| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
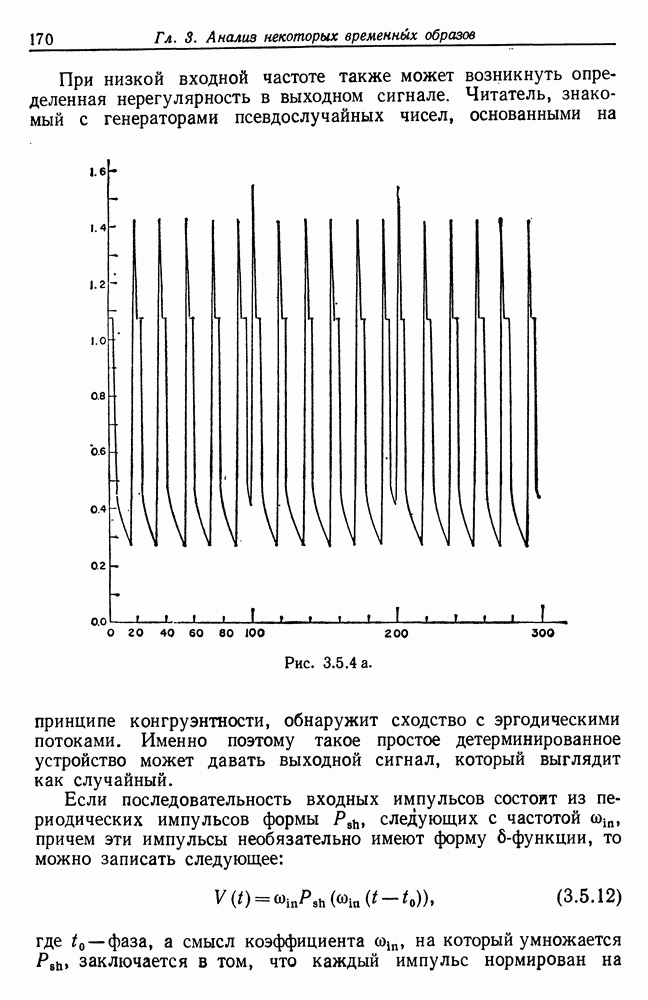
5.4. Логика признаков бесконечного порядка
Теперь перейдем к рассмотрению менее жестких алгебр изображений, воспользовавшись разложением макрообразующих. Допустив логики признаков бесконечного порядка, но отталкиваясь по-прежнему от образующих-полуплоскостей и правила  идентифицирующего пересечение множеств, мы приходим к замкнутым множествам в смысле теоремы 3.9.7 (т. 1, гл. 3).
идентифицирующего пересечение множеств, мы приходим к замкнутым множествам в смысле теоремы 3.9.7 (т. 1, гл. 3).
В таком случае нецелесообразно пользоваться  в качестве восстановленного образа
в качестве восстановленного образа  поскольку
поскольку  конечное точечное множество (в данном случае рассматривается
конечное точечное множество (в данном случае рассматривается  ) и, следовательно,
) и, следовательно,  Вместо этого следует «вставить» в незаполненные части деформированного изображения небольшие множества положительных площадей.
Вместо этого следует «вставить» в незаполненные части деформированного изображения небольшие множества положительных площадей.

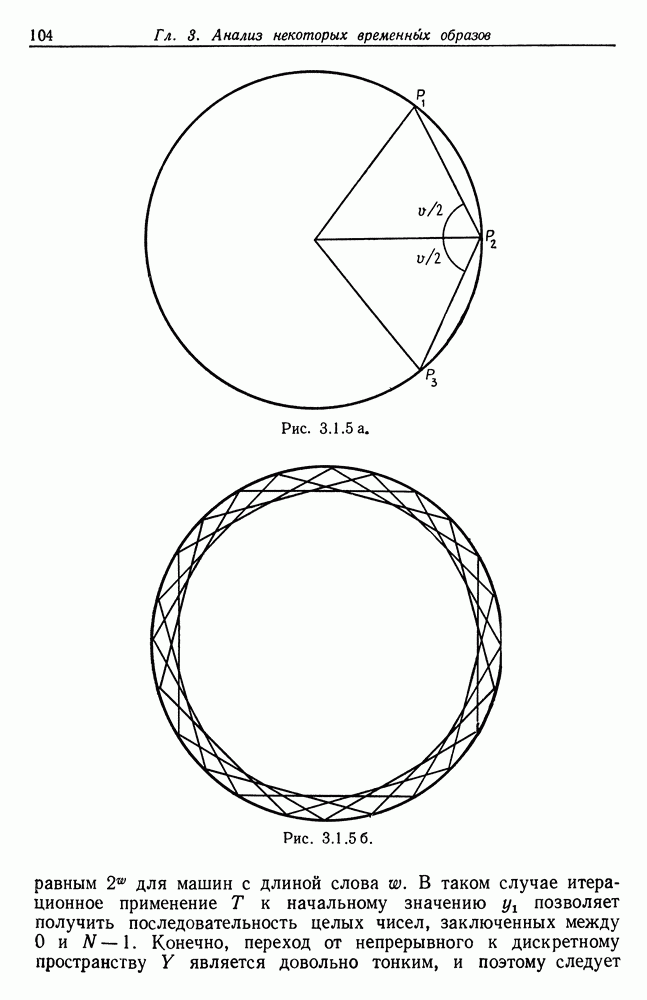
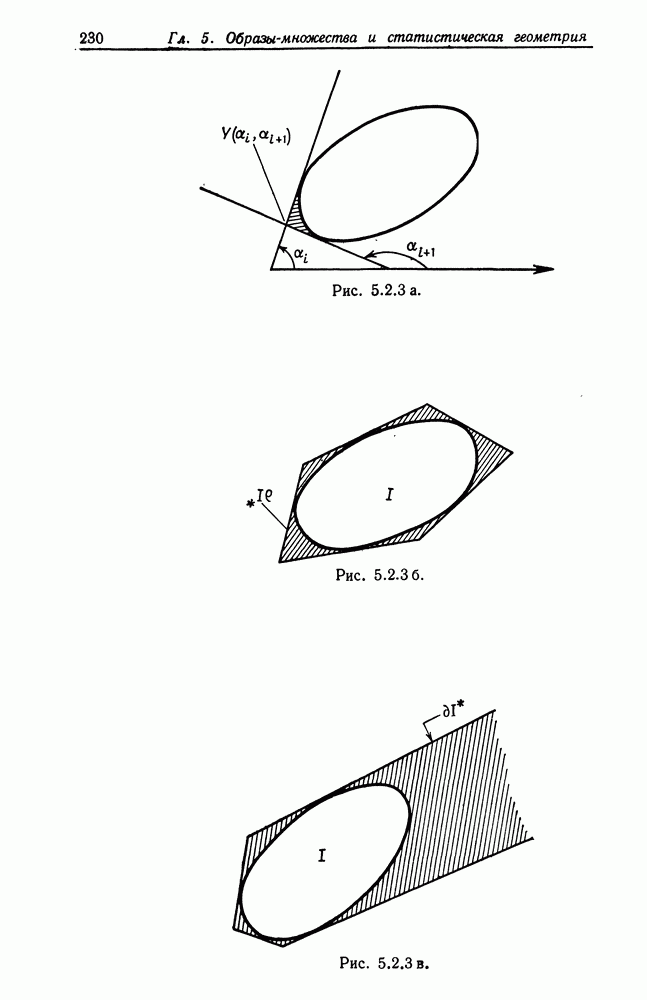
Рис. 5.4.1.
Один из способов осуществления этого заключается в следующем. Обозначим через  произвольный круг радиуса
произвольный круг радиуса  и через
и через  — круг радиуса
— круг радиуса  с центром в точке
с центром в точке  Сформируем объединение
Сформируем объединение

и пусть радиус  стремится к нулю при
стремится к нулю при  Мы покажем, что соотношение (5.4.1) обеспечивает при должном выборе радиуса
Мы покажем, что соотношение (5.4.1) обеспечивает при должном выборе радиуса  состоятельное восстановление (см. разд. 1.3). Все множества должны принадлежать некоторому ограниченному
состоятельное восстановление (см. разд. 1.3). Все множества должны принадлежать некоторому ограниченному  (см. разд. 5.1).
(см. разд. 5.1).
Обратимся к рис. 5.4.1, где с помощью соотношений

(сложение осуществляется по Минковсксому) введены внутреннее  и внешнее
и внешнее  изображения (на рис.
изображения (на рис.  ). Будм предполагать, что граница
). Будм предполагать, что граница  является тонкой в том смыслу
является тонкой в том смыслу  Тогда справедлива следующая теорема.
Тогда справедлива следующая теорема.
Теорема 5.4.1, Пусть  ограниченнее замкнутое множество с тонкой границей. Тогда восстановление в соответствии с (5.1) является состоятельным в области
ограниченнее замкнутое множество с тонкой границей. Тогда восстановление в соответствии с (5.1) является состоятельным в области

если  .
.
Доказательство. Известно, что

где  — индикаторная функция
— индикаторная функция  Для
Для  однако получаем следующее:
однако получаем следующее:

 Аналогично для
Аналогично для  получаем, что
получаем, что

Обратившись к оставшимся частям интегралов из  Достаточно заметить то обстоятельство, что подынтегральные выражения ограничены единицей, и доказать, что области, по которым ведется интегрирование этих частей, стремятся к нулю.
Достаточно заметить то обстоятельство, что подынтегральные выражения ограничены единицей, и доказать, что области, по которым ведется интегрирование этих частей, стремятся к нулю.  можно сделать, представив оставшиеся области как
можно сделать, представив оставшиеся области как

Поскольку, однако, при  множества
множества  сокращается
сокращается  замыкания
замыкания  которое представляет собой само
которое представляет собой само  то
то  Аналогично
Аналогично  Следовательно,
Следовательно,

и доказательство закончено.
Для случая  необходимо, как монсет убедиться читатель, слегка изменить утверждение.
необходимо, как монсет убедиться читатель, слегка изменить утверждение.  интенсивности пуассоновского потока (внутренняя) и
интенсивности пуассоновского потока (внутренняя) и  (внешняя) представляем
(внешняя) представляем
в виде

где и  постоянные,
постоянные,  . Введем показатель
. Введем показатель  число точек
число точек  находящихся внутри
находящихся внутри 
Теорема 5.4.2. Восстановление

является состоятельным в области, если

Доказательство. Если  то
то

где  случайная величина, подчиняющаяся распределению Пуассона с математическим ожиданием
случайная величина, подчиняющаяся распределению Пуассона с математическим ожиданием 

Тогда из (5.4.11) следует, что  Однако хорошо известно, что для пуассоновской переменной
Однако хорошо известно, что для пуассоновской переменной  по вероятности и, следовательно,
по вероятности и, следовательно,

по вероятности. Таким образом,

Аналогично очевидно, что

Закончить доказательство данной теоремы можно так же, как это было сделано при доказательстве теоремы 5.4.1.
Две последние теоремы справедливы при слабых структурных ограничениях; можно было бы, однако, заметить, что их столь значительная общность делает их менее удобными в случае специфических структур образов, когда возникает возможность предложить специализированные алгоритмы восстановления. Поясним это с помощью нескольких примеров.
Если известно, что  это просто
это просто  задано,
задано,  неизвестна и
неизвестна и  принадлежит группе переносов, то как будто бы естественно восстанавливать
принадлежит группе переносов, то как будто бы естественно восстанавливать  с помощью пересечения всех
с помощью пересечения всех  содержащих
содержащих  где
где  (см. рис. 5.4.2). Тогда
(см. рис. 5.4.2). Тогда  ограничено круговыми дугами и имеет сплошную внутреннюю часть.
ограничено круговыми дугами и имеет сплошную внутреннюю часть.
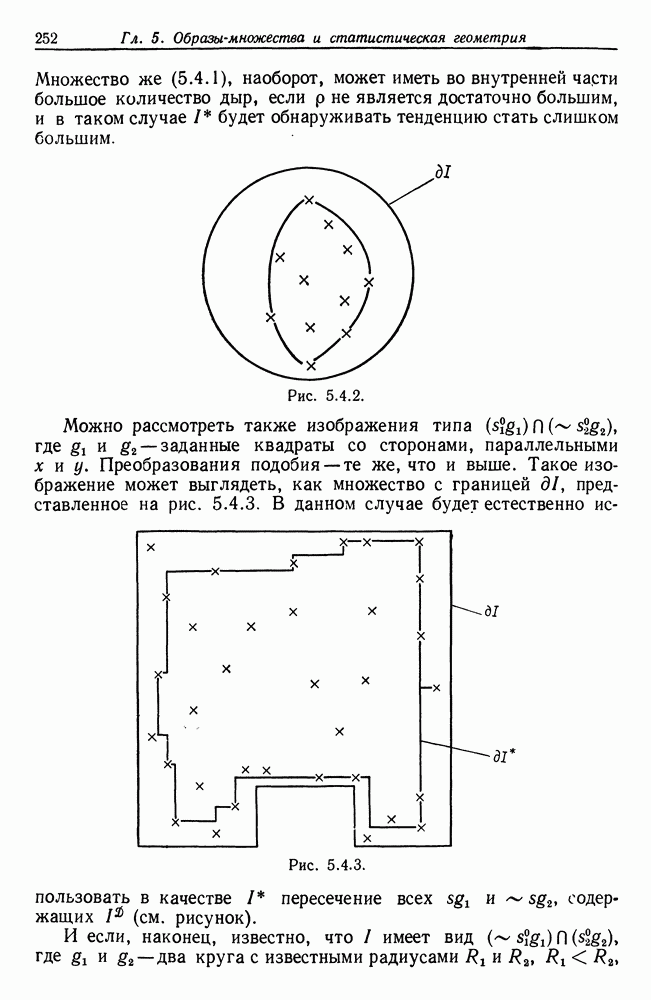
Множество же (5.4.1), наоборот, может иметь во внутренней части большое количество дыр, если  не является достаточно большим, и в таком случае
не является достаточно большим, и в таком случае  будет обнаруживать тенденцию стать слишком большим.
будет обнаруживать тенденцию стать слишком большим.

Рис. 5.4.2.
Можно рассмотреть также изображения типа  где
где  и — заданные квадраты со сторонами, параллельными х и у. Преобразования подобия — те же, что и выше. Такое изображение может выглядеть, как множество с границей
и — заданные квадраты со сторонами, параллельными х и у. Преобразования подобия — те же, что и выше. Такое изображение может выглядеть, как множество с границей  представленное на рис. 5.4.3. В данном случае будет естественно использовать в качестве
представленное на рис. 5.4.3. В данном случае будет естественно использовать в качестве  пересечение всех
пересечение всех  содержащих
содержащих  (см. рисунок).
(см. рисунок).

Рис. 5.4.3.
И если, наконец, известно, что  имеет вид
имеет вид  , где
, где  — два круга с известными радиусами и
— два круга с известными радиусами и 
то мы получаем области, имеющие форму круговых колец, как это показано на рис. 5.4.4. В этом случае можно попытаться восстановить  строя пересечение всех
строя пересечение всех  содержащих
содержащих  на рисунке не показано).
на рисунке не показано).

Рис. 5.4.4.
Остановимся более подробно на мощности тех алгоритмов восстановления, которые в большей степени, чем алгоритмы (5.4.1) и (5.4.10), используют структуру образа. Пусть  причем
причем  включает некоторые множества с границами, построенными из конечного числа ограниченных аналитических дуг. Пусть арность в
включает некоторые множества с границами, построенными из конечного числа ограниченных аналитических дуг. Пусть арность в  задана так:
задана так:  . Множество
. Множество  представляет собой совокупность булевых функций множества; здесь
представляет собой совокупность булевых функций множества; здесь  равна числу переменных,
равна числу переменных,  . Следовательно, элементы, входящие в
. Следовательно, элементы, входящие в  могут представлять собой композиции объединения, пересечения и дополнения. Кроме того,
могут представлять собой композиции объединения, пересечения и дополнения. Кроме того,  перенос, как и выше, для
перенос, как и выше, для  а для
а для  .
.
Воспользовавшись типом соединения  -древовидный, при соединении всех входных связей
-древовидный, при соединении всех входных связей  или
или  и
и  получаем некоторое пространство конфигураций, являющееся обобщением евклидовых образов из случая 2.3.3 т.1. В данном случае индекс класса образующих
получаем некоторое пространство конфигураций, являющееся обобщением евклидовых образов из случая 2.3.3 т.1. В данном случае индекс класса образующих  используется только для того, чтобы различать множества и функции множеств. Обратившись к более тонкому делению пространства а, можно было бы получить на результирующей алгебре изображений более жесткие структуры образов, однако здесь мы не будем этим заниматься.
используется только для того, чтобы различать множества и функции множеств. Обратившись к более тонкому делению пространства а, можно было бы получить на результирующей алгебре изображений более жесткие структуры образов, однако здесь мы не будем этим заниматься.
Мы будем идентифицировать две конфигурации  оценивая множества, вычислимые по схеме конфигурации, начиная с нижних узлов и далее вверх. Если два полученные в результате такого вычисления множества согласуются, то мы отождествляем
оценивая множества, вычислимые по схеме конфигурации, начиная с нижних узлов и далее вверх. Если два полученные в результате такого вычисления множества согласуются, то мы отождествляем  т. е.
т. е. 
Рассмотрим теперь принадлежащий этой алгебре изображений  некоторый класс образов 90 с ограниченными изображениями
некоторый класс образов 90 с ограниченными изображениями  Другими словами, мы имеем дело с некоторым классом ограниченных множеств, характеризуемых определенными структурными описаниями — примером можно считать один из трех рассмотренных выше случаев. Как же можно, располагая этими сведениями, восстановить
Другими словами, мы имеем дело с некоторым классом ограниченных множеств, характеризуемых определенными структурными описаниями — примером можно считать один из трех рассмотренных выше случаев. Как же можно, располагая этими сведениями, восстановить  по наблюдаемым
по наблюдаемым 
Как и раньше,  и мы хотели бы окружить Р границами, связанными с теми, которые возникают в множестве образующих Мы хотим, чтобы восстановленное изображение
и мы хотели бы окружить Р границами, связанными с теми, которые возникают в множестве образующих Мы хотим, чтобы восстановленное изображение  сходилось по мере к
сходилось по мере к  при
при 
Попробуем воспользоваться следующим алгоритмом.
Алгоритм. I вычисляется как пересечение всех тех изображений  принадлежащих которые содержат
принадлежащих которые содержат  Интуитивно кажется, что этот алгоритм использует структуру образов и можно рассчитывать на благоприятный результат восстановления. Ситуация, однако, не так проста, и необходимо заранее принять меры против тех возможных последствий, которые могут не быть очевидными с первого взгляда. Может оказаться, что
Интуитивно кажется, что этот алгоритм использует структуру образов и можно рассчитывать на благоприятный результат восстановления. Ситуация, однако, не так проста, и необходимо заранее принять меры против тех возможных последствий, которые могут не быть очевидными с первого взгляда. Может оказаться, что  включает изображение
включает изображение  дополнение которого снабжено длинными и тонкими «иглами», направленными внутрь
дополнение которого снабжено длинными и тонкими «иглами», направленными внутрь  Если это действительно так, то, комбинируя (посредством объединения) иглы ряда изображений
Если это действительно так, то, комбинируя (посредством объединения) иглы ряда изображений  из мы можем исключить из
из мы можем исключить из  значительную часть
значительную часть  и при
и при  сходимость к идеальному изображению может не иметь места.
сходимость к идеальному изображению может не иметь места.
Чтобы избежать этого, необходимо обеспечить выполнение определенных условий, и мы предложим один способ преодоления этого затруднения. Пусть задан некоторый ограниченный треугольник  одна из вершин которого обозначена Р и угол при ней равен
одна из вершин которого обозначена Р и угол при ней равен  рассмотрим класс подобразов 0, для которого существует такой поворот
рассмотрим класс подобразов 0, для которого существует такой поворот  что при
что при  повернутый треугольник
повернутый треугольник  также содержится в
также содержится в  .
.
Используя этот класс подобразов, мы предложим модифицированный алгоритм, единственное отличие которого от описанного выше заключается в том, что заменяется на 
Теорема 5.4.3. Модифицированный алгоритм сходится в области.
Доказательство. Рассмотрим некоторую точку  (см. рис. 5.4.5). Все изображение
(см. рис. 5.4.5). Все изображение  состоит из конечного числа связанных элементов и
состоит из конечного числа связанных элементов и  — один из них. Пусть
— один из них. Пусть  — расстояние от
— расстояние от  до
до  поэтому
поэтому  Рассмотрим круг
Рассмотрим круг  содержащийся в
содержащийся в  Чтобы обеспечить
Чтобы обеспечить  необходимо располагать некоторым
необходимо располагать некоторым  дополнение которого
дополнение которого  покрывает
покрывает  Если Iе покрывает
Если Iе покрывает  то существует некоторый
то существует некоторый 
угольник  обладающий определенной ориентацией
обладающий определенной ориентацией  Принцип действия алгоритма, однако, исключает наличие в
Принцип действия алгоритма, однако, исключает наличие в  точки
точки  из Следовательно, в множестве
из Следовательно, в множестве  не может быть точек
не может быть точек  . С другой стороны, условное распределение вероятностей на
. С другой стороны, условное распределение вероятностей на  является равномерным, и
является равномерным, и 

Рис. 5.4.5.
Следовательно, вероятность по крайней мере для  точек в
точек в  стремится к единице при
стремится к единице при  Для заданного числа точек в
Для заданного числа точек в  их условное распределение на
их условное распределение на  является равномерным. Вероятность же того, что углы между
является равномерным. Вероятность же того, что углы между  и теми
и теми  , для которых выполняется
, для которых выполняется  не покрывают угол
не покрывают угол  стремится, однако, к нулю при стремлении
стремится, однако, к нулю при стремлении  к бесконечности, так что
к бесконечности, так что

и

отсюда следует, что теорема доказана, см. доказательство теоремы 5.4.1.
Теорема 5.4.3 показывает, что можно обеспечить с помощью модифицированного алгоритма восстановление, состоятельное в смысле площади. Все это прекрасно, но хочется выяснить, нельзя ли выдвинуть более сильного утверждения. Можно считать, что подобные методы восстановления, обеспечивающие сохранение структуры, должны быть эффективнее общих методов типа (5.4.1). Итак, речь идет о компромиссе между общностью и эффективностью в частных случаях.
Чтобы несколько прояснить эту ситуацию, обратимся к конкретному случаю, а именно к случаю, о котором шла речь в
теореме 5.3.1. Пусть изображение соответствует указанной постановке; сформируем восстановленное изображение

где  — квадрат с центром в точке
— квадрат с центром в точке  и со стороной
и со стороной  Причина использования квадратов, а не кругов, как в (5.4.1), несомненно, состоит в том, что квадрат — более естественная фигура с точки зрения формы границы (см., например, рис. 5.3.1). Отметим, однако, что
Причина использования квадратов, а не кругов, как в (5.4.1), несомненно, состоит в том, что квадрат — более естественная фигура с точки зрения формы границы (см., например, рис. 5.3.1). Отметим, однако, что  вообще говоря, не принадлежит
вообще говоря, не принадлежит  мы не пользуемся алгоритмом восстановления, обеспечивающим сохранение структуры.
мы не пользуемся алгоритмом восстановления, обеспечивающим сохранение структуры.
Определим теперь математическое ожидание площади множества ошибок:

(обозначения здесь те же, что и выше). Чтобы обеспечить восстановление, состоятельное по площади, необходимо, конечно, считать, что  при
при  За счет некоторой потери общности будем полагать, что при
За счет некоторой потери общности будем полагать, что при  Но довод, аналогичный использованному при доказательстве теоремы 5.4.1, указывает, что необходимо потребовать, чтобы
Но довод, аналогичный использованному при доказательстве теоремы 5.4.1, указывает, что необходимо потребовать, чтобы  и, следовательно,
и, следовательно,  .
.
Для этого необходим асимптотический прием того же типа, что использовался для доказательства теоремы 5.3.1, конечно, в некоторых деталях они будут различаться. Мы не будем приводить здесь довольно трудоемкое доказательство и сформулируем лишь результат (доказательство можно найти в отчете Гренандера и Лавина 
Теорема 5.4.4. Алгоритм восстановления (5.4.19) имеет при  ошибку восстановления
ошибку восстановления

где  — периметр
— периметр 
Этот результат относится к изображению  обладающему конечной числовой сложностью. В случае гладкой границы выражение (5.4.21) следует заменить другим.
обладающему конечной числовой сложностью. В случае гладкой границы выражение (5.4.21) следует заменить другим.
Теорема свидетельствует о том, что алгоритм (5.4.19) имеет асимптотическую ошибку восстановления порядка  сопоставив эту оценку с величиной
сопоставив эту оценку с величиной  что соответствует алгоритму, обеспечивающему сохранение структуры, убеждаемся, что последний лучше.
что соответствует алгоритму, обеспечивающему сохранение структуры, убеждаемся, что последний лучше.
Это хорошо, но следует помнить, что данный результат доказан лишь для частного случая. Следующий пример позволяет убедиться в том, что он не обладает общностью в полном смысле этого слова. Пусть алгебра изображений состоит изо всех тех множеств, которые замкнуты относительно логики признаков  порядка при
порядка при  или
или  и все
и все  полуплоскости.
полуплоскости.
Тогда пределом при  является само и при
является само и при  мы не получим состоятельного по площади восстановления. Несомненно, этот пример — скорее крайний случай, и, вероятно, можно было бы найти лучшие примеры.
мы не получим состоятельного по площади восстановления. Несомненно, этот пример — скорее крайний случай, и, вероятно, можно было бы найти лучшие примеры.
К этому следует добавить, что восстановленные изображения типа (5.4.1) или (5.4.19) неудобны в обращении, поскольку в них используется столько же информации, сколько содержит само И наоборот, восстановление типа того, которое применяется для выпуклой оболочки в среднем требует много меньше информации.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
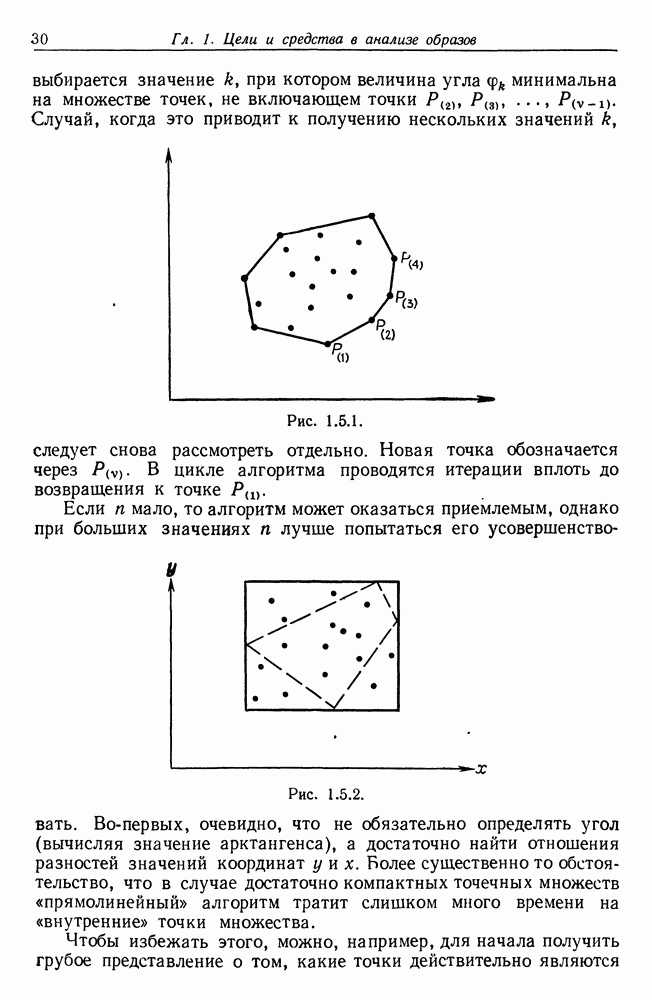
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
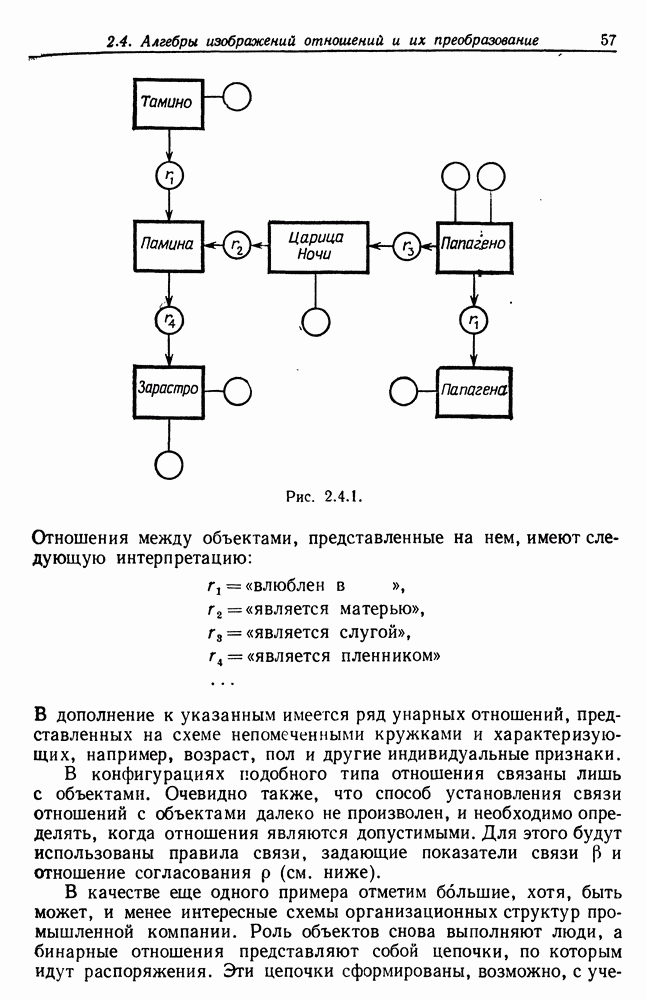
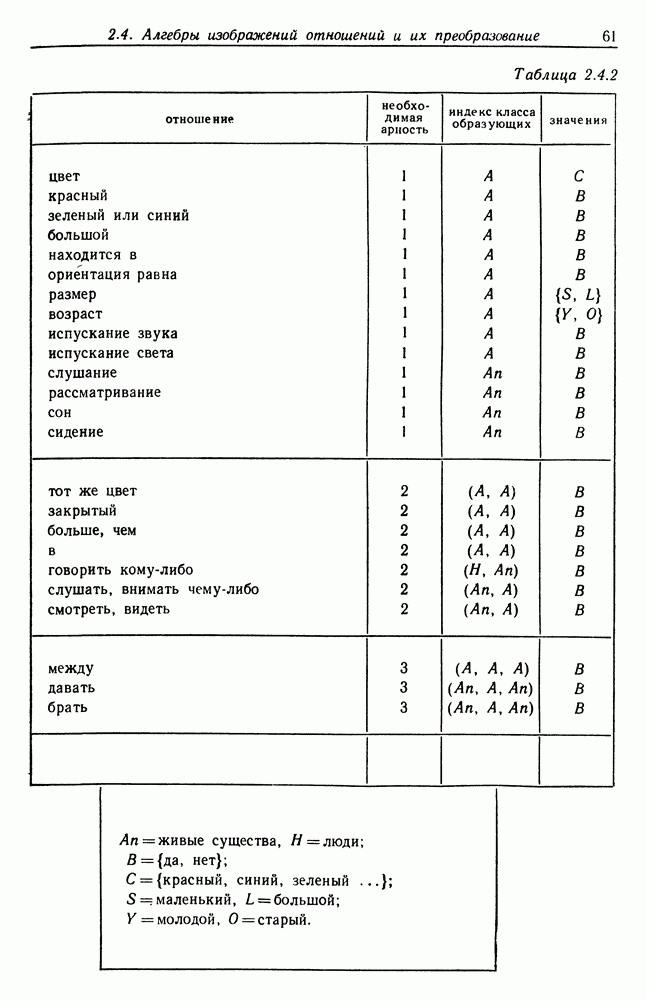
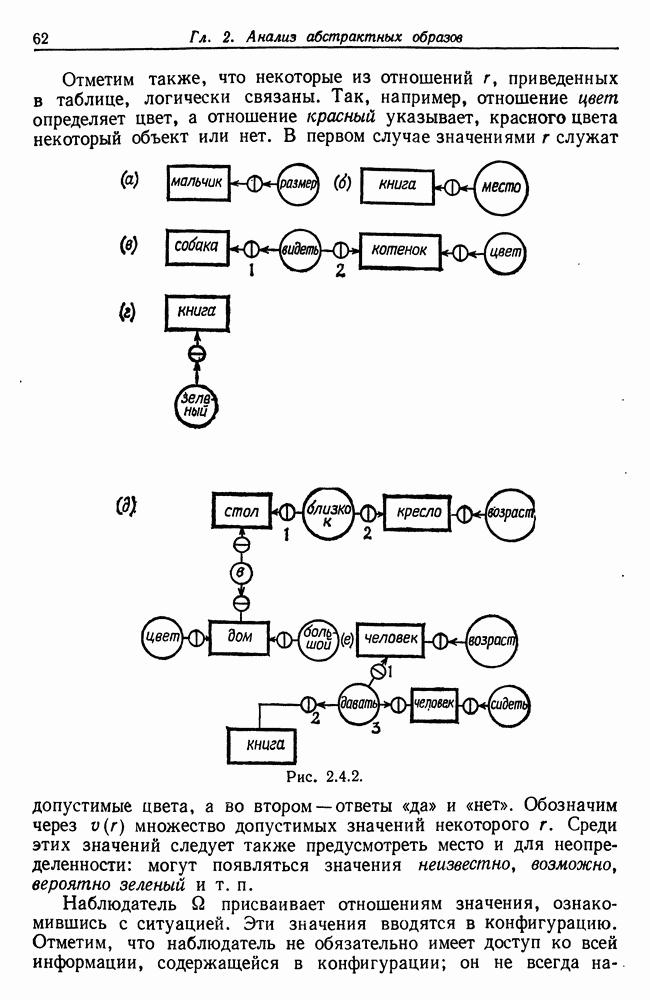
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
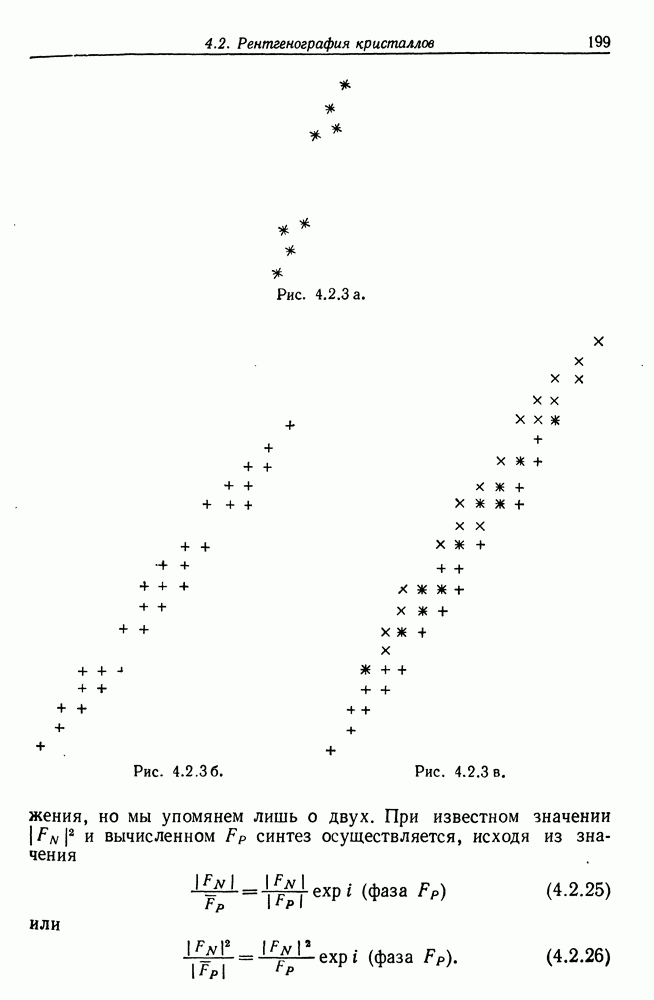
- 4.2. Рентгенография кристаллов
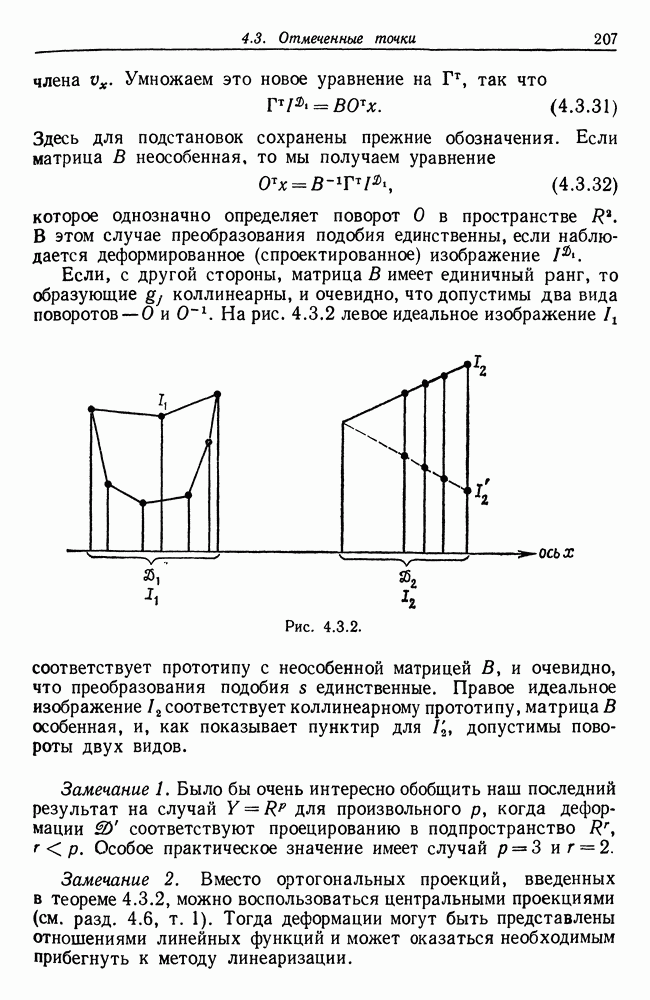
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
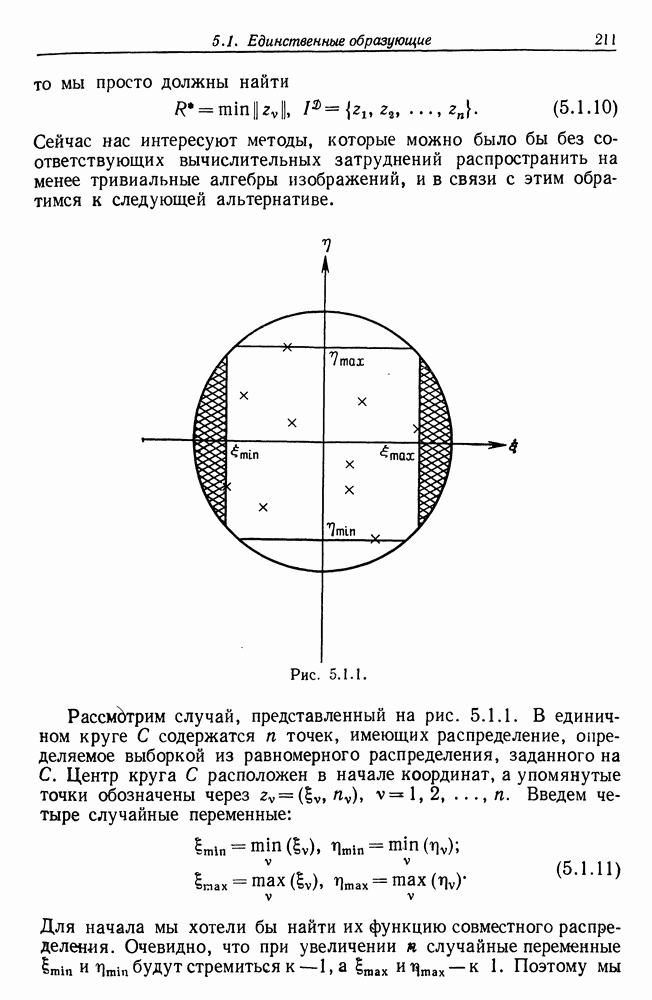
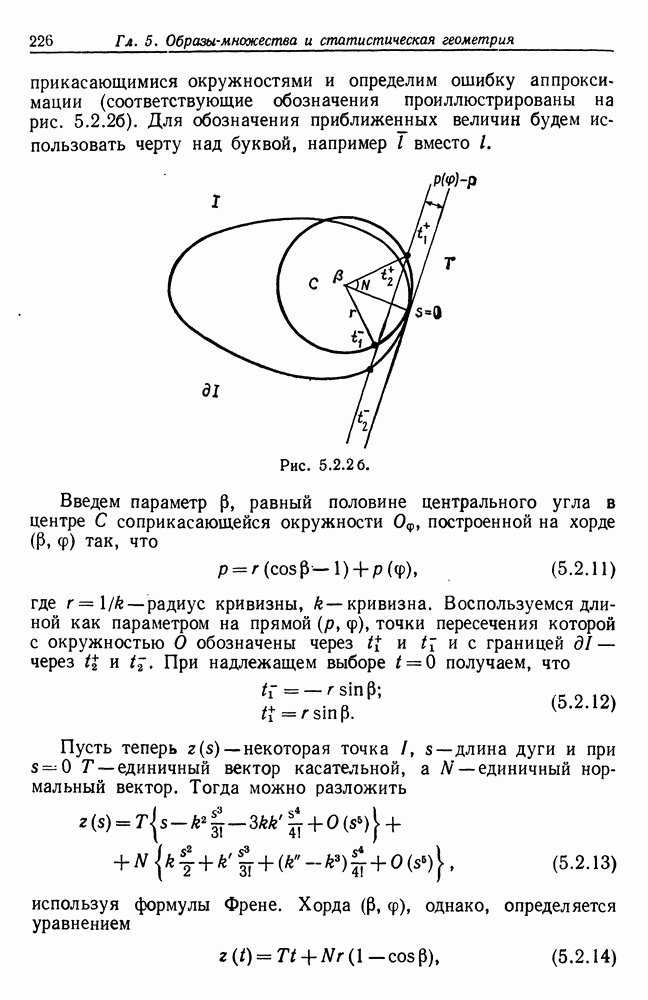
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
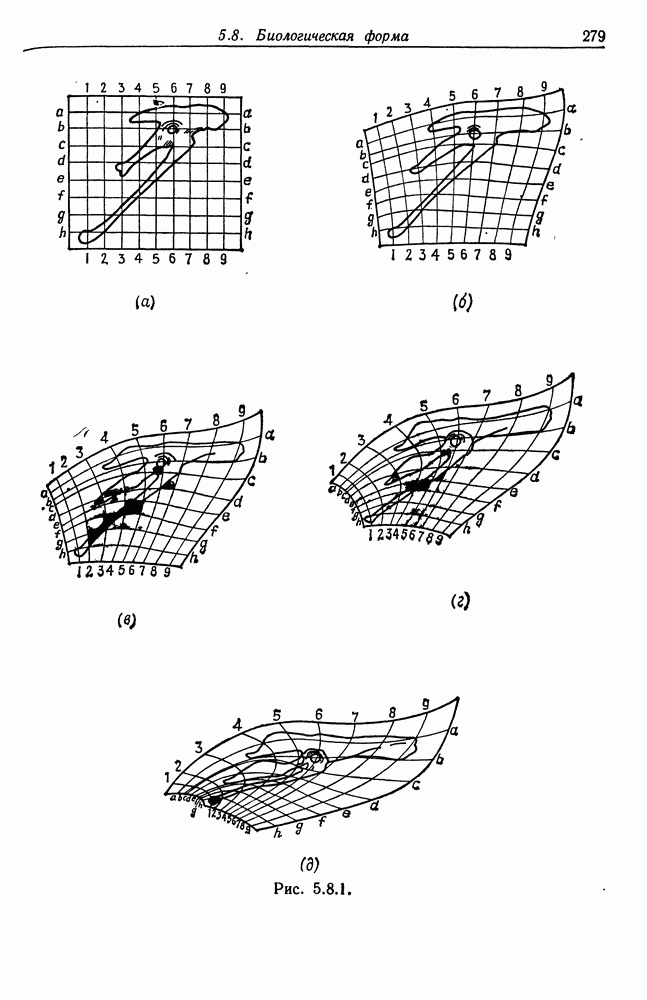
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
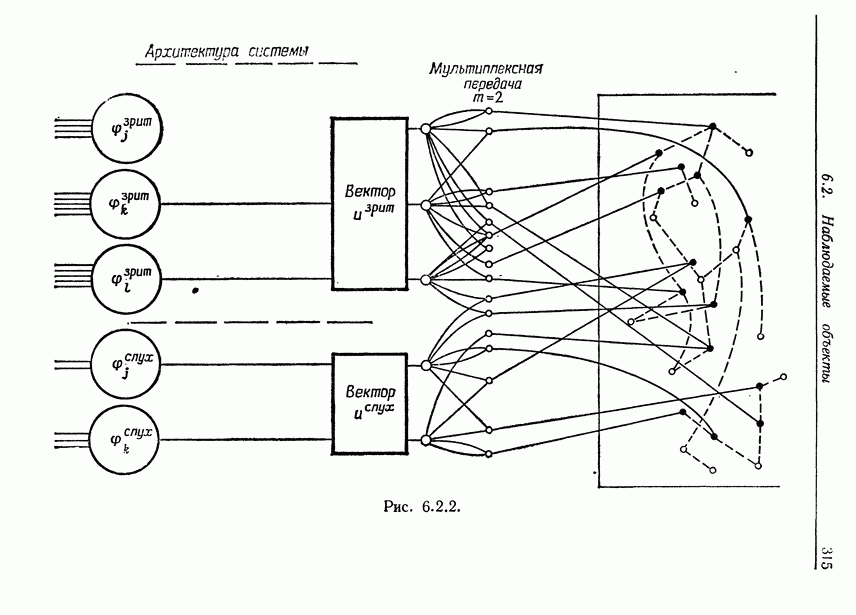
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы