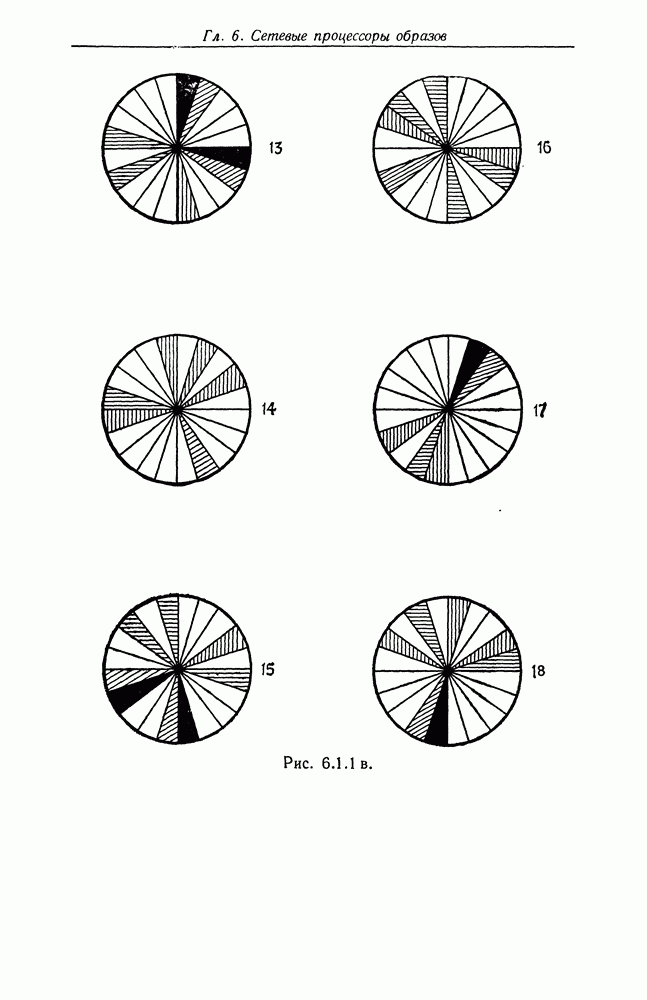| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Примечания
2.1. Алгоритм (2.1.18)-(2.1.20) применялся в статье Гренандера (1970).
2.2. Теорема 2.2.1 и утверждение (2.2.26) теоремы 2.2.2 заимствованы из работы Робински (1975), в которой, однако, условие, налагаемое на дисперсию, в явном виде не сформулировано,
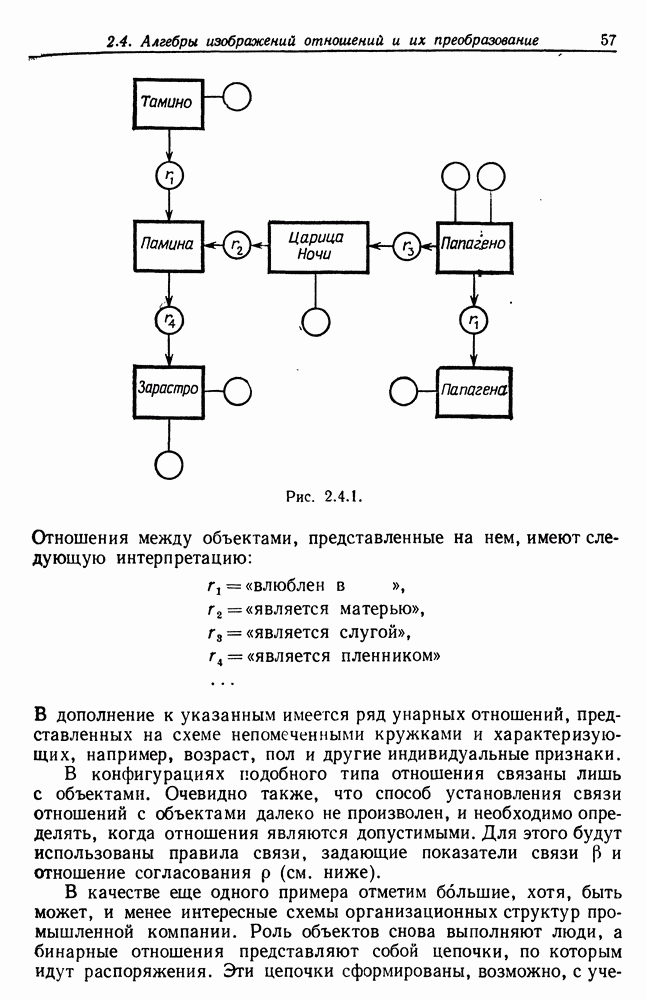
2.4. Формализованные рикромиры» и их описания изучались многими авторами, в частности Виноградом (1976). См. также Росс (1974).
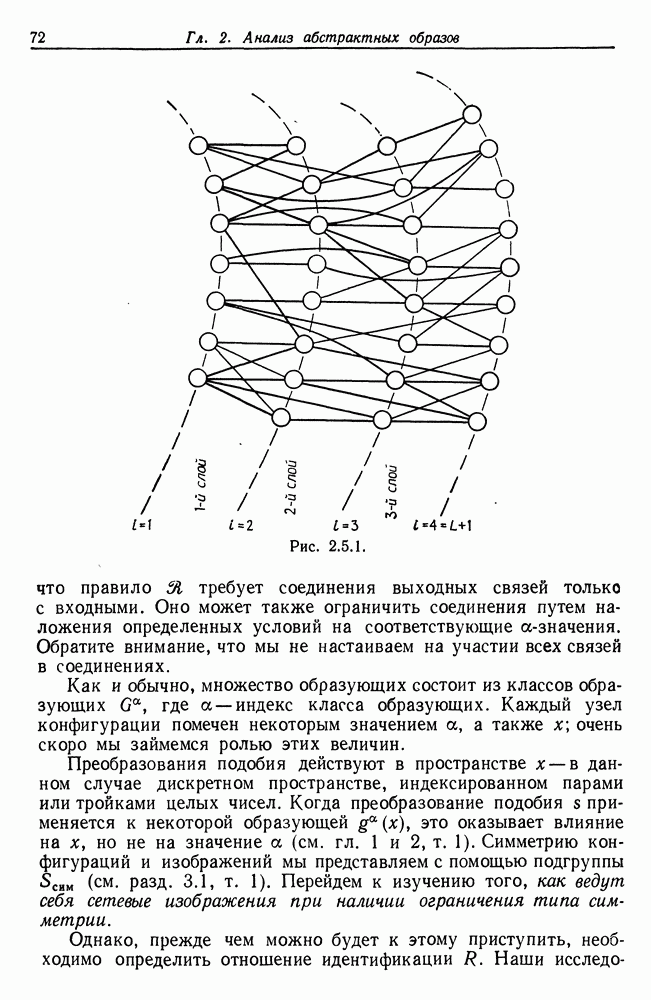
К условиям (i)-(iv), обеспечивающим регулярность конфигурации, состоящей из  многие склонны добавлять некоторое правило, налагающее дополнительные ограничения на тип соединения 2- При таком подходе следует также допускать соединения типа
многие склонны добавлять некоторое правило, налагающее дополнительные ограничения на тип соединения 2- При таком подходе следует также допускать соединения типа  Сравните с исчислением предикатов.
Сравните с исчислением предикатов.
Вопрос о выборе правила идентификации также остается открытым; возможно, естественнее были бы менее строгие правила.
2.5. Более наглядно теорему 2.5.1 можно интерпретировать следующим образом. Матрица энергии  в частном случае
в частном случае  превращается в циркулянтную матрицу, и тогда, конечно, собственные значения можно найти непосредственно. Это соответствует выражению (2.5.60). В общем случае при
превращается в циркулянтную матрицу, и тогда, конечно, собственные значения можно найти непосредственно. Это соответствует выражению (2.5.60). В общем случае при  матрица
матрица  не обладает свойством циркулянтности, однако здесь решить задачу можно, воспользовавшись тем обстоятельством, что эта матрица поддается разбиению на циркулянтные блоки. Именно в этом заключается истинная причина справедливости теоремы. См. по этому поводу также статью Ханта в журнале IEEE Trans. Computers, С-22, 9, 1973.
не обладает свойством циркулянтности, однако здесь решить задачу можно, воспользовавшись тем обстоятельством, что эта матрица поддается разбиению на циркулянтные блоки. Именно в этом заключается истинная причина справедливости теоремы. См. по этому поводу также статью Ханта в журнале IEEE Trans. Computers, С-22, 9, 1973.
При таком подходе возникает вопрос о возможной модификации теоремы, если допустить задание образующих интегралом Фурье:

Мы не изучали эту проблему, однако отметим ее близость к результатам, изложенным в монографии Гренандера и Сеге ((1957) разд. 6.5).
3.2. Подробные сведения об анализе авторегрессионных схем можно найти в монографии Андерсона (1976), в частности в гл. 5.
3.3. Материал разд. 3.3 заимствован из работы Маклура (1975). См. также работу Маклура и Вайтала (1975).
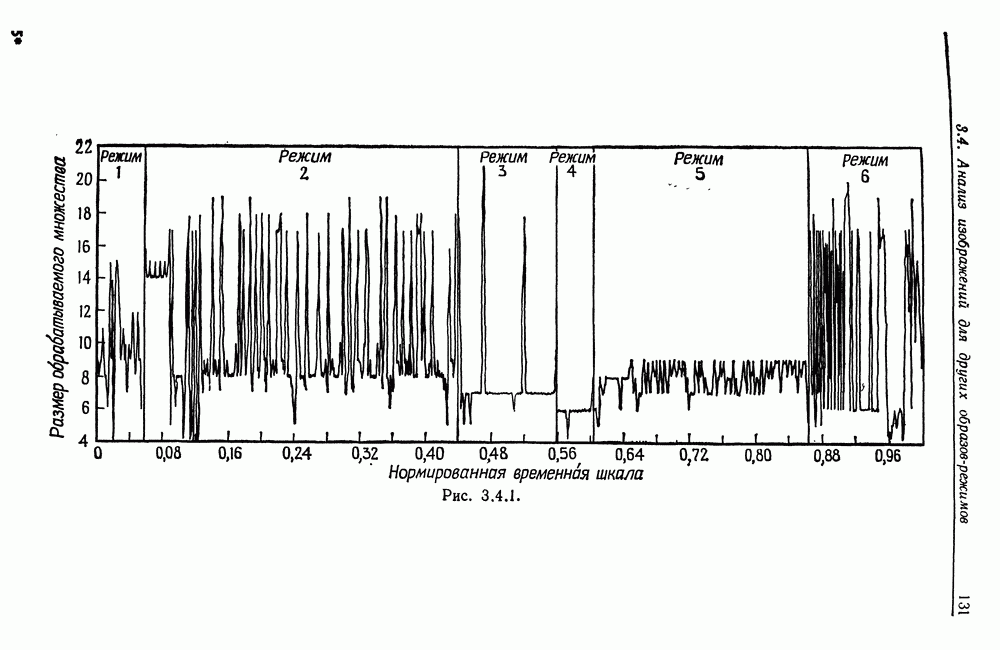
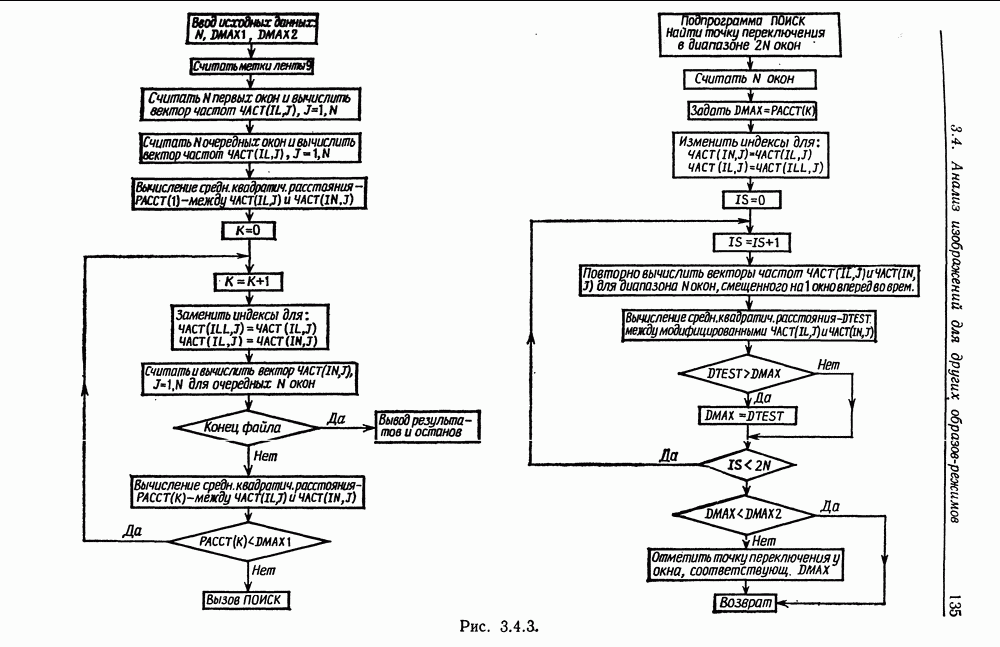
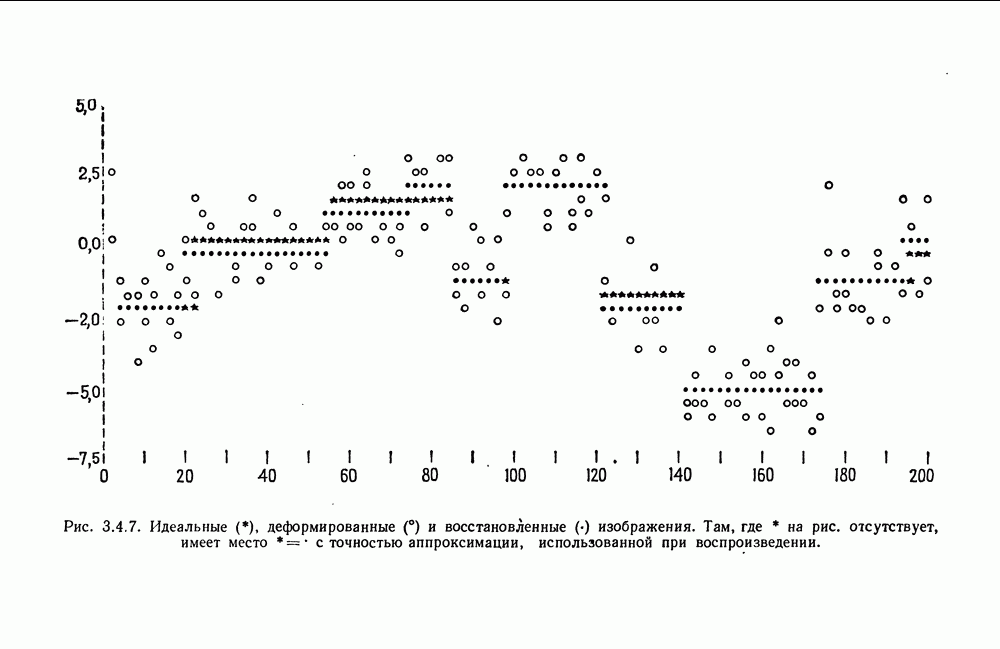
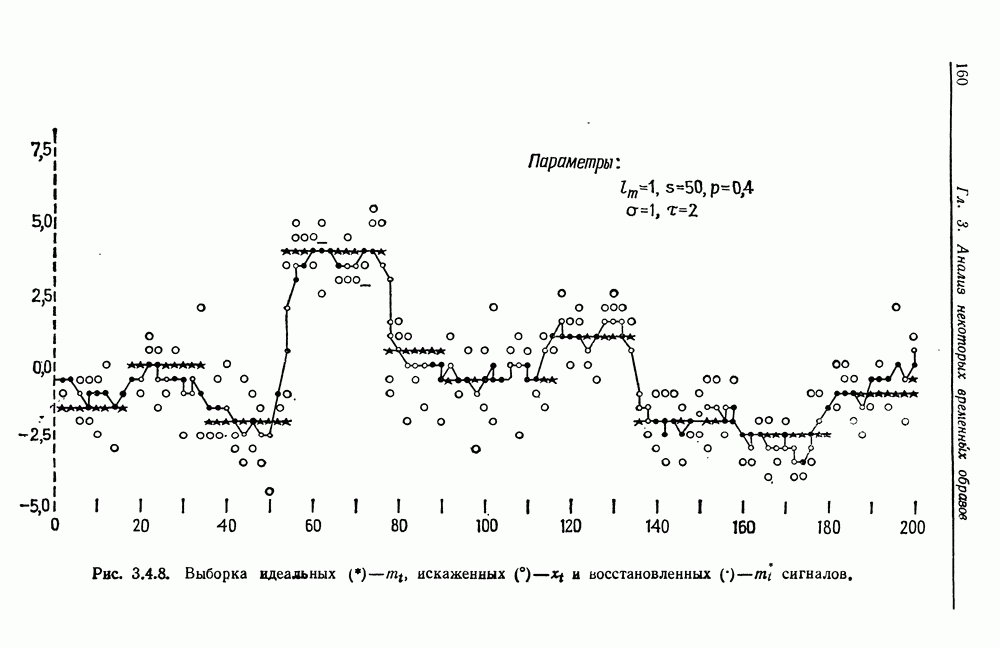
3.4. Большая часть результатов этого раздела, связанных с адаптивным эвристическим алгоритмом, получена в трех работах: Анг (1974, 1975) и Гренандер (1950). В отчете Анга (1974) подробно описана организация численного эксперимента, посвященного проверке этого алгоритма и сравнению его с методом фильтрации.
Модифицированная версия алгоритма в работе Лин (1974) была использована для изучения рабочих характеристик одной операционной системы.
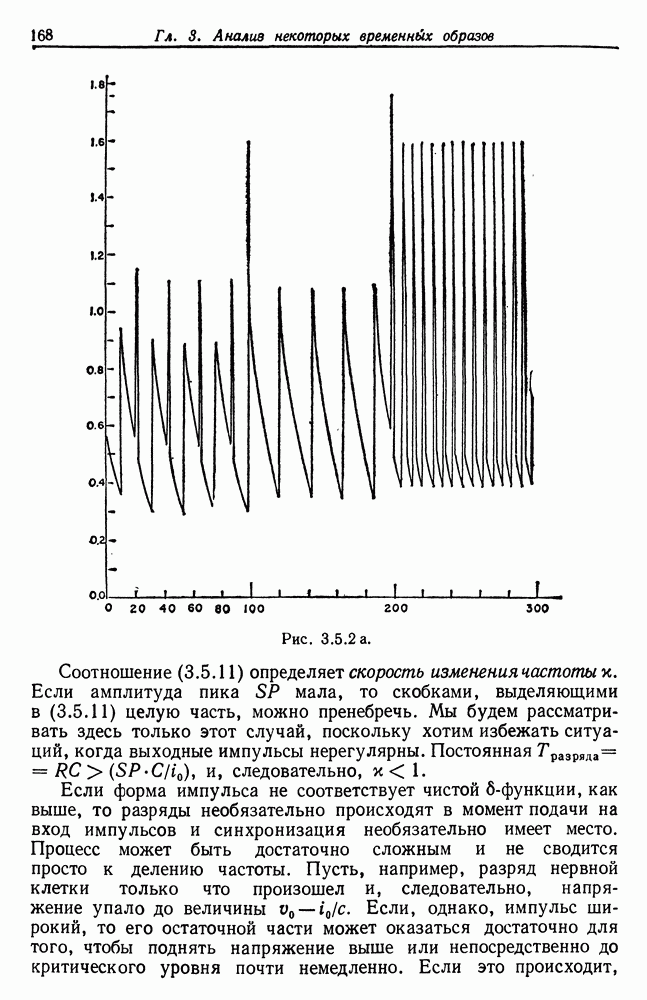
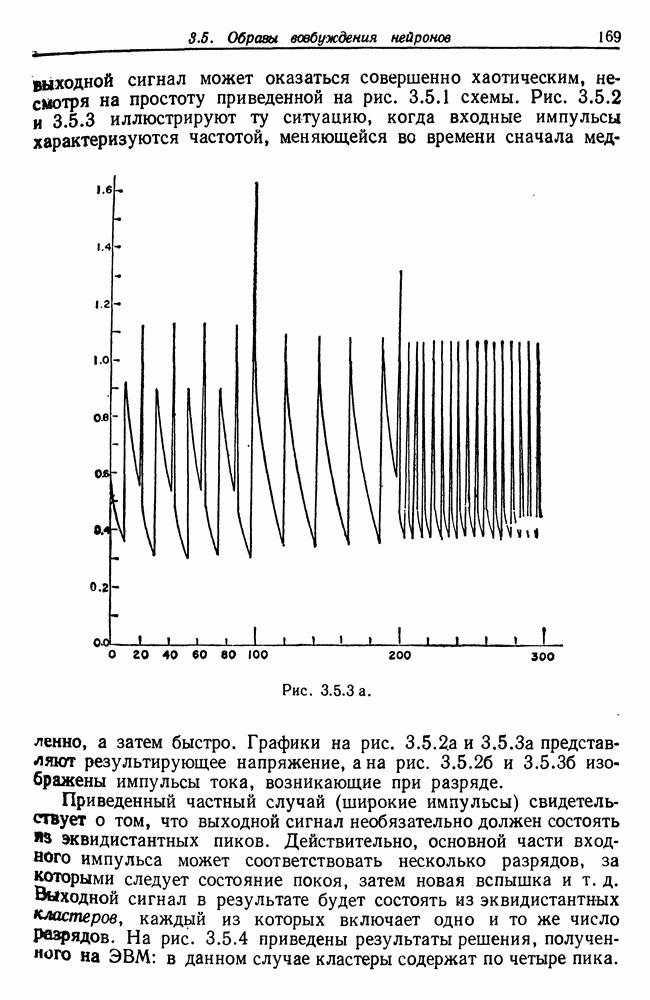
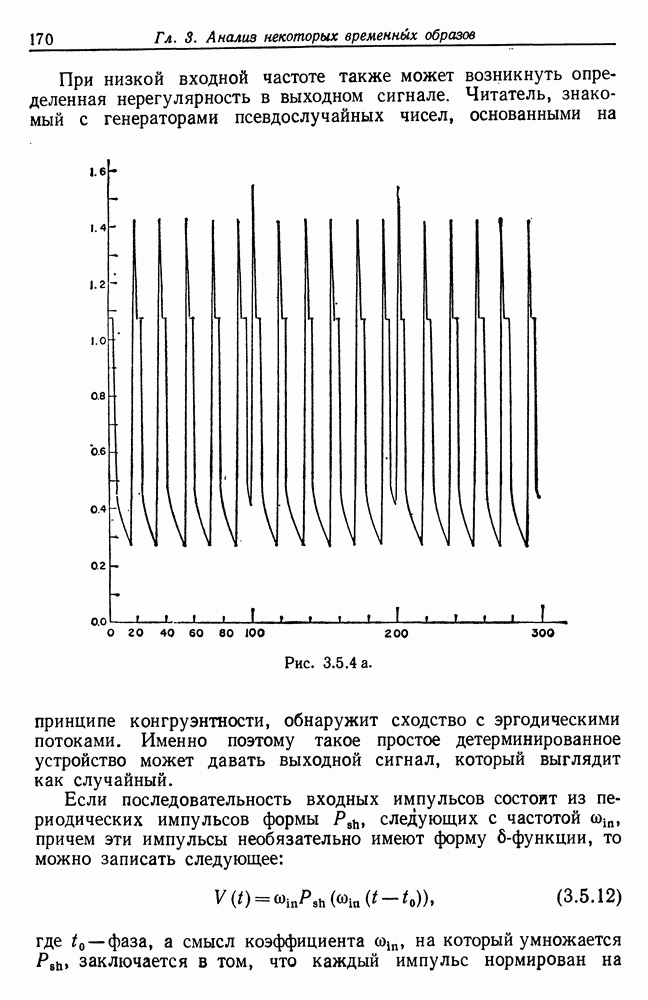
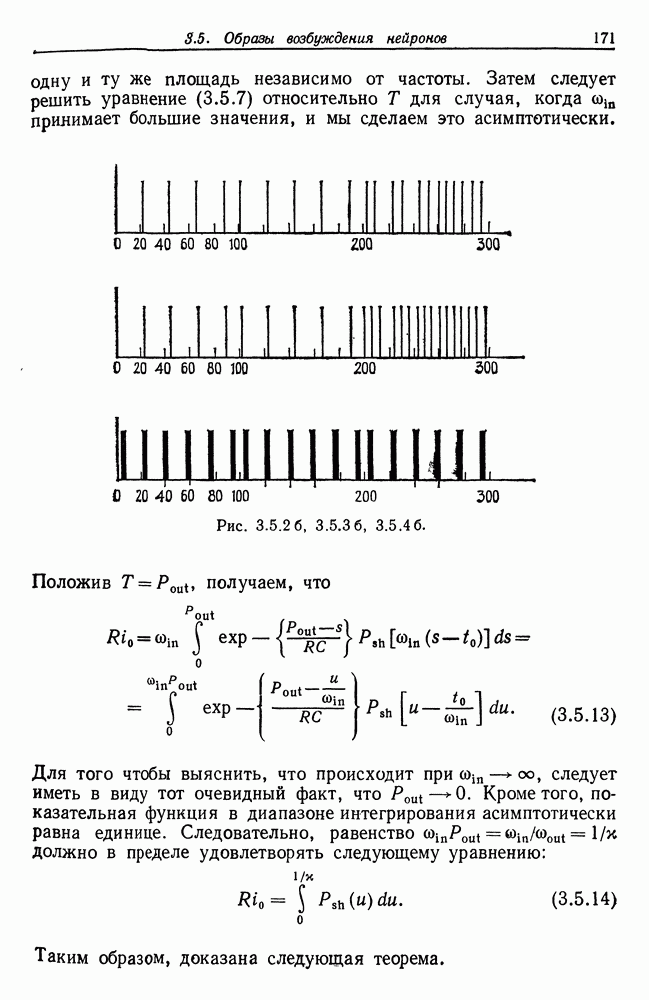
3.5. Многое написано относительно формальных нейронов и их временных образов (см., например, монографию Гриффита (1971)). Анализ, проведенный в разд. 3.5, потребуется нам в гл. 6.
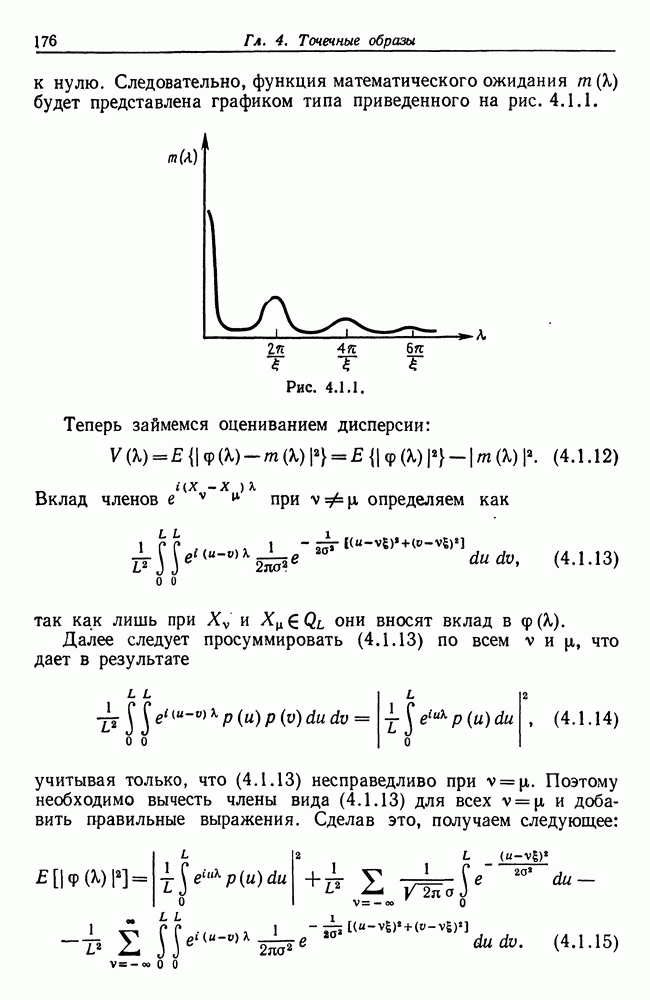
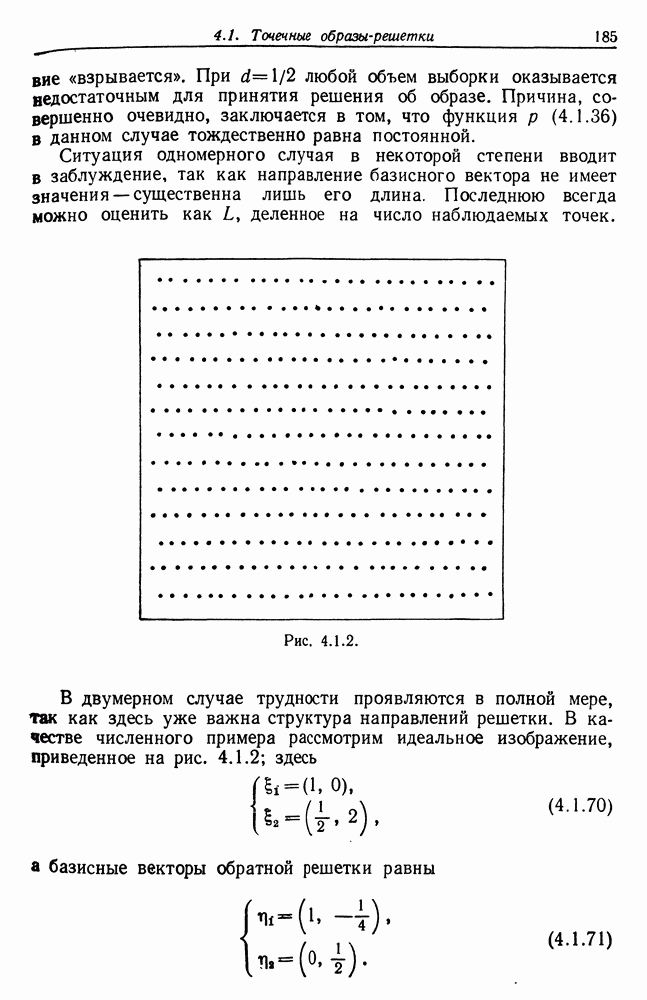
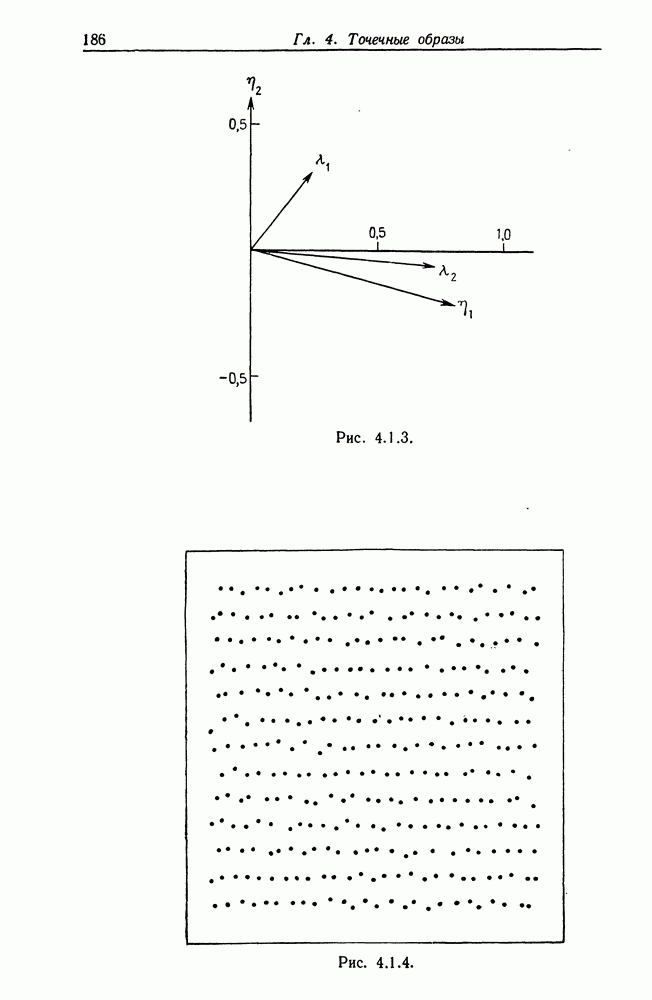
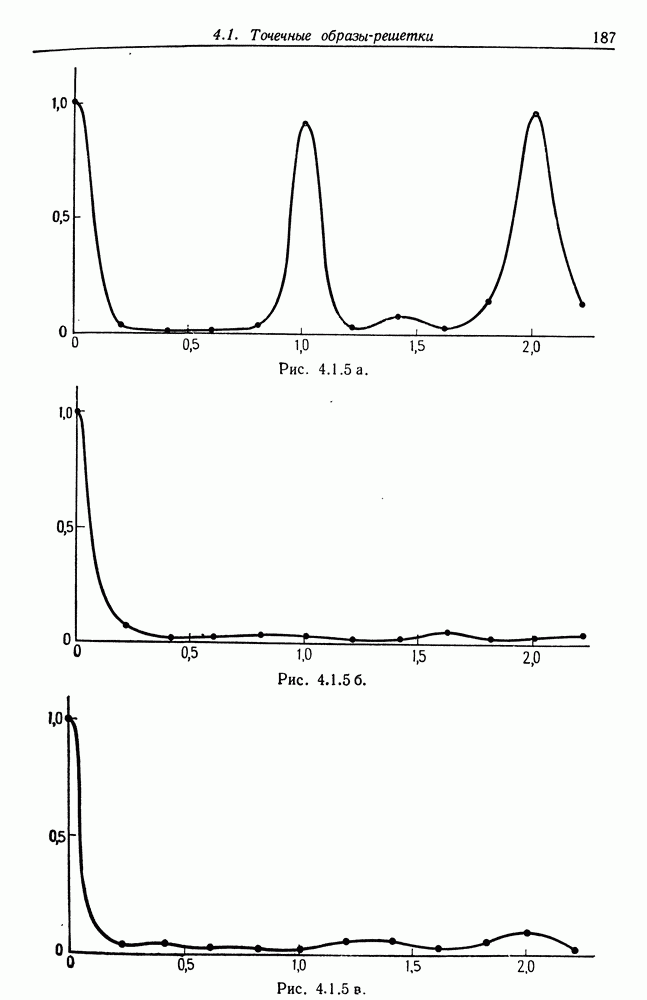
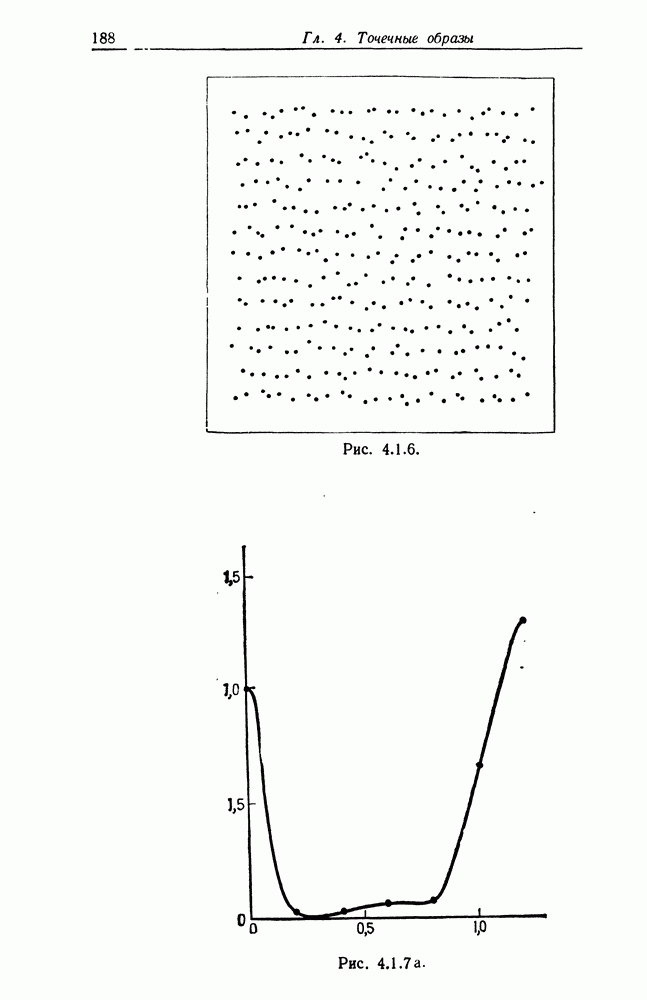
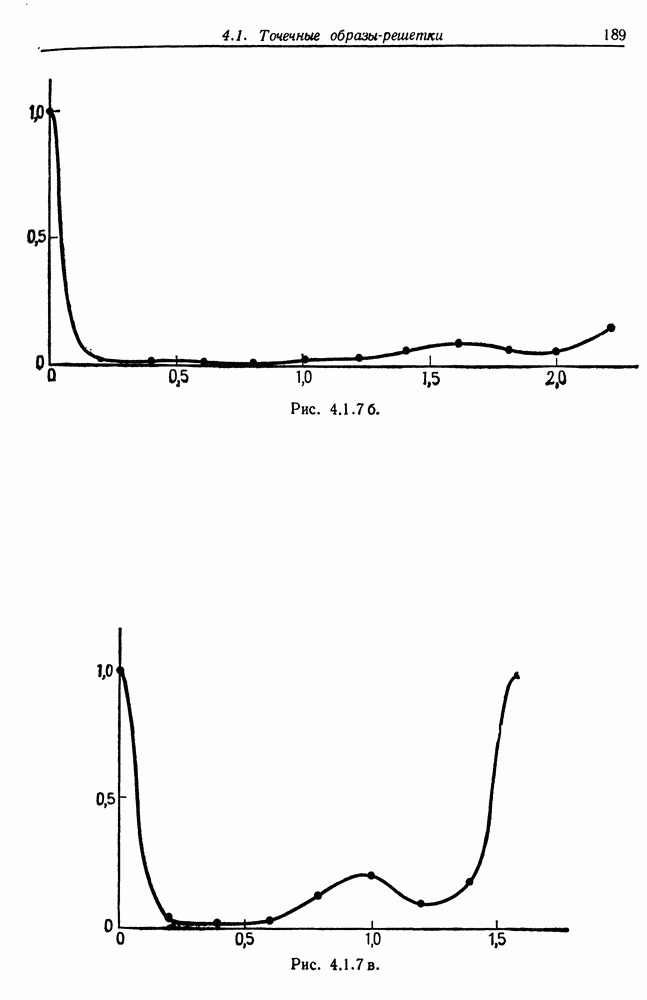
4.1. Теоремы, изложенные в этом разделе, заимствованы из работы Гренандера (1973в). Они не обеспечивают полного восстановления изображения, а позволяют определить только структуру регулярности через векторы базиса.
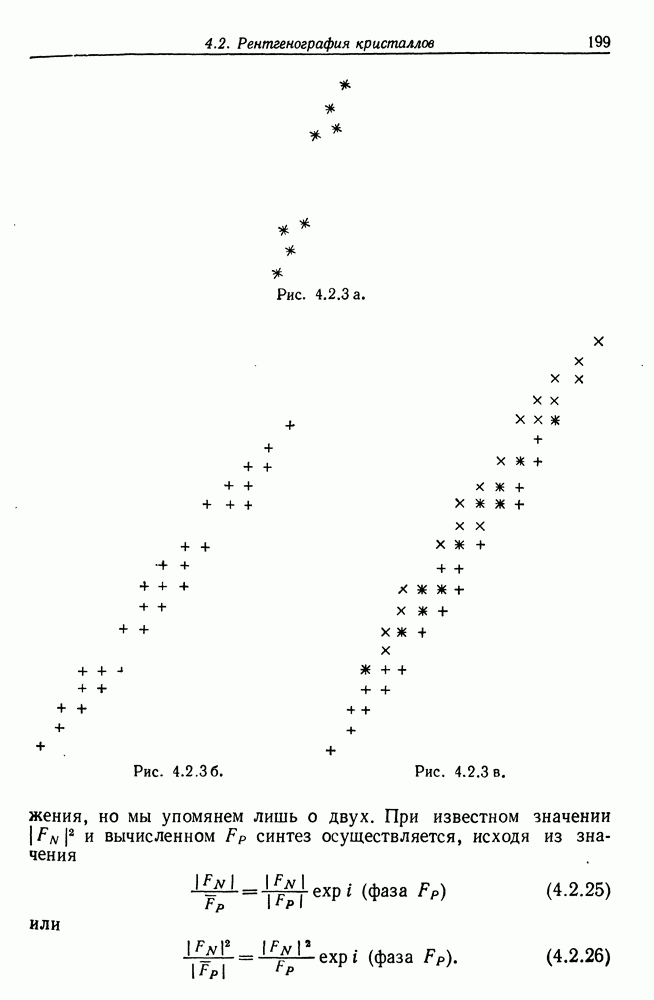
4.2. Читатель, желающий углубиться в джунгли литературы по дифракции рентгеновских лучей на кристаллах, может обратиться к двум обзорам, подготовленным весьма авторитетными специалистами: Боуман (1957) и Вулфсон (1971). Более подробное, элементарное и удобочитаемое изложение кристаллографического анализа можно найти в монографии Бюргера (1960).
Что касается фурье-анализа дифракции рентгеновских лучей, то наиболее ясное его изложение дано, по мнению автора, в монографии Рамачандрана и Сринивасана (1972), где досконально описаны некоторые наиболее важные виды анализа, основанного на дифракции рентгеновских лучей.
Автору не удалось в литературе по кристаллографическому анализу обнаружить теорему 4.2.1, сформулированную в точной форме. Почти полную формулировку можно найти у Рамачандрана и Сринивасана (1971); см. также две небольшие статьи Ринча (1939).
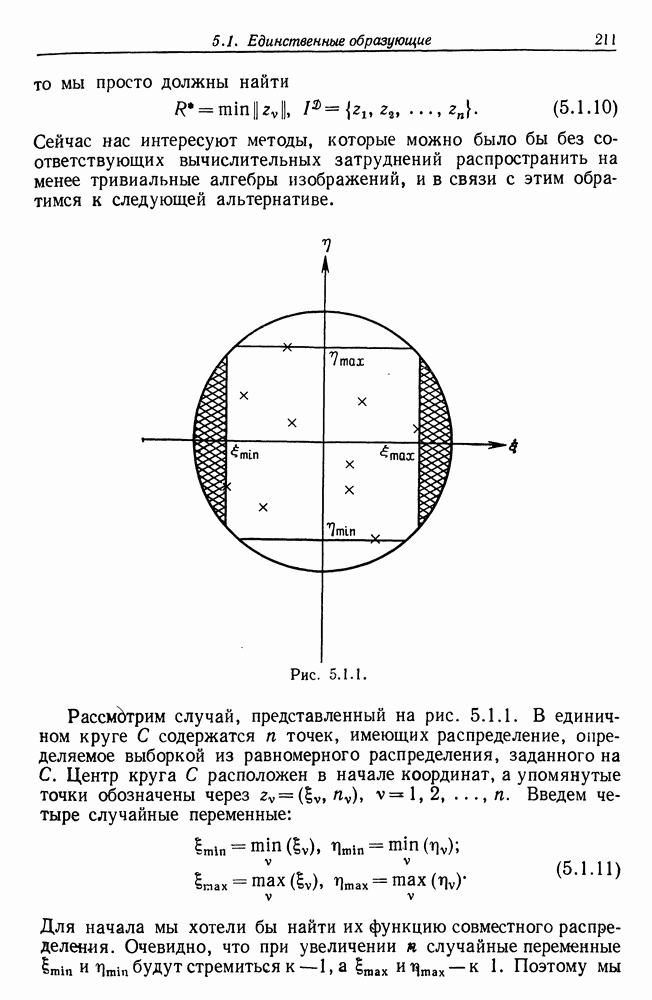
5.1. Общая идея статистической геометрии предложена в статье Гренандера (1973а), которая содержит также и большую часть материала данного раздела, и некоторую часть разд. 5.4.
Задачи, рассматриваемые в гл. 5, относятся к областям
интегральной геометрии и статистической геометрии. Чрезвычайно полно и изящно эта тематика представлена в работе Санталб (1976).
Производную Радона—Никодима можно получить другим способом. Для этого следует воспользоваться приемом, приведенным в статье Гренандера (1950, с. 225), и параметризовать изображение, деформированное, скажем, с помощью механизма деформации  посредством
посредством  Отметим, что это не есть вектор конечномерного пространства, и, следовательно, снова потребуется теорема 1.2.1 из гл. 1.
Отметим, что это не есть вектор конечномерного пространства, и, следовательно, снова потребуется теорема 1.2.1 из гл. 1.
Мы не рассматривали случай, когда прототип является множеством бесконечной площади. Пусть, например, это полуплоскость с  Тогда оказывается возможным определить
Тогда оказывается возможным определить  с вероятностью единица по наблюдениям
с вероятностью единица по наблюдениям  Вероятно, это справедливо и для но это не доказано.
Вероятно, это справедливо и для но это не доказано.
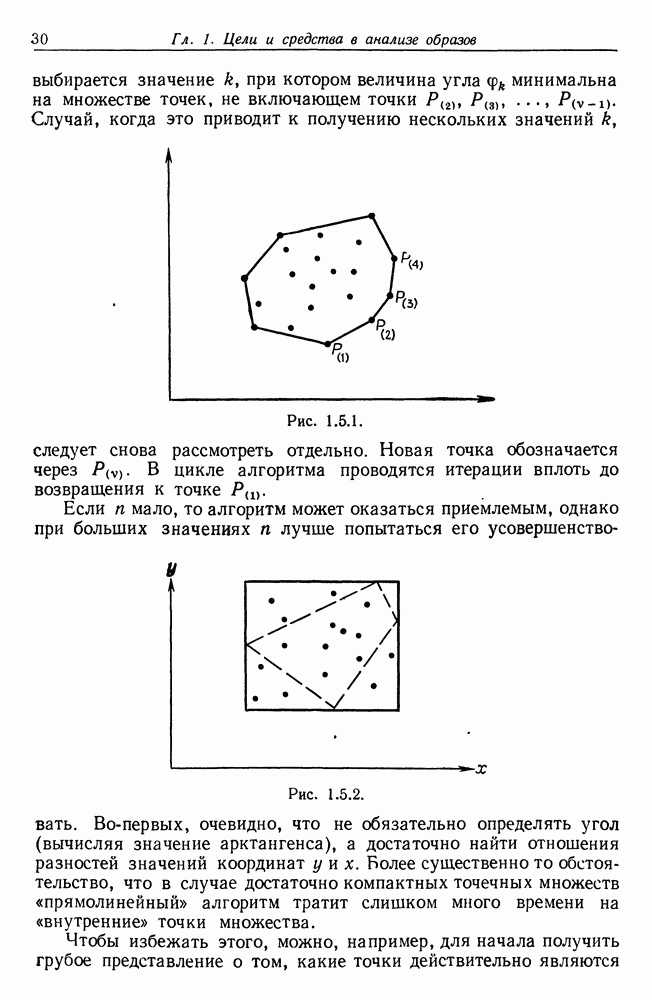
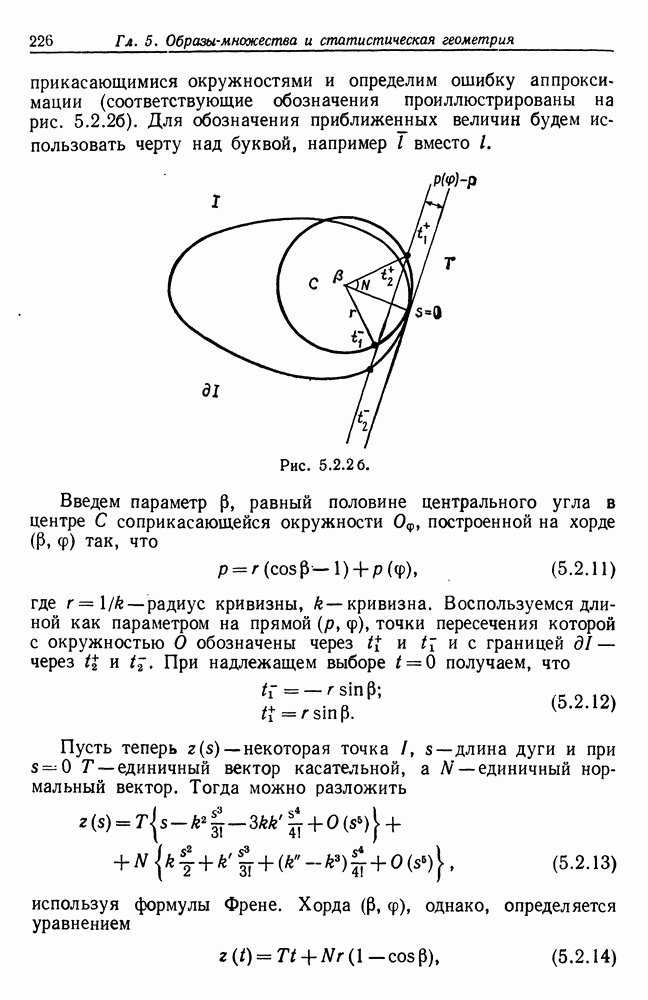
5.2. Другой алгоритм построения выпуклой оболочки читатель может найти в статье Джарвиса (1973). В работе Шамоса содержится много сведений о геометрических алгоритмах.
Математическое ожидание числа экстремальных точек  можно найти в работе Реньи и Сьюланке (1964).
можно найти в работе Реньи и Сьюланке (1964).
5.3. Нам не известен ни один быстрый алгоритм для построения замыкания по признакам, однако считается, что его можно получить, опираясь на принцип, заложенный в алгоритме быстрого построения выпуклой оболочки.
Мы не занимались проблемой отыскания эффективных алгоритмов для построения замыкания по признакам второго порядка для точечного множества на плоскости.
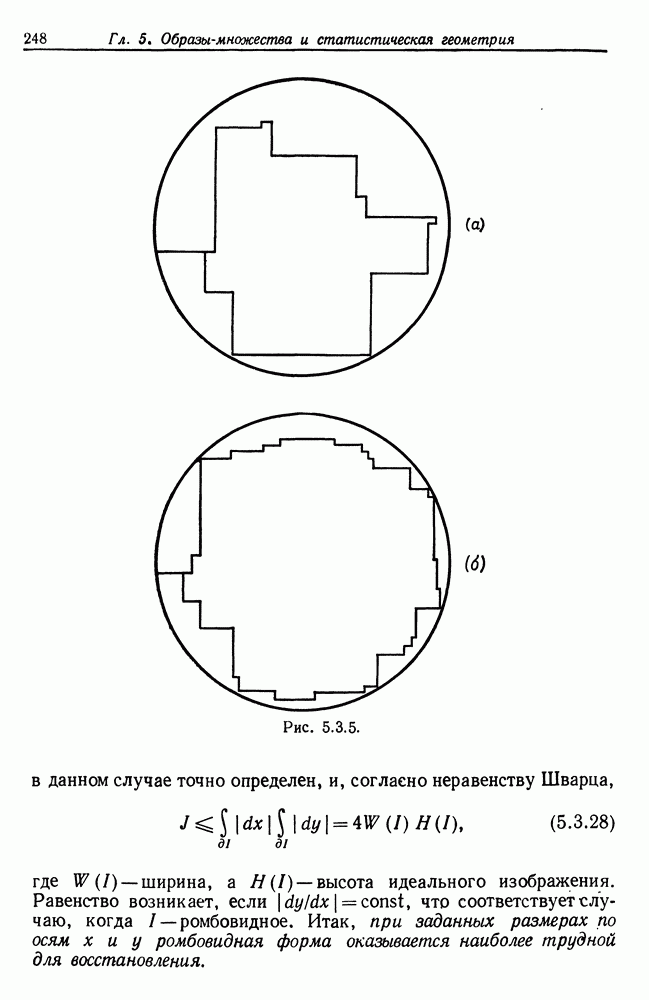
Обе приведенные теоремы заимствованы из работы Гренандера и Лавина; здесь только скорректировано уравнение (5.3.26).
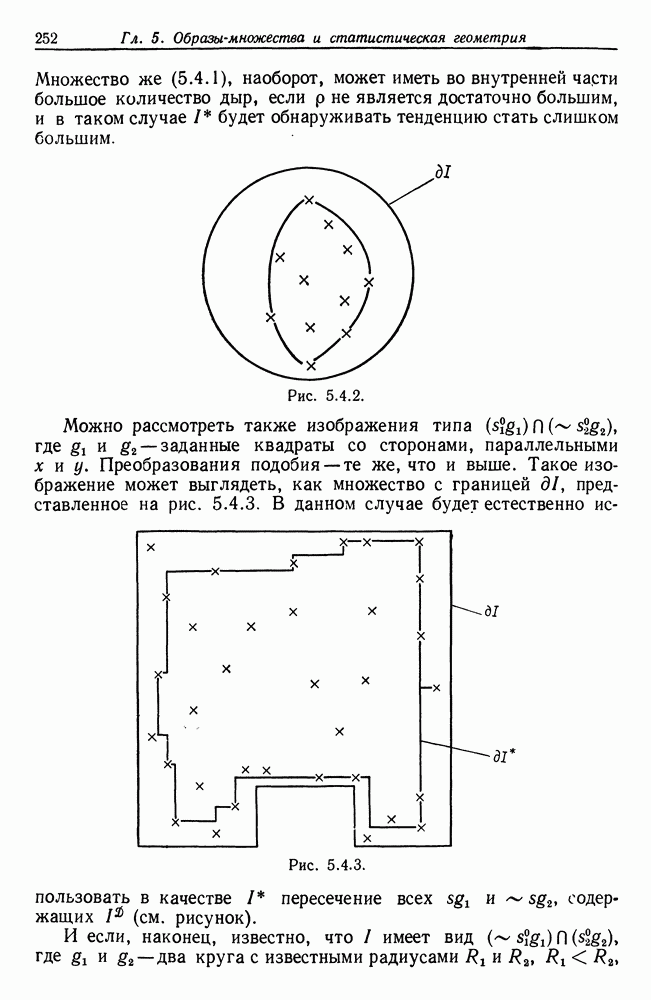
5.4. В теореме 5.4.3 мы были вынуждены ограничить изображения принадлежностью подобразу чтобы обеспечить восстановление, состоятельное по площади. Это связано с предложенным автором понятием  которое будет введено в т. 3.
которое будет введено в т. 3.
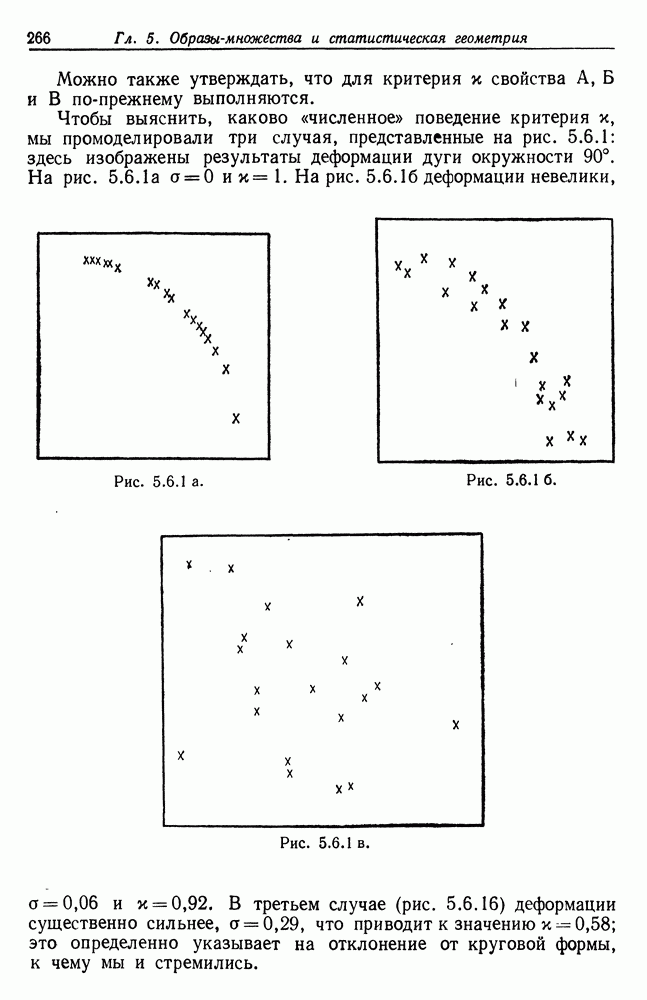
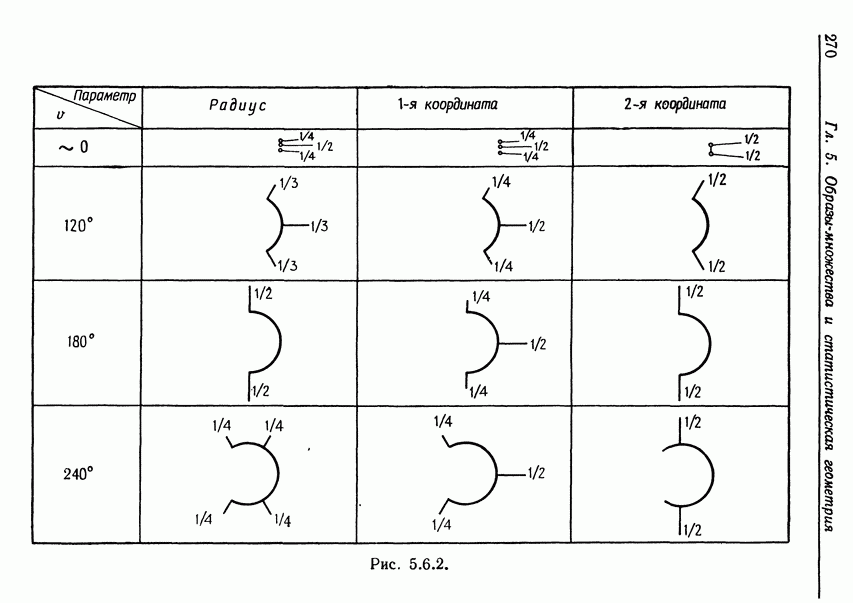
5.6. Результаты, рассмотренные в этом разделе, приведены в работе Гренандера (1974а).
5.7. С помощью того же метода, который был использован при доказательстве теоремы 5.7.2, можно получить асимптотические выражения для смещения и дисперсии  С их помощью можно попытаться определить вид окна оптимальной оценки
С их помощью можно попытаться определить вид окна оптимальной оценки  аналогично процедуре, описанной в статье Гренандера (19736), сс. 183-187. Перспективным кандидатом на роль окна оценки было бы
аналогично процедуре, описанной в статье Гренандера (19736), сс. 183-187. Перспективным кандидатом на роль окна оценки было бы

где

6.8 (добавлено при корректуре). Как только что стало известно автору, У. Р. Тоблер с географического отделения Мичиганского университета выступил с идеями, очень близкими изложенным в данном разделе. Он также выполнил ряд вычислений, которые, судя по всему, подтвердили пригодность метода.
6.1. Математический анализ процессов мышления имеет долгую историю. В книге Рашевски «Математическая биофизика» (Rashevsky «Mathematical Biophysics» (1948)), в высшей степени незаурядной работе, которую в свое время очень сильно недооценили, описаны некоторые ранние попытки в этом направлении. Оригинальные идеи Ф. Розенблатта, связанные с перцептронами (1962), привлекли множество последователей (и вызвали много критики!), и сейчас по этому предмету имеется необъятная литература. Подробную библиографию можно найти у Гриффита (1971) и Скотта (1975). В этой же связи следует отметить книгу Минского и Пейперта (1969), продемонстрировавших наличие жестких ограничений на перцептроны при некоторых видах обработки информации. Их результаты, в частности, показали, что организация периферийной обработки информации по перцептронному принципу маловероятна. В этой же связи необходимо отметить большую серию работ Гроссберга (см., например, Гроссберг (1969) и (1974)), в которых можно найти дополнительные ссылки.
Идея, состоящая в том, что такие процессоры образов должны быть основаны на предположении о существенной регулярности структуры среды в смысле алгебр изображений в противовес некоторому множеству произвольных векторов в пространстве  была выдвинута в работе Гренандера (1972б), но лишь схематично; там же высказано допущение о параллельности логики, используемой
была выдвинута в работе Гренандера (1972б), но лишь схематично; там же высказано допущение о параллельности логики, используемой  и алгебры операторов проекций в гильбертовом пространстве. В предшествовавшей работе Гренандера (1972а) содержатся некоторые предварительные и менее структурированные подходы к изучению логики
и алгебры операторов проекций в гильбертовом пространстве. В предшествовавшей работе Гренандера (1972а) содержатся некоторые предварительные и менее структурированные подходы к изучению логики 
Вопрос о том, как использовать  для введения какой-либо вероятностной меры на
для введения какой-либо вероятностной меры на  был рассмотрен в разд.
был рассмотрен в разд.  . Там мы имели дело со случаем
. Там мы имели дело со случаем  но если отношения связи менее жестки, то требуется менее общий подход.
но если отношения связи менее жестки, то требуется менее общий подход.
Одна из возможностей заключается в следующем. Допустим для простоты, что  конечно и все показатели связи (3 принимают значения из одного и того же множества В. Введем интенсивности вероятностей и причем
конечно и все показатели связи (3 принимают значения из одного и того же множества В. Введем интенсивности вероятностей и причем  означает,
означает,
что  Никакой нормализации здесь не требуется, мы лишь предполагаем, что
Никакой нормализации здесь не требуется, мы лишь предполагаем, что

Для заданной конфигурации с, имеющей набор замкнутых связей  и разомкнутых связей
и разомкнутых связей  определяем
определяем

Отметим, что второе произведение берется по всем замкнутым внутренним связям, соответствующим ориентации стрелок на графе связности. Постоянная задается так, чтобы выполнялось 
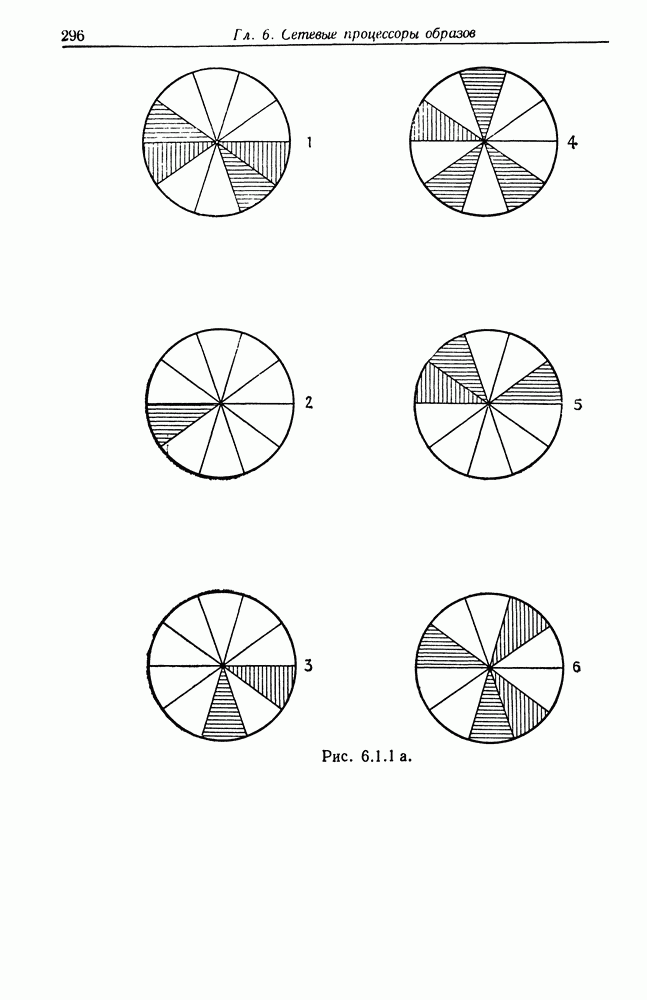
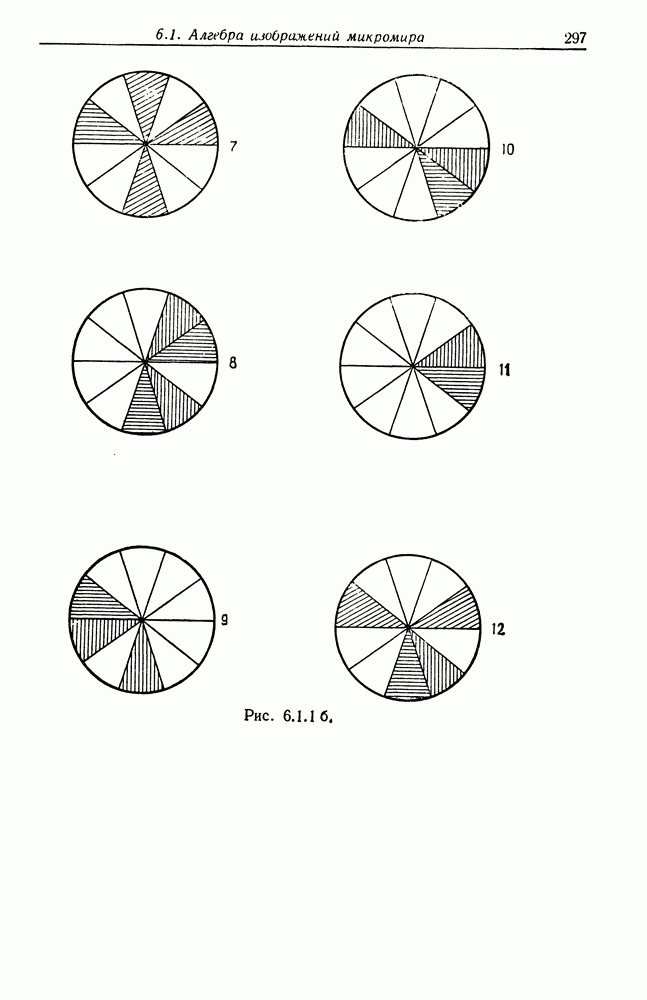
В примере, рассматривавшемся в конце разд. 6.1, стрелки соединений имеют ориентацию  конфигурация с построена из соединенных подконфигураций со следующими локализациями:
конфигурация с построена из соединенных подконфигураций со следующими локализациями:

сложение здесь всегда осуществляется по модулю  и
и  -цветовой признак в
-цветовой признак в  Тогда
Тогда  пропорциональна
пропорциональна

Если расширить область определения  от множества
от множества  на множество
на множество  где
где  обозначает нулевую образующую, то значения
обозначает нулевую образующую, то значения  новой функции представляют собой подходящий объект для изучения:
новой функции представляют собой подходящий объект для изучения:

В данном разделе мы использовали это и другие предложения Купера (1974).
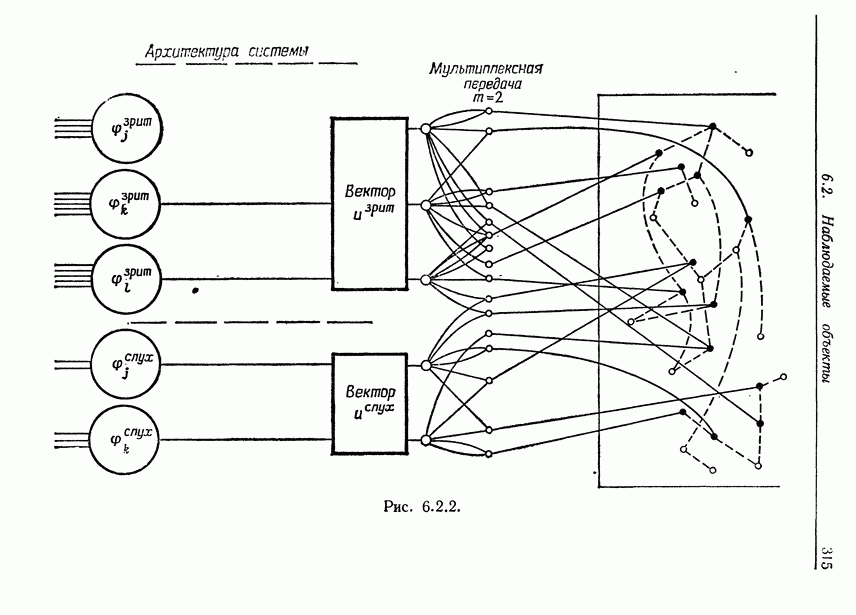
6.2. Возможность формулировки предложения 6.2.4 как экстремального результата была указана Вайталом, предложившим, кроме того, использовать при доказательстве для упрощения вы ражения (6.2.30) ортогональное преобразование.
При моделировании использовался когерентный аддитивный передаточный шум, хотя предлагалось и было бы целесообразнее работать с некогерентным шумом. Единственным следствием когерентности аддитивного шума является некоторое увеличение влияния члена, представляющего шум. Здесь закон больших чисел реализуется не так быстро.
Л. Купер предложил и обосновал идею о том, что именно матричнозначные стохастические дифференциальные уравнения представляют отличия активности в пиках по сравнению с состоянием покоя (см. также предложение 6.5.4).
Этой же теме посвящена статья Силверстайна (1976а).
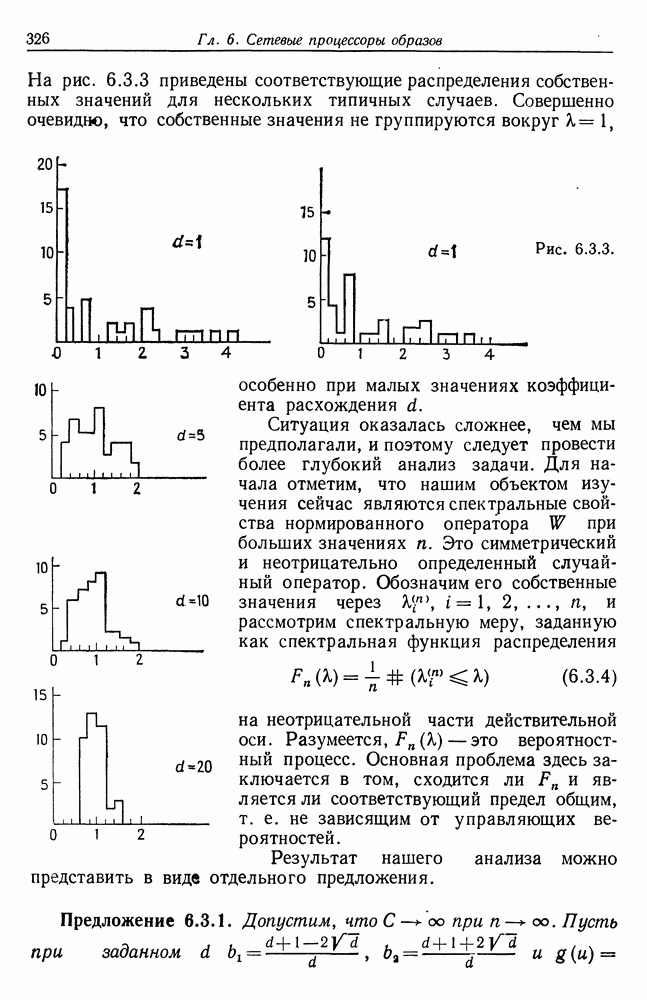
6.3. Результаты, изложенные в разд. 6.3, получены совместно автором и Дж. Силверстайном. Несколько подробнее они описаны в отчете Гренандера и Силверстайна (1974).
Доказательство предложения 6.3.1, надо признаться, длинно и сложно. Представляется маловероятным, что при использовании данного метода его можно было бы сделать короче. И комбинаторный анализ, и метод производящих функций кажутся необходимыми, а лемма 6.3.6 нужна, только если нас не удовлетворяет математическое ожидание спектральной меры. Следовательно, чтобы получить существенно более короткое доказательство, требуется принципиально иной метод.
Мы нашли распределение собственных значений (асимптотически), однако поведение собственных векторов пока неизвестно. Даже точное утверждение об асимптотическом поведении всех собственных векторов одновременно связано с определенными трудностями. Читателю, интересующемуся этой проблемой, следует обратиться к монографии Гренандера и Сеге (1958).
Случайные матрицы изучались многими авторами. Полезно, в частности, обратиться к работам Уигнера (1958), Арнольда (1967), Гренандера (1965) и Архарова (1971).
Нормирование оператора  с помощью множителя
с помощью множителя  следует интерпретировать как уменьшение прочности соединений в сети
следует интерпретировать как уменьшение прочности соединений в сети  на множитель
на множитель  . В последующих разделах мы предполагаем, что это сделано.
. В последующих разделах мы предполагаем, что это сделано.
6.5. Аксиому  следует рассматривать исключительно как первое приближение. Предпочтительнее было бы заменить ее уравнением, в котором первый член (6.5.2) не содержал бы символа математического ожидания. Тогда мы пришли бы к
следует рассматривать исключительно как первое приближение. Предпочтительнее было бы заменить ее уравнением, в котором первый член (6.5.2) не содержал бы символа математического ожидания. Тогда мы пришли бы к

и получили бы

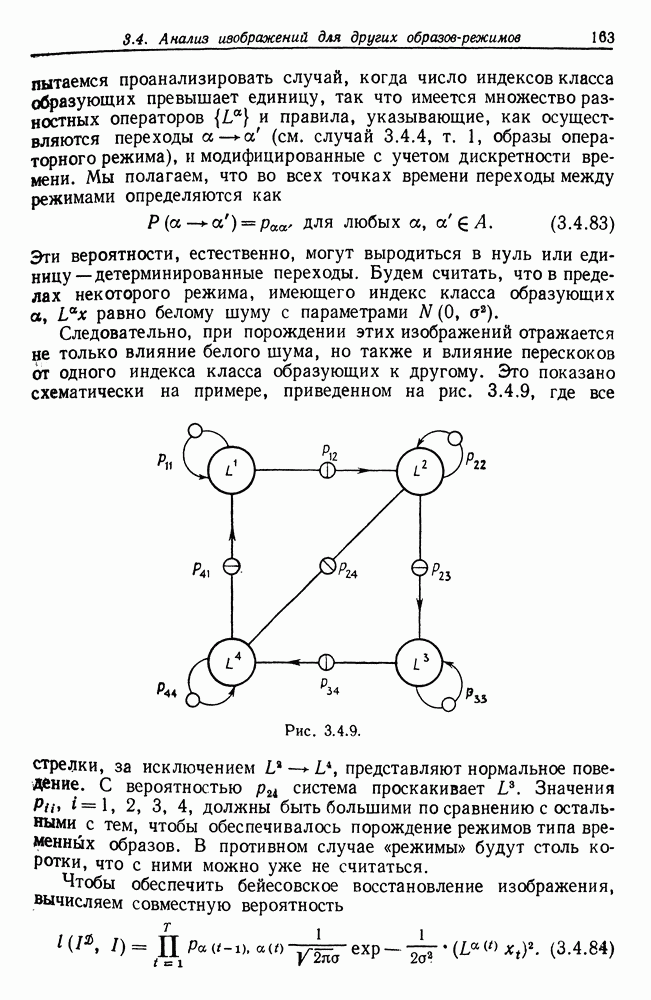
Это означает, что конфигурация обладает вероятностной структурой марковской цепи с вероятностями перехода  , причем на нее наложено условие периодичности с периодом
, причем на нее наложено условие периодичности с периодом  Именно так конфигурации порождались в машинном эксперименте.
Именно так конфигурации порождались в машинном эксперименте.
Было бы заманчиво подробно рассмотреть другие типы соединения — эта задача еще ждет своего решения.
Аксиому  можно усилить с тем, чтобы идентифицировать вектор уровня внимания двух конфигураций.
можно усилить с тем, чтобы идентифицировать вектор уровня внимания двух конфигураций.
6.6. При моделировании получаемую в результате энергию мы вычисляли как  Было бы естественно также попробовать сделать это, заменив
Было бы естественно также попробовать сделать это, заменив  на
на  или
или 
Если сеть  не обладает полной связностью и, следовательно,
не обладает полной связностью и, следовательно,  нейроны соединены лишь в определенных парах
нейроны соединены лишь в определенных парах  то уравнение модификации (6.5.2) не может быть справедливо при всех
то уравнение модификации (6.5.2) не может быть справедливо при всех  Отсюда следует, что, в то время как уравнение (6.5.2) приводит к (6.5.7) со сложением, умножением на скаляр, обращением и умножением матриц, новую модификацию представить через эти элементарные операции не представляется возможным. Следует выяснить, действительно ли это так и можно ли предложить альтернативные методы анализа этого нового важного уравнения.
Отсюда следует, что, в то время как уравнение (6.5.2) приводит к (6.5.7) со сложением, умножением на скаляр, обращением и умножением матриц, новую модификацию представить через эти элементарные операции не представляется возможным. Следует выяснить, действительно ли это так и можно ли предложить альтернативные методы анализа этого нового важного уравнения.
6.7. Дж. Силверстайн недавно показал, что гипотеза о временной оптимальности импульсного лечения неверна. См. Силверстайн (1977б).
В данном разделе мы не занимались проблемами лечения «органических» нарушений. В работе Гренандера (1972а) была предпринята попытка выяснить, что произойдет при разрушении существенной части оператора запоминания. При этом, конечно, автор опирался на понятие распределенной памяти, часто встречающееся в литературе и возникшее в какой-то степени благодаря классическим экспериментам Лешли. Наша попытка не имела аналитического характера, но предусматривала проведение машинных экспериментов. К сожалению, результаты оказались отрицательными. Согласно идее распределенной памяти, частичное разрушение оператора запоминания на 10 — 20% должно приводить лишь к небольшой потере памяти. Мы же, наоборот, наблюдали существенные повреждения ассоциативной памяти.
Несколько критических замечаний относительно гл. 6
(1) Структура среды описывалась как некоторая алгебра изображений физических объектов с регулярностью  Это рациональный подход, но он страдает тем недостатком, что фактор времени не учитывается в полной мере. Изображения следуют друг за другом, но мы не вводили физические ограничения на временную зависимость в
Это рациональный подход, но он страдает тем недостатком, что фактор времени не учитывается в полной мере. Изображения следуют друг за другом, но мы не вводили физические ограничения на временную зависимость в  Так, например, мы не формализовали такие понятия, как «непрерывность движения», «неизменность объектов», «nullus motus sine causam» (нет движения без причины — лат.). Для того чтобы устранить этот недостаток, необходимо расширить опорное пространство так, чтобы оно включало время, а преобразования подобия должны быть превращены в пространственно временные отображения. В таком случае можно было бы изучить, например, вопрос о том, может ли
Так, например, мы не формализовали такие понятия, как «непрерывность движения», «неизменность объектов», «nullus motus sine causam» (нет движения без причины — лат.). Для того чтобы устранить этот недостаток, необходимо расширить опорное пространство так, чтобы оно включало время, а преобразования подобия должны быть превращены в пространственно временные отображения. В таком случае можно было бы изучить, например, вопрос о том, может ли  обнаруживать каузальные отношения.
обнаруживать каузальные отношения.
(2) Мы представляли аксиоматически кратковременную память как вектор состояния  а долговременную память — как линейный оператор. Обучение означает, что геометрия пространств состояния постепенно изменяется, а операторы проекций — наблюдаемые высказывания - определены. Очевидно, и необходимо отдавать себе в этом полный отчет, что при реализации этого процесса
а долговременную память — как линейный оператор. Обучение означает, что геометрия пространств состояния постепенно изменяется, а операторы проекций — наблюдаемые высказывания - определены. Очевидно, и необходимо отдавать себе в этом полный отчет, что при реализации этого процесса  обобщает свой конечный опыт на потенциально бесконечную совокупность допустимых объектов и отношений. Математической подоплекой этого обстоятельства служит линейный характер операторов: они соответствуют подмножествам, содержащим бесконечное число точек. Мы отметили лишь, между прочим, что множество
обобщает свой конечный опыт на потенциально бесконечную совокупность допустимых объектов и отношений. Математической подоплекой этого обстоятельства служит линейный характер операторов: они соответствуют подмножествам, содержащим бесконечное число точек. Мы отметили лишь, между прочим, что множество  не обязательно должно быть линейно замкнутым, а также что возможно обучение «фиктивным» объектам. Следует рассмотреть более глубокие последствия этого факта. В частности, при каких обстоятельствах множество будет линейно замкнутым и что это говорит нам об алгебре изображений.
не обязательно должно быть линейно замкнутым, а также что возможно обучение «фиктивным» объектам. Следует рассмотреть более глубокие последствия этого факта. В частности, при каких обстоятельствах множество будет линейно замкнутым и что это говорит нам об алгебре изображений.
(3) В нашем эксперименте операторы проекций коммутативны. Автор полагает, что если они некоммутативны, то возникают интересные следствия, которые можно исследовать по крайней мере частично, с помощью метода возмущений (аналогично тому, как это сделано в разд. 6.6). С этим же связан и такой важный вопрос, как характер влияния на результирующее отображение памяти неопределенностей при выборе изображений из алгебры изображений и шума, возникающего при передаче и в основной сети. Для полного ответа на этот вопрос потребовалось бы глубокое изучение случайного дифференциального уравнения, рассмотренного в разд. 6.5; условия предложения 6.5.4 явно неудовлетворительны. Другими словами, вопрос можно было бы
сформулировать так: если и  имеют (статистически) идентичную исходную внутреннюю структуру и живут в одной и той же статистической среде, насколько мы можем быть уверены в том, что они придут к почти одному и тому же насыщенному отображению памяти?
имеют (статистически) идентичную исходную внутреннюю структуру и живут в одной и той же статистической среде, насколько мы можем быть уверены в том, что они придут к почти одному и тому же насыщенному отображению памяти?
(4) Мы предполагали, что оператор сети симметрический. В то время когда это допущение вводилось, единственным мотивом была математическая элегантность. Оно, однако, не кажется естественным, и следовало бы попытаться модифицировать эту аксиому. Мы вполне можем работать с несимметричными матрицами, хотя нам придется использовать каноническую жорданову форму с ее несколько неудобными свойствами. Собственные векторы отображения памяти уже не обязаны быть взаимно ортогональными, что может привести к ряду интересных модификаций, связанных с проблемой обучения.
(5) Аналогично, полная связность сети  которая требовалась в некоторых разделах данной главы, неестественна и от нее следовало бы отказаться. В настоящее время мы не знаем способа сделать это аналитически, однако можно по крайней мере попытаться провести машинные эксперименты с тем, чтобы получить некоторое представление о последствиях предположения о неполной связности. Здесь первостепенное значение будет иметь внутренняя обратная связь сети
которая требовалась в некоторых разделах данной главы, неестественна и от нее следовало бы отказаться. В настоящее время мы не знаем способа сделать это аналитически, однако можно по крайней мере попытаться провести машинные эксперименты с тем, чтобы получить некоторое представление о последствиях предположения о неполной связности. Здесь первостепенное значение будет иметь внутренняя обратная связь сети  и, в частности, то обстоятельство, что граф сети
и, в частности, то обстоятельство, что граф сети  должен быть транзитивно замкнутым.
должен быть транзитивно замкнутым.
(6) На протяжении всей главы мы считали, что пространства  , так же как и пространство состояний
, так же как и пространство состояний  конечномерны. Однако совершенно очевидно, что размерности множества реальных нейронных сетей колоссальны. Быть может, нам следовало бы лучше воспользоваться формализмом гильбертова пространства. Эта проблема становится действительно важной только тогда, когда у нас есть основания ожидать столкновения с какими-либо истинными различиями между гильбертовым пространством и евклидовым пространством высокой размерности. Будем ли мы, например, использовать (почти) неограниченные операторы? Будем ли мы сталкиваться с операторами с (почти) непрерывным спектром и т. д.?
конечномерны. Однако совершенно очевидно, что размерности множества реальных нейронных сетей колоссальны. Быть может, нам следовало бы лучше воспользоваться формализмом гильбертова пространства. Эта проблема становится действительно важной только тогда, когда у нас есть основания ожидать столкновения с какими-либо истинными различиями между гильбертовым пространством и евклидовым пространством высокой размерности. Будем ли мы, например, использовать (почти) неограниченные операторы? Будем ли мы сталкиваться с операторами с (почти) непрерывным спектром и т. д.?
(7) Мы установили, что необходима определенная степень уплотнения для того, чтобы  обучилось логике признаков высшего порядка. Мы никоим образом не утверждаем, что использованное нами уплотнение — объединение векторов и и посредством умножения — единственно возможное. Совсем наоборот — может быть, имеет смысл рассмотреть альтернативы, когда комбинирование достигается при помощи других функций. Кроме того, системы частичного уплотнения следует изучить тщательнее.
обучилось логике признаков высшего порядка. Мы никоим образом не утверждаем, что использованное нами уплотнение — объединение векторов и и посредством умножения — единственно возможное. Совсем наоборот — может быть, имеет смысл рассмотреть альтернативы, когда комбинирование достигается при помощи других функций. Кроме того, системы частичного уплотнения следует изучить тщательнее.
7.1. На подход, которому мы следовали в данном разделе, в значительной степени повлияли идеи покойного Шпачека относительно дедуктивно-индуктивных построений в условиях неполноты информации. Примеры можно найти в работе Шпачека (1960). К сожалению, Шпачек не имел возможности завершить разработку своих новаторских представлений. Работа, которую он опубликовал по этому поводу, заслуживает большей известности.
В принципе вывод образов, в том числе абдукцию образов, можно рассматривать как индуктивное поведение подобно тому, как Нейман (1966, 1968) предложил описывать этим термином статистический вывод.
Очень интересная попытка формализовать индуктивный процесс была предпринята Р. Соломоновым (1964а,б).
Имеется также определенная связь этой проблемы с работами в области искусственного интеллекта: автоматизация доказательств, эвристические программы и т. п. Читатель может обратиться, например, к монографии Ханта (1975) (см., в частности, гл. 9—12 и библиографию).
В уравнении (7.1.4) мы допускаем в качестве образующих пустой символ с различными входными и выходными связями в отличие от наших обычных допущений.
7.2. Вообще говоря, грамматический вывод — это то, чем филологи занимались тысячелетиями. Вывод в формальных грамматиках появился не так давно, но даже и здесь соответствующая литература достигла уже чудовищного объема. Большая ее часть лишь косвенно связана с изучением абдукции, которое проводится в данном разделе. Читателю, интересующемуся этой литературой, можно рекомендовать книги Ханта (1975), гл. 7, и Фу (1974), в которых приведено множество соответствующих ссылок (см. также Пейтл (1972) и Мариански (1974)). На трактовку этой проблемы  данной главе оказали влияния дискуссии с Кучерой.
данной главе оказали влияния дискуссии с Кучерой.
Более близкое отношение к данному разделу имеет старая работа Миллера и Хомского (1957), в которой подстановка предложена в качестве естественного принципа, на котором может основываться алгоритм. Другим важным источником является работа Соломонова (1964), базирующаяся на теореме  Автору неизвестно, последовал ли за этими первыми попытками подробный анализ устойчивости, чувствительности к ошибкам, реализация на вычислительных машинах и т. п.
Автору неизвестно, последовал ли за этими первыми попытками подробный анализ устойчивости, чувствительности к ошибкам, реализация на вычислительных машинах и т. п.
Материал, помещенный в разд. 7.2. — 7.5, основан на исследовании, начатом в 1974 г. в результате обсуждения, проведенного  Купером, У. Фрайбергером,
Купером, У. Фрайбергером,  Кучерой и автором. Некоторые предварительные результаты были приведены в отчете Гренандера (19746), однако сам алгоритм не был подвергнут достаточно
Кучерой и автором. Некоторые предварительные результаты были приведены в отчете Гренандера (19746), однако сам алгоритм не был подвергнут достаточно
детальному анализу. Более полный анализ проведен у Шрира (1977); там же представлены и математические эксперименты, иллюстрирующие достоинства и недостатки одной конкретной схемы абдукции.
Выбор автоматных языков вносит существенные ограничения. Следует заметить, что нашей целью является не изучение абдукции естественного языка, но выяснение того, каким образом можно организовать абдукцию при одной конкретной постановке и что представляют собой возникающие при этом математические затруднения, в частности определение  устойчивость, сходимость.
устойчивость, сходимость.
При выборе преобразований подобия необходимо определить, на какие именно существенные свойства мы хотим обратить внимание, какого рода «одинаковость» интересует нас в данном случае. Часто приходится работать более чем с одними S. В данном разделе мы хотим изучить общую значимость связей, определяющих выбор использованных 
7.4. Было бы полезно получить полное выражение для пределов, фигурирующих в (7.4.3) и (7.4.4), при ей  Это можно сделать, модифицировав доказательство Силверстайна.
Это можно сделать, модифицировав доказательство Силверстайна.
7.5 (добавлено при корректуре). Проведенные недавно машинные эксперименты указывают, что иерархическая организация алгоритма не приводит к ускорению сходимости алгоритма, как предполагалось в тексте. Следовательно, может быть лучше осуществлять обработку образа в один этап, чем начинать с классификации слов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
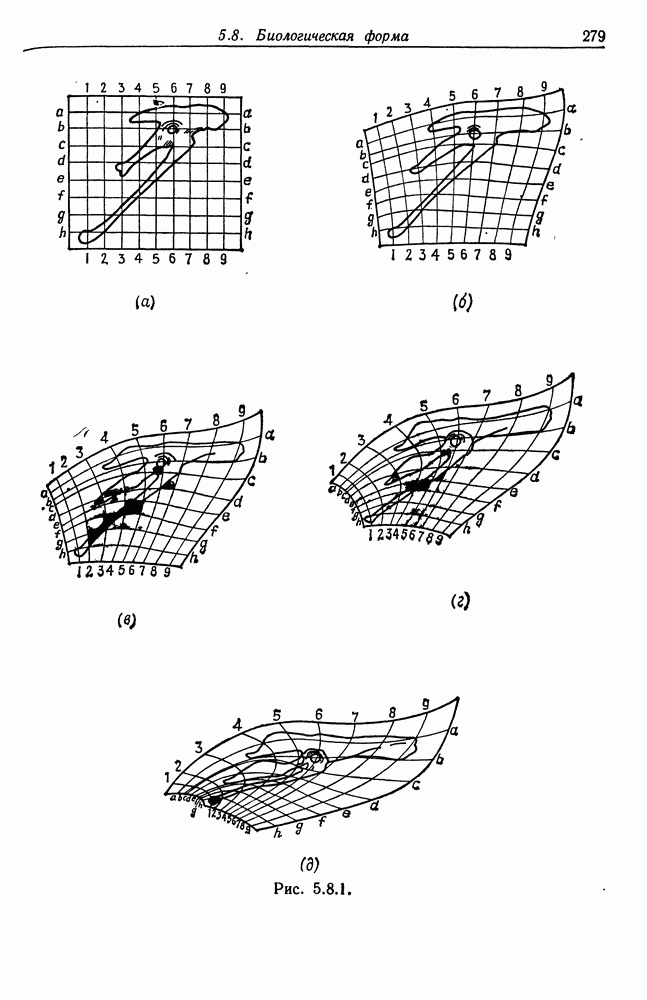
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
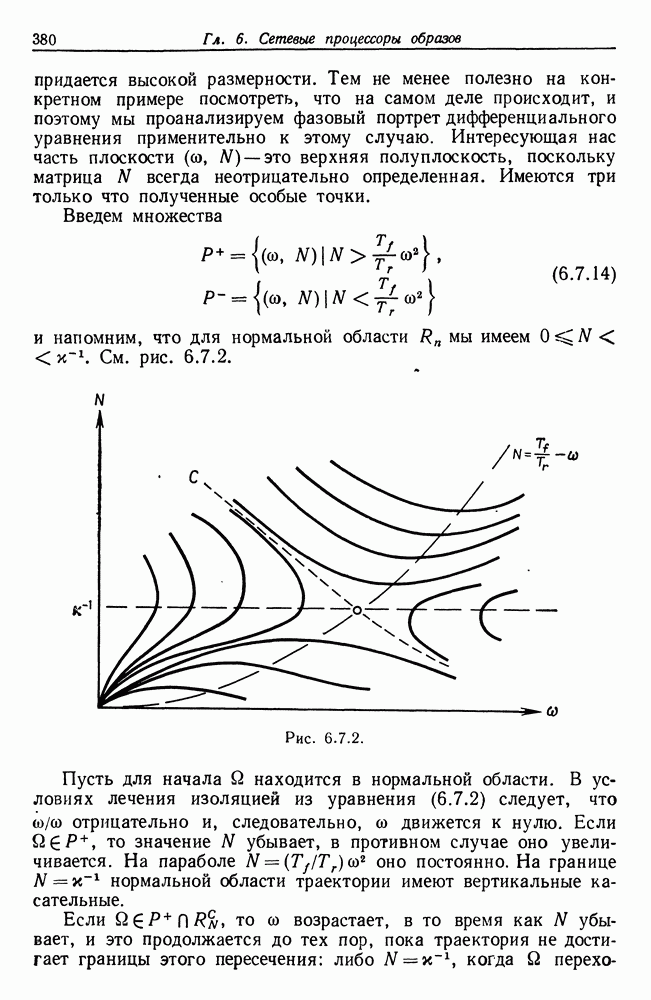
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
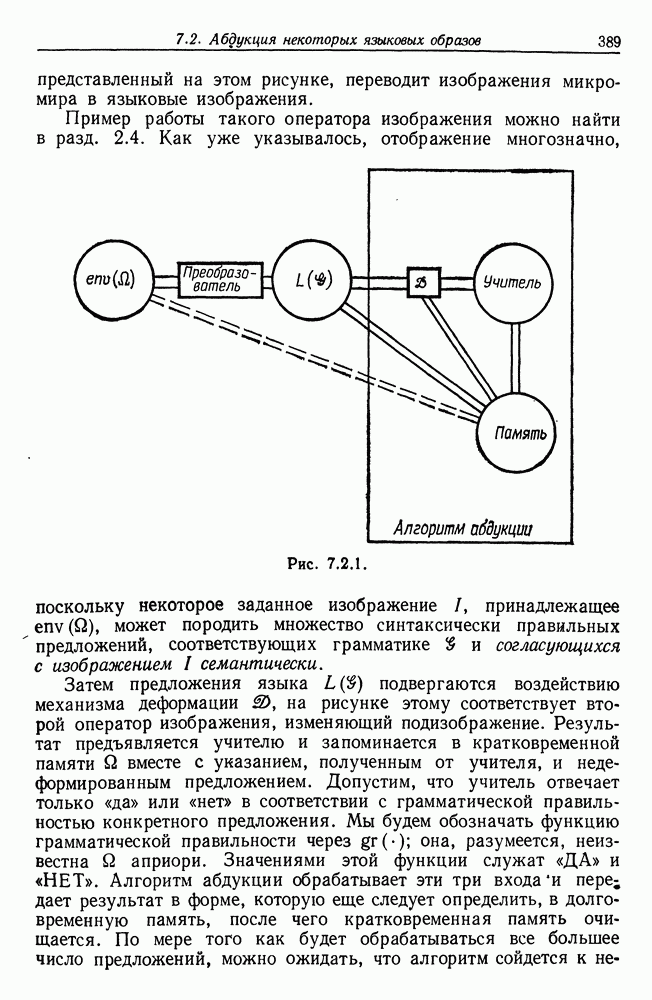
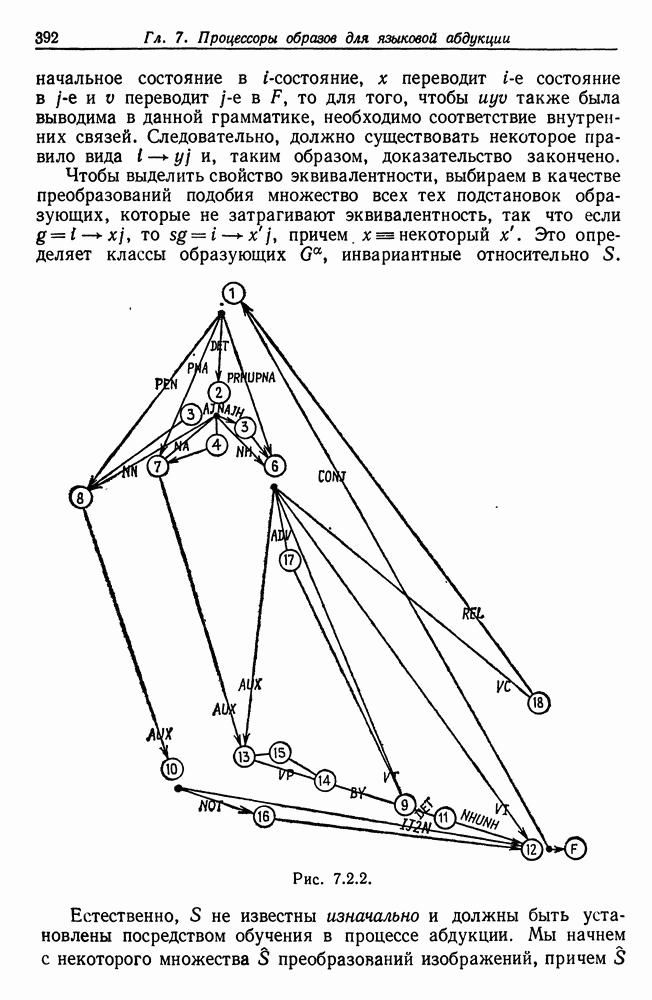
- 7.2. Абдукция некоторых языковых образов
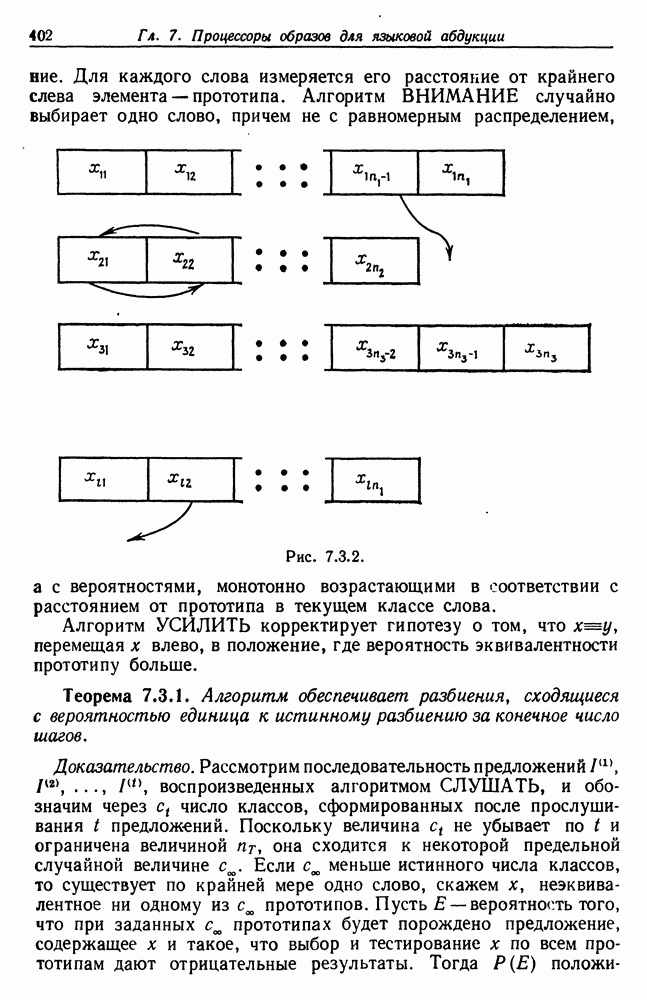
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы