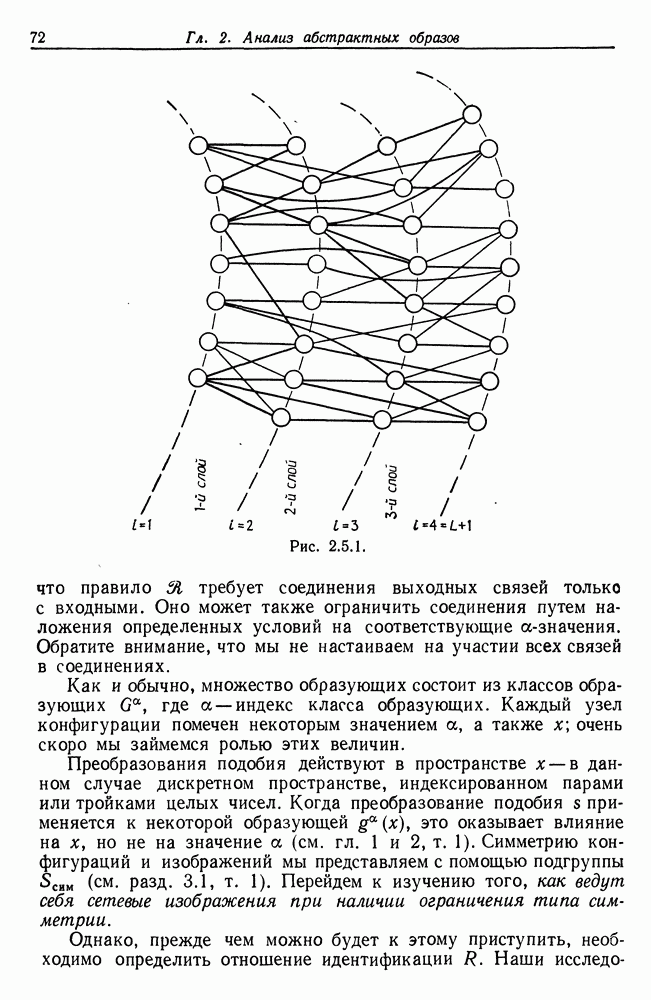
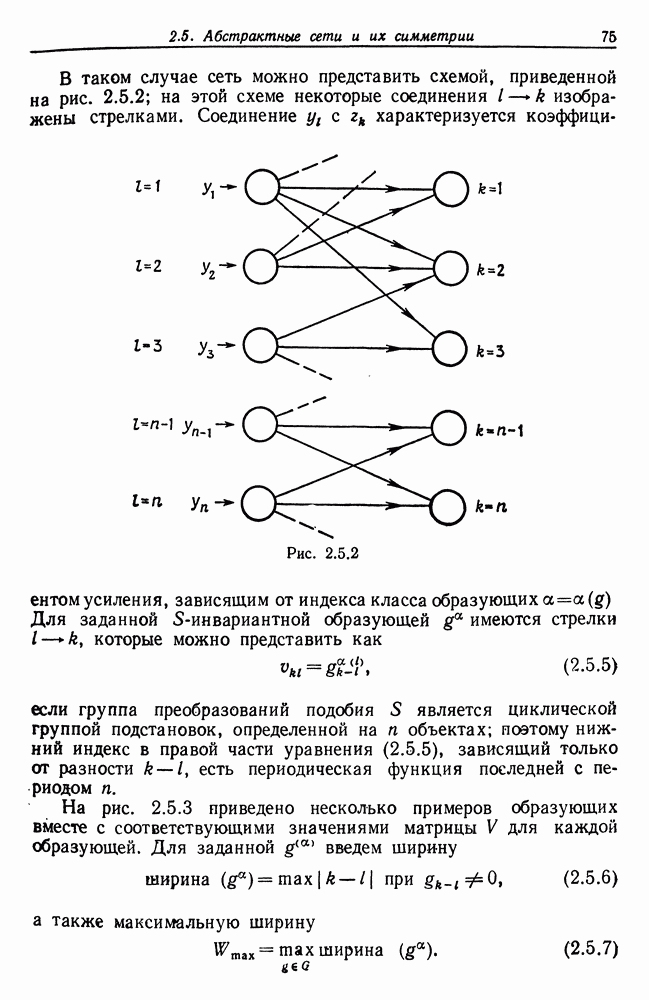
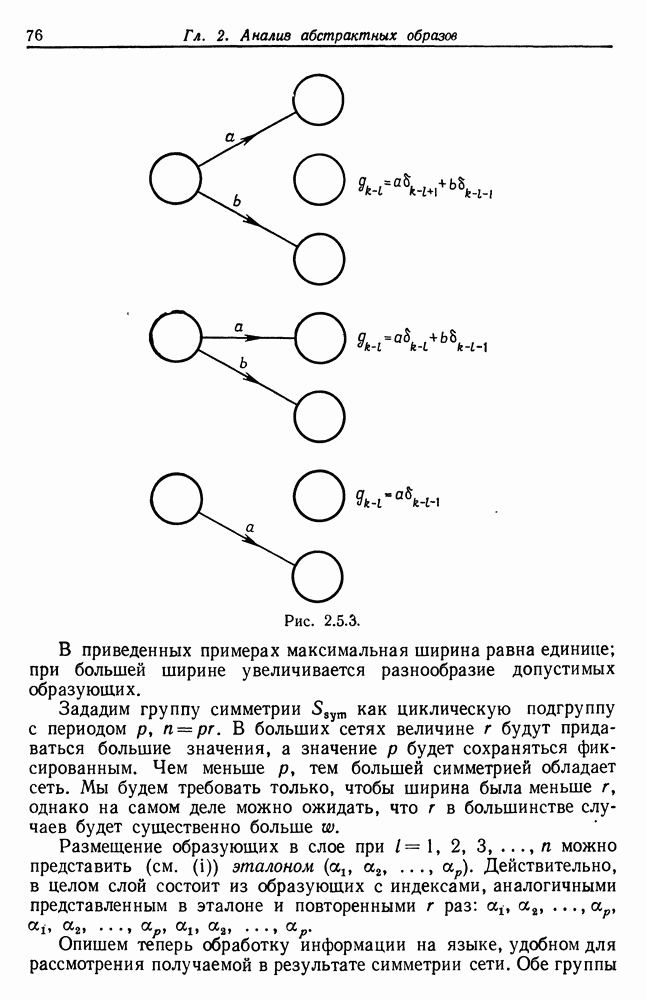
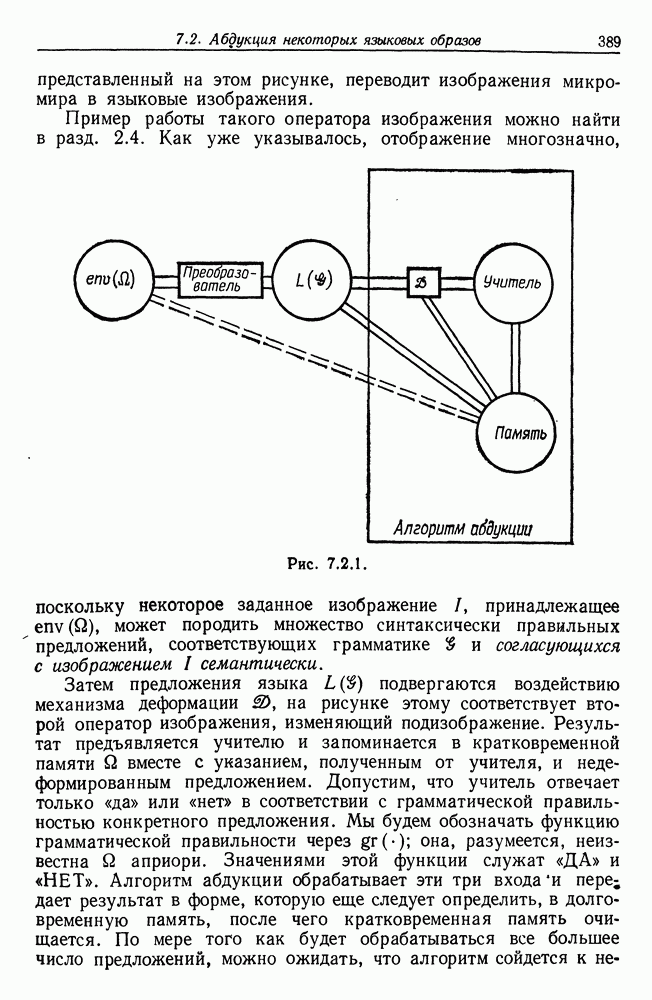
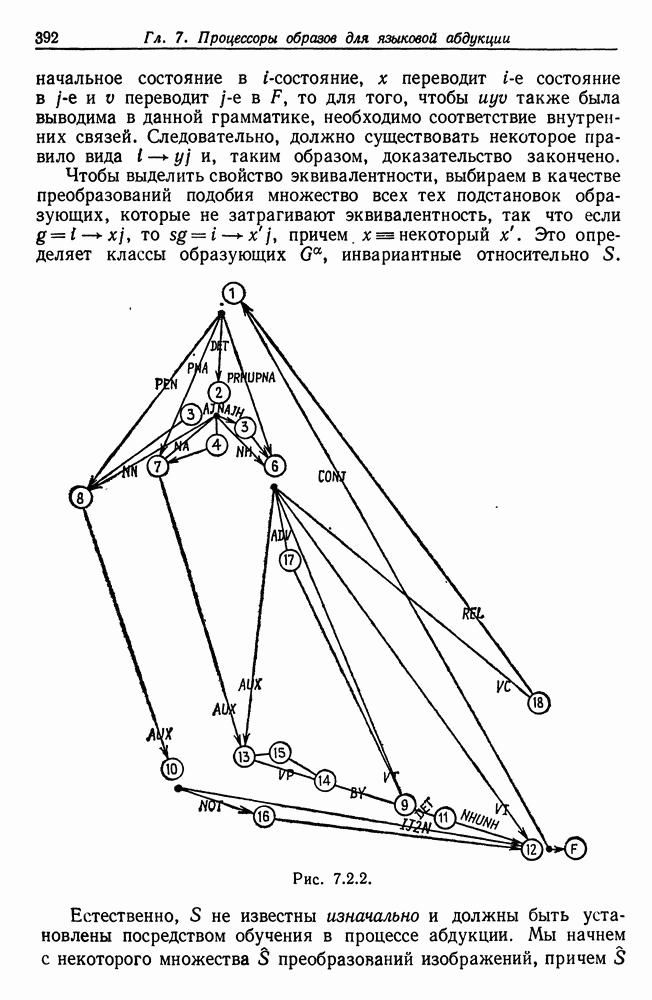
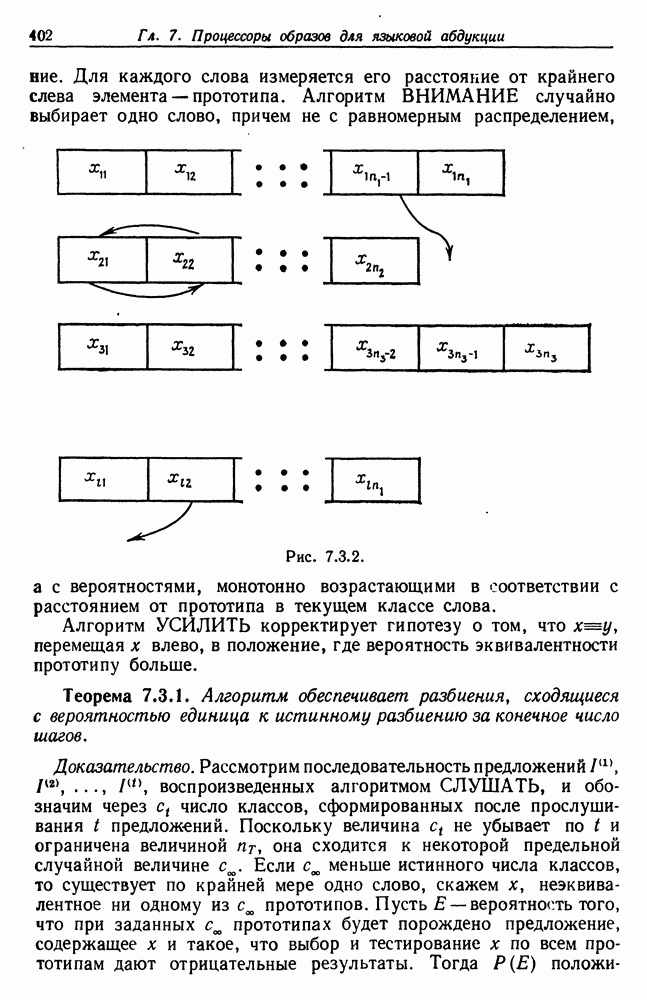
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 4. Точечные образы
4.1. Точечные образы-решетки
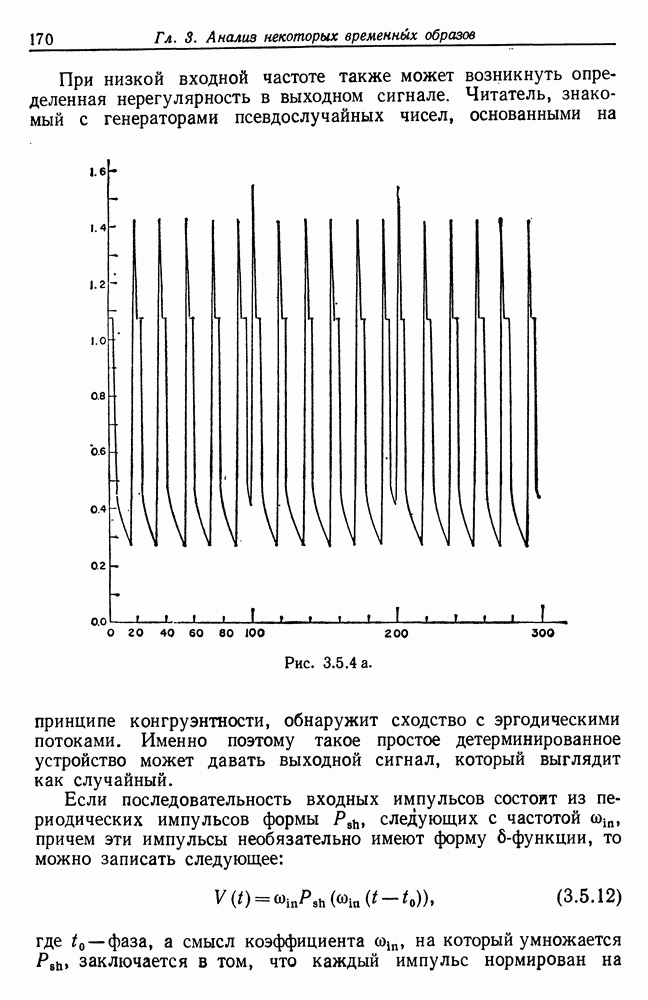
Рассмотрим точечные образы-решетки, подобные описанным в разд. 3.5 т. 1, на которые воздействуют деформации типа «пульсирующий кристалл» (см. разд. 4.2, т. 1).
Допустим, что идеальное изображение I представляет собой регулярную решетку в  и, следовательно, ее точки имеют вид
и, следовательно, ее точки имеют вид

здесь  -фазовый вектора
-фазовый вектора  — векторы базиса решетки
— векторы базиса решетки  — произвольные целые числа. Естественно, векторы базиса не определяются однозначно.
— произвольные целые числа. Естественно, векторы базиса не определяются однозначно.
Допустим теперь, что фазовые и базисные векторы неизвестны и наблюдению доступны лишь пульсации

где векторы шума  статистически независимы и характеризуются нормальным распределением с нулевым вектором математического ожидания и ковариационной матрицей
статистически независимы и характеризуются нормальным распределением с нулевым вектором математического ожидания и ковариационной матрицей  Мы хотим
Мы хотим  деформированному изображению
деформированному изображению  восстановить идеальное изображение
восстановить идеальное изображение  т. е., другими словами, определить векторы базиса (а может быть, также и фазовый вектор).
т. е., другими словами, определить векторы базиса (а может быть, также и фазовый вектор).
Ситуация такова. В некоторой заданной области, скажем кубе  размера
размера  мы наблюдаем пульсирующие точки решетки, оказавшиеся в
мы наблюдаем пульсирующие точки решетки, оказавшиеся в  . С первого взгляда может показаться, что возникает регрессионная задача хорошо известного типа, поскольку соотношения (4.1.1) и (4.1.2) образуют линейную модель. Это действительно так, но лишь при низком уровне шума.
. С первого взгляда может показаться, что возникает регрессионная задача хорошо известного типа, поскольку соотношения (4.1.1) и (4.1.2) образуют линейную модель. Это действительно так, но лишь при низком уровне шума.
Если уровень шума значителен, то возникает на порядок более трудная задача. Во-первых, число наблюдений не фиксировано и заранее неизвестно, какие точки идеального изображения попадут в  после воздействия пульсаций. Этот вопрос требует отдельного анализа.
после воздействия пульсаций. Этот вопрос требует отдельного анализа.
Во-вторых, если влияние пульсаций существенно, то упорядочение может оказаться нарушенным: мы не знаем, какие индексы  соответствуют данному наблюдаемому
соответствуют данному наблюдаемому  Это затруднение, насколько автору известно, не нашло еще
Это затруднение, насколько автору известно, не нашло еще 
вещения в литературе. Процедуры прямого оценивания оказываются вычислительно нереализуемыми, если они связаны с полным перебором перестановок индексов.
Может создаться впечатление, что эта задача неразрешима, но в данном разделе мы убедимся в том, что можно отыскать удовлетворительное решение, но только не с помощью традиционных методов регрессии.
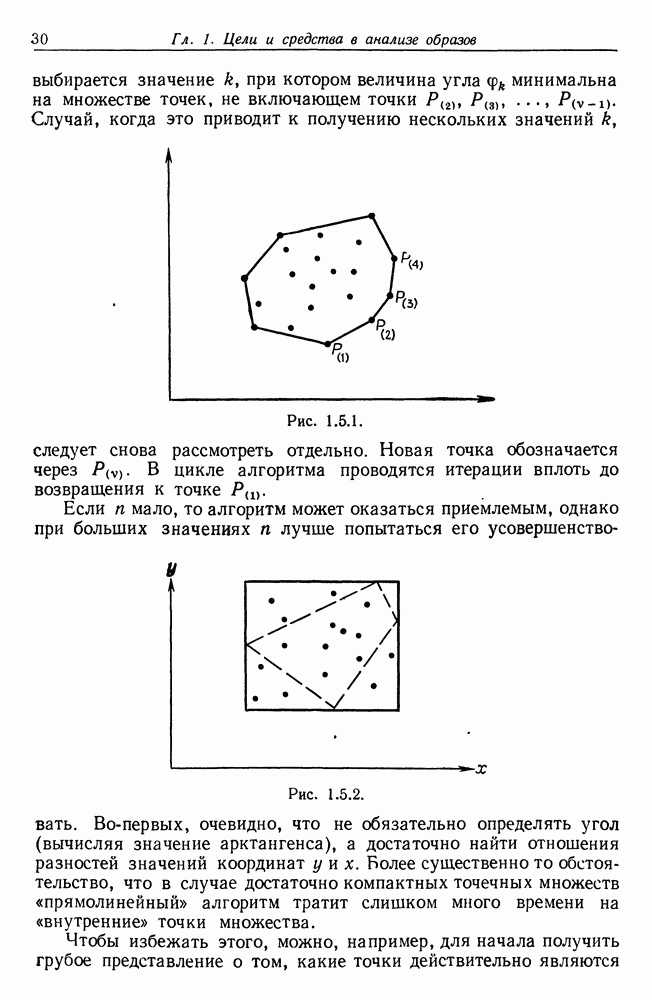
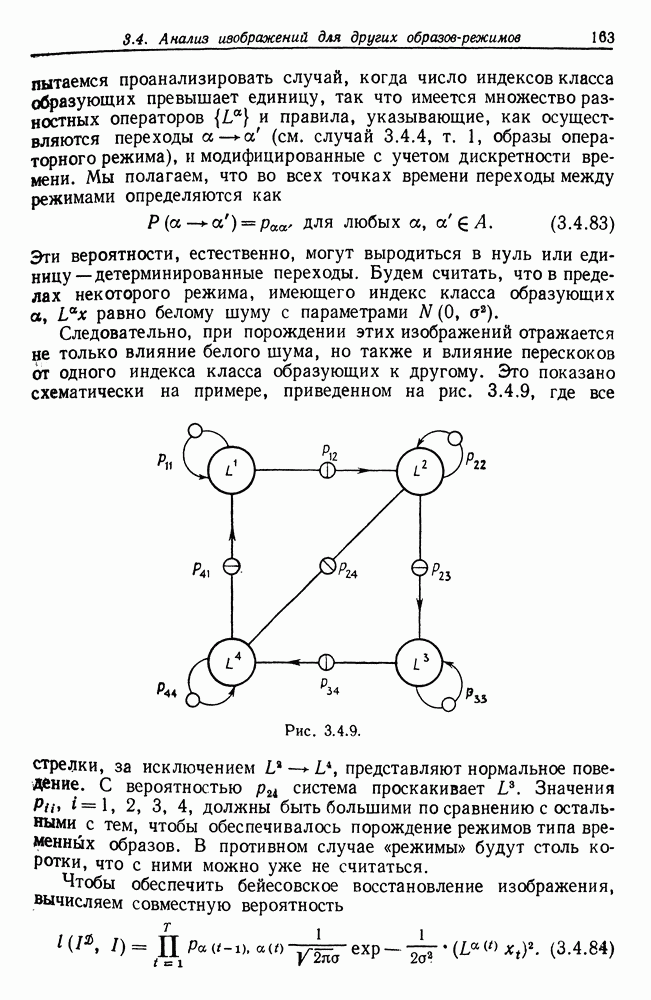
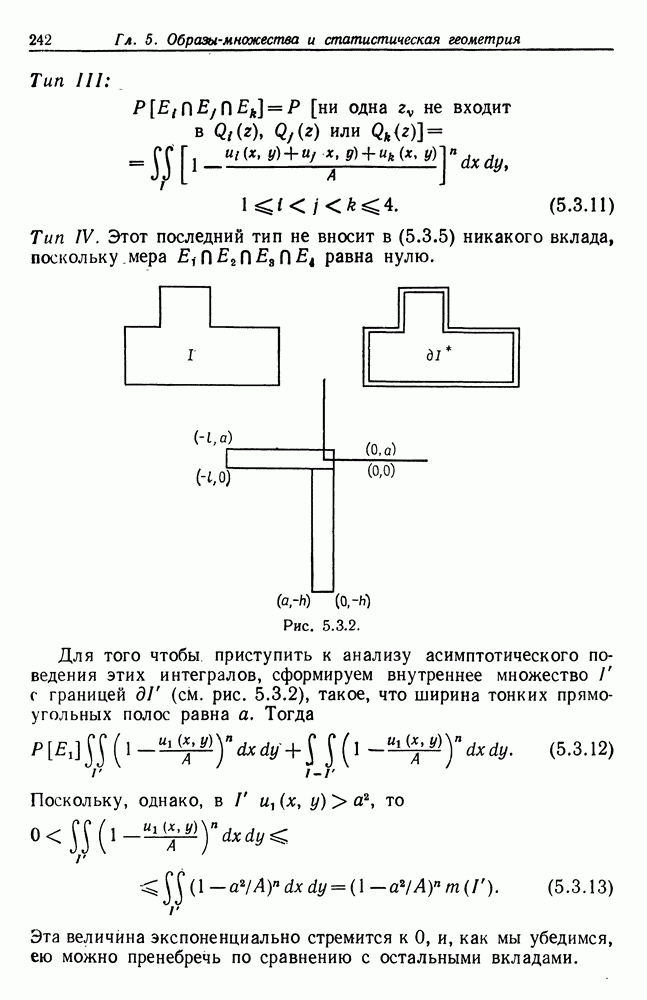
Мы действительно имеем дело с составным механизмом деформаций  причем представляет пульсации, вызванные аддитивным шумом, как в уравнении (4.1.2), а — маскирование, исключающее все наблюдения вне
причем представляет пульсации, вызванные аддитивным шумом, как в уравнении (4.1.2), а — маскирование, исключающее все наблюдения вне 
Наш анализ должен быть инвариантным относительно перестановок: и мы положим в его основу функцию (4.1.4), обладающую сходством с фурье-анализом. Однако на самом деле это не есть фурье-анализ стандартного типа: отметим, что тригонометрические функции при наблюдениях не перемножаются — вместо этого они появляются в показателе степени.
При анализе должен учитываться также и эффект маскирования, и для этого будет применен специально разработанный метод.
Мы начнем с простейшего случая, когда опорное пространство — ось действительных чисел, а шум — гауссов. Одномерный случай в действительности представляет незначительный интерес, так как его можно проанализировать более прямым способом (см. ниже). Будет поучительно, однако, рассмотреть сначала этот случай и выяснить, какого типа анализ необходим, а затем распространить его на двумерную задачу, которая собственно и представляет интерес.
Деформированное изображение представляет собой в данном случае множество точек:

где  — интервал
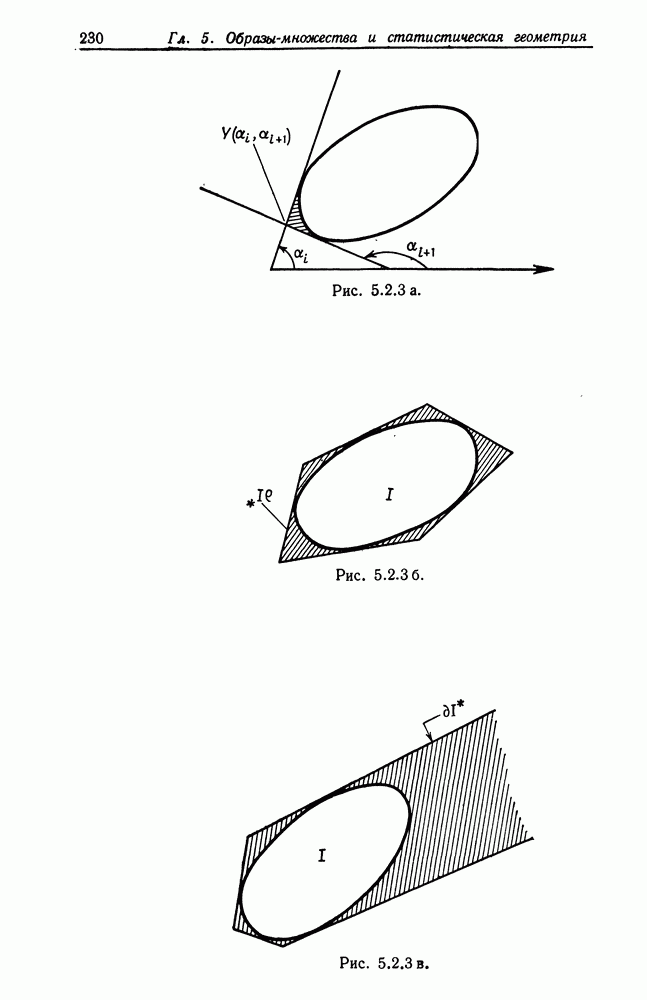
— интервал  Как указывалось выше, механизм деформации
Как указывалось выше, механизм деформации  состоит из
состоит из  аддитивного шума и — экранировки пространства, окружающего Разумеется, число наблюдаемых точек заранее неизвестно. Мы принимаем допущение о том, что
аддитивного шума и — экранировки пространства, окружающего Разумеется, число наблюдаемых точек заранее неизвестно. Мы принимаем допущение о том, что  но результаты можно распространить на случай шумов, обладающих распределениями более общего вида.
но результаты можно распространить на случай шумов, обладающих распределениями более общего вида.
Сформируем «преобразование Фурье» по Бартлетту (1964) (см. также Бартлетт (1975):

Нам будет удобно реализовать анализ в комплексной форме.
Математическое ожидание  определяется как
определяется как

здесь мы положили  что будет скомпенсировано позже умножением на
что будет скомпенсировано позже умножением на  Введем теперь функцию
Введем теперь функцию

Благодаря равномерной сходимости (4.1.6) функция  непрерывна; кроме того, она положительная и периодическая с периодом
непрерывна; кроме того, она положительная и периодическая с периодом  . Тогда
. Тогда

и, введя абсолютно сходящийся ряд Фурье

можно записать, что

при этом случай, когда знаменатель равен нулю, интерпретируется обычным образом.
Теперь мы должны выделить случай, когда  -это
-это  кратное
кратное  тогда
тогда

Отметим, что если пользоваться определением  (4.1.8), то
(4.1.8), то

Это означает, что  убывая, стремится к нулю чрезвычайно быстро при стремлении
убывая, стремится к нулю чрезвычайно быстро при стремлении  к бесконечности. Если же, с другой стороны, А, не есть кратное
к бесконечности. Если же, с другой стороны, А, не есть кратное  то сумма в (4.1.9) стремится
то сумма в (4.1.9) стремится
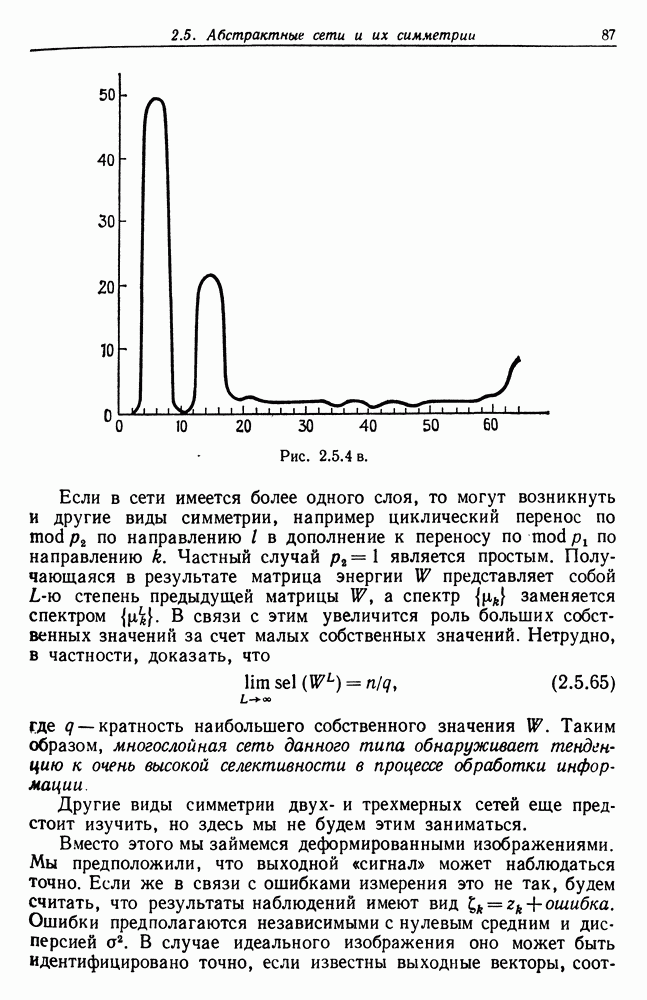
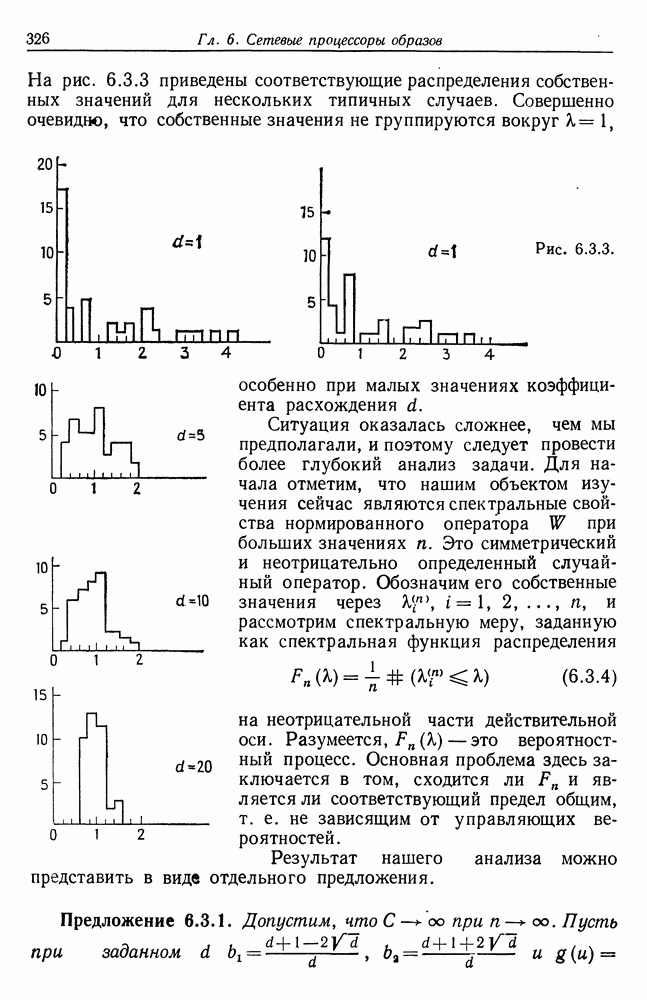
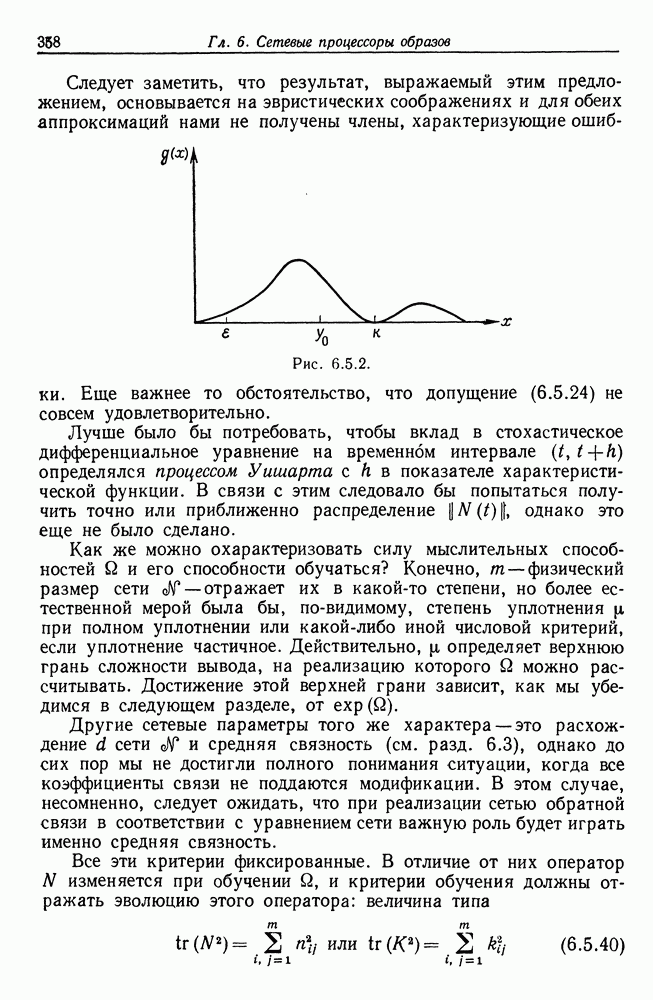
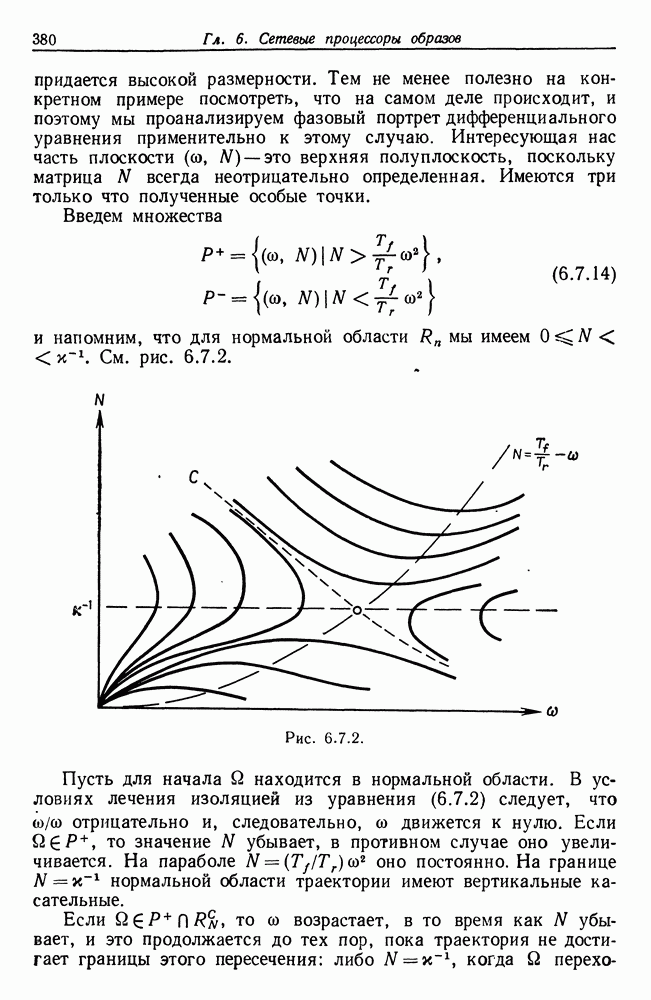
к нулю. Следовательно, функция математического ожидания  будет представлена графиком типа приведенного на рис. 4.1.1.
будет представлена графиком типа приведенного на рис. 4.1.1.

Рис. 4.1.1.
Теперь займемся оцениванием дисперсии:

Вклад членов  при определяем как
при определяем как

так как лишь при  и они вносят вклад в
и они вносят вклад в 
Далее следует просуммировать (4.1.13) по всем  что дает в результате
что дает в результате

учитывая только, что (4.1.13) несправедливо при  Поэтому необходимо вычесть члены вида (4.1.13) для всех
Поэтому необходимо вычесть члены вида (4.1.13) для всех  и добавить правильные выражения. Сделав это, получаем следующее:
и добавить правильные выражения. Сделав это, получаем следующее:

С использованием (4.1.7) и (4.1.12) данное выражение удается ввести к следующему:

поскольку

и мы ввели

— периодическую непрерывную и положительную функцию.
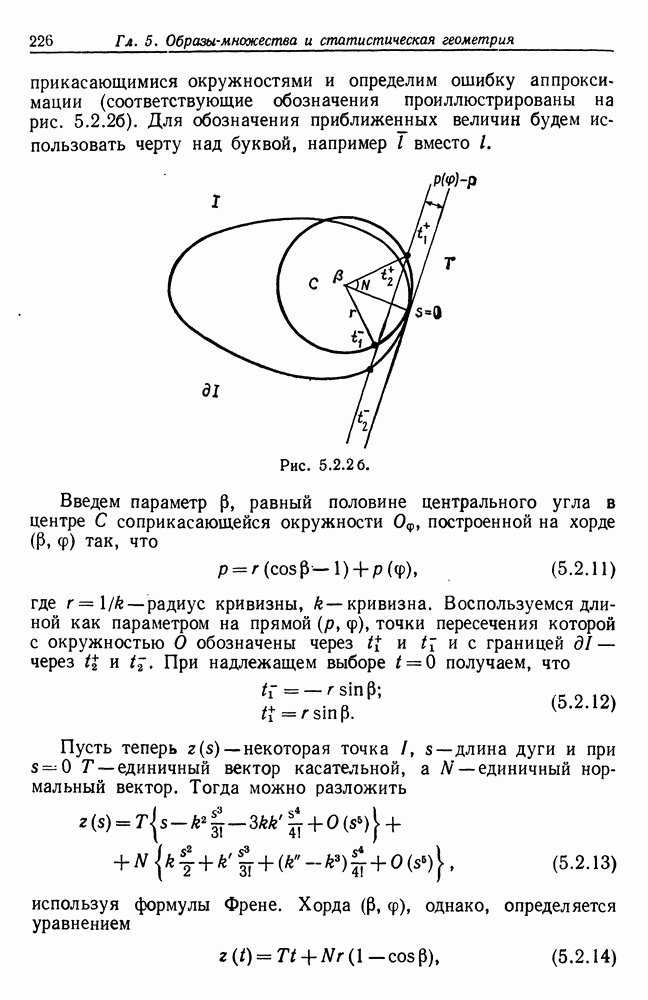
Покажем, что  стремится к пределу при
стремится к пределу при  Очевидно, что
Очевидно, что

Для второго интеграла в (4.1.16) можно, не учитывая один М множителей  знаменателя, записать, что
знаменателя, записать, что

где использована замена переменных

а множитель 2 в знаменателе порождается якобианом преобразования (4.1.21). Интервал интегрирования имеет вид

так что  при фиксированных
при фиксированных  Тогда на основании сходимости мажоранты в качестве предела (4.1.20) получаем, что
Тогда на основании сходимости мажоранты в качестве предела (4.1.20) получаем, что

Но из (4.1.18) следует, что

Объединяя последнее выражение  (4.1.16), получаем, что
(4.1.16), получаем, что

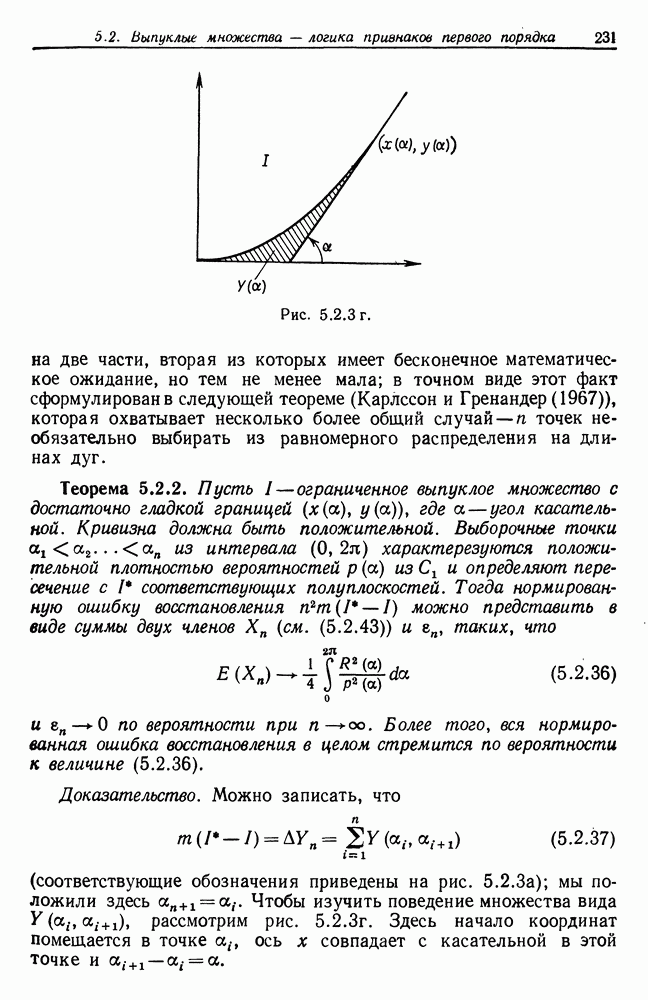
Это означает, что мы доказали следующую теорему.
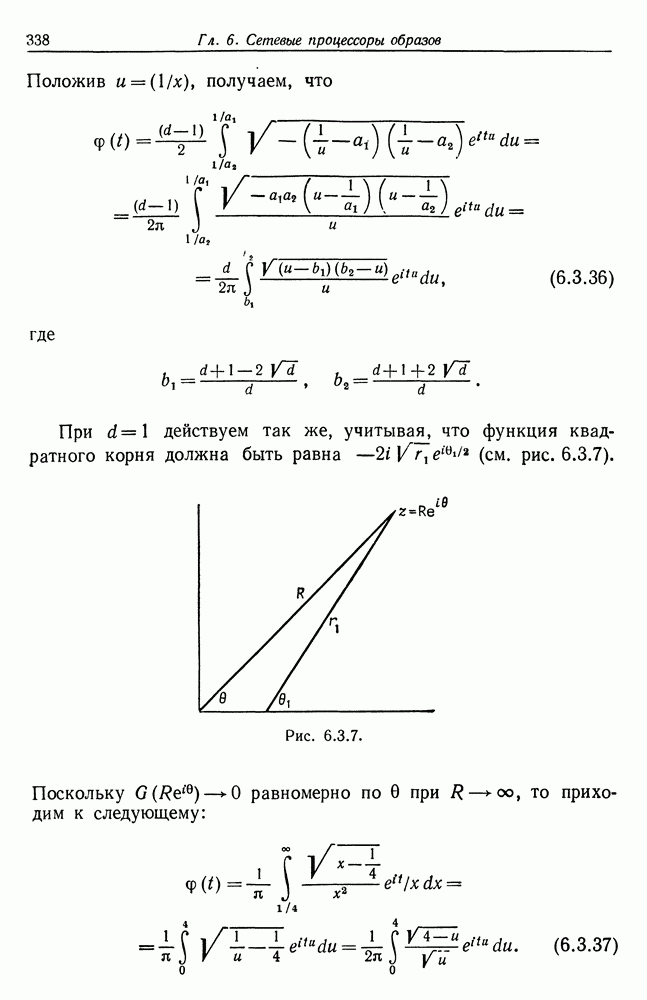
Теорема 4.1.1. Для восстановления идеального изображения решетки по деформированному изображению (4.1.3) мы строим функцию  (4.1.4). Тогда при
(4.1.4). Тогда при  справедливо следующее:
справедливо следующее:

и

Для дисперсии справедливо соотношение:

Важность данной теоремы определяется тем обстоятельством, что оно может служить нам средством, позволяющим избавиться от осложнений, возникающих в связи с маскирующим эффектом второго механизма деформации  и отсутствием сведений об «истинном» упорядочении точек в
и отсутствием сведений об «истинном» упорядочении точек в  Автору известно (Маклур (1975)), что ковариации также асимптотически стремятся к нулю в соответствии с (4.1.28).
Автору известно (Маклур (1975)), что ковариации также асимптотически стремятся к нулю в соответствии с (4.1.28).
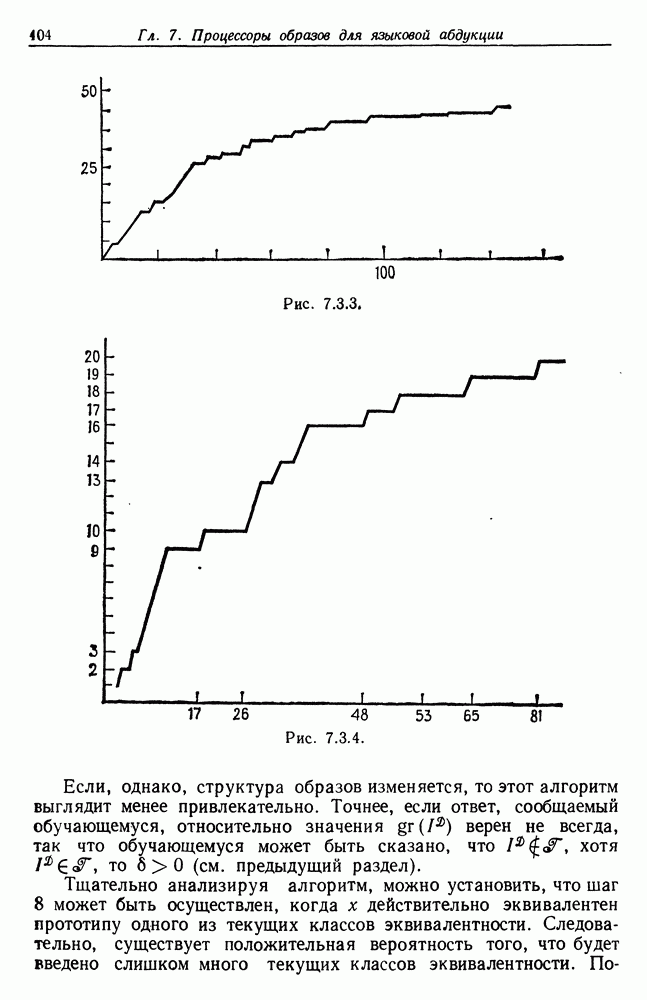
Кроме того, данный метод при правильном применении показывает, как можно обнаруживать отклонения от постулируемой модели. Мы обсудим это позже.
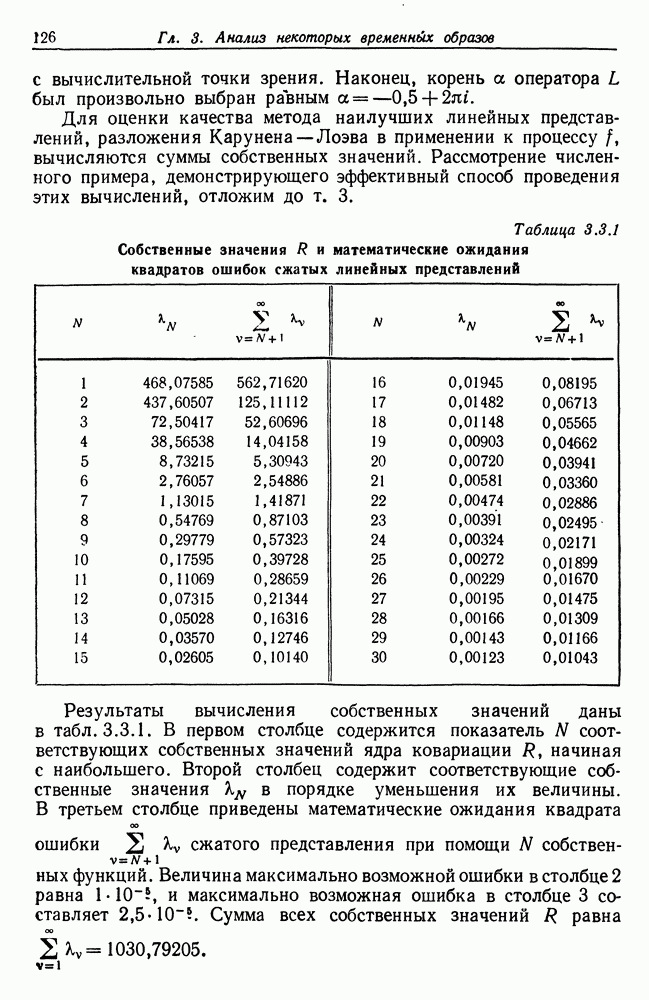
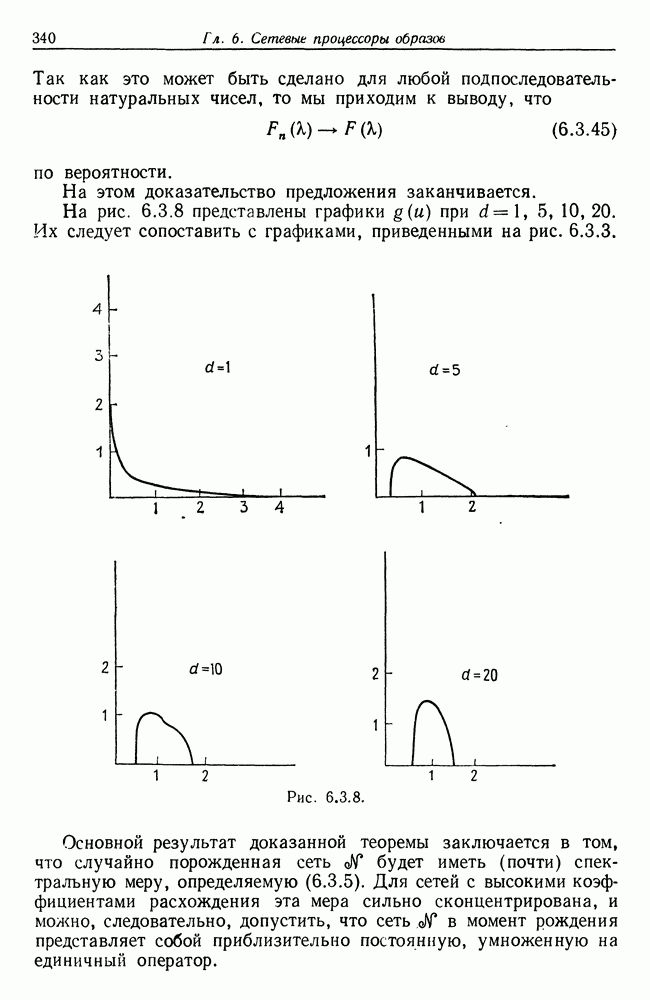
Нужно вычислить функцию  для довольно большого набора значений
для довольно большого набора значений  , зависящего от того, какими априорными сведениями относительно идеальной решетки мы располагаем. Затем следует построить графики действительной и мнимой частей
, зависящего от того, какими априорными сведениями относительно идеальной решетки мы располагаем. Затем следует построить графики действительной и мнимой частей  и попытаться определить максимумы
и попытаться определить максимумы  особенно первый, который
особенно первый, который
должен быть близок к  если длина
если длина  достаточно велика. Величины нескольких первых максимумов позволяют нам также получить некоторое представление о
достаточно велика. Величины нескольких первых максимумов позволяют нам также получить некоторое представление о  , исходя из характера убывания ординат (см. (4.1.26)). Могут оказаться полезными некоторые процедуры сглаживания, но здесь мы не будем обсуждать эту возможность.
, исходя из характера убывания ординат (см. (4.1.26)). Могут оказаться полезными некоторые процедуры сглаживания, но здесь мы не будем обсуждать эту возможность.
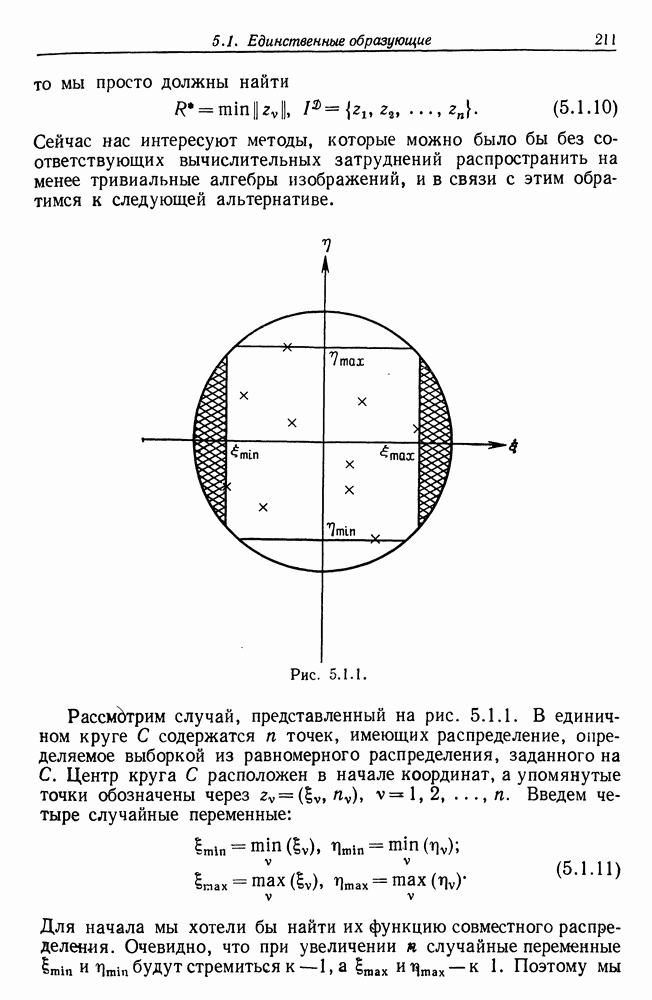
Допустим теперь, что наблюдаются образы, которые порождены не деформацией линейной решетки, а имеют более хаотический характер. Предположим для начала, что пуассоновский процесс с интенсивностью  порождает множество
порождает множество  Тогда получаем, что
Тогда получаем, что

Эта величина стремится к нулю при любом ненулевом значении  Следовательно, ее поведение резко отличается от наблюдаемого в случае изображений решеток.
Следовательно, ее поведение резко отличается от наблюдаемого в случае изображений решеток.
Дисперсию можно получить также, если записать

где  считающий процесс, соответствующий пуассоновскому процессу. Поскольку
считающий процесс, соответствующий пуассоновскому процессу. Поскольку  ортогональный процесс, для которого
ортогональный процесс, для которого  то
то

Эта величина стремится к нулю при  Изучение
Изучение  должно помочь нам при решении вопроса о том, соответствует ли имеющимся данным образ регулярной решетки или более хаотическая пуассоновская модель.
должно помочь нам при решении вопроса о том, соответствует ли имеющимся данным образ регулярной решетки или более хаотическая пуассоновская модель.
В более общем случае для стационарного процесса восстановления мы получаем аналогичный результат для  . В самом деле, пусть распределение промежуточных интервалов
. В самом деле, пусть распределение промежуточных интервалов  не арифметрическое и характеризуется математическим ожиданием
не арифметрическое и характеризуется математическим ожиданием  так что расстояние от начала до первой наблюдаемой точки определяется как
так что расстояние от начала до первой наблюдаемой точки определяется как

Тогда

Воспользовавшись классическим результатом (см. Феллер (1957), т. 2, с. 354), получаем следующее:

поэтому

точно так же, как и для пуассоновского процесса.
В данном случае функцию дисперсии мы не получили. Теперь посмотрим, как можно перейти к негауссовому случаю. Вместо предположения о нормальности шума вводится весьма общее допущение о том, что члены, представляющие в (4.1.3) шум, характеризуются функцией распределения  которая предполагается четной и интегрируемой с квадратом. Эти условия не являются необходимыми, но упрощают рассмотрение. Введем функцию
которая предполагается четной и интегрируемой с квадратом. Эти условия не являются необходимыми, но упрощают рассмотрение. Введем функцию

этот ряд сходится почти везде. Очевидно, что функция неотрицательная и периодическая с периодом Теперь мы можем проанализировать этот случай так же, как и выше, опуская детали, представляющие собой непосредственные обобщения. Вместо (4.1.7) получаем следующее:

и при

если к не есть кратное  это выражение стремится к нулю. В противном случае
это выражение стремится к нулю. В противном случае  и
и

Для дисперсии, аналогично уже рассмотренному частному цафчаю, получаем следующее:

где

Сделав замену переменных, записываем второй интеграл в (4.1.40) как

Здесь

при  аналогичное выражение справедливо для отрицателных
аналогичное выражение справедливо для отрицателных  . Благодаря периодичности для любого
. Благодаря периодичности для любого 

Кроме того, поскольку функция распределения  положительна,
положительна,  мажорируется кратным ядра
мажорируется кратным ядра  Однако К принадлежит поэтому
Однако К принадлежит поэтому

 преобразование Фурье от
преобразование Фурье от  обозначить через
обозначить через  то мы прижим к следующей теореме.
то мы прижим к следующей теореме.
Теорема 4.1.2. Если шум характеризуется четной и интегрируемой с квадратом функцией распределения то

кроме того,

Пусть теперь идеальное изображение состоит из точек:

где фаза а и векторы базиса и  принадлежат
принадлежат  Эти векторы, естественно, не определяются решеткой однозначно. Введем также обратную решетку
Эти векторы, естественно, не определяются решеткой однозначно. Введем также обратную решетку  с базисными векторами
с базисными векторами  так, что
так, что

Деформированное изображение снова вводится с помощью но члены, представляющие шум, являются в данном случае векторами на плоскости и характеризуются двумерной функцией распределения  определяет маскирование за пределами квадрата
определяет маскирование за пределами квадрата  со стороной
со стороной  Введем
Введем

где X — фиксированный вектор на плоскости. Для математического ожидания имеем следующее:

Здесь

Этот ряд почти везде сходится к неотрицательной функции с периодами и  , принадлежащей
, принадлежащей  Теперь снова свернем
Теперь снова свернем  на одном из фундаментальных параллелограммов Р исходной решетки, учитывая, что
на одном из фундаментальных параллелограммов Р исходной решетки, учитывая, что

где и  так что
так что

если  представляется через параметры обратной решетки
представляется через параметры обратной решетки 

то означает, что при суммировании геометрического ряда по параллелограммам, принадлежащим  (сравните с (4.1.38)),
(сравните с (4.1.38)),

и, следовательно, если  то
то

Если  так что
так что  где
где  целые,
целые, 

где  — угол между двумя базисными векторами в исходной решетке.
— угол между двумя базисными векторами в исходной решетке.
Итак, для дисперсии имеем следующее:

где u и v принадлежат  , а
, а

Эти выражения аналогичны выражениям (4.1.40) и (4.1.41) и, проводя анализ подобно тому, как это было сделано выше, приходим к непосредственному аналогу выражения (4.1.45).
Теорема 4.1.3. Для двумерной решетки с базисными векторами и и обратной решетки  (см. (4.1.49)) среднее функции (4.1.50) определяется асимптотически как
(см. (4.1.49)) среднее функции (4.1.50) определяется асимптотически как

Асимптотическая дисперсия равна

где Р — фундаментальный параллелограмм исходной решетки, а  двумерное преобразование Фурье
двумерное преобразование Фурье 
В приложениях значение фазы а неизвестно, но так как это влияет лишь на  то при помощи умножения на множитель
то при помощи умножения на множитель  абсолютная величина которого равна единице, мы получаем возможность работать с
абсолютная величина которого равна единице, мы получаем возможность работать с  и отыскивать наибольшие локальные максимумы. Рассмотрим первый локальный максимум
и отыскивать наибольшие локальные максимумы. Рассмотрим первый локальный максимум  в (4.1.46) и обратимся для начала к одномерному случаю.
в (4.1.46) и обратимся для начала к одномерному случаю.
Можно ожидать, что значение ординаты приближенно равно (при  )
)

Это значение следует сравнить с приближенным средним квадратическим отклонением

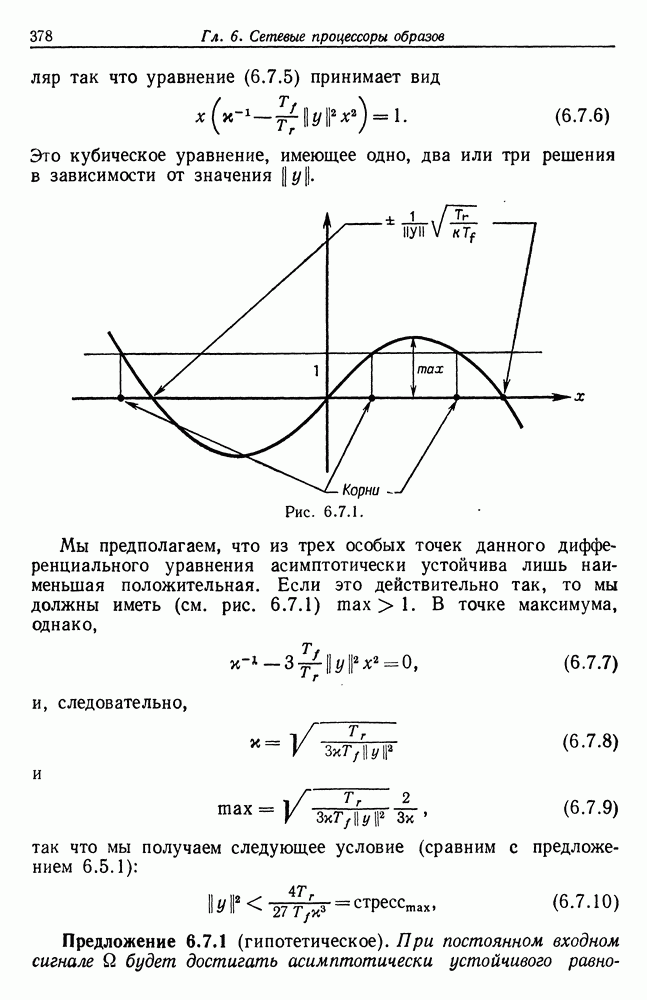
Если (4.1.64) по порядку совпадает с (4.1.63) или превышает его, то мы не можем рассчитывать на обнаружение максимума. Такая ситуация возникнет, если

откуда следует, что

При  мы имеем
мы имеем

и неравенство (4.1.66) принимает вид

Если, с другой стороны,  то
то

Следовательно, учитывая (4.1.66), можно считать допустимыми такие значения  при которых справедливо неравенство
при которых справедливо неравенство

Если  мало, то это условие, конечно, приводит к малым значениям
мало, то это условие, конечно, приводит к малым значениям  однако, когда
однако, когда  достигает значения 1/2, это условие
достигает значения 1/2, это условие
«взрывается». При  любой объем выборки оказывается недостаточным для принятия решения об образе. Причина, совершенно очевидно, заключается в том, что функция
любой объем выборки оказывается недостаточным для принятия решения об образе. Причина, совершенно очевидно, заключается в том, что функция  в данном случае тождественно равна постоянной.
в данном случае тождественно равна постоянной.
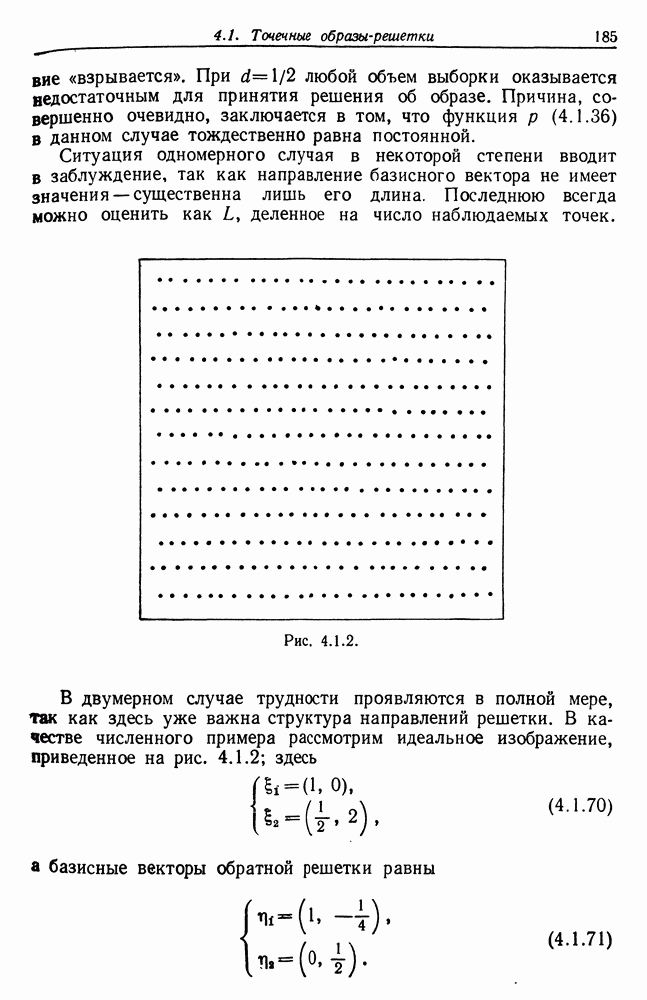
Ситуация одномерного случая в некоторой степени вводит в заблуждение, так как направление базисного вектора не имеет значения — существенна лишь его длина. Последнюю всегда можно оценить как  деленное на число наблюдаемых точек.
деленное на число наблюдаемых точек.

Рис. 4.1.2.
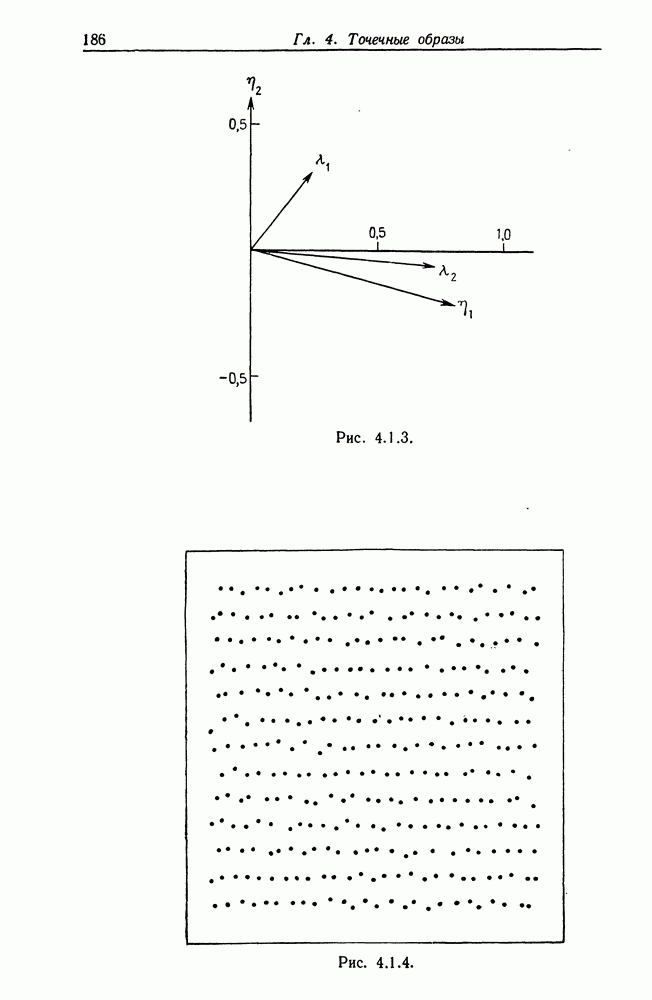
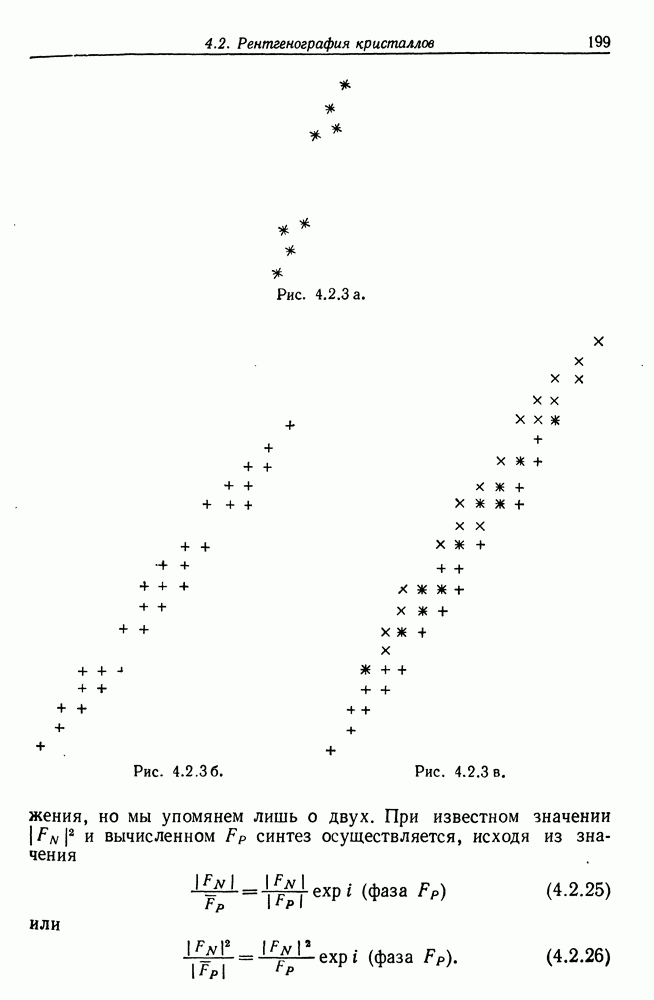
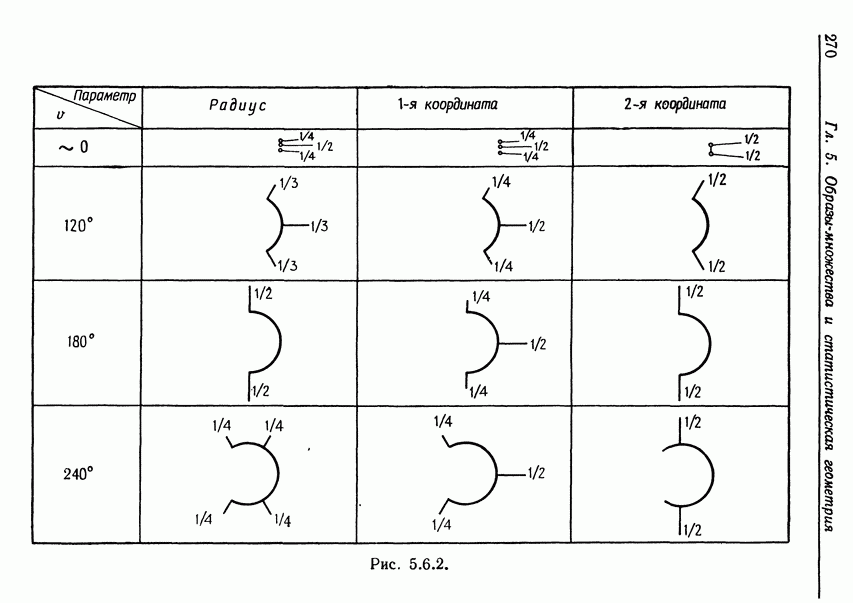
В двумерном случае трудности проявляются в полной мере, так как здесь уже важна структура направлений решетки. В качестве численного примера рассмотрим идеальное изображение, приведенное на рис. 4.1.2; здесь

а базисные векторы обратной решетки равны


(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
Вычислим значение  для кратных векторов и
для кратных векторов и  и для векторов
и для векторов

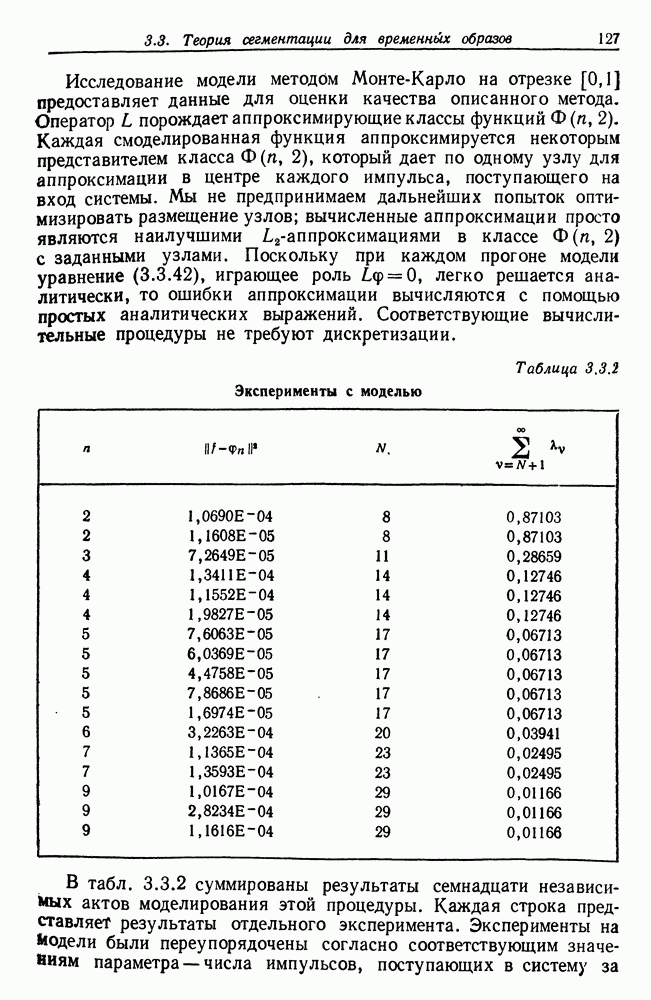
представленных на рис. 4.1.3. Известно, что с шумом, который характеризуется прямоугольным распределением, работать трудно, и именно поэтому мы используем его в данном случае.
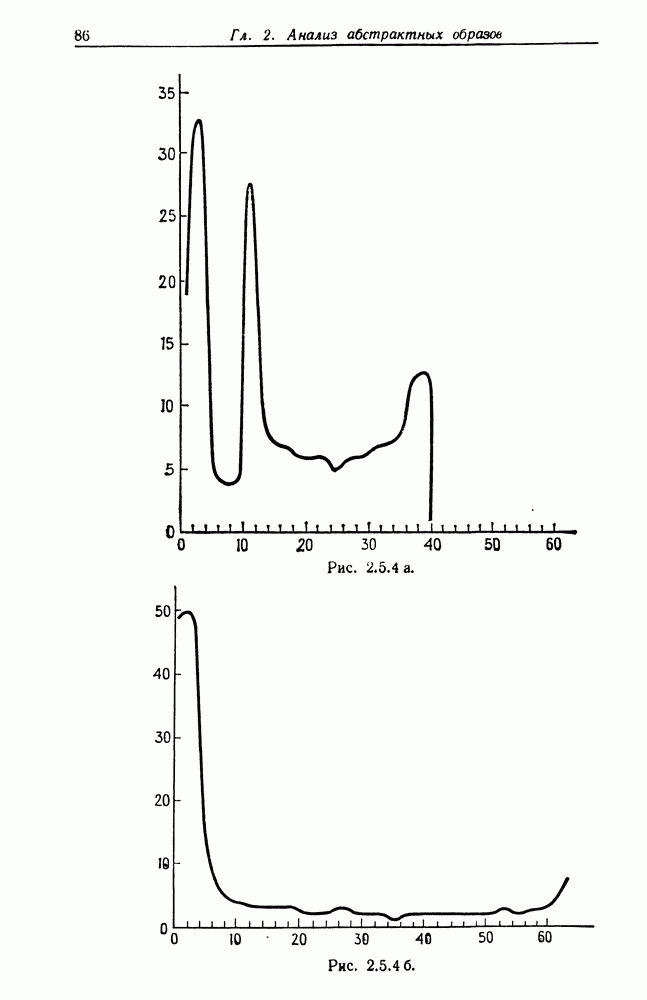
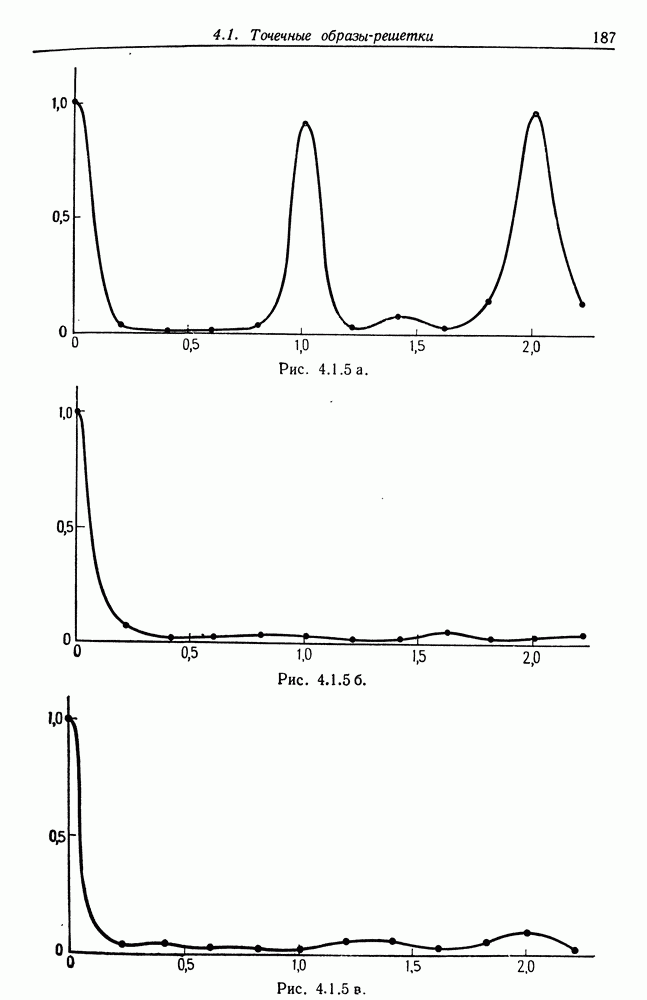
Деформированная решетка, приведенная на рис. 4.1.4, дает графики  соответствующие ориентациям
соответствующие ориентациям  Эти графики показав на рис. 4.1.5 а, б и в соответственно.
Эти графики показав на рис. 4.1.5 а, б и в соответственно.
Мы видим, что умеренно деформированная решетка, приведенная на рис. 4.1.4, приводит к появлению функций имеющих вполне определенный максимум около 1 в случае  , но не имеющих его в случаях
, но не имеющих его в случаях  и
и  . Это именно тот тип поведения, который нас инресовал.
. Это именно тот тип поведения, который нас инресовал.
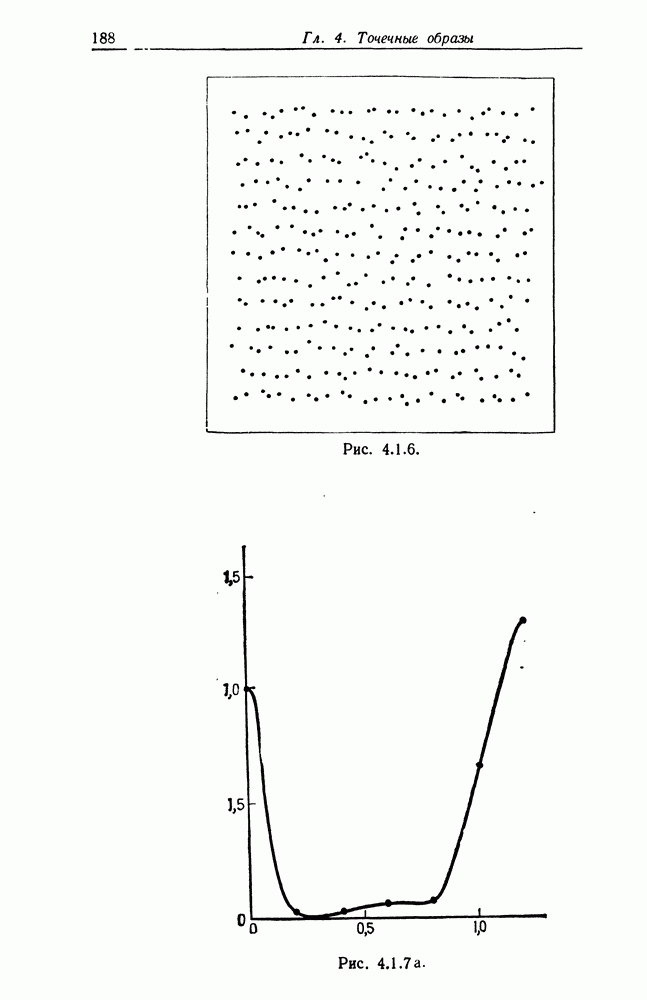
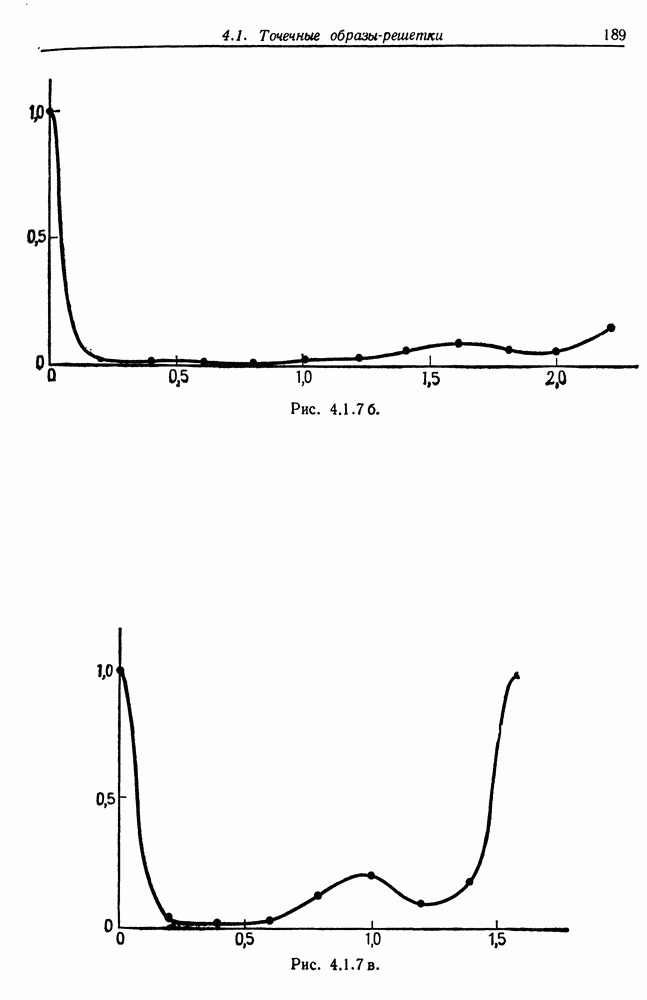
Что касается хаотической картины типа представленной на рис. 4.1.6, где изображена сильно деформированная решетка, то с функцией  соответствующей ориентации и имеющей максимум вблизи 1 (см. рис. 4.1.7а), все в порядке: точно так же все в порядке и с функцией соответствующей ориентации
соответствующей ориентации и имеющей максимум вблизи 1 (см. рис. 4.1.7а), все в порядке: точно так же все в порядке и с функцией соответствующей ориентации  и не имеющей явных максимумов (см. рис. 4.1.76). С другой стороны, показанный на рис. 4.1.7в график, соответствующий ориентации
и не имеющей явных максимумов (см. рис. 4.1.76). С другой стороны, показанный на рис. 4.1.7в график, соответствующий ориентации  рмеет слабо выраженный максимум в точке 1,0 и более выраженный максимум в точке 1,5. Следовательно, деформации оказались слишком велики для того, чтобы оказалось возможным восстановление с хорошим качеством при выборке заданного размера.
рмеет слабо выраженный максимум в точке 1,0 и более выраженный максимум в точке 1,5. Следовательно, деформации оказались слишком велики для того, чтобы оказалось возможным восстановление с хорошим качеством при выборке заданного размера.
Судя по всему» данный метод восстановления позволяет справляться с умеренными деформациями. При сильных деформациях могут возникать ложные максимумы. Аналитические выражения для математического ожидания и дисперсии позволяют нам судить о том,  этого можно ожидать.
этого можно ожидать.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому переводу
- Введение
- Глава 1. Цели и средства в анализе образов
- 1.2. Свойства операторов изображений
- 1.3. Критерии качества для операторов изображения
- 1.4. Выбор операторов изображения
- 1.5. Алгоритмы анализа образов
- Глава 2. Анализ абстрактных образов
- 2.2. Синтаксические деформации
- 2.3. Измерение синтаксического стиля
- 2.4. Алгебры изображений отношений и их преобразование
- 2.5. Абстрактные сети и их симметрии
- Глава 3. Анализ некоторых временных образов
- 3.2. Образы числовых последовательностей
- 3.3. Теория сегментации для временных образов
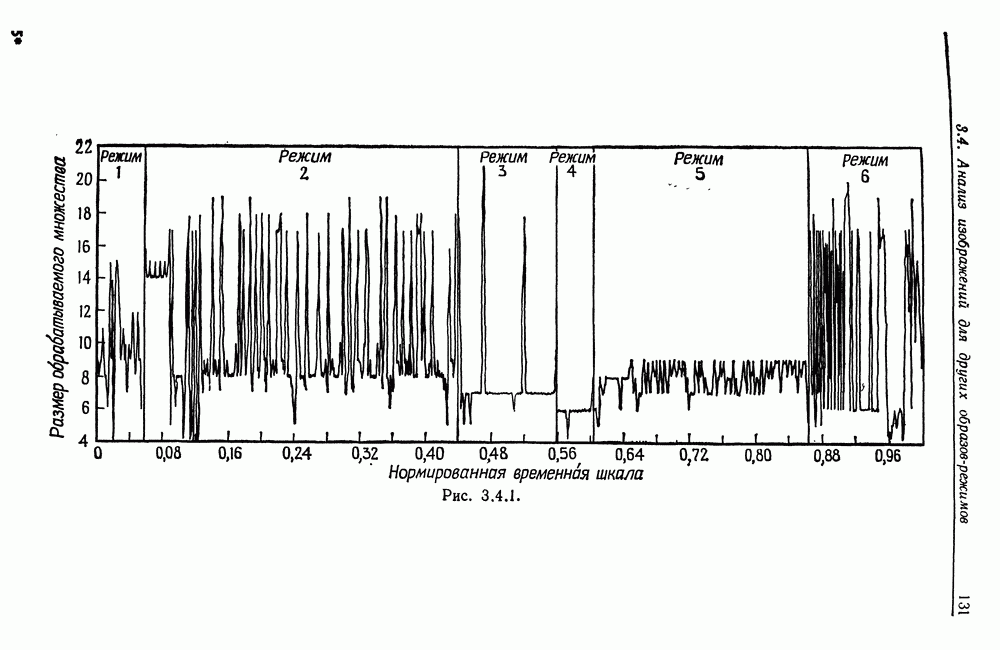
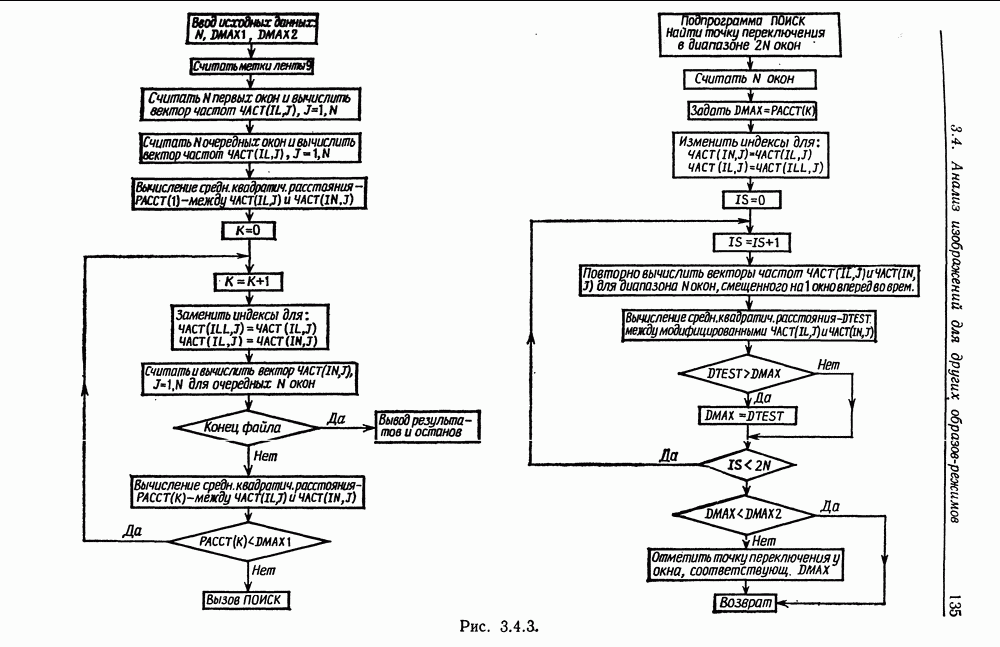
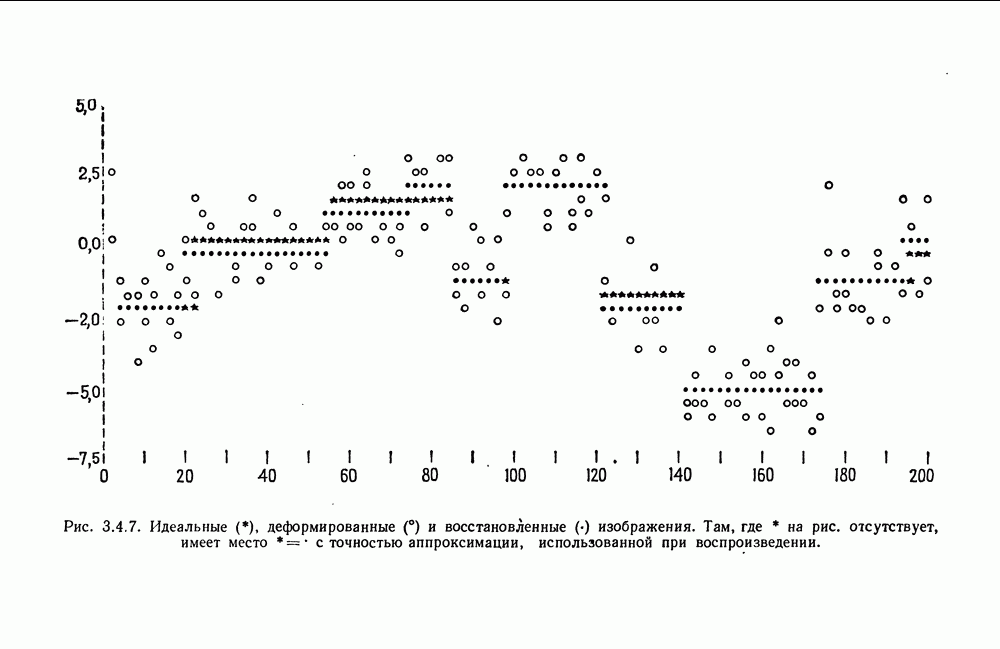
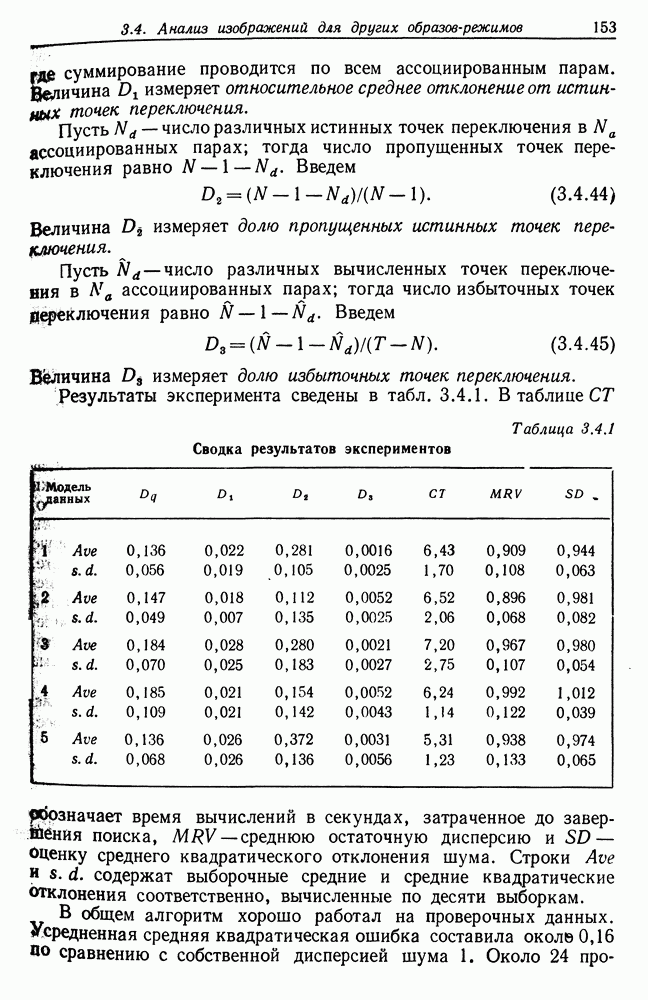
- 3.4. Анализ изображений для других образов-режимов
- Глава 4. Точечные образы
- 4.2. Рентгенография кристаллов
- 4.3. Отмеченные точки
- Глава 5. Образы-множества и статистическая геометрия
- 5.2. Выпуклые множества — логика признаков первого порядка
- 5.3. Логика признаков второго порядка
- 5.4. Логика признаков бесконечного порядка
- 5.5. Один результат, относящийся к аппроксимации изображения
- 5.6. Зондирование границ
- 5.7. Немного стереологии
- 5.8. Биологическая форма
- Глава 6. Сетевые процессоры образов
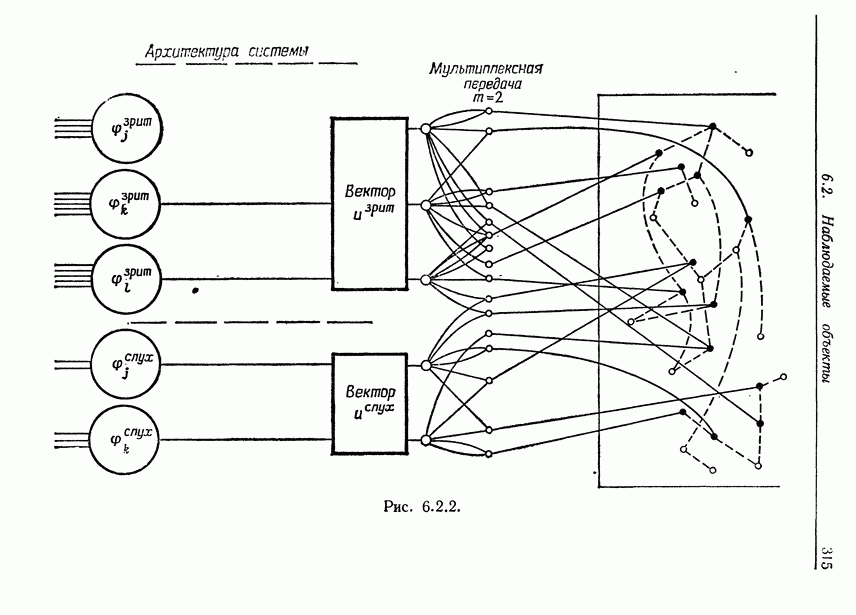
- 6.2. Наблюдаемые объекты
- 6.3. Исходная сеть
- 6.4. Действующая сеть
- 6.5. Обучающаяся сеть
- 6.6. Вывод алгебры изображений
- 6.7. Сеть, функционирующая неверно
- Глава 7. Процессоры образов для языковой абдукции
- 7.2. Абдукция некоторых языковых образов
- 7.3. Разбиение слов на классы
- 7.4. Разбиение на классы слов посредством сетей
- 7.5. Обнаружение синтаксических переменных
- Примечания
- Список литературы