| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
2.1. Введение
Наиболее прямой способ решения кластерной проблемы заключается в полном переборе всех возможных разбиений на кластеры и отыскании такого разбиения, которое ведет к оптимальному (минимальному) значению целевой функции. Однако такая процедура практически невыполнима за исключением тех случаев, когда  (число объектов) и
(число объектов) и  (число кластеров) не велико. Этот способ называют кластеризацией с помощью полного перебора. Например, если
(число кластеров) не велико. Этот способ называют кластеризацией с помощью полного перебора. Например, если  , то число возможных разбиений равно 1701; другими словами, существует 1701 способов разбить 8 объектов на 4 группы. Число разбиений обозначается через
, то число возможных разбиений равно 1701; другими словами, существует 1701 способов разбить 8 объектов на 4 группы. Число разбиений обозначается через  и называется числом Стирлинга второго рода. Оно может быть вычислено по формулам, которые будут нами получены в следующем параграфе. Данная глава лишь частично имеет отношение к проблеме кластеризации и поэтому при первом чтении может быть опущена.
и называется числом Стирлинга второго рода. Оно может быть вычислено по формулам, которые будут нами получены в следующем параграфе. Данная глава лишь частично имеет отношение к проблеме кластеризации и поэтому при первом чтении может быть опущена.
2.2. Число разбиений n объектов на m непустых подмножеств
Процесс разбиения множества из  объектов на
объектов на  непустых подмножеств можно представить как распределение
непустых подмножеств можно представить как распределение  различных шаров по
различных шаров по  одинаковым урнам, ни одна из которых не должна остаться пустой.
одинаковым урнам, ни одна из которых не должна остаться пустой.
Обозначим число таких разбиений через w. Тогда  есть число всех возможных размещений
есть число всех возможных размещений  различных
различных
объектов по  разным урнам (ни одна из которых не остается пустой).
разным урнам (ни одна из которых не остается пустой).
Один из наиболее эффективных методов решения задач, связанных с этой проблемой ( т. е. разбиение  объектов на
объектов на  непустых подмножеств), основан на методе производящих функций.
непустых подмножеств), основан на методе производящих функций.
Рассмотрим функцию

Раскрывая скобки, мы получим полином от t, в котором коэффициент при  представляет собой сумму произведений всех комбинаций по k множителей из
представляет собой сумму произведений всех комбинаций по k множителей из  .
.
Если, далее,  , то коэффициент при
, то коэффициент при  равен
равен  — числу способов отбора (сочетаний) k объектов из п. Таким образом, последовательность Си можно получить при помощи производящей функции
— числу способов отбора (сочетаний) k объектов из п. Таким образом, последовательность Си можно получить при помощи производящей функции

- Этой же функцией можно воспользоваться в случае, когда порядок элементов в группе существен:

здесь  (число размещений).
(число размещений).
Функция (2.2) называется экспоненциальной производящей функцией. Если допускаются повторения, то для подсчета результата перебора служит ряд,  член которого равен
член которого равен  , где k — число повторений. Таким образом, если число повторений не ограничено, то счетчиком для каждого объекта служит ряд
, где k — число повторений. Таким образом, если число повторений не ограничено, то счетчиком для каждого объекта служит ряд

Следовательно, число различных перестановок  различных объектов в группе из k объектов равно коэффициенту при
различных объектов в группе из k объектов равно коэффициенту при  в производящей функции
в производящей функции

Как видим, это число равно  . Если число повторений не ограничено и каждый объект повторяется не менее одного раза, то счетчиком будет
. Если число повторений не ограничено и каждый объект повторяется не менее одного раза, то счетчиком будет

Тогда число перестановок определяется формулой

Производящая функция, применяемая для получения числа способов распределения  различных шаров по
различных шаров по  различным урнам (порядок расположения шаров в урнах несуществен), при котором урна i содержит
различным урнам (порядок расположения шаров в урнах несуществен), при котором урна i содержит  шаров,
шаров,  задается как
задается как

где суммирование производится по всем  -разбиениям
-разбиениям  (так что
(так что  ). Коэффициент при
). Коэффициент при  равен числу таких распределений
равен числу таких распределений  шаров, при которых урна 1 содержит
шаров, при которых урна 1 содержит  шаров, урна 2 содержит
шаров, урна 2 содержит  , урна
, урна  содержит
содержит  шаров. Таким образом, величина
шаров. Таким образом, величина

есть число способов размещения  шаров в
шаров в  урне,
урне,  .
.
Число способов размещения  различных шаров по
различных шаров по  различным урнам может быть найдено с помощью производящей функции
различным урнам может быть найдено с помощью производящей функции

В этом случае  множитель
множитель

соответствует числу способов размещения шаров в  урне. Раскрывая скобки в (2.7), находим, что коэффициент при
урне. Раскрывая скобки в (2.7), находим, что коэффициент при  равен
равен

где суммирование производится по всем  -разбиениям
-разбиениям  . Таким образом, коэффициент при
. Таким образом, коэффициент при  в (2.7) равен
в (2.7) равен

Как следует из (2.6), число способов размещения  шаров по
шаров по  урнам, при которых
урнам, при которых  урна содержит
урна содержит  шаров
шаров  равно
равно  , так как
, так как  отвечает некоторому частному способу размещения. Полагая в
отвечает некоторому частному способу размещения. Полагая в  получаем, что коэффициент при
получаем, что коэффициент при  в выражении
в выражении

есть число способов размещения  различных шаров по m различным урнам. Однако этот коэффициент равен коэффициенту при
различных шаров по m различным урнам. Однако этот коэффициент равен коэффициенту при  в выражении
в выражении

Отсюда следует, что число возможных размещений  шаров по
шаров по  урнам равно
урнам равно  .
.
Число разбиений множества из  объектов на
объектов на  подмножеств, ни одно из которых не будет пустым, определяется в следующей теореме.
подмножеств, ни одно из которых не будет пустым, определяется в следующей теореме.
Теорема 1.1. Число способов размещения  шаров по
шаров по  урнам (ни одна из урн не будет пустой, а порядок расположения шаров в урне несуществен) равно
урнам (ни одна из урн не будет пустой, а порядок расположения шаров в урне несуществен) равно

Доказательство. Число шаров, содержащихся в  урне, определяется из уравнения
урне, определяется из уравнения

поскольку каждая урна содержит по крайней мере один шар. Соответствующая экспоненциальная производящая функция, которую обозначим через  равна:
равна:

Число способов размещения  шаров по
шаров по  урнам так, чтобы ни одна урна не была пустой, равно коэффициенту при
урнам так, чтобы ни одна урна не была пустой, равно коэффициенту при  и при условии
и при условии  . В этом случае производящая функция (2.9) превращается в
. В этом случае производящая функция (2.9) превращается в

которая совпадает с (2.3). Поэтому

Коэффициент при  равен
равен

что приводит к требуемому результату.
В теореме 1.1  урн предполагаются различными. Однако при разбиении
урн предполагаются различными. Однако при разбиении  объектов на
объектов на  подмножеств, каждое из которых не пусто, порядок подмножеств не играет роли. С учетом теоремы 1.1 отсюда следует, что число разбиений
подмножеств, каждое из которых не пусто, порядок подмножеств не играет роли. С учетом теоремы 1.1 отсюда следует, что число разбиений  объектов на
объектов на  подмножеств равно:
подмножеств равно:

Осталось показать, каким образом числа Стирлинга второго рода связаны с соотношением (2.11).
Числа Стирлинга второго рода возникают при вычислении конечных разностей и связаны с нахождением показателя  в факториальных многочленах. Факториальный многочлен определяется следующим образом:
в факториальных многочленах. Факториальный многочлен определяется следующим образом:

Определение 2.1. Числами Стирлинга второго рода называются числа  удовлетворяющие уравнениям
удовлетворяющие уравнениям

По теореме Ньютона [172, гл. 6] полином  степени
степени  может быть записан в виде:
может быть записан в виде:

где  определяется как
определяется как

Разлагая  по формуле (2.12), получим:
по формуле (2.12), получим:

Из определения  имеем:
имеем:

Осталось показать, что

Для этой цели введем оператор смещения  , где
, где  Пользуясь введенными обозначениями, получим:
Пользуясь введенными обозначениями, получим:

Таким образом, имеем  .
.
Если число подмножеств разбиения  известно заранее, то общее число разбиений
известно заранее, то общее число разбиений  объектов на
объектов на  кластеров равно
кластеров равно  . Если же значение
. Если же значение  неизвестно, то общее число всех разбиений равно
неизвестно, то общее число всех разбиений равно

| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
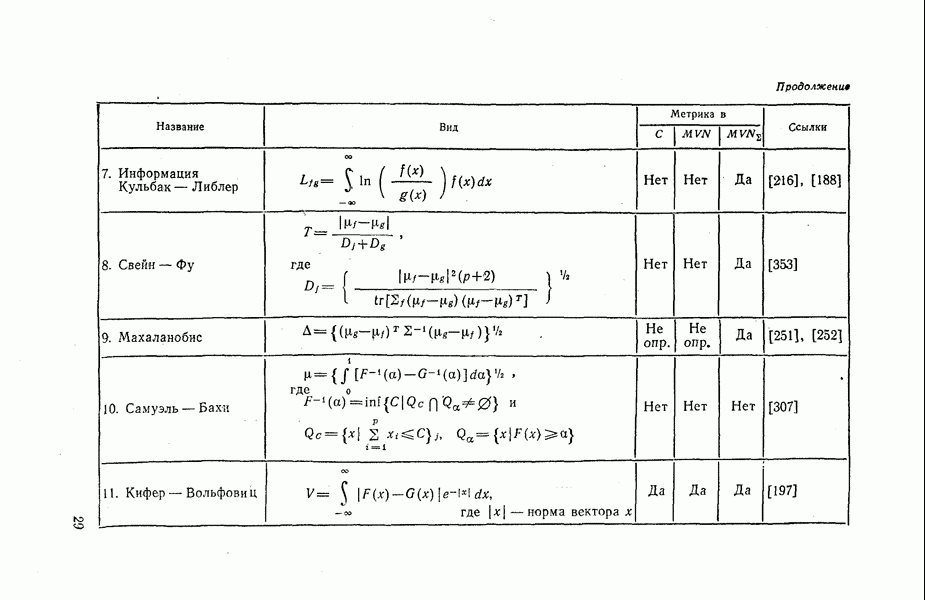
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
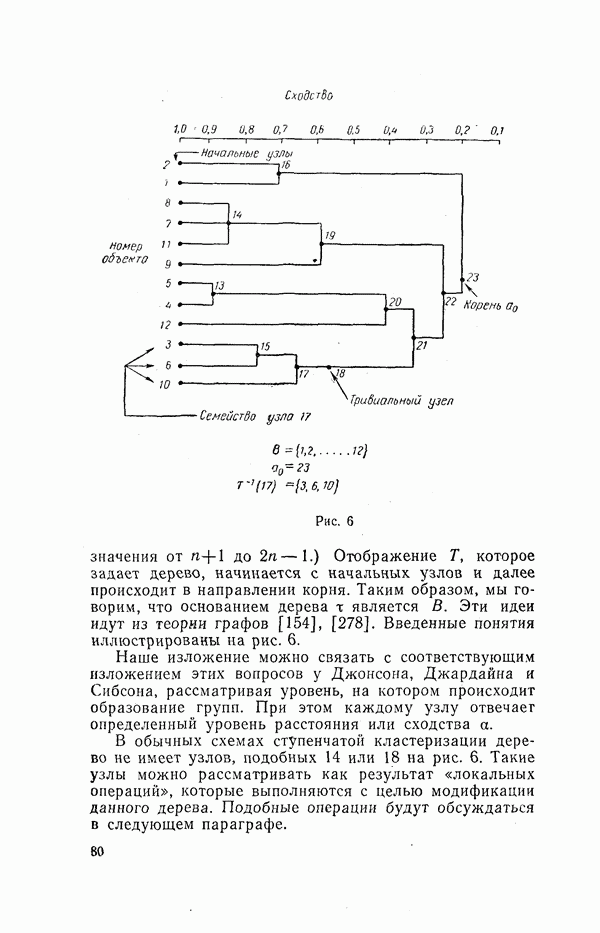
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
- ГЛАВА 6. ПРИЛОЖЕНИЯ
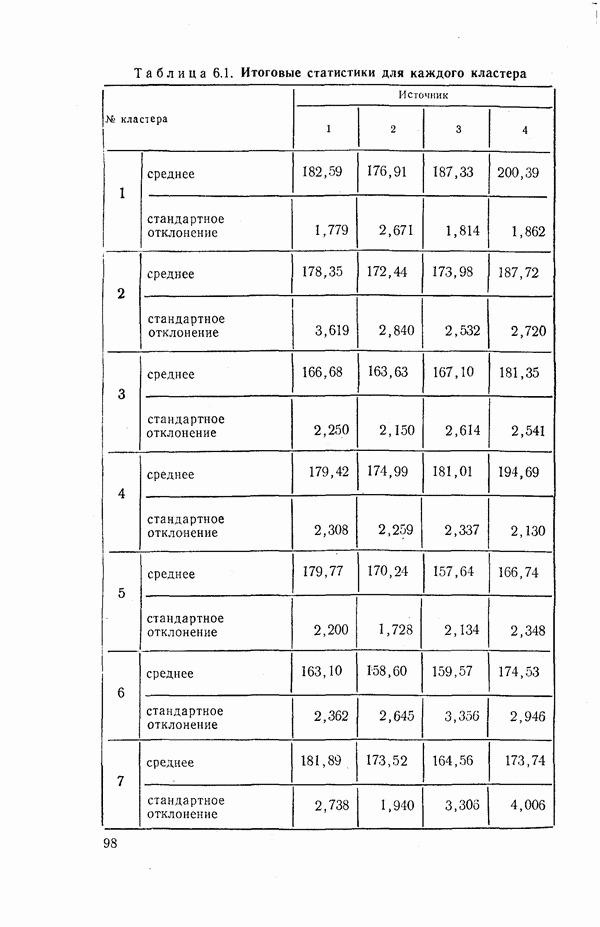
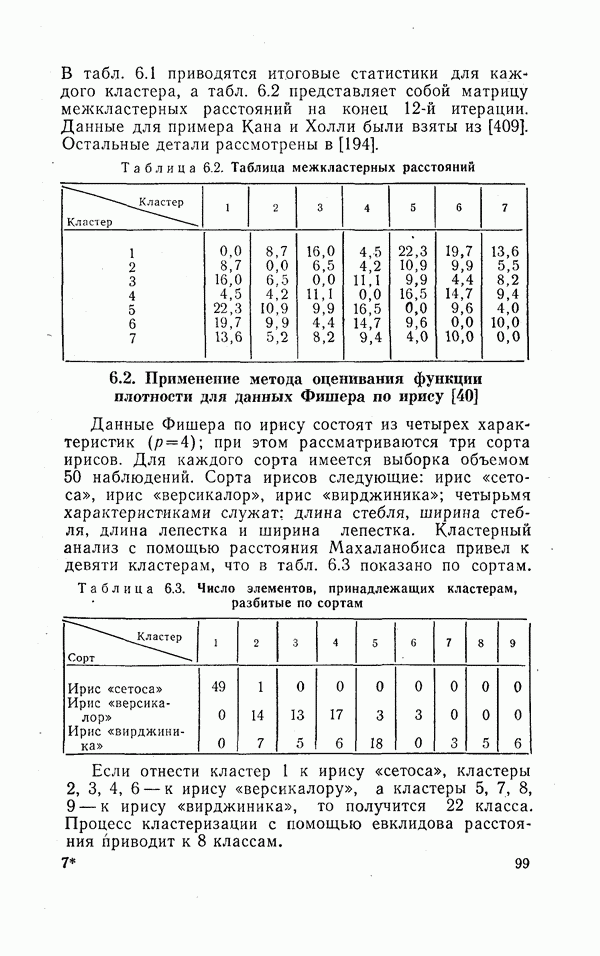
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература