| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
Напомним, что решением кластерной задачи является такое разбиение  объектов на
объектов на  , непересекающихся подмножеств, которое удовлетворяет некоторому критерию однородности внутри кластеров. Один из способов отыскания такого разбиения был рассмотрен в предыдущей главе: он заключался в полном переборе всех возможных разбиений на
, непересекающихся подмножеств, которое удовлетворяет некоторому критерию однородности внутри кластеров. Один из способов отыскания такого разбиения был рассмотрен в предыдущей главе: он заключался в полном переборе всех возможных разбиений на  кластеров и выбора из них оптимального. К сожалению, указанный метод практически неосуществим даже для небольших
кластеров и выбора из них оптимального. К сожалению, указанный метод практически неосуществим даже для небольших  .
.
В качестве альтернативы метода полного перебора можно предложить другие методы, составляющие содержание так называемого математического программирования; эти методы позволяют сократить общий объем вычислений и в то же время приводят к оптимальному решению. Заметим, что большинство из ранее рассмотренных методов кластеризации (гл. 1) дает оптимальное решение в классе меньшем, чем класс всех возможных разбиений (кластеров), поэтому нет гарантии, что найденное решение будет оптимально в классе всех разбиений. Различные применения математического программирования читатель найдет, например, у Дженсена [183], Вайнода [380] и Рао [291].
3.1. Применение динамического программирования к кластерному анализу
В этом параграфе мы рассмотрим задачу разбиения множества из 6 объектов на 3 подмножества; в качестве меры расстояния между объектами выберем евклидову метрику, что соответствует критерию минимизации внутригрупповой суммы квадратов (ВСК).
Напомним, что ВСК вычисляется по формуле

где  обозначает
обозначает  матрицу рассеяния
матрицу рассеяния  кластера,
кластера,  . Таким образом, имеем:
. Таким образом, имеем:

где 
Суть методов динамического программирования состоит в целенаправленном поиске разбиения, дающего минимальное значение величины W, при этом разбиения, которые приводят к большему значению W, отбрасываются.
Подробнее остановимся на проблеме разбиения  объектов на
объектов на  группы с помощью полного перебора. На этом же примере мы рассмотрим применения методов динамического программирования, которые приведены в работе Дженсена [183].
группы с помощью полного перебора. На этом же примере мы рассмотрим применения методов динамического программирования, которые приведены в работе Дженсена [183].
Общее число способов разбиения 6 объектов на 3 группы определяется из уравнения (2.11):

90 альтернатив кластеризации может быть классифицировано соответственно формам распределения [183]. В нашем примере существуют три формы распределения, которые обозначим,

Каждая компонента формы распределения обозначает число объектов в некотором кластере. Компоненты в форме распределения всегда будем записывать в убывающем порядке. В нашем примере имеется 90 альтернатив разбиения и 3 формы распределения. В общем
случае число форм распределения значительно меньше чем число возможных разбиений.
Всего существует  видов разбиения, соответствующих первой форме распределения
видов разбиения, соответствующих первой форме распределения  видов разбиения, соответствующих второй форме распределения
видов разбиения, соответствующих второй форме распределения  соответствующих третьей форме
соответствующих третьей форме  . Приведем теперь полный список разбиений, соответствущих всем видам распределений.
. Приведем теперь полный список разбиений, соответствущих всем видам распределений.
Форма распределения {4}, {1}, {1}
 (1)
(1)
Форма распределения {3}, {2}, {1}
 (6)
(6)
Продолжение
 (3)
(3)
Форма распределения {2}, {2}, {2}

При полном переборе целевую функцию (ВСК) необходимо вычислить для каждой из 90 альтернатив разбиения, приведенных выше; затем отыскивается такоз разбиение, которое приводит W к минимуму. Из приведенного списка возможных альтернатив разбиения видно, что ВСК для некоторых кластеров, например для (1, 2, 3), будет вычисляться больше одного раза.
Применение методов динамического программирования к проблеме кластеризации представляет собой последовательное нахождение оптимальной группировки, на каждом шаге которой вычисляется целевая функция; при этом лишние вычисления, присутствующие при методике полного перебора, исключаются. Другими словами, оптимальное решение находится поэтапно. Подход с помощью динамического программирования ускоряет обработку массива информации.
Описанный выше пример рассмотрим в качестве иллюстраций применения динамического программирования. Прежде всего все альтернативы кластеризации классифицируются соответственно формам распределения. Напомним, что компоненты форм распределения располагаются в убывающем порядке. На первом шаге для каждой компоненты первой формы распределения вычисляется и запоминается соответствующая целевая функция. На втором шаге для кластеров, соответствующих первым двум компонентам формы распределения вычисляются новые значения целевых функций; при этом привлекается вся информация, полученная на первом шаге; таким образом, внутригрупповая сумма квадратов не вычисляется заново для каждого кластера, а ее значение берется из предыдущего шага.
Для иллюстрации решения с помощью динамического программирования рассмотрим табл. 3.1. Второй столбец таблицы соответствует первой компоненте формы распределения, т. е. кластерам, образованным на первом шаге. Число кластеров первого шага равно:  . Функция W на первом шаге вычисляется для каждых из пяти кластеров. На втором шаге мы будем иметь 2 кластера, соответствующих первым двум компонентам формы распределения, размеры этих кластеров будут
. Функция W на первом шаге вычисляется для каждых из пяти кластеров. На втором шаге мы будем иметь 2 кластера, соответствующих первым двум компонентам формы распределения, размеры этих кластеров будут  или
или  или
или  . Таким образом, общее число объектов на втором шаге равно 5 или 4. Число способов получения 5 объектов равно:
. Таким образом, общее число объектов на втором шаге равно 5 или 4. Число способов получения 5 объектов равно:  . Число способов получения 4 объектов равно:
. Число способов получения 4 объектов равно:  , а общее число объектов на втором шаге равно 240. На втором шаге существует
, а общее число объектов на втором шаге равно 240. На втором шаге существует  способов образования кластеров с компонентами формы распределения
способов образования кластеров с компонентами формы распределения  это означает, что мы имеем 45 повторений. На третьем шаге необходимо к компонентам
это означает, что мы имеем 45 повторений. На третьем шаге необходимо к компонентам  из второго шага добавить еще
из второго шага добавить еще  , что приведет к форме
, что приведет к форме  или эквивалентно
или эквивалентно  . Таким образом, общее число способов разбиения на втором шаге равно:
. Таким образом, общее число способов разбиения на втором шаге равно:

вместо 105.
Число различных множеств, содержащих 4 или 5 объектов, на втором шаге равно:  Эти множества приведены в табл. 3.1 (шаг 2) и называются состояниями. Итак, на втором шаге имеется 21 состояние. На первом шаге число состояний равно 50. В табл. 3.1 показано 5 из 135 допустимых способов получения состояний на втором шаге.
Эти множества приведены в табл. 3.1 (шаг 2) и называются состояниями. Итак, на втором шаге имеется 21 состояние. На первом шаге число состояний равно 50. В табл. 3.1 показано 5 из 135 допустимых способов получения состояний на втором шаге.
Третий шаг является окончательным. Он состоит из 3 кластеров. На последнем этапе имеется одно состояние, содержащее все 6 объектов. Число способов получения шести объектов на последнем шаге равно:

т. е. имеется  допустимая дуга, связывающая шаг 2 с шагом 3.
допустимая дуга, связывающая шаг 2 с шагом 3.
Например, если  , то общее число допустимых дуг равно:
, то общее число допустимых дуг равно:  . При включении первоначальных состояний число их будет:
. При включении первоначальных состояний число их будет: 
Таблица 3.1
(см. скан)
Каждая допустимая дуга приводит к переходным вычислениям по формуле

где  обозначает группу из
обозначает группу из  объектов,
объектов,  — расстояние между
— расстояние между  .
.
В нашем примере всего 90 альтернатив разбиения, для каждой из которых необходимо произвести 3 переходные вычисления (всего 270). Решение с помощью динамического программирования требует 206 или по крайней мере 64 переходных вычислений.
Предположим, что на некотором шаге k имеется некоторое распределение объектов  . В процедуре динамического программирования запоминается оптимальный способ разбиения q объектов на k непустых непересекающихся подмножеств. На следующих шагах, на которых требуется разбить q объектов на k групп, уже не будет необходимости решать эту задачу, перебирая все возможные способы их разбиения.
. В процедуре динамического программирования запоминается оптимальный способ разбиения q объектов на k непустых непересекающихся подмножеств. На следующих шагах, на которых требуется разбить q объектов на k групп, уже не будет необходимости решать эту задачу, перебирая все возможные способы их разбиения.
В качестве иллюстрации рассмотрим наш пример, в котором 
Таблица 3.2

Напомним, что при  и
и  имеется
имеется  альтернатив разбиения. Три из 90 возможных альтернатив приведены в табл. 3.2. При полном переборе для трех альтернатив потребовалось бы 9 переходных вычислений. При оптимальном разбиении множества (1, 2, 3, 4) на две группы размера 2 требуется только 6 переходных вычислений. Если запомнить оптимальное разбиение
альтернатив разбиения. Три из 90 возможных альтернатив приведены в табл. 3.2. При полном переборе для трех альтернатив потребовалось бы 9 переходных вычислений. При оптимальном разбиении множества (1, 2, 3, 4) на две группы размера 2 требуется только 6 переходных вычислений. Если запомнить оптимальное разбиение  , то для определения
, то для определения  требуется только одно вычисление
требуется только одно вычисление  . Для трех альтернатив применение динамического программирования дает возможность, таким образом, сократить число вычислений на
. Для трех альтернатив применение динамического программирования дает возможность, таким образом, сократить число вычислений на  Естественно, при увеличении
Естественно, при увеличении  число сокращаемых вычислений
число сокращаемых вычислений
значительно увеличивается, однако по отношению к общему числу переходных вычислений это увеличение может быть не столь значительным.
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
- ГЛАВА 6. ПРИЛОЖЕНИЯ
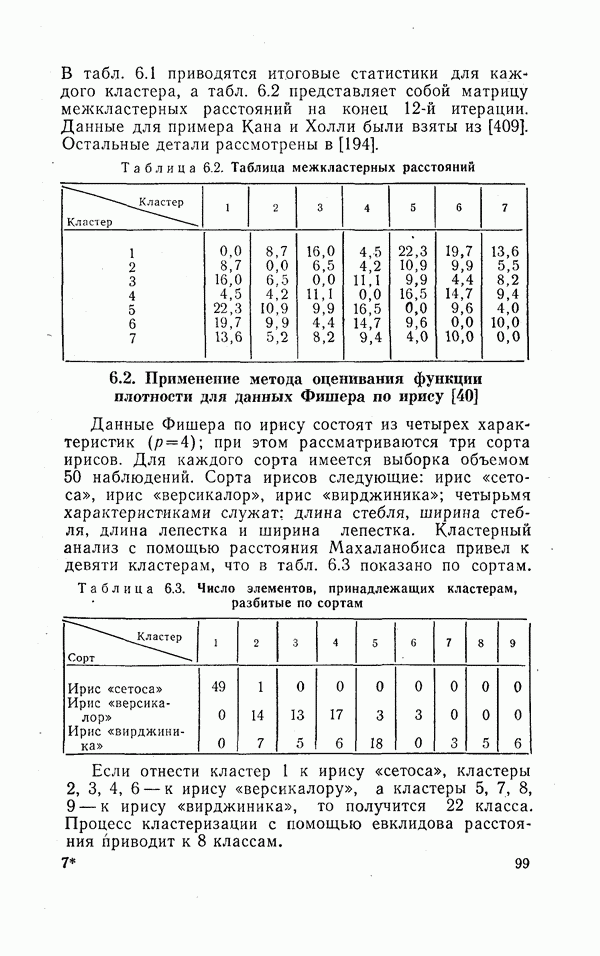
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература