| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. Оценивание функции плотности вероятности
По вопросу оценивания функции плотности вероятности имеется много работ. Мы не ставим себе цели дать обзор методов оценивания функций плотности. За коротким обзором существующих методов отсылаем читателя к Брайену [40]. Брайен предлагает один метод оценивания многомерных функций плотности вероятности, который называет методом ядра; он также строит метод кластеризации, который основывается на оценке функции плотности.
Метод ядра оценивания функции плотности связан с линейным интегральным преобразованием

Это преобразование устанавливает соответствие между функциями  . Функция
. Функция  называется ядром преобразования (см. [209]). Метод ядра также иногда называют оцениванием с взвешенным средним (см. [95], [283], [298]).
называется ядром преобразования (см. [209]). Метод ядра также иногда называют оцениванием с взвешенным средним (см. [95], [283], [298]).
В методе ядра функция плотности вероятности f(x) оценивается по формуле

где  — ядро,
— ядро,  — эмпирическая функция распределения. Розенблат [298] предложил само ядро рассматривать как некоторую функцию плотности, т. е.
— эмпирическая функция распределения. Розенблат [298] предложил само ядро рассматривать как некоторую функцию плотности, т. е.

Сейчас мы рассмотрим основные моменты процедуры оценивания плотности вероятности, предложенной Брайеном [40].
Пусть  обозначает случайную выборку объема
обозначает случайную выборку объема  из некоторой функции плотности f(x), имеющей невырожденную матрицу ковариаций
из некоторой функции плотности f(x), имеющей невырожденную матрицу ковариаций  . С помощью
. С помощью
рассматриваемого метода, который аналогичен методу Какоулоса [42], оценивается функция плотности в виде:

где К — ядро. В качестве ядра выбирается функция плотности многомерного нормального распределения с математическим ожиданием, равным нулю, а ковариационной матрицей S, т. е.

Оценкой тогда будет:

где  обозначают векторы наблюдений, а
обозначают векторы наблюдений, а  — выборочная матрица ковариаций, которая предполагается невырожденной, откуда следует, что
— выборочная матрица ковариаций, которая предполагается невырожденной, откуда следует, что  положительно определена.
положительно определена.
Легко показать, что  из (5.2) является функцией плотности вероятности, другими словами,
из (5.2) является функцией плотности вероятности, другими словами,

Квадратичная форма  в экспоненте
в экспоненте  в (5.1) является расстоянием Махаланобиса между
в (5.1) является расстоянием Махаланобиса между  и 0. Вместо матрицы S можно привлечь матрицу
и 0. Вместо матрицы S можно привлечь матрицу  это приведет к квадрату евклидова расстояния между
это приведет к квадрату евклидова расстояния между  . Выбор S и I эквивалентен выбору между расстоянием Махаланобиса и евклидовым расстоянием.
. Выбор S и I эквивалентен выбору между расстоянием Махаланобиса и евклидовым расстоянием.
Евклидово расстояние проще и легче вычисляется. Однако расстояние Махаланобиса имеет много преимуществ. Например, как показано в параграфе 1,3, это расстояние инвариантно по отношению ко всем невырожденным преобразованиям. Это означает, что f(x)
совпадает с  , где А — невырождено. Таким образом, выбор масштаба не влияет на f(x).. Это перестает быть верным для евклидова расстояния.
, где А — невырождено. Таким образом, выбор масштаба не влияет на f(x).. Это перестает быть верным для евклидова расстояния.
Другим, свойством расстояния Махаланобиса является то, что оно делает некоторые критерии кластеризации эквивалентными. Следующие три критерия кластеризации при пользовании расстоянием Махаланобиса эквивалентны:  где T, В и W — соответственно матрицы полного, межгруппового и внутригруппового расстояния, которые обсуждались в параграфе 1.4. Критерии (2) и (3) были предложены Фридманом и Рубиным [122], ими же были исследованы свойства этих критериев. В следующем
где T, В и W — соответственно матрицы полного, межгруппового и внутригруппового расстояния, которые обсуждались в параграфе 1.4. Критерии (2) и (3) были предложены Фридманом и Рубиным [122], ими же были исследованы свойства этих критериев. В следующем  параграфе мы рассмотрим процедуру кластеризации, которая приводит к оптимальному, по меньшей мере в локальном смысле, разбиению на группы относительно критериев (2) и (3). Метод, который был рассмотрен в параграфе 1.5, приводит к оптимальному разбиению с точки зрения критерия (1).
параграфе мы рассмотрим процедуру кластеризации, которая приводит к оптимальному, по меньшей мере в локальном смысле, разбиению на группы относительно критериев (2) и (3). Метод, который был рассмотрен в параграфе 1.5, приводит к оптимальному разбиению с точки зрения критерия (1).
Одной из проблем применения оценки f(x) в (5.2) является выбор значения а. Выбор того или иного значения очень важен, и в случае плохого выбора оценка будет неудовлетворительной.
Выбор а основан на неравенстве теории информацию

Кульбак [217] доказал, что равенство в (5.3) достигается тогда и только тогда, когда  для почти всех
для почти всех  Процедура заключается в том, чтобы минимизировать
Процедура заключается в том, чтобы минимизировать  . Неравенство (5.3) можно переписать следующим образом:
. Неравенство (5.3) можно переписать следующим образом:

причем равенство достигается в том и только в том случае, когда  для почти всех
для почти всех  . Как видим, минимизация
. Как видим, минимизация  эквивалентна максимизации
эквивалентна максимизации  . Процедура выбора
. Процедура выбора  заключается в максимизации не самого значения
заключается в максимизации не самого значения
 , а его оценки. Если
, а его оценки. Если  построено на
построено на 
— другая выборка объема k, то оценка  равна:
равна:

Если второй выборки не существует, то оценку для  строят на основе
строят на основе  в этом случае она равна:
в этом случае она равна:

Однако эта оценка будет смещена и может привести к: отрицательным значениям  . Смещение оценки (5.4) может быть уменьшено методом складного ножа (jackk-nifing) [81], [141]. Пусть
. Смещение оценки (5.4) может быть уменьшено методом складного ножа (jackk-nifing) [81], [141]. Пусть  — оценка f(x) (допущен). Тогда
— оценка f(x) (допущен). Тогда

а  определяется равенством:
определяется равенством:

Производная  после преобразований равна:
после преобразований равна:

где

Оптимальное значение  находят из уравнения
находят из уравнения 
Для решения этого уравнения могут быть применены различные методы, например метод Ньютона—Рафсона. Эти методы рассматриваются в главе 3, Изаксона и Келлера [172].
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
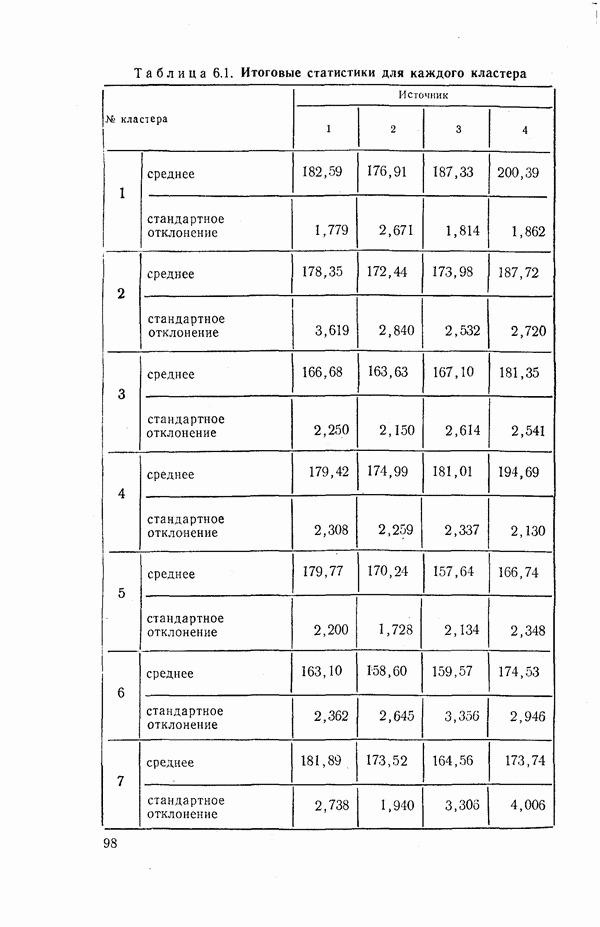
- ГЛАВА 6. ПРИЛОЖЕНИЯ
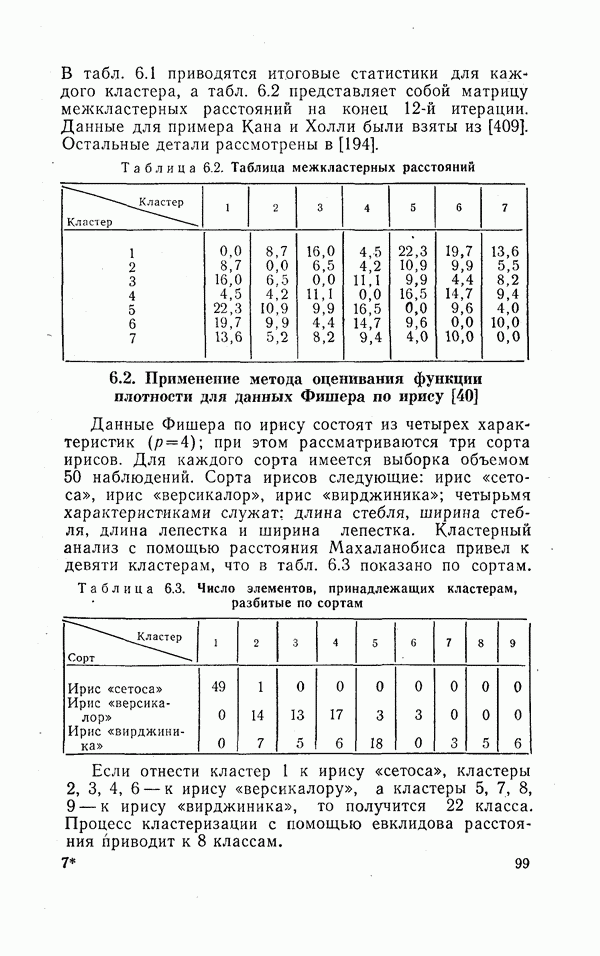
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература