| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.7. Алгоритм последовательной кластеризации
Схема последовательной кластеризации может быть описана следующим образом. Рассмотрим  как множество кластеров выберем два из них, скажем
как множество кластеров выберем два из них, скажем  , которые в некотором смысле наиболее близки друг к другу, и объединим их в один кластер. Новое множество кластеров, состоящее уже из
, которые в некотором смысле наиболее близки друг к другу, и объединим их в один кластер. Новое множество кластеров, состоящее уже из  кластеров, будет
кластеров, будет

Повторяя процесс, мы получим последовательные множества кластеров, состоящие из  и т. д. кластеров. В конце этой процедуры получится кластер, состоящий из
и т. д. кластеров. В конце этой процедуры получится кластер, состоящий из  объектов и совпадающий с первоначальным множеством
объектов и совпадающий с первоначальным множеством 
В качестве меры расстояния примем квадрат евклидовой метрики  . Для наглядности вычислим матрицу
. Для наглядности вычислим матрицу  , где
, где  -квадрат расстояния между
-квадрат расстояния между 
Таблица 1.4. Значения 

Предположим, что расстояние между  минимально, т. е. что
минимально, т. е. что  образуем с помощью
образуем с помощью  новый кластер
новый кластер  Построим новую
Построим новую  матрицу расстояния (см. табл. 1.5).
матрицу расстояния (см. табл. 1.5).
Таблица 1.5. Значения  после первого объединения
после первого объединения

Легко видеть, что  строки для этой матрицы можно непосредственно взять из старой, однако первую строку необходимо вычислить заново. Очевидно, вычисления будут сведены к минимуму, если удастся выразить
строки для этой матрицы можно непосредственно взять из старой, однако первую строку необходимо вычислить заново. Очевидно, вычисления будут сведены к минимуму, если удастся выразить  через элементы первоначальной матрицы.
через элементы первоначальной матрицы.
Ланс и Уильямс [223] предложили рекурсивную процедуру, в которой вычисления матрицы расстояний опираются только на значения расстояний в предыдущей матрице. Их рекурсивная схема предполагает использование минимального и максимального локальных расстояний, медианы, групповых средних и центра. Все пять случаев, за исключением минимального локального расстояния и медианы, были описаны в параграфе 1.6. Минимальное локальное расстояние между двумя кластерами  было определено в параграфе 1.5; схема предусматривает объединение двух кластеров, имеющих наименьшее минимальное локальное расстояние. Медианный метод такой же, как и центроидный, за исключением того, что здесь при объединении кластеров
было определено в параграфе 1.5; схема предусматривает объединение двух кластеров, имеющих наименьшее минимальное локальное расстояние. Медианный метод такой же, как и центроидный, за исключением того, что здесь при объединении кластеров  предполагается, что
предполагается, что  и поэтому центр нового кластера лежит точно посередине между центрами старых кластеров.
и поэтому центр нового кластера лежит точно посередине между центрами старых кластеров.
Уишарт [394] считает, что процедуру Уорда [387] можно объединить с пятью, рассмотренными выше. Как было показано в параграфе 1.5, объединение кластеров
 ведет к увеличению ВСК на величину
ведет к увеличению ВСК на величину  , которая задается равенством
, которая задается равенством

где  Если кластер
Если кластер  объединяется с
объединяется с  , то можно показать, что
, то можно показать, что  и
и

Более того, из (1.13) следует, что

Подставляя выражение (1.15). для каждого  в уравнение (1.14), получим:
в уравнение (1.14), получим:

Уравнение (1.16) определяет величину приращения ВСК при объединении  и
и  .
.
Начиная с матрицы квадратов евклидовых расстояний (табл. 1.4)  процедура заключается в объединении таких кластеров
процедура заключается в объединении таких кластеров  , для которых
, для которых  минимально. Кластер
минимально. Кластер  состоящий из одного объекта, заменяется на
состоящий из одного объекта, заменяется на  , а расстояния
, а расстояния  в матрице D заменяются на
в матрице D заменяются на  . Элементы
. Элементы  столбца и строки полагаются равными нулю, т. е.
столбца и строки полагаются равными нулю, т. е.  становится «недействительным» [394]. Соответственно пр заменяется на
становится «недействительным» [394]. Соответственно пр заменяется на  приравнивается нулю. Равенство
приравнивается нулю. Равенство

выполняется для всех  .
.
Подставляя  (фактически
(фактически  ) из уравнения (1.16) в уравнение (1.17), получим
) из уравнения (1.16) в уравнение (1.17), получим


где  . Если на каждом шаге объединения
. Если на каждом шаге объединения  столбцы и строки матрицы D преобразовываются по формуле (1.18), то равенство (1.17) будет выполняться для всех
столбцы и строки матрицы D преобразовываются по формуле (1.18), то равенство (1.17) будет выполняться для всех  и всех действительных множеств
и всех действительных множеств  и
и  . Заметим, что
. Заметим, что  в (1.17) не является евклидовым расстоянием, если не рассматриваются только два кластера, содержащих по одному элементу.
в (1.17) не является евклидовым расстоянием, если не рассматриваются только два кластера, содержащих по одному элементу.
Алгоритм группирбвки окончательно может быть записан следующим образом [394]:
1) Найдем 
2) Увеличение целевой функции при объединении двух кластеров  равно
равно 
3)  заменяется на
заменяется на  строка
строка  и столбец
и столбец  матрицы D пересчитываются по формуле (1.18),
матрицы D пересчитываются по формуле (1.18), 
4) Полагаем  превращая
превращая  в недействительное множество;
в недействительное множество;
5) Записываем элементы кластера  в кластер
в кластер  возвращаемся к (1) и повторяем процедуру
возвращаемся к (1) и повторяем процедуру  раз.
раз.
Ланс и Уильямс [223] получили общее уравнение (1.19), аналогичное (1.18) и верное для всех пяти процессов кластеризации, описанных выше. Это уравнение может быть записано в следующем виде:
 (1.19)
(1.19)
где  — параметры, задающие вид процесса. В уравнении
— параметры, задающие вид процесса. В уравнении  обозначает меру расстояния между кластерами
обозначает меру расстояния между кластерами 
Значения параметров, входящих в общую формулу (1.19), соответствующие шести различным процессам кластеризации, приведены ниже:
минимальное локальное расстояние: 
максимальное локальное расстояние: 
медиана: 
среднее группы:  ;
;
центроидный метод:  ;
;
метод Уорда:  .
.
Первые пять значений параметров приводятся в работе Ланса и Уильямса [223]. Значения параметров в методе Уорда найдены Уишартом [394] и получаются из уравнения (1.19). Все шесть методов были объединены в одну вычислительную программу с параметрами  и
и  [398], [399].
[398], [399].
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
- ГЛАВА 6. ПРИЛОЖЕНИЯ
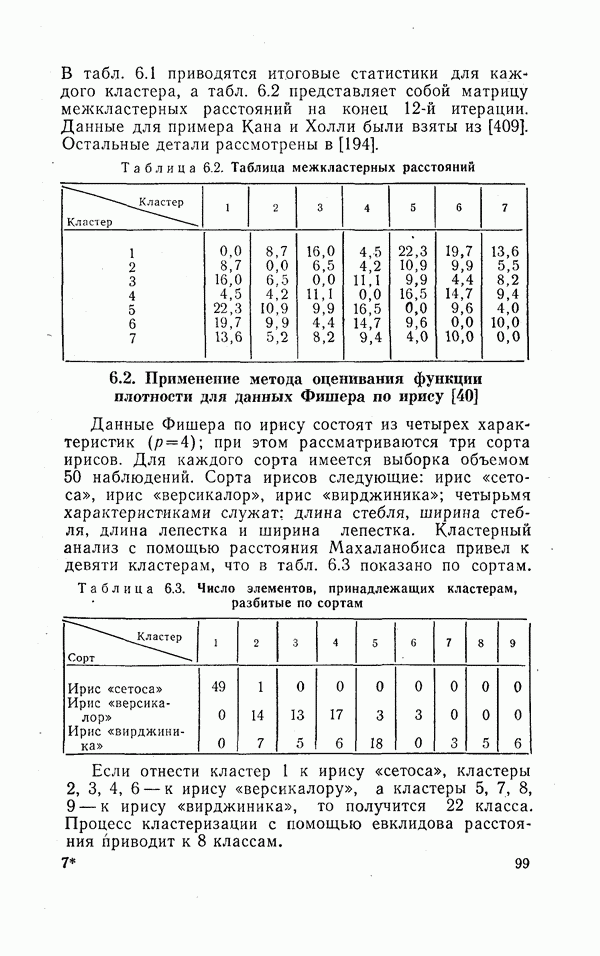
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература