4.4. Деревья

Дерево определим как , где обозначает корень, А — множество (конечное) узлов, включая — отображение А в себя, такое, что для любого тогда и только тогда, когда . Для данной дендограммы соответствует кластеру (узлу), содержащему все объектов. Для данного узла b отображение Т устанавливает, в какой узел переходит b после преобразования (группировки); это отображение тесно связано с данной процедурой кластеризации. Узлы объединяются и образуют новый кластер (узел b) и называются семейством b, а b называется образующим (parent) узлов . Узел b называется тривиальным, если состоит из одного узла. Узел b называется начальным (barren), если множество пусто. Множество начальных узлов обозначим буквой В. Число начальных узлов обозначим , а общее число узлов — , (Очевидно, принимают целые

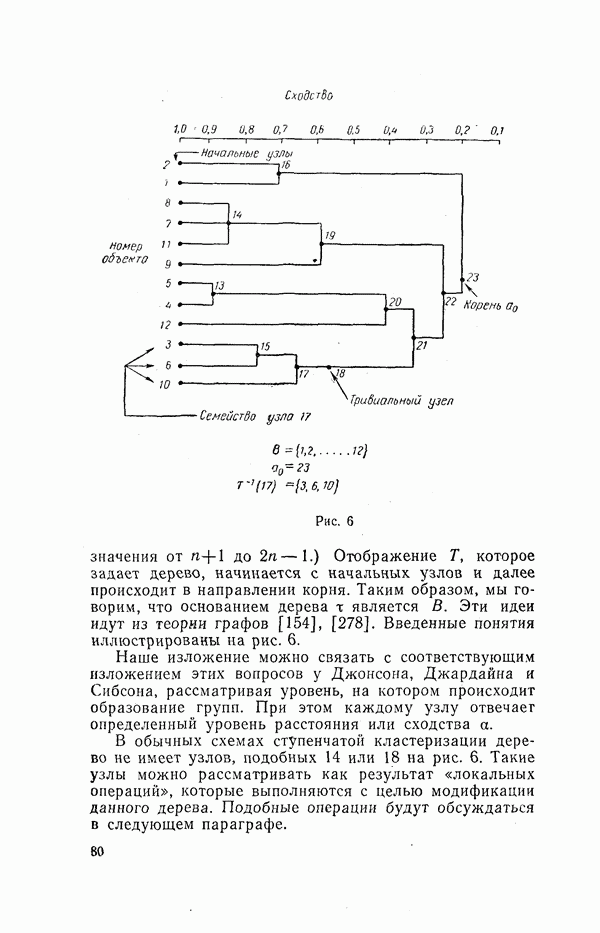
Рис. 6

значения от до Отображение Т, которое задает дерево, начинается с начальных узлов и далее происходит в направлении корня. Таким образом, мы говорим, что основанием дерева является В. Эти идеи идут из теории графов [154], [278]. Введенные понятия иллюстрированы на рис. 6.

Наше изложение можно связать с соответствующим изложением этих вопросов у Джонсона, Джардайна и Сибсона, рассматривая уровень, на котором происходит образование групп. При этом каждому узлу отвечает определенный уровень расстояния или сходства .

В обычных схемах ступенчатой кластеризации дерево не имеет узлов, подобных 14 или 18 на рис. 6. Такие узлы можно рассматривать как результат «локальных операций», которые выполняются с целью модификации данного дерева. Подобные операции будут обсуждаться в следующем параграфе.

Если два узла таковы, что для , то будем писать . Отношение задает на А частичное упорядочение. Если , то существует элемент такой, что и из следует другими словами, с есть первый узел, который содержит а и b, т. е. минимально. В терминах этих понятий дерево может быть определено как частичное упорядочение А, которое имеет единственный максимальный элемент и для которого множество линейно упорядочено для всех .

Дерево сходства, которое обозначим как , состоит из дерева и вещественнозначной функции на А, такой, что

Действительное число называется сходством узла . Любое дерево сходства может быть представлено дендограммой. В дендограмме узлам одного семейства присваивается порядок, соответствующий их узлам сходства, т. е. значениям; крайние значения задаются произвольно. С помощью этой процедуры, которая начинается с корня, в начальных узлах можно установить линейный порядок. Начальные узлы располагаются вертикально в порядке вычислений и горизонтально соответственно значениям своего сходства, узлы с большим сходством располагаются левее. Другие узлы располагаются вертикально в центрах соответствующих семейств, которые также располагаются вертикально и горизонтально соответственно значениям сходства. На основе дендограммы может быть построено полное дерево сходства . Действительно, дендограмма есть не что иное, как графическое представление абстрактного дерева

Матрица сходства S имеет точную структуру дерева на В, т. е. если для некоторого есть дерево сходства

для всех . Другими словами, величина сходства между двумя узлами равна сходству первого узла, в котором они кластеризуются с помощью -отображения. Это определение аналогично определению Джонсона [186] и Джардайна и Сибсона [179];

расстояние между двумя узлами i и полагается равным тому уровню расстояния, на котором происходит объединение i и Если матрица сходства имеет точную структуру дерева, то элементов матрицы могут быть определены по значениям .

Расстояние между двумя матрицами сходства S и определяется как

где W — симметричная весовая функция.

Расстояние между матрицей и деревом определяется как

где означает, что S имеет точную структуру дерева. Матрица сходства S, которая минимизирует называется приближением S по . Итак, есть сходство первого узла, в котором i и j группируются впервые, т. е. , где — некоторая вещественнозначная функция на А, такая, что если Отсюда следует, что

где а может быть выбрано произвольно и единственным ограничением является выполнение определенных неравенств. Такое определение приводит нас к задаче квадратичного программирования; при этом существует единственное решение, которое и приводит Томпсон [358]. Однако если единственным условием минимизации является для произвольного а, то

Если эта функция удовлетворяет неравенству для то S является приближением S по дереву т. В действительности наибольший интерес представляют такие деревья , для которых это неравенство выполняется (см. [162]).

Нахождение приближения S по эквивалентно отысканию

таких деревьев , для которых величина принимает минимальные значения. Определение расстояния позволяет нам выбрать «оптимальное» представление S деревом. Расстояние естъсредний Квадрат ошибки при подстановке вместо S матрицы близости с точной структурой дерева .

Для любого дерева на В обобщение W, S на производится следующим образом:

Веса узлов приближения и их коэффициенты сходства определяются следующим образом:

определенные из уравнений (4.8) и (4.12), совпадают, поскольку

Поэтому

Таким же образом

Теперь средний квадрат ошибки может быть записан как

поскольку

Уравнения (4.9) — (4.13) применяются для приближения дерева к матрице сходства S. Для данного S цель заключается в том, чтобы найти такие деревья , для которых минимально, т. е. найти такие коэффициенты сходства узлов приближения которые минимизируют взвешенную сумму квадратов (среднее квадрата ошибки):