| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
Как было отмечено в предыдущих главах, задачи кластерного анализа можно решать как в терминах матрицы расстояний D, так и в терминах матрицы сходства S. В этой главе мы рассмотрим различные аспекты представления результатов кластеризации, матриц сходства и расстояния.
Параграфы 4.1 и 4.2 служат неформальным введением в более строгое изложение соответствующих вопросов с точными формулировками (Хартиген), которые читатель найдет в параграфе 4.3.
4.1. Дендограммы
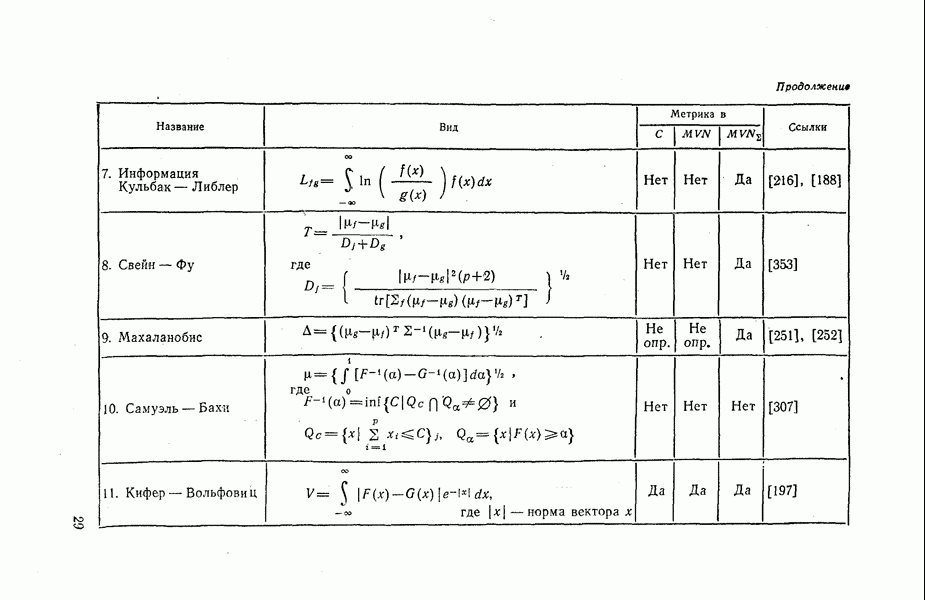
Последовательный процесс кластеризации начинается с рассмотрения  объектов; затем два наименее удаленных (ближайших) объекта объединяются в один кластер и число кластеров становится равным
объектов; затем два наименее удаленных (ближайших) объекта объединяются в один кластер и число кластеров становится равным  . Процесс повторяется до тех пор, пока все
. Процесс повторяется до тех пор, пока все  объектов не попадут в один кластер, содержащий все объекты. Идеи, изложенные в этой главе, имеют в виду применение методов последовательной (стратифицированной) кластеризации.
объектов не попадут в один кластер, содержащий все объекты. Идеи, изложенные в этой главе, имеют в виду применение методов последовательной (стратифицированной) кластеризации.
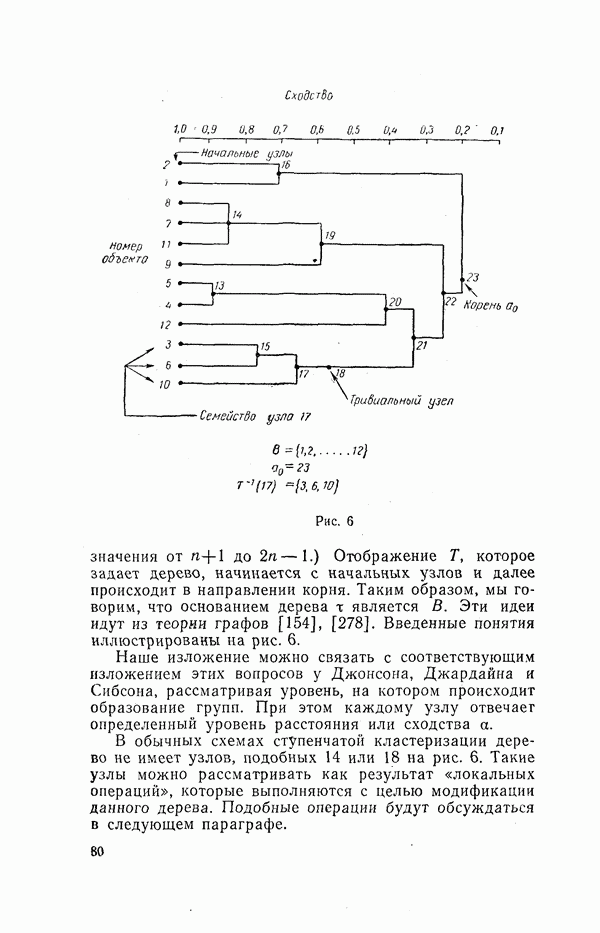
Наиболее известный метод представления матрицы расстояний (разнородности) или сходства основан на идее «дендограммы», или «диаграммы-дерева».
Дендограмму можно определить как графическое изображение результатов процесса последовательной кластеризации, который осуществляется в терминах матрицы расстояний или сходства. В дальнейшем процесс такой кластеризации будем рассматривать, как процедуру с матрицей расстояний или сходства. Таким образом, с помощью дендограммы можно графически
или геометрически изображать процедуру кластеризации при условии, что эта процедура оперирует только с элементами матрицы расстояний или сходства.
Существует много способов построения диаграмм-деревьев, соответствующих данной дендограмме. В диаграмме-дереве объекты располагаются вертикально слева, а результаты кластеризации справа. Значения расстояний или сходства, отвечающие построению новых кластеров, изображаются на горизонтальной прямой поверх дендограммы. Имея  объектов, можно построить большое количество диаграмм-деревьев, которые соответствуют данной процедуре кластеризации, однако для данной конкретной матрицы расстояний или сходства существует только одна диаграмма-дерево.
объектов, можно построить большое количество диаграмм-деревьев, которые соответствуют данной процедуре кластеризации, однако для данной конкретной матрицы расстояний или сходства существует только одна диаграмма-дерево.

Рис. 3
На рис. 3 показан один из примеров диаграммы-дерева. В дальнейшем мы будем рассматривать диаграммы-деревья только одного вида, и поэтому дендограммы и диаграммы-деревья будут отождествляться. Рис. 3 соответствует случаю шести объектов  характеристик (признаков). Объекты 1 и 3 наиболее близки (наименее удалены друг от друга), и поэтому объединяются в один кластер на уровне близости, равном 0,9. Объекты 4 и 5 объединяются при уровне 0,8. На этом шаге имеются 4 кластера: (1, 3), (6), (5, 4) (2). На
характеристик (признаков). Объекты 1 и 3 наиболее близки (наименее удалены друг от друга), и поэтому объединяются в один кластер на уровне близости, равном 0,9. Объекты 4 и 5 объединяются при уровне 0,8. На этом шаге имеются 4 кластера: (1, 3), (6), (5, 4) (2). На  третьем и четвертом шаге процесса образуются кластеры (1, 3, 6) и (5, 4, 2), соответствующие уровню близости, равному 0,7 и 0,6. Окончательно все объекты группируются в один кластер при уровне 0,5. С некоторыми специальными вопросами представления результатов кластеризации читатель может ознакомиться по работе
третьем и четвертом шаге процесса образуются кластеры (1, 3, 6) и (5, 4, 2), соответствующие уровню близости, равному 0,7 и 0,6. Окончательно все объекты группируются в один кластер при уровне 0,5. С некоторыми специальными вопросами представления результатов кластеризации читатель может ознакомиться по работе
Сокала и Спита [336]. Вид дендограммы зависит от выбора меры сходства или расстояния между объектом и кластером и методом кластеризации. Наиболее важным моментом является выбор меры сходства или меры расстояния между объектом и кластером. Некоторые меры расстояния обсуждались в главе 1. Дендограмму можно построить для любой из этих мер.
Джонсон [186] рассматривает различные последовательные процедуры кластеризации и их связь с одной специальной метрикой. Рассмотрим последовательность множества кластеров  и связанные с ними числа
и связанные с ними числа  . В терминах примера, показанного на рис. 3.
. В терминах примера, показанного на рис. 3.  соответствует точке ответвления,
соответствует точке ответвления,  уровню, при котором производится кластеризация. Множество
уровню, при котором производится кластеризация. Множество  содержит n кластеров, состоящих из одного объекта, а
содержит n кластеров, состоящих из одного объекта, а  . Таким образом,
. Таким образом,  а каждый кластер из
а каждый кластер из  - представляет собой объединение кластеров из
- представляет собой объединение кластеров из  Подобные процедуры будем называть схемами иерархической кластеризации (СИК).
Подобные процедуры будем называть схемами иерархической кластеризации (СИК).
Далее Джонсон показывает, что каждая СИК приводит к специальному виду метрики между объектами и, наоборот, СИК может быть получена на основе этой метрики. Таким образом, СИК может быть исследована с помощью изучения соответствующей метрики.
Пусть в  даны
даны  со значениями
со значениями  определим меры расстояния
определим меры расстояния  как
как

где i — наименьшее целое из множества  такое, что
такое, что  . Например, из рис. 3 видим, что
. Например, из рис. 3 видим, что  . Матрица расстояний, соответствующая этой мере, будет следующей:
. Матрица расстояний, соответствующая этой мере, будет следующей:

Можно показать, что мера расстояния (4.1) является «действенной» (bona fide) метрикой (см. определение
1.1). Наибольший интерес представляет проверка выполнимости неравенства треугольника. Пусть X, Y и Z — любые три объекта и  . Отсюда следует, что X и Y принадлежат некоторым кластерам, содержащимся в
. Отсюда следует, что X и Y принадлежат некоторым кластерам, содержащимся в  , а У и Z — некоторым кластерам из
, а У и Z — некоторым кластерам из  . Однако кластер, содержащийся в
. Однако кластер, содержащийся в  где
где  содержит и другой кластер, что следует из свойств
содержит и другой кластер, что следует из свойств  . Таким образом, X, Y и Z принадлежат одному кластеру из
. Таким образом, X, Y и Z принадлежат одному кластеру из  . Далее
. Далее

и

Неравенство (4.3) называется ультраметрическим неравенством. Поскольку  неравенство (4.3) сильнее обычного неравенства треугольника, поэтому
неравенство (4.3) сильнее обычного неравенства треугольника, поэтому

Каждой  соответствует единственная «действенная» метрика. Наоборот, имея матрицу расстояний, например (4.2), можно построить соответствующую диаграмму-дерево (рис. 3), т. е.
соответствует единственная «действенная» метрика. Наоборот, имея матрицу расстояний, например (4.2), можно построить соответствующую диаграмму-дерево (рис. 3), т. е.  .
.
Неотъемлемой частью процедуры Джонсона является определение расстояния между кластерами. Два кластера, имеющие минимальное расстояние, объединяются. Джонсон пользуется в качестве межкластерного расстояния минимальным и максимальным локальным расстоянием между кластерами (определения 1.8 и 1.9). Эти меры приводят к инвариантным методам кластеризации, т. е. результаты кластеризации инвариантны относительно монотонных преобразований матрицы сходства.
Джардайн и Сибсон [179] определяют дендограмму как функцию, отображающую интервал  ) в множество отношений эквивалентности на
) в множество отношений эквивалентности на  (множество
(множество  объектов), удовлетворяющую следующим условиям:
объектов), удовлетворяющую следующим условиям:
1) каждый кластер для данного уровня h есть объединение кластеров на уровне h, где 
2) для достаточно больших  все объекты объединены в один кластер;
все объекты объединены в один кластер;
3) для данного h существуют  такое, что множества кластеров для h и
такое, что множества кластеров для h и  совпадают.
совпадают.
Условия (1), (2), (3) аналогичны соответствующим условиям Джонсона. Однако в определениях Джардайна
и Сибсона не требуется, чтобы все объекты на уровне h = 0 были различны, h в определениях Джардайна и Сибсона соответствует а в определении Джонсона, у которого предполагается, что  Джардайн и Сибсон обсуждают также ультраметрическое неравенство и связывают свои результаты с различными методами кластеризации. Аналогичные вопросы рассматриваются в [175], [176], [178] и [180]. В некоторых из них обсуждается также аксиоматический подход к кластерному анализу.
Джардайн и Сибсон обсуждают также ультраметрическое неравенство и связывают свои результаты с различными методами кластеризации. Аналогичные вопросы рассматриваются в [175], [176], [178] и [180]. В некоторых из них обсуждается также аксиоматический подход к кластерному анализу.
Гауер и Росс [139] вводят понятие минимального дерева и рассматривают его связь с односвязным кластерным анализом (минимальное локальное расстояние между кластерами, определение 1.8).
Определение 4.1. Пусть даны  точек в
точек в  деревом, натянутым на данные точки, называется множество отрезков прямых (ребер), связывающих попарно эти точки таким образом, что
деревом, натянутым на данные точки, называется множество отрезков прямых (ребер), связывающих попарно эти точки таким образом, что
1) не существует замкнутых контуров;
2) через каждую точку проходит по крайней мере одна прямая;
3) дерево связано, т. е. любые две точки соединены прямой. Идеи этого определения идут из теории графов (см. [154] или [278]). Длиной дерева называется сумма длин отрезков прямых, составляющих дерево. Минимальным деревом называется дерево минимальной длины. Гауер и Росс предлагают два алгоритма для отыскания минимального дерева; там же рассматривается алгоритм, описанный в [299].
Пусть  обозначает множество длин ребер минимального дерева; число ребер равно h. На основе множества
обозначает множество длин ребер минимального дерева; число ребер равно h. На основе множества  можно построить дендограмму, группируя такие две точки, которым соответствует минимальное ребро; далее процедура совпадает с методом кластеризации по минимальному локальному расстоянию.
можно построить дендограмму, группируя такие две точки, которым соответствует минимальное ребро; далее процедура совпадает с методом кластеризации по минимальному локальному расстоянию.

Рис. 4. Минимальное дерево для семи точек

Рис. 5. Дендограмма минимального дерева из рис. 4
Рис. 4 и 5 иллюстрируют эту процедуру. Описанный метод кластеризации по минимальному локальному расстоянию на минимальном дереве эквивалентен методу кластеризации на матрице расстояний, при этом элементы матрицы, которые не соответствуют ребрам дерева, во внимание не принимаются. Отсюда следует, что кластеризация на минимальном дереве эквивалент - на кластеризации на матрице расстояний (Джонсон [186], Зан [408] изучает свойства минимального дерева и возможные приложения этого понятия, в том числе к методам ступенчатой кластеризации.
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
- ГЛАВА 6. ПРИЛОЖЕНИЯ
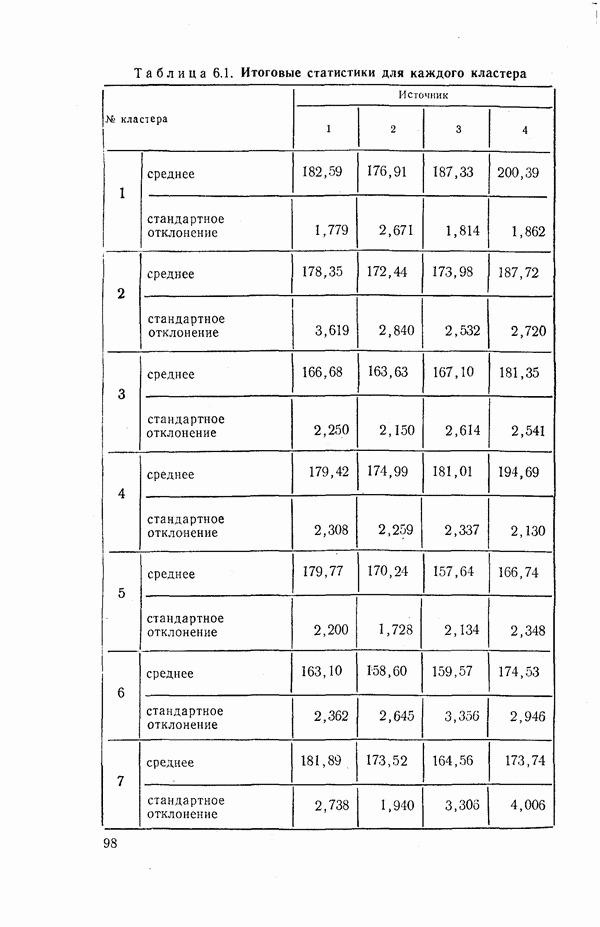
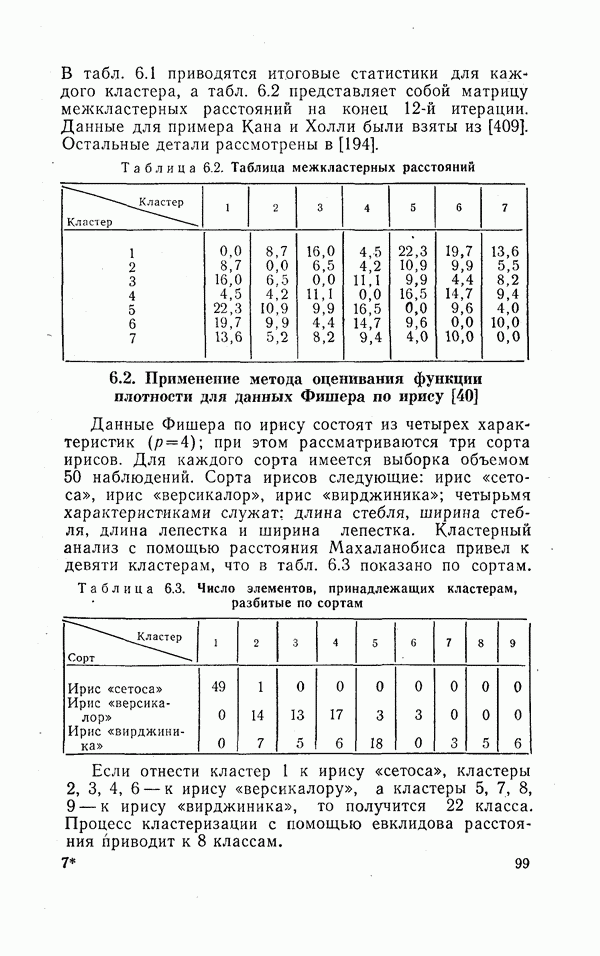
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература