| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.3. Кластеризация на основе оценивания функции плотности
В предыдущем параграфе было указано, что одним из преимуществ применения оценки плотности f (х) (5.1) является то, что при этом три критерия группировки (1) W;  становятся эквивалентными. Для этого векторы наблюдений
становятся эквивалентными. Для этого векторы наблюдений  необходимо заменить на
необходимо заменить на  и так что новое семейство векторов будет иметь среднее, равное 0; а затем векторы
и так что новое семейство векторов будет иметь среднее, равное 0; а затем векторы  преобразовать по закону СХ, где С — невырожденная матрица, такая, что СТСТ
преобразовать по закону СХ, где С — невырожденная матрица, такая, что СТСТ  Как следует из теоремы, доказанной в [40], евклидово расстояние в преобразованном пространстве пропорционально расстоянию Махаланобиса первоначального пространства. Отсюда можно сделать следующий вывод: алгоритмом кластеризации можно пользоваться в соответствии с одним из трех критериев без предварительного преобразования, если первоначально пользовались расстоянием Махаланобиса.
Как следует из теоремы, доказанной в [40], евклидово расстояние в преобразованном пространстве пропорционально расстоянию Махаланобиса первоначального пространства. Отсюда можно сделать следующий вывод: алгоритмом кластеризации можно пользоваться в соответствии с одним из трех критериев без предварительного преобразования, если первоначально пользовались расстоянием Махаланобиса.
Большинство из методов кластеризации, которые обсуждались в предыдущих главах, были сформулированы на эвристической и интуитивной основе и имели детерминированную природу. Методы, основанные на оценивании функции плотности, составляют содержание статистического подхода и приводят к хорошо обоснованному понятию кластера (по крайней мере не хуже, чем в детерминированном случае). Один из основных моментов в статистическом подходе — оценивание моды. При этом имеются два способа: 1) моды оцениваются непосредственно из наблюдений; 2) сначала оценивается многомерная функция плотности f(x), на основе которой затем вычисляются моды.
При эвристических подходах выбор метода кластеризации зависит в основном от данных. При статистическом подходе кластер определяется в терминах характеристик функции плотности, которой соответствуют наблюдения. Этот подход более точен, так как при этом мы можем более точно сказать, что является целью кластерирования; статистическое оценивание даст объективный подход к достижению этой цели, а статистическая проверка поможет ответить на вопрос, как близко результат лежит от цели.
При статистическом подходе к кластеризации, предложенном в [40], в первую очередь оценивается многомерная функция плотности для произведенных наблюдений. Затем с целью распределения наблюдений по кластерам применяется метод «подъема на холм» (hill chimbing); кластеры определяются в терминах моды плотности f(x). Процедура «подъема на холм» заключается в следующем. Сначала оценивается f(x). Затем для каждого наблюдения  определяются два ближайших элемента (по минимальному расстоянию). Наблюдение становится частью «пути» или «холма» f(x), если ближайшее дает большее значение f(x). В результате перебора всех наблюдений получатся пути, которые поднимаются на «холмы» (или-холм)
определяются два ближайших элемента (по минимальному расстоянию). Наблюдение становится частью «пути» или «холма» f(x), если ближайшее дает большее значение f(x). В результате перебора всех наблюдений получатся пути, которые поднимаются на «холмы» (или-холм)  Наблюдения на каждом пути группируются и образуют кластеры.
Наблюдения на каждом пути группируются и образуют кластеры.
Путь заканчивается наблюдением, для которого ближайшее другое приводит к меньшему значению f(x). Алгоритм, основанный на минимальном расстоянии, может привести к большому числу путей (кластеров). Для устранения подобной ситуации для каждого наблюдения выбирается другое, расстояние до которого равно второму минимальному значению. Если для элемента (наблюдения)  первый ближайший элемент равен
первый ближайший элемент равен  а второй
а второй  то путь продолжается. Процедура первых двух ближайших наблюдений применяется для построения начального приближения разбиения на группы.
то путь продолжается. Процедура первых двух ближайших наблюдений применяется для построения начального приближения разбиения на группы.
Два пути по обеим сторонам «холма» (моды) в этой процедуре будут всегда несвязанными. Для устранения последствий этой ситуации сравним f(x) в трех точках между каждой вершиной и ее ближайшей вершиной.
Значения f(x) в этих точках указывают либо на то, что две ближайшие вершины составляют «холм» (в этом случае наблюдения, соответствующие двум путям, объединяются), либо на «долину», которая лежит между холмами, — в этом случае пути оставляем разомкнутыми. Процедура повторяется до тех пор, пока все наблюдения не будут соответствовать одному холму или пока между каждой вершиной и ближайшей к ней не будет
долины. Три точки между ближайшими вершинами могут быть выбраны, например, по следующему правилу: первая точка соответствует одной четвертой отрезка прямой, соединяющей вершины, вторая — одной второй отрезка, третья — трем четвертым отрезка.
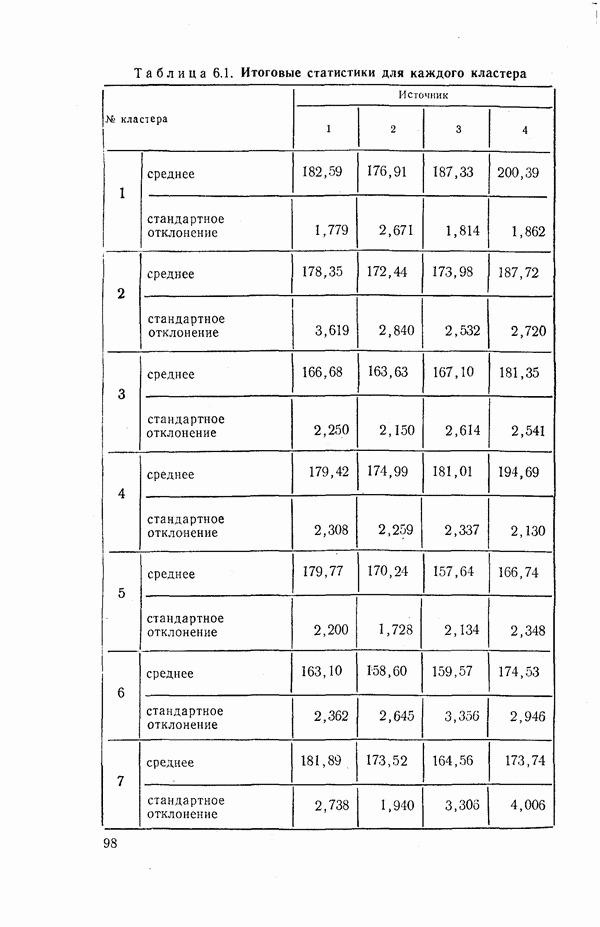
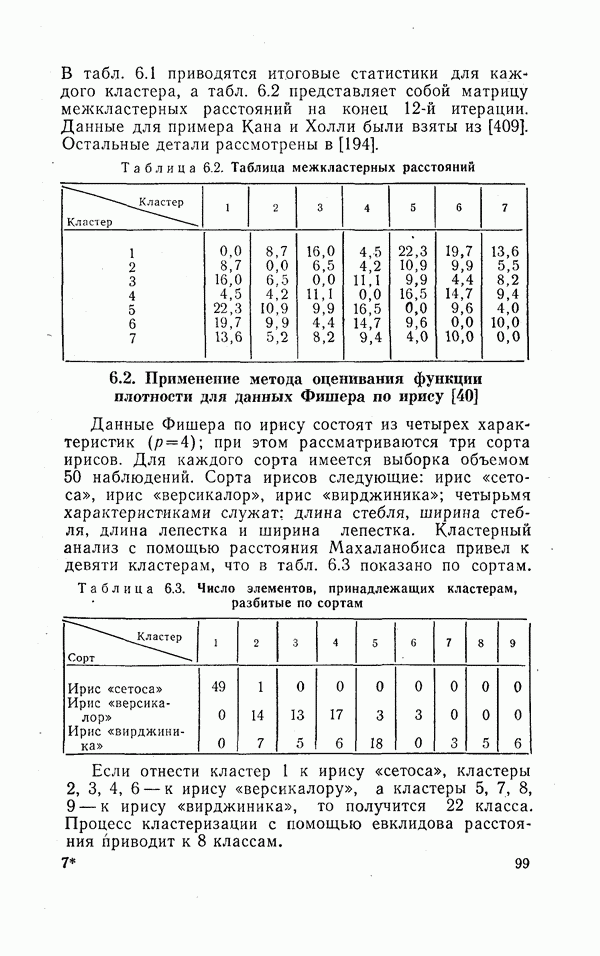
Брайен [40] описывает вычислительную программу, которая выполняет оценивание функции плотности и производит кластеризацию по методу, изложенному выше. Он приводит примеры, для которых этот метод привел к удовлетворительным результатам. В одном из этих примеров привлекаются хорошо известные данные наблюдений Фишера за ирисами; этот пример будет описан в следующей главе.
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
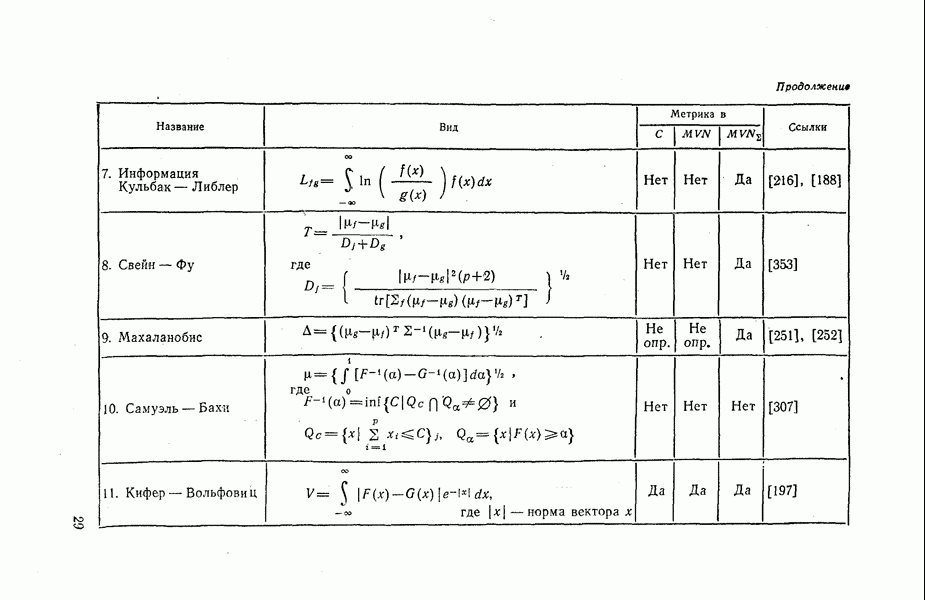
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
- ГЛАВА 6. ПРИЛОЖЕНИЯ
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература