| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. Задача кластерного анализа
Пусть m — целое число, меньшее, чем  . Задача кластерного анализа заключается в том, чтобы на основании данных, содержащихся в множестве X, разбить множество объектов
. Задача кластерного анализа заключается в том, чтобы на основании данных, содержащихся в множестве X, разбить множество объектов  на
на  кластеров (подмножеств)
кластеров (подмножеств)  так, чтобы каждый объект h принадлежал одному и только одному подмножеству разбиения и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными, в то время как объекты, принадлежащие разным кластерам, были разнородными (несходными).
так, чтобы каждый объект h принадлежал одному и только одному подмножеству разбиения и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными, в то время как объекты, принадлежащие разным кластерам, были разнородными (несходными).
Решением задачи кластерного анализа является разбиение, удовлетворяющее некоторому критерию оптимальности. Этот критерий может представлять собой некоторый функционал, - выражающий уровни желательности различных разбиений и группировок. Этот функционал часто называют целевой функцией. Например, в качестве целевой функции может быть взята внутригрупповая сумма квадратов отклонений (см. параграф 1.5). В качестве примера рассмотрим  объектов, обладающих одной характеристикой (т. е.
объектов, обладающих одной характеристикой (т. е.  результаты измерения пусть представляют собой множество Х={3, 4, 7, 4, 3, 3, 4, 4}. Сумма квадратов отклонений вычисляется по формуле
результаты измерения пусть представляют собой множество Х={3, 4, 7, 4, 3, 3, 4, 4}. Сумма квадратов отклонений вычисляется по формуле

где  представляет собой измерение
представляет собой измерение  объекта. Для нашего примера, содержащего 8 объектов, получим:
объекта. Для нашего примера, содержащего 8 объектов, получим:

Если множество X разбить на три группы:  , то все внутригрупповые суммы квадратов отклонений будут равны нулю:
, то все внутригрупповые суммы квадратов отклонений будут равны нулю:

где  обозначает сумму квадратов, соответствующую группе
обозначает сумму квадратов, соответствующую группе  Оптимальное значение для этого примера равно нулю при условии, что ведется разбиение натри группы. В общем случае следует рассматривать значение целевой функции в сочетании с желаемым числом групп. Далее будут определены различные виды целевых функций, многие из которых могут быть записаны в универсальной и общей форме.
Оптимальное значение для этого примера равно нулю при условии, что ведется разбиение натри группы. В общем случае следует рассматривать значение целевой функции в сочетании с желаемым числом групп. Далее будут определены различные виды целевых функций, многие из которых могут быть записаны в универсальной и общей форме.
Очевидно, для того чтобы «решить» задачу кластерного анализа, необходимо количественно определить понятия сходства и разнородности. Что означает «два объекта  различны»? Задача была бы решена, если бы
различны»? Задача была бы решена, если бы  объекты попадали в один и тот же кластер всякий раз, когда расстояние (отдаленность) между соответствующими точками и
объекты попадали в один и тот же кластер всякий раз, когда расстояние (отдаленность) между соответствующими точками и  было бы «достаточно малым», и, наоборот, попадали в разные кластеры, если бы расстояние между точками
было бы «достаточно малым», и, наоборот, попадали в разные кластеры, если бы расстояние между точками  было бы, «достаточно большим». Таким образом, для нашей цели следует рассмотреть понятие расстояния между точками
было бы, «достаточно большим». Таким образом, для нашей цели следует рассмотреть понятие расстояния между точками  из
из  с абстрактных позиций.
с абстрактных позиций.
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
- ГЛАВА 6. ПРИЛОЖЕНИЯ
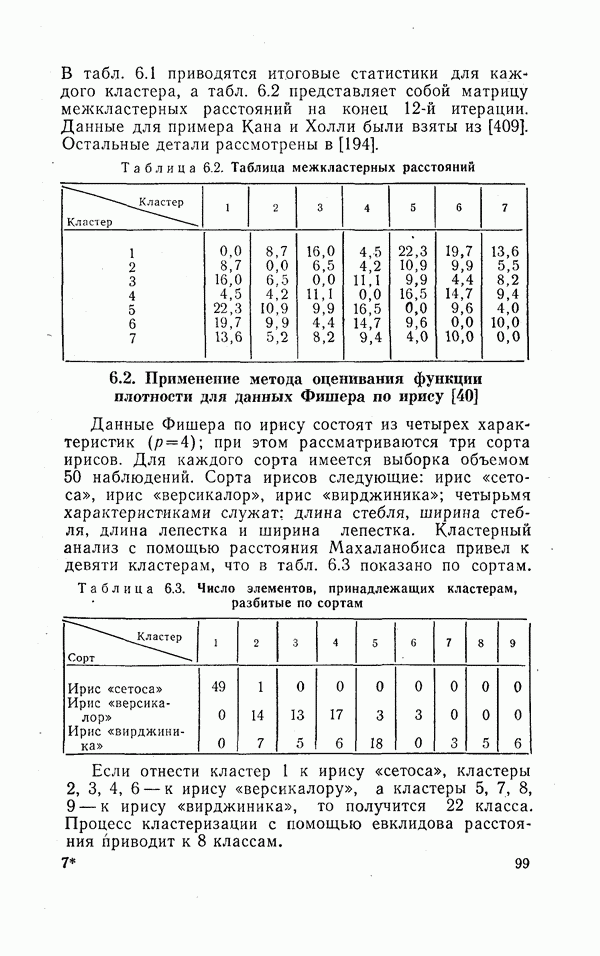
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература