| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.6. Кластерные методы, основанные на евклидовой метрике
Основные усилия в развитии методов кластеризации и классификации были направлены на построение методов, основанных на минимизации внутригрупповых сумм квадратов (отклонений). Они могут быть выражены в терминах евклидовых расстояний и называются методами минимальной дисперсии [396]. В этом параграфе мы рассмотрим различные методы кластеризации. Кроме
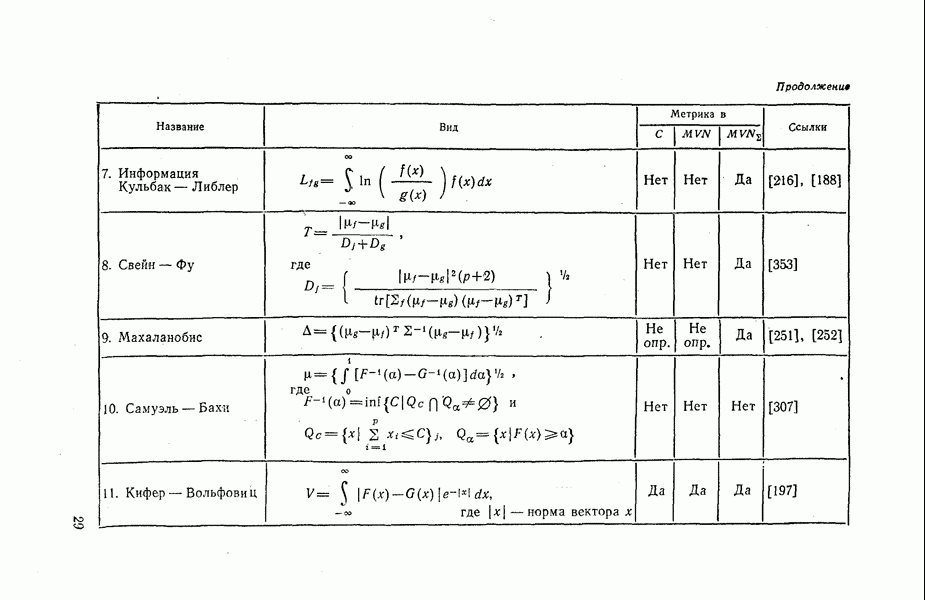
Таблица 1.3. Многомерные меры расстояния и их метрические свойства
(см. скан)
Продолжение
(см. скан)
того, мы увидим, что многие приемы кластеризации могут быть охвачены одним алгоритмом посредством общего соотношения, содержащего меры расстояния 
Рассмотрим матрицу наблюдений  . Квадрат евклидова расстояния между
. Квадрат евклидова расстояния между  определяется по формуле
определяется по формуле

Сейчас мы рассмотрим различные кластерные методы, основанные на этой мере расстояния. Наше описание методов весьма кратко и за деталями отсылаем читателей к соответствующим источникам.
Соренсен [338] описывает так называемый метод полных связей (complete linkage). Суть этого метода заключается в том, что два объекта, принадлежащих одной и той же группе (кластеру), имеют коэффициент сходства, который меньше некоторого порогового значения s. В терминах евклидова расстояния d это означает, что расстояние между двумя точками (объектами) кластера не должно превышать некоторого порогового значения  . В этом случае
. В этом случае  определяет максимально допустимый диаметр подмножества, образующего кластер.
определяет максимально допустимый диаметр подмножества, образующего кластер.
МакНотон-Смит [234] предлагает последовательную процедуру, которую назвал методом максимального локального расстояния (см. определение 1.9); этот метод имеет много общего с предыдущим. Каждый индивид (объект) рассматривается как одноточечный кластер. Объекты группируются последовательно по следующему правилу: два кластера объединяются, если максимальное расстояние между точками одного кластера и точками другого минимально. Процедура состоит из  шагов и результатом являются разбиения, которые совпадают со всевозможными разбиениями в методе Соренсена для любых пороговых значений.
шагов и результатом являются разбиения, которые совпадают со всевозможными разбиениями в методе Соренсена для любых пороговых значений.
Ворд [387] в качестве целевой функции применяет внутригрупповую сумму квадратов (ВСК) отклонений, которая есть не что иное, как сумма квадратов расстояний между каждой точкой (объектом) и средней по кластеру, содержащему этот объект. Его метод также представляет собой последовательную процедуру; на каждом шаге объединяются такие два кластера, которые приводят к минимальному увеличению целевой
функции, т. е. ВСК. При объединении кластеров  элементов) и
элементов) и  элементов) это увеличение, как следует из параграфа 1.5, равно:
элементов) это увеличение, как следует из параграфа 1.5, равно:

где X и Y обозначают векторы средних по кластерам J и  Метод Ворда направлен на объединение близко расположенных кластеров.
Метод Ворда направлен на объединение близко расположенных кластеров.
Сокал и Миченер [334] описывают процедуру, которую назвали центроидным методом. Расстояние между двумя кластерами I и  в этом методе определяется как евклидово расстояние между центрами (средними) этих кластеров, т. е. как
в этом методе определяется как евклидово расстояние между центрами (средними) этих кластеров, т. е. как  Кластеризация осуществляется поэтапно [223]: на каждом из
Кластеризация осуществляется поэтапно [223]: на каждом из  шагов объединяют два кластера
шагов объединяют два кластера  имеющие минимальное значение
имеющие минимальное значение  Если
Если  много больше
много больше  то центры
то центры  близки друг к другу и характеристики
близки друг к другу и характеристики  при объединении кластеров практически игнорируются. Это наталкивает на мысль назвать этот метод методом «взвешенных групп».
при объединении кластеров практически игнорируются. Это наталкивает на мысль назвать этот метод методом «взвешенных групп».
Другой метод, предложенный Сокалом и Миченером [334], называется двухгрупповым и опирается на связь между объектом i и кластером I. Эта связь выражается в виде среднего коэффициента сходства между объектом i и всеми объектами, входящими в кластер  . Для того чтобы средний коэффициент сходства выразить через евклидово расстояние, обозначим векторы, входящие в кластер
. Для того чтобы средний коэффициент сходства выразить через евклидово расстояние, обозначим векторы, входящие в кластер  соответственно через
соответственно через  , а через
, а через  -центр кластера
-центр кластера  . Тогда среднее расстояние
. Тогда среднее расстояние  между объектом
между объектом  и всеми объектами из I будет равно:
и всеми объектами из I будет равно:

где Y обозначает вектор, соответствующий  . Далее
. Далее

Первое слагаемое правой части уравнения обозначим  и назовем внутригрупповой дисперсией объектов из
и назовем внутригрупповой дисперсией объектов из  второе слагаемое представляет собой квадрат расстояния между объектом i и центром кластера
второе слагаемое представляет собой квадрат расстояния между объектом i и центром кластера  . Процедура последовательной кластеризации заключается в том, что объект
. Процедура последовательной кластеризации заключается в том, что объект  , для которого
, для которого  минимально, присоединяется к кластеру I. Из (1.11) легко видеть, что если два кластера имеют сравнимые дисперсии, то среднее расстояние
минимально, присоединяется к кластеру I. Из (1.11) легко видеть, что если два кластера имеют сравнимые дисперсии, то среднее расстояние  минимизирует расстояние между объектом i и центром кластера
минимизирует расстояние между объектом i и центром кластера  . Для кластеров с различными дисперсиями объединение происходит в первую очередь с кластером меньшей дисперсии.
. Для кластеров с различными дисперсиями объединение происходит в первую очередь с кластером меньшей дисперсии.
Ланс и Уильямс [225] обобщают двухгрупповой метод и определяют среднее сходство между двумя кластерами  как среднее сходство между всеми парами объектов из
как среднее сходство между всеми парами объектов из  Этот метод они назвали методом групповых средних. Кластеры строятся последовательно; два кластера с минимальным средним коэффициентом сходства объединяются. Для того чтобы среднее сходство выразить в_терминах евклидова расстояния, обозначим через X и Y соответственно средние кластеров
Этот метод они назвали методом групповых средних. Кластеры строятся последовательно; два кластера с минимальным средним коэффициентом сходства объединяются. Для того чтобы среднее сходство выразить в_терминах евклидова расстояния, обозначим через X и Y соответственно средние кластеров  . Средний квадрат расстояний между объектами кластеров
. Средний квадрат расстояний между объектами кластеров  обозначенный через
обозначенный через  будет равен
будет равен

Первое слагаемое правой части выражения есть внутригрупповая дисперсия кластера  , а второе слагаемое — средний квадрат расстояний между
, а второе слагаемое — средний квадрат расстояний между 
 . Таким образом, второе слагаемое может быть переписано как
. Таким образом, второе слагаемое может быть переписано как

откуда

т. е. минимизация среднего сходства эквивалентна минимизации (1.12).
Боннер [33] описывает метод, в котором объект, служащий начальной точкой, выбирается случайно. Все объекты, лежащие на расстоянии от начальной точки не больше  , принимаются за первый кластер. Из оставшихся точек снова случайным образом выбирается объект и процесс повторяется, как и предшествовавший. В результате все точки будут разбиты на группы.
, принимаются за первый кластер. Из оставшихся точек снова случайным образом выбирается объект и процесс повторяется, как и предшествовавший. В результате все точки будут разбиты на группы.
Хиверинен [171] рассматривает процедуру, аналогичную Боннеру, но в качестве начального объекта кластеризации выбирает не случайную, а так называемую «типическую» точку. Для определения «типических» точек он пользуется статистикой потери информации, причем эти точки лежат на минимальном расстоянии от центра оставшегося множества объектов.
В процедуре Болла и Холла [18] первоначальные К кластеров формируются случайным отбором К точек, к которым затем присоединяется каждая из оставшихся  точек — по минимальному расстоянию к той или иной из них. Затем находятся центры кластеров и два кластера
точек — по минимальному расстоянию к той или иной из них. Затем находятся центры кластеров и два кластера  объединяются, если
объединяются, если  меньше некоторого порогового значения
меньше некоторого порогового значения  . Наоборот, если внутригрупповая дисперсия кластера
. Наоборот, если внутригрупповая дисперсия кластера  по некоторой переменной
по некоторой переменной  превосходит пороговое значение
превосходит пороговое значение  то кластер разбивается. Таким образом, дисперсии
то кластер разбивается. Таким образом, дисперсии  кластеров, получающихся в результате этой процедуры, ограничены:
кластеров, получающихся в результате этой процедуры, ограничены:

где  — число переменных. Вместо центра первоначального кластера рассматриваются центры новых образовавшихся
— число переменных. Вместо центра первоначального кластера рассматриваются центры новых образовавшихся
кластеров и процесс продолжается до тех пор пока не сойдется. Процедура Болла и Холла становится довольно популярной.
МакКвин [237] предлагает метод, аналогичный методу Болла и Холла. Случайным образом отбирается k объектов, которые принимаются в качестве центров кластеризации. Для каждого объекта отыскивается ближайшая точка кластеризации, и если расстояние от выбранного объекта до этой точки не больше заданного уровня  , то объект приписывают к кластеру найденной точки кластеризации. Если это расстояние больше
, то объект приписывают к кластеру найденной точки кластеризации. Если это расстояние больше  , то объект образует новый кластер. После этого вычисляются новые центры кластеров. Если расстояние между цен трами двух кластеров меньше другого априорно заданного уровня, то соответствующие кластеры объединяются. Процесс продолжается до сходимости.
, то объект образует новый кластер. После этого вычисляются новые центры кластеров. Если расстояние между цен трами двух кластеров меньше другого априорно заданного уровня, то соответствующие кластеры объединяются. Процесс продолжается до сходимости.
Метод Себестьена [315] имеет много общего с предыдущим. Однако по Себестьену объект принадлежит кластеру, если расстояние d до центра - кластера меньше  ; если же это расстояние больше
; если же это расстояние больше  то этот объект образует новую точку кластеризации. Однако если
то этот объект образует новую точку кластеризации. Однако если  , то объект выбывает из рассмотрения до следующей итерации.
, то объект выбывает из рассмотрения до следующей итерации.
Дженси [174] предложил процедуру, сходную с предложенной МакКвином. Однако в методе Дженси случайным образом выбирается k течек не из  рассматриваемых объектов, как в методе МакКвина, а из всего пространства
рассматриваемых объектов, как в методе МакКвина, а из всего пространства  В качестве минимизируемой целевой функции берется внутригрупповая сумма квадратов отклонений.
В качестве минимизируемой целевой функции берется внутригрупповая сумма квадратов отклонений.
Форджи [114] рассматривает метод, сходный с методом Дженси. Разбиение объектов на кластеры в этом методе близко к разбиению, предложенному Дженси. Здесь также пользуются минимизацией внутригрупповой суммы квадратов.
Основная причина популярности евклидовой метрики в кластерном анализе заключается скорее всего в том, что она наиболее близка к интуитивному представлению о расстоянии, а также, как следует из уравнения (1.7), в том, что она тесно связана с ВСК.
Имеются также и возражения против подхода, основанного на минимальной дисперсии в кластерном анализе. Так, изменение масштаба приведет к другому разбиению на кластеры. С этими и другими возражениями
и их обсуждением читатель может ознакомиться по работе Уишарта [396]. Там же рассматриваются методы, описанные выше. Фридман и Рубин [122] обсуждают некоторые инвариантные критерии группировки наблюдений.
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
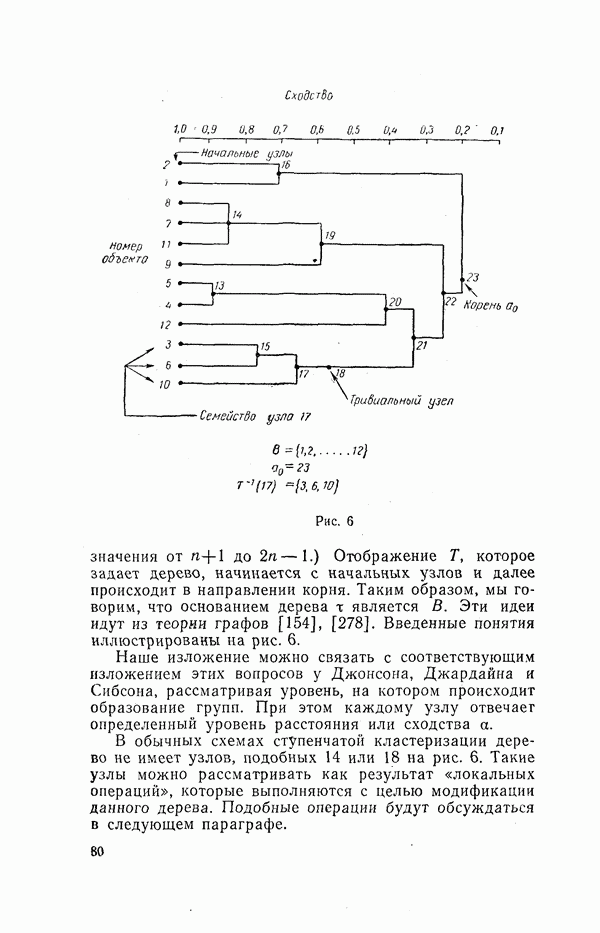
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
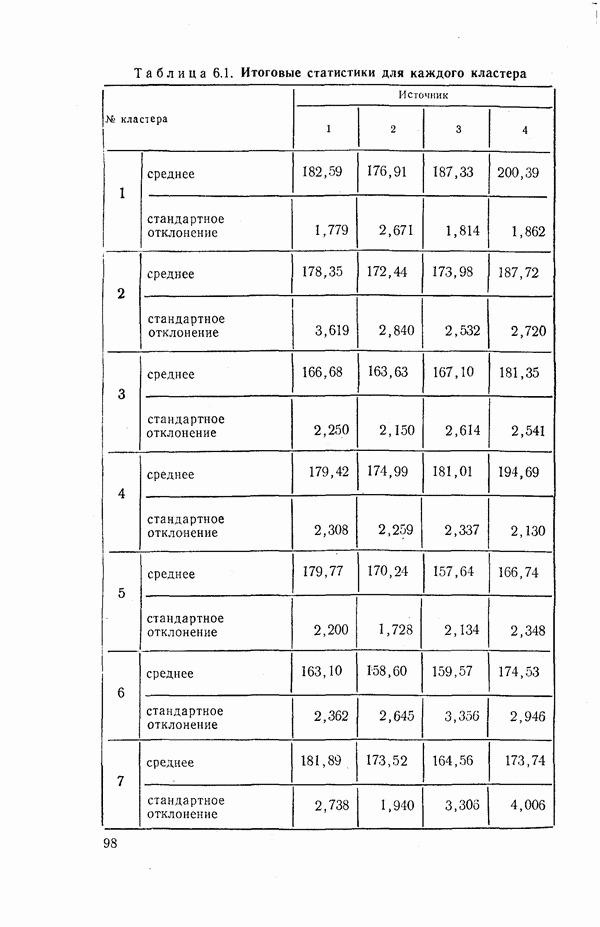
- ГЛАВА 6. ПРИЛОЖЕНИЯ
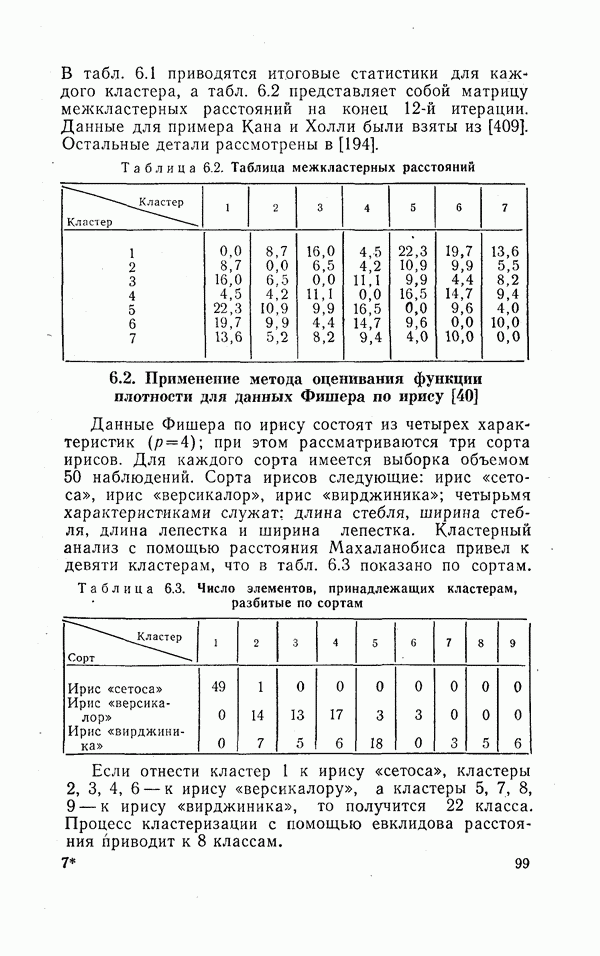
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература