| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.3. Функции расстояния
Определение 1.1. Неотрицательная вещественнозначная функция  называется функцией расстояния (метрикой), если:
называется функцией расстояния (метрикой), если:

Значение  для заданных
для заданных  называется
называется  расстоянием между
расстоянием между  и эквивалентно расстоянию между U и
и эквивалентно расстоянию между U и  соответственно выбранным характеристикам
соответственно выбранным характеристикам 
В таблице 1.1 приводятся примеры некоторых наиболее употребительных функций расстояния.
Евклидова метрика очень популярна и наиболее употребительна. Метрика  абсолютных значений наиболее простая с вычислительной точки зрения. Сюпремум-норма также легко вычисляется и включает в себя процедуру упорядочивания.
абсолютных значений наиболее простая с вычислительной точки зрения. Сюпремум-норма также легко вычисляется и включает в себя процедуру упорядочивания.  -норма охватывает функции расстояния 1, 2 и 3, соответственно
-норма охватывает функции расстояния 1, 2 и 3, соответственно 
Расстояние Махаланобиса часто называют обобщенным евклидовым расстоянием.  обычно обозначает
обычно обозначает
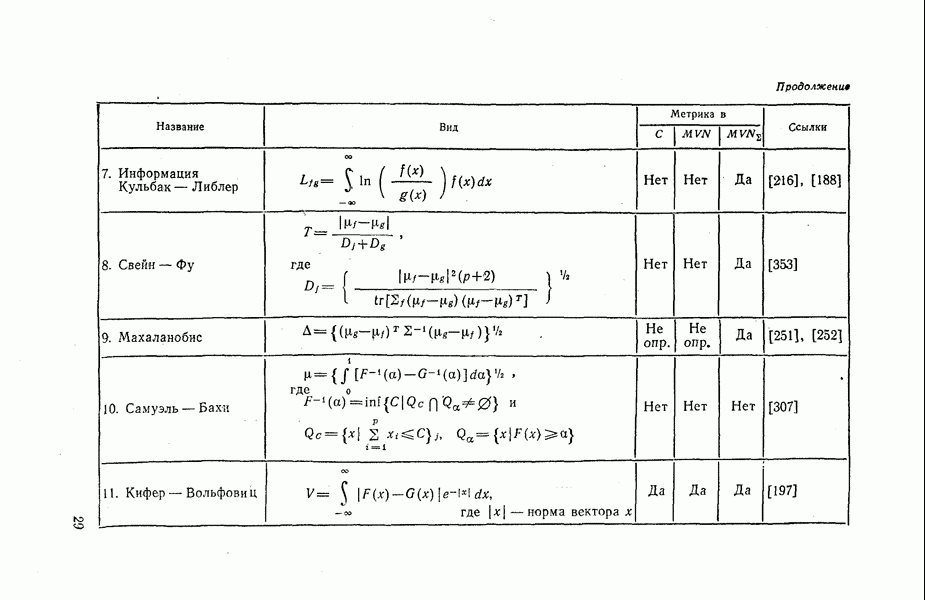
Таблица 1.1. Некоторые функции расстояния

матрицу, обратную к матрице рассеяния (см. параграф 1.5). Расстояние Махаланобиса инвариантно относительно невырожденных линейных преобразований. Рассмотрим преобразование  . Тогда
. Тогда

Существуют другие, эвристические, меры отдаленности, не являющиеся расстояниями с точки зрения определения 1.1, которые, однако, также применяются на практике. Например, мера Джеффриса — Матуситы [81], [82], [259], которая определяется по формуле

и другая мера, известная под названием «коэффициент дивергенции» [55].

Мера Джеффриса — Матуситы первоначально была введена в качестве расстояния между двумя функциями плотностей вероятности, однако в форме (1.1) она может быть применена и как мера расстояния между парой векторов. В первоначальном применении коэффициента дивергенции  были действительными средними
были действительными средними  и рассматривались как расстояние между выборочными средними двух выборок.
и рассматривались как расстояние между выборочными средними двух выборок.
Следующая теорема позволяет упорядочить функции расстояния, определяемые по  -норме.
-норме.
Теорема 1.1. Неравенство  выполняется для всех
выполняется для всех  из
из  тогда и только тогда, когда
тогда и только тогда, когда 
Напомним, что из определения расстояния следует, что для 
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
- ГЛАВА 6. ПРИЛОЖЕНИЯ
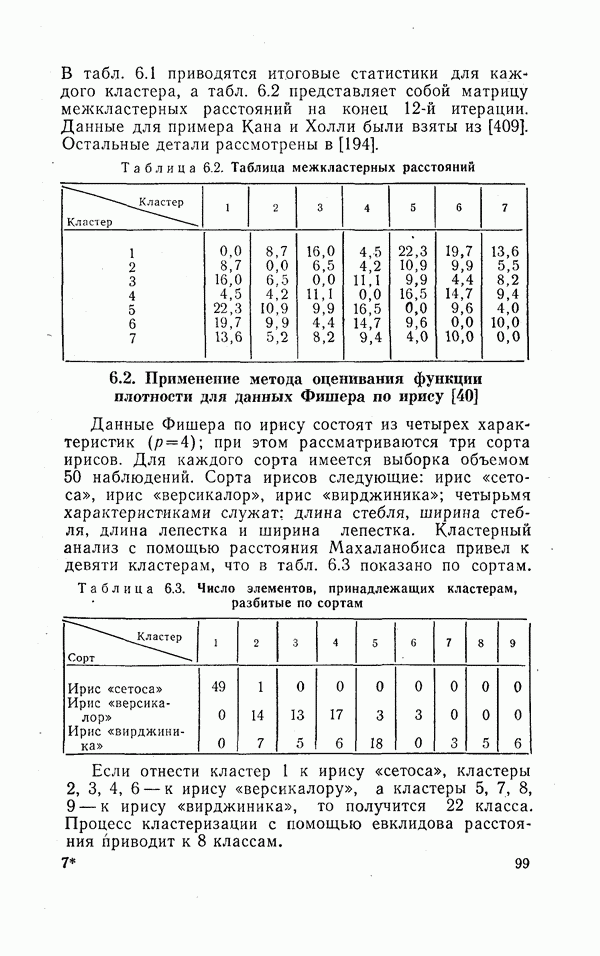
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература