| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5. Расстояние между кластерами и их сходство
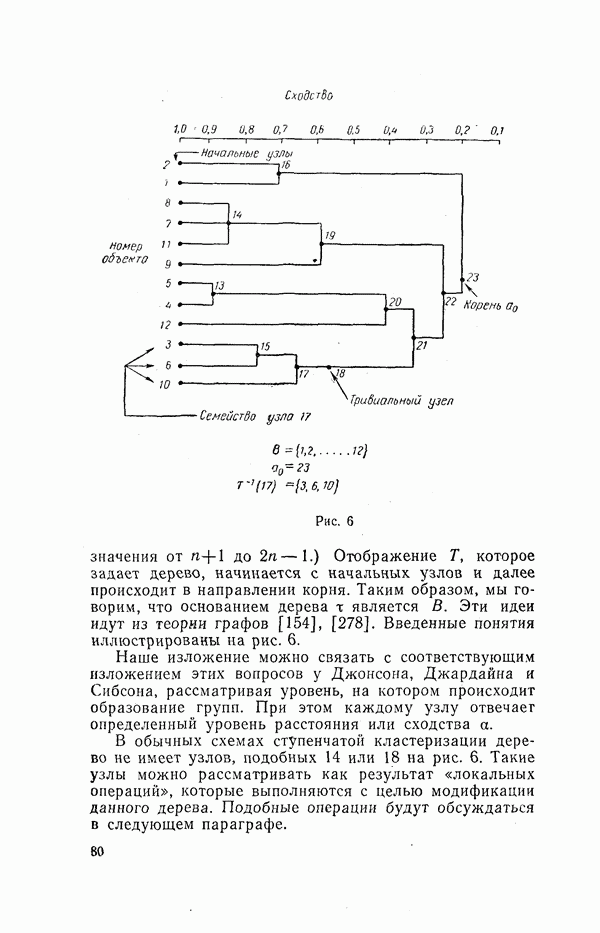
Как мы увидим позднее, многие процедуры при кластеризации совершаются ступенчато. Это означает, что два наиболее близко расположенных объекта  объединяются и рассматриваются как один кластер. Это приводит к тому, что число объектов уменьшается и становится равным
объединяются и рассматриваются как один кластер. Это приводит к тому, что число объектов уменьшается и становится равным  причем один кластер будет содержать два объекта, а
причем один кластер будет содержать два объекта, а  остальных по одному. Процесс можно повторять до тех пор, пока все объекты не сгруппируются в один кластер. В рассмотренной
остальных по одному. Процесс можно повторять до тех пор, пока все объекты не сгруппируются в один кластер. В рассмотренной
последовательной процедуре пользуются интуитивным представлением о расстоянии между объектом и кластером и расстоянии между двумя кластерами.
Неотъемлемой частью задачи кластерного анализа является понятие оптимального критерия (целевой функции), которое позволяет установить, когда достигается желательное разбиение. Для введения подобного критерия необходимо найти меру внутренней однородности кластера и меру разнородности кластеров между собой.
Пусть  обозначают два кластера объектов, принадлежащих некоторой популяции
обозначают два кластера объектов, принадлежащих некоторой популяции  . Пусть
. Пусть  будет множеством характеристик, которые генерируют два множества измерений
будет множеством характеристик, которые генерируют два множества измерений  соответствующие I и
соответствующие I и 
Определение 1.8. Обозначим через  множество всех расстояний. Величину
множество всех расстояний. Величину

будем называть минимальным локальным расстоянием (nearest neighbor distance) [395] между кластерами  соответствующим данной функции расстояния
соответствующим данной функции расстояния 
Определение 1.9. Пусть  определено так же, как и в определении 1.8. Тогда
определено так же, как и в определении 1.8. Тогда 

назовем максимальным локальным расстоянием (furthest neighbor distance) [234] между 
Определение 1.10. Величина

есть среднее расстояние [225] между  соответствующее данной функции расстояния d.
соответствующее данной функции расстояния d.
При оперировании понятием статистического рассеяния иногда пользуются следующей мерой расстояния между кластерами 
Определение 1.11. Величину

где

называют статистическим расстоянием между кластерами I и 
Меру  очевидно, можно обосновать следующим образом. Рассмотрим два кластера
очевидно, можно обосновать следующим образом. Рассмотрим два кластера  которые в свою очередь составляют кластер К, где
которые в свою очередь составляют кластер К, где  (значок
(значок  означает объединение); тогда по формуле
означает объединение); тогда по формуле 

где 
Поэтому

поскольку  . Заметим, что
. Заметим, что

поэтому

и

Окончательно

Последнее выражение будем называть матрицей межгруппового рассеяния.
В результате получим:

где  обозначают внутригрупповое рассеяние
обозначают внутригрупповое рассеяние  Матрицу
Матрицу

назовем матрицей межгруппового рассеяния, а след этой матрицы

- статистическим расстоянием между кластерами  . След матрицы (1.10) называют внутригрупповой суммой квадратов (ВСК). При объединении
. След матрицы (1.10) называют внутригрупповой суммой квадратов (ВСК). При объединении  в один кластер К, очевидно, ВСК возрастает.
в один кластер К, очевидно, ВСК возрастает.
Уравнение (1.9) статистики интерпретируют следующим образом: «общая сумма квадратов равна внутригрупповой сумме квадратов плюс межгрупповая сумма квадратов». Сумма  есть «внутригрупповая сумма квадратов», а выражение (1.10) представляет «межгрупповую сумму квадратов», записанную в матричной форме. Подобным образом можно было бы построить новые меры расстояния между кластерами, воспользовавшись другими функциями расстояния, рассмотренными в параграфе 1.3.
есть «внутригрупповая сумма квадратов», а выражение (1.10) представляет «межгрупповую сумму квадратов», записанную в матричной форме. Подобным образом можно было бы построить новые меры расстояния между кластерами, воспользовавшись другими функциями расстояния, рассмотренными в параграфе 1.3.
Рассмотрим теперь несколько иной подход к проблеме измерения расстояния между кластерами. Предположим, что каждый кластер представляет собой выборку из некоторой генеральной совокупности (популяции). Обозначим через  функции плотности вероятности, соответствующие кластерам
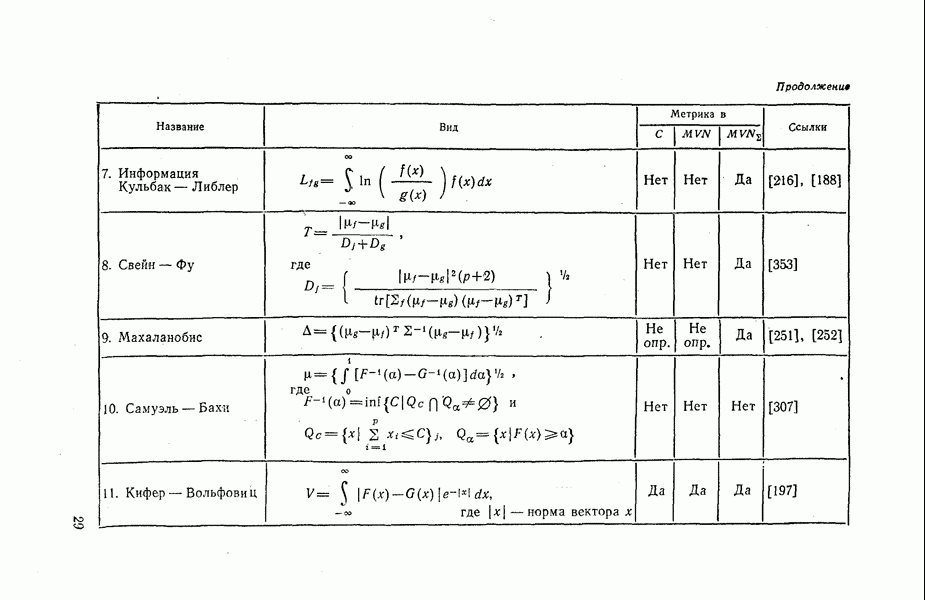
функции плотности вероятности, соответствующие кластерам  . Уоккер и Лангриб [383] рассматривают различные многомерные формы мер расстояния и их метрические свойства. Их результаты сведены в табл. 1.3, где С обозначает класс всех
. Уоккер и Лангриб [383] рассматривают различные многомерные формы мер расстояния и их метрические свойства. Их результаты сведены в табл. 1.3, где С обозначает класс всех  -мерных абсолютно непрерывных функций распределения, MVN — класс многомерных нормальных распределений, MVN — класс многомерных нормальных распределений с одинаковыми матрицами ковариаций. В таблице также приводятся метрические свойства мер расстояния соответственно для трех классов функций распределения.
-мерных абсолютно непрерывных функций распределения, MVN — класс многомерных нормальных распределений, MVN — класс многомерных нормальных распределений с одинаковыми матрицами ковариаций. В таблице также приводятся метрические свойства мер расстояния соответственно для трех классов функций распределения.
Эти меры межкластерного расстояния могут оказаться весьма полезными в случае нормального распределения. В этом случае оценкам  и
и  служат соответственно X и
служат соответственно X и  и меры табл. 1.3 могут быть легко вычислены. Коэффициент дивергенции применяется в приложениях дискриминантного (классификационного) анализа [226]. Мера Джеффриса — Матуситы применялась в приложениях дискриминантного анализа к сельскохозяйственным данным для классификации полей [169].
и меры табл. 1.3 могут быть легко вычислены. Коэффициент дивергенции применяется в приложениях дискриминантного (классификационного) анализа [226]. Мера Джеффриса — Матуситы применялась в приложениях дискриминантного анализа к сельскохозяйственным данным для классификации полей [169].
В большинстве работ, указанных в табл. 1.3, рассматриваются одномерные виды мер расстояния. Эти меры обсуждаются в работе Уоккера и Лангриба [383]; там же предлагается их обобщение на многомерный случай. Для более полного ознакомления с мерами, представленными в табл. 1.3, отсылаем читателя к работе [383].
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
- ГЛАВА 6. ПРИЛОЖЕНИЯ
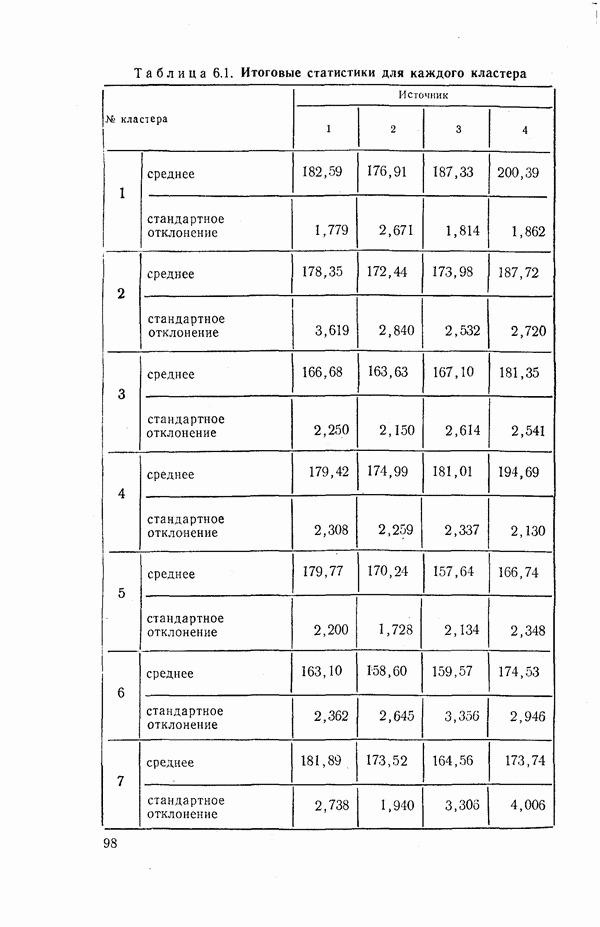
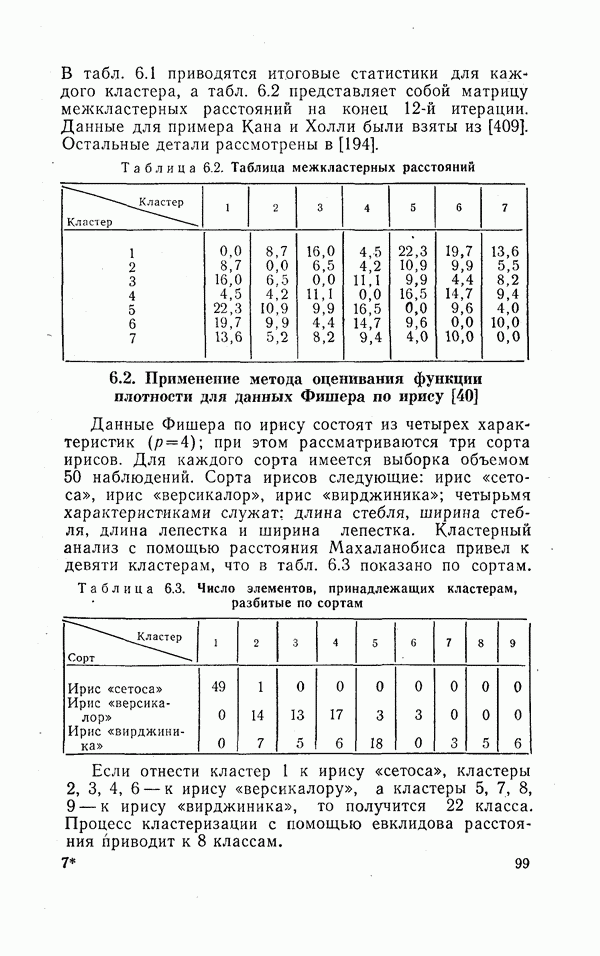
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература