| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. Модель динамического программирования Дженсена
В отличие от линейного программирования, для которого существует точная стандартная формулировка задачи, в динамическом программировании таковая отсутствует.
В задачах динамического программирования соответствующие формулы и уравнения зависят от конкретной постановки проблемы. При этом, как правило, задачу сводят к последовательности рекурсивны формул или уравнений, отражающих связи, имевших место в задаче, по которым и отыскивается «оптимальное» решение. Рао [291] приводит формулировку применения динамического программирования для решения кластерной проблемы при  Дженсен [183] описывает более общую ситуацию, которую мы сейчас и рассмотрим.
Дженсен [183] описывает более общую ситуацию, которую мы сейчас и рассмотрим.
На языке динамического программирования задачу кластеризации Дженсен описывает в виде следующих рекурсивных уравнений:

где  — число непересекающихся непустых подмножеств, на которые разбивается
— число непересекающихся непустых подмножеств, на которые разбивается  объектов;
объектов;
 — индекс или переменная шага;
— индекс или переменная шага;
 если
если  и равно
и равно  если
если 
 — переменная состояния, характеризующая данное множество объектов на шаге
— переменная состояния, характеризующая данное множество объектов на шаге 
 — переменная состояния, характеризующая данное множество объектов на шаге
— переменная состояния, характеризующая данное множество объектов на шаге  — подмножество всех объектов, содержащихся в z и не содержащихся в у;
— подмножество всех объектов, содержащихся в z и не содержащихся в у;
 — «переходные издержки» (transition cost) объектов в кластере
— «переходные издержки» (transition cost) объектов в кластере 
Переменные у и z представляют собой два состояния (множества объектов) на шаге  и k соответственно.
и k соответственно.
Разность  представляет собой те объекты, которые содержатся на шаге k и не содержатся на шаге
представляет собой те объекты, которые содержатся на шаге k и не содержатся на шаге  означает «переходные издержки», т. е. ВСК объектов, объединенных на шаге
означает «переходные издержки», т. е. ВСК объектов, объединенных на шаге  дает минимальное значение ВСК при разбиении объектов, содержащихся в
дает минимальное значение ВСК при разбиении объектов, содержащихся в  , на k непустых непересекающихся подмножеств. Очевидно, формула (3.3) приводит к большому числу вычислений. Напомним читателю, что, как следует из уравнения (3.2) параграфа 3.1, где
, на k непустых непересекающихся подмножеств. Очевидно, формула (3.3) приводит к большому числу вычислений. Напомним читателю, что, как следует из уравнения (3.2) параграфа 3.1, где  обозначает кластер из
обозначает кластер из  объектов, переходные издержки
объектов, переходные издержки  равны:
равны:

что совпадает в ВСК кластера 
Заметим, что число шагов равно  если
если  если
если  Это объясняется тем, что если
Это объясняется тем, что если  то обязательно существуют по крайней мере
то обязательно существуют по крайней мере  кластеров, состоящих из одного объекта. Переходные издержки Т для кластера из одного объекта равны нулю, поэтому вклад такого кластера в W также равен нулю. Следовательно, процесс может закончиться на шаге
кластеров, состоящих из одного объекта. Переходные издержки Т для кластера из одного объекта равны нулю, поэтому вклад такого кластера в W также равен нулю. Следовательно, процесс может закончиться на шаге  при этом все оставшиеся кластеры будут содержать по одному объекту. При вычислении
при этом все оставшиеся кластеры будут содержать по одному объекту. При вычислении  необходимо подчеркнуть, что объекты, соответствующие любому состоянию на шаге k, состоят из объектов некоторого множества, соответствующего некоторому состоянию у на шаге
необходимо подчеркнуть, что объекты, соответствующие любому состоянию на шаге k, состоят из объектов некоторого множества, соответствующего некоторому состоянию у на шаге  и объектов, содержащихся в другом множестве, содержащемся в
и объектов, содержащихся в другом множестве, содержащемся в 
В качестве примера, иллюстрирующего рекурсивные уравнения (3.3), рассмотрим 37-е состояние первого шага и 15-е состояние второго шага; напомним, что  (табл. 3.1). В этом случае
(табл. 3.1). В этом случае  обозначает объекты
обозначает объекты  состояния первого шага, z — объекты
состояния первого шага, z — объекты  состояния второго шага,а
состояния второго шага,а  — объекты (5, 6). «Переходными издержками» из 37-го состояния в 15-е будут:
— объекты (5, 6). «Переходными издержками» из 37-го состояния в 15-е будут:

Переходными издержками из 37-го состояния первого шага в первое состояние второго шага будут:

На первом шаге алгоритма динамического программирования для данного множества кластеров вычисляется значение  . В этом случае
. В этом случае

где  обозначает данное множество объектов. Значение
обозначает данное множество объектов. Значение  вычисляется для каждого из кластеров первого шага. Максимальное число объектов, содержащихся в кластере на первом шаге, обозначим через
вычисляется для каждого из кластеров первого шага. Максимальное число объектов, содержащихся в кластере на первом шаге, обозначим через 

это означает, что максимальный кластер содержит  объектов, а все остальные кластеры по одному. Минимальное число объектов в кластере на первом шаге, которое обозначим через
объектов, а все остальные кластеры по одному. Минимальное число объектов в кластере на первом шаге, которое обозначим через  равно:
равно:

если  делится надело наш, и
делится надело наш, и

если  не делится нацело на
не делится нацело на  ;
;  обозначает наибольшее число, меньшее или равное
обозначает наибольшее число, меньшее или равное  Общее число кластеров на первом шаге, которое обозначим через NS (1), равно:
Общее число кластеров на первом шаге, которое обозначим через NS (1), равно:

На первом шаге алгоритма для всех возможных кластеров NS (1) вычисляется значение 
В общем случае максимальное число объектов в одном состоянии на шаге k равно максимальной сумме компонент всех форм распределения с первого по  шаг включительно. Минимальное число состояний равно минимальной сумме компонент форм распределения,
шаг включительно. Минимальное число состояний равно минимальной сумме компонент форм распределения,  определяются из следующих уравнений:
определяются из следующих уравнений:

и

если  делится на
делится на  нацело. В противном случае
нацело. В противном случае

Число состояний на шаге k определяется как

Общее число состояний при динамическом программировании равно

В рассмотренном подходе большое значение имеет общее число значений  при переходе от шага
при переходе от шага  к шагу k, т. е. число способов построения состояния на шаге k. Состояния последовательных шагов связываются дугами. Два состояния на шаге k и
к шагу k, т. е. число способов построения состояния на шаге k. Состояния последовательных шагов связываются дугами. Два состояния на шаге k и  связываются допустимыми дугами, если объекты состояния на шаге k связаны с состоянием на шаге
связываются допустимыми дугами, если объекты состояния на шаге k связаны с состоянием на шаге  Отсюда следует, что допустимая дуга не может связывать состояние на шаге
Отсюда следует, что допустимая дуга не может связывать состояние на шаге  и состояние на шаге k, если
и состояние на шаге k, если  некоторого состояния на шаге
некоторого состояния на шаге  не связан ни с одним состоянием на шаге k для 2
не связан ни с одним состоянием на шаге k для 2
В алгоритме динамического программирования общее число допустимых дуг равно:

где  обозначает общее число дуг между шагами k и
обозначает общее число дуг между шагами k и  для
для  . Значение
. Значение  находится по формуле
находится по формуле

где

В уравнениях (3.11) и (3.12) i обозначает число объектов в классе (допустимых) состояний шага 6. Всего имеется  таких состояний, содержащих i объектов; это следует из того факта, что число подмножеств, содержащих i объектов, равно
таких состояний, содержащих i объектов; это следует из того факта, что число подмножеств, содержащих i объектов, равно  . Символом j обозначена число объектов, которые комбинируются с i объектами и образуют новое состояние шага
. Символом j обозначена число объектов, которые комбинируются с i объектами и образуют новое состояние шага  Очевидно, для состояния порядка
Очевидно, для состояния порядка  присутствующего на шаге
присутствующего на шаге  Если
Если  удовлетворяет приведенному условию, то существует
удовлетворяет приведенному условию, то существует  множеств порядка
множеств порядка  которые добавляются к i объектам 6 раз.
которые добавляются к i объектам 6 раз.
Дженсен предлагает способ вычисления эффективности динамического программирования по сравнению с методом полного перебора. Эта эффективность измеряется отношением общего числа переходных вычислений при динамическом программировании к соответствующему числу вычислений при полном переборе. В качестве альтернативы в числителе можно взять общее число допустимых дуг. В любом случае процедура динамического программирования довольно эффективна. Однако применение методов динамического программирования требует привлечения дополнительной памяти ЭВМ; соответственно увеличивается время вычислений за счет обращения к памяти машины, что в конечном счете может привести к тому, что метод полного перебора окажется более предпочтительным. В любом случае для больших пят, может быть, целесообразнее воспользоваться другими методами, например ISODATA [18] или ступенчатым.
Для иллюстрации методики, предложенной Дженсеном, рассмотрим наш пример, в котором  . В этом случае
. В этом случае  и поэтому нам необходимо рассмотреть
и поэтому нам необходимо рассмотреть  шага, т. е.
шага, т. е.  . Кроме того,
. Кроме того,

как следует из табл. 3.1.
Общее число состояний на шаге 0, 1, 2 и 3 находятся из формул:

Эти состояния приведены в табл. 3.1. Таким образом, общее число состояний равно 73. Это число можно было бы получить непосредственным подсчетом состояний в табл. 
Для  из уравнения (3.12) находим:
из уравнения (3.12) находим:

и общее число допустимых дуг между шагами 1 и 2 равно  .
.
Для  получим:
получим:

Таким образом, общее число допустимых дуг в нашем примере, как следует из (3.10), равно:

В параграфе 3.1 было показано, что половина состояний на шаге  соответствующихкомпонентам форм распределения
соответствующихкомпонентам форм распределения  лишние, и 60 дуг, соответствующие компонентам
лишние, и 60 дуг, соответствующие компонентам  в конечном счете приводят к форме распределения
в конечном счете приводят к форме распределения  которая эквивалентна форме
которая эквивалентна форме  . Таким образом, при редуцировании число допустимых дуг, которое обозначим через NA, равно:
. Таким образом, при редуцировании число допустимых дуг, которое обозначим через NA, равно: 
Число допустимых дуг между шагами k и  после исключения равно:
после исключения равно:

где

Общее число дуг после редуцирования равно:

Легко проверить, что при  уравнение (3.13) приведет к значению
уравнение (3.13) приведет к значению  Итак, максимальное число допустимых дуг, которые необходимо рассмотреть при динамическом программировании, для нашего при мера равно 206.
Итак, максимальное число допустимых дуг, которые необходимо рассмотреть при динамическом программировании, для нашего при мера равно 206.
Чтобы показать, как работает алгоритм динамического программирования, допустим  шесть объектов равны (1, 1), (3, 4), (5, 5), (4, 4), (1, 2) и (5, 6), т. е.
шесть объектов равны (1, 1), (3, 4), (5, 5), (4, 4), (1, 2) и (5, 6), т. е.

Квадраты расстояний равны:

Следуя алгоритму динамического программирования, будем иметь:
шаг 0. 
шаг 1. Вычислим  для каждого множества объектов шага 1. Например,
для каждого множества объектов шага 1. Например,

На данном шаге мы должны получить 50 таких значений;
шаг 2. Для каждого множества объектов этого шага вычислим 
Например,

шаг 3. Для каждого множества объектов этого шага вычислим  На этом шаге
На этом шаге  обозначает единственное множество объектов (1, 2, 3, 4, 5, 6). Всего существует 21 допустимая дуга, соединяющая состояния шага 2 с состоянием шага 3. Таким образом, нам необходимо выбрать, как минимум, 21 значение. Одно из этих значений равно
обозначает единственное множество объектов (1, 2, 3, 4, 5, 6). Всего существует 21 допустимая дуга, соединяющая состояния шага 2 с состоянием шага 3. Таким образом, нам необходимо выбрать, как минимум, 21 значение. Одно из этих значений равно

Оно соответствует состоянию под номером 15 (см. табл. 3.1), для которого у соответствует множеству (1, 3, 5, 6), z соответствует (1, 2, 3, 4, 5, 6), а  множеству (2, 4).
множеству (2, 4).
Результатом применения процедуры динамического программирования будут кластеры (1, 1) и (1, 2), (3, 4) и (4, 4), (5, 5) и (5, 6) с формой распределения {2}, {2}, {2}. Максимальное значение равно:

Решение показано на рис. 2.
| << Предыдущий параграф | Следующий параграф >> |
- О МЕТОДОЛОГИЧЕСКИХ ПРИНЦИПАХ И МНОГОМЕРНОМ АНАЛИЗЕ (вместо предисловия)
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА КЛАСТЕРНОГО АНАЛИЗА. ОСНОВНЫЕ ИДЕИ
- 1.2. Задача кластерного анализа
- 1.3. Функции расстояния
- 1.4. Меры сходства
- 1.5. Расстояние между кластерами и их сходство
- 1.6. Кластерные методы, основанные на евклидовой метрике
- 1.7. Алгоритм последовательной кластеризации
- 1.8. Другие вопросы кластерного анализа
- ГЛАВА 2. КЛАСТЕРИЗАЦИЯ ПОЛНЫМ ПЕРЕБОРОМ
- 2.3. Рекурсивное соотношение между числами Стирлинга второго рода
- 2.4. Вычислительные аспекты полного перебора
- ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И КЛАСТЕРНЫЙ АНАЛИЗ
- 3.2. Модель динамического программирования Дженсена
- 3.3. Применение целочисленного программирования в кластерном анализе
- ГЛАВА 4. ПРЕДСТАВЛЕНИЯ МАТРИЦ СХОДСТВ
- 4.2. Сравнения дендограмм и матриц сходства
- 4.3. Основные определения
- 4.4. Деревья
- 4.5. Локальные операции на деревьях
- ГЛАВА 5. КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ОЦЕНИВАНИЯ ФУНКЦИИ ПЛОТНОСТИ
- 5.2. Оценивание функции плотности вероятности
- 5.3. Кластеризация на основе оценивания функции плотности
- 5.4. Замечания
- ГЛАВА 6. ПРИЛОЖЕНИЯ
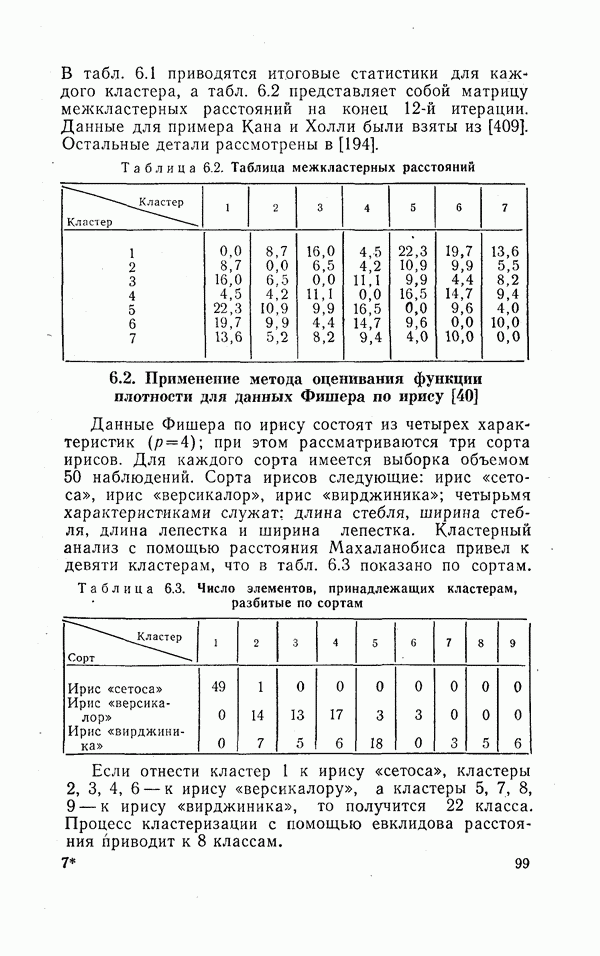
- 6.2. Применение метода оценивания функции плотности для данных Фишера по ирису [40]
- ГЛАВА 7. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- Литература