ДЕТЕРМИНИРОВАННОЕ НЕПЕРИОДИЧЕСКОЕ ТЕЧЕНИЕ

Эдвард Н. Лоренц

Резюме. Конечномерные системы обыкновенных дифференциальных уравнений могут быть использованы для описания вынужденного вязкого гидродинамического течения. Для таких систем с ограниченными решениями установлено, что непериодические движения обычно неустойчивы, в результате чего решения с близкими начальными условиями могут через некоторое время сильно различаться. Показано, что системы с ограниченными решениями имеют и ограниченные численные решения.

Численно исследуется простая система, описывающая ячеистую конвекцию. Обнаружено, что все решения неустойчивы, и почти все непериодические.

В свете этих результатов обсуждается возможность долго срочного прогноза погоды.

1. ВВЕДЕНИЕ

Некоторые гидродинамические системы демонстрируют постоянные во времени картины течения, другие — регулярные осцилляции. Однако многие меняются нерегулярно, внешне случайно и, даже если их наблюдать достаточно долго, не повторяют свою предшествующую историю.

Все эти типы поведения могут наблюдаться в известных экспериментах с вращающимися сосудами, описанных Фульцем с соавторами [3] и Хайдом [5]. В этих экспериментах цилиндрический сосуд с водой вращается вокруг своей оси и стационарно и симметрично подогревается с края и охлаждается в центре. При одних условиях получающееся течение столь же симметрично и стационарно, как и вызывающий его подогрев. При других условиях развивается система регулярно расположенных волн, которые движутся с постоянной скоростью, не меняя своей формы. А при некоторых условиях

образуется нерегулярная картина течения, которая движется и меняет свою форму нерегулярным непериодическим образом.

Отсутствие периодичности часто встречается в природе и является одной из отличительных особенностей турбулентного течения. Поскольку мгновенная картина турбулентного потока весьма нерегулярна, внимание обычно ограничивается статистикой турбулентности, которая в противоположность деталям турбулентного течения часто характеризуется регулярностью и высокой степенью упорядоченности. Однако человек, занимающийся краткосрочным прогнозом погоды, волей-неволей вынужден предсказывать именно детали крупномасштабных вихрей — циклонов и антициклонов, — которые постоянно образуют все новые картины. Таким образом, есть ситуации, в которых реальный интерес представляют более тонкие свойства, чем статистика нерегулярного течения.

В данной работе мы будем иметь дело с детерминированными системами уравнений, которые являются идеализациями гидродинамических систем. Нас будут особенно интересовать непериодические решения, т. е. решения, которые никогда точно не повторяются и у которых все приблизительные повторения имеют конечную продолжительность. Таким образом, мы должны рассматривать установившееся поведение решений в отличие от переходного поведения, связанного с различными начальными условиями.

Замкнутую гидродинамическую систему с конечной массой можно, казалось бы, с математической точки зрения считать конечным набором молекул (обычно очень большим конечным набором) и тогда законы движения записываются в виде конечной системы обыкновенных дифференциальных уравнений. В общем случае эти уравнения весьма сложны, и совокупность молекул обычно аппроксимируют непрерывным распределением масс. Законы движения при этом представляют собой систему уравнений в частных производных, содержащую в качестве переменных такие величины, как скорость, плотность, давление.

Иногда удается аналитически получить частные решения этих уравнений, особенно если эти решения периодичны или не зависят от времени. Действительно, множество работ посвящено нахождению таких решений тем или иным способом. Однако непериодические решения обычно невозможно получить иначе, как с помощью численных методов. В этих методах непрерывные переменные заменяют новым конечным набором функций времени, которые могут, например, совпадать с непрерывными переменными в выбранной сетке точек или являться коэффициентами разложения этих переменных

по ортогональным функциям. Законы движения тогда снова описываются конечной системой обыкновенных дифференциальных уравнений, но гораздо более простой, чем система, описывающая индивидуальные движения молекул.

В любой реальной гидродинамической системе всегда есть вязкая диссипация, если только система не движется как твердое тело, и тепловая диссипация, если только температура в системе непостоянна. Для определенных целей многие системы можно считать консервативными, в них энергия или какая-нибудь аналогичная величина сохраняется во времени. При рассмотрении установившегося поведения системы консервативные законы движения не проходят, поскольку предельное значение сохраняющейся величины оказывается равным произвольно выбранному начальному значению. Эту трудность можно преодолеть, если учесть диссипативные процессы, т. е. сделать уравнения неконсервативными, а также включить внешнее механическое или тепловое воздействие, чтобы система не пришла в конце концов в состояние покоя. Чтобы система была детерминированной, вынуждающие силы должны или не зависеть от времени или подчиняться детерминированным законам.

В данной работе мы будем иметь дело с конечномерными системами детерминированных обыкновенных дифференциальных уравнений, которые соответствуют диссипативным гидродинамическим течениям с внешним воздействием. При этом основное внимание будет сосредоточено на изучении свойств непериодических решений этих уравнений.

Совсем неочевидно, что такие решения могут вообще существовать. В самом деле, в диссипативных системах, описываемых конечной системой линейных уравнений, постоянное внешнее воздействие приводит в конце концов к постоянному отклику, а периодическое воздействие — к периодическому отклику. Поэтому иногда считают, что непериодическое течение — это результат непериодического или случайного воздействия.

Аргументы, приводящие к подобным выводам, не годятся, когда уравнения движения нелинейны. Если эти уравнения содержат члены, отвечающие адвекции — переносу некоторой характеристики жидкого потока самим течением жидкости, — то постоянное воздействие может привести к различным откликам. В уже упоминавшихся экспериментах с вращающимися сосудами как периодическое, так и непериодическое течения возникали в результате теплового воздействия, которое в пределах экспериментальных ошибок было постоянным. Точное периодическое решение упрощенных систем уравнений, описывающих диссипативное течение с постоянным

тепловым воздействием, было аналитически найдено автором в работе [7]. В подобных системах уравнений автором [8] численным методом были найдены и непериодические решения.

2. ФАЗОВОЕ ПРОСТРАНСТВО

Рассмотрим систему, состояние которой описывается М переменными Пусть они подчиняются уравнениям

где время t — единственная независимая переменная, а функции имеют непрерывные первые производные. Такую систему можно изучать с помощью фазового пространства — -мерного евклидова пространства Г с координатами

Каждой точке фазового пространства отвечает возможное мгновенное состояние системы. Изменение состояния в соответствии с (1) представляется движением изображающей точки в фазовом пространстве вдоль траектории. Стационарное положение изображающей точки, отвечающее установившемуся состоянию, для полноты также будем считать траекторией.

Понятие о фазовом пространстве оказалось полезным при изучении конечномерных систем и использовалось многими математиками: Гиббсом [4] в работах по статистической механике, Пуанкаре [10] при исследовании решений дифференциальных уравнений и Биркгофом [1] в его трактате о динамических системах.

Из теории дифференциальных уравнений следует (см., например, книгу Форда [2], гл. 6), что если непрерывны, то для любого момента времени и любой точки в Г уравнения (1) имеют единственное решение

определенное на некотором временном интервале, включающем точку и удовлетворяющее условию

Функции непрерывны по и t. Следовательно, через каждую точку Г проходит только одна траектория. Две или большее число траекторий могут, однако, асимптотически приближаться к одной и той же точке или к одной и той же кривой при или при Более того, поскольку функции непрерывны, каждому интервалу времени отвечает

непрерывная деформация любой области Г в некоторую другую область.

В случае консервативной системы, когда некоторая положительно определенная величина Q, представляющая, например, энергию в той или иной форме, не зависит от времени, каждая траектория принадлежит какой-нибудь поверхности постоянного уровня Q. Эти поверхности могут иметь вид вложенных друг в друга замкнутых «сфер».

Если же в системе есть диссипация и внешнее воздействие и если всякий раз, когда Q больше или равно некоторой фиксированной величине уменьшение Q за счет диссипации происходит быстрее, чем увеличение за счет внешнего воздействия, то строго положительно при и каждая траектория обязательно должна войти в область, где Таким образом, поведение траектории, представляющей диссипативное течение с внешним воздействием, может существенно отличаться от поведения траекторий в консервативной системе.

Типичным представителем диссипативных систем с внешним воздействием является следующая система уравнений:

    (4)

где тождественно равно нулю, положительно определено, а — постоянные . Если

    (5)

и — корни уравнения

то из (4) следует, что

Правая часть (7) равна нулю только на поверхности некоего эллипсоида Е и положительна только внутри Е. Поверхности — это концентрические сферы. Если через S обозначить одну из этих сфер, внутренность которой R содержит эллипсоид Е, то, очевидно, каждая траектория рано или поздно попадет в

3. НЕУСТОЙЧИВОСТЬ НЕПЕРИОДИЧЕСКОГО ТЕЧЕНИЯ

В этом разделе мы установим одно из наиболее важных Свойств детерминированного непериодического течения, а Именно его неустойчивость по отношению к малым изменениям начальных условий. Исследование удобно будет проводить, рассматривая решение уравнений движения как траекторию в фазовом пространстве. Будем обозначать символом (переменный аргумент) траекторию, а символами Р или (нет аргумента или постоянный аргумент) точки, причем последний символ обозначает точку, через которую траектория РЦ) проходит в момент

Мы будем иметь дело с фазовым пространством Г, в котором через каждую точку проходит единственная траектория, и в котором интервал времени определяет непрерывное преобразование каждой области Г в другую область, так что если точки в пределе приближаются к то точки должны в пределе приближаться к . Потребуем далее, чтобы все траектории были равномерно ограничены при , т. е. должна существовать ограниченная область R, такая, что каждая траектория в конце концов остается внутри R. На ход наших рассуждений оказала влияние книга Биркгофа [1] о динамических системах; основное отличие в том, что Биркгоф имел дело в основном с консервативными системами. Детальное описание динамических систем дано Немыцким и Степановым [9], в их книге можно найти строгие доказательства некоторых из приводимых ниже теорем.

Мы будем проводить классификацию траекторий по трем различным признакам, а именно: по наличию или отсутствию свойств установления, по устойчивости или неустойчивости и по наличию или отсутствию свойства периодичности.

Поскольку каждая положительная полутраектория ограничена, она должна иметь по крайней мере одну предельную точку — точку, к которой она сколь угодно много раз приближается на сколь угодно малое расстояние. Более строго, есть предельная точка для если для любого и любого времени U существует время такое, что . Здесь знак абсолютной величины означает расстояние в фазовом пространстве. Ясно, что каждая точка траектории, проходящей через также является предельной точкой для и множество предельных точек образует траекторию или множество траекторий,

называемых предельными траекториями Предельная траектория, естественно лежит внутри

Траектория, содержащаяся в множестве своих собственных предельных траекторий, называется центральной, остальные траектории называются нецентральными. Центральная траектория сколь угодно много раз проходит сколь угодно близко к тем точкам, через которые она проходила ранее, и в этом смысле отдельные разнесенные куски центральной траектории статистически подобны. Нецентральная траектория остается на некотором расстоянии от любой точки, через которую она раньше проходила. Она должна асимптотически приближаться к своему полному множеству предельных точек, хотя может и не приближаться асимптотически к какой-то одной предельной траектории. Мгновенное расстояние от нее до ближайшей предельной точки меняется и становится сколь угодно малым при

Траекторию назовем устойчивой в точке если любая другая траектория, проходящая достаточно близко к в момент времени остается близкой к при устойчива в если для любого существует , такое, что если то . В противном случае траекторию назовем неустойчивой в Ясно, что траектория, устойчивая в одной точке, устойчива во всех точках, поэтому назовем ее устойчивой траекторией. Неустойчивая в одной точке траектория неустойчива во всех точках, мы назовем ее неустойчивой траекторией. В том частном случае, когда состоит из одной точки, это определение устойчивости согласуется с обычным определением устойчивости стационарного течения.

Устойчивую траекторию назовем равномерно устойчивой, если расстояние, на котором соседняя траектория должна проходить вблизи точки чтобы оставаться близкой к при само имеет положительную нижнюю грань при равномерно устойчива, если для любого существует и время такое, что если Предельная траектория равномерно устойчивой траектории должна быть сама равномерно устойчивой, поскольку

скольку проходящие достаточно близко к траектории должны проходить сколь угодно близко к некоторой точке и, следовательно, должны оставаться вблизи при

Так как каждая точка лежит только на одной траектории, то любая траектория, проходящая через уже пройденную ранее точку, должна повторить свое прежнее поведение и поэтому должна быть периодической. Траекторию назовем квазипериодической, если для некоторого произвольно большого интервала времени остается все время вблизи квазипериодическая, если для любого и любого интервала времени то существует и время такое, что при . Периодическая траектория есть частный случай квазипериодической.

Траекторию, не являющуюся квазипериодической, мы назовем непериодической. Если непериодическая, то точка может быть сколь угодно близка к но при этом не может оставаться сколь угодно близким к при . Непериодические траектории представляют детерминированное непериодическое течение и являются основным предметом данной работы.

Периодические траектории, очевидно, являются центральными. В множество квазипериодических центральных траекторий входят многопериодические траектории с несоизмеримыми периодами, а в множество квазипериодических нецентральных траекторий входят траектории, асимптотически приближающиеся к периодическим. Непериодические траектории могут быть как центральными, так и нецентральными.

Приведем теперь теорему о том, что траектория, имеющая устойчивую предельную траекторию, квазипериодична. Если — предельная траектория для , то две различные точки , где сколь угодно велико, могут быть выбраны сколь угодно близкими к любой точке Поскольку устойчива, должны оставаться сколь угодно близкими к и, следовательно, друг к другу при — квазипериодическая траектория.

Отсюда сразу следует, что устойчивая предельная траектория квазипериодическая, или, что то же самое, непериодическая центральная траектория должна быть неустойчивой.

Этот результат очень важен с точки зрения предсказания будущего состояния системы с непериодическим поведением.

Получается, что два незначительно отличающихся состояния могут в конце концов перейти в два совершенно различных. Тогда, если при наблюдении данного состояния есть какие-нибудь ошибки — а в реальных системах ошибки неизбежны, приемлемое предсказание мгновенных состояний оказывается невозможным.

Что касается нецентральных траекторий, то равномерно устойчивая нецентральная траектория квазипериодична, или, что то же самое, непериодическая нецентральная траектория не является равномерно устойчивой. Остается, однако, возможность того, что непериодическая нецентральная траектория устойчива, но неравномерно устойчива. Автору, впрочем, кажется, что такие траектории хотя и возможны теоретически, но не характерны для реальных гидродинамических течений. Любая попытка, например, представить атмосферное течение такой траекторией приводит к невероятному выводу, что мы должны делать долгосрочный прогноз погоды как можно быстрее, так как чем дольше мы ждем, тем сложнее становится наша задача.

Итак, мы показали, что центральная траектория, удовлетворяющая приведенным вначале условиям единственности, непрерывности и ограниченности и в некотором смысле не обладающая переходными свойствами, неустойчива, если она непериодична. Нецентральная траектория, характеризуемая переходными свойствами, не является равномерно устойчивой, если она непериодична, и если она все же устойчива, то устойчивость — одно из переходных свойств, исчезающих с течением времени. Ввиду невозможности точно измерить начальные условия и, следовательно, отличить центральную траекторию от близкой нецентральной, все непериодические траектории эффективно неустойчивы с точки зрения практического предсказания.

4. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ НЕКОНСЕРВАТИВНЫХ СИСТЕМ

Приведенные в последнем параграфе теоремы представляют интерес, только если непериодические решения рассматриваемых уравнений действительно существуют. Поскольку статистически стационарные непериодические функции времени нелегко описать аналитически, частные непериодические решения легче всего, видимо, искать численно. В этом разделе мы опишем алгоритм численного интегрирования, специально предназначенный для систем вида (4). В следующем разделе мы используем этот алгоритм для нахождения непериодических решений простой системы уравнений.

Для численного решения системы (1) выберем начальное время и временной шаг и положим

Введем теперь вспомогательные аппроксимации

где — точки с координатами

Простейший численный алгоритм нахождения приближенных решений - это прямая разностная схема

Во многих случаях более хорошее приближение к решениям (1) может быть получено с помощью центрально-разностной схемы

Эта схема, однако, не подходит в том случае, когда особое внимание уделяется детерминистской природе (1), так как величины неоднозначно определяют

Преодолеть недостатки как прямой разностной, так и центрально-разностной схемы нам поможет алгоритм двойной аппроксимации, определяемый соотношением

Здесь коэффициент при — это аппроксимация производной по времени в момент . Из (9) и (10) следует, что (13) можно переписать в виде

Естественный путь автоматического вычисления — это последовательное определение величин в соответствии с (9), (10) и (14). Мы использовали этот алгоритм во всех приводимых в данной работе расчетах.

В фазовом пространстве численное решение уравнений (1) следует рассматривать скорее как прыгающую, а не непрерывно движущуюся изображающую точку. Более того, если каждое число в памяти ЦВМ представлено заданным фиксированным набором битов, то в фазовом пространстве могут быть заняты только определенные точки. Если численное

решение ограничено, то обязательно должны начаться повторения, так что, строго говоря, любое численное решение будет периодическим. На практике этим обстоятельством можно пренебречь, если число различных возможных состояний гораздо больше числа итераций, которые когда-либо можно произвести. Неизбежность повторений можно преодолеть и довольно неэкономичным способом, увеличивая точность вычислений с ростом п.

Рассмотрим теперь численные решения уравнений (4), полученные с помощью прямой разностной схемы (11). Для этих решений

Пусть S — некая поверхность постоянного уровня Q, во внутренности которой R содержится эллипсоид Е, на котором равно нулю, и пусть — любая поверхность постоянного уровня, чья внутренность R содержит

Поскольку ограничены сверху в можно выбрать настолько малым, чтобы лежало в R, если лежит в R. Более того, так как имеет верхнюю границу, имеет отрицательную верхнюю границу в R — R, мы можем выбрать настолько малым, чтобы неравенство выполнялось, если лежит в Следовательно, может быть выбрано настолько малым, чтобы любая попадающая в R прыгающая изображающая точка оставалась захваченной внутри R и численное решение не уходило на бесконечность. Уход может, впрочем, произойти, если вначале точка не принадлежит

Рассмотрим теперь схему с двойной аппроксимацией (14). Из проведенных рассуждений следует не только то, что лежит в R, если лежит в R, но также, что лежит в R, если ) лежит в R. Так как область R выпуклая, точка задаваемая (14), лежит в R, если лежит в R. Следовательно, если выбрано настолько малым, что при использовании прямой разностной схемы не происходит ухода на бесконечность, то в случае схемы с двойной аппроксимацией тоже не произойдет ухода.

Заметим мимоходом, что если бы мы применили прямую разностную схему к консервативной системе, для которой то имели бы

В данном случае при любом фиксированном выборе численное решение неизбежно стремится к бесконечности, если только не приближается асимптотически к состоянию равновесия. Аналогичный результат получится, если к консервативной системе применить схему с двойной аппроксимацией (14).

5. УРАВНЕНИЯ КОНВЕКЦИИ СОЛЬЦМЕНА

В этом разделе мы введем систему трех обыкновенных дифференциальных уравнений, решения которой дают простейший известный автору пример детерминированного непериодического течения. Она представляет собой упрощение системы, использованной Сольцменом [12] для описания конечно-амплитудной конвекции. Хотя нас больше интересует непериодическая природа решений, а не связь с проблемами конвекции, мы опишем вкратце физические основы.

Рэлей [11] рассмотрел течение, возникающее в слое жидкости постоянной толщины при условии, что разность температур между нижней и верхней границами поддерживается равной постоянной величине Такая система допускает равновесное решение, когда нет движения, а температура линейно меняется с глубиной. Если это решение неустойчиво, развивается конвекция.

Если все движения происходят в плоскости , а от координаты у ничего не зависит, уравнения движения можно записать в следующем виде (см. Сольцмен [12]):

Здесь — функция тока плоского течения, — отклонение температуры от равновесной, постоянные g, a, v и к обозначают соответственно ускорение силы тяжести, коэффициент теплового расширения, кинематическую вязкость и температуропроводность. В самой простой постановке задачи верхняя и нижняя границы считаются свободными, тогда на них равны нулю.

Рэлей обнаружил, что система будет неустойчивой по отношению к возмущениям вида

если величина

называемая числом Релея, превышает критическое значение

Минимальное значение равное получается при

Систему обыкновенных дифференциальных уравнений, описывающую конвекцию, Сольцмен [12] получил следующим образом: он разложил и 0 в двойные ряды Фурье по с зависящими от времени коэффициентами и подставил эти ряды в (17) и (18), затем выразил правые части получившихся уравнений двойными рядами Фурье, заменив произведения тригонометрических функций от (или ) суммами, и приравнял коэффициенты при одинаковых функциях после этого он, следуя работе автора [6], свел получившуюся бесконечную систему к конечной, положив не равным нулю только определенное число функций времени.

Далее Сольцмен численно получил зависящие от времени решения. В некоторых случаях все переменные, кроме трех, в конце концов стремились к нулю, а три отмеченных испытывали нерегулярные, явно непериодические флюктуации.

Эти же самые решения можно получить, если с самого начала обрезать ряды так, чтобы они состояли из трех членов. Поэтому в данной работе положим

Здесь X, Y и Z зависят только от времени. Если выражения (23), (24) подставить в (17), (18) и отбросить тригонометрические члены, отличные от тех, что учтены в (23) и (24), то получим

Здесь точка обозначает производную по безразмерному времени — число Прандтля, . С точностью до постоянных сомножителей наши переменные X, Y и Z соответствуют переменным Сольцмена A, D и G. Уравнения (25), (26), (27) и есть те уравнения конвекции, решения которых мы будем исследовать.

В этих уравнениях X пропорционально интенсивности конвективного движения, а У — разности температур между восходящим и нисходящим потоками, одинаковые знаки X и Y отвечают подъему теплой жидкости и опусканию холодной. Переменная Z пропорциональна отклонению вертикального профиля температуры от линейного, положительным Z отвечает увеличение градиентов температуры вблизи границ.

Уравнения (25)-(27) могут дать реалистические результаты только при небольшом превышении числа Рэлея над критическим. Из-за слишком сильного упрощения исходных уравнений нельзя ожидать, что и при сильной конвекции их решения будут соответствовать решениям (17) и (18).

6. РЕЗУЛЬТАТЫ ЛИНЕЙНОГО АНАЛИЗА

Хотя уравнения (25) — (27) в том виде, как они написаны, не совпадают по форме с (4), их можно привести к виду (4) различными линейными преобразованиями. Одно из простейших таких преобразований:

Поэтому решения (25) — (27) остаются ограниченными внутри области R при и общие результаты предыдущих разделов применимы к этим уравнениям.

Устойчивость решения можно формально исследовать, рассматривая поведение малых возмущений Изменение этих возмущений во времени описывается линеаризованными уравнениями

Поскольку коэффициенты в (29) зависят от времени, то, кроме того случая, когда основное решение X, Y, Z есть состояние равновесия системы (25) — (27), общее решение (29) найти не удается. Однако изменение объема малой области фазового пространства, каждая точка которой движется в соответствии с (25) — (27), определяется диагональной суммой матрицы коэффициентов, а именно

Возможно, это изменение объема легче себе представить, если смотреть на движение в фазовом пространстве как на течение жидкости с дивергенцией

Поэтому любой малый объем стремится к нулю при со скоростью, не зависящей от X, Y и Z. Но это не означает, что каждый малый объем стягивается в точку, он может просто растекаться по поверхности. Отсюда следует, что объем области, первоначально ограниченной поверхностью S, стремится к нулю с той же самой скоростью. Поэтому все траектории в конце концов притягиваются к некоторому подмножеству, имеющему нулевой объем. Это подмножество содержит все траектории, лежащие внутри R, и, следовательно, все центральные траектории.

Уравнения (25) — (27) имеют стационарное решение отвечающее отсутствию конвекции. Для него характеристическое уравнение имеет вид

Это уравнение при имеет три действительных корня, при все они отрицательны, но при один корень положителен. Критерий возникновения конвекции есть, таким образом, или в согласии с результатами Релея.

При система (25) — (27) имеет еще два состояния равновесия Для каждого из этих решений характеристическое уравнение имеет вид

У уравнения (33) при один действительный отрицательный корень и два комплексно-сопряженных корня. Комплексно-сопряженные корни будут чисто мнимыми, если произведение коэффициентов при равно свободному члену, т. е. если

Это — критическое значение , при котором стационарная конвекция становится неустойчивой. Таким образом, если то ни при одном положительном (34) не выполняется и стационарная конвекция всегда устойчива, а при стационарная конвекция теряет устойчивость при достаточно больших числах Рэлея. Этот вывод, конечно, справедлив для идеализированной конвекции, описываемой уравнениями не для решений уравнений в частных производных (17) и (18).

Комплексность корней (33) показывает, что если слегка возмутить неустойчивую стационарную конвекцию, интенсивность движения начнет осциллировать. Что происходит, когда возмущение становится большим, линейная теория сказать

не может. Чтобы исследовать конечно-амплитудную конвекцию и подмножество, к которому в конце концов притягиваются траектории, обратимся к численным расчетам.

7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ КОНВЕКЦИИ

Чтобы получить численные решения уравнений конвекции, мы должны выбрать числовые значения констант. Следуя Сольцмену [12], положим так что . При этом критическое число Рэлея для неустойчивости стационарной конвекции равно

Мы выберем слегка надкритическое значение Стационарная конвекция тогда представляется точками в фазовом пространстве, а отсутствию конвекции соответствует начало координат (0, 0, 0).

Для численного интегрирования мы использовали метод двойной аппроксимации, определяемый формулами (9), (10), (14). Безразмерный шаг по времени равнялся Вычисления проводились на ЭВМ Роял На одну итерацию тратилась примерно секунда, не считая времени вывода.

В качестве начальной мы выбрали точку, незначительно отличающуюся от состояния покоя, а именно (0, 1, 0). Таблица 1 составлена с помощью ЭВМ. В ней представлены величины N (число шагов), X, Y и Z в каждой пятой итерации для первых 160 шагов. Перед выходной печатью (но не при вычислениях) величины X, Y и Z умножены на десять и напечатаны только цифры слева от десятичной точки. В такой записи состояния стационарной конвекции — это состояние покоя

Ясно видна начальная неустойчивость состояния покоя. Все три переменные быстро растут, опускающаяся холодная жидкость замещается еще более холодной сверху, а поднимающаяся теплая — еще более теплой снизу, так что к шагу интенсивность конвективного движения превышает интенсивность стационарной конвекции. Затем, когда теплая жидкость проходит верхнюю часть конвективной ячейки, У уменьшается, и к шагу, когда X и Y имеют противоположные знаки, теплая жидкость уже опускается, а холодная жидкость поднимается. Вследствие этого движение приостанавливается и меняет направление, о чем свидетельствуют отрицательные значения X после шага. К 85-му шагу система достигает состояния, близкого к стационарной конвекции.

Таблица 1. Численное решение уравнений конвекции. Величины X, Y, Z даны на каждом пятом шаге для первых 160 итераций (см. скан)

Между 85-м и 150-м шагами происходит одно полное колебание интенсивности, небольшое увеличение амплитуды почти незаметно.

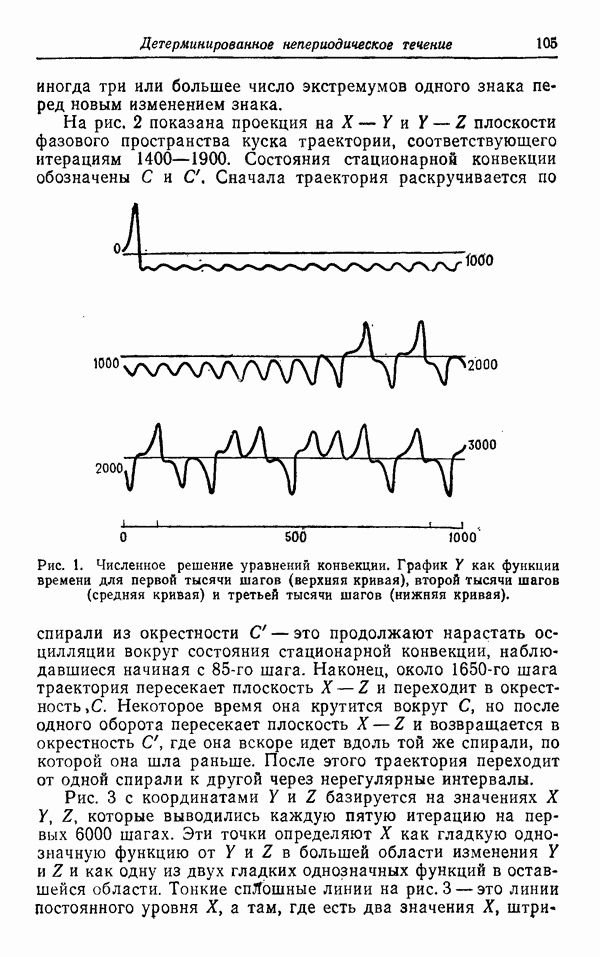
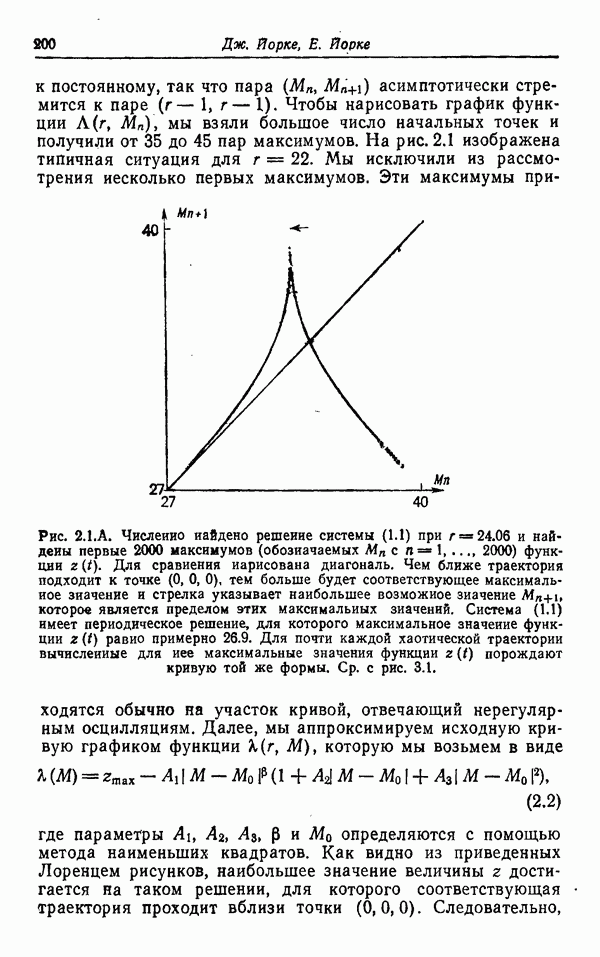
Последующее поведение системы иллюстрируется рис. 1, на котором показано, как ведет себя У на первых 3000 итерациях. После достижения первого пика вблизи 35-го шага и затем приближения к состоянию равновесия вблизи 85-го шага У претерпевает систематическое усиление осцилляций вплоть до 1650-го шага. Здесь система достигает критического состояния, и после этого У меняет знак через внешне нерегулярные интервалы, имея иногда один, иногда два, а

иногда три или большее число экстремумов одного знака перед новым изменением знака.

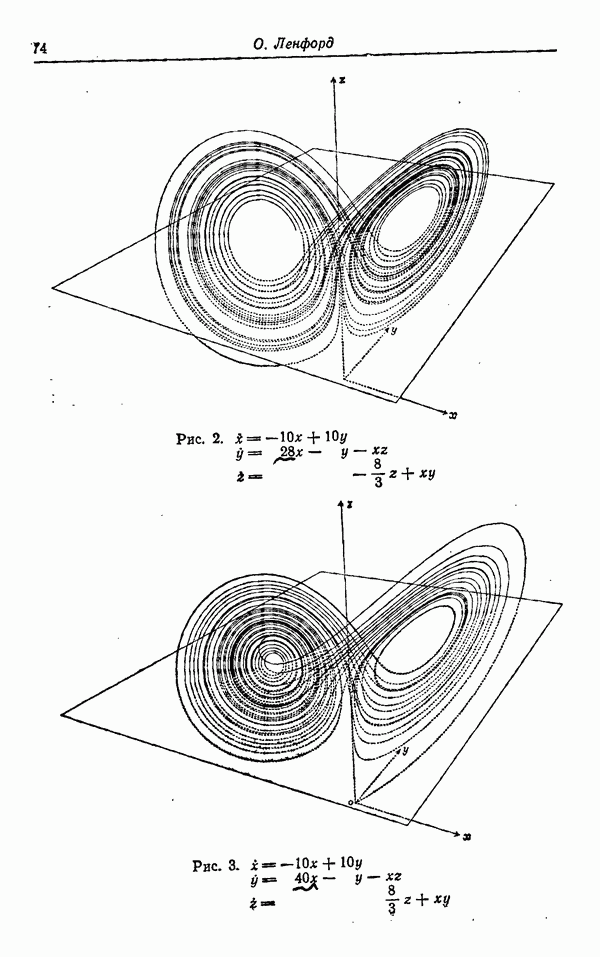
На рис. 2 показана проекция на и плоскости фазового пространства куска траектории, соответствующего итерациям 1400—1900. Состояния стационарной конвекции обозначены С и С, Сначала траектория раскручивается по спирали из окрестности С — это продолжают нарастать осцилляции вокруг состояния стационарной конвекции, наблюдавшиеся начиная с шага.

Рис. 1. Численное решение уравнений конвекции. График Y как функции времени для первой тысячи шагов (верхняя кривая), второй тысячи шагов (средняя кривая) и третьей тысячи шагов (нижняя кривая).

Наконец, около 1650-го шага траектория пересекает плоскость и переходит в окрестность С. Некоторое время она крутится вокруг С, но после одного оборота пересекает плоскость и возвращается в окрестность С, где она вскоре идет вдоль той же спирали, по которой она шла раньше. После этого траектория переходит от одной спирали к другой через нерегулярные интервалы.

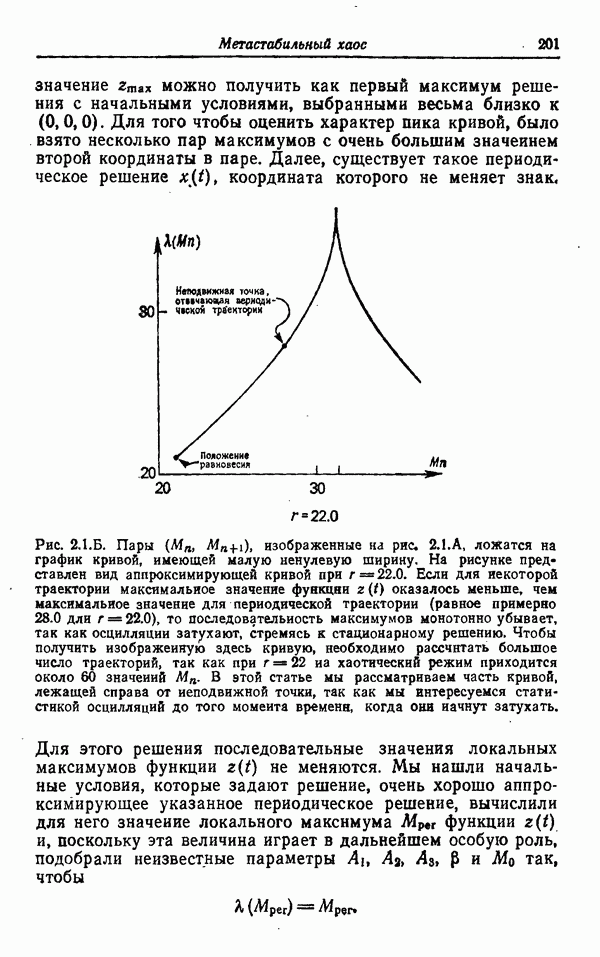
Рис. 3 с координатами Y и Z базируется на значениях X У, Z, которые выводились каждую пятую итерацию на первых 6000 шагах. Эти точки определяют X как гладкую однозначную функцию от Y и Z в большей области изменения Y и Z и как одну из двух гладких однозначных функций в оставшейся области. Тонкие сплошные линии на рис. 3 — это линии постоянного уровня X, а там, где есть два значения X, штрихованные

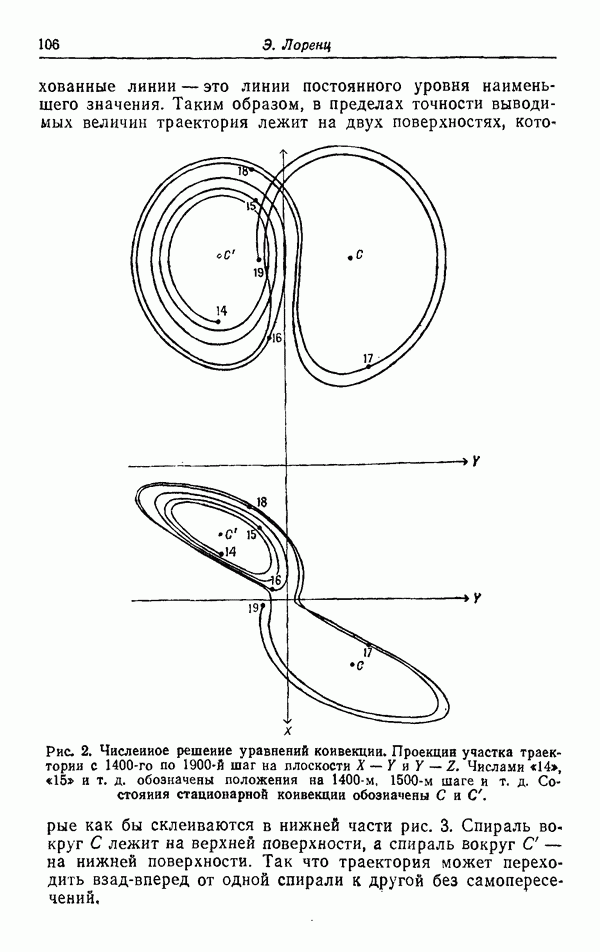
линии — это линии постоянного уровня наименьшего значения. Таким образом, в пределах точности выводимых величин траектория лежит на двух поверхностях, которые как бы склеиваются в нижней части рис. 3.

Рис. 2. Численное решение уравнений конвекции. Проекции участка траектории с 1400-го по 1900-й шаг на плоскости и Числами «14», «15» и т. д. обозначены положения на 1400-м, 1500-м шаге и т. д. Состояния стационарной конвекции обозначены С и С.

Спираль вокруг С лежит на верхней поверхности, а спираль вокруг С — на нижней поверхности. Так что траектория может переходить взад-вперед от одной спирали к другой без самопересечений.

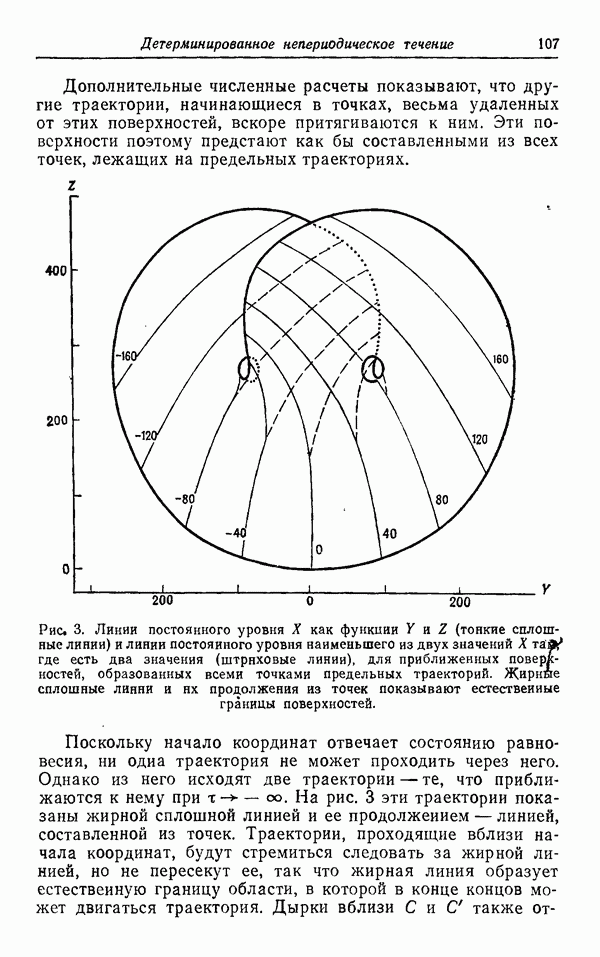
Дополнительные численные расчеты показывают, что другие траектории, начинающиеся в точках, весьма удаленных от этих поверхностей, вскоре притягиваются к ним. Эти поверхности поэтому предстают как бы составленными из всех точек, лежащих на предельных траекториях.

Рис. 3. Линии постоянного уровня X как функции Y и Z (тонкие сплошные линии) и линии постоянного уровня наименьшего из двух значений X там, где есть два значения (штриховые линии), для приближенных поверхностей, образованных всеми точками предельных траекторий. Жирные сплошные линии и их продолжения из точек показывают естественные границы поверхностей.

Поскольку начало координат отвечает состоянию равновесия, ни одна траектория не может проходить через него. Однако из него исходят две траектории — те, что приближаются к нему при . На рис. 3 эти траектории показаны жирной сплошной линией и ее продолжением — линией, составленной из точек. Траектории, проходящие вблизи начала координат, будут стремиться следовать за жирной линией, но не пересекут ее, так что жирная линия образует естественную границу области, в которой в конце концов может двигаться траектория. Дырки вблизи С и также отвечают

областям, в которые траектория не может попасть после того, как она их однажды покинула.

Возвращаясь к рис. 2, мы обнаруживаем, что траектория покидает одну из спиралей после того, как она отойдет на некоторое критическое расстояние от центра. Более того, похоже, что степень, на которую превышается это расстояние, определяет точку, в которой траектория попадает в другую спираль; эта точка в свою очередь как бы задает число оборотов, совершаемых перед новым изменением знака.

Таким образом, получается, что по некоторой одной характеристике данного оборота можно предсказать такую же характеристику следующего оборота. Подходящей характеристикой такого рода является максимальное значение Z, которое достигается, когда оборот почти завершен. Таблица 2 также приготовлена с помощью компьютера, она показывает величины X, Y и Z только при тех итерациях N, когда Z достигает относительного максимума. Последовательность оборотов вокруг С и С определяется последовательностью положительных и отрицательных значений X и У. Видно, что X и Y меняют знаки после максимума, который превышает некоторое критическое значение — примерно 385 (в выводимых величинах).

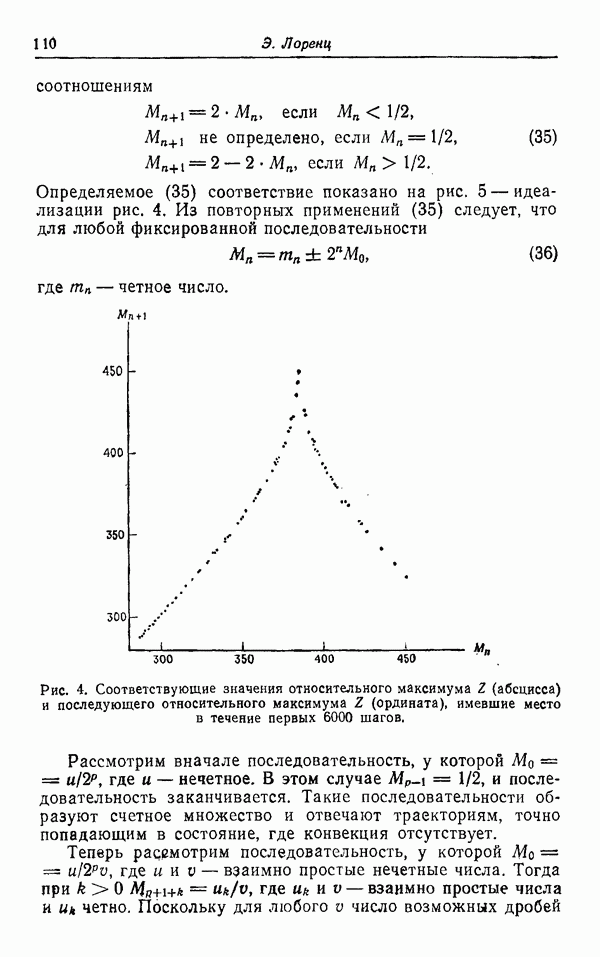
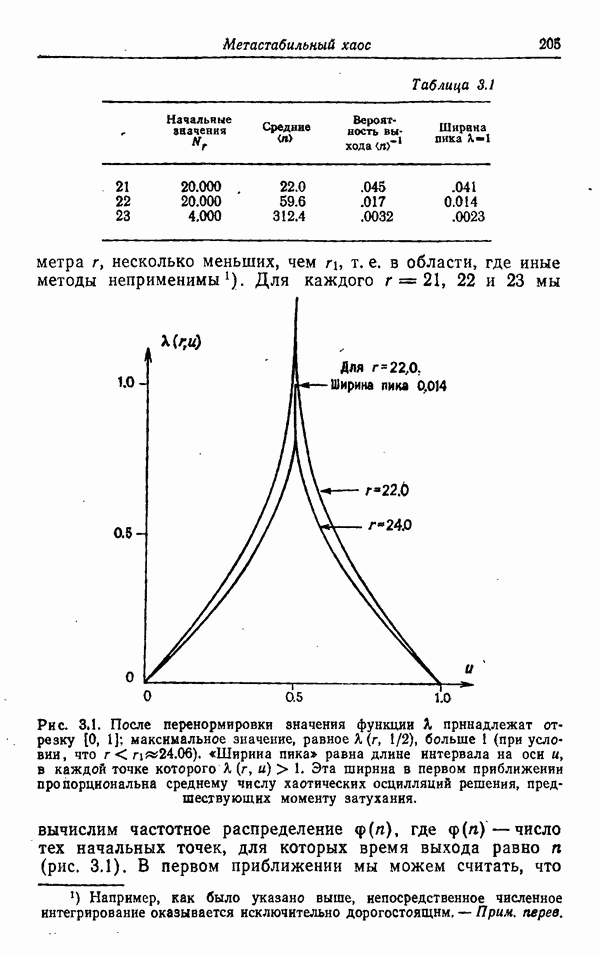
Рис. 4 сделан по табл. 2. Абсцисса — это величина максимума Z, а ордината — это — величина следующего максимума. Каждая точка представляет пару последовательных значений Z, взятых из табл. 2. В пределах округлений протабулированных значений Z имеется точное соответствие между двумя точками и одной Начальный максимум изображен так, как будто он следовал за максимумом так как максимумы вблизи 385 сменяются близким приближением к нулю и затем исключительно большими максимумами.

Отсюда следует, что исследователь, даже не зная ничего о природе уравнений движения, может сформулировать эмпирическую схему предсказания по «данным», приведенным на рис. 2 и 4. Из величины самого последнего максимума Z повторными применениями рис. 4 могут быть получены величины последующих максимумов. А значения X, Y и Z между максимумами Z могут быть найдены из рис. 2 интерполированием между близкими кривыми. Конечно, точность сделанных этим методом предсказаний ограничена точностью рис. 2 и 4 и, как мы увидим, точностью, с которой задается начальное значение X, Y и Z.

Чтобы лучше понять свойства рис. 4, обратимся к исследованию идеализированного переводящего две точки в одну соответствия между следующими друг за другом членами

Таблица 2. Численное решение уравнений конвекции. Величины X, Y, Z даны при тех итерациях , при которых Z достигает относительного максимума, для первых 6000 итераций (см. скан)

последовательностей состоящих из чисел между нулем и единицей. Эти последовательности удовлетворяют

соотношениям

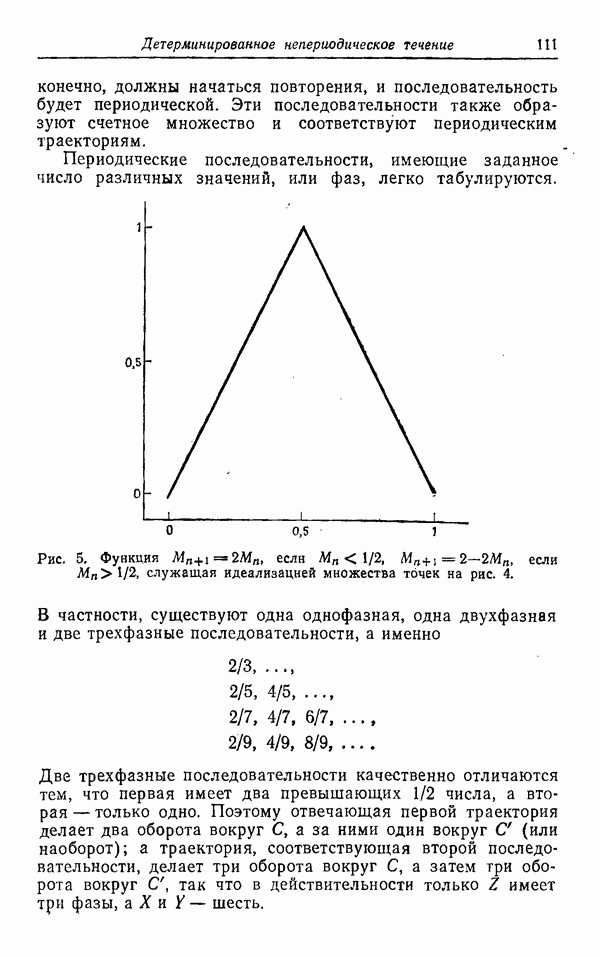
Определяемое (35) соответствие показано на рис. 5 — идеализации рис. 4. Из повторных применений (35) следует, что для любой фиксированной последовательности

где — четное число.

Рис. 4. Соответствующие значения относительного максимума 2 (абсцисса) и последующего относительного максимума 1 (ордината), имевшие место в течение первых 6000 шагов.

Рассмотрим вначале последовательность, у которой где — нечетное. В этом случае и последовательность заканчивается. Такие последовательности образуют счетное множество и отвечают траекториям, точно попадающим в состояние, где конвекция отсутствует.

Теперь рассмотрим последовательность, у которой где и взаимно простые нечетные числа. Тогда при где и v — взаимно простые числа и четно. Поскольку для любого v число возможных дробей

конечно, должны начаться повторения, и последовательность будет периодической. Эти последовательности также образуют счетное множество и соответствуют периодическим траекториям.

Периодические последовательности, имеющие заданное число различных значений, или фаз, легко табулируются.

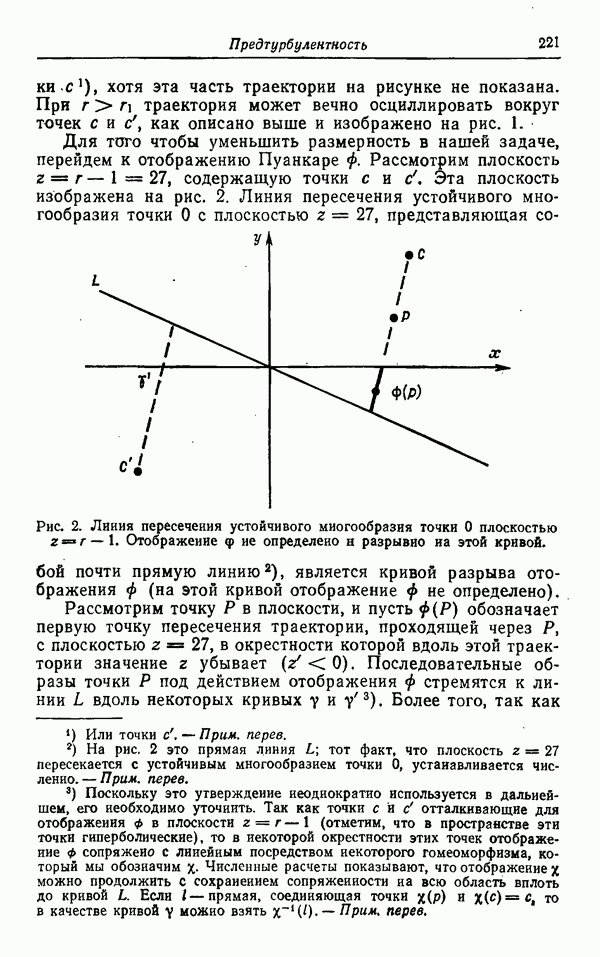
Рис. 5. Функция если если служащая идеализацией множества точек на рис. 4.

В частности, существуют одна однофазная, одна двухфазная и две трехфазные последовательности, а именно

Две трехфазные последовательности качественно отличаются тем, что первая имеет два превышающих 1/2 числа, а вторая — только одно. Поэтому отвечающая первой траектория делает два оборота вокруг С, а за ними один вокруг С (или наоборот); а траектория, соответствующая второй последовательности, делает три оборота вокруг С, а затем три оборота вокруг С, так что в действительности только Z имеет три фазы, а X и Y — шесть.

Обратимся теперь к последовательности, у которой не является рациональной дробью. В этом случае из (36) следует, что не может быть равным при так что повторения не наступают. Эти последовательности образуют несчетное множество и могут, вообще говоря, приближаться асимптотически к периодическим последовательностям или же быть квазипериодическими или непериодическими.

Наконец, рассмотрим две последовательности , у которых Тогда для данного если достаточно мало. Все последовательности, таким образом, неустойчивы по отношению к малым возмущениям. В частности, все периодические последовательности неустойчивы и никакая другая последовательность не может асимптотически приближаться к периодической. Поэтому все последовательности, кроме множества меры нуль, являются непериодическими, и они соответствуют непериодическим траекториям.

Возвращаясь к рис. 4, мы видим, что здесь тоже имеются периодические последовательности, аналогичные протабулированным выше. Они приближенно задаются величинами

Траектории, которым соответствуют эти или другие периодические последовательности, сами, по-видимому, являются периодическими или квазипериодическими.

Описанные последовательности возникают в численном решении на короткое время в виде последовательностей, начинающихся при итерациях 5340, 4881, 3625 и 3926. Поскольку численное решение в конце концов отходит от каждой из этих последовательностей, все они, видимо, неустойчивы.

В общем случае, если достаточно мало, то где — произведение наклонов кривых рис. 4 в точках с абсциссами Поскольку внешне величина наклона кривой везде больше единицы, все последовательности максимумов и, следовательно, все траектории неустойчивы. В частности, периодические траектории, чьи последовательности максимумов образуют счетное множество, неустойчивы, и только некоторые траектории, имеющие такие же последовательности максимумов, могут приближаться к ним асимптотически. Остальные траектории, у которых последовательности максимумов образуют несчетное

множество, представляют, таким образом, детерминированное непериодическое течение.

Эти выводы были получены на основе численного исследования решений на конечном промежутке времени. Их нельзя считать математически доказанными, хотя они весьма обоснованны. Одно явное противоречие требует более детального исследования.

Трудно совместить слияние двух поверхностей, каждая из которых содержит по одной спирали, с невозможностью слияния отдельных траекторий. Нетрудно, однако, объяснить кажущееся слияние поверхностей. Объемы, занятые некоторым множеством точек в моменты то и в соответствии с (30) удовлетворяют соотношению

Типичный оборот вокруг занимает 70 итераций, так что для него и, учитывая, что а получаем

Две точки, вначале отделенные в соответствующем направлении, могут, таким образом, очень быстро сблизиться, и внешне это выглядит как слияние.

Тогда, видимо, слияние двух поверхностей только кажущееся, на самом же деле они остаются разными поверхностями. Следуя за ними вдоль траектории и делая оборот вокруг С и С, мы видим, что в действительности каждая поверхность состоит из пары поверхностей, так что когда они опять как бы сливаются, на самом деле есть четыре поверхности. Повторяя этот процесс и делая следующий оборот, мы получаем восемь поверхностей и т. д., и в конце концов напрашивается вывод о существовании бесконечного комплекса поверхностей, каждая из которых очень близка к одной из двух сливающихся.

Бесконечное множество точек, в которых линия, параллельная оси X, пересекает эти поверхности, может быть уподоблено множеству всех чисел между нулем и единицей, чьи десятичные разложения (или какие-нибудь другие разложения, кроме двоичных) содержат только нули и единицы. Это множество очевидно, несчетно ввиду своего соответствия множеству всех чисел между нулем и единицей, выраженных в двоичной системе. Тем не менее это множество имеет меру нуль. Последовательность нулей и единиц, соответствующая определенной поверхности, содержит историю лежащих на этой верхности траекторий: единица или нуль, стоящие сразу после запятой в десятичном разложении, показывают, то последний оборот был соответственно вокруг С или С, единица или

нуль на втором месте дают такую же информацию о предыдущем обороте и т. д. Повторяющиеся десятичные разложения представляют периодические или квазипериодические траектории и, поскольку они задаются рациональными дробями, образуют счетное множество.

Если кому-нибудь удастся изобразить этот бесконечный комплекс поверхностей, будет нетрудно нарисовать и непериодические детерминированные траектории, лежащие на этих поверхностях.

8. ЗАКЛЮЧЕНИЕ

Определенные механически или термически возбуждаемые неконсервативные гидродинамические системы могут вести себя как периодически, так и нерегулярно, даже если в вынуждающей силе нет соответствующей явной периодичности или нерегулярности. И периодическое, и непериодическое течения наблюдаются в некоторых экспериментальных моделях, когда вынуждающая сила поддерживается постоянной в пределах экспериментальных ошибок. В некоторых конечномерных системах обыкновенных дифференциальных уравнений, предназначенных для описания этих гидродинамических систем, при строгом постоянстве внешней силы удается аналитически получить периодические решения. Непериодические решения других подобных систем находятея численно.

Конечномерные системы обыкновенных дифференциальных уравнений, описывающие вынужденное диссипативное течение, часто имеют следующее свойство: все решения в конце концов сосредоточиваются в одном и том же объеме. Мы в деталях исследовали свойства решений таких систем. Наши основные результаты относятся к вопросу, связанному с устойчивостью непериодических решений. Установившееся непериодическое решение должно быть неустойчивым в том смысле, что близкие к нему в какой-то момент решения не останутся близкими навсегда. Неустановившееся непериодическое решение иногда устойчиво, но в этом случае устойчивость — одно из переходных свойств, стремящееся исчезнуть.

Для подтверждения существования детерминированного непериодического течения мы численно решали систему трех обыкновенных дифференциальных уравнений, предназначенную для описания конвекции. Эти уравнения допускают три стационарных решения и счетное бесконечное множество периодических решений. Обнаружено, что все решения и, в частности, периодические решения, неустойчивы. Поэтому остальные решения не могут, в общем, приближаться асимптотически к периодическим решениям, и, следовательно, они непериодические,

Если наши результаты, касающиеся неустойчивости непериодического течения, применить к атмосфере, которая явно не периодична, то получается, что предсказать погоду на достаточно отдаленное будущее невозможно никаким методом, если только теперешнее состояние не известно точно. Из-за неизбежной неточности и неполноты наблюдений погоды точное предсказание на очень долгий срок, видимо, невозможно.

Остается вопрос: можно ли в действительности применить наши результаты к атмосфере? Атмосферу обычно не рассматривают ни как детерминированную, ни как конечную систему, и отсутствие периодичности не математически строгий факт, поскольку наблюдения велись не всегда.

Наш основной результат основан на том, что любое ограниченное решение конечномерной системы должно рано или поздно подойти сколь угодно близко к состоянию, которое у него было ранее. Если система устойчива, ее последующее движение останется произвольно близким к прошлому и поведение будет квазипериодическим.

В случае атмосферы решающий вопрос в том, отмечались ли с тех пор, как начали наблюдать ее состояние, какие-либо аналоги. Под аналогами мы в данном случае подразумеваем два или более состояния атмосферы, которые так похожи друг на друга, что отличия могут быть приписаны ошибкам в наблюдениях. Чтобы быть аналогами, два состояния должны быть очень похожи в областях, где наблюдения точны и обильны, но они могут быть не похожи в областях, где наблюдений нет совсем. Если некие ненаблюдавшиеся черты проявляются в последовательности состояний, две последовательности должны быть похожими, чтобы быть аналогами.

Пусть два аналога действительно наблюдались с тех пор, как впервые начались атмосферные наблюдения. Тогда, поскольку, согласно наблюдениям, атмосфера непериодична, следующие за этими аналогами последовательности состояний должны в конце концов отличаться друг от друга и ни одним методом нельзя было выполнить предсказания на такие времена. Если, наоборот, аналогов не было, то в принципе может существовать некая аккуратная схема очень долгосрочного прогноза, использующая доступные в данный момент наблюдения. Но если такая схема все же существует, то при появлении аналога атмосфера достигнет квазипериодического поведения и никогда не сойдет с него. Это квазипериодическое поведение не обязательно установится даже при осуществимости очень долгосрочного прогноза, если множество атмосферных состояний так необъятно, что аналогия может и не наступить. Следует отметить, что наши выводы не зависят от того, является атмосфера детерминированной или нет.

Остается весьма важный вопрос — насколько долгим может быть «очень долгий срок»? Для атмосферы наши результаты не дают ответа, этот срок может составлять несколько дней или несколько столетий. В идеализированной системе независимо от того, описанная ли это конвективная модель или сложная система, предназначенная для как можно более точного описания атмосферы, ответ может быть получен при сравнении двух численных решений с почти одинаковыми начальными условиями. В случае атмосферы, если все остальные методы ничего не дадут, мы должны ждать аналога.

Благодарности. Автор признателен доктору Барри Сольцмену, который привлек его внимание к существованию непериодических решений уравнений конвекции. Особая благодарность выражается мисс Элен Феттер за проведение многих численных расчетов и приготовление графического представления численных материалов.

СПИСОК ЛИТЕРАТУРЫ

[1] Birkhoff G. О. Dynamical Systems, New York, Amer. Math. Soc., Colloq. Publ., 1927, 295 pp. (Русский перевод: Биркгоф Дж. Динамические системы. Пер. с англ. М.: ОГИЗ, 1941.)

[2] Ford L. R. Differential Equations, New York, McGraw-Hill. 1933.

[3] Fultz D., Long R. R., Owens G. V., Bohan W., Kaylor R., Weil J. Studies of thermal convection in a rotating cylinder with some implications for large-scale atmospheric motions, Meteor. Monog., 4 (21) (1959), Amer. Meteor. Soc., 104 pp.

[4] Gibbs J. W. Elementary principles in statistical mechanics, New York, Scribner, 1902, 207 pp. (Русский перевод: Гиббс Дж. В. Основные принципы статистической механики. Пер. с англ. М. — Л.: Гостех-издат, 1946.)

[5] Hide R. An experimental study of thermal convection in a rotating liquid, Phil Trans. Roy. Soc. London, 250A, (1958), 441—478.

f6] Lorenz E. N. Maximum simplification of the dynamic equations, Tellus, 12 (1960), 243—254.

[7] Lorenz E. N. Simplified dynamic equations applied to the rotating-basin experimencs, J. atmos. Sci., 19 (1962), 39—51.

[8] Lorenz E. N. The statistical prediction of solutions of dynamic equations, Proc. Internat. Symposium Numerical Weather Prediction, Tokyo, 1962, 629—635.

[9] Немыцкий В. В., Степанов В. В. Качественная теория дифференциальных уравнений. М.: Гостехиздат, 1947.

[10] Пуанкаре А. О кривых, определяемых дифференциальными уравнениями. Пер. с фраиц. М.: ОГИЗ, 1947.

[11] Rayleigh. On convective currents in a horizontal layer of fluid when the higher temperature is on the under side, Phil. Mag., 32 (1916), 529—546.

[12] Saltzman B. Finite amplitude free convection as an initial value problem I, J. atmos. Sci., 19 (1962), 329—341.

[13] Андронов А. А. Собрание трудов. М.: Изд. АН СССР, 1956, 85.

[14] Markoff A. Stabilitat im Liapunoffschen Sinne und FastenperiodizitSt, Math. Zeitschr., Bd. 36, 1933.