ТОПОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ АТТРАКТОРОВ ЛОРЕНЦА

Дэвид Рэнд 1. ВВЕДЕНИЕ

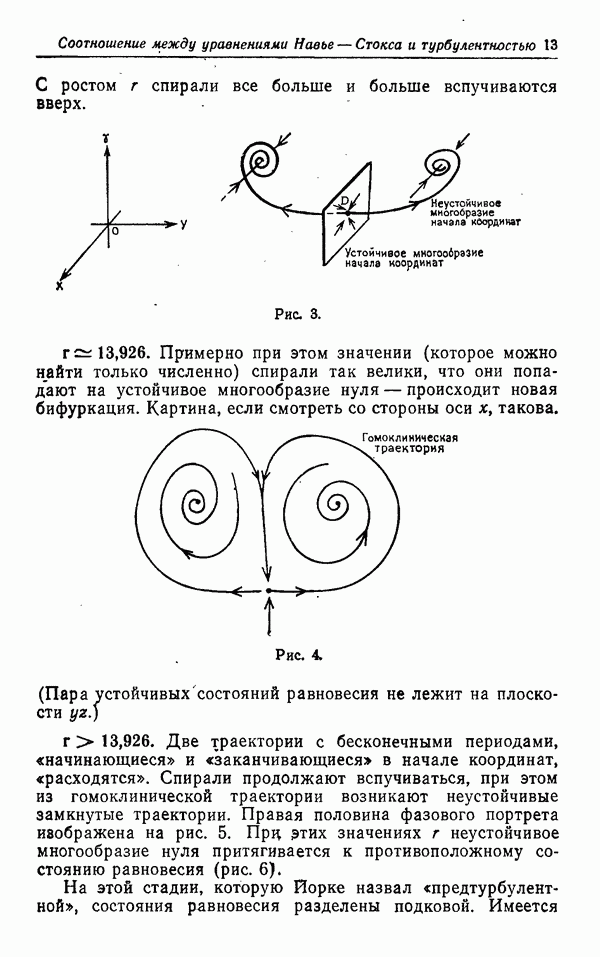
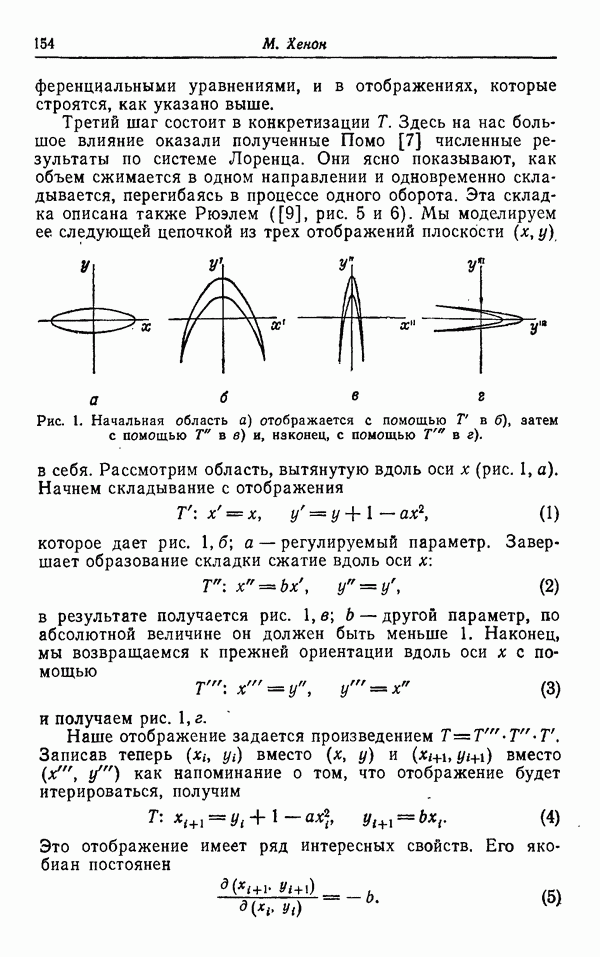
Аттрактор Лоренца — это представитель класса странных аттракторов, предложенный в качестве наглядной модели турбулентности ([4], см. также [5]). Впервые рассмотренный Лоренцем в модельной системе, полученной из уравнений Навье — Стокса с помощью галеркинской процедуры [2], он привлек внимание математиков своими весьма интересными динамическими свойствами.

Аттракторы этого типа, называемые в дальнейшем аттракторами Лоренца, особенно чувствительны к возмущениям векторного поля. Подробное описание аттракторов Лоренца дано Дж. Гуккенхеймером [1], более детальное исследование их свойств проводилось Р. Ф. Уильямсом [6].

Чувствительность аттракторов Лоренца проявляется следующим образом: любое открытое множество векторных полей, имеющих аттрактор Лоренца, содержит такое двупараметрическое семейство полей, что два любых аттрактора топологически не эквивалентны.

Это семейство выделяется при помощи так называемых нидипг-рядов, которые описывают совершаемый траекториями вблизи аттрактора характерный танец вращений. Нидинг-ряды были впервые введены Дж. Милнором и У. Тёрстоном при исследовании динамических свойств некоторых эндоморфизмов интервала на действительной оси. Р. Ф. Уильямс [6] использовал этот подход при исследовании аттракторов Лоренца.

В данной работе содержится ответ на некоторые поставленные в [6] вопросы, в частности показывается, что нидингряды определяют топологический тип аттрактора. Для этого мы вводим нидинг-инвариант, который хотя в основном совпадает с предложенными Уильямсом последовательностями, но все же ближе к конструкции Милнора [3]. В том случае, когда аттрактор симметричен (как в исходной модели

Лоренца), мы строим кусочно-линейную модель отображения Пуанкаре и описываем некоторые свойства периодических траекторий.

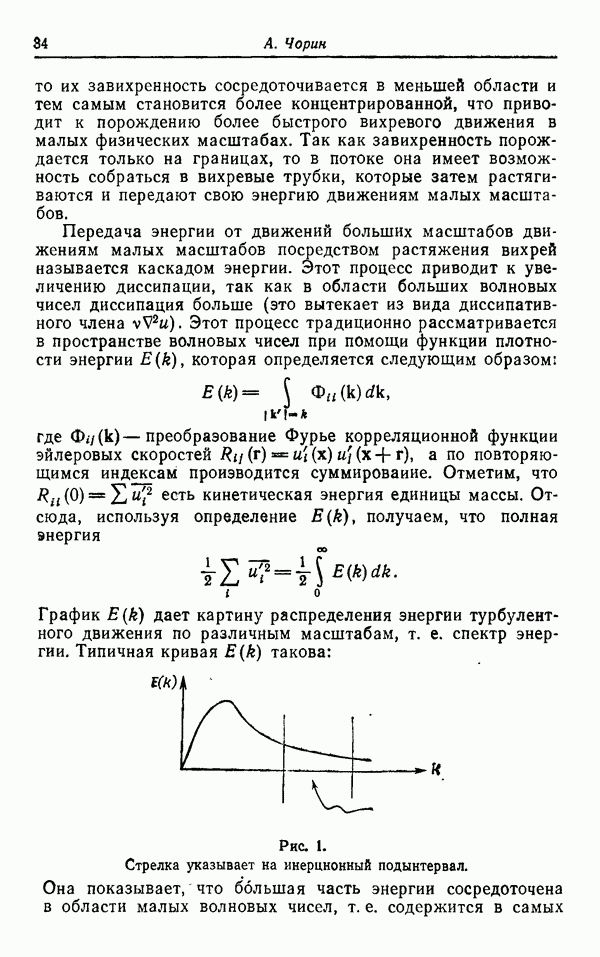
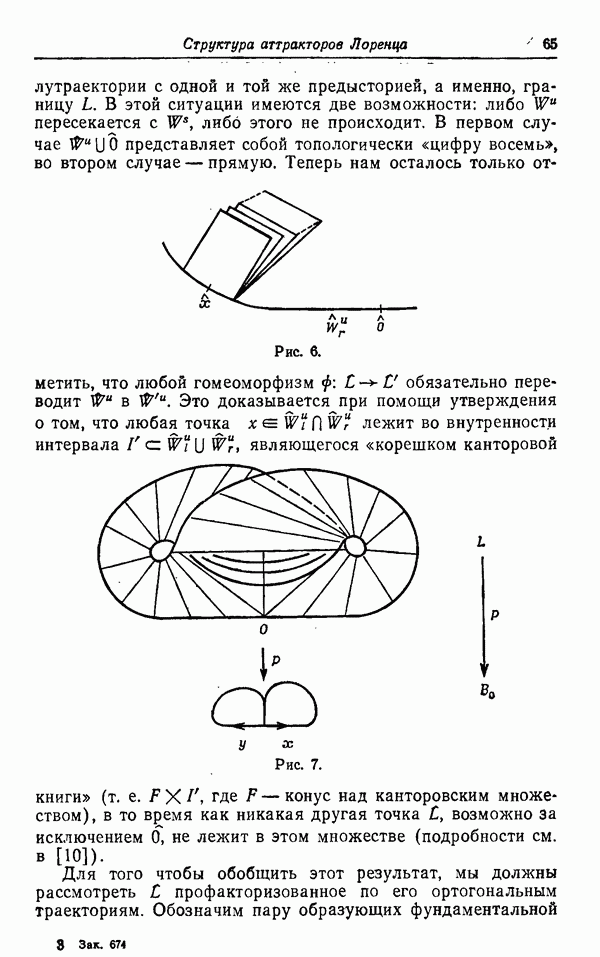
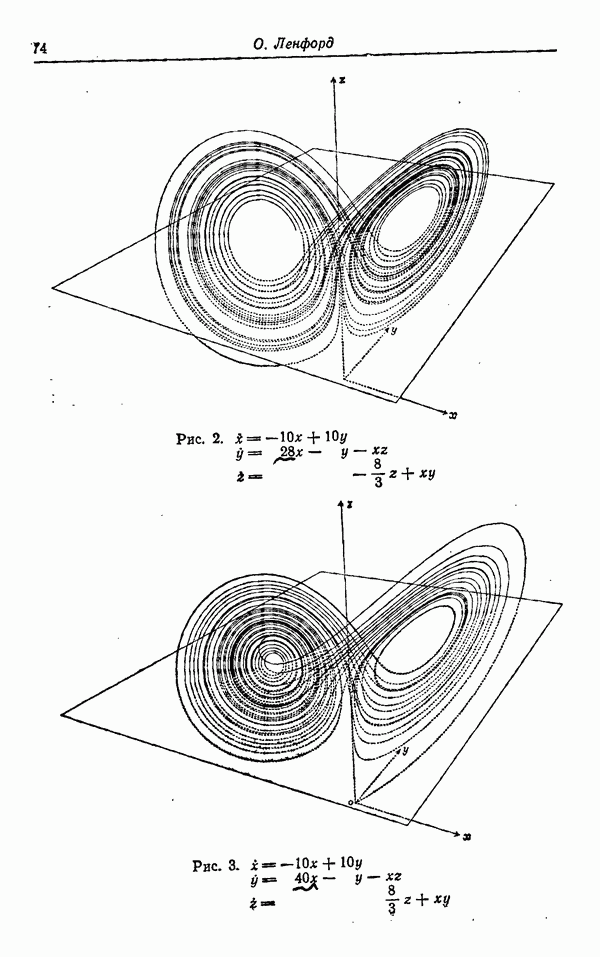
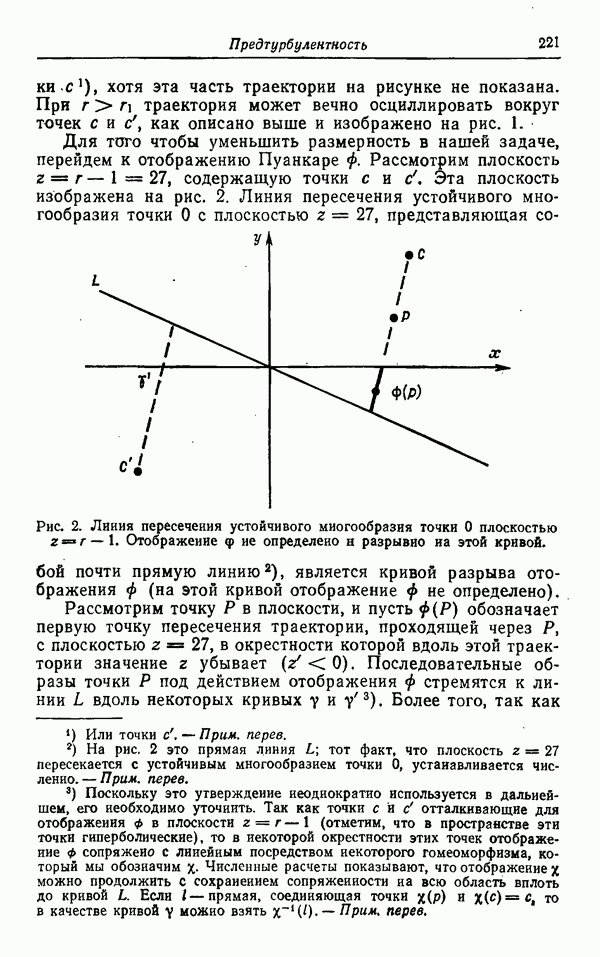
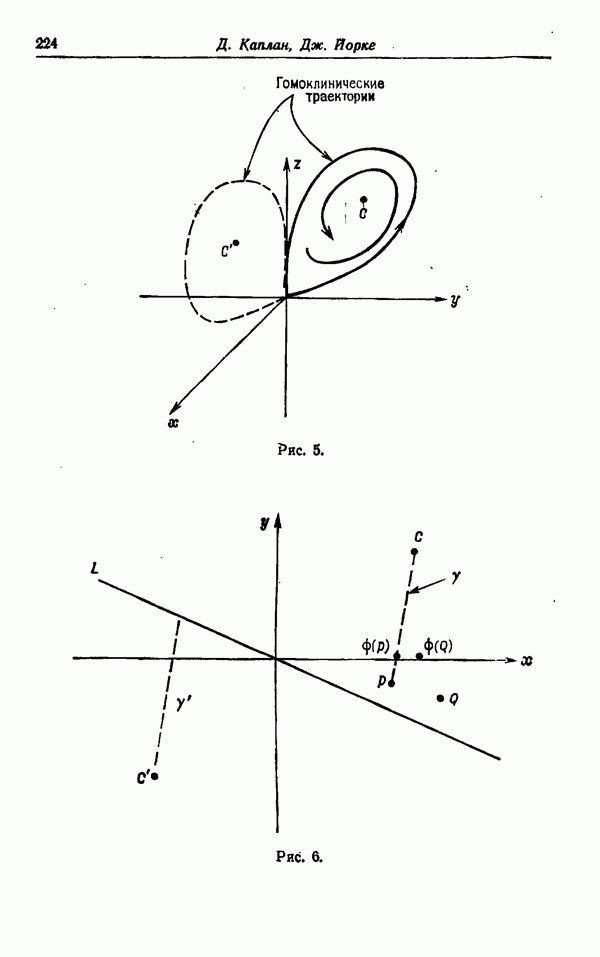
Опишем вкратце предложенный Уильямсом способ построения аттракторов Лоренца. Пусть L — показанная на рис. 1 ветвящаяся поверхность (ср. [6], рис. 1 и 2, стр. 138). Пусть — определенный на L полупоток, такой, что О — седловая точка, устойчивое и неустойчивое многообразия которой ведут себя, как показано на рисунке, а отображение Пуанкаре имеет вид, как на рис. 2, и удовлетворяет условиям (1) — (3) разд. 2.

Рис. 1.

Рис. 2.

Тогда определяемый по аттрактор Лоренца является обратным пределом L по отношению к Он представляет собой сингулярное пространство вместе с потоком . В типичном случае окрестность каждой точки на С есть либо декартово произведение канторова множества на двумерный диск, либо произведение одномерного диска на канторовский конус (последнее в том случае, если к принадлежит неустойчивому многообразию точки но ).

Конечно, фактически вся информация об аттракторе содержится в отображении Пуанкаре f, и именно его мы будем исследовать в дальнейшем. Способ перехода от к аттрактору Лоренца достаточно хорошо описан Уильямсом [6].

2. ОТОБРАЖЕНИЕ ЛОРЕНЦА

В последующих разделах мы будем изучать отображение Пуанкаре где удовлетворяет следующим условиям:

Из условия следует, что если любой подынтервал то существует целое положительное k, такое, что содержит 0.

3. НИДИНГ-ИНВАРИАНТ ОТОБРАЖЕНИЯ f

Для положим

и пусть при

Определение 1. Формальный степенной ряд называется нидинг-рядом точки

Отображение будет монотонным строго возрастающим (т. е. если то ), если мы в кольце нидинг-рядов введем следующее отношение порядка:

если первый ненулевой коэффициент в

положителен. Тогда тогда и только тогда, когда где - полином степени по

Далее, если в ввести топологию, индуцированную метрикой

то будут существовать следующие пределы:

Определение 2. Пара называется нидинг-инвариантом отображения

В тех случаях, когда неясно, о каком отображении идет речь, будем писать

Конечно, вводя это определение, мы исходим из предложенных Р. Ф. Уильямсом нидинг-последовательностей [6]. Однако следует отметить, что между двумя конструкциями

есть различие: в гомоклиннческом случае, когда или они не совпадают, хотя между ними существует довольно простое соответствие. Причина, по которой выбрано именно такое определение, станет очевидной из приводимых ниже результатов, в частности из содержания разд. 6, 7. Мы придерживаемся подхода, предложенного Милнором [3].

Отображение непрерывно в тех точках х, для которых для всех . Если — минимальное из чисел, для которых , то

если только и

если только

Свойства k могут быть описаны достаточно просто. Если

Но так что для всех

Заметим также, что для ряда выполняется одно из трех условий:

для каждого .

Определение 3. Формальный степенной ряд

с коэффициентами из множества называется -допустимым тогда и только тогда, когда он удовлетворяет соотношениям (1) и (2) при всех .

Лемма 1. Для каждого является Недопустимым. Обратно, любой -допустимый ряд совпадает с для некоторого

Доказательство. В доказательстве нуждается только второе утверждение. Пусть

- - допустимый ряд, и пусть Тогда вследствие определено. Ясно, что

так что если k непрерывно в точке то будем иметь Теперь пусть для некоторого . Выбирая минимальное из этих , получим

Отсюда следует, что при и

Из последнего соотношения получаем, что при всех , так как 0 является допустимым рядом. Следовательно, при всех и поэтому

Таким образом, между периодическими допустимыми последовательностями и периодическими точками есть биекция, следовательно, определяют периодические точки f. Обратное утверждение также верно при следовательно, нидинг-инвариант является топологическим инвариантом аттрактора [6].

Лемма 2. Если то периодические точки f плотны в I

Доказательство. Покажем, что в любом открытом интервале содержится периодическая точка. Без ограничения общности можно положить

Пусть — самая длинная из компонент или, если эти. компоненты имеют одинаковую длину, пусть это будет компонента, лежащая по ту же сторону от 0, что и

Для каждого i есть сжатие, переводящее в . Теперь из следует, что при достаточно больших (см., например, [6]). Поэтому имеем

так что содержит точку периода .

Предложение - определяют периодические траектории, Периодические траектории определяют если

Доказательство. В доказательстве нуждается только утверждение Оно вытекает из следующей леммы.

Лемма 3. Предположим, что Для каждого целого существуют такие периодические точки х и у в I, что

Доказательство. Зафиксируем п. Пусть — наименьшее из чисел, для которых Тогда для всех Но по предыдущей лемме существует периодическая точка Следовательно,

Доказательство предложения 1. Пусть Р — множество всех периодических точек в (0, 1). Тогда если , то Пусть . Тогда Если существует n 0, такое, что . Но по лемме 3 - существует такое, что . Получается, что это противоречит определению k. Следовательно, Рассуждения для k - проводятся аналогично.

4. ЗАВИСИМОСТЬ ИНДИНГ-ИНВАРИАНТА ОТ f

Множество отображений Пуанкаре, удовлетворяющих сформулированным в разд. 2 условиям, обозначим через т. Введем на метрику класса

Для будем писать если при всех

Предложение 2. Если , то

Доказательство. Если , то, очевидно, при всех . Следовательно, . Возможность равенства мы можем исключить, показав, что если таковы, что при всех то из следует, что

а из следует, что при всех .

Итак, предположим, что . Если для всех , то сразу получаем, что при всех . В самом деле, если при некотором минимальном и, скажем, то при некотором . Тогда из следует, что Но при лежат по одну сторону 0, так что если выбрано минимальное , то

Если то применяя те же рассуждения, получаем, что если то для всех Если же то получается, что и, следовательно, имеют периодические коэффициенты. Отсюда следует, что —1 — периодическая точка, что противоречит условию Следовательно,

для всех . Аналогичным образом доказательство проводится в случае и для Этим завершается доказательство предложения 2.

Следствие 1. В любом открытом подмножестве класса существует несчетное подмножество, элементы которого имеют отличные друг от друга нидинг-инварианты.

Следствие 2. В любом открытом подмножестве класса существует несчетное множество классов топологической сопряженности.

Замечание. Два отображения топологически сопряжены, если существует гомеоморфизм такой, что

Замечание. Мы работаем здесь только с -метрикой, потому что возможна ситуация, когда

Это как раз тот случай, который рассматривал Гуккенхеймер в [1] в связи с исследованием аттрактора Лоренца. Однако из следствия 1 ясно, что следствие 2 справедливо для любой разумной метрики, учитывающей дифференцируемость; например, для метрики, индуцированной из метрики в пространстве векторных полей, порождающих полупотоки на ветвящемся многообразии L. Поэтому после небольшой работы из предложения 1 можно вывести, что в любой -окрестности

векторного поля с аттрактором Лоренца имеется несчетное множество векторных полей с топологически не сопряженными аттракторами (см. [6]).

5. НИДИНГ-ИНВАРИАНТ ЯВЛЯЕТСЯ ПОЛНЫМ ИНВАРИАНТОМ

Теорема 1. Если имеют одинаковые нидинг-инва-рианты, то они сопряжены при помощи сохраняющего ориентацию гомеоморфизма.

Доказательство. Положим

Из равенства нидинг-инвариантов f и g следует существование сохраняющей ориентацию биекции такой, что При этом используется тот факт, что, согласно лемме 1, эти точки соответствуют допустимым полиномам степени . Далее, если то принадлежат и имеют одинаковые нидинг-ряды по g, так что Таким образом, на

Пусть кусочно-линейный гомеоморфизм, такой, что

и линейно вне

Поскольку отображение строго монотонно, плотны в Принимая это во внимание, мы видим, что — это последовательность Коши в -топологии на пространстве непрерывных отображений I в I. Следовательно, предел существует и является непрерывным отображением.

Так как h совпадает с на а А плотно, то h строго монотонно и, следовательно, является гомеоморфизмом. Далее, на при любом , так что совпадают на плотном подмножестве Из непрерывности следует, что Таким образом, h обеспечивает требуемое сопряжение и теорема доказана.

Замечание. Построенное при доказательстве теоремы 1 сопряжение сохраняет ориентацию. Если то подобным образом можно построить сопряжение, обращающее ориентацию,

Следствие 1. Множество является полным топологическим инвариантом аттрактора Лоренца при

Доказательство. То, что множество является топологическим инвариантом, следует из работы Уильямса [6] (ср. предложение 1). Обратное утверждение вытекает из теоремы 1, очевидным образом дополненной рассмотрением случая обращения ориентации, и из детального анализа конструкций, приведенных в [8, 6].

Конечно, из теоремы следует и более сильное утверждение.

Следствие 2. Два аттрактора Лоренца с топологически эквивалентны тогда и только тогда, когда два множества

нидинг-рядов совпадают.

6. ИНВАРИАНТ РАЗРЕЗАНИЯ

Числа разрезаний показывают, сколько раз интервал разрезался точкой разрыва после некоторого числа итераций.

Определение число разрезаний отображения f есть мощность множества

Инвариант разрезания отображения — это формальный степенной ряд

Теорема 2. В Z [[f]]

Доказательство. Функция есть ступенчатая функция с разрывами в тех точках для которых при . Если выбрано минимальным, то размер скачка есть (см. разд. 3). Всего таких скачков Суммируя их, мы видим, что

Устремляя получаем

откуда сразу следует утверждение теоремы. Скорость роста чисел при определяется величиной Так как то Мы можем дать и более точную оценку.

Лемма

Доказательство. Поскольку непусто при всех то при всех .

Имеем Поэтому после итераций должно быть не менее разрезов. Следовательно,

Но при всех , поэтому

Следовательно,

откуда сразу получаем, что

7. ПЕРИОДИЧЕСКИЕ ТОЧКИ СИММЕТРИЧНОГО ОТОБРАЖЕНИЯ

Предположим, что Очевидно, в этом симметричном случае

Если то через обозначим шах Тогда из определения 3 сразу следует, что если

и если для всех

то ряд является -допустимым. В действительности условие можно опустить, если заменить условие

Отсюда сразу следует, что если имеет периодические коэффициенты то 0 является -допустимым, если и только если для всех

Таким образом, мы получили следующее

Предложение 3. Если то отображение индуцирует биекцию между периодическими точками f и периодическими формальными степенными рядами

с коэффициентами из удовлетворяющими условию (3) при всех .

Определение 6. Формальный степенной ряд

назовем самодопустимым, если при всех

Мы приведем сейчас несколько примеров самодопустимых рядов. Следующие замечания в значительной степени -принадлежат Л. Джонкеру.

Примеры. (1) Пусть Тогда

периодично с периодом и самодопустимо.

(2) Если и нечетно, положим

Тогда периодично с периодом и самодопустимо.

Теорема Для любого положительного целого является максимальным элементом в множестве всех периодических самодопустимых рядов, минимальный период которых равен .

(ii) Предположим, что Тогда если f имеет периодическую точку периода k, то существует и периодическая точка периода I.

(iii) Ряды а располагаются в следующем порядке:

Доказательство. Мы докажем только доказательство остальных утверждений появится в работе Л. Джонкера [7].

Предположим, что имеет период k. Тогда ряд у лежит на траектории -самодопустимый и Из следует, что так что

Тогда удовлетворяет условию (3) для

всех и, следовательно, является -допустимым. Применяя лемму 1, получаем отсюда, что для некоторого и доказательство завершено, поскольку — периодическая точка с периодом I.

Я хотел бы отметить, что многим обязан работам Гуккенхеймера, Уильямса и Милнора, и поблагодарить Дэвида Фаулера, Лео Джонкера и Кристофера Зимана за ряд полезных обсуждений, касавшихся аттрактора Лоренца.

Замечание. После завершения данной статьи автор получил препринт Гуккенхеймера, в котором другим способом доказана теорема 1.

СПИСОК ЛИТЕРАТУРЫ

(см. скан)