| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
МЕТАСТАБИЛЬНЫЙ ХАОС: ПЕРЕХОД К УСТОЙЧИВОМУ ХАОТИЧЕСКОМУ ПОВЕДЕНИЮ В МОДЕЛИ ЛОРЕНЦА
Дж. Йорке и Е. Йорке
Аннотация. В настоящей статье изучается поведение траекторий системы уравнений, введенной Лоренцем для описания турбулентной конвекции, при значениях чисел Рэлея, несколько меньших, чем то критическое значение, при котором возникает устойчивое хаотическое движение. Численно исследуются некоторые статистические свойства решений при этих переходных значениях параметра. Находится среднее время, в течение которого поведение траектории является хаотическим и изучается зависимость этого времени от параметра  . Это изучение проводится либо численно, либо (для значений
. Это изучение проводится либо численно, либо (для значений  , близких к критическому) аналитически.
, близких к критическому) аналитически.
§ 1. ВВЕДЕНИЕ
Хаотическое поведение траекторий динамической системы представляет интерес во многих отношениях и было исследовано большей частью в связи с проблемой турбулентности. При построении идеализированной модели неустойчивой конвекции жидкости между двумя параллельными пластинами Лоренц ввел систему обыкновенных дифференциальных уравнений, определяющую поток, который при подходящих значениях параметров ведет себя как «детерминированный непериодический поток». Хотя решения полностью определяются своими начальными данными, они с течением времени меняются чрезвычайно нерегулярным образом. Более того, малые отклонения начальных условий вызывают большие отклонения в поведении решений через достаточно большое время. Таким образом, для наблюдателя, следящего за грубыми свойствами системы, картина поведения ее траекторий выглядит полностью хаотической.
Система уравнений, введенных Лоренцем, имеет вид

См. также Марсден и Мак-Кракен [12] и Марсден [13]. Хотя более поздние работы (Мартин и Маклолин [14], Кэрри [1]) показали, что эти уравнения не адекватно описывают конвекцию жидкости в тех случаях, для которых они первоначально были написаны, эти уравнения могут описывать некоторые явления в лазерах, а также конвекцию жидкости в случаях, которые мы опишем в § 2. Более того, они представляют собой относительно простую модель, дающую богатую пищу для изучения нерегулярного поведения.
Эта статья посвящена детальному численному анализу системы Лоренца в «предтурбулентной» области изменения параметров. Мы ограничимся значениями  которыми пользовался в своих расчетах Лоренц. Он показал, что при
которыми пользовался в своих расчетах Лоренц. Он показал, что при  стационарное решение (0,0,0), не соответствующее конвекции, устойчиво, в то время как при
стационарное решение (0,0,0), не соответствующее конвекции, устойчиво, в то время как при  существуют три стационарных решения:
существуют три стационарных решения:  , где
, где  Для значений
Для значений  , лежащих между
, лежащих между  (от
(от  и для выбранных выше значений а и
и для выбранных выше значений а и  две ненулевые неподвижные точки устойчивы и являются притягивающими, а при
две ненулевые неподвижные точки устойчивы и являются притягивающими, а при  все три неподвижные точки неустойчивы. При
все три неподвижные точки неустойчивы. При  Лоренц наблюдал устойчивые хаотические осцилляции решений системы (1.1), подробно описал поведение траекторий в фазовом пространстве и странное притягивающее множество, к которому эти траектории стремятся.
Лоренц наблюдал устойчивые хаотические осцилляции решений системы (1.1), подробно описал поведение траекторий в фазовом пространстве и странное притягивающее множество, к которому эти траектории стремятся.
Этот странный аттрактор наблюдался вполне отчетливо для значений параметра  , больших критического значения
, больших критического значения  да 24.74, и в частности для случая
да 24.74, и в частности для случая  рассмотренного Лоренцем. Почти для каждого начального условия
рассмотренного Лоренцем. Почти для каждого начального условия  задаваемая этнм начальным условием траектория стремится к странному аттрактору. Подобное явление в действительности наблюдается для значений параметра
задаваемая этнм начальным условием траектория стремится к странному аттрактору. Подобное явление в действительности наблюдается для значений параметра  , немного меньших, чем
, немного меньших, чем  А именно, в области
А именно, в области  некоторые траектории стремятся асимптотически к странному аттрактору, в то время как другие стремятся к притягивающим точкам. Решения, отвечающие траекториям первого типа, осциллируют нерегулярным образом без затухания. При малых изменениях начальных данных наблюдаются значительные отклонения в форме этих осцилляций. Следовательно, можно сказать, что для значений
некоторые траектории стремятся асимптотически к странному аттрактору, в то время как другие стремятся к притягивающим точкам. Решения, отвечающие траекториям первого типа, осциллируют нерегулярным образом без затухания. При малых изменениях начальных данных наблюдаются значительные отклонения в форме этих осцилляций. Следовательно, можно сказать, что для значений  наблюдается «устойчивый хаос». (Для достаточно больших
наблюдается «устойчивый хаос». (Для достаточно больших  характер поведения траекторий изменяется, но эту область значений параметров мы не рассматриваем.) Цель настоящей работы — описать характер поведения траекторий для значений
характер поведения траекторий изменяется, но эту область значений параметров мы не рассматриваем.) Цель настоящей работы — описать характер поведения траекторий для значений  , немного меньших, чем
, немного меньших, чем  , и указать, как он изменяется при переходе через это значение.
, и указать, как он изменяется при переходе через это значение.
Каплан и Йорке [8], [9] показали, что значение  да да 13.926 является переходным. По поводу этого предтурбулентного режима см. также Роббинс [16], [17]. При значениях
да да 13.926 является переходным. По поводу этого предтурбулентного режима см. также Роббинс [16], [17]. При значениях  , больших
, больших  возникает «исключительное» множество (т. е. множество меры нуль) хаотических решений системы (1.1), которые осциллируют в течение всего времени. Множество хаотических траекторий неустойчиво для значений параметра
возникает «исключительное» множество (т. е. множество меры нуль) хаотических решений системы (1.1), которые осциллируют в течение всего времени. Множество хаотических траекторий неустойчиво для значений параметра  , заключенных между
, заключенных между  : поведение траекторий в окрестности этого множества напоминает поведение траекторий в окрестности седловой точки, так что траектория, начальная точка которой лежит в окрестности этого множества, но не в самом множестве, с течением времени удаляется от этой окрестности. Если начальная точка
: поведение траекторий в окрестности этого множества напоминает поведение траекторий в окрестности седловой точки, так что траектория, начальная точка которой лежит в окрестности этого множества, но не в самом множестве, с течением времени удаляется от этой окрестности. Если начальная точка  принадлежит окрестности хаотического множества и выбирается случайным образом, то вероятность того, что соответствующее решение будет осциллировать без затухания в течение всего времени, равна нулю. Хотя множество все время
принадлежит окрестности хаотического множества и выбирается случайным образом, то вероятность того, что соответствующее решение будет осциллировать без затухания в течение всего времени, равна нулю. Хотя множество все время
осциллирующих (хаотических) траекторий непосредственно не наблюдается, его существование устанавливается косвенно через то воздействие, которое оно оказывает на характер поведения траекторий и которое проявляется в наших численных экспериментах, в особенности для значений  , лишь немного меньших
, лишь немного меньших  .
.

Рис. 1.1. Это решение системы (1.1), вычисленное при  проявляет свойство переходного хаотического поведения, хаотические осцнллиции внезапно обрываются и переходят в затухающие осцилляции; решение стремится к стационарному
проявляет свойство переходного хаотического поведения, хаотические осцнллиции внезапно обрываются и переходят в затухающие осцилляции; решение стремится к стационарному  Среднее число осцилляций в хаотическом режиме равно примерно 60. При
Среднее число осцилляций в хаотическом режиме равно примерно 60. При  , приближающемся (снизу) к
, приближающемся (снизу) к  это число увеличивается и составляет около 300 осцилляций при
это число увеличивается и составляет около 300 осцилляций при 
При этих значениях  «время затухания» осцилляций траектории, проходящей вблизи хаотического множества, чрезвычайно велико, и на эту «метастабильную» особенность поведения траекторий мы и обращаем внимание в настоящей статье. Рис. 1.1 иллюстрирует обсуждаемый нами тип поведения траекторий, и в частности внезапный переход от нерегулярных осцилляций к их затуханию.
«время затухания» осцилляций траектории, проходящей вблизи хаотического множества, чрезвычайно велико, и на эту «метастабильную» особенность поведения траекторий мы и обращаем внимание в настоящей статье. Рис. 1.1 иллюстрирует обсуждаемый нами тип поведения траекторий, и в частности внезапный переход от нерегулярных осцилляций к их затуханию.
§ 2. ПРЕДСТАВЛЕНИЕ СИСТЕМЫ ЛОРЕНЦА ПОСРЕДСТВОМ СКАЛЯРНЫХ ФУНКЦИЙ
Лоренц показал, что в пространстве  существует такой эллипсоид Е, что каждая траектория, попавшая однажды внутрь этого эллипсоида, остается там навсегда. Это означает, что множество Е инвариантно под действием потока, задаваемого системой дифференциальных уравнений (1.1), при положительных значениях времени t. Обозначим через
существует такой эллипсоид Е, что каждая траектория, попавшая однажды внутрь этого эллипсоида, остается там навсегда. Это означает, что множество Е инвариантно под действием потока, задаваемого системой дифференциальных уравнений (1.1), при положительных значениях времени t. Обозначим через  точку, в которую приходит через время t траектория системы (1.1), начинающаяся в точке
точку, в которую приходит через время t траектория системы (1.1), начинающаяся в точке  Если
Если  — некоторое множество, то обозначим через
— некоторое множество, то обозначим через  множество
множество  Через
Через  обозначим трехмерный объем множества 5. Лоренц заметил, что дивергенция векторного поля, задаваемого функциями, стоящими в правых частях уравнений (1.1), постоянна и равна — (а
обозначим трехмерный объем множества 5. Лоренц заметил, что дивергенция векторного поля, задаваемого функциями, стоящими в правых частях уравнений (1.1), постоянна и равна — (а  Следовательно,
Следовательно,

Пусть Е будет упомянутым выше эллипсоидом, инвариантным при  . Так как
. Так как  для
для  то
то

Таким образом, траектория асимптотически стремится к предельному множеству

при t, стремящемся к бесконечности, причем множество Д» в силу (2.1) имеет меру нуль. Форма множества Я» при значениях  чрезвычайно сложна. Оно содержит апериодические траектории, причем соответствующие решения осциллируют без затухания в течение всего времени, не стремясь к какому-либо постоянному или периодическому решению. Для
чрезвычайно сложна. Оно содержит апериодические траектории, причем соответствующие решения осциллируют без затухания в течение всего времени, не стремясь к какому-либо постоянному или периодическому решению. Для  среднее время, приходящееся на одну осцилляцию (т. е. среднее время между двумя последовательными максимумами какой-либо координаты решения, скажем,
среднее время, приходящееся на одну осцилляцию (т. е. среднее время между двумя последовательными максимумами какой-либо координаты решения, скажем,  ), полученное в результате численных расчетов, равно примерно 2/3. За это характеристическое для системы (1.1) время объем уменьшается в
), полученное в результате численных расчетов, равно примерно 2/3. За это характеристическое для системы (1.1) время объем уменьшается в  раз. Следовательно, любая начальная точка, лежащая в интересующей нас области, задает траекторию, которая быстро приближается к множеству
раз. Следовательно, любая начальная точка, лежащая в интересующей нас области, задает траекторию, которая быстро приближается к множеству  при этом она может асимптотически стремиться либо
при этом она может асимптотически стремиться либо
к некоторой точке, либо к некоторому подмножеству в  и при известных обстоятельствах она может, закручиваясь, сколь угодно близко подходить к каждой точке «странного» множества
и при известных обстоятельствах она может, закручиваясь, сколь угодно близко подходить к каждой точке «странного» множества 
Систему Лоренца мы интегрировали численно. Для нахождения решений мы использовали локальную экстраполяцию в модифицированной форме Адамса — Писа, взятую из программы Шампине.
При  легко обнаруживались траектории, которые нерегулярно осциллировали в течение всего времени, пока длился численный счет. Это есть как раз такое поведение решений, которое было теоретически предсказано. С другой стороны, при значениях
легко обнаруживались траектории, которые нерегулярно осциллировали в течение всего времени, пока длился численный счет. Это есть как раз такое поведение решений, которое было теоретически предсказано. С другой стороны, при значениях  , немного меньших, чем
, немного меньших, чем  , наблюдались решения, имеющие подобные нерегулярные осцилляции с большим числом циклов; впоследствии эти решения начинали затухать, стремясь к одному из двух стационарных решений
, наблюдались решения, имеющие подобные нерегулярные осцилляции с большим числом циклов; впоследствии эти решения начинали затухать, стремясь к одному из двух стационарных решений  . В частности, численные расчеты показали, что функция
. В частности, численные расчеты показали, что функция  — первая координата решения — редко меняет знак в интервале времени, где она нерегулярно осциллирует, но в конце концов знак
— первая координата решения — редко меняет знак в интервале времени, где она нерегулярно осциллирует, но в конце концов знак  перестает меняться после того, как решение начинает стремиться к одному из стационарных решений. Обозначим через Т момент времени, когда функция
перестает меняться после того, как решение начинает стремиться к одному из стационарных решений. Обозначим через Т момент времени, когда функция  последний раз меняет знак перед тем, как начать затухать, и назовем его концом интервала нерегулярности (см. рис. 1.1). Если перемен знака не происходит, то мы положим
последний раз меняет знак перед тем, как начать затухать, и назовем его концом интервала нерегулярности (см. рис. 1.1). Если перемен знака не происходит, то мы положим  Для заданной точки
Для заданной точки  подсчитаем число локальных максимумов на интервале нерегулярности (0, Т) функции
подсчитаем число локальных максимумов на интервале нерегулярности (0, Т) функции  Мы обозначим это число через
Мы обозначим это число через  и назовем числом осцилляций точки Р.
и назовем числом осцилляций точки Р.
Для значений  , немного меньших, чем
, немного меньших, чем  , наблюдается явная дихотомия решений. Для многих начальных точек
, наблюдается явная дихотомия решений. Для многих начальных точек  или 1 и существуют такие начальные точки, что определяемые ими траектории почти сразу же начинают затухать. Например, для точек, лежащих в окрестности устойчивых неподвижных точек,
или 1 и существуют такие начальные точки, что определяемые ими траектории почти сразу же начинают затухать. Например, для точек, лежащих в окрестности устойчивых неподвижных точек,  а для точек, лежащих в окрестности неустойчивой точки,
а для точек, лежащих в окрестности неустойчивой точки,  Существует другой тип начальных точек Р с большим значением
Существует другой тип начальных точек Р с большим значением  . Например, при
. Например, при  подсчет дает среднее значение
подсчет дает среднее значение  на множестве точек, где
на множестве точек, где  равное примерно 300.
равное примерно 300.
Анализ этой дихотомии с помощью непосредственного численного интегрирования системы (1.1) весьма затруднен, поскольку среднее значение  быстро стремится к бесконечности при
быстро стремится к бесконечности при  и необходимое для этого машинное время весьма велико даже при
и необходимое для этого машинное время весьма велико даже при  Итак, решения
Итак, решения
весьма неустойчивы; малым отклонениям начальных данных отвечают большие отклонения формы осцилляций, проявляющиеся уже после нескольких первых циклов. Неизбежные ошибки вычислений порождают некоторую неуверенность в правильности полученных нами результатов, и эта неуверенность растет с ростом  , так как с каждым новым циклом точность вычислений уменьшается примерно в два раза, так что со временем накопленные ошибки становятся недопустимо большими. Поэтому вычисленные нами значения величины
, так как с каждым новым циклом точность вычислений уменьшается примерно в два раза, так что со временем накопленные ошибки становятся недопустимо большими. Поэтому вычисленные нами значения величины  хоть и являются весьма показательными, все же им нельзя слишком доверять. Точно так же простое вычисление среднего значения
хоть и являются весьма показательными, все же им нельзя слишком доверять. Точно так же простое вычисление среднего значения  не позволяет даже на интуитивном уровне понять, что происходит при переходе параметра
не позволяет даже на интуитивном уровне понять, что происходит при переходе параметра  через критическое значение
через критическое значение 
Лоренц предложил довольно неожиданный метод, позволяющий свести описание поведения решений системы обыкновенных дифференциальных уравнений (1.1) к исследованию некоторых функций одной переменной. Интегрируя численно систему уравнений (1.1), он выписывал последовательные максимумы функции  . (Совершенно безразлично, какую именно координату решения выбирать.) Обозначая
. (Совершенно безразлично, какую именно координату решения выбирать.) Обозначая  максимум функции
максимум функции  через
через  он последовательно нанес на чертеже точки
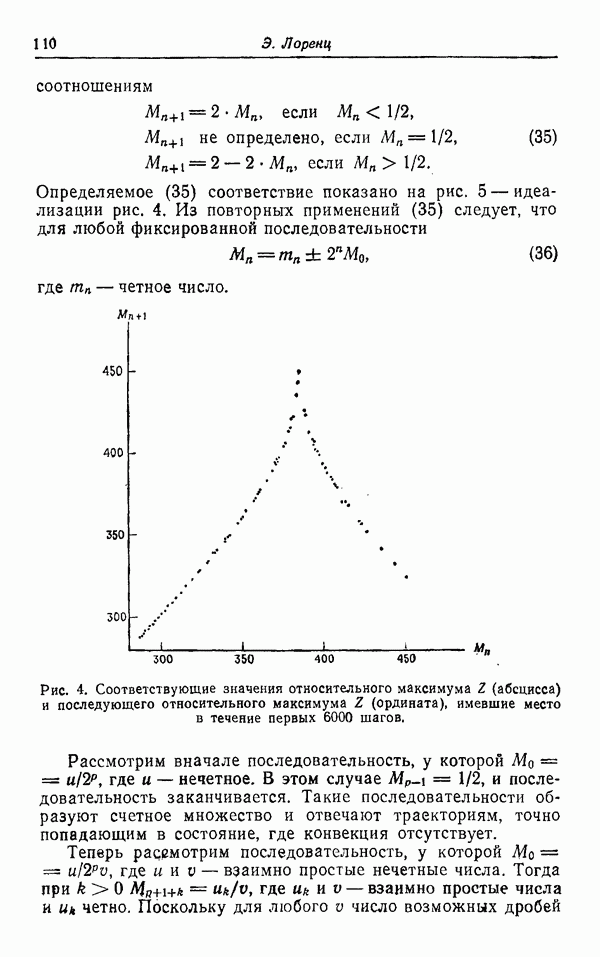
он последовательно нанес на чертеже точки  и обнаружил, что они лежат на кривой, имеющей форму буквы А с острым пиком. Он сообщил, что «в пределах точности, с которой вычисляется г», существует точное взаимно-однозначное соответствие между
и обнаружил, что они лежат на кривой, имеющей форму буквы А с острым пиком. Он сообщил, что «в пределах точности, с которой вычисляется г», существует точное взаимно-однозначное соответствие между  Это означает, что построенная кривая является графиком функции
Это означает, что построенная кривая является графиком функции  Это равенство не является абсолютно точным (даже еслн решение вычисляется абсолютно точно), но величина отклонения весьма мала. Если при том же значении параметра
Это равенство не является абсолютно точным (даже еслн решение вычисляется абсолютно точно), но величина отклонения весьма мала. Если при том же значении параметра  мы рассмотрим другую траекторию и вычислим для нее последовательные значения максимумов
мы рассмотрим другую траекторию и вычислим для нее последовательные значения максимумов  то точки
то точки  будут располагаться на той же кривой
будут располагаться на той же кривой  (за исключением первых одной или двух точек). Взяв длинную последовательность локальных максимумов, мы убедимся, что соответствующие точки с большой точностью ложатся на график функции А. Обсуждение возможной картины распределения точек
(за исключением первых одной или двух точек). Взяв длинную последовательность локальных максимумов, мы убедимся, что соответствующие точки с большой точностью ложатся на график функции А. Обсуждение возможной картины распределения точек  при
при  имеется у Ли и Иорке [9]. См. также Шарковский
имеется у Ли и Иорке [9]. См. также Шарковский 
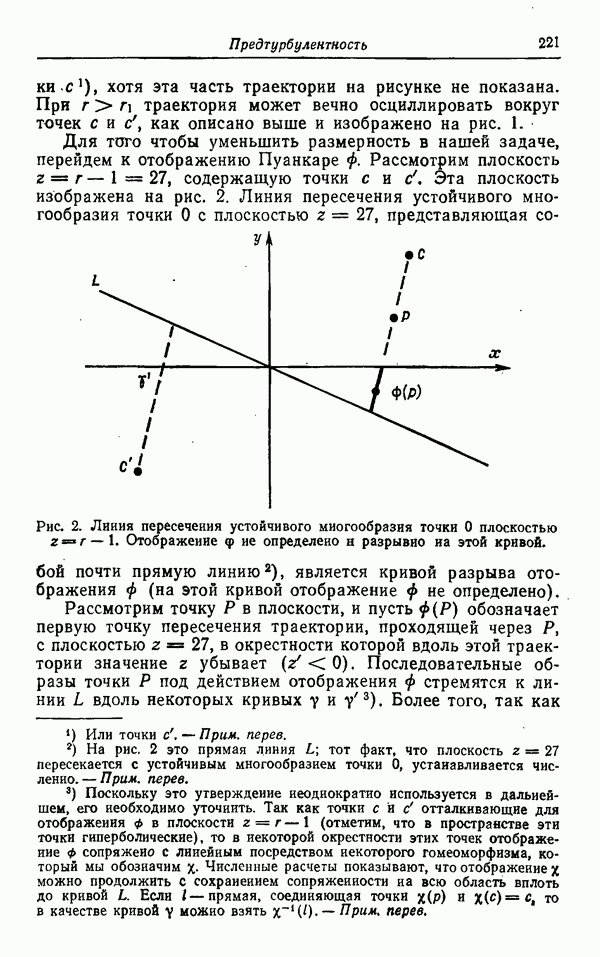
При  мы не можем воспроизвести график функции
мы не можем воспроизвести график функции  , используя одну траекторию, так как спустя некоторое время соответствующее решение стремится асимптотически
, используя одну траекторию, так как спустя некоторое время соответствующее решение стремится асимптотически
к постоянному, так что пара  асимптотически стремится к паре
асимптотически стремится к паре  . Чтобы нарисовать график функции
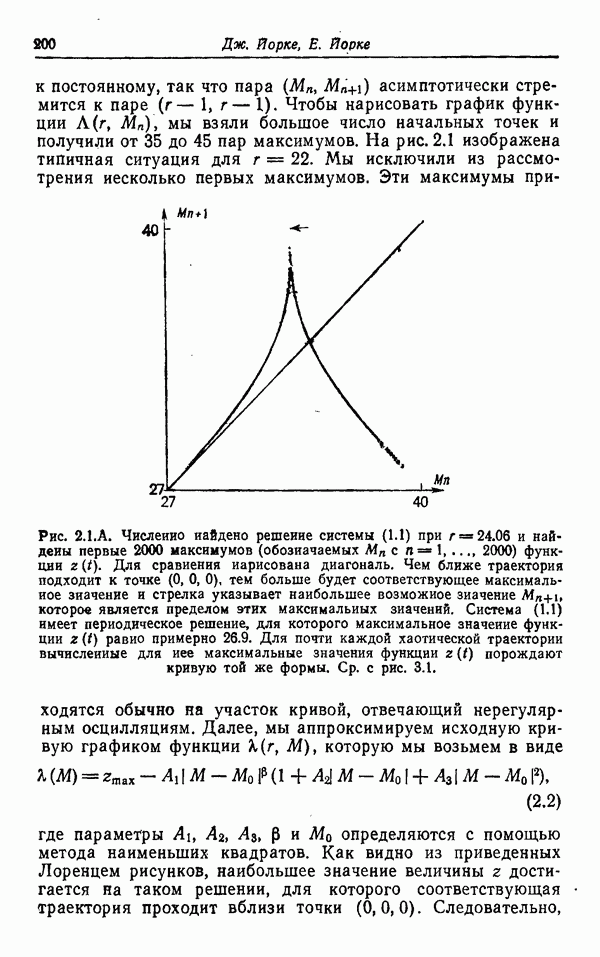
. Чтобы нарисовать график функции  мы взяли большое число начальных точек и получили от 35 до 45 пар максимумов. На рис. 2.1 изображена типичная ситуация для
мы взяли большое число начальных точек и получили от 35 до 45 пар максимумов. На рис. 2.1 изображена типичная ситуация для  Мы исключили из рассмотрения несколько первых максимумов.
Мы исключили из рассмотрения несколько первых максимумов.

Рис. 2.1. А. Численно найдено решение системы (1.1) при  и найдены первые 2000 максимумов (обозначаемых
и найдены первые 2000 максимумов (обозначаемых  функции 2 (t). Для сравнения нарисована диагональ. Чем ближе траектория подходит к точке (0, 0, 0), тем больше будет соответствующее максимальное значение и стрелка указывает наибольшее возможное значение
функции 2 (t). Для сравнения нарисована диагональ. Чем ближе траектория подходит к точке (0, 0, 0), тем больше будет соответствующее максимальное значение и стрелка указывает наибольшее возможное значение  которое является пределом этих максимальных значений. Система (1.1) имеет периодическое решение, для которого максимальное значение функции
которое является пределом этих максимальных значений. Система (1.1) имеет периодическое решение, для которого максимальное значение функции  равно примерно 26.9. Для почти каждой хаотической траектории вычисленные для нее максимальные значения функции
равно примерно 26.9. Для почти каждой хаотической траектории вычисленные для нее максимальные значения функции  порождают кривую той же формы.
порождают кривую той же формы.  с рис. 3.1.
с рис. 3.1.
Эти максимумы приходятся обычно на участок кривой, отвечающий нерегулярным осцилляциям. Далее, мы аппроксимируем исходную кривую графиком функции  , которую мы возьмем в виде
, которую мы возьмем в виде

где параметры  определяются с помощью метода наименьших квадратов. Как видно из приведенных Лоренцем рисунков, наибольшее значение величины z достигается на таком решении, для которого соответствующая траектория проходит вблизи точки (0,0,0). Следовательно,
определяются с помощью метода наименьших квадратов. Как видно из приведенных Лоренцем рисунков, наибольшее значение величины z достигается на таком решении, для которого соответствующая траектория проходит вблизи точки (0,0,0). Следовательно,
значение  можно получить как первый максимум решения с начальными условиями, выбранными весьма близко к (0,0,0). Для того чтобы оценить характер пика кривой, было взято несколько пар максимумов с очень большим значением второй координаты в паре. Далее, существует такое периодическое решение
можно получить как первый максимум решения с начальными условиями, выбранными весьма близко к (0,0,0). Для того чтобы оценить характер пика кривой, было взято несколько пар максимумов с очень большим значением второй координаты в паре. Далее, существует такое периодическое решение  координата которого не меняет знак.
координата которого не меняет знак.

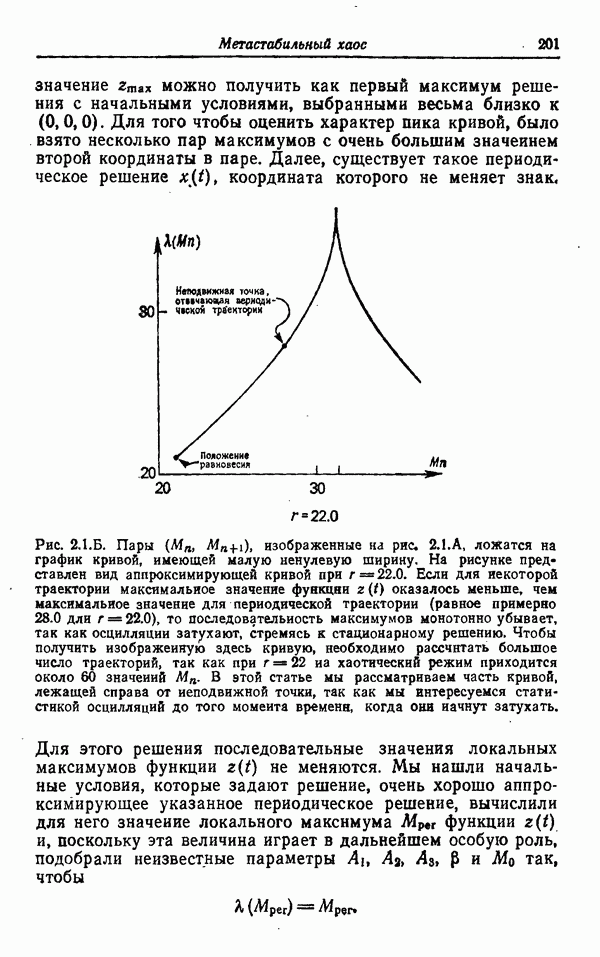
Рис. 2.1. Б. Пары  изображенные
изображенные  рис. 2.1.А, ложатся на график кривой, имеющей малую ненулевую ширину. На рисунке представлен вид аппроксимирующей кривой при
рис. 2.1.А, ложатся на график кривой, имеющей малую ненулевую ширину. На рисунке представлен вид аппроксимирующей кривой при  . Если для некоторой траектории максимальное значение функции
. Если для некоторой траектории максимальное значение функции  оказалось меньше, чем максимальное значение для периодической траектории (равное примерно
оказалось меньше, чем максимальное значение для периодической траектории (равное примерно  то последовательность максимумов монотонно убывает, так как осцилляции затухают, стремясь к стационарному решению. Чтобы получить изображенную здесь кривую, необходимо рассчитать большое число траекторий, так как при
то последовательность максимумов монотонно убывает, так как осцилляции затухают, стремясь к стационарному решению. Чтобы получить изображенную здесь кривую, необходимо рассчитать большое число траекторий, так как при  на хаотический режим приходится около 60 значений
на хаотический режим приходится около 60 значений  . В этой статье мы рассматриваем часть кривой, лежащей справа от неподвижной точки, так как мы интересуемся статистикой осцилляций до того момента времени, когда они начнут затухать.
. В этой статье мы рассматриваем часть кривой, лежащей справа от неподвижной точки, так как мы интересуемся статистикой осцилляций до того момента времени, когда они начнут затухать.
Для этого решения последовательные значения локальных максимумов функции  не меняются. Мы нашли начальные условия, которые задают решение, очень хорошо аппроксимирующее указанное периодическое решение, вычислили для него значение локального максимума
не меняются. Мы нашли начальные условия, которые задают решение, очень хорошо аппроксимирующее указанное периодическое решение, вычислили для него значение локального максимума  функции
функции  и, поскольку эта величина играет в дальнейшем особую роль, подобрали неизвестные параметры
и, поскольку эта величина играет в дальнейшем особую роль, подобрали неизвестные параметры  так, чтобы
так, чтобы

Если очередное найденное значение локального максимума  таково, что
таково, что  то рассматриваемое решение находится в стадии стремления к стационарному решению. Напротив, выбранная выше периодическая траектория не затухает по определению. Указанные вычисления проводились для значений параметра
то рассматриваемое решение находится в стадии стремления к стационарному решению. Напротив, выбранная выше периодическая траектория не затухает по определению. Указанные вычисления проводились для значений параметра  равных
равных  .
.
Результаты вычислений сведены в табл. 2.1 и 2.2. Чтобы получить эти данные, при каждом значении  было вычислено в среднем около 45 пар локальных максимумов. Кроме того, для каждого
было вычислено в среднем около 45 пар локальных максимумов. Кроме того, для каждого  величина квадратного корня из среднего числа квадратов отклонений была меньше, чем 0.01.
величина квадратного корня из среднего числа квадратов отклонений была меньше, чем 0.01.
Таблица 2.1

Таблица 2.2

Полученное нами очень хорошее совпадение результатов счета с функцией К тем более удивительно, что эта функция была выбрана симметричной. Мы не можем объяснить, почему полученные нами данные оказались симметричными.
Коэффициенты  являются почти линейными функциями параметра
являются почти линейными функциями параметра  . Весьма трудно аккуратно определить показатель степени
. Весьма трудно аккуратно определить показатель степени  . Однако упомянутое выше совпадение результатов сохраняется при небольших изменениях величины
. Однако упомянутое выше совпадение результатов сохраняется при небольших изменениях величины  . Форма графика функции
. Форма графика функции  вблизи пика зависит от того, - какая именно траектория, проходящая в окрестности точки (0,0,0), была выбрана, ибо в силу сказанного выше наибольшее значение локального максимума
вблизи пика зависит от того, - какая именно траектория, проходящая в окрестности точки (0,0,0), была выбрана, ибо в силу сказанного выше наибольшее значение локального максимума  определяется с помощью этой траектории. Линеаризируя систему (1.1) 9 точке (0,0,0), получим три собственных вектора
определяется с помощью этой траектории. Линеаризируя систему (1.1) 9 точке (0,0,0), получим три собственных вектора 
и  где
где  . В интересующей нас области изменения параметров
. В интересующей нас области изменения параметров  Траектории выходят из точки (0, 0, 0) в направлении собственного вектора, отвечающего собственному значению
Траектории выходят из точки (0, 0, 0) в направлении собственного вектора, отвечающего собственному значению  . Можно показать с помощью некоторых правдоподобных рассуждений, что число
. Можно показать с помощью некоторых правдоподобных рассуждений, что число  должно равняться отношению
должно равняться отношению  . В таком случае пока траектория проходит в окрестности точки (0,0,0), она будет лежать почти в плоскости, натянутой на собственные векторы, отвечающие собственным значениям
. В таком случае пока траектория проходит в окрестности точки (0,0,0), она будет лежать почти в плоскости, натянутой на собственные векторы, отвечающие собственным значениям  Следовательно, в соответствующем промежутке времени она будет приближенно удовлетворять линейной системе дифференциальных уравнений
Следовательно, в соответствующем промежутке времени она будет приближенно удовлетворять линейной системе дифференциальных уравнений

причем координаты выбраны таким образом, что точки (0.1) и (0.0) совпадают с концами собственных векторов. Решения этой системы уравнений удовлетворяют соотношению  , так что траектория, которая попадает в малую окрестность точки (0.0), пройдя через некоторую точку
, так что траектория, которая попадает в малую окрестность точки (0.0), пройдя через некоторую точку  (
( — маленькое, но отличное от нуля число), покинет эту окрестность, пройдя через точку
— маленькое, но отличное от нуля число), покинет эту окрестность, пройдя через точку  где
где  Отметим, что максимальное значение
Отметим, что максимальное значение  в линейном приближении достигается на траекториях, проходящих через точки
в линейном приближении достигается на траекториях, проходящих через точки  и можно ожидать, что значение
и можно ожидать, что значение  для соответствующих решений нелинейной системы будет меньше на величину, пропорциональную
для соответствующих решений нелинейной системы будет меньше на величину, пропорциональную 
При  что отличается от значения
что отличается от значения  приведенного в таблице. Следовательно, значению Р, найденному теоретически, должен отвечать более острый пик графика функции
приведенного в таблице. Следовательно, значению Р, найденному теоретически, должен отвечать более острый пик графика функции  чем значению
чем значению  , найденному нами численно. Это противоречие не сказывается сильно из-за слабой зависимости функции к от параметра
, найденному нами численно. Это противоречие не сказывается сильно из-за слабой зависимости функции к от параметра  , и действительно относительно большим изменениям
, и действительно относительно большим изменениям  отвечают весьма малые ошибки при вычислении пар
отвечают весьма малые ошибки при вычислении пар 
§ 3. МЕТОД ИССЛЕДОВАНИЯ ДЛИННЫХ УЧАСТКОВ ТРАЕКТОРИЙ С ХАОТИЧЕСКИМ ПОВЕДЕНИЕМ
Функция  построенная в § 3, является тем инструментом, который позволяет нам исследовать для некоторых значений
построенная в § 3, является тем инструментом, который позволяет нам исследовать для некоторых значений  природу временных хаотических осцилляций решений системы (1.1), изображенных на рис. 1.1, Если бы мы исследовали различные случаи поведения системы (1.1)
природу временных хаотических осцилляций решений системы (1.1), изображенных на рис. 1.1, Если бы мы исследовали различные случаи поведения системы (1.1)
путем непосредственного численного интегрирования, то нам пришлось бы вычислить в общей сложности около миллиона осцилляций. С помощью итераций функций ЦАТ) удается избежать этой исключительно дорогостоящей процедуры, Рассмотрим последовательность

Перейдем к нормализованной величине

Последовательности  соответствует последовательность
соответствует последовательность  причем на интервале, где происходят нерегулярные осцилляции, каждый член этой последовательности принадлежит [0, 1]. Мы будем писать также
причем на интервале, где происходят нерегулярные осцилляции, каждый член этой последовательности принадлежит [0, 1]. Мы будем писать также  или
или  . В этих обозначениях функция к симметрична относительно
. В этих обозначениях функция к симметрична относительно  ее максимальное значение
ее максимальное значение  в то время как
в то время как  Определим также ширину пика
Определим также ширину пика  как длину интервала (с центром в
как длину интервала (с центром в  ), на котором
), на котором

См. рис. 2.1. Критическое значение  — это первое значение, для которого к осуществляет отображение [0, 1] в [0, 1], и следовательно,
— это первое значение, для которого к осуществляет отображение [0, 1] в [0, 1], и следовательно, 
Для каждого из трех значений параметра  разобьем отрезок
разобьем отрезок  подынтервалов равной длины. В каждом подынтервале выберем начальную точку, используя датчик случайных чисел с равномерным распределением. Для каждого такого начального значения
подынтервалов равной длины. В каждом подынтервале выберем начальную точку, используя датчик случайных чисел с равномерным распределением. Для каждого такого начального значения  вычислим (с двойной точностью), итерируя функцию к, последовательность чисел
вычислим (с двойной точностью), итерируя функцию к, последовательность чисел  Вычисления ведутся до тех пор, пока полученное значение
Вычисления ведутся до тех пор, пока полученное значение  станет больше 1 либо
станет больше 1 либо  станет равным 2000 или какому-нибудь меньшему фиксированному значению; полученное значение
станет равным 2000 или какому-нибудь меньшему фиксированному значению; полученное значение  обозначим через
обозначим через  . Следовательно, для каждого из
. Следовательно, для каждого из  начальных значений «о получено время выхода
начальных значений «о получено время выхода  Среднее из значений
Среднее из значений  мы назовем средним временем затухания
мы назовем средним временем затухания  .
.
Наши результаты сведены в табл. 3.1. Значение  выбирается тем меньше, чем больше
выбирается тем меньше, чем больше  , поскольку в этом случае число необходимых итераций увеличивается. В конце этого параграфа мы укажем метод, позволяющий оценить среднее время затухания в зависимости от
, поскольку в этом случае число необходимых итераций увеличивается. В конце этого параграфа мы укажем метод, позволяющий оценить среднее время затухания в зависимости от  для значений параметра
для значений параметра
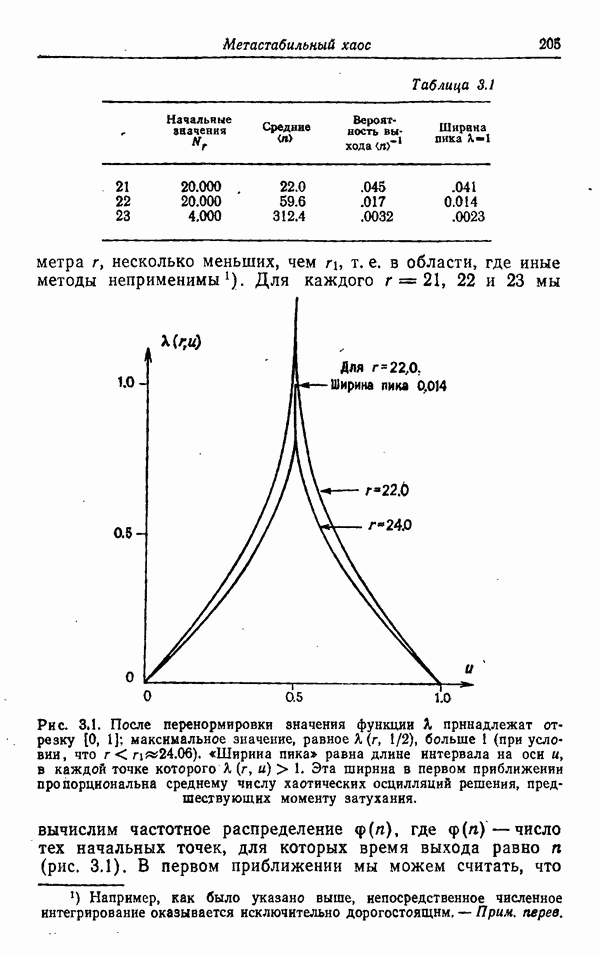
Таблица 3.1

 , несколько меньших, чем
, несколько меньших, чем  , т. е. в области, где иные методы неприменимы.
, т. е. в области, где иные методы неприменимы.

Рис. 3.1. После перенормировки значения функции к принадлежат отрезку [0, 1]; максимальное значение, равное  больше 1 (при условии, что
больше 1 (при условии, что  . «Ширина пика» равна длине интервала на оси и, в каждой точке которого
. «Ширина пика» равна длине интервала на оси и, в каждой точке которого  Эта ширина в первом приближении пропорциональна среднему числу хаотических осцилляций решения, предшествующих моменту затухания.
Эта ширина в первом приближении пропорциональна среднему числу хаотических осцилляций решения, предшествующих моменту затухания.
Для каждого  мы вычислим частотное распределение
мы вычислим частотное распределение  где
где  -число тех начальных точек, для которых время выхода равно
-число тех начальных точек, для которых время выхода равно  (рис. 3.1). В первом приближении мы можем считать, что
(рис. 3.1). В первом приближении мы можем считать, что
время выхода распределено по экспоненциальному закону. Простой, но не строгий способ проверить это утверждение состоит в том, чтобы подсчитать число точек, для которых время выхода превосходит  , и затем нарисовать график зависимости логарифма этого числа от
, и затем нарисовать график зависимости логарифма этого числа от  . Полученные на чертеже точки будут располагаться почти вдоль прямой линии. Далее, нами была проведена более точная проверка, состоящая в установлении того факта, что вероятность
. Полученные на чертеже точки будут располагаться почти вдоль прямой линии. Далее, нами была проведена более точная проверка, состоящая в установлении того факта, что вероятность  выхода после
выхода после  итерации не зависит от п. Взяв
итерации не зависит от п. Взяв  в соответствии со средним временем выхода, получим, что ожидаемое значение
в соответствии со средним временем выхода, получим, что ожидаемое значение  должно быть равно
должно быть равно  Получив необходимые численные значения, мы воспользовались критерием
Получив необходимые численные значения, мы воспользовались критерием  Для того, чтобы определить, будут ли отклонения наблюдаемых значений
Для того, чтобы определить, будут ли отклонения наблюдаемых значений  от ожидаемых значений достаточно малы. Проверка показала, что с вероятностью 90% полученные отклонения вполне допустимы.
от ожидаемых значений достаточно малы. Проверка показала, что с вероятностью 90% полученные отклонения вполне допустимы.
Если начальные точки распределялись на отрезке [0, 1] с некоторой начальной вероятностной плотностью  то образы
то образы  которые также принадлежат [0, 1], будут распределяться с некоторой (вообще говоря, другой) вероятностной плотностью, которую мы обозначим через
которые также принадлежат [0, 1], будут распределяться с некоторой (вообще говоря, другой) вероятностной плотностью, которую мы обозначим через  . Выше был рассмотрен случай, когда начальные точки распределяются равномерно, так что
. Выше был рассмотрен случай, когда начальные точки распределяются равномерно, так что  Обозначим через
Обозначим через  плотность, отвечающую
плотность, отвечающую  итерации
итерации  оставшейся по-прежнему на [0,1]; мера, задаваемая плотностью
оставшейся по-прежнему на [0,1]; мера, задаваемая плотностью  нормирована, так что
нормирована, так что  Если
Если  есть интервал, на котором
есть интервал, на котором  то
то  при условии, что Пп
при условии, что Пп  равен вероятности того, что
равен вероятности того, что  попадает в интервал около пика. Следовательно,
попадает в интервал около пика. Следовательно,  равно вероятности того, что точка, оставшаяся в течение
равно вероятности того, что точка, оставшаяся в течение  итераций, появится при
итераций, появится при  Экспоненциальное затухание будет наблюдаться в том случае, когда
Экспоненциальное затухание будет наблюдаться в том случае, когда  быстро сходится к некоторой постоянной
быстро сходится к некоторой постоянной  Число
Число  назовем средним временем выхода. Пьянигьяни и Йорке [16] доказали, что последовательность плотностей
назовем средним временем выхода. Пьянигьяни и Йорке [16] доказали, что последовательность плотностей  сходится к «гладкой» (бесконечно дифференцируемой) предельной плотности f, которая не зависит от начальной плотности
сходится к «гладкой» (бесконечно дифференцируемой) предельной плотности f, которая не зависит от начальной плотности  если только
если только  непрерывна и строго положительна. Поскольку эти авторы имели дело с более общей ситуацией, то, чтобы доказать это утверждение, им пришлось предположить, что функция К удовлетворяет следующим условиям:
непрерывна и строго положительна. Поскольку эти авторы имели дело с более общей ситуацией, то, чтобы доказать это утверждение, им пришлось предположить, что функция К удовлетворяет следующим условиям:

2. Существуют такие числа  что функция
что функция  бесконечно дифференцируема на каждом интервале
бесконечно дифференцируема на каждом интервале  для
для 
3. Существуют такие  , что
, что  при
при  .
.
В нашем случае  Требуемые условия выполнены; их проверка проводится так же, как для отображения
Требуемые условия выполнены; их проверка проводится так же, как для отображения  при условии, что
при условии, что  Предельная функция f зависит как от
Предельная функция f зависит как от  так и от
так и от  . Следовательно,
. Следовательно,

Если начальное распределение равномерно (т. е.  ), то наблюдается быстрая сходимость в том смысле, что с каждой итерацией
), то наблюдается быстрая сходимость в том смысле, что с каждой итерацией  уменьшается примерно в 0,9 раза и так вплоть до
уменьшается примерно в 0,9 раза и так вплоть до  Хотя эти оценки довольно грубые, они указывают на то, что
Хотя эти оценки довольно грубые, они указывают на то, что  станет достаточно малым за время
станет достаточно малым за время  , меньшее, чем время выхода. На рис. 3.2 показаны малые отклонения от хорошего экспоненциального затухания, полученные для значений
, меньшее, чем время выхода. На рис. 3.2 показаны малые отклонения от хорошего экспоненциального затухания, полученные для значений  в пределах от 5 до 10. Мы можем принять соответствующие
в пределах от 5 до 10. Мы можем принять соответствующие  за
за 
Для описания того, что происходит при переходе параметра  через критическое значение
через критическое значение  , полезно иметь аналитические выражения, дающие при
, полезно иметь аналитические выражения, дающие при  , близких к
, близких к  примерную зависимость среднего времени выхода от
примерную зависимость среднего времени выхода от  . Как видно из уравнения (3.1), время выхода зависит как от ширины пика, так и от предельного распределения в интервале ширины пика. Уравнение (3.1) можно переписать в виде
. Как видно из уравнения (3.1), время выхода зависит как от ширины пика, так и от предельного распределения в интервале ширины пика. Уравнение (3.1) можно переписать в виде

где  есть среднее значение f на интервале ширины пика. Еслй предположить, что
есть среднее значение f на интервале ширины пика. Еслй предположить, что  стремится к конечному ненулевому значению при
стремится к конечному ненулевому значению при  то для
то для  , достаточно близких к
, достаточно близких к  , будем иметь
, будем иметь

и в первом приближении ширина пика стремится к нулю при 
Ширину пика можно оценить, воспользовавшись уравнением для функции  . В нашем случае уравнение (2.2) принимает вид
. В нашем случае уравнение (2.2) принимает вид

где  и коэффициенты
и коэффициенты  являются функциями параметра
являются функциями параметра  . Положив
. Положив  перепишем предыдущее равенство в виде круглых скобках.
перепишем предыдущее равенство в виде круглых скобках.

где  обозначает функцию, которая стремится к нулю при
обозначает функцию, которая стремится к нулю при  . В общем случае
. В общем случае  обозначает члены более высокого порядка малости, чем любые другие, оставшиеся в
обозначает члены более высокого порядка малости, чем любые другие, оставшиеся в

Рис. 3.2. Частотное распределение времени выхода  при
при  Для сравнения начерчен график функции
Для сравнения начерчен график функции  где
где 
В следующем утверждении будет использоваться только информация о поведении функции К в окрестности пика, и поэтому оно применимо к более широкому классу функций, чем те, которые рассматривались в § 2. Мы будем писать  вместо
вместо  . Предположим, что функция А, имеет вид (3.2), где
. Предположим, что функция А, имеет вид (3.2), где  . Предположим далее, что
. Предположим далее, что  для
для  для
для  , а также
, а также  при
при  . Положим
. Положим

Заметим, что  так что функция
так что функция  обратима в окрестности
обратима в окрестности 
Ширина w определяется из равенства

Запишем  равенство, используя (3.2) в виде
равенство, используя (3.2) в виде

Следовательно, при  , достаточно близких к
, достаточно близких к  ,
,

Таким образом, время затухания примерно равно  где а — некоторая постоянная. Для упрощения выкладок мы считали, что
где а — некоторая постоянная. Для упрощения выкладок мы считали, что  постоянно, но наши рассуждения легко переносятся на случай, когда
постоянно, но наши рассуждения легко переносятся на случай, когда  является функцией параметра
является функцией параметра  , при условии, что
, при условии, что  Окончательные результаты при этом не меняются.
Окончательные результаты при этом не меняются.
Полученные нами приближенные формулы справедливы только для  , достаточно близких к
, достаточно близких к  Значения параметра
Значения параметра  , приведенные в табл. 3.1, выходят за пределы этой области.
, приведенные в табл. 3.1, выходят за пределы этой области.
§ 4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
В предыдущих параграфах мы исследовали метастабильное хаотическое поведение траектории в модели Лоренца при значениях чисел Рэлея, несколько меньших, чем критическое значение  при котором происходит обратная бифуркация. При этих значениях система допускает метастабильные хаотические решения, изображенные на рис. 1.1. После достаточно большого числа нерегулярных осцилляций решения системы затухают к какому-либо из двух ее стационарных решений. «Время жизни» хаотического режима данного решения зависит от начального значения, задающего это решение, и распределяется в фазовом пространстве по экспоненциальному закону. Мы исследовали численно поведение решений, а также получили аналитические выражения для оценки времени затухания при значениях параметра
при котором происходит обратная бифуркация. При этих значениях система допускает метастабильные хаотические решения, изображенные на рис. 1.1. После достаточно большого числа нерегулярных осцилляций решения системы затухают к какому-либо из двух ее стационарных решений. «Время жизни» хаотического режима данного решения зависит от начального значения, задающего это решение, и распределяется в фазовом пространстве по экспоненциальному закону. Мы исследовали численно поведение решений, а также получили аналитические выражения для оценки времени затухания при значениях параметра  , очень близких (снизу) к критическому значению
, очень близких (снизу) к критическому значению  . Время затухания очень быстро стремится к
. Время затухания очень быстро стремится к  при
при  . При
. При
 наблюдались устойчивые хаотические осцилляции. Время убывания пропорционально
наблюдались устойчивые хаотические осцилляции. Время убывания пропорционально  и при выбранных у нас значениях параметров
и при выбранных у нас значениях параметров  число
число  заключено между 3,5 и 4. Метастабильное хаотическое поведение траекторий, возникающих при
заключено между 3,5 и 4. Метастабильное хаотическое поведение траекторий, возникающих при  предвещает ситуацию, возникающую при
предвещает ситуацию, возникающую при  которая характеризуется наличием двух типов режимов: хаотического режима и устойчивого (ламинарного) режима. При
которая характеризуется наличием двух типов режимов: хаотического режима и устойчивого (ламинарного) режима. При  возникающий метастабильный хаос можно представлять себе состоящим из хаотических траекторий, которые спустя некоторое время проскакивают через маленькое «окошко» из хаотической области в ламинарную.
возникающий метастабильный хаос можно представлять себе состоящим из хаотических траекторий, которые спустя некоторое время проскакивают через маленькое «окошко» из хаотической области в ламинарную.
Из соображений преемственности мы выбрали «канонические» значения параметров, фигурирующих при описании модели Лоренца, которые, как оказалось, широко используются в литературе, посвященной численному исследованию уравнений Лоренца (см. Люкке [12]).
Вообще говоря, можно отыскать метастабильные решения, варьируя параметры в физической системе, в которой сосуществуют устойчивый и хаотический режимы. При изменении некоторых контрольных параметров хаотический режим может прекратить свое существование и перейти в метастабильный хаотический режим. Кревелинг и др. исследовали, что происходит при уменьшении числа Рэлея ниже критического значения (соответствующего нашему  ). Они проделали переход от неустойчивой ситуации к устойчивой, но все же при этом наблюдали нерегулярные осцилляции, которые иногда не ослабевали в течение двух часов (что соответствует 100—200 осцилляциям). Это и есть как раз тот тип поведения, который следует ожидать в случае метастабильного хаоса. Хотя различные ограничения, имевшие место при постановке этого эксперимента, приводили к тому, что полученную физическую систему нельзя было описывать с помощью уравнений Лоренца, не следует думать, что метастабильный хаотический режим присущ только модели Лоренца или, например, только системам, в которых возникает обратная бифуркация. Мы предполагаем, что Кревелинг и его помощники наблюдали метастабильный хаос.
). Они проделали переход от неустойчивой ситуации к устойчивой, но все же при этом наблюдали нерегулярные осцилляции, которые иногда не ослабевали в течение двух часов (что соответствует 100—200 осцилляциям). Это и есть как раз тот тип поведения, который следует ожидать в случае метастабильного хаоса. Хотя различные ограничения, имевшие место при постановке этого эксперимента, приводили к тому, что полученную физическую систему нельзя было описывать с помощью уравнений Лоренца, не следует думать, что метастабильный хаотический режим присущ только модели Лоренца или, например, только системам, в которых возникает обратная бифуркация. Мы предполагаем, что Кревелинг и его помощники наблюдали метастабильный хаос.
Из чего в системах иного типа может возникать метастабильный хаос? Подходящими системами являются такие, в которых существуют по меньшей мере два устойчивых состояния, одио из которых является регулярным, описываемым простой временной зависимостью (устойчивое положение
равновесия или периодическая траектория), в то время как другое должно быть турбулентным. В этом случае в системе имеются неустойчивые решения, осуществляющие хаотические осцилляции с конечной амплитудой и достаточно малого возмущения, чтобы перевести один режим в другой. Существование неустойчивых решений с хаотическими осцилляциями конечной амплитуды гарантирует существование по меньшей мере двух режимов. Подобным образом в системах с гистерезисом должны существовать по меньшей мере два режима, поскольку состояние системы в данный момент времени зависит от ее предыстории. В частности, движение жидкости в трубе или канале является ламинарным, но оно может быть превращено в турбулентное течение при помощи малого, однако же, конечного возмущения. Точно так же при изучении движения жидкости, заключенной между двумя вращающимися в противоположных направлениях цилиндрами, Колисс (Д. Колисс [1]) обнаружил такие состояния, в которых сосуществовал как турбулентный, так и ламинарный режим. В этих случаях удается наблюдать метастабильное хаотическое движение, возникающее в тот момент, когда система переходит от устойчивого турбулентного режима к устойчивому ламинарному. (Как видно из результатов настоящей работы, на практике может оказаться весьма трудным определить достаточно точно те критические значения параметров, при которых происходит переход от турбулентного движения к ламинарному, поскольку метаустойчивое хаотическое движение с очень большим временем жизни фактически неотличимо от устойчивого хаотического.)
Мы благодарим Р. Ф. Чанда, позволившего нам воспользоваться его программой, имеющей широкие возможности и составленной им для вычисления критических индексов для фазовых переходов в бинарных жидкостях, И. Р. Кейлора за его помощь в программировании. Мы благодарны также А. Феллеру за полезные обсуждения и ознакомление нас с работами Лоренца в 1968 г.
СПИСОК ЛИТЕРАТУРЫ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- ПОПЫТКИ УСТАНОВИТЬ СООТНОШЕНИЕ МЕЖДУ УРАВНЕНИЯМИ НАВЬЕ-СТОКСА И ТУРБУЛЕНТНОСТЬЮ
- ПРИЛОЖЕНИЕ К СТАТЬЕ МАРСДЕНА БИФУРКАЦИИ, ПОЛУПОТОКИ И УРАВНЕНИЯ НАВЬЕ—СТОКСА
- ТЕОРИИ ТУРБУЛЕНТНОСТИ
- ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ РАСЧЕТА ТУРБУЛЕНТНЫХ СДВИГОВЫХ ТЕЧЕНИЙ
- ФРАКТАЛЫ И ТУРБУЛЕНТНОСТЬ: АТТРАКТОРЫ И РАЗБРОС
- СТРУКТУРА АТТРАКТОРОВ ЛОРЕНЦА
- ПРИЛОЖЕНИЕ К СТАТЬЕ Р. ВИЛЬЯМСА. «ИЗОБРАЖЕНИЕ АТТРАКТОРА ЛОРЕНЦА, ПОЛУЧЕННОЕ С ПОМОЩЬЮ КОМПЬЮТЕРА»
- ДВА ПОДХОДА К МОДЕЛИРОВАНИЮ ДВУМЕРНОЙ ТУРБУЛЕНТНОСТИ
- ДЕТЕРМИНИРОВАННОЕ НЕПЕРИОДИЧЕСКОЕ ТЕЧЕНИЕ
- О ПРИРОДЕ ТУРБУЛЕНТНОСТИ
- ДВУМЕРНОЕ ОТОБРАЖЕНИЕ СО СТРАННЫМ АТТРАКТОРОМ
- СИСТЕМА ДВУХДИСКОВОГО ДИНАМО РИКИТАКЕ
- МЕТАСТАБИЛЬНЫЙ ХАОС: ПЕРЕХОД К УСТОЙЧИВОМУ ХАОТИЧЕСКОМУ ПОВЕДЕНИЮ В МОДЕЛИ ЛОРЕНЦА
- ПРЕДТУРБУЛЕНТНОСТЬ: РЕЖИМ, НАБЛЮДАЕМЫЙ В ТЕЧЕНИИ ЖИДКОСТИ, ОПИСЫВАЕМОЙ МОДЕЛЬЮ ЛОРЕНЦА
- ТОПОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ АТТРАКТОРОВ ЛОРЕНЦА