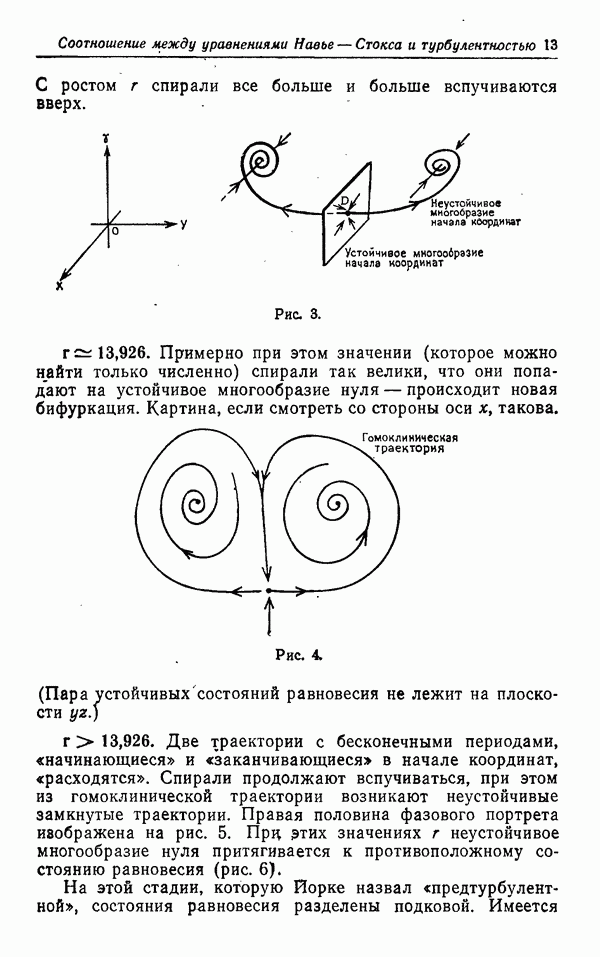
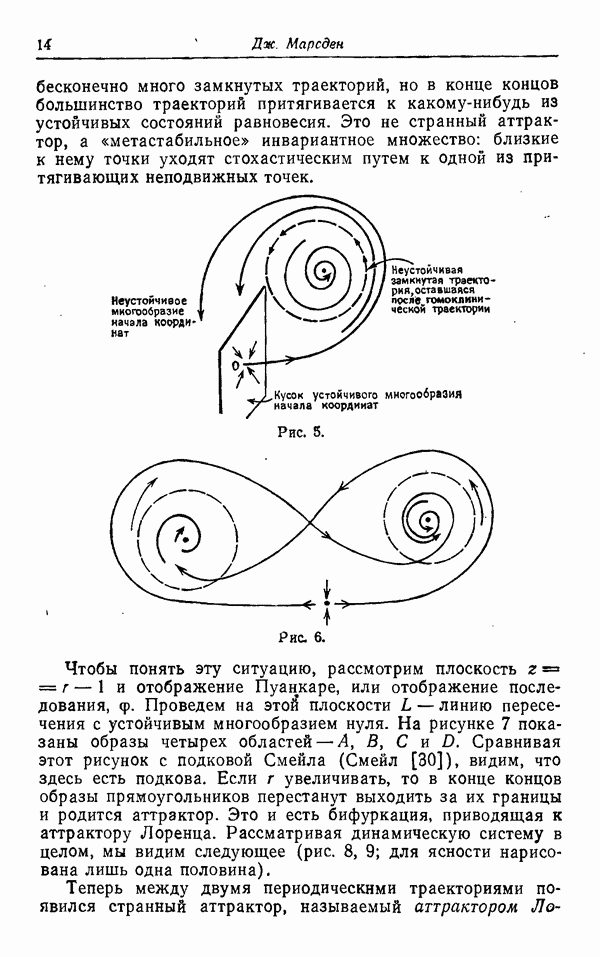
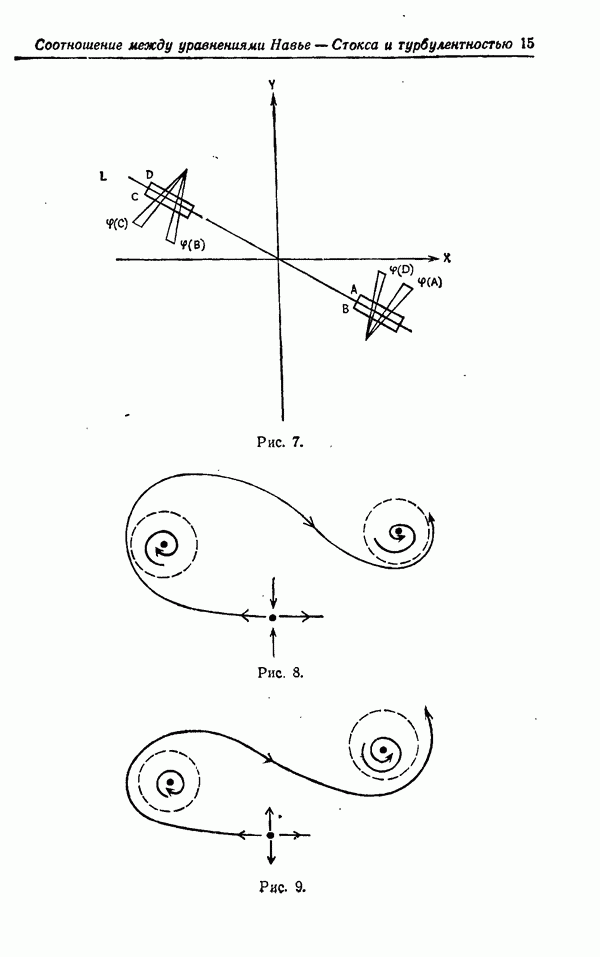
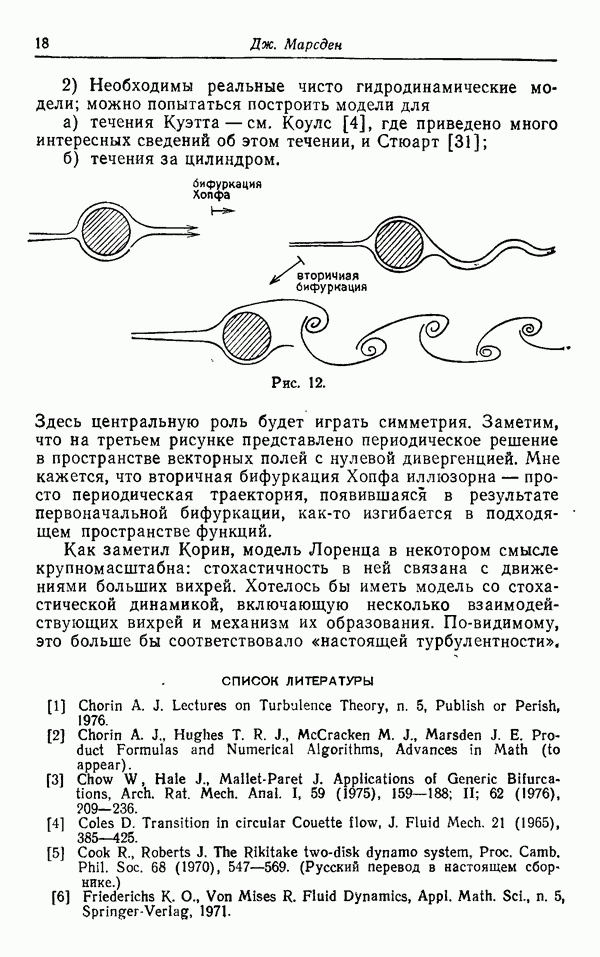
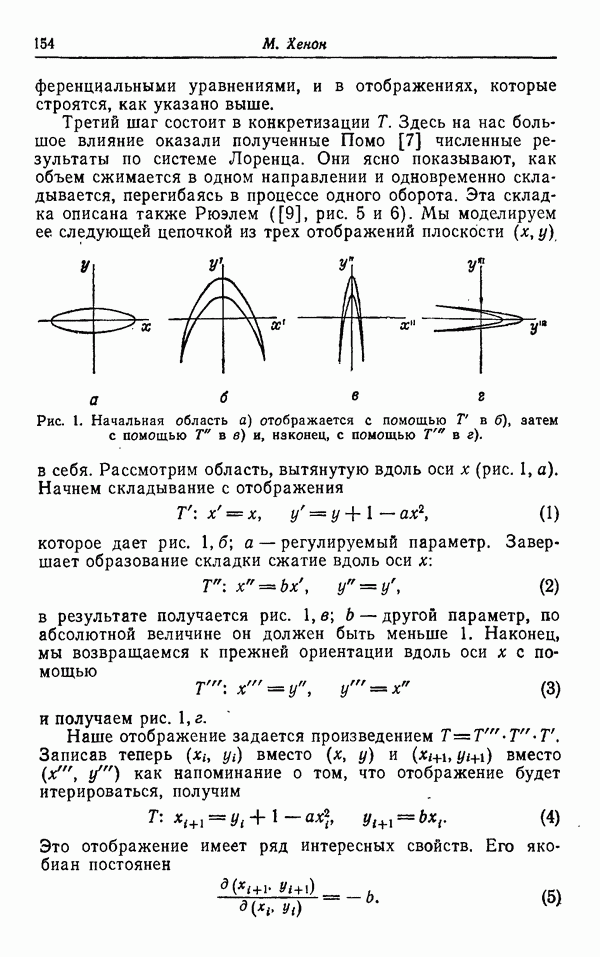
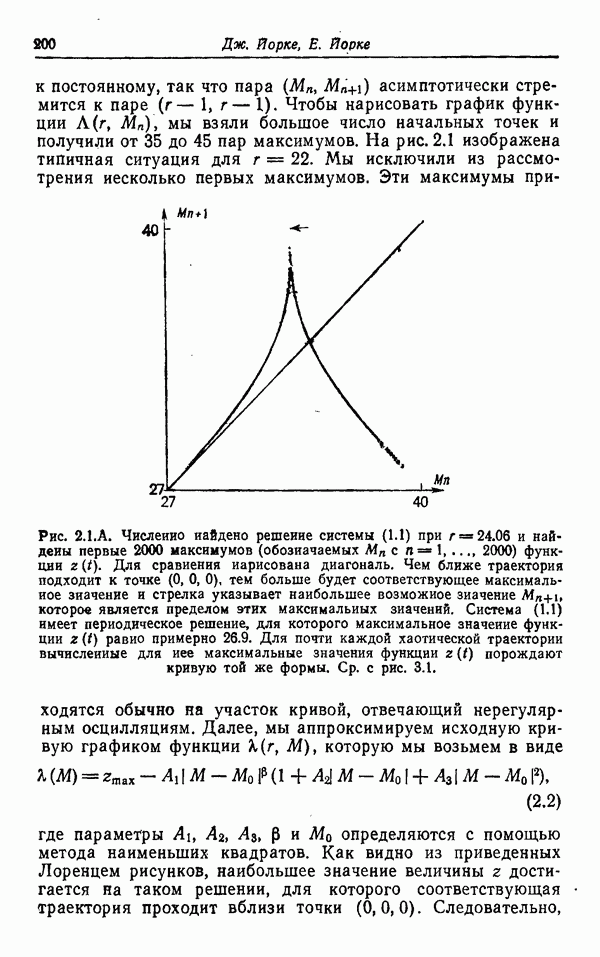
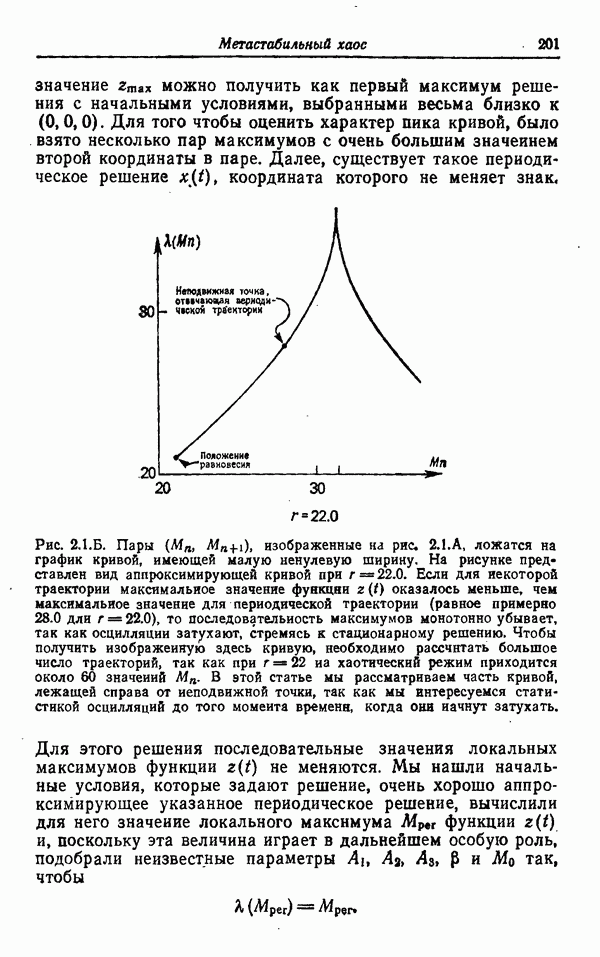
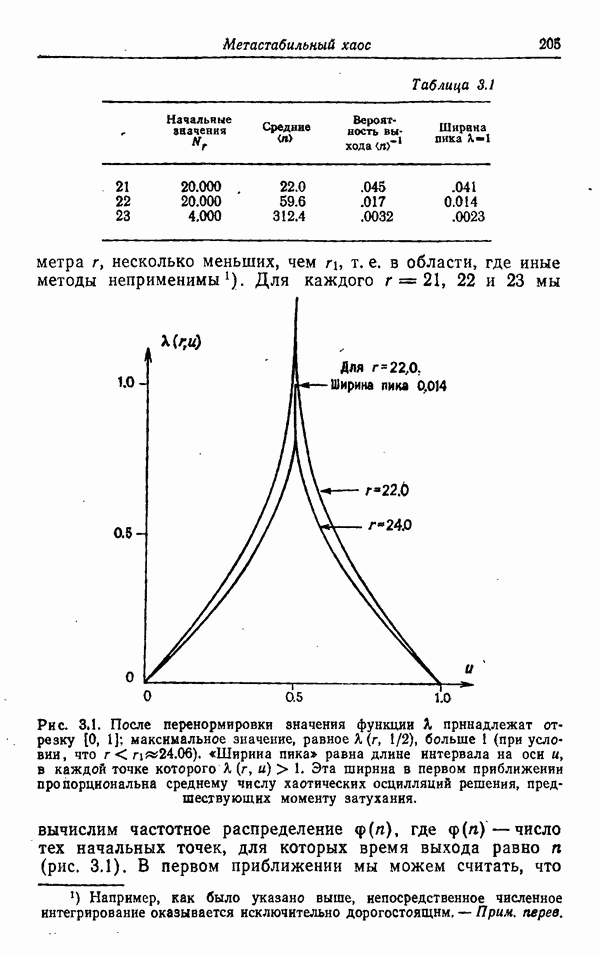
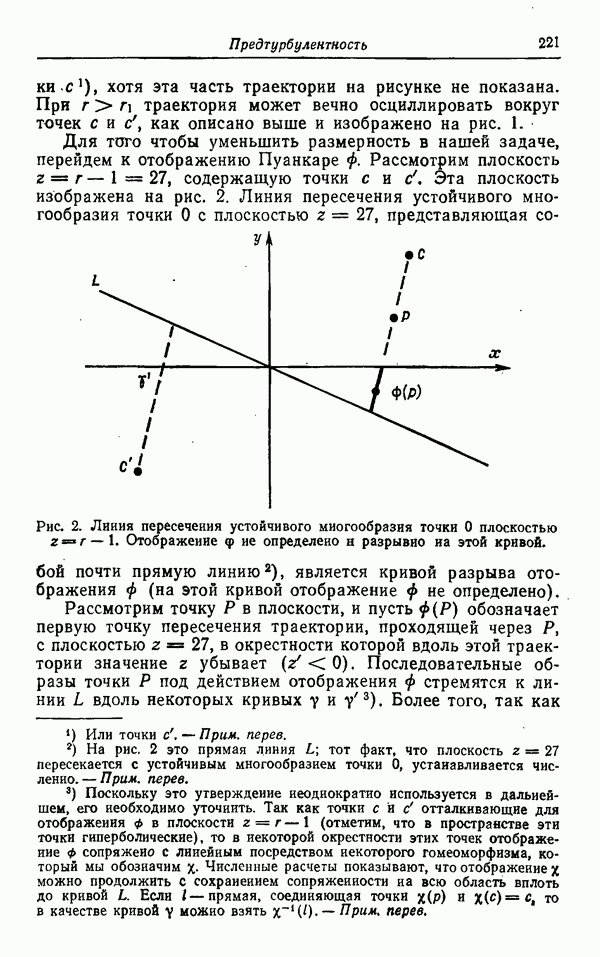
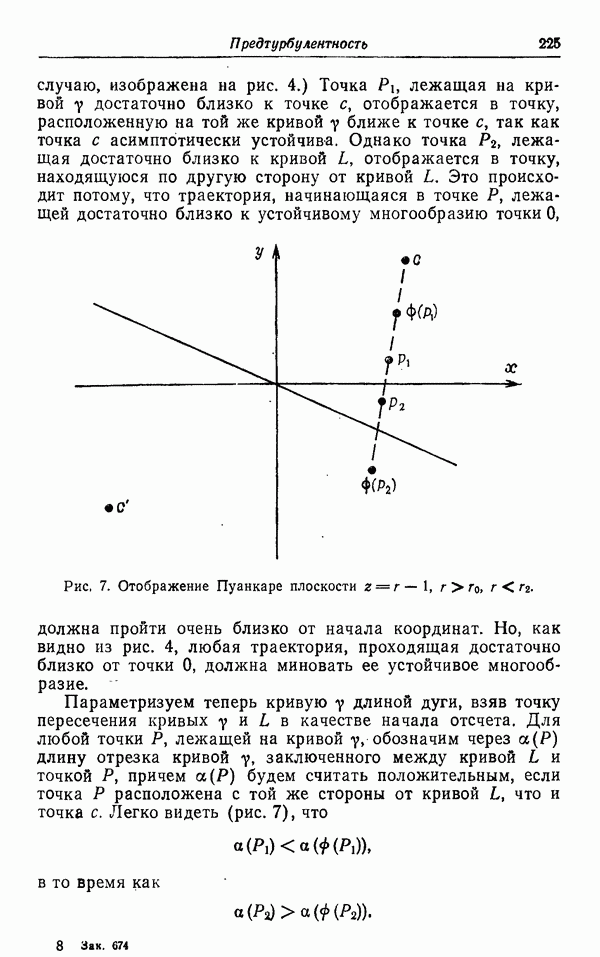
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СИСТЕМА ДВУХДИСКОВОГО ДИНАМО РИКИТАКЕ
А. Е. Кук и П. X. Робертс
Резюме. Показано, что решение системы двухдискового динамо Рикитаке может быть описано траекторией точки, которая при достаточно больших временах подходит как угодно близко к предельной поверхности, имеющей ограниченную площадь. Показано, что перемена полярности электрического поля в катушках динамо происходит в сообщающихся областях двух листов предельной поверхности. При помощи прямого метода Ляпунова показано, что две сингулярные точки системы представляют собой неустойчивые фокусы. В случае малой разности скоростей динамо развита асимптотическая теория. Эта теория применяется к ситуации малой диссипации, когда траектории стремятся к периодическому движению с единственной осцилляцией между последовательными сменами направления движения на противоположное.
1. Введение. При рассмотрении палеомагнитных записей создается впечатление, что диполь Земли много раз и нерегулярным образом изменял свою полярность на противоположную, а археомагнитные исследования показывают, что даже при сохранении знака его величина флуктуирует. Данные, полученные из глубин океана, охватывающие последние десять миллионов лет, были представлены и подробно обсуждены Коксом [1], предложившим статистическую модель распределения интервалов полярности. Он разделил переориентации на «эпохи полярности», когда интервал между последовательными переменами полярности имеет порядок миллиона лет, и на «события полярности» для интервалов длительности от  до
до  лет. В течение последних четырех миллионов лет мы имеем по меньшей мере шестнадцать таких интервалов, из которых семь представляют собой события полярности и девять — эпохи полярности.
лет. В течение последних четырех миллионов лет мы имеем по меньшей мере шестнадцать таких интервалов, из которых семь представляют собой события полярности и девять — эпохи полярности.
Согласно общепринятой точке зрения, статистика перемен полярности не претерпела существенных изменений за последние десять миллионов лет. Тем не менее в течение более длительного интервала времени, очевидно, произошли некоторые перемены. Например, не было зарегистрировано ни одного изменения полярности в течение семнадцати миллионов лет пермского периода (см. Ирвинг [2]).
В настоящее время господствующим является представление, согласно которому нерегулярность изменений полярности есть неотъемлемая черта магнитогидродинамики земного динамо, а не результат причуд динамических сил, действующих на ядро. Вследствие сложности этого нелинейного механизма в качестве возможных аналогий были предложены гомополярные дисковые динамо. Буллард [3] предложил и исследовал систему однодискового самовозбуждающегося динамо, но обнаружил, что в такой системе невозможны изменения полярности. Рикитаке [4] рассмотрел ситуацию, при которой два одинаковых дисковых динамо соединены таким образом, что ток от каждого диска заряжает катушку другого динамо. При помощи численного интегрирования он обнаружил, что токи могут изменять знак. Позднее Аллан [5] тоже при помощи численного интегрирования подтвердил наличие этого свойства у системы двухдискового динамо Рикитаке. Несмотря на то что просчитанные им временные траектории системы были значительно длиннее, чем просчитанные Рикитаке, Аллану удалось обнаружить только несколько более общие черты действительно имеющего место процесса изменения полярности. Самервиль [6], резюмируя содержание работы Аллана и свои обобщения, утверждает: «...ясно, что даже простейшая система спаренных динамо в настоящее время еще совершенно недостаточно исследована».
В настоящей работе приведены результаты, основанные на длительных по времени интегрированиях, использующих численные и аналоговые методы. Топология множества траекторий решений в фазовом пространстве определена для интервала значений основного параметра  представляющего собой омическую диссипацию. Показано, что топологическое представление значительно проясняет природу процесса перемены полярности. С помощью второго метода Ляпунова исследована устойчивость траекторий около стационарных точек. Оказалось, что для всех реалистических с точки зрения физики значений
представляющего собой омическую диссипацию. Показано, что топологическое представление значительно проясняет природу процесса перемены полярности. С помощью второго метода Ляпунова исследована устойчивость траекторий около стационарных точек. Оказалось, что для всех реалистических с точки зрения физики значений  траектории являются неустойчивыми. Для случая малого отличия
траектории являются неустойчивыми. Для случая малого отличия  угловых скоростей
угловых скоростей
динамо получено соотношение между периодом колебаний и максимальным отклонением величины тока. При очень малой диссипации траектории почти периодичны и совершают единственное колебание между изменениями полярности.
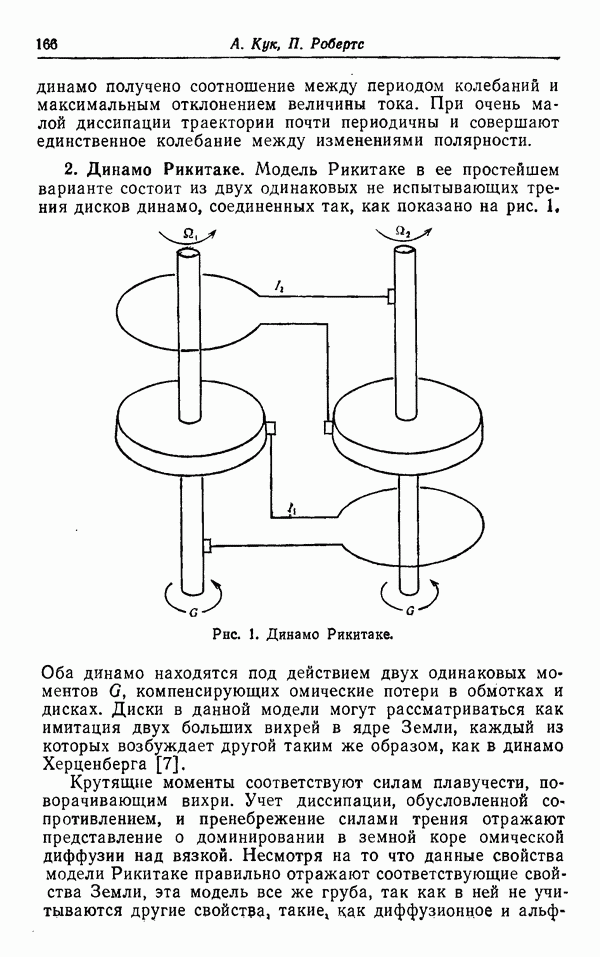
2. Динамо Рикитаке. Модель Рикитаке в ее простейшем варианте состоит из двух одинаковых не испытывающих трения дисков динамо, соединенных так, как показано на рис. 1,

Рис. 1. Динамо Рикитаке.
Оба динамо находятся под действием двух одинаковых моментов G, компенсирующих омические потери в обмотках и дисках. Диски в данной модели могут рассматриваться как имитация двух больших вихрей в ядре Земли, каждый из которых возбуждает другой таким же образом, как в динамо Херценберга [7].
Крутящие моменты соответствуют силам плавучести, поворачивающим вихри. Учет диссипации, обусловленной сопротивлением, и пренебрежение силами трения отражают представление о доминировании в земной коре омической диффузии над вязкой. Несмотря на то что данные свойства модели Рикитаке правильно отражают соответствующие свойства Земли, эта модель все же груба, так как в ней не учитываются другие свойства, такие, как диффузионное и альфвеновское
запаздывания при взаимодействии между вихрями в ядре и эффекты, обусловленные действием сил Кориолиса.
Уравнения, описывающие эволюцию токов  и угловых скоростей
и угловых скоростей  имеют вид
имеют вид

где L — самоиндукция, R — сопротивление, соответствующие каждому динамо и соединяющему их контуру, М — «общая взаимная индукция» между контурами динамо, С — момент инерции динамо относительно его оси,  пара сил, приложенная к этой оси. Из уравнений (3) и (4) вытекает, что разность угловых скоростей постоянна
пара сил, приложенная к этой оси. Из уравнений (3) и (4) вытекает, что разность угловых скоростей постоянна

где А — константа, при фиксированном значении которой система имеет два состояния равновесия:

В этих выражениях знаки плюс или минус должны браться одновременно. Они отвечают соответственно нормальному (N) и обратному (R) состояниям. Эти обозначения произвольны в том смысле, что любое утверждение о переходе между состояниями N и R остается справедливым при замене буквы N на R и наоборот.
Система имеет два масштаба времени. Первый «механический масштаб времени»  — это время, за которое диски разгоняются до типичного значения угловой скорости
— это время, за которое диски разгоняются до типичного значения угловой скорости  состояния (6) под действием приложенной пары и в отсутствие сил Лоренца, т. е.
состояния (6) под действием приложенной пары и в отсутствие сил Лоренца, т. е.
 (7)
(7)
Второй масштаб времени может быть назван «временем электромагнитной диффузии» те. Если диски остановить при заданной величине магнитных полей, то эти поля, согласно (1) и (2), исчезнут за характерное время порядка

Важным параметром системы является отношение этих времен

которое тем самым равно отношению запасенной механической энергии к запасенной электромагнитной энергии.
Уравнения приводятся к безразмерному виду, если измерять t в единицах  токи — в единицах
токи — в единицах  а угловые скорости — в единицах
а угловые скорости — в единицах  Положив
Положив

получим уравнение (5) в следующем виде:

При этом уравнения (1) — (3) приводятся к виду

Стационарные решения (6) теперь принимают вид

где

Без ограничения общности можно предположить, что  в противном случае рассматриваемые динамо просто меняются ролями. В общем случае не известно аналитических решений уравнений (12) — (14). Единственная ситуация
в противном случае рассматриваемые динамо просто меняются ролями. В общем случае не известно аналитических решений уравнений (12) — (14). Единственная ситуация  в которой известно точное решение, рассматривалась Алланом [5].
в которой известно точное решение, рассматривалась Алланом [5].
Рассматривая  как время, которое требуется медленным альфвеновским волнам для прохождения ядра, и предполагая, что альфвеновская скорость обусловливается полоидальным полем величиной в
как время, которое требуется медленным альфвеновским волнам для прохождения ядра, и предполагая, что альфвеновская скорость обусловливается полоидальным полем величиной в  получаем
получаем  лет. Используя это значение
лет. Используя это значение  и предполагая, что
и предполагая, что  лет, получаем
лет, получаем  Несмотря на то что эта процедура противоречит определению (7) величины
Несмотря на то что эта процедура противоречит определению (7) величины  она дает возможность оценить величину
она дает возможность оценить величину  . С другой стороны, может быть определено как отношение плотностей механической и магнитной энергии. Используя значения величин этих плотностей, вычисленные Буллардом и Геллманом [8], получаем
. С другой стороны, может быть определено как отношение плотностей механической и магнитной энергии. Используя значения величин этих плотностей, вычисленные Буллардом и Геллманом [8], получаем  . Аллан [5] и Лауэс (отмечено в [9]) приводят значение
. Аллан [5] и Лауэс (отмечено в [9]) приводят значение  Таким образом, наиболее подходящие для Земли значения
Таким образом, наиболее подходящие для Земли значения  заключены в интервале от
заключены в интервале от  до 10. Предполагая, что для Земли величина К равна 2, получаем, что значение
до 10. Предполагая, что для Земли величина К равна 2, получаем, что значение  заключенное между 1 и 2, для модели Рикитаке наиболее достоверно описывает наблюдаемые изменения полярности.
заключенное между 1 и 2, для модели Рикитаке наиболее достоверно описывает наблюдаемые изменения полярности.
Тем не менее следует отметить, что даже при  лет и
лет и  лет временная шкала Утетт описанного здесь процесса очень коротка по сравнению со средней продолжительностью эпохи полярности. Поэтому, по-видимому, нецелесообразно проводить очень детальное сравнение между данной моделью и Землей.
лет временная шкала Утетт описанного здесь процесса очень коротка по сравнению со средней продолжительностью эпохи полярности. Поэтому, по-видимому, нецелесообразно проводить очень детальное сравнение между данной моделью и Землей.
3. Поведение в окрестности стационарной точки. Решения, как угодно близкие к стационарному состоянию, можно наиболее просто найти с помощью преобразований

Подставляя (1) в уравнения (12)-(14) и используя (16), получаем первую каноническую форму Ляпунова

где  — элементы матрицы
— элементы матрицы

а
 (19)
(19)
Одним из двух стационарных решений системы уравнений (18) является  Пренебрегая членами
Пренебрегая членами  получаем из (18) укороченную систему линейных уравнений
получаем из (18) укороченную систему линейных уравнений

Характеристическое уравнение укороченной системы имеет вид

откуда получаем характеристические корни

где 
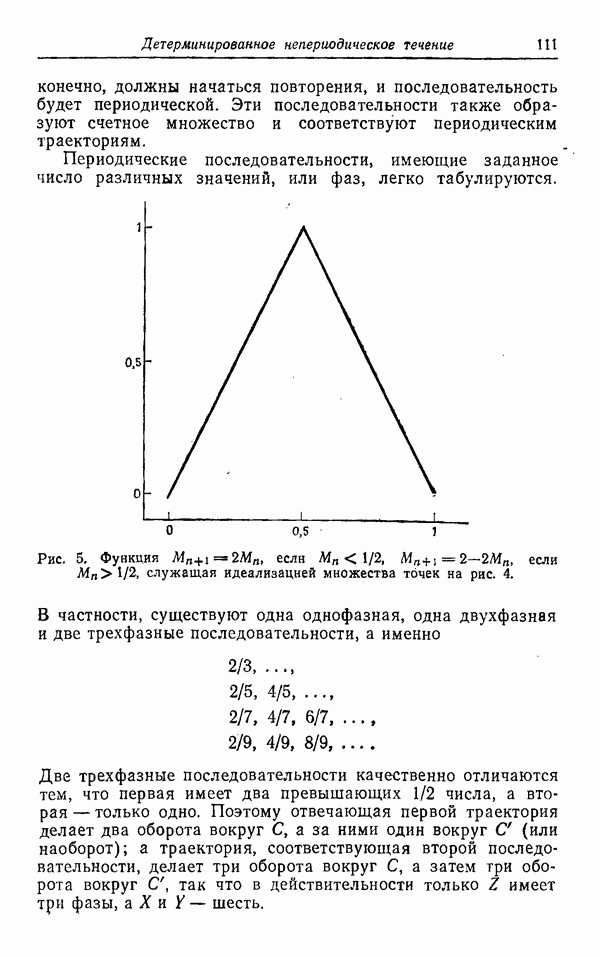
Соответственно этим корням получаем следующие решения:

где С и  произвольные постоянные, a t выбрано так, что
произвольные постоянные, a t выбрано так, что

Остальные коэффициенты определяются из равенств

Уравнения (24) описывают, траекторию точки в пространстве  которая приближается к плоскости
которая приближается к плоскости  при t, стремящемся к бесконечности, где
при t, стремящемся к бесконечности, где

Траектории, лежащие в этой плоскости, являются замкнутыми орбитами, охватывающими точку  Заменяя в уравнении (17) величину К на —К, можно найти линейные решения, близкие к стационарному решению R. Линеаризованная система обладает решениями, которые как угодно близко подходят к предельной поверхности, состоящей из двух плоскостей, одна из которых содержит стационарную точку N, а другая содержит стационарную точку
Заменяя в уравнении (17) величину К на —К, можно найти линейные решения, близкие к стационарному решению R. Линеаризованная система обладает решениями, которые как угодно близко подходят к предельной поверхности, состоящей из двух плоскостей, одна из которых содержит стационарную точку N, а другая содержит стационарную точку 
4. Поведение системы около состояния N. Вопрос об устойчивости стационарной точки N и аналогично R не может быть решен при помощи исследования укороченной системы (21) из-за вида характеристических корней (23). Ляпунов [10] исследовал устойчивость систем уравнений такого типа, и последующий анализ основан на одном из его прямых методов.
При помощи преобразования

и обратного к нему

система уравнений (18) преобразуется ко второй канонической форме

где  .
.
Для исследования устойчивости системы (28) вводится следующая функция:

где

и

Коэффициенты (30) выбраны (однозначно) так, что в силу (28) только члены четвертого порядка остаются в правой части уравнения

Устойчивость траекторий около состояния N теперь исследуется с использованием однозначного линейного приближения

правой части (31). В силу этого приближения следующий далее анализ справедлив только для орбит на листе  и не годится для траекторий, стремящихся к N во время обращения движения с листа R. Используя преобразование
и не годится для траекторий, стремящихся к N во время обращения движения с листа R. Используя преобразование

я подставляя в (3) выражение (32) для W, получаем

Согласно теории Ляпунова, устойчивость определяется знаком интеграла

Проводя интегрирование, получаем

Следует отметить, что если  или
или  то существуют решения типа Булларда, для которых
то существуют решения типа Булларда, для которых 
(см. скан)
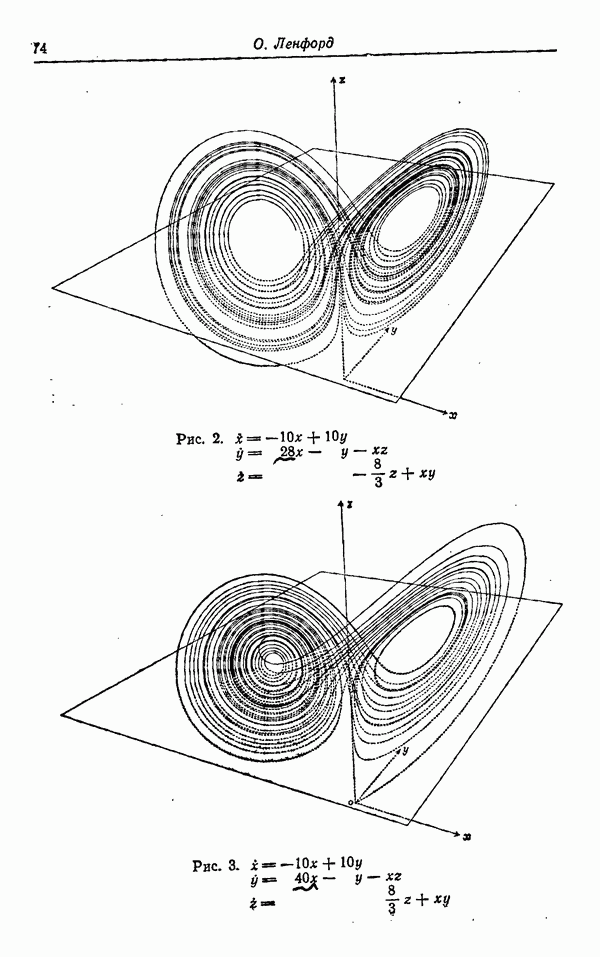
Рис. 2. Типичные кривые, описывающие временною эволюцию  при
при 
Эти решения обладают замкнутыми траекториями, для которых величина G обязана обращаться в нуль, и, как видно из (36), в этих случаях действительно равна нулю. Для всех других, имеющих физический смысл значений К и величина
G положительна, и поэтому N является неустойчивым фокусом.
5. Топология траекторий в фазовом пространстве. В соответствии с результатами п. 4 во всех случаях, для которых было проведено численное интегрирование уравнений (12)- (14), было обнаружено, что вне зависимости от того, насколько близко к состоянию N система находится в начальный момент, она будет систематически отклоняться от него посредством колебаний возрастающей амплитуды и приближаться к окрестности состояния R. Число промежуточных осцилляций может быть как угодно большим, если начальная точка достаточно близка к N. Рис. 2 иллюстрирует поведение системы при  и ясно обнаруживает изменения направлений движения в моменты времени
и ясно обнаруживает изменения направлений движения в моменты времени  и т. д. Несмотря на информативность рис. 2, он не дает компактного или ясного описания поведения динамо. Более информативно изображать поведение системы при помощи орбит в пространстве
и т. д. Несмотря на информативность рис. 2, он не дает компактного или ясного описания поведения динамо. Более информативно изображать поведение системы при помощи орбит в пространстве  , или, как мы будем называть его, фазовом пространстве. Ансамбль всех таких орбит описывает «фазовую жидкость», эйлерова скорость которой
, или, как мы будем называть его, фазовом пространстве. Ансамбль всех таких орбит описывает «фазовую жидкость», эйлерова скорость которой  в соответствии с уравнениями (12) — (14) дается выражением
в соответствии с уравнениями (12) — (14) дается выражением

Объем фазовой жидкости может быть определен при помощи якобиана

где индекс 0 означает, что значения соответствующих переменных берутся в некоторый фиксированный момент времени. Они являются лагранжевыми координатами фазовой жидкости. Уравнение непрерывности в лагранжевой форме имеет вид

откуда, используя (37), получаем результат Аллана [5]

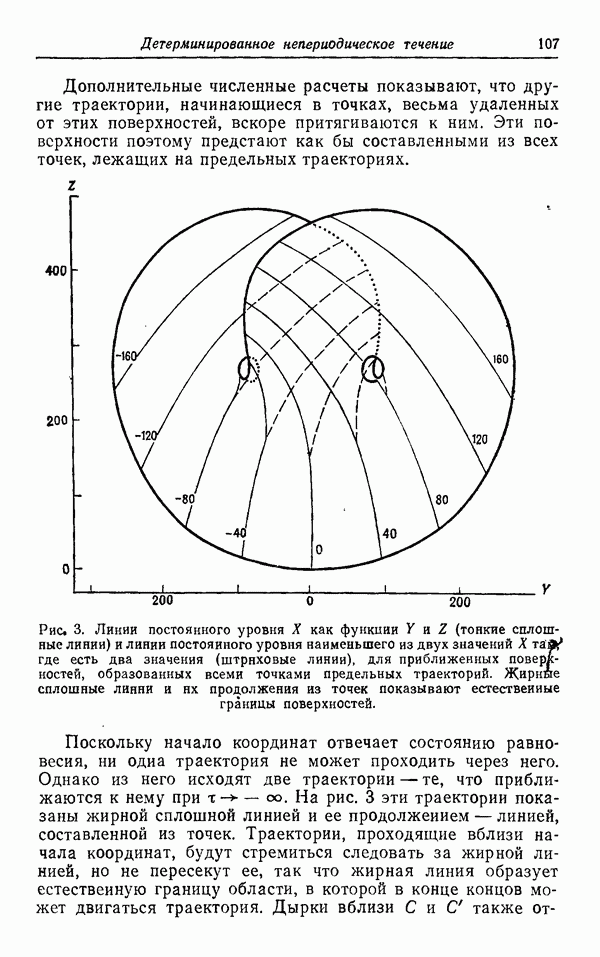
Таким образом, объем, занимаемый любым элементов фазовой жидкости стремится к нулю с характерным временем порядка  . Тем самым должна существовать предельная поверхность S, обладающая таким свойством, что с точностью до множества меры нуль точки любого элемента фазовой
. Тем самым должна существовать предельная поверхность S, обладающая таким свойством, что с точностью до множества меры нуль точки любого элемента фазовой
жидкости будут подходить как угодно близко к  Оговорка, касающаяся множества меры нуль, важна, что можно ясно увидеть на следующем примере. Если сингулярная траектория
Оговорка, касающаяся множества меры нуль, важна, что можно ясно увидеть на следующем примере. Если сингулярная траектория

проходит через  , то точки, лежащие в V и на этой траектории, будут отходить как угодно далеко от остальных точек V при t, стремящемся к бесконечности. Нам не известно никаких других сингулярных траекторий.
, то точки, лежащие в V и на этой траектории, будут отходить как угодно далеко от остальных точек V при t, стремящемся к бесконечности. Нам не известно никаких других сингулярных траекторий.
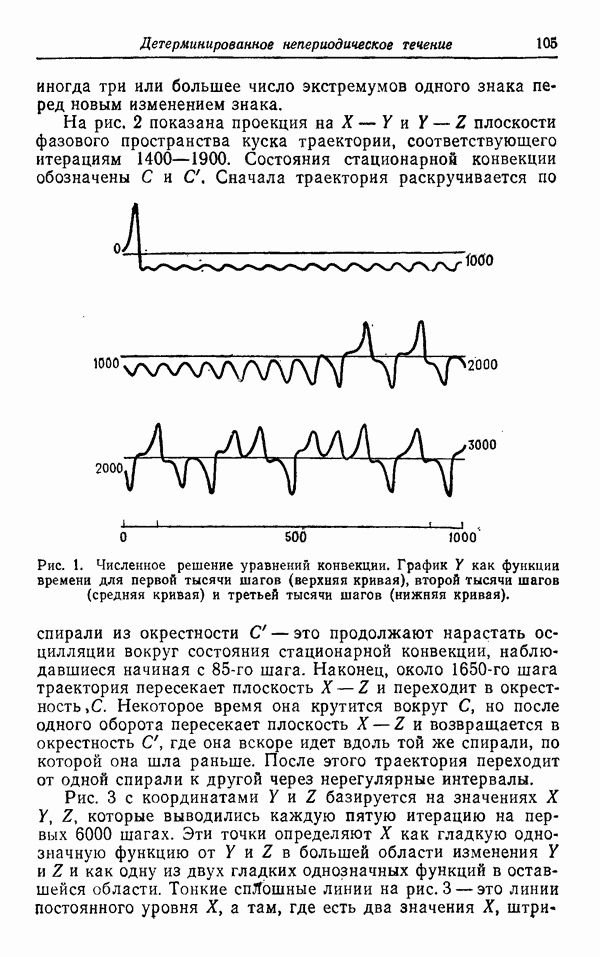
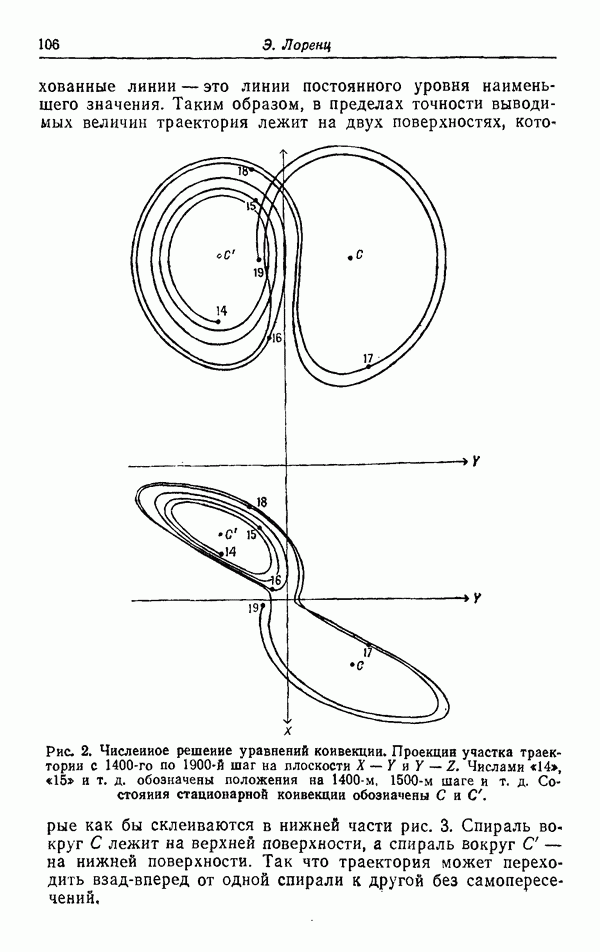
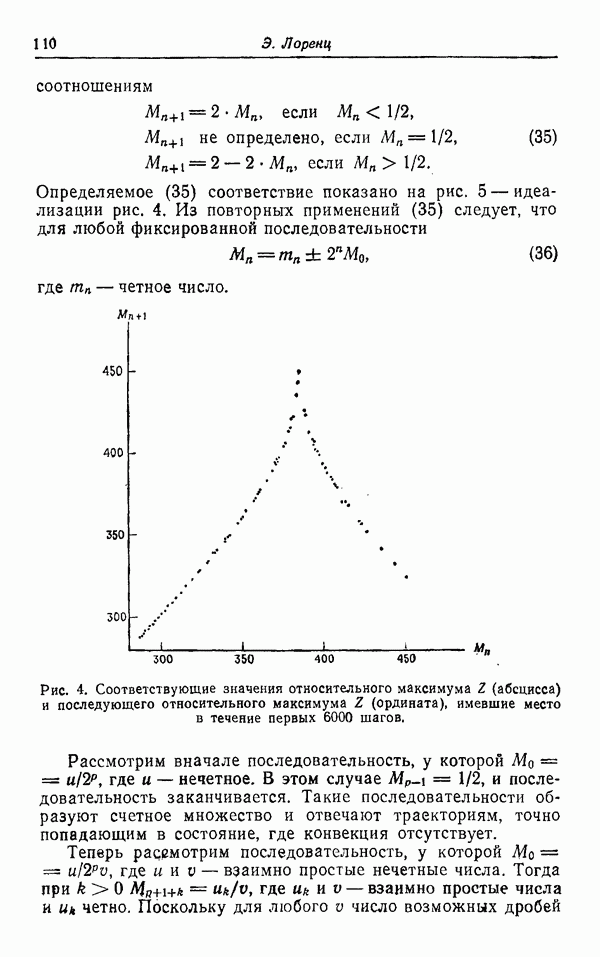
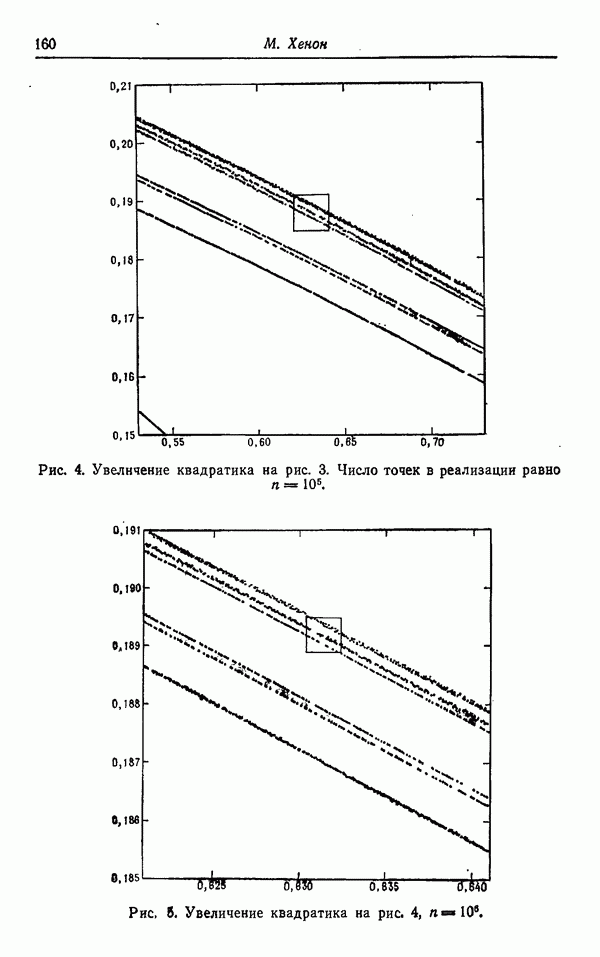
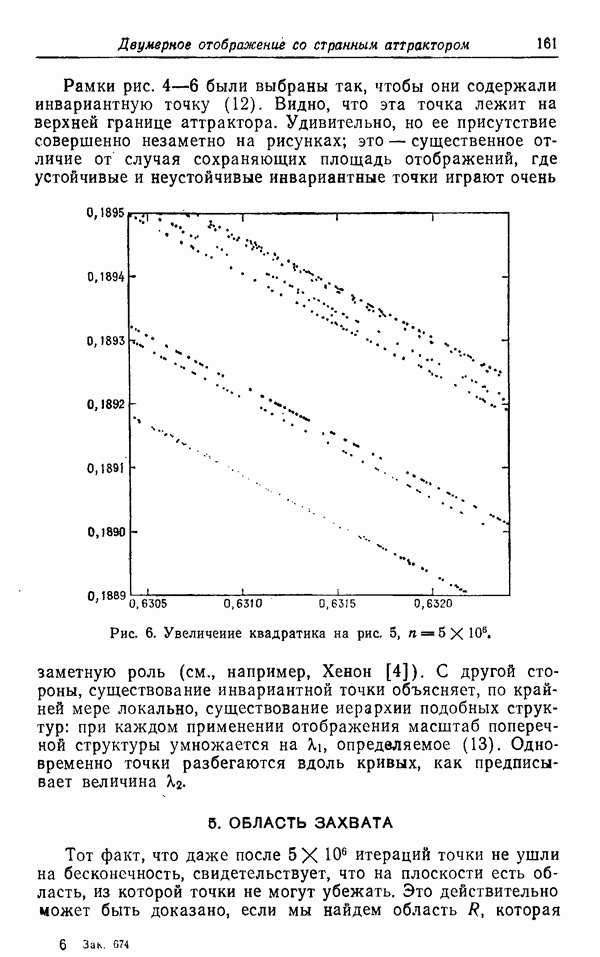
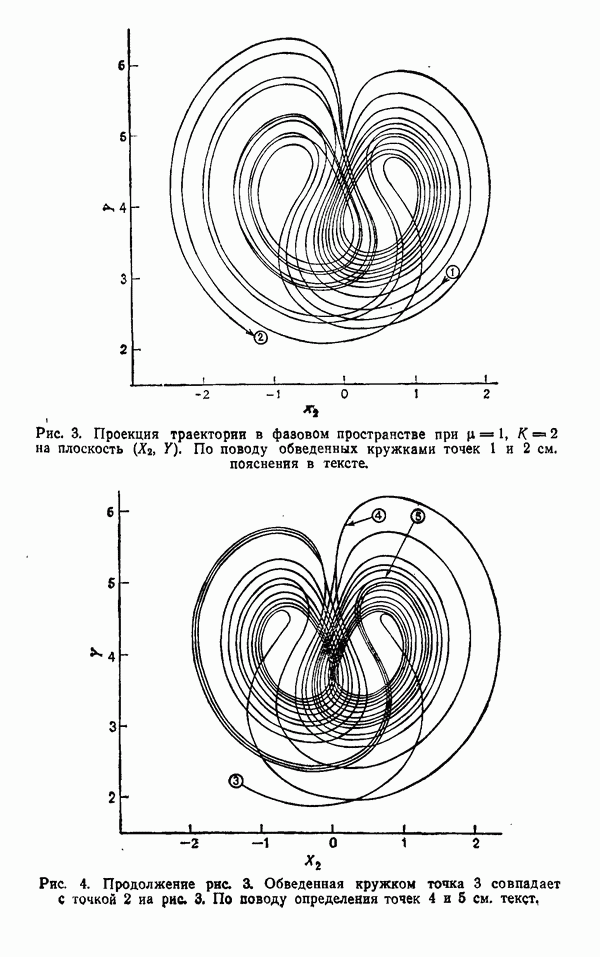
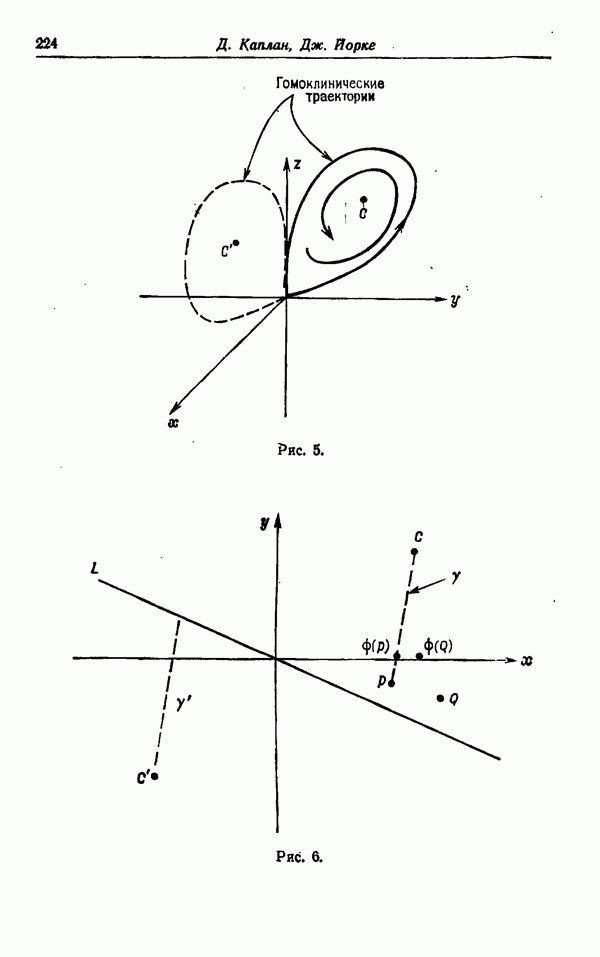
На рис. 3 и 4 изображена проекция траектории на плоскость  в случае
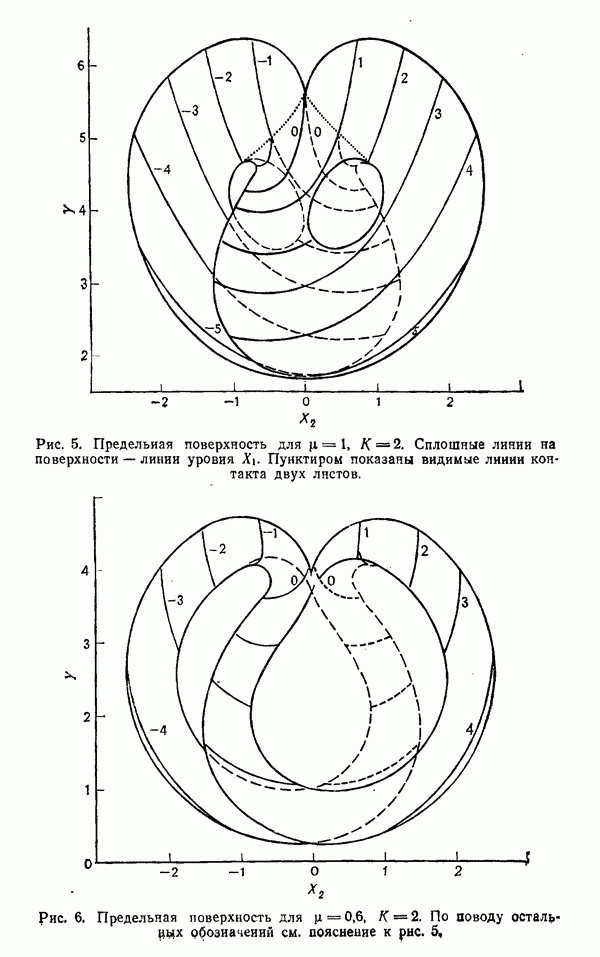
в случае  Рис. 4 есть продолжение по времени рис. 3, точки 2 и 3 на соответствующих рисунках отвечают одному и тому же моменту времени. Как видно, существует область около состояния N и около состояния R, в которую не попадает ни одна траектория. Несмотря на то что траектория может начинаться в одной из этих областей и несмотря на то что такая траектория, очевидно, может попасть на поверхность, содержащую локальную стационарную точку, эти области в действительности являются «дырками» в предельной поверхности и не лежат на ней. Траектория, начинавшаяся в какой-либо из этих областей, будет раскручиваться, пока она не выйдет из соответствующей области. Аналогично, траектория, начинающаяся вне большой внешней огибающей этих орбит, всегда будет идти к плотно заполненным областям и оставаться там. На рис. 5 и 6 изображены предельные поверхности соответственно для случаев
Рис. 4 есть продолжение по времени рис. 3, точки 2 и 3 на соответствующих рисунках отвечают одному и тому же моменту времени. Как видно, существует область около состояния N и около состояния R, в которую не попадает ни одна траектория. Несмотря на то что траектория может начинаться в одной из этих областей и несмотря на то что такая траектория, очевидно, может попасть на поверхность, содержащую локальную стационарную точку, эти области в действительности являются «дырками» в предельной поверхности и не лежат на ней. Траектория, начинавшаяся в какой-либо из этих областей, будет раскручиваться, пока она не выйдет из соответствующей области. Аналогично, траектория, начинающаяся вне большой внешней огибающей этих орбит, всегда будет идти к плотно заполненным областям и оставаться там. На рис. 5 и 6 изображены предельные поверхности соответственно для случаев  Предельная поверхность состоит из двух листов, верхнего правого листа и нижнего левого листа. Их границы нанесены пунктиром, когда они являются невидимыми линиями. Правая внутренняя петля окружает точку
Предельная поверхность состоит из двух листов, верхнего правого листа и нижнего левого листа. Их границы нанесены пунктиром, когда они являются невидимыми линиями. Правая внутренняя петля окружает точку  а левая внутренняя петля окружает точку обратного движения
а левая внутренняя петля окружает точку обратного движения  Внешние границы левого и правого листов являются частями траекторий, а внутренние петли, окружающие N и R, не являются. Область между внешней петлей и двумя внутренними петлями в проекции довольно равномерно пересекается траекторией, хотя наблюдается некоторое сгущение около внутренних петель и в окрестности почти периодических решений. Решения уравнений (12) — (14), разумеется, не могут пересекаться или касаться, но есть примеры, когда они кажутся сливающимися (например, точки
Внешние границы левого и правого листов являются частями траекторий, а внутренние петли, окружающие N и R, не являются. Область между внешней петлей и двумя внутренними петлями в проекции довольно равномерно пересекается траекторией, хотя наблюдается некоторое сгущение около внутренних петель и в окрестности почти периодических решений. Решения уравнений (12) — (14), разумеется, не могут пересекаться или касаться, но есть примеры, когда они кажутся сливающимися (например, точки

Рис. 3. Проекция траектории в фазовом пространстве при  на плоскость
на плоскость  . По поводу обведенных кружками точек 1 и 2 см. пояснения в тексте.
. По поводу обведенных кружками точек 1 и 2 см. пояснения в тексте.

Рис. 4. Продолжение рис. 3. Обведенная кружком точка 3 совпадает С точкой 2 на рис. 3. По поводу определения точек 4 и 5 см. текст,

Рис. 5. Предельная поверхность для  . Сплошные линии на поверхности — линии уровня
. Сплошные линии на поверхности — линии уровня  Пунктиром показаны видимые лииии контакта двух листов.
Пунктиром показаны видимые лииии контакта двух листов.

Рис. 6. Предельная поверхность для  По поводу остальных обозначений см. пояснение к рис. 5,
По поводу остальных обозначений см. пояснение к рис. 5,
4 и 5 на рис. 4). В связи с этим важно различать проекцию  на эту поверхность траектории, идущей около 5, и саму поверхность. Практически невозможно исследовать траекторию, лежащую в точности на S, но если это можно было бы сделать, то обнаружилось бы, что такая траектория не может перейти с одного листа на другой, так как такой переход противоречит уравнениям
на эту поверхность траектории, идущей около 5, и саму поверхность. Практически невозможно исследовать траекторию, лежащую в точности на S, но если это можно было бы сделать, то обнаружилось бы, что такая траектория не может перейти с одного листа на другой, так как такой переход противоречит уравнениям 
Топологически  как видно на рис. 5 и 6, представляет собой конечный симплициальный комплекс, не содержащий стационарных точек группы преобразования g, определяемой дифференциальными уравнениями (12) — (14).
как видно на рис. 5 и 6, представляет собой конечный симплициальный комплекс, не содержащий стационарных точек группы преобразования g, определяемой дифференциальными уравнениями (12) — (14).

Рис. 7. Схематическое изображение предельной поверхности  Дуги АВ на каждом листе должны быть отождествлены (склеены) друг с другом, то же самое относится к дугам ВС.
Дуги АВ на каждом листе должны быть отождествлены (склеены) друг с другом, то же самое относится к дугам ВС.
На рис. 7 дано схематическое идеализированное изображение  . Луч АВ слева отождествляется с дугой АВ справа, а дуга ВС слева — с лучом ВС справа. Траектории переходят с одного листа на другой через эти общие кривые. Поверхность, изображенная на рис. 7, принадлежит к тому же гомотопическому классу, что и букет двух окружностей, а его фундаментальная группа является свободной группой с двумя образующими (в действительности интересно рассматривать каждую достаточно длинную траекторию как элемент этой группы).
. Луч АВ слева отождествляется с дугой АВ справа, а дуга ВС слева — с лучом ВС справа. Траектории переходят с одного листа на другой через эти общие кривые. Поверхность, изображенная на рис. 7, принадлежит к тому же гомотопическому классу, что и букет двух окружностей, а его фундаментальная группа является свободной группой с двумя образующими (в действительности интересно рассматривать каждую достаточно длинную траекторию как элемент этой группы).
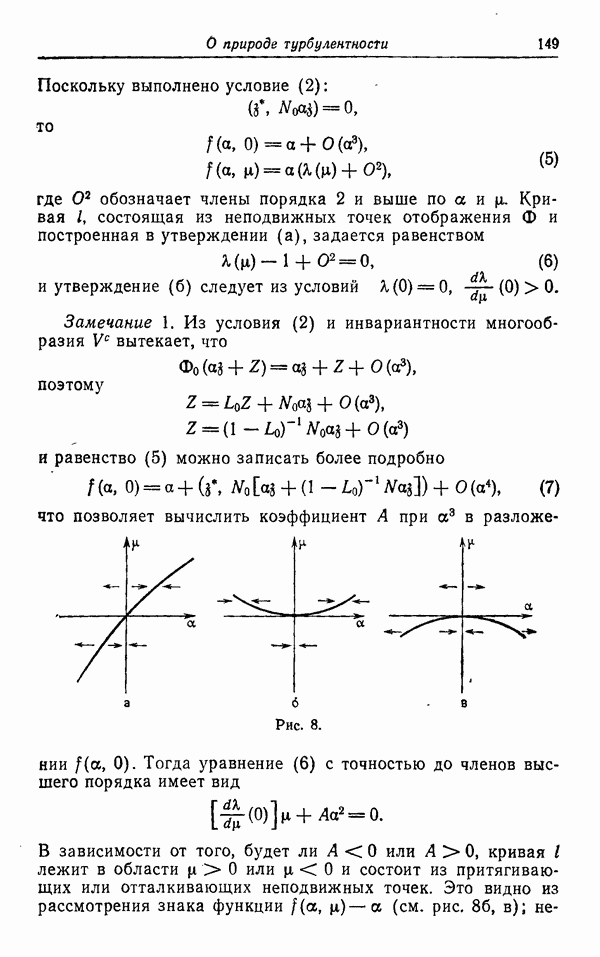
Важно было бы обнаружить, что S не может иметь такого вида. Если бы это было так, то нульмерное и одномерное числа Бетти должны быть равны соответственно 1 и 2, а характеристика Эйлера — Пуанкаре поверхности не равна нулю  Преобразование S, определяемое g, тем не менее гомотопно
Преобразование S, определяемое g, тем не менее гомотопно  Это следует из теоремы Лефшеца о неподвижной точке, что противоречит предположению о том, что
Это следует из теоремы Лефшеца о неподвижной точке, что противоречит предположению о том, что  содержит неподвижные точки. Отождествление АВ и CD слева и справа на рис. 7 поэтому невозможно для S, и траектории не могут переходить с одного листа на другой. Если траектория попадает в точности на S, то она продолжает
содержит неподвижные точки. Отождествление АВ и CD слева и справа на рис. 7 поэтому невозможно для S, и траектории не могут переходить с одного листа на другой. Если траектория попадает в точности на S, то она продолжает
крутиться вокруг N или R все время, либо представляя собой замкнутую орбиту, либо притягиваясь к предельному циклу на внешней или внутренней границе рассматриваемого листа.
Система дифференциальных уравнений, похожая на (12) — (14), обладающая свойством, аналогичным (39), исследовалась Лоренцем  ). Построенные им графики решений аналогичны по форме нашим предельным поверхностям.
). Построенные им графики решений аналогичны по форме нашим предельным поверхностям.
6. Численные результаты. Диаграммы траекторий движущихся точек были построены на основании численных результатов, полученных с помощью метода Рунге — Кутта четвертого порядка. Следует отметить, что значительная часть исследования была проведена на аналоговой машине. Численное интегрирование было проведено на протяжении 200—? 500 шагов по времени так, чтобы с достаточной точностью определить предельную поверхность и получить приемлемые оценки количества осцилляций между обращением направления. Авторам не известно других работ, за исключением некоторых неопубликованных результатом Ф. Дж. Лауэса, в которых интегрирования были бы столь протяженными по времени. Обсуждаемые ниже результаты, если не оговорено противное, относятся к случаю 
При  число осцилляций между обращением направления заключено между 1 и 11, а среднее их число равно 4. Если траектория сразу перескакивает с
число осцилляций между обращением направления заключено между 1 и 11, а среднее их число равно 4. Если траектория сразу перескакивает с  -листа на
-листа на  -лист, то это происходит на пунктирной кривой так далеко от точки R (см. рис. 5), что она почти мгновенно возвращается на
-лист, то это происходит на пунктирной кривой так далеко от точки R (см. рис. 5), что она почти мгновенно возвращается на  -лист. Такое изменение направления соответствует событию полярности, описанному Коксом [1]. Если траектория уходит с
-лист. Такое изменение направления соответствует событию полярности, описанному Коксом [1]. Если траектория уходит с  -листа около его границы, то она попадает на
-листа около его границы, то она попадает на  -лист в той части пунктирной кривой, которая близка к точке R. Следовательно, произойдет большое число осцилляций прежде, чем траектория вернется обратно на
-лист в той части пунктирной кривой, которая близка к точке R. Следовательно, произойдет большое число осцилляций прежде, чем траектория вернется обратно на  -лист. Это соответствует эпохе полярности Кокса.
-лист. Это соответствует эпохе полярности Кокса.
Некоторая статистическая информация о поведении изменений полярности может быть описана следующим образом. Пусть  обозначает максимальное значение
обозначает максимальное значение  на петле около N, непосредственно предшествующей переходу на
на петле около N, непосредственно предшествующей переходу на  -лист. Число осцилляций
-лист. Число осцилляций  , которое она испытывает в этом состоянии до возвращения к первоначальной полярности, дается целой частью следующего выражения:
, которое она испытывает в этом состоянии до возвращения к первоначальной полярности, дается целой частью следующего выражения:

(при замене К на  функции а и b, разумеется, не меняются). При
функции а и b, разумеется, не меняются). При  оказалось, что и 5—4, а при
оказалось, что и 5—4, а при  получилось
получилось 

Рис. 8. Среднее число колебаний  между изменениями ориентации как функция от
между изменениями ориентации как функция от  при
при 

Рис. 9. Среднее число колебаний  между изменениями ориентации как функция от К при
между изменениями ориентации как функция от К при 
Значение среднего числа осцилляций  между изменениями полярности приведено на рис. 8 и 9. По-видимому,
между изменениями полярности приведено на рис. 8 и 9. По-видимому,  имеет глобальный максимум при
имеет глобальный максимум при 
Поиск чисто периодических решений проводился с помощью модифицированного метода Дэвидона (Дэвидон [12],
Флетчер и Пауэлл [13]), основанного на минимизации функции

для решений, близких к стационарным точкам. F можно рассматривать как меру удаления траектории от состояния N в течение одного витка около N. Начальное расстояние траектории от состояния N можно определить следующим образом:

Минимизация  была проведена по начальным значениям
была проведена по начальным значениям  и по независимой переменной
и по независимой переменной  . Величина
. Величина  может быть хорошо аппроксимирована периодом
может быть хорошо аппроксимирована периодом  получающимся из линейной теории.
получающимся из линейной теории.
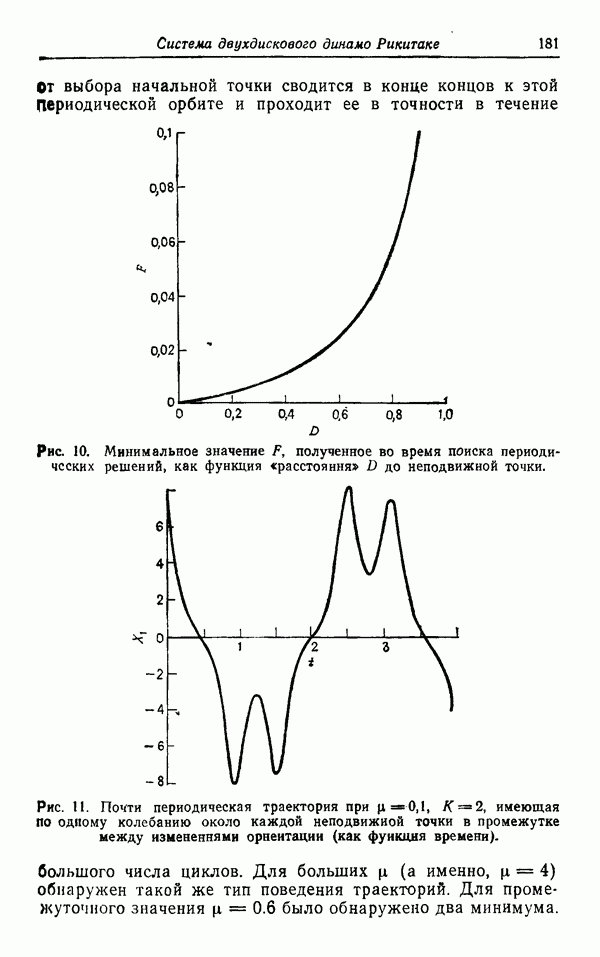
На рис. 10 приведен график минимального значения F в зависимости от D для  Для значений
Для значений  обнаружено, что F есть приблизительно
обнаружено, что F есть приблизительно  что находится в хорошем соответствии с результатами, полученными с помощью теории устойчивости. Для больших значений
что находится в хорошем соответствии с результатами, полученными с помощью теории устойчивости. Для больших значений  зависимость F от D более близка к линейной. Из рис. 10 следует, что траектории, начинающиеся близко к N, раскручиваются сначала медленно, а затем с возрастанием D более быстро.
зависимость F от D более близка к линейной. Из рис. 10 следует, что траектории, начинающиеся близко к N, раскручиваются сначала медленно, а затем с возрастанием D более быстро.
Для нахождения периодических решений, на которых происходит изменение полярности, минимизируется функция

Различные знаки в скобках в выражении (44) обусловлены тем, что однопериодическим решениям по  соответствуют двойные периодические решения по У. Оценки
соответствуют двойные периодические решения по У. Оценки  были получены при помощи длительных интегрирований, проведенных для предельной поверхности.
были получены при помощи длительных интегрирований, проведенных для предельной поверхности.
Наличие нуля у F в (44) отвечает периодическому решению с изменением полярности. Тем не менее нет уверенности, что такие решения существуют. Было обнаружено, что локальные минимумы отвечают «почти периодическим» решениям с большей (малые F) или меньшей (большие F) степенью постоянства на «почти периоде». Для малых  (порядка 0.1 или меньше) был найден только один минимум. Для
(порядка 0.1 или меньше) был найден только один минимум. Для  пример приведен на рис. 11 и 12. Вопреки видимости, траектории совершают только один оборот около стационарной точки до возвращения к другой стационарной точке. Для этих значений
пример приведен на рис. 11 и 12. Вопреки видимости, траектории совершают только один оборот около стационарной точки до возвращения к другой стационарной точке. Для этих значений  любая траектория вне зависимости
любая траектория вне зависимости
От выбора начальной точки сводится в конце концов к этой Периодической орбите и проходит ее в точности в течение большого числа циклов.

Рис. 10. Минимальное значение F, полученное во время поиска периодических решений, как функция «расстояния» D до неподвижной точки.

Рис. 11. Почти периодическая траектория при  имеющая по одному колебанию около каждой неподвижной точки в промежутке между изменениями ориентации (как функция времени).
имеющая по одному колебанию около каждой неподвижной точки в промежутке между изменениями ориентации (как функция времени).
Для больших  (а именно,
(а именно,  ) обнаружен такой же тип поведения траекторий. Для промежуточного значения
) обнаружен такой же тип поведения траекторий. Для промежуточного значения  было обнаружено два минимума.
было обнаружено два минимума.
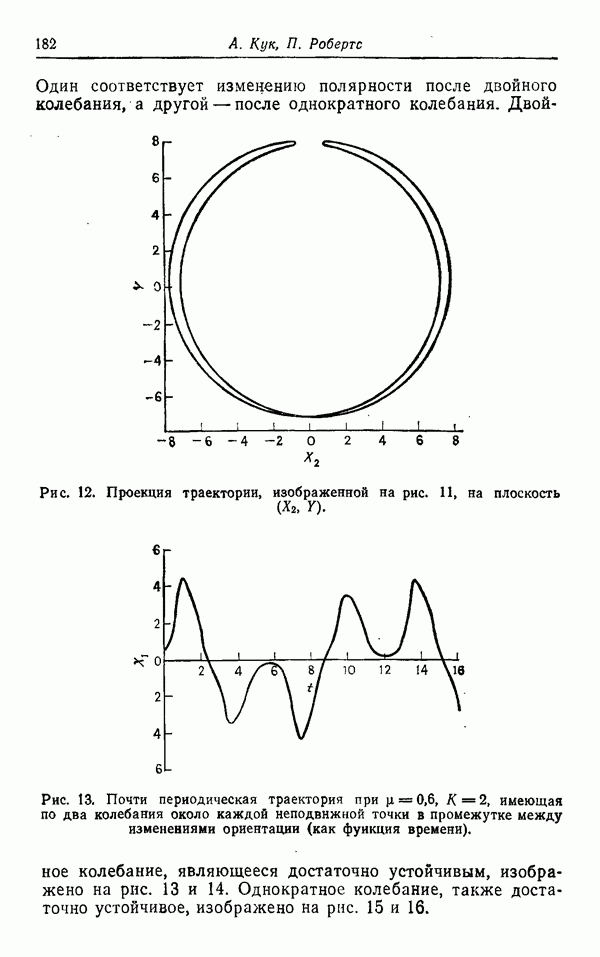
Один соответствует изменению полярности после двойного колебания, а другой — после однократного колебания.

Рис. 12. Проекция траектории, изображенной на рис. 11, на плоскость 

Рис. 13. Почти периодическая траектория при  имеющая по два колебания около каждой неподвижной точки в промежутке между изменениями ориентации (как функция времени).
имеющая по два колебания около каждой неподвижной точки в промежутке между изменениями ориентации (как функция времени).
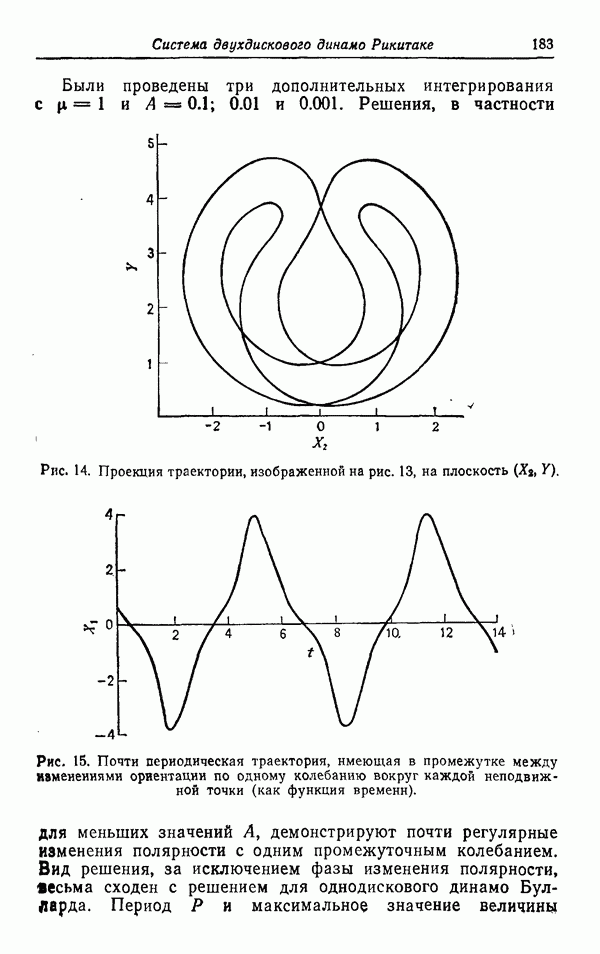
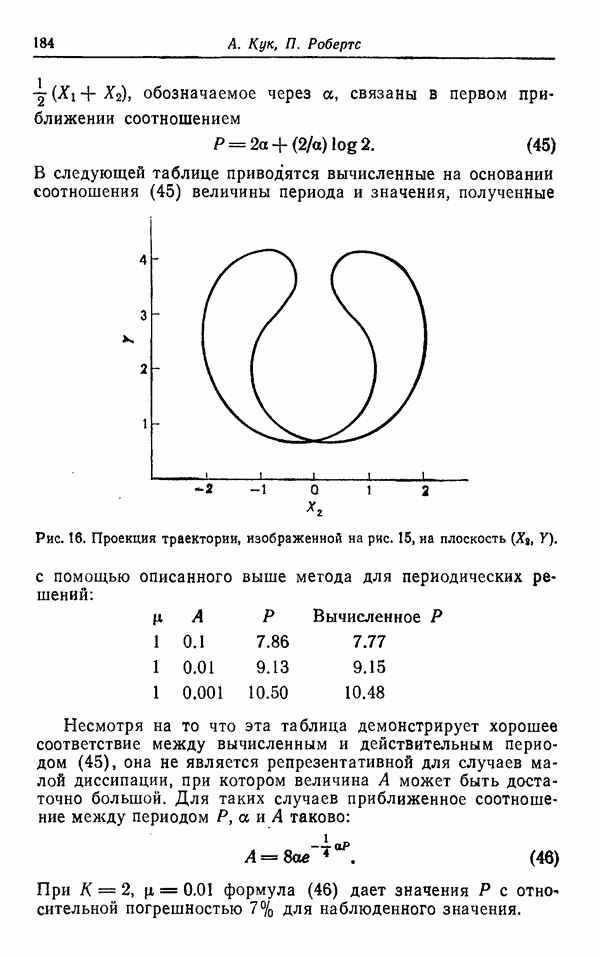
Двойное колебание, являющееся достаточно устойчивым, изображено на рис. 13 и 14. Однократное колебание, также достаточно устойчивое, изображено на рис. 15 и 16.
Были проведены три дополнительных интегрирования с  и 0.001.
и 0.001.

Рис. 14. Проекция траектории, изображенной на рис. 13, на плоскость  .
.

Рис. 15. Почти периодическая траектория, имеющая в промежутке между изменениями ориентации по одному колебанию вокруг каждой неподвижной точки (как функция времени).
Решения, в частности для меньших значений А, демонстрируют почти регулярные изменения полярности с одним промежуточным колебанием. Вид решения, за исключением фазы изменения полярности, весьма сходен с решением для однодискового динамо Бул-Ларда. Период Р и максимальное значение величины
 обозначаемое через а, связаны в первом приближении соотношением
обозначаемое через а, связаны в первом приближении соотношением

В следующей таблице приводятся вычисленные на основании соотношения (45) величины периода и значения, полученные с помощью описанного выше метода для периодических решений:


Рис. 16. Проекция траектории, изображенной на рис. 15, на плоскость  .
.
Несмотря на то что эта таблица демонстрирует хорошев соответствие между вычисленным и действительным периодом (45), она не является репрезентативной для случаев малой диссипации, при котором величина А может быть достаточно большой. Для таких случаев приближенное соотношение между периодом Р, а и А таково:

При  формула (46) дает значения Р с относительной погрешностью 7% для наблюденного значения.
формула (46) дает значения Р с относительной погрешностью 7% для наблюденного значения.
Приложение: Динамо Рикитаке при малых А
В (6) уже отмечалось, что для фиксированного К при достаточно малых  траектории близки к периодическим с единственным колебанием между изменениями полярности. В связи с этим возникает интересная возможность рассматривать их как приближения к строго периодическим орбитам, полученным на основании асимптотических методов при
траектории близки к периодическим с единственным колебанием между изменениями полярности. В связи с этим возникает интересная возможность рассматривать их как приближения к строго периодическим орбитам, полученным на основании асимптотических методов при  Прежде чем детально обсуждать эту идею, необходимо исследовать однодисковое динамо Булларда и связанное с ним антидинамо.
Прежде чем детально обсуждать эту идею, необходимо исследовать однодисковое динамо Булларда и связанное с ним антидинамо.
Динамо Булларда. Однодисковое динамо Булларда [3] описывается следующими дифференциальными уравнениями:

Здесь U обозначает ток,  — разность между угловой скоростью У и эффектом омической диссипации
— разность между угловой скоростью У и эффектом омической диссипации  .
.

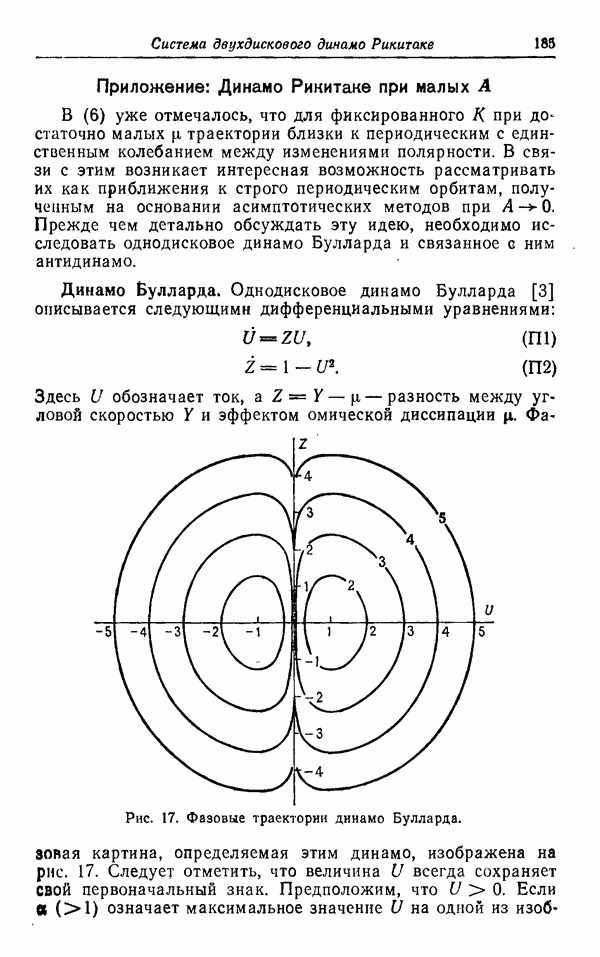
Рис. 17. Фазовые траектории динамо Булларда.
Фазовая картина, определяемая этим динамо, изображена на рис. 17. Следует отметить, что величина U всегда сохраняет свой первоначальный знак. Предположим, что  Если а
Если а  означает максимальное значение U на одной из изображенных
означает максимальное значение U на одной из изображенных
кривых, то из  следует, что сама кривая задается уравнением
следует, что сама кривая задается уравнением

Кроме максимума  эта кривая имеет минимальное значение по U, а именно
эта кривая имеет минимальное значение по U, а именно

При  уравнение (П3) дает асимптотическую формулу
уравнение (П3) дает асимптотическую формулу

Из  и (ПЗ) получаем следующее выражение для времени прохождения точкой одной из полных орбит, изображенных на рис. 17:
и (ПЗ) получаем следующее выражение для времени прохождения точкой одной из полных орбит, изображенных на рис. 17:

При малых  кривая представляет собой окружность с центром в стационарной точке
кривая представляет собой окружность с центром в стационарной точке  изображающая точка проходит эту окружность равномерно. Период соответствующего простого гармонического движения равен
изображающая точка проходит эту окружность равномерно. Период соответствующего простого гармонического движения равен  При
При  движение по кривой ни в коем случае не равномерно. Оказалось, что
движение по кривой ни в коем случае не равномерно. Оказалось, что  соответствует почти равномерному движению с единичной скоростью вдоль части кривой, близкой к оси Z. Оставшаяся часть кривой проходится за время порядка
соответствует почти равномерному движению с единичной скоростью вдоль части кривой, близкой к оси Z. Оставшаяся часть кривой проходится за время порядка 
Случай а  может быть исследован методом асимптотических разложений. Для
может быть исследован методом асимптотических разложений. Для  из
из  и (П3) в первом приближении получается уравнение
и (П3) в первом приближении получается уравнение

где должен быть взят знак, который имеет величина  нение
нение  можно использовать для определения величин U и Z при
можно использовать для определения величин U и Z при  При этих начальных данных, интегрируя
При этих начальных данных, интегрируя  получаем
получаем

Последующие члены в разложении U могут быть получены при помощи итераций. Приближение второго порядка дается
выражением

При  из
из  и (П3) получаем в первом порядке
и (П3) получаем в первом порядке

где снова берется знак величины Z. Решение уравнения первого приближения имеет вид

где

 есть момент времени, когда достигается максимум
есть момент времени, когда достигается максимум  Как и раньше, приближения высших порядков могут быть получены при помощи итераций. Приближение второго порядка имеет вид
Как и раньше, приближения высших порядков могут быть получены при помощи итераций. Приближение второго порядка имеет вид

полупериод  может быть определен в первом порядке при Помощи (П8) — (П11), а во втором порядке — из (П9) - (П13). Подставляя
может быть определен в первом порядке при Помощи (П8) — (П11), а во втором порядке — из (П9) - (П13). Подставляя  получаем
получаем

Так как  то в первом порядке из (П14) получаем
то в первом порядке из (П14) получаем

Из (П11) при  имеем
имеем

Выражения (П15) и (П16) согласуются, если

Аналогично из (П9) и (П13) получаем

Антидинамо. Обращая связи в динамо Булларда или обращая направление, в котором движется динамо, получаем вместо  следующие уравнения:
следующие уравнения:

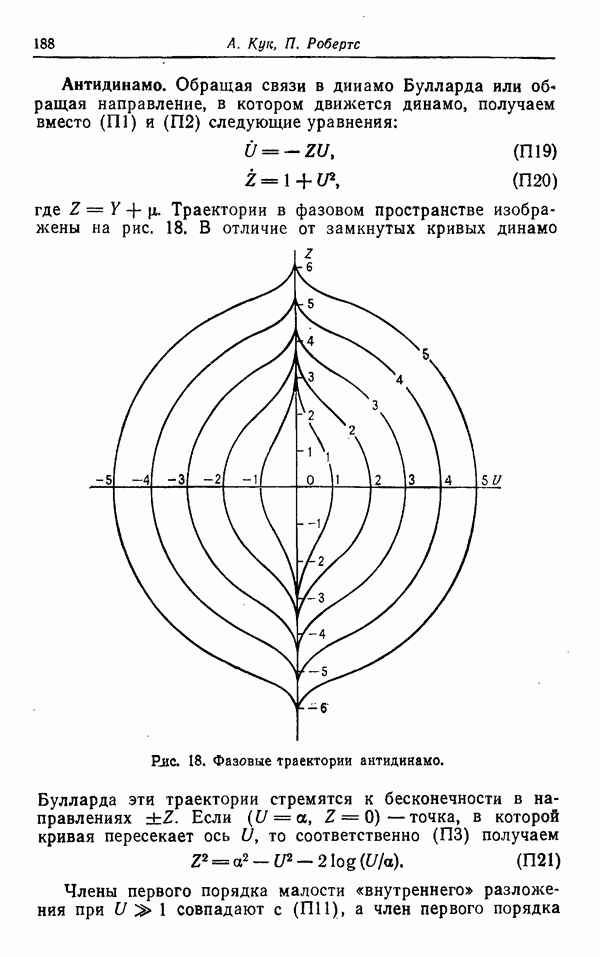
где  Траектории в фазовом пространстве изображены на рис. 18.
Траектории в фазовом пространстве изображены на рис. 18.

Рис. 18. Фазовые траектории антидинамо.
В отличие от замкнутых кривых динамо Булларда эти траектории стремятся к бесконечности в направлениях  Если
Если  - точка, в которой кривая пересекает ось U, то соответственно (П3) получаем
- точка, в которой кривая пересекает ось U, то соответственно (П3) получаем

Члены первого порядка малости «внутреннего» разложения при  совпадают с
совпадают с  а член первого порядка
а член первого порядка
«внешнего» разложения имеет теперь вид

Выбор начала отсчета t не имеет здесь особого значения, как это было для динамо Булларда.
Спаренные динамо. Уравнения (12) и (13) спаренного динамо могут быть приведены к более симметричному виду:

где  отвечает величине
отвечает величине  а не
а не  как в основном тексте.
как в основном тексте.
Рассмотрим функции  определяемые уравнениями
определяемые уравнениями

Подставляя  получаем
получаем

Существуют два различных семейства решений, отвечающих  Для первого из них
Для первого из них  Тогда динамика величин
Тогда динамика величин  описывается уравнениями
описывается уравнениями  которые теперь сводятся к уравнениям Булларда. Для второго семейства
которые теперь сводятся к уравнениям Булларда. Для второго семейства  Тогда уравнения
Тогда уравнения  для величин
для величин  сводятся к уравнениям антидинамо. При малом, но не равном нулю
сводятся к уравнениям антидинамо. При малом, но не равном нулю  существуют такие решения уравнений
существуют такие решения уравнений  в которых могут быть выделены три фазы:
в которых могут быть выделены три фазы:
(a)  велико,
велико,  мало. U и У быстро меняются, как во «внутреннем» решении уравнений Булларда;
мало. U и У быстро меняются, как во «внутреннем» решении уравнений Булларда;  определяется этими величинами.
определяется этими величинами.
(в) U мало,  велико.
велико.  и У быстро изменяются, как во «внутреннем» решении уравнений антидинамо;
и У быстро изменяются, как во «внутреннем» решении уравнений антидинамо;  определяется
определяется  и
и  .
.
(с) У велико и медленно меняется,  остаются промежуточными по величине за счет экспоненциального возрастания и убывания.
остаются промежуточными по величине за счет экспоненциального возрастания и убывания.
(Использованные здесь прилагательные «большой» и «малый» относятся к модулям соответствующих величин.)
Ищем периодические решения в следующем виде: они состоят из двух частей, удовлетворяющих (А) и (В), имеющих разные знаки, и каждая из них длится время порядка  Величина а выбирается на основании теории и соответствует амплитуде
Величина а выбирается на основании теории и соответствует амплитуде  для случая (а) и амплитуде
для случая (а) и амплитуде  для случая (b). Каждый переход от фазы (а) к фазе (b) содержит фазу (с). Рассмотрим полупериод, который содержит последовательные фазы (а), (с), (Ь) и (с), начинающийся в момент времени
для случая (b). Каждый переход от фазы (а) к фазе (b) содержит фазу (с). Рассмотрим полупериод, который содержит последовательные фазы (а), (с), (Ь) и (с), начинающийся в момент времени  из состояния, в котором значение
из состояния, в котором значение  максимально, а величины У и
максимально, а величины У и  равны нулю. (Здесь и далее считается, что
равны нулю. (Здесь и далее считается, что  пренебрежимо мало по сравнению с У.)
пренебрежимо мало по сравнению с У.)
В фазе (а) величины  и У в первом приближении равны
и У в первом приближении равны

Согласно  величина
величина  в первом приближении является подходящим решением уравнения
в первом приближении является подходящим решением уравнения

а именно

Очевидно, что при  , т. e. в случае, когда решение впервые входит в фазу (с), справедливы следующие приближенные равенства:
, т. e. в случае, когда решение впервые входит в фазу (с), справедливы следующие приближенные равенства:

В первом приближении соотношения  имеют место на всем протяжении фазы (с). Если длительность этой фазы равна
имеют место на всем протяжении фазы (с). Если длительность этой фазы равна  , то амплитуда
, то амплитуда  уменьшается в
уменьшается в  раз, а амплитуда
раз, а амплитуда  увеличивается (по абсолютной величине) в
увеличивается (по абсолютной величине) в  раз. Если теперь изменить начало отсчета t так, чтобы оно соответствовало эпохе максимума
раз. Если теперь изменить начало отсчета t так, чтобы оно соответствовало эпохе максимума  в последующей фазе (b), то для этой фазы при
в последующей фазе (b), то для этой фазы при  имеем
имеем 

В фазе  величина
величина  значительно превосходит
значительно превосходит  и, согласно изложенной выше теории антидинамо, вместо (А30) имеем
и, согласно изложенной выше теории антидинамо, вместо (А30) имеем

Подставляя выражения  для
для  получаем вместо (П31)
получаем вместо (П31)

Соотношения (П34) и (П35) могут выполняться при  одновременно с (П33) тогда и только тогда, когда
одновременно с (П33) тогда и только тогда, когда

Из  вытекает, что период Р, амплитуда а и величина А связаны соотношением
вытекает, что период Р, амплитуда а и величина А связаны соотношением

Предположение о постоянстве У в течение фазы  как будто бы противоречит
как будто бы противоречит  Строго говоря, это так и есть. Однако изменение У в течение этой фазы на основании
Строго говоря, это так и есть. Однако изменение У в течение этой фазы на основании  равно
равно

где начало отсчета t то же, что и в первоначальном распределении. Из  получаем, что основной член в выражении для У имеет порядок
получаем, что основной член в выражении для У имеет порядок  и равен
и равен

В силу  это выражение равно нулю. Поэтому изменение У в течение фазы
это выражение равно нулю. Поэтому изменение У в течение фазы  имеет порядок
имеет порядок  что и требуется.
что и требуется.
Уравнение (П37) представляет собой единственное соотношение между двумя неизвестными величинами а и Р. Из равенств

и

(полученных с помощью (П27) и (П29)) вытекает, что для вычисления величины Р нужно отказаться от симметрии решений первого приближения.
Авторы признательны профессору Дж. Хорроксу за помощь в топологическом описании предельной поверхности. Мы также хотим поблагодарить мистера Дж. Добсона за проведение всего исследования на аналоговой машине и проявленный им интерес к рассмотренной проблеме, а также Ф. Дж. Лауэса за полезные замечания,
СПИСОК ЛИТЕРАТУРЫ
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- ПОПЫТКИ УСТАНОВИТЬ СООТНОШЕНИЕ МЕЖДУ УРАВНЕНИЯМИ НАВЬЕ-СТОКСА И ТУРБУЛЕНТНОСТЬЮ
- ПРИЛОЖЕНИЕ К СТАТЬЕ МАРСДЕНА БИФУРКАЦИИ, ПОЛУПОТОКИ И УРАВНЕНИЯ НАВЬЕ—СТОКСА
- ТЕОРИИ ТУРБУЛЕНТНОСТИ
- ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ РАСЧЕТА ТУРБУЛЕНТНЫХ СДВИГОВЫХ ТЕЧЕНИЙ
- ФРАКТАЛЫ И ТУРБУЛЕНТНОСТЬ: АТТРАКТОРЫ И РАЗБРОС
- СТРУКТУРА АТТРАКТОРОВ ЛОРЕНЦА
- ПРИЛОЖЕНИЕ К СТАТЬЕ Р. ВИЛЬЯМСА. «ИЗОБРАЖЕНИЕ АТТРАКТОРА ЛОРЕНЦА, ПОЛУЧЕННОЕ С ПОМОЩЬЮ КОМПЬЮТЕРА»
- ДВА ПОДХОДА К МОДЕЛИРОВАНИЮ ДВУМЕРНОЙ ТУРБУЛЕНТНОСТИ
- ДЕТЕРМИНИРОВАННОЕ НЕПЕРИОДИЧЕСКОЕ ТЕЧЕНИЕ
- О ПРИРОДЕ ТУРБУЛЕНТНОСТИ
- ДВУМЕРНОЕ ОТОБРАЖЕНИЕ СО СТРАННЫМ АТТРАКТОРОМ
- СИСТЕМА ДВУХДИСКОВОГО ДИНАМО РИКИТАКЕ
- МЕТАСТАБИЛЬНЫЙ ХАОС: ПЕРЕХОД К УСТОЙЧИВОМУ ХАОТИЧЕСКОМУ ПОВЕДЕНИЮ В МОДЕЛИ ЛОРЕНЦА
- ПРЕДТУРБУЛЕНТНОСТЬ: РЕЖИМ, НАБЛЮДАЕМЫЙ В ТЕЧЕНИИ ЖИДКОСТИ, ОПИСЫВАЕМОЙ МОДЕЛЬЮ ЛОРЕНЦА
- ТОПОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ АТТРАКТОРОВ ЛОРЕНЦА