| << Предыдущий параграф | Следующий параграф >> |
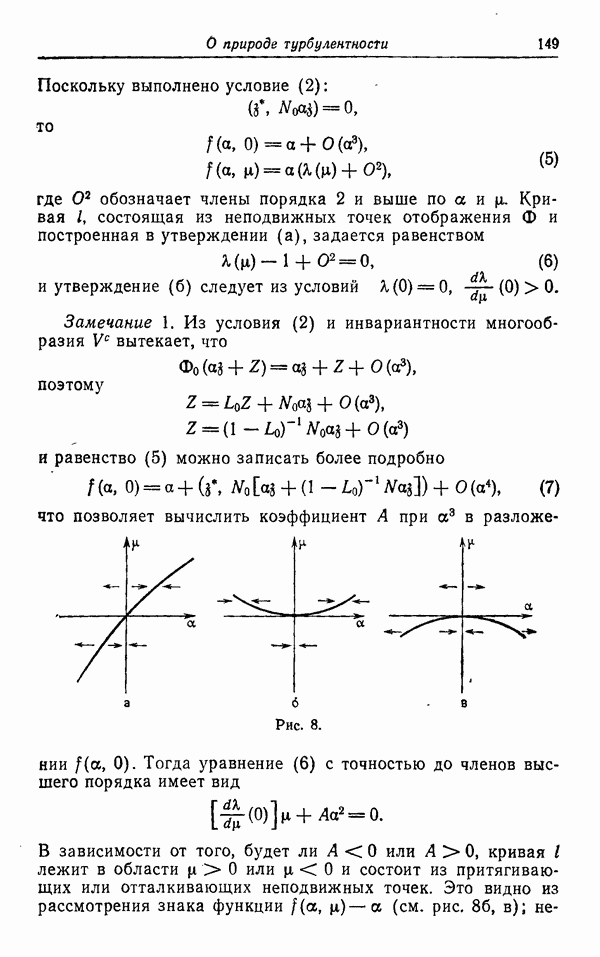
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СТРУКТУРА АТТРАКТОРОВ ЛОРЕНЦА
Р. Ф. Вильямс
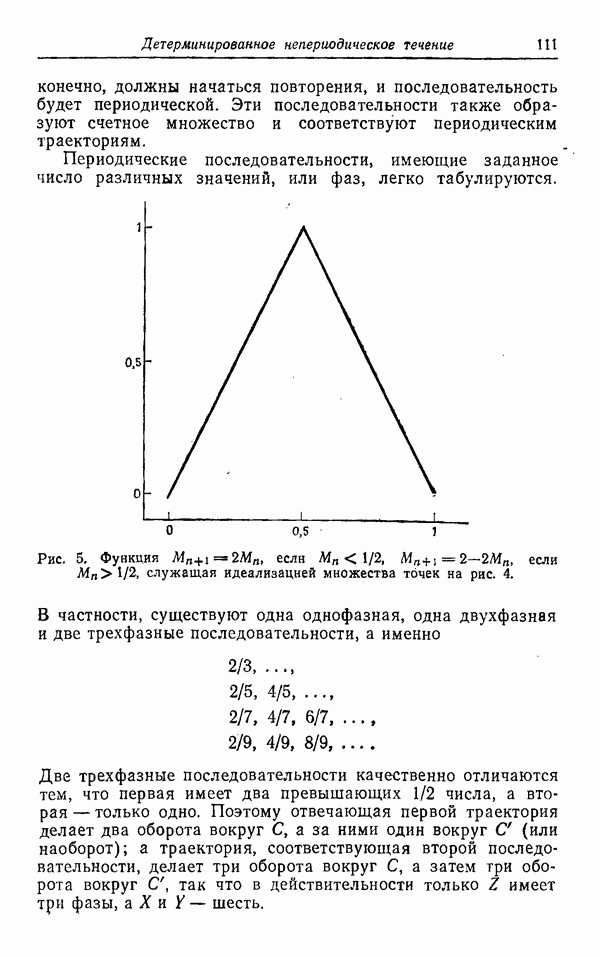
Система уравнений

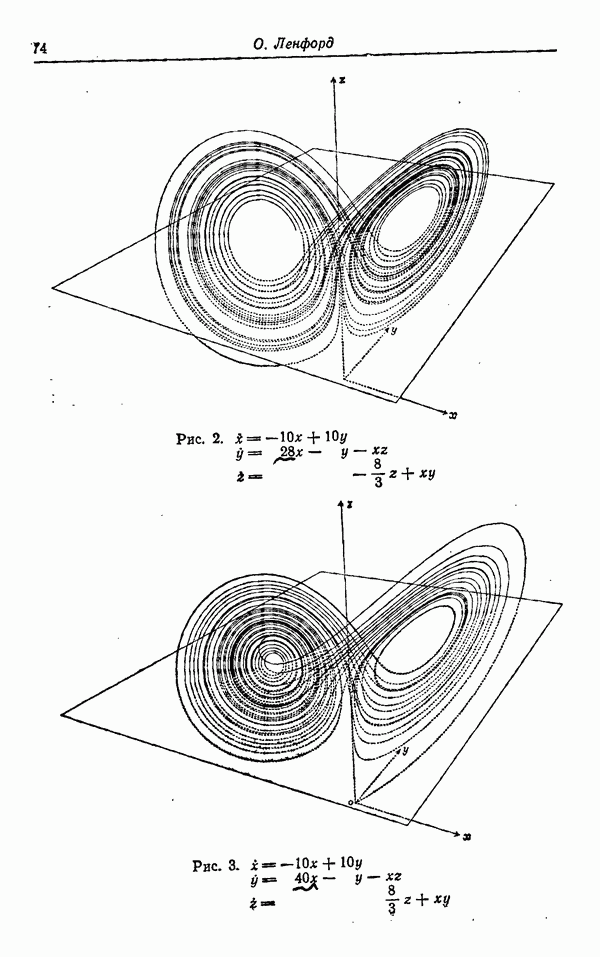
выведенная Е. Н. Лоренцем [7], позднее вызвала значительный интерес, в частности из-за ее предполагаемой связи с турбулентностью. Как было отмечено в статье Дж. Е. Марсдена (см. настоящий сб., стр. 7—20), эта система была получена путем обрезания уравнений Навье — Стокса. В настоящее время неизвестно, как эта система в действительности связана с проблемой турбулентности, и, как видно из предыдущих работ настоящего сборника, здесь существует много аргументов как «за», так и «против». Несомненно только, что эта система действительно обладает аттрактором нового типа, который не только не является классическим, но даже не является странным в смысле Смейла. Отметим, что, согласно классификации бифуркаций, данной в работе Дж. Марсдена, приведенная выше система обладает «стандартным» аттрактором Лоренца. Цель настоящей статьи — изучить его строение.
Наша первая задача — определить понятие «аттрактор» для потока. Это определение все время опускалось, на что есть свои причины. (Понятие аттрактора было определено в работе Смейла, но только для диффеоморфизмов, удовлетворяющих аксиоме А и с использованием теоремы Смейла о спектральном разложении.) С физической точки зрения
все, что наблюдаемо, т. е. проявляется с ненулевой вероятностью, тем или иным образом ассоциируется с чем-то «притягивающим» и поэтому называется «аттрактором». Мы будем использовать следующее определение, которое, по-видимому, в настоящее время принимается большинством специалистов по динамическим системам (см., напрнмер, [2], [9], [11]). Мы начнем с введения некоторых предварительных понятий.
Определение. Пусть М — компактное риманово многообразие и  — гладкий поток. Замкнутое
— гладкий поток. Замкнутое  -инвариантное множество
-инвариантное множество  , не содержащее неподвижных точек, называется гиперболическим, если ограничение на
, не содержащее неподвижных точек, называется гиперболическим, если ограничение на  касательного пучка
касательного пучка  может быть разложено в непрерывную сумму Уитни
может быть разложено в непрерывную сумму Уитни

где все три непрерывных подпучка  -инвариантны, Е — одномерный подпучок, касательный к траекториям потока и существуют постоянные
-инвариантны, Е — одномерный подпучок, касательный к траекториям потока и существуют постоянные  такие, что
такие, что

Пусть теперь  — замкнутое
— замкнутое  -инвариантное множество. Рассмотрим следующие свойства:
-инвариантное множество. Рассмотрим следующие свойства:
(a)  — топологически транзитивный поток, т. е.
— топологически транзитивный поток, т. е.  , такой, что множество
, такой, что множество  плотно в
плотно в  (существование всюду плотной траектории);
(существование всюду плотной траектории);
(b) периодические орбиты  плотны в
плотны в  ;
;
(c) существует открытое множество  , такое, что
, такое, что 
(d)  может быть выбрано таким, что
может быть выбрано таким, что 
 не содержит неподвижных точек и гиперболично.
не содержит неподвижных точек и гиперболично.
Если  удовлетворяет условиям (b), (с), (d), то оно называется аттрактором (здесь следует отметить, что большинство специалистов считает, что свойство
удовлетворяет условиям (b), (с), (d), то оно называется аттрактором (здесь следует отметить, что большинство специалистов считает, что свойство  должно быть теоремой, т. е. нужно сделать более слабое предположение
должно быть теоремой, т. е. нужно сделать более слабое предположение  а затем показать, что из (b), (с), (d) вытекает
а затем показать, что из (b), (с), (d) вытекает  если выполнено (а), (b), (с), (е), то называется базисным гиперболическим множеством;
если выполнено (а), (b), (с), (е), то называется базисным гиперболическим множеством;  ) —
) —  -гиперболическим аттрактором
-гиперболическим аттрактором  -базисным гиперболическим аттрактором.
-базисным гиперболическим аттрактором.
Определим для  , где
, где  — гиперболическое множество, следующие объекты:
— гиперболическое множество, следующие объекты:

где d — метрика, индуцированная римановой метрикой на М.  (соответственно
(соответственно  ) называется сильно устойчивым многообразием (соответственно локальным сильно устойчивым, сильно неустойчивым, локальным сильно неустойчивым многообразием) точки
) называется сильно устойчивым многообразием (соответственно локальным сильно устойчивым, сильно неустойчивым, локальным сильно неустойчивым многообразием) точки 
Теорема о локальном сильно устойчивом многообразии (Смейл, Хирш, Пэйлис, Пью, Шуб).
Пусть  — гиперболическое множество потока
— гиперболическое множество потока  принадлежащего классу
принадлежащего классу  Тогда для
Тогда для  справедливы равенства
справедливы равенства  Если e достаточно мало, то
Если e достаточно мало, то
(1°)  —
—  -вложенные диски, такие, что
-вложенные диски, такие, что

(2°)  при всех
при всех 
 при всех
при всех 
где X — константа, входящая в условия гиперболичности 
(3°)  непрерывно зависят от
непрерывно зависят от 
(4°) если  — гиперболический аттрактор, то множество
— гиперболический аттрактор, то множество  является окрестностью А.
является окрестностью А.
Отметим также, что 
Сформулированная теорема утверждает, что мы можем выбрать замкнутую окрестность N гиперболического аттрактора
 таким образом, что пересечения
таким образом, что пересечения  расслаивают N вдоль
расслаивают N вдоль  . Определим на N отношение эквивалентности таким образом, что
. Определим на N отношение эквивалентности таким образом, что  тогда и только тогда, когда
тогда и только тогда, когда  принадлежат одной и той же связной компоненте пересечения
принадлежат одной и той же связной компоненте пересечения  Обозначим через
Обозначим через  каноническое отображение на факторпространство. Тогда
каноническое отображение на факторпространство. Тогда  является, вообще говоря, разветвленным многообразием. Мы воздержимся здесь от точных определений и отсылаем любознательного читателя к [11].
является, вообще говоря, разветвленным многообразием. Мы воздержимся здесь от точных определений и отсылаем любознательного читателя к [11].

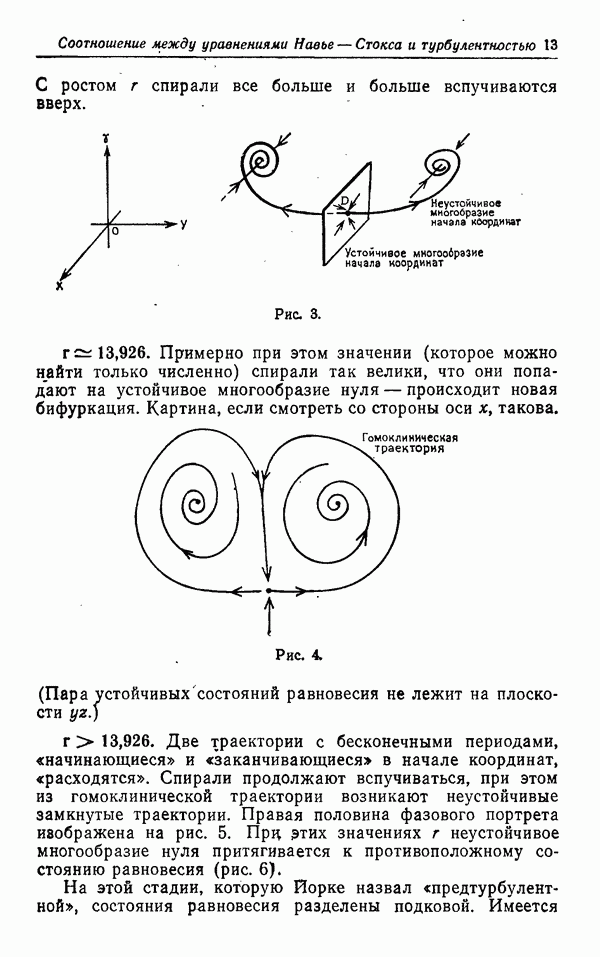
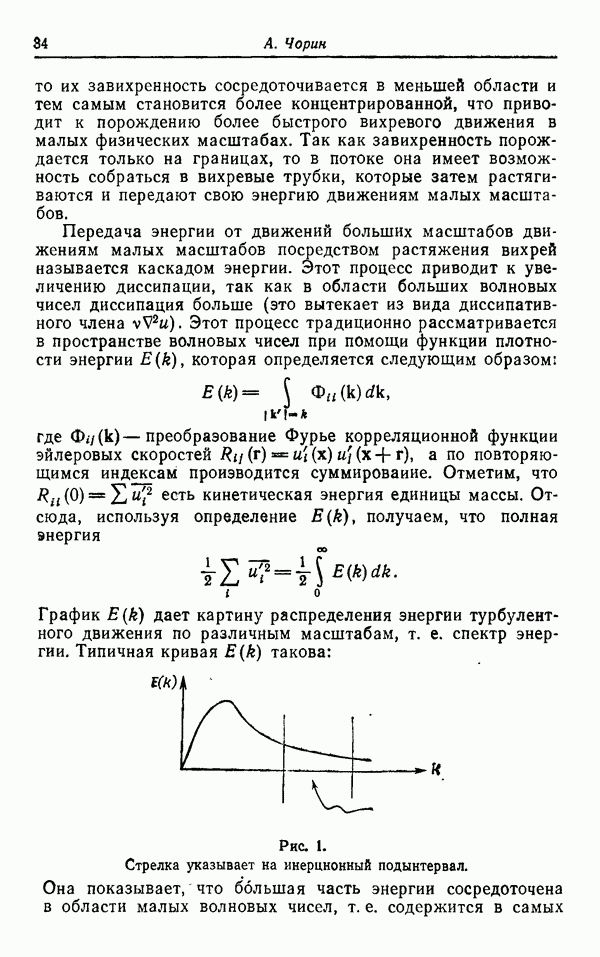
Рис. I.
Приведенный рисунок дает достаточно полное представление о том, что такое разветвленное многообразие.
Напомним, что мы рассматриваем поток на многообразии М. По определению  — инвариантное множество, а N нет. Действительно, N инвариантно только относительно полупотока
— инвариантное множество, а N нет. Действительно, N инвариантно только относительно полупотока  Определим теперь отображение
Определим теперь отображение  для
для  при помощи равенства
при помощи равенства  и заметим, что, согласно предыдущей теореме, это определение корректно. Таким образом, мы получили полупоток
и заметим, что, согласно предыдущей теореме, это определение корректно. Таким образом, мы получили полупоток  на разветвленном многообразии
на разветвленном многообразии  который имитирует поведение нашего начального потока в окрестности гиперболического аттрактора
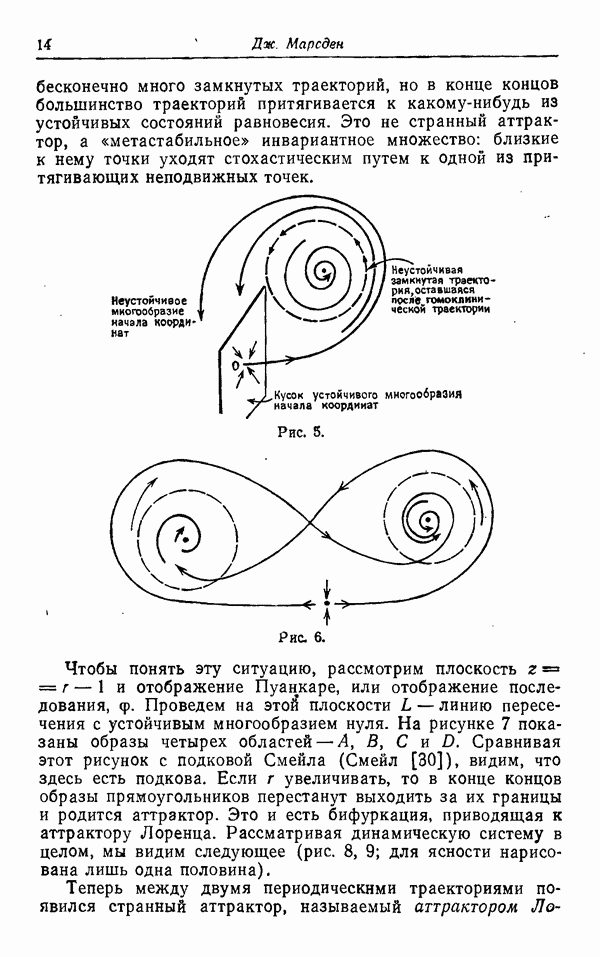
который имитирует поведение нашего начального потока в окрестности гиперболического аттрактора  . Обращение с аттракторами такого вида имеет несколько преимуществ. Во-первых, они естественно возникают и снижают размерность. Во-вторых, они реально существуют и, следовательно, дают хорошее интуитивное представление о поведении потока. После отображения проектирования аттрактор Лоренца представляет собой следующее разветвленное многообразие: такой рисунок был приведен уже в работе Лоренца [7]. Сравним этот рисунок с приведенным в работе Марсдена рис. 10 для того, чтобы
. Обращение с аттракторами такого вида имеет несколько преимуществ. Во-первых, они естественно возникают и снижают размерность. Во-вторых, они реально существуют и, следовательно, дают хорошее интуитивное представление о поведении потока. После отображения проектирования аттрактор Лоренца представляет собой следующее разветвленное многообразие: такой рисунок был приведен уже в работе Лоренца [7]. Сравним этот рисунок с приведенным в работе Марсдена рис. 10 для того, чтобы
представить себе, каким образом осуществляется проектирование. Локальные устойчивые многообразия расположены перпендикулярно этому разветвленному многообразию. Вычисление на ЭВМ, основанное на программе обнаружения аттрактора системы (L), дает такую же картину с точностью до гладкой деформации.

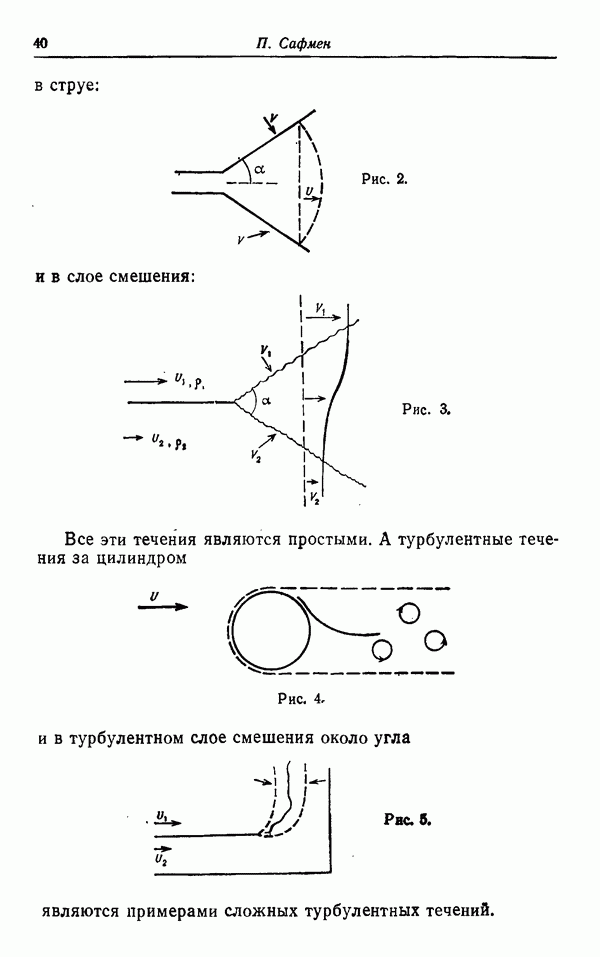
Рис. 2.
Таким образом, мы свели задачу изучения аттрактора к задаче исследования разветвленного многообразия с заданным на нем полупотоком. Теперь нам потребуется проделать другое каноническое построение. Пусть задана точка k на нашем разветвленном многообразии. Мы хотим найти множество всех ее возможных «предысторий» относительно полупотока  . Тем самым мы должны рассмотреть множество
. Тем самым мы должны рассмотреть множество

являющееся обратным пределом  системы
системы  , где
, где  — и при всех t и
— и при всех t и  при
при  . Тогда при 20 отображение
. Тогда при 20 отображение  естественным образом индуцирует отображение
естественным образом индуцирует отображение  так как
так как  Более точно,
Более точно,  Наиболее приятной особенностью этого отображения является его обратимость. Именно
Наиболее приятной особенностью этого отображения является его обратимость. Именно  и тем самым
и тем самым  становится потоком на
становится потоком на  !
!
Теорема. Пусть А — гиперболический аттрактор потока  на многообразии
на многообразии  для всех
для всех  замкнутая окрестность А, расслоенная вдоль А при помощи локальных сильно устойчивых многообразий,
замкнутая окрестность А, расслоенная вдоль А при помощи локальных сильно устойчивых многообразий,  полупоток на
полупоток на  индуцированный потоком
индуцированный потоком 

Рис. 3.

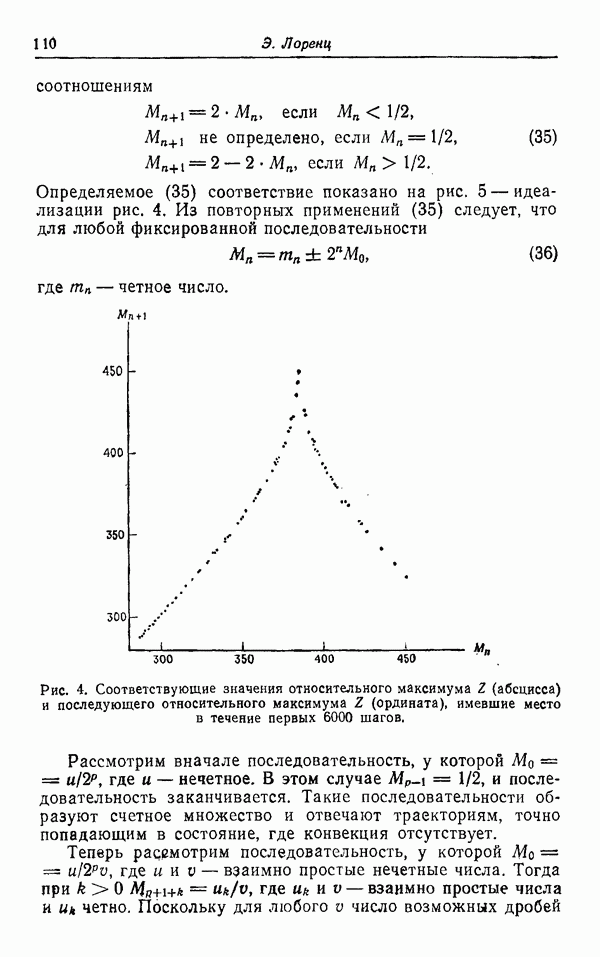
Рис. 4.
Тогда следующая диаграмма коммутативна: где вертикальные стрелки соответствуют гомеоморфизму  — естественное отображение на факторпространство
— естественное отображение на факторпространство 
Доказательство. Непрерывность и обратимость h получаются тривиально (согласно композиции). Из определения множества к вытекает, что любой его элемент имеет вид  при
при  . Следовательно,
. Следовательно,  или
или  при всех
при всех  . Положив в этом равенстве
. Положив в этом равенстве  получим
получим  при всех
при всех  . Отсюда вытекает, что любой элемент из
. Отсюда вытекает, что любой элемент из  имеет вид
имеет вид  и, следовательно, отображение h сюръективно. До сих пор мы не использовали того, что
и, следовательно, отображение h сюръективно. До сих пор мы не использовали того, что  при всех
при всех  , Из этого условия вытекает инъективность отображения h. Тем самым искомое утверждение доказано, так как мы могли бы встретиться со случаем, когда
, Из этого условия вытекает инъективность отображения h. Тем самым искомое утверждение доказано, так как мы могли бы встретиться со случаем, когда  содержит плотное подмножество
содержит плотное подмножество  Эта патологическая ситуация исключается с помощью наших предположений.
Эта патологическая ситуация исключается с помощью наших предположений.
Отсюда следует, что с точностью до канонического гомеоморфизма поведение потока на нашем гиперболическом аттракторе Л описывается обратным пределом  на котором действует поток
на котором действует поток 
В качестве общего принципа, полезного для уяснения понятий обратного предела и потока на разветвленном многообразии, мы сформулируем следующие утверждения:
— если точка имеет единственную «предысторию», то в ней не происходит «раздвоения»;
— если существует много «предысторий», то имеется и много «раздвоений» в процессе взятия 
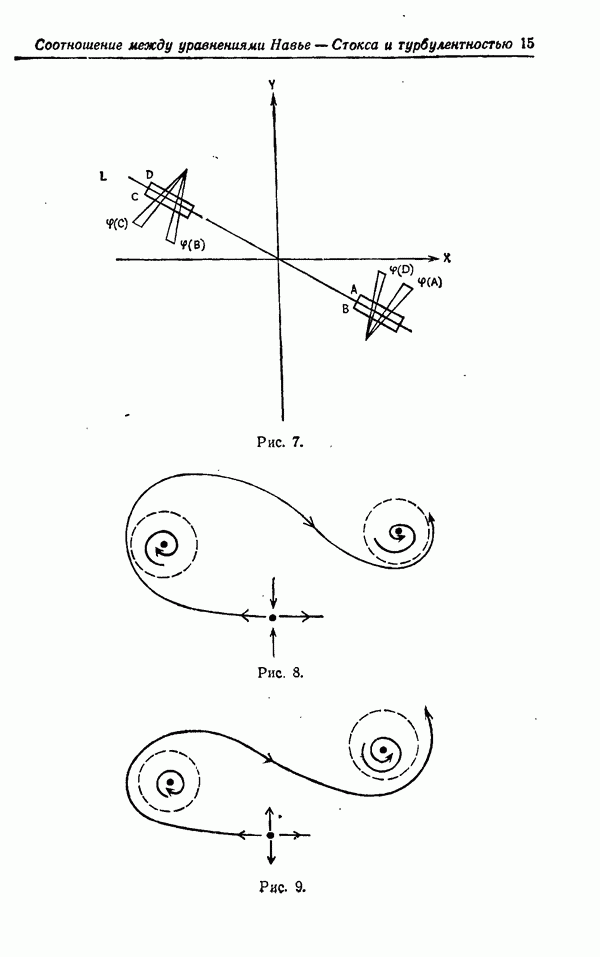
В дальнейшем мы собираемся применить эту технику к изучению аттрактора Лоренца. Мы уже видели, что как разветвленное многообразие аттрактор Лоренца представляет собой следующее образование:

Рис. 5.
Полезно отметить, что L канонически вложен в  . То же самое имеет место для
. То же самое имеет место для  , т. е., хотя наше построение
, т. е., хотя наше построение  по L абстрактно, получившееся в результате многообразие С может быть вложено в
по L абстрактно, получившееся в результате многообразие С может быть вложено в  и (по модулю неэквивалентности, существующей между этими конструкциями и начальными уравнениями, которые мы будем исследовать позднее) совпадает с аттрактором Лоренца с точностью до топологической (возможно, гладкой) сопряженности (см. доказанную выше теорему), предположения которой легко проверяются.
и (по модулю неэквивалентности, существующей между этими конструкциями и начальными уравнениями, которые мы будем исследовать позднее) совпадает с аттрактором Лоренца с точностью до топологической (возможно, гладкой) сопряженности (см. доказанную выше теорему), предположения которой легко проверяются.
Основной вклад в выяснение структуры аттрактора Лоренца был сделан Гукенхаймером, который догадался до основных геометрических свойств аттрактора Лоренца и доказал следующую теорему (см. [3]).
Теорема. (Гукенхаймер). Существует два топологически различных типа аттракторов Лоренца.
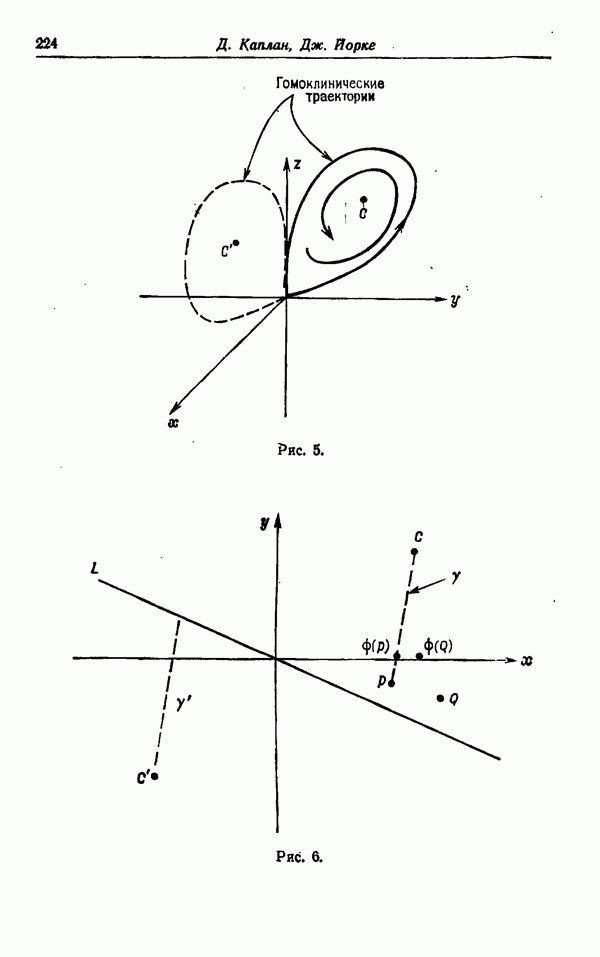
Набросок доказательства. Для того чтобы выяснить, как устроены эти аттракторы, мы должны проследить за поведением неустойчивого многообразия  точки 0. Это многообразие мы разобьем на две части: правое неустойчивое многообразие
точки 0. Это многообразие мы разобьем на две части: правое неустойчивое многообразие  и левое неустойчивое многообразие
и левое неустойчивое многообразие  Многообразие
Многообразие  пересекается с линией ветвления в ее самой правой точке,
пересекается с линией ветвления в ее самой правой точке,  в первый раз пересекается с ней в самой левой ее точке (см. приведенный выше рис. 5). Отличительным признаком
в первый раз пересекается с ней в самой левой ее точке (см. приведенный выше рис. 5). Отличительным признаком  является то, что оно содержит только две
является то, что оно содержит только две
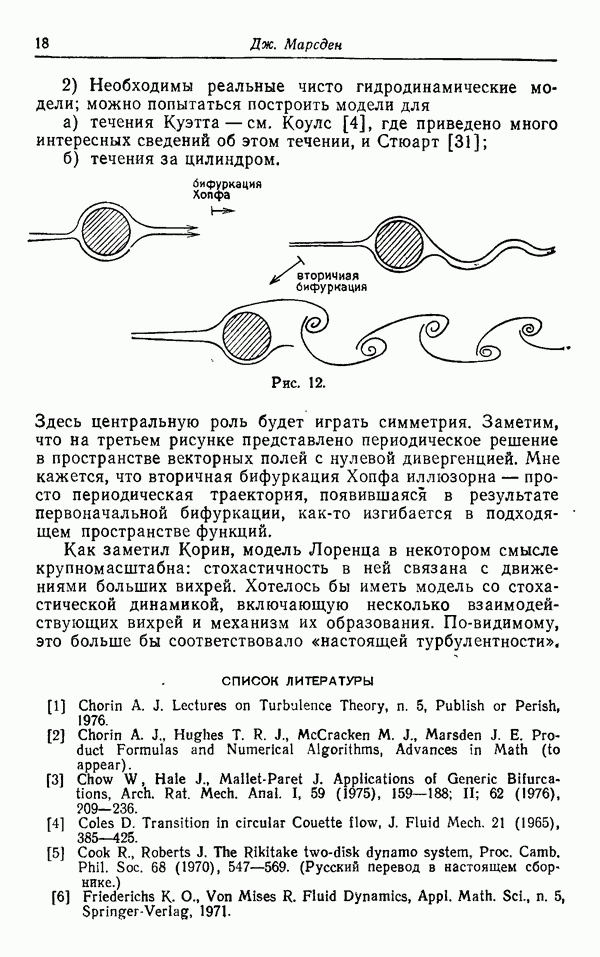
полутраектории с одной и той же предысторией, а именно, границу L. В этой ситуации имеются две возможности: либо  пересекается с
пересекается с  , либо этого не происходит. В первом случае
, либо этого не происходит. В первом случае  представляет собой топологически «цифру восемь», во втором случае — прямую.
представляет собой топологически «цифру восемь», во втором случае — прямую.

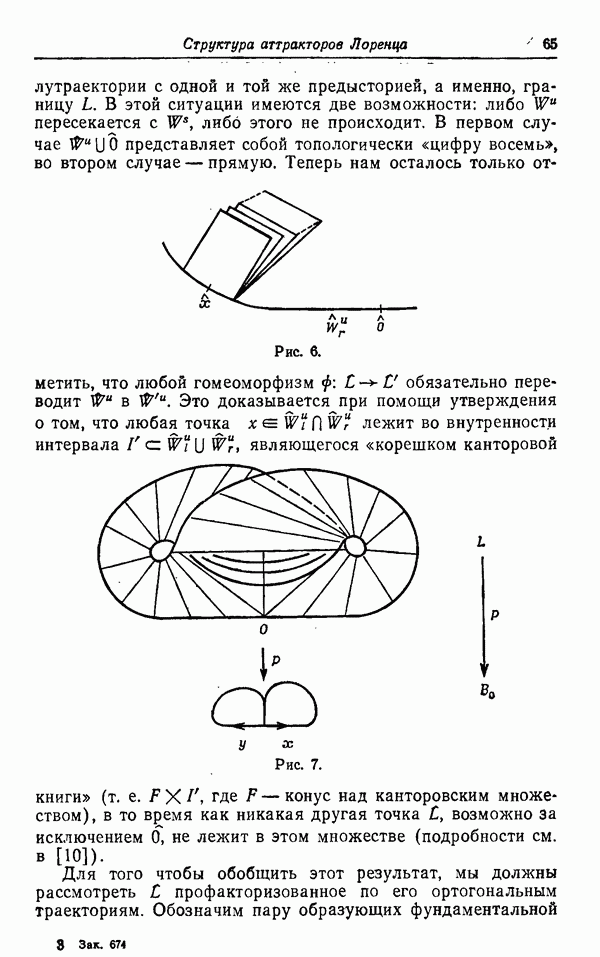
Рис. 6.
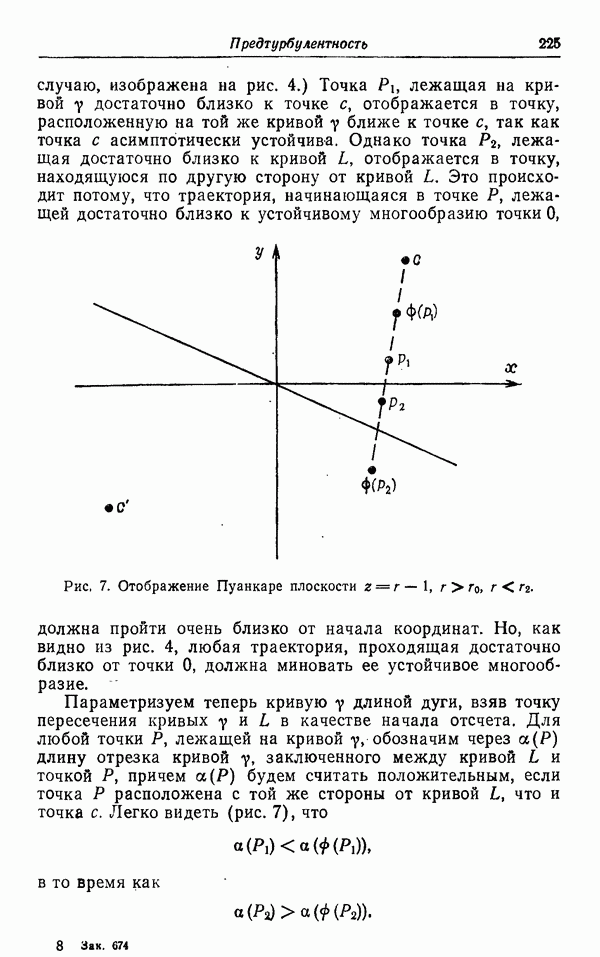
Теперь нам осталось только отметить, что любой гомеоморфизм  обязательно переводит
обязательно переводит  в
в  Это доказывается при помощи утверждения о том, что любая точка
Это доказывается при помощи утверждения о том, что любая точка  лежит во внутренности интервала
лежит во внутренности интервала  являющегося «корешком канторовой книги» (т. е.
являющегося «корешком канторовой книги» (т. е.  где
где  - конус над канторовским множеством), в то время как никакая другая точка
- конус над канторовским множеством), в то время как никакая другая точка  , возможно за исключением 0, не лежит в этом множестве (подробности см. в [10]).
, возможно за исключением 0, не лежит в этом множестве (подробности см. в [10]).

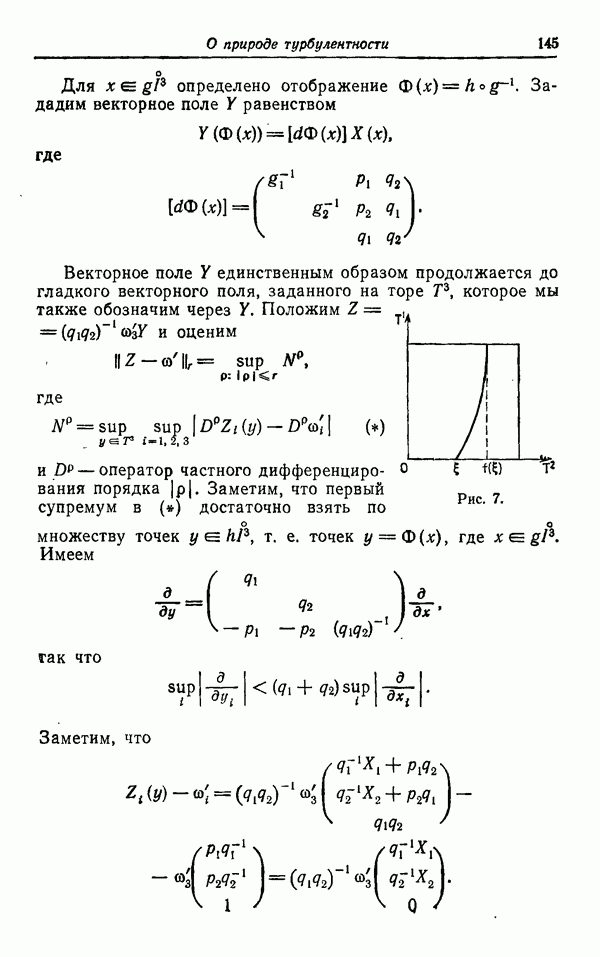
Рис. 7.
Для того чтобы обобщить этот результат, мы должны рассмотреть  профакторизованное по его ортогональным траекториям. Обозначим пару образующих фундаментальной
профакторизованное по его ортогональным траекториям. Обозначим пару образующих фундаментальной
группы многообразия  через
через  Определим нидинг k как пару
Определим нидинг k как пару  , где
, где  есть (возможно бесконечное) слово, составленное из х и у, и аналогично определяется
есть (возможно бесконечное) слово, составленное из х и у, и аналогично определяется  Отметим, что
Отметим, что  .
.
Теперь результат Гукенхаймера может быть переформулирован следующим образом: два топологически различных типа аттракторов Лоренца соответствуют случаям, когда  оба конечны или оба бесконечны.
оба конечны или оба бесконечны.
Пусть А — периодическая траектория, полупотока на L. Тогда  можно представить как положительное слово
можно представить как положительное слово  , определенное с точностью до циклической перестановки. Положим
, определенное с точностью до циклической перестановки. Положим

где суммирование производится по всем замкнутым орбитам А и для каждой фиксированной А вторая сумма берется по всем циклическим перестановкам Г слова до (А). Допускается ретракция орбиты А, но при этом получается периодическое слово, имеющее меньшее число перестановок.
Мы покажем далее, что определение  по существу навеяно
по существу навеяно  -функцией отображения Пуанкаре f линии ветвления.
-функцией отображения Пуанкаре f линии ветвления.
Напомним, что дзета-функция отображения f определяется как

где  есть число неподвижных точек отображения
есть число неподвижных точек отображения  Мы докажем теперь, что
Мы докажем теперь, что

Действительно, если  — неподвижная точка отображения имеющая минимальный период
— неподвижная точка отображения имеющая минимальный период  , то
, то  Обозначим через А замкнутую орбиту, содержащую точку
Обозначим через А замкнутую орбиту, содержащую точку  . Она определяет слово до (А) длины
. Она определяет слово до (А) длины  . Повторим его q раз. Тогда его вклад в сумму будет равен
. Повторим его q раз. Тогда его вклад в сумму будет равен  так как число возможных циклических перестановок равно
так как число возможных циклических перестановок равно  и тем самым все другие циклические перестановки дублируют уже имеющиеся. Поэтому, согласно нашей договоренности, они не принимаются
и тем самым все другие циклические перестановки дублируют уже имеющиеся. Поэтому, согласно нашей договоренности, они не принимаются
во внимание. Вычислив это выражение  получим
получим  Но, согласно определению замкнутая траектория
Но, согласно определению замкнутая траектория  рассматривается как множестве из
рассматривается как множестве из  точек, а именно
точек, а именно  точек, в которых
точек, в которых  пересекает линию ветвления. Взяв теперь в обоих случаях сумму по всем замкнутым орбитам
пересекает линию ветвления. Взяв теперь в обоих случаях сумму по всем замкнутым орбитам  и просуммировав затем по
и просуммировав затем по  получившиеся суммы, получаем требуемый результат.
получившиеся суммы, получаем требуемый результат.
Мы покажем теперь, как может быть вычислена величина  . Рассмотрим для этого
. Рассмотрим для этого  , т. е. F есть ортогональная траектория, проходящая через точку 0 и образованная двумя прямолинейными отрезками. Обозначим через
, т. е. F есть ортогональная траектория, проходящая через точку 0 и образованная двумя прямолинейными отрезками. Обозначим через  точку пересечения
точку пересечения  . Заметим, что
. Заметим, что  . Определим теперь символическое пространство 2 следующим образом
. Определим теперь символическое пространство 2 следующим образом 

(2)  тогда и только тогда, когда U и
тогда и только тогда, когда U и  лежат по одну сторону от точки 0,
лежат по одну сторону от точки 0,

Введем в 2 лексикографическое упорядочение и определим (вообще говоря) бесконечную матрицу

где  означает, что вместо нее может быть подставлено любое допустимое число.
означает, что вместо нее может быть подставлено любое допустимое число.
Прямое формальное вычисление дает

Следующее предложение показывает, сколь тесно нидинг связан с функцией 
Теорема. Если пары  определяют два аттрактора Лоренца, то
определяют два аттрактора Лоренца, то  тогда и только тогда, когда
тогда и только тогда, когда 
Основным результатом, связывающим обратный предел С с нидингом, является следующая
Теорема. С гомеоморфен С тогда и только тогда, когда 
В силу предыдущей теоремы это утверждение эквивалентно тому, что  Мы хотим подчеркнуть, что в приведенной теореме гомеоморфизм может быть произвольным.
Мы хотим подчеркнуть, что в приведенной теореме гомеоморфизм может быть произвольным.
При этом не предполагается, что он коммутирует с действием потоков. Мы приведем здесь только основные этапы доказательства и отсылаем любознательного читателя к работе [10].
— Первый этап. Любой гомеоморфизм гомеоморфно отображает  на Изменим h так, чтобы
на Изменим h так, чтобы  . Используя теорему о симплициальной аппроксимации и переходя к фундаментальной группе, получаем следующую диаграмму:
. Используя теорему о симплициальной аппроксимации и переходя к фундаментальной группе, получаем следующую диаграмму:

где  проекция на нулевую координату в обратном пределе. Диаграмма определяет отображение
проекция на нулевую координату в обратном пределе. Диаграмма определяет отображение 
— Второй этап. Покажем, что J есть либо  либо
либо  Это наиболее утомительная часть доказательства, которая сводится к рассмотрению пяти подслучаев. Вначале доказывается, что
Это наиболее утомительная часть доказательства, которая сводится к рассмотрению пяти подслучаев. Вначале доказывается, что  либо строго положительно, либо строго отрицательно, как слово, образованное из х и у. Отображение
либо строго положительно, либо строго отрицательно, как слово, образованное из х и у. Отображение  обязано быть изоморфизмом. Поэтому послесимметризации
обязано быть изоморфизмом. Поэтому послесимметризации  задается матрицей
задается матрицей  где
где  . Отсюда с помощью тщательного анализа, использующего структуру Р как клеточного комплекса, можно вывести наше утверждение.
. Отсюда с помощью тщательного анализа, использующего структуру Р как клеточного комплекса, можно вывести наше утверждение.
— Третий этап. Используя соотношение  , где
, где  — замкнутая траектория, и второй этап, получаем, что
— замкнутая траектория, и второй этап, получаем, что  или
или 
— Четвертый этап. Из предыдущей теоремы и третьего этапа имеем: либо  либо
либо  .
.
Клеточная структура P позволяет доказать следующее предложение.
Теорема. В любом аттракторе Лоренца L периодические траектории всюду плотны.
Как уже отмечалось ранее, каждое из равенств  и гомеоморфность С и
и гомеоморфность С и  эквивалентны. Поэтому заманчиво сформулировать гипотезу, что
эквивалентны. Поэтому заманчиво сформулировать гипотезу, что  тогда и только тогда, когда
тогда и только тогда, когда  где индекс а обозначает, что функция
где индекс а обозначает, что функция  симметризована. Следующий контрпример показывает, что эта гипотеза неверна.
симметризована. Следующий контрпример показывает, что эта гипотеза неверна.
Положим  где
где  как и раньше, образующие фундаментальной группы многообразия В. Ясно, что
как и раньше, образующие фундаментальной группы многообразия В. Ясно, что  Тем не менее мы покажем, что
Тем не менее мы покажем, что 
Докажем прежде всего, что k и  — действительно нидинги, т. е. выполнены следующие две аксиомы:
— действительно нидинги, т. е. выполнены следующие две аксиомы:

2)  для любого конечного слова w из
для любого конечного слова w из  или
или 
Упорядочение, используемое в этих двух аксиомах, может быть пояснено следующим образом:  — минимальный символ, у — максимальный, а пустой символ
— минимальный символ, у — максимальный, а пустой символ  является промежуточным. Например,
является промежуточным. Например,  Отметим также, что нидинги, определенные раньше для аттрактора Лоренца, всегда удовлетворяют этим двум аксиомам. Легко видеть, что k и
Отметим также, что нидинги, определенные раньше для аттрактора Лоренца, всегда удовлетворяют этим двум аксиомам. Легко видеть, что k и  оба удовлетворяют аксиомам 1 и 2.
оба удовлетворяют аксиомам 1 и 2.
Это упорядочение позволяет нам построить траектории, отвечающие k и  . Для этого упорядочим слева направо линию ветвления F, будем считать, что траектория, начинающаяся из 1, соответствует страницам аттрактора Лоренца, и расположим все символы, соответствующие
. Для этого упорядочим слева направо линию ветвления F, будем считать, что траектория, начинающаяся из 1, соответствует страницам аттрактора Лоренца, и расположим все символы, соответствующие  слева, а соответствующие у — справа. Например, для k на Р получаются следующие числа:
слева, а соответствующие у — справа. Например, для k на Р получаются следующие числа:

Матрица А в формуле для  имеет при этом размерность
имеет при этом размерность  .
.
Заметим теперь, что если w конечное слово, то до дает вклад в  тогда и только тогда, когда
тогда и только тогда, когда

где t отвечает «конечным последовательностям».
В соответствии с упорядочением напишем теперь  следующим образом:
следующим образом:

Под А мы подразумеваем множество  конечное, удовлетворяющее
конечное, удовлетворяющее  Промежуток, обозначенный «same» состоит из слов до, которые встречаются как в
Промежуток, обозначенный «same» состоит из слов до, которые встречаются как в  , так и в
, так и в  . Множество А определяется аналогично А. Таким образом, для того чтобы показать, что
. Множество А определяется аналогично А. Таким образом, для того чтобы показать, что  нам нужно установить взаимно-однозначное соответствие между А и А, так, чтобы соответствующие друг другу слова совпадали после симметризации.
нам нужно установить взаимно-однозначное соответствие между А и А, так, чтобы соответствующие друг другу слова совпадали после симметризации.
Далее мы поступаем следующим образом: любое слово  должно начинаться с а и в силу
должно начинаться с а и в силу  включать в себя все конечные последовательности
включать в себя все конечные последовательности  любое слово
любое слово  должно кончаться у, т. е. иметь вид
должно кончаться у, т. е. иметь вид  Аналогичное
Аналогичное  имеет вид
имеет вид  . Поэтому первыми кандидатами являются слова
. Поэтому первыми кандидатами являются слова  и, в самом деле, они являются единственными словами длины 8 в
и, в самом деле, они являются единственными словами длины 8 в  . Итак,
. Итак, 
Пусть теперь  — слова длины i, представляющие собой соответственно концы слов
— слова длины i, представляющие собой соответственно концы слов  . Имеем
. Имеем  Наконец, можно сделать так, что
Наконец, можно сделать так, что  при
при  . Таким образом, (симметризованные) слова из
. Таким образом, (симметризованные) слова из  длины 15 совпадают. Используя теперь выражение функции
длины 15 совпадают. Используя теперь выражение функции

для нашего случая (матрицы  для
для  имеют размерность
имеют размерность  ), получаем, что после симметризации
), получаем, что после симметризации  при
при  . Следовательно, это равенство имеет место
. Следовательно, это равенство имеет место  всех
всех  и поэтому
и поэтому 
Для полноты мы приводим последние 5 выражений для 
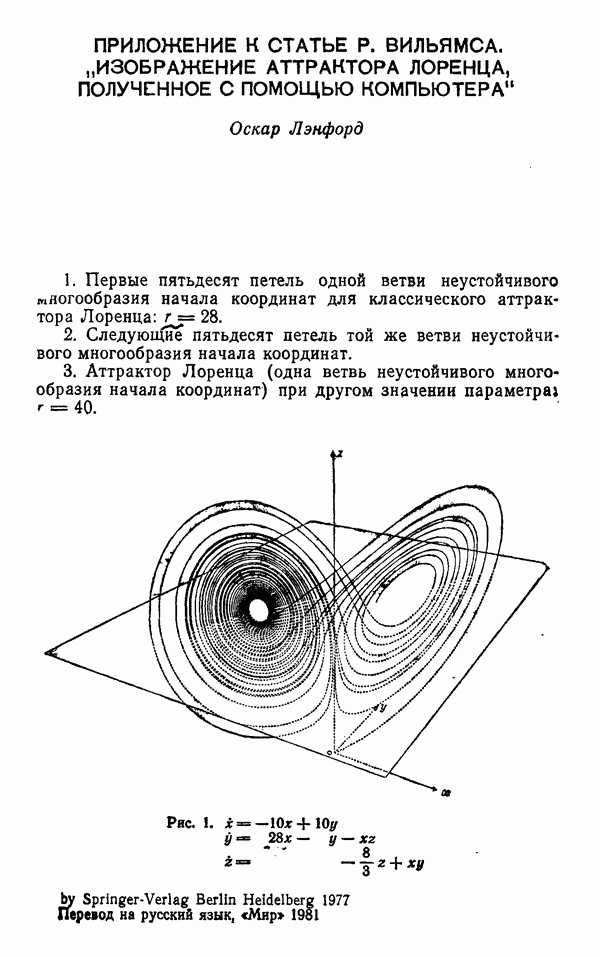
На этом мы заканчиваем качественное исследование аттрактора Лоренца и в заключение сделаем несколько замечаний относительно соответствия между уравнениями Лоренца (L) и нашими предыдущими рассмотрениями. Как уже было отмечено в работе Марсдена (см. стр. 7—20 настоящего сборника), большая часть работ, проделанных с целью обнаружения аттрактора, была выполнена на ЭВМ. Поэтому имеется много недоказанных утверждений, наиболее важное из которых следующее: строго доказать, что аттрактор, определяемый уравнениями (L), имеет вид, приведенный на рис. 10 работы Марсдена  ) (т. е. после стягивания вдоль сильно устойчивого многообразия совпадает с нашим разветвленным многообразием
) (т. е. после стягивания вдоль сильно устойчивого многообразия совпадает с нашим разветвленным многообразием  ).
).
Второе важное утверждение, нуждающееся в доказательстве, состоит в следующем: показать, что существует поле строго устойчивых направлений, в некотором смысле «нормальное» к С. Другими словами, доказать существование слоения на строго устойчивые многообразия.
Наконец, мы сформулируем две гипотезы. Как отмечалось ранее, периодические траектории плотны в L. Я думаю, что они
а) зацеплены друг с другом и
б) заузлены.
ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Несколько лет назад Джим Йорк произвел некоторые вычисления с уравнениями Лоренца и привлек к ним интерес других математиков. Он прочел по этому вопросу несколько лекций, в том числе одну здесь, в Беркли. Рюэль, Ланфорд и Гукенхаймер, заинтересовавшись, попытались исследовать эти уравнения. К сожалению, за исключением недавнего препринта Рюэля [8], работа Гукенхаймера [3], насколько мне известно, является единственной, написанной об аттракторе Лоренца этими четырьмя людьми.
СПИСОК ЛИТЕРАТУРЫ
1. Bowen R. Equilibrium states and the Ergodic Theory of Anosov Dif-feomorphisms, Springer Lecture Notes in Math., 470.
2. Bowen R., Ruelle D. The Ergodic Theory of Axiom A Flows, Inventiones Math., v. 29, 181—202 (1975).
3. Guckenheimer J., A Strange, Strange Attractor, in Marsden, McCracken, The Hopf Bifurcation and Applications, Applied Math., Sciences, 19, Springer Verlag, 1976.
4. Hirsch M„ Pugh C. The Stable Manifold Theorem, Global Analysis, Proc. Symposia in Pure Math., v. 14, American Math. Soc., 1970.
5. Hirsch М., Pugh C., Shub M. Invariant Manifolds (to appear).
6. Hirsch М., Palis J., Pugh C., Shub М., Neighborhoods of Hyperbolic Sets, Inventiones Math., v. 9, 121—134 (1970).
7. Lorenz E. N. Deterministic Nonperiodic flow, J. of Atmospheric Sci., v. 20, 130—141 (1963).
8. Ruelle D. The Lorenz Attractor and The Problem of Turbulence, Proc. conf. «Quantum dynamics models and mathematics» in Bielfeld, 1975.
9. Smale S. Differentiable Dynamical Systems, Bull. AMS, v. 13, 767—817 (1964).
10. Williams R. The Structure of Lorenz Attractors, preprint Northwestern Univ., 1976.
11. Williams R. Expanding Attractors, Publications Math§matiques IHES, no. 43, 169—203 (1974).
12. Williams R. One Dimensional Non-Wandering Sets, Topology, v. 6, 473— 487 (1967).
13.Dankner A. On Smale’s Axiom A dynamical systems, Ann. Math., 1978, 107, N 3, 517—553.
14. Лесин Я. Б. Семейство инвариантных многообразий, отвечающее ненулевым характеристическим показателям, Изв. АН СССР, серия ма-тем, 40-6 (1976), 1332—1379.
15. Рохлин В. А. Точные эндоморфизмы пространства Лебега, Изв. АН СССР, сер. матем., 25, № 4 (1961), 499—530.
16. Афраймович В. С., Быков В. В., Шильников Л. П. О возникновении и структуре аттрактора Лоренца, ДАН СССР, т. 234, № 2, (1977), стр. 336—339.
17.Milnor J., Thurston W. P. Neding-invariant, preprint, Prinstone.
18. Симонов Л. А. Исследование бифуркаций в некоторых динамических системах методами символической динамики, ДАН СССР, т. 240, № 6.1978, 1297—1300.
19. Sinai J. G., Vul Е. В. Discovery of close orbits of dynamical systems with the helps of computers, J. of Stat. Phys. 1980 (in press).
20. Sinai J. G., Vul E. V. Verification of hyperbolisity condition for the Lorenz model, Physics reports, 1980 (in press).
21. Бунимович Л. А., Синай Я. Г. Стохастичность аттрактора Лоренца. В сб. Нелинейные волны. — М.: Наука, 1979.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- ПОПЫТКИ УСТАНОВИТЬ СООТНОШЕНИЕ МЕЖДУ УРАВНЕНИЯМИ НАВЬЕ-СТОКСА И ТУРБУЛЕНТНОСТЬЮ
- ПРИЛОЖЕНИЕ К СТАТЬЕ МАРСДЕНА БИФУРКАЦИИ, ПОЛУПОТОКИ И УРАВНЕНИЯ НАВЬЕ—СТОКСА
- ТЕОРИИ ТУРБУЛЕНТНОСТИ
- ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ РАСЧЕТА ТУРБУЛЕНТНЫХ СДВИГОВЫХ ТЕЧЕНИЙ
- ФРАКТАЛЫ И ТУРБУЛЕНТНОСТЬ: АТТРАКТОРЫ И РАЗБРОС
- СТРУКТУРА АТТРАКТОРОВ ЛОРЕНЦА
- ПРИЛОЖЕНИЕ К СТАТЬЕ Р. ВИЛЬЯМСА. «ИЗОБРАЖЕНИЕ АТТРАКТОРА ЛОРЕНЦА, ПОЛУЧЕННОЕ С ПОМОЩЬЮ КОМПЬЮТЕРА»
- ДВА ПОДХОДА К МОДЕЛИРОВАНИЮ ДВУМЕРНОЙ ТУРБУЛЕНТНОСТИ
- ДЕТЕРМИНИРОВАННОЕ НЕПЕРИОДИЧЕСКОЕ ТЕЧЕНИЕ
- О ПРИРОДЕ ТУРБУЛЕНТНОСТИ
- ДВУМЕРНОЕ ОТОБРАЖЕНИЕ СО СТРАННЫМ АТТРАКТОРОМ
- СИСТЕМА ДВУХДИСКОВОГО ДИНАМО РИКИТАКЕ
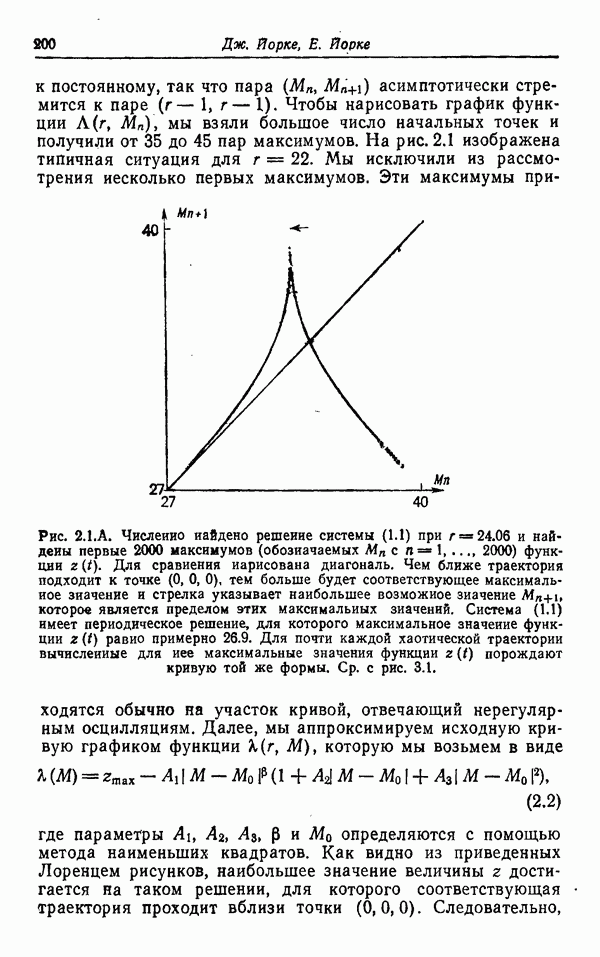
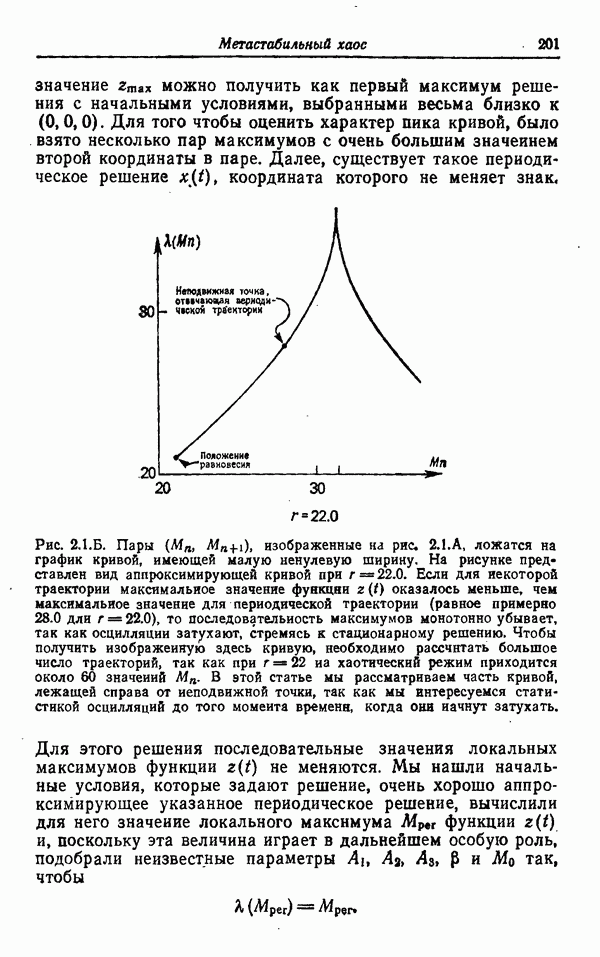
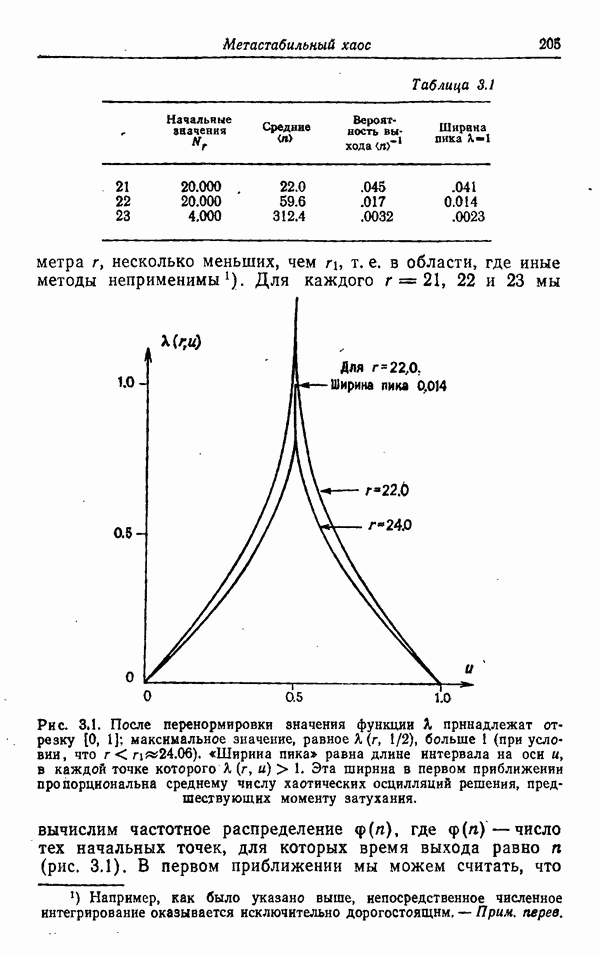
- МЕТАСТАБИЛЬНЫЙ ХАОС: ПЕРЕХОД К УСТОЙЧИВОМУ ХАОТИЧЕСКОМУ ПОВЕДЕНИЮ В МОДЕЛИ ЛОРЕНЦА
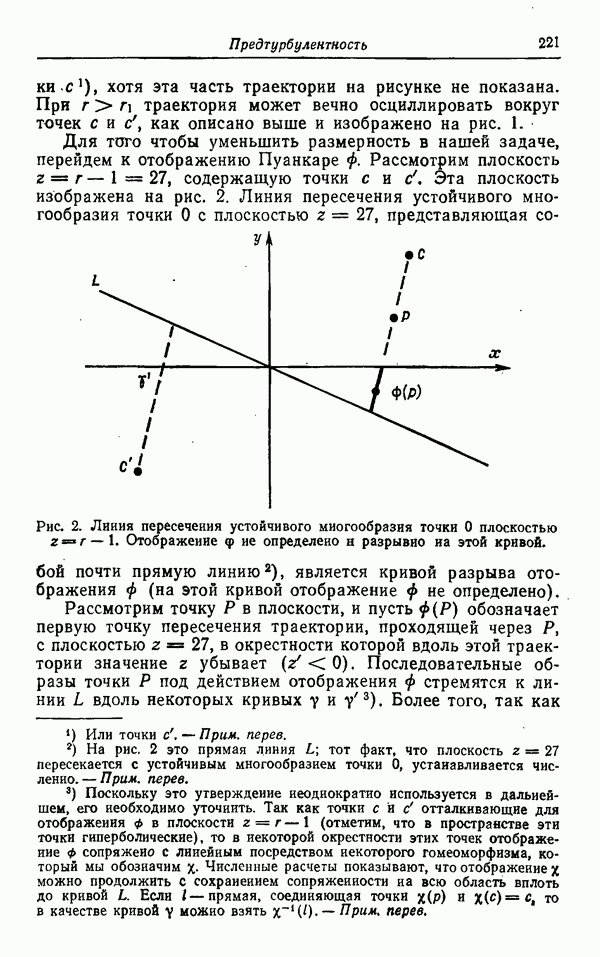
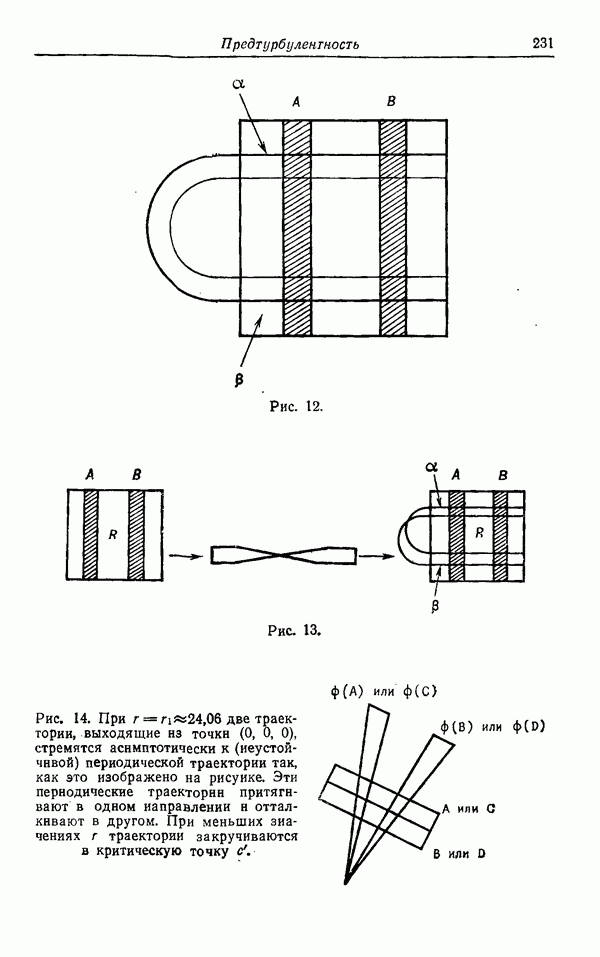
- ПРЕДТУРБУЛЕНТНОСТЬ: РЕЖИМ, НАБЛЮДАЕМЫЙ В ТЕЧЕНИИ ЖИДКОСТИ, ОПИСЫВАЕМОЙ МОДЕЛЬЮ ЛОРЕНЦА
- ТОПОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ АТТРАКТОРОВ ЛОРЕНЦА