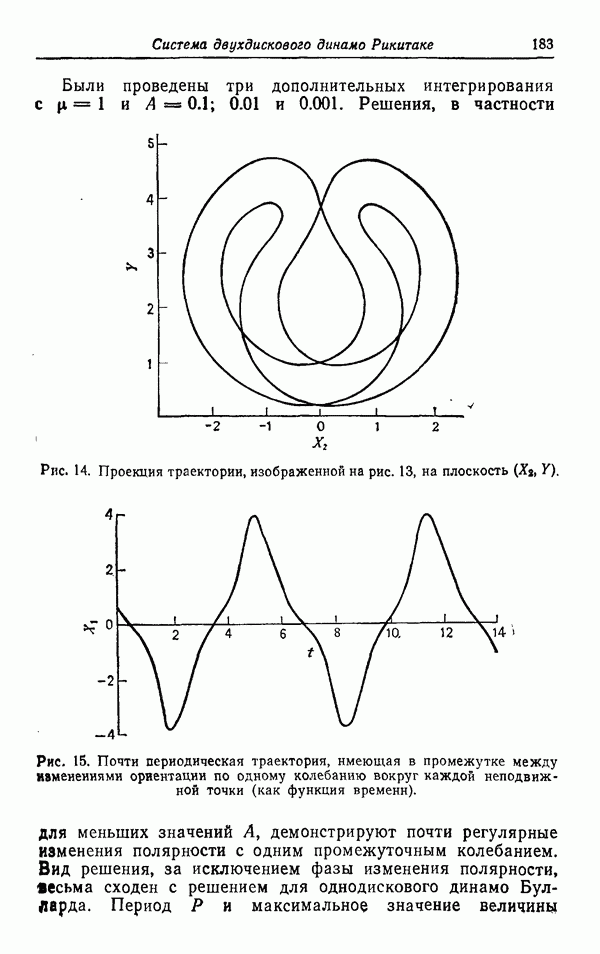
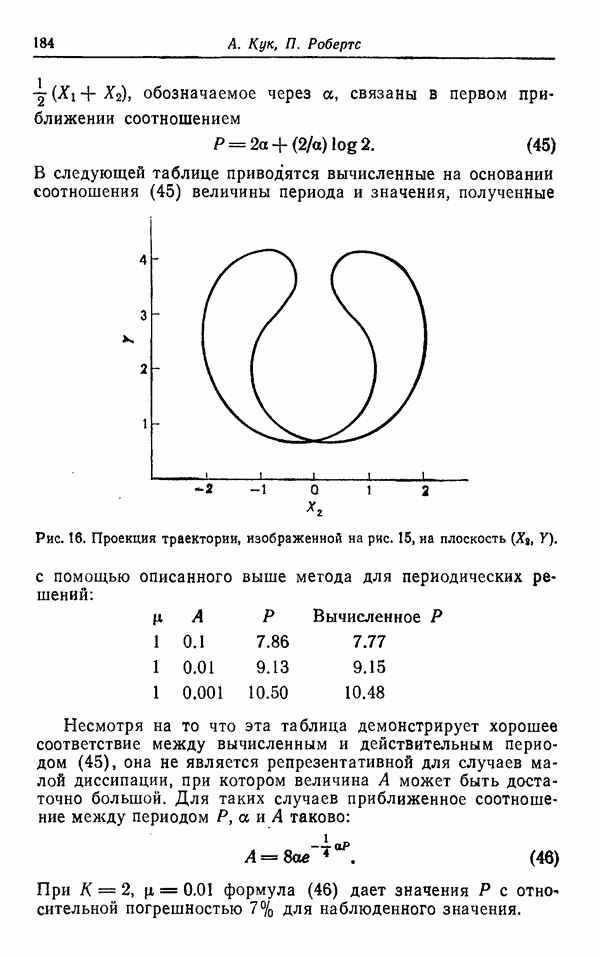
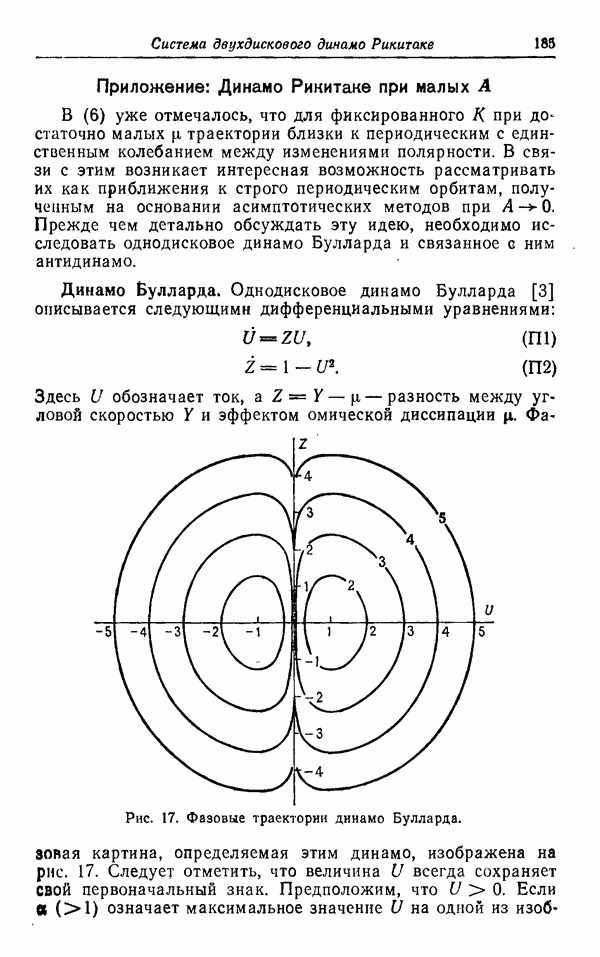
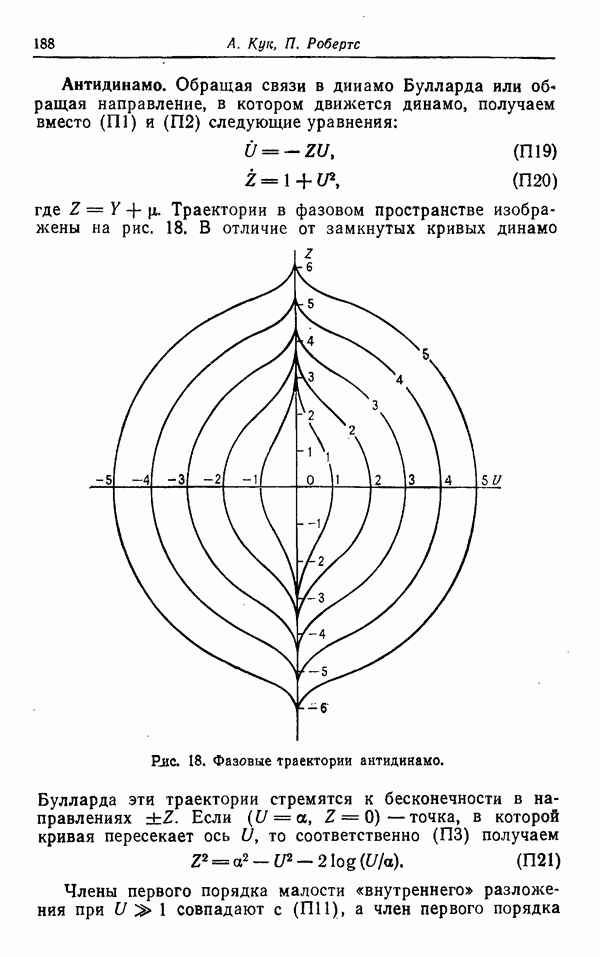
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
О ПРИРОДЕ ТУРБУЛЕНТНОСТИ
Д. Рюэль и Ф. Такенс
Аннотация. Предлагается механизм, описывающий процесс возникновения турбулентности и связанных с ней явлений в диссипативных системах.
§ 1. ВВЕДЕНИЕ
Если физическая система, состоящая из вязкой жидкости (и твердых тел), не подвергается какому-либо внешнему воздействию, то она стремится к состоянию покоя (равновесия). Подчиним теперь систему устойчивому воздействию (накачке, нагреву и т. п.), характеризуемому параметром  При
При  жидкость покоится. При
жидкость покоится. При  сначала возникает установившееся течение, характеризуемое тем, что описывающие жидкость физические параметры (скорость, температура и т. д.) не меняются со временем, хотя сама жидкость не находится более в состоянии покоя. Такое состояние сохраняется при малых значениях
сначала возникает установившееся течение, характеризуемое тем, что описывающие жидкость физические параметры (скорость, температура и т. д.) не меняются со временем, хотя сама жидкость не находится более в состоянии покоя. Такое состояние сохраняется при малых значениях  При возрастании
При возрастании  могут возникать различные новые явления: (а) течение жидкости может остаться установившимся, но изменяются его свойства симметрии; (б) течение жидкости может стать периодическим во времени; (в) при достаточно больших
могут возникать различные новые явления: (а) течение жидкости может остаться установившимся, но изменяются его свойства симметрии; (б) течение жидкости может стать периодическим во времени; (в) при достаточно больших  течение жидкости становится очень сложным, нерегулярными хаотичным, т. е. иозникает турбулентность.
течение жидкости становится очень сложным, нерегулярными хаотичным, т. е. иозникает турбулентность.
Турбулентное течение жидкости как физическое явление получило различные математические интерпретации. Согласно представлениям Лере [9], турбулентность связана с нарушением уравнений (Навье — Стокса), используемых для описания системы. Хотя такое нарушение возможно и происходит, мы полагаем, что оно не обязательно связано с турбулентностью. Ландау и Лифшиц [8] предположили, что физический параметр  описывающий жидкость в турбулентном
описывающий жидкость в турбулентном
течении, является квазипериодической функцией времени:

где функция f имеет период 1 по каждому из своих аргументов в отдельности, а частоты он,  рационально независимы. При этом число k становится большим для достаточно больших значений
рационально независимы. При этом число k становится большим для достаточно больших значений  и это ведет к сложному и нерегулярному поведению, характеризующему турбулентное течение. Мы увидим, однако, что некоторые диссипативные системы, похожие на вязкую жидкость, вообще говоря, не имеют квазипериодических движений. Поэтому идея Ландау и Лифшица должна быть модифицирована.
и это ведет к сложному и нерегулярному поведению, характеризующему турбулентное течение. Мы увидим, однако, что некоторые диссипативные системы, похожие на вязкую жидкость, вообще говоря, не имеют квазипериодических движений. Поэтому идея Ландау и Лифшица должна быть модифицирована.
Рассмотрим для определенности вязкую несжимаемую жидкость, занимающую область D в  Если тепловыми эффектами можно пренебречь, то течение жидкости описывается при помощи вектора скорости в каждой точке области D. Пусть Н — это бесконечномерное векторное пространство. Эволюция во времени поля скоростей задается уравнениями Навье — Стокса
Если тепловыми эффектами можно пренебречь, то течение жидкости описывается при помощи вектора скорости в каждой точке области D. Пусть Н — это бесконечномерное векторное пространство. Эволюция во времени поля скоростей задается уравнениями Навье — Стокса

где  — векторное поле на Н. В этой статье нам не понадобится более точных представлений о пространстве Н и векторном поле
— векторное поле на Н. В этой статье нам не понадобится более точных представлений о пространстве Н и векторном поле 
Ниже мы исследуем поведение решений уравнения (1), сделав предположения весьма общего характера относительно векторного поля  При этом окажется, что течение жидкости, как ожидалось, становится хаотическим, когда параметр
При этом окажется, что течение жидкости, как ожидалось, становится хаотическим, когда параметр  возрастает. Это обстоятельство служит оправданием нашей модели турбулентности и открывает некоторую возможность для проникновения в механизм ее возникновения. Чтобы изучить уравнение (1), мы заменим пространство Н конечномерным многообразием и воспользуемся качественной теорией дифференциальных уравнений.
возрастает. Это обстоятельство служит оправданием нашей модели турбулентности и открывает некоторую возможность для проникновения в механизм ее возникновения. Чтобы изучить уравнение (1), мы заменим пространство Н конечномерным многообразием и воспользуемся качественной теорией дифференциальных уравнений.
При  каждое решение
каждое решение  уравнения (1) стремится К решению
уравнения (1) стремится К решению  когда время стремится к
когда время стремится к 
Рассмотрим теперь какой-либо способ изменения векторного поля  т. е. переход от векторного поля
т. е. переход от векторного поля  к некоторому векторному полю с
к некоторому векторному полю с  Если этот переход осуществляется произвольным образом, то об изменении в характере поведения решений уравнения (1) мало что известно. Естественно поэтому ограничиться рассмотрением лишь типичных переходов, т. е. пренебречь темн из них, которые в некотором смысле можно считать исключительными. Эта точка зрения могла бы привести к серьезным ошибкам, если из-за некоторых законов природы, действием которых мы пренебрегаем, векторное поле окажется в специальном классе векторных полей с исключительными свойствами. Однако нам кажется, что те переходы от векторного поля
Если этот переход осуществляется произвольным образом, то об изменении в характере поведения решений уравнения (1) мало что известно. Естественно поэтому ограничиться рассмотрением лишь типичных переходов, т. е. пренебречь темн из них, которые в некотором смысле можно считать исключительными. Эта точка зрения могла бы привести к серьезным ошибкам, если из-за некоторых законов природы, действием которых мы пренебрегаем, векторное поле окажется в специальном классе векторных полей с исключительными свойствами. Однако нам кажется, что те переходы от векторного поля  к векторному полю
к векторному полю  которые описывают изменения в поведении трехмерной вязкой жидкости с ростом
которые описывают изменения в поведении трехмерной вязкой жидкости с ростом  должны быть типичными. Эти переходы мы и обсудим ниже. Наше рассмотрение применимо в действительности к весьма общим диссипативным системам.
должны быть типичными. Эти переходы мы и обсудим ниже. Наше рассмотрение применимо в действительности к весьма общим диссипативным системам.
Настоящая статья состоит из двух глав. Глава I по своему характеру более физическая и соответственно технически менее сложная. В § 2 мы приведем некоторые результаты о дифференциальных уравнениях; в § 3—4 применим эти результаты к изучению решений уравнения (1). Глава II содержит доказательства некоторых теорем, использованных в гл. I. В § 5 используется теория центральных многообразий для перехода от пространства Н к конечномерному многообразию. В § 6—8 изложена теория бифуркаций Хопфа как для векторных полей, так и для диффеоморфизмов. В § 9 указан пример «турбулентного» аттрактора.
Благодарности. Авторы считают своим приятным долгом выразить благодарность Р. Тому за ценные обсуждения, в частности за ознакомление одного из нас  с теорией бифуркаций Хопфа. К написанию настоящей статьи нас вдохновила в известном смысле готовящаяся к выходу в свет книга Тома [12].
с теорией бифуркаций Хопфа. К написанию настоящей статьи нас вдохновила в известном смысле готовящаяся к выходу в свет книга Тома [12].
§ 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Пусть  — открытый шар в конечномерном евклидовом пространстве Н. Пусть X — векторное поле с непрерывными производными до порядка
— открытый шар в конечномерном евклидовом пространстве Н. Пусть X — векторное поле с непрерывными производными до порядка  на
на  число
число  фиксировано. Такие векторные поля образуют банахово пространство
фиксировано. Такие векторные поля образуют банахово пространство  с нормой
с нормой

где

 Множество Е из
Множество Е из  называется массивным, если оно содержит счетное пересечение открытых множеств, которые плотны в
называется массивным, если оно содержит счетное пересечение открытых множеств, которые плотны в  . В силу теоремы Бэра массивное множество также плотно в
. В силу теоремы Бэра массивное множество также плотно в  Поэтому массивное множество Е может рассматриваться в некотором смысле как «большое» подмножество множества
Поэтому массивное множество Е может рассматриваться в некотором смысле как «большое» подмножество множества  . Свойство векторного поля
. Свойство векторного поля  которое выполняется для некоторого массивного множества в называется типичным.
которое выполняется для некоторого массивного множества в называется типичным.
Интегральная кривая  проходящая через точку
проходящая через точку  удовлетворяет условиям
удовлетворяет условиям  она определена по крайней мере для достаточно малых
она определена по крайней мере для достаточно малых  Зависимость
Зависимость  от
от  выражается при помощи записи
выражается при помощи записи  называют интегралом векторного поля X;
называют интегралом векторного поля X;  — это интеграл за единицу времени. Если
— это интеграл за единицу времени. Если  то решение
то решение  определяет неподвижную точку интеграла векторного поля X. Если
определяет неподвижную точку интеграла векторного поля X. Если  для
для  то решение
то решение  определяет замкнутую траекторию периода т. Естественным обобщением понятия замкнутой траектории является понятие квазипериодического движения:
определяет замкнутую траекторию периода т. Естественным обобщением понятия замкнутой траектории является понятие квазипериодического движения:

где f — периодическая функция периода 1 по каждому из своих аргументов в отдельности, а частоты  рационально
рационально
независимы. Мы предположим, что f — функция класса  а ее значения пробегают
а ее значения пробегают  -мерный тор
-мерный тор  вложенный в В. Отметим, однако, что квазипериодическое движение не типично. В частности, для
вложенный в В. Отметим, однако, что квазипериодическое движение не типично. В частности, для  из теоремы Пейксото вытекает, что квазипериодические движения на двумерном торе содержатся в дополнении к открытому плотному подмножеству 2 в банаховом пространстве векторных полей класса
из теоремы Пейксото вытекает, что квазипериодические движения на двумерном торе содержатся в дополнении к открытому плотному подмножеству 2 в банаховом пространстве векторных полей класса  на торе: множество S состоит из векторных полей, неблуждающее множество Й которых составлено только из конечного числа неподвижных точек и замкнутых траекторий.
на торе: множество S состоит из векторных полей, неблуждающее множество Й которых составлено только из конечного числа неподвижных точек и замкнутых траекторий.

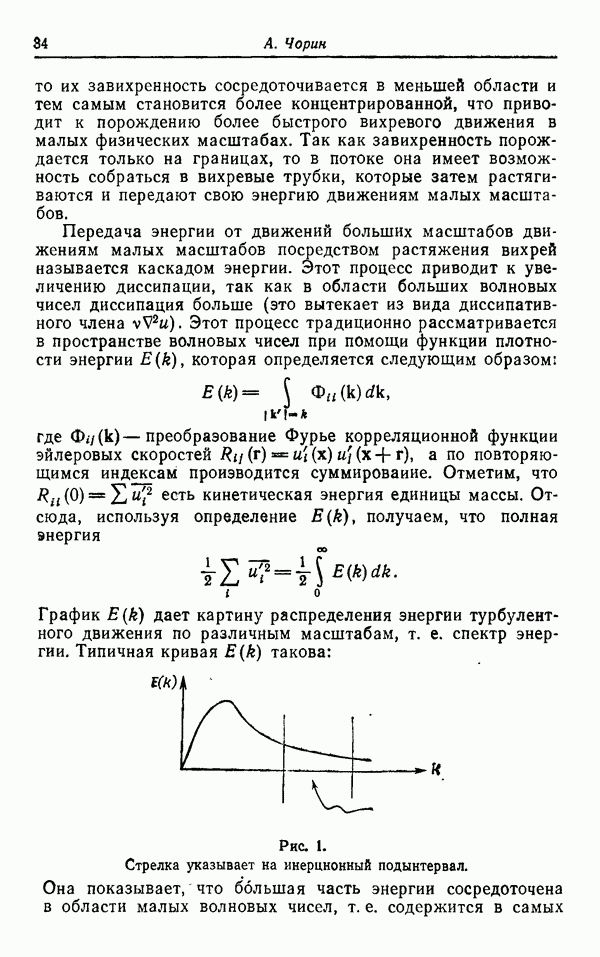
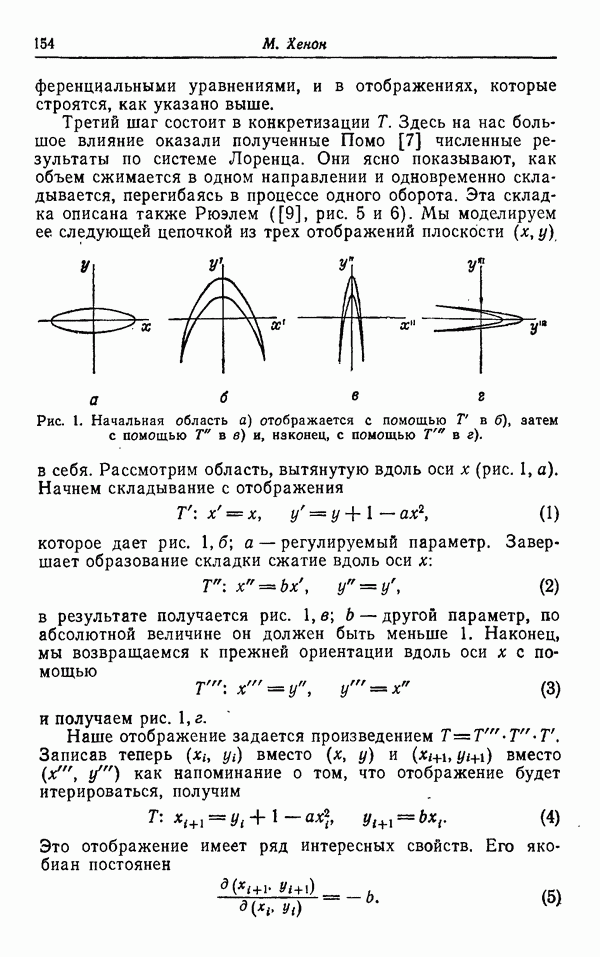
Рис. 1.
При  интегральная кривая
интегральная кривая  векторного поля X может притягиваться к неподвижной точке или замкнутой траектории векторного поля, или к аттракторам более общего типа. Она, по-видимому, не может притягиваться к квазипериодическим траекториям, поскольку последние встречаются редко. Возможно, однако, что траектория притягивается к множеству, которое не является многообразием. Чтобы проиллюстрировать эту ситуацию в размерности
векторного поля X может притягиваться к неподвижной точке или замкнутой траектории векторного поля, или к аттракторам более общего типа. Она, по-видимому, не может притягиваться к квазипериодическим траекториям, поскольку последние встречаются редко. Возможно, однако, что траектория притягивается к множеству, которое не является многообразием. Чтобы проиллюстрировать эту ситуацию в размерности  , вообразим, что интегральные кривые векторного поля проходят приблизительно параллельно и пересекают трансверсально некоторый кусок (
, вообразим, что интегральные кривые векторного поля проходят приблизительно параллельно и пересекают трансверсально некоторый кусок ( -мерной поверхности S (рис. 1). Пусть
-мерной поверхности S (рис. 1). Пусть  обозначает первую точку пересечения интегральной кривой, проходящей через
обозначает первую точку пересечения интегральной кривой, проходящей через  с поверхностью S (Р — отображение Пуанкаре).
с поверхностью S (Р — отображение Пуанкаре).
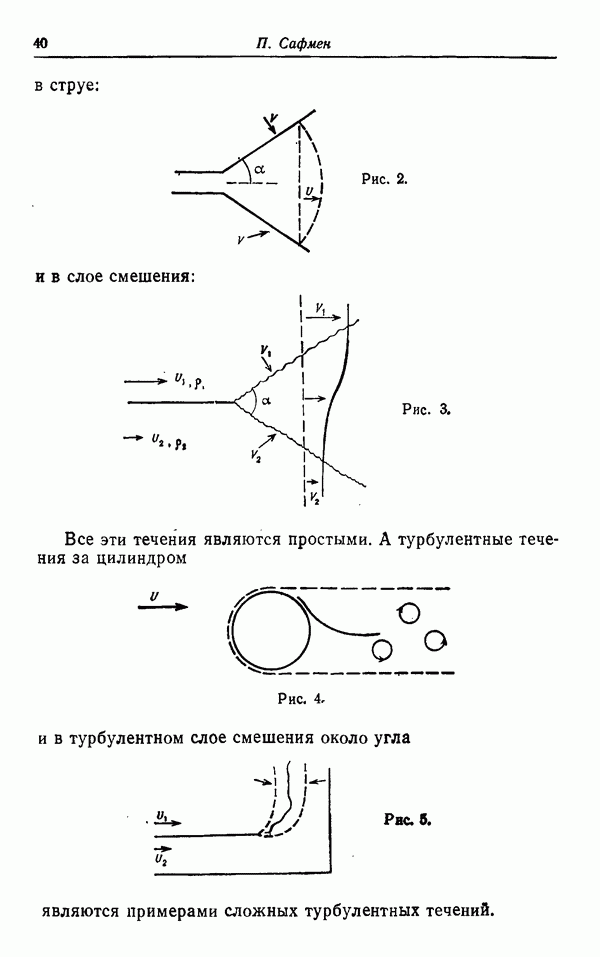
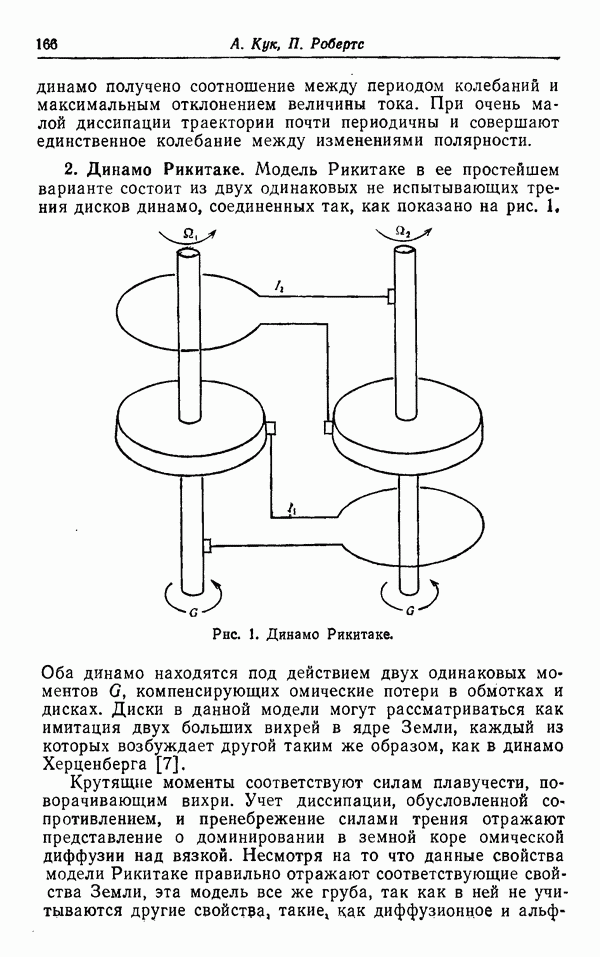
Возьмем теперь  и предположим, что Р отображает полноторий По в себя, как показано на рис. 2,
и предположим, что Р отображает полноторий По в себя, как показано на рис. 2,

Множество  является аттрактором; локально оно представляется произведением канторова множества и отрезка прямой (см. Смейл [11], § 1.9). Возвращаясь вновь к векторному полю X, мы получим в этом случае «странный» аттрактор, который локально представляется как произведение канторова множества и куска двумерного многообразия. Отметим, что картина сохранится, если заменить векторное поле X векторным полем У, которое достаточно близко к X в норме банахова пространства, выбранного подходящим образом. Поэтому аттракторы только что рассмотренного типа не могут быть изъяты из рассмотрения под тем предлогом, что они представляют собой нетипичное явление.
является аттрактором; локально оно представляется произведением канторова множества и отрезка прямой (см. Смейл [11], § 1.9). Возвращаясь вновь к векторному полю X, мы получим в этом случае «странный» аттрактор, который локально представляется как произведение канторова множества и куска двумерного многообразия. Отметим, что картина сохранится, если заменить векторное поле X векторным полем У, которое достаточно близко к X в норме банахова пространства, выбранного подходящим образом. Поэтому аттракторы только что рассмотренного типа не могут быть изъяты из рассмотрения под тем предлогом, что они представляют собой нетипичное явление.

Рис. 2.
§ 3. ОБ ОДНОМ МАТЕМАТИЧЕСКОМ МЕХАНИЗМЕ ПОЯВЛЕНИЯ ТУРБУЛЕНТНОСТИ
Пусть  векторное поле, зависящее от параметра
векторное поле, зависящее от параметра  Мы сохраним те же предположения, что и в § 2, но отныне будем интерпретировать как правую часть уравнений Навье — Стокса. При изменении параметра
Мы сохраним те же предположения, что и в § 2, но отныне будем интерпретировать как правую часть уравнений Навье — Стокса. При изменении параметра  векторное поле может меняться различными способами. Здесь мы опишем один способ изменения поля
векторное поле может меняться различными способами. Здесь мы опишем один способ изменения поля  который физически вполне приемлем, и покажем, что происходящие при этом изменения в характере поведения решений уравнения (1) приводят к такой картине поведения траекторий, которая очень похожа на турбулентность.
который физически вполне приемлем, и покажем, что происходящие при этом изменения в характере поведения решений уравнения (1) приводят к такой картине поведения траекторий, которая очень похожа на турбулентность.
Пусть при  о уравнение
о уравнение

имеет решение  . Предположим, что все собственные значения матрицы Якоби определяемой с помощью формулы
. Предположим, что все собственные значения матрицы Якоби определяемой с помощью формулы

имеют строго отрицательные действительные части; это соответствует тому, что неподвижная точка 0 притягивающая. Определитель матрицы Якоби отличен от нуля, и поэтому (в силу теоремы о неявной функции) существует такая непрерывная зависящая от  функция
функция  что
что

В гидродинамической интерпретации функция  описывает установившееся течение.
описывает установившееся течение.
Мы проследим теперь за функцией  ПРИ возрастании параметра
ПРИ возрастании параметра  Для достаточно малых
Для достаточно малых  матрица Якоби
матрица Якоби  задаваемая равенством
задаваемая равенством

(в силу непрерывности) имеет только собственные значения со строго отрицательными действительными частями. Предположим, что при возрастании параметра  пары комплексно сопряженных собственных значений матрицы (2) пересекают мнимую ось последовательно одна за другой при значениях
пары комплексно сопряженных собственных значений матрицы (2) пересекают мнимую ось последовательно одна за другой при значениях  . Для
. Для  неподвижная точка
неподвижная точка
 не является более притягивающей. Когда пара комплексно сопряженных собственных значений матрицы (2) пересекает мнимую ось при значении параметра, равном
не является более притягивающей. Когда пара комплексно сопряженных собственных значений матрицы (2) пересекает мнимую ось при значении параметра, равном  существует, как показано Хопфом, однопараметрическое семейство замкнутых траекторий векторного поля, лежащих в некоторой окрестности
существует, как показано Хопфом, однопараметрическое семейство замкнутых траекторий векторного поля, лежащих в некоторой окрестности  Более точно, существуют непрерывные функции
Более точно, существуют непрерывные функции  определенные для
определенные для  и такие, что
и такие, что

б) для  интегральная кривая векторного поля проходящая через точку
интегральная кривая векторного поля проходящая через точку  является замкнутой траекторией.
является замкнутой траекторией.
В общем случае  или
или  для
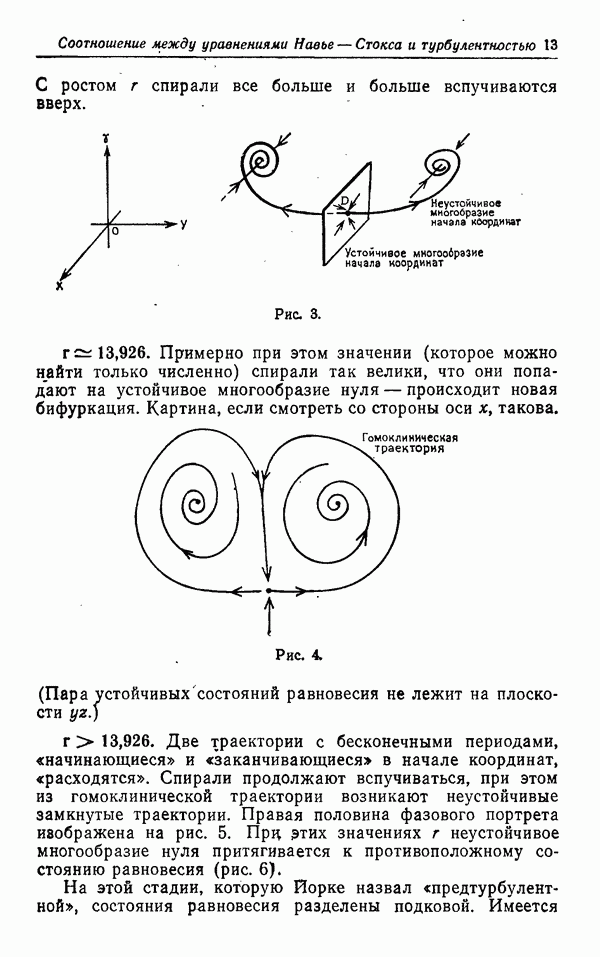
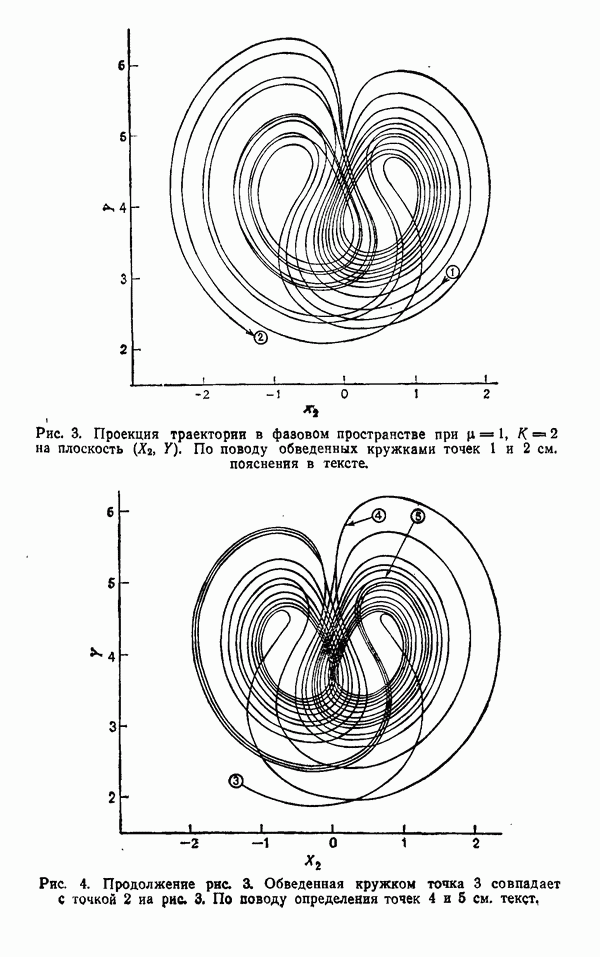
для  . Чтобы увидеть, как возникают замкнутые траектории, мы проследим в двумерном случае за окрестностью точки
. Чтобы увидеть, как возникают замкнутые траектории, мы проследим в двумерном случае за окрестностью точки  для
для  (рис. 3) и
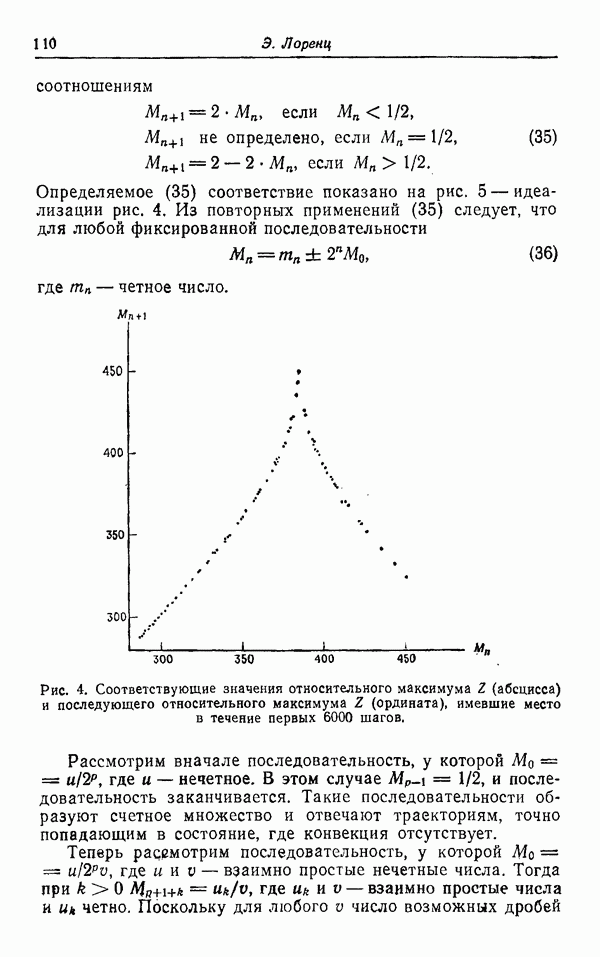
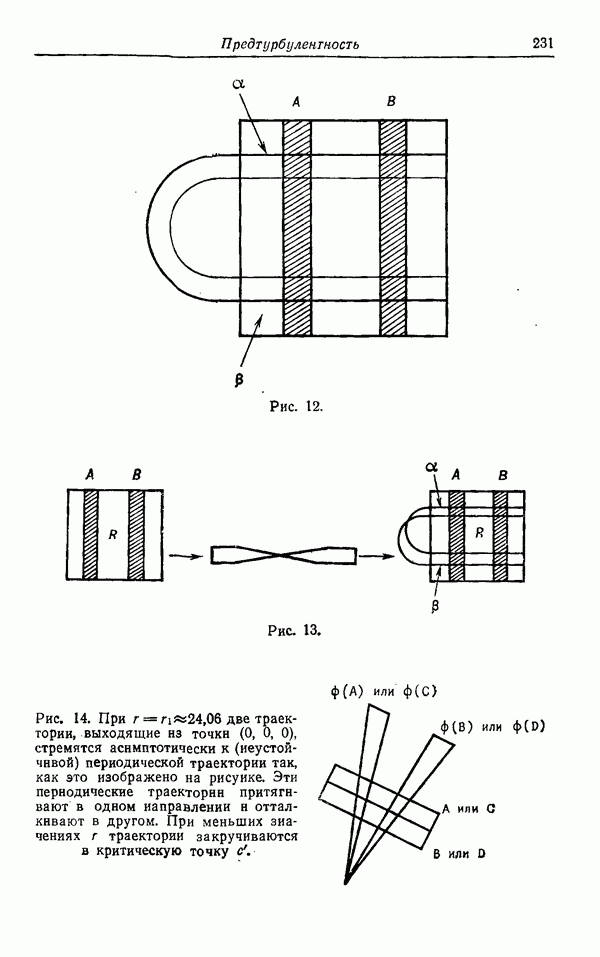
(рис. 3) и  (рис. 4).
(рис. 4).

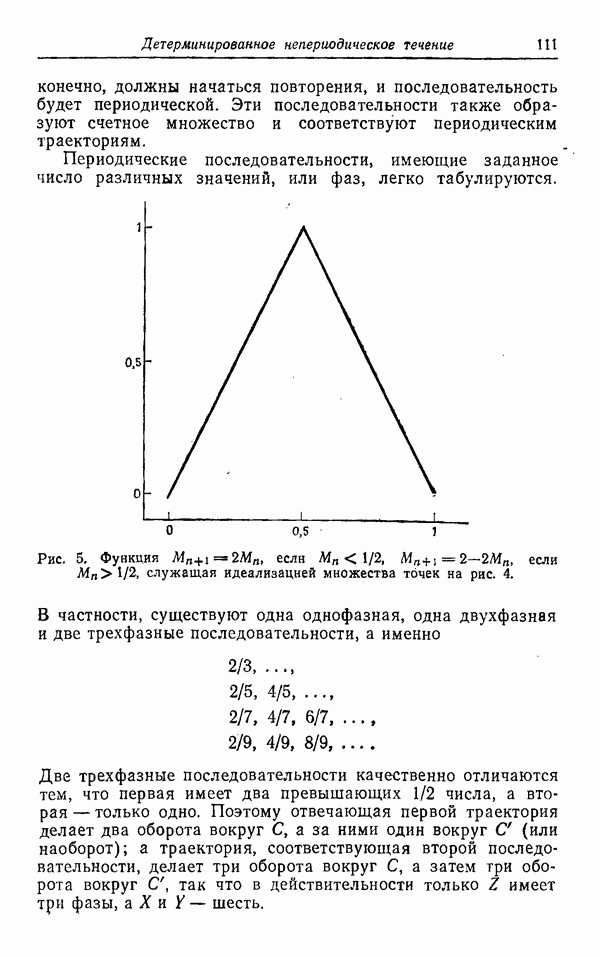
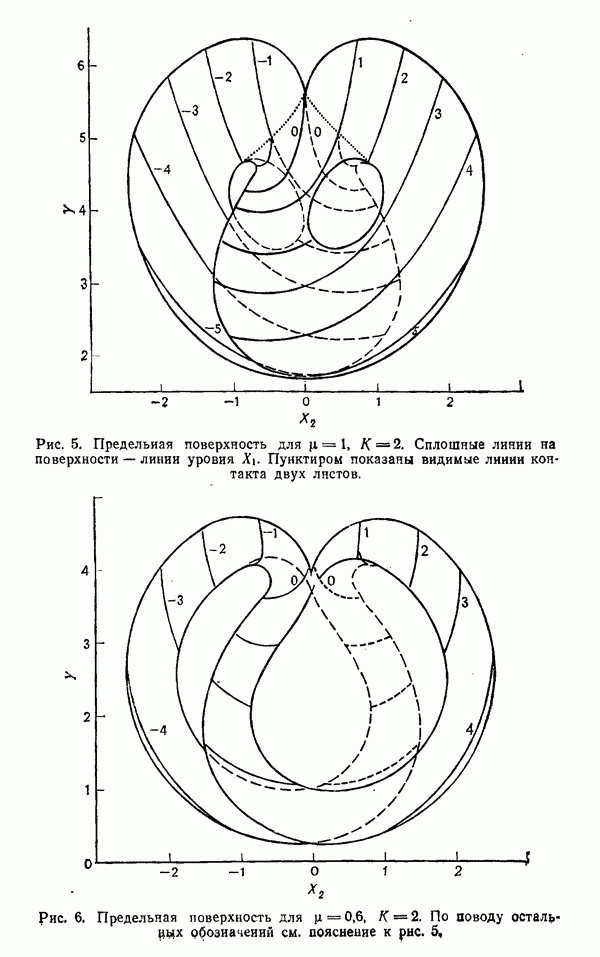
Рис. 

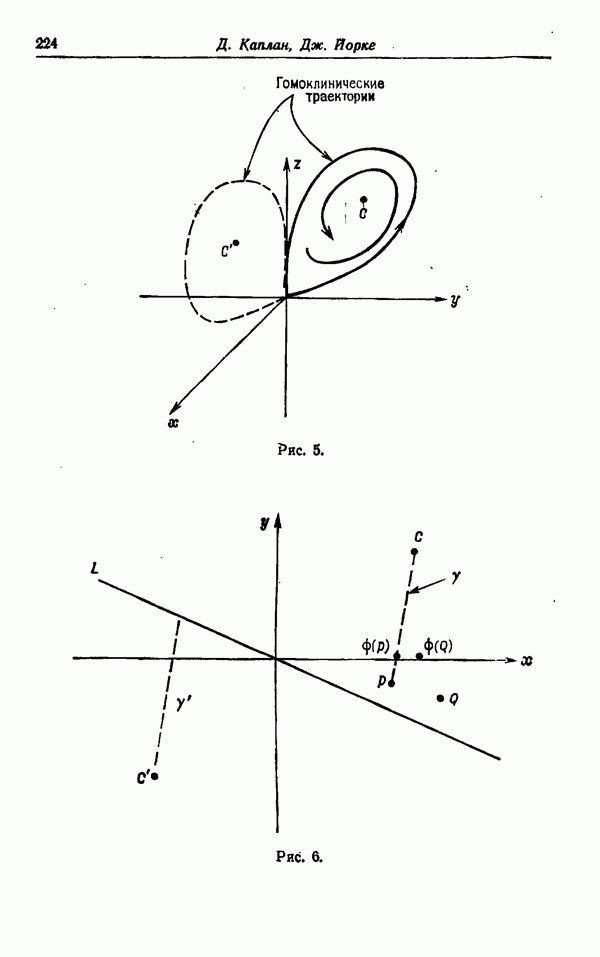
Рис. 5.
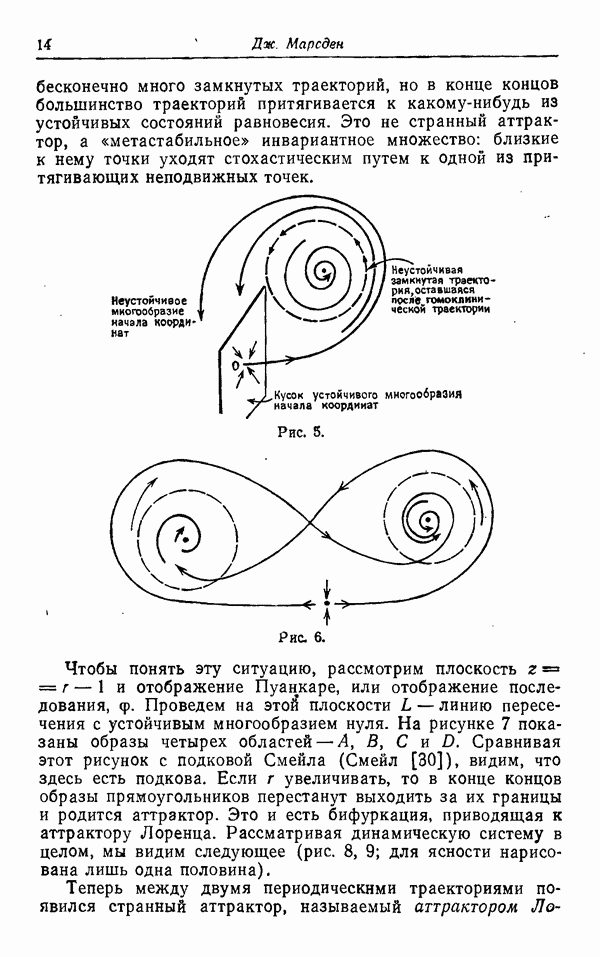
Предположим, что когда параметр и переходит через значение  векторное поле на больших расстояниях от точки
векторное поле на больших расстояниях от точки  имеет вид, изображенный на рис. 3; замкнутая траектория рождается так, как изображено на рис. 5. Отметим, что рис. 4 отвечает случаю
имеет вид, изображенный на рис. 3; замкнутая траектория рождается так, как изображено на рис. 5. Отметим, что рис. 4 отвечает случаю  и что замкнутая траектория является притягивающей. Обычно мы будем предполагать, что замкнутые траектории возникают при
и что замкнутая траектория является притягивающей. Обычно мы будем предполагать, что замкнутые траектории возникают при  так, что векторное поле на больших расстояниях от точки
так, что векторное поле на больших расстояниях от точки  остается притягивающим в соответствии с физическими представлениями. Когда параметр
остается притягивающим в соответствии с физическими представлениями. Когда параметр  переходит через бифуркационное значение, происходит замена притягивающей неподвижной точки на притягивающую
переходит через бифуркационное значение, происходит замена притягивающей неподвижной точки на притягивающую
периодическую траекторию. Замкнутая траектория интерпретируется физически как периодическое движение, его амплитуда увеличивается с ростом параметра 
§ 3 а). ИЗУЧЕНИЕ ОКРЕСТНОСТИ БИФУРКАЦИОННОГО ЗНАЧЕНИЯ
Для того чтобы проследить за тем, что происходит, когда параметр  . последовательно переходит через значения мы рассмотрим двумерное линейное пространство натянутое на
. последовательно переходит через значения мы рассмотрим двумерное линейное пространство натянутое на  пару собственных значений матрицы Якоби. В первом приближении векторное поле X вблизи точки
пару собственных значений матрицы Якоби. В первом приближении векторное поле X вблизи точки  имеет вид
имеет вид

где  — компоненты и
— компоненты и  в пространстве Для значений параметра
в пространстве Для значений параметра  лежащих в интервале
лежащих в интервале  интеграл векторного поля имеет инвариантное множество
интеграл векторного поля имеет инвариантное множество  , представляющее собой декартово произведение замкнутых траекторий
, представляющее собой декартово произведение замкнутых траекторий  в пространствах
в пространствах  При подходящем выборе координат на
При подходящем выборе координат на  движение, задаваемое векторным полем на
движение, задаваемое векторным полем на  является квазипериодическим (частоты
является квазипериодическим (частоты  замкнутых траекторий в пространствах
замкнутых траекторий в пространствах  вообще говоря, рационально независимы).
вообще говоря, рационально независимы).
Замена векторного поля  векторным полем
векторным полем  может рассматриваться как некоторое возмущение. Предположим, что это возмущение мало, т. е. что векторное поле вблизи бифуркационного значения представимо в виде (3). В этом случае существует многообразие — тор Тк класса
может рассматриваться как некоторое возмущение. Предположим, что это возмущение мало, т. е. что векторное поле вблизи бифуркационного значения представимо в виде (3). В этом случае существует многообразие — тор Тк класса  близкий к тору
близкий к тору  , который инвариантен относительно и является притягивающим. Справедливость предположения о малости векторного поля
, который инвариантен относительно и является притягивающим. Справедливость предположения о малости векторного поля  определяется тем, будут ли замкнутые траектории
определяется тем, будут ли замкнутые траектории  притягивающими траекториями векторных полей
притягивающими траекториями векторных полей  соответственно, поэтому это предположение может оказаться неверным, если параметр
соответственно, поэтому это предположение может оказаться неверным, если параметр  . будет достаточно близок к одному из значений
. будет достаточно близок к одному из значений 
Рассмотрим теперь ограничение векторного поля  на тор
на тор  . В связи со сказанным выше мы не надеемся на то, что движение на этом торе будет по-прежнему квазипериодическим.
. В связи со сказанным выше мы не надеемся на то, что движение на этом торе будет по-прежнему квазипериодическим.
Например, если  то из теоремы Пейксото следует, что в общем случае неблуждающее множество на торе
то из теоремы Пейксото следует, что в общем случае неблуждающее множество на торе  состоит из конечного числа неподвижных точек и замкнутых траекторий. В рассматриваемом случае можно надеяться лишь на то, что будет существовать одна или несколько притягивающих замкнутых траекторий с такими частотами
состоит из конечного числа неподвижных точек и замкнутых траекторий. В рассматриваемом случае можно надеяться лишь на то, что будет существовать одна или несколько притягивающих замкнутых траекторий с такими частотами  что отношение
что отношение  проходит непрерывно через рациональные значения.
проходит непрерывно через рациональные значения.
Пусть  . В этом случае векторные поля на торе Тк, неблуждающее множество которых состоит из конечного числа неподвижных точек и замкнутых траекторий, не образуют более плотного множества в соответствующем банаховом пространстве. Реализуется другая возможность, соответствующая более сложной структуре траекторий; возникают «странные» аттракторы, похожие на тот, который рассмотрен в конце § 2. Как мы покажем в § 9, в случае тора 74, снабженного
. В этом случае векторные поля на торе Тк, неблуждающее множество которых состоит из конечного числа неподвижных точек и замкнутых траекторий, не образуют более плотного множества в соответствующем банаховом пространстве. Реализуется другая возможность, соответствующая более сложной структуре траекторий; возникают «странные» аттракторы, похожие на тот, который рассмотрен в конце § 2. Как мы покажем в § 9, в случае тора 74, снабженного  -топологией, в любой окрестности квазипериодического векторного поля К существует открытое множество векторных полей, обладающих странными аттракторами.
-топологией, в любой окрестности квазипериодического векторного поля К существует открытое множество векторных полей, обладающих странными аттракторами.
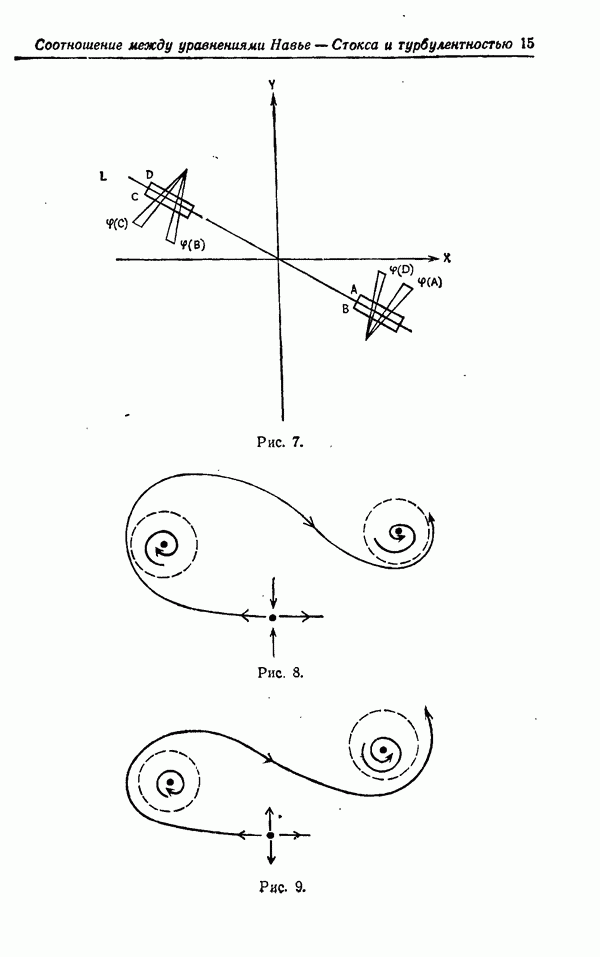
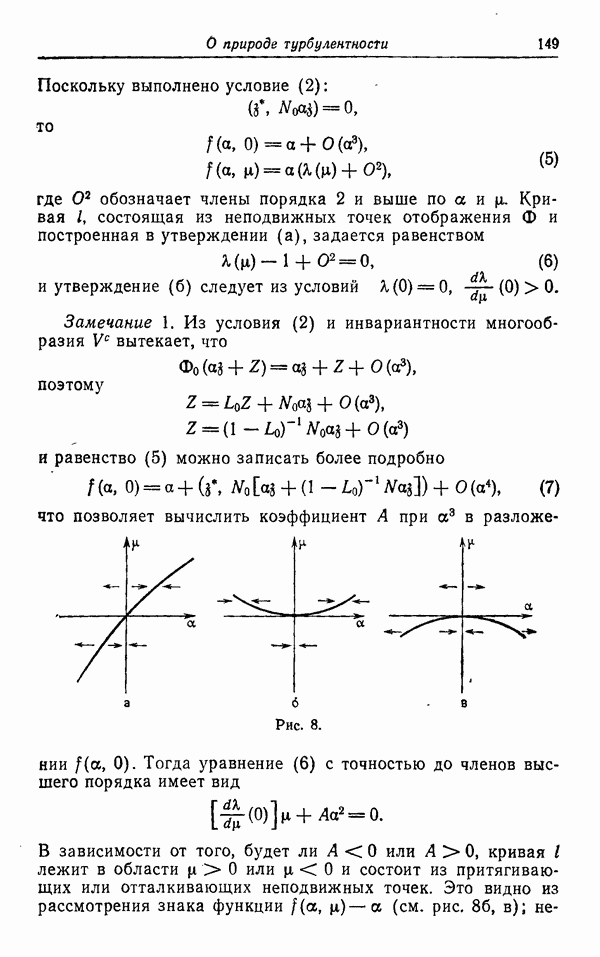
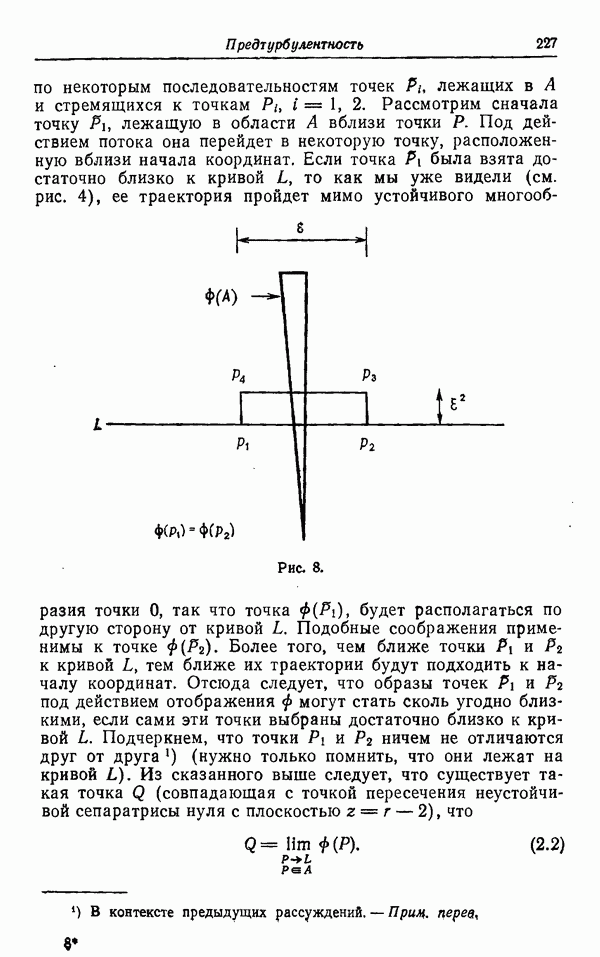
Мы предлагаем определять турбулентное течение жидкости как такое, которое описывается интегральной кривой векторного поля  стремящейся к некоторому множеству Л, причем это множество не пусто и не сводится к неподвижной точке или замкнутой траектории. При таком подходе мы пренебрегаем отдельными случаями (например, когда множество А имеет вид, изображенный на рис. 8, и т. д.), которые являются нетипичными.
стремящейся к некоторому множеству Л, причем это множество не пусто и не сводится к неподвижной точке или замкнутой траектории. При таком подходе мы пренебрегаем отдельными случаями (например, когда множество А имеет вид, изображенный на рис. 8, и т. д.), которые являются нетипичными.
Это определение основано на следующих соображениях:
а) Как мы указывали, кажется весьма вероятным, что при возрастании параметра и появляется аттрактор А, который не является ни неподвижной точкой, ни замкнутой траекторией.
б) В известных примерах, являющихся типичными, в которых множество А не является ни неподвижной точкой, ни замкнутой траекторией, поведение интегральных кривых на или вблизи множества А является сложным и неустойчивым (см. Смейл [11]) и Вильямс [13]).
В § 4 мы продолжим обсуждение данного выше определения турбулентного течения.
§ 3 б). БИФУРКАЦИИ ЗАМКНУТЫХ ТРАЕКТОРИЙ
Мы видели выше, как притягивающая неподвижная точка векторного поля  заменяется на притягивающую замкнутую траекторию
заменяется на притягивающую замкнутую траекторию  когда параметр проходит через значение
когда параметр проходит через значение  (бифуркация Хопфа).
(бифуркация Хопфа).
Рассмотрим теперь детально следующую бифуркацию; мы предположим, что она происходит при значении параметра, равном  и что lim у является замкнутой траекторией
и что lim у является замкнутой траекторией  векторного поля X.
векторного поля X.
Пусть — отображение Пуанкаре, заданное на куске гиперповерхности S, трансверсальной  при
при  Так как траектория
Так как траектория  притягивающая, то точка
притягивающая, то точка  является неподвижной притягивающей точкой отображения
является неподвижной притягивающей точкой отображения  для
для  Производная
Производная  отображения
отображения  в точке
в точке  — это линейное отображение в себя касательной гиперплоскости к поверхности S в точке
— это линейное отображение в себя касательной гиперплоскости к поверхности S в точке  .
.
Предположим, что спектр отображения  распадается на две части: первая состоит из изолированных собственных значений, равных по модулю 1, а вторая содержится в открытом единичном диске
распадается на две части: первая состоит из изолированных собственных значений, равных по модулю 1, а вторая содержится в открытом единичном диске  Согласно § 5, замечание (5.6), мы можем предположить, что гиперповерхность S конечномерна. Опираясь на это предположение, можно предсказать, какова типичная бифуркация при
Согласно § 5, замечание (5.6), мы можем предположить, что гиперповерхность S конечномерна. Опираясь на это предположение, можно предсказать, какова типичная бифуркация при  . Мы опишем такие бифуркации, указав притягивающие множества векторного поля X (или отображения Ф) вблизи замкнутой траектории (или точки
. Мы опишем такие бифуркации, указав притягивающие множества векторного поля X (или отображения Ф) вблизи замкнутой траектории (или точки  ), когда
), когда  . В общем случае множество Е собственных значений отображения
. В общем случае множество Е собственных значений отображения  равных по модулю 1, имеет вид
равных по модулю 1, имеет вид

3.  , где числа
, где числа  отличны друг от друга.
отличны друг от друга.
В случаях 1 и 2 мы можем воспользоваться результатами Бруновски [3]. В первом случае отсутствуют притягивающие замкнутые траектории (как отсутствуют и гиперболические замкнутые траектории); при  векторное поле
векторное поле  вообще говоря, не имеет аттракторов вблизи кривой у Во втором случае при
вообще говоря, не имеет аттракторов вблизи кривой у Во втором случае при  имеется притягивающая (соответственно гиперболическая) замкнутая траектория, но в два раза большего периода.
имеется притягивающая (соответственно гиперболическая) замкнутая траектория, но в два раза большего периода.
В случае 3 для значений  немного превышающих
немного превышающих  отображение
отображение  имеет неподвижную точку причем в общем случае выполняются условия (а) — (д) теоремы 7.2. Отсюда вытекает, что если траектория
имеет неподвижную точку причем в общем случае выполняются условия (а) — (д) теоремы 7.2. Отсюда вытекает, что если траектория  является неопределенным аттрактором, (т. е. если выполнено еще и условие (е)), то при
является неопределенным аттрактором, (т. е. если выполнено еще и условие (е)), то при  отображение
отображение  имеет притягивающую окружность; последнее эквивалентно существованию инвариантного притягивающего тора
имеет притягивающую окружность; последнее эквивалентно существованию инвариантного притягивающего тора  для векторного поля
для векторного поля  Если траектория
Если траектория  не является «неопределенным аттрактором», то в общем случае векторное поле
не является «неопределенным аттрактором», то в общем случае векторное поле  при
при  не имеет притягивающих множеств вблизи кривой
не имеет притягивающих множеств вблизи кривой
§ 4. НЕСКОЛЬКО ЗАМЕЧАНИЙ ПО ПОВОДУ ОПРЕДЕЛЕНИЯ ТУРБУЛЕНТНОСТИ
В заключение мы сделаем несколько замечаний:
1. Представление об общности, основанное на понятии массивного множества, может оказаться неубедительным с точки зрения физика. Действительно, дополнение к массивному на оси  множеству не обязательно имеет нулевую лебеговскую меру. В частности, квазипериодические движения, которые мы исключили из рассмотрения, на самом деле могут составлять на оси
множеству не обязательно имеет нулевую лебеговскую меру. В частности, квазипериодические движения, которые мы исключили из рассмотрения, на самом деле могут составлять на оси  множество, имеющее ненулевую лебеговскую меру. Такие квазипериодические движения должны считаться турбулентными согласно нашему определению, но «турбулентность» должна быть слабой при малых
множество, имеющее ненулевую лебеговскую меру. Такие квазипериодические движения должны считаться турбулентными согласно нашему определению, но «турбулентность» должна быть слабой при малых  Однако имеются доводы, заставляющие считать квазипериодические движения, как и периодические, не турбулентными (см. замечание (4) ниже).
Однако имеются доводы, заставляющие считать квазипериодические движения, как и периодические, не турбулентными (см. замечание (4) ниже).
2. Согласно нашему определению, периодическое движение (замкнутая траектория векторного поля  ) не является турбулентным. Однако оно может быть весьма сложным и казаться турбулентным (представьте себе периодическое движение, аппроксимирующее квазипериодическое, см. § 36), вторая сноска).
) не является турбулентным. Однако оно может быть весьма сложным и казаться турбулентным (представьте себе периодическое движение, аппроксимирующее квазипериодическое, см. § 36), вторая сноска).
3. Мы показали, что при определенных условиях векторное поле  имеет притягивающий тор
имеет притягивающий тор  , когда
, когда  лежит между
лежит между  . Переход от тора
. Переход от тора  к тору
к тору  описан в § 36), но переход от тора
описан в § 36), но переход от тора  к тору
к тору  при
при  может оказаться более сложным. В общем случае складывается впечатление, что поведение траекторий, не вкладывающихся в нашу схему, является более сложным, трудно описываемым и, вероятно, турбулентным.
может оказаться более сложным. В общем случае складывается впечатление, что поведение траекторий, не вкладывающихся в нашу схему, является более сложным, трудно описываемым и, вероятно, турбулентным.
4. Интересный вопрос возникает при исследовании, основанном на индивидуальной эргодической теореме, статистических свойств движения, связанных с эргодической мерой, сосредоточенной на притягивающем множестве А. Предположим, что наблюдаемая в некоторой физической системе в момент времени t величина описывается функцией  заданной на пространстве
заданной на пространстве  , и ее среднее значение равно
, и ее среднее значение равно  . Если мера m перемешивающая, то корреляционные функции
. Если мера m перемешивающая, то корреляционные функции  стремятся к нулю при
стремятся к нулю при  Такое поведение корреляционных функций должно свидетельствовать о том, что движение является турбулентным; «псевдослучайные» величины с корреляционными функциями, стремящимися к нулю на бесконечности изучались Бассом. С этой точки зрения квазипериодические движения не следует считать турбулентными.
Такое поведение корреляционных функций должно свидетельствовать о том, что движение является турбулентным; «псевдослучайные» величины с корреляционными функциями, стремящимися к нулю на бесконечности изучались Бассом. С этой точки зрения квазипериодические движения не следует считать турбулентными.
5. В приведенных выше рассуждениях совершенно не учитывалась конкретная структура уравнений, описывающих вязкую жидкость. В действительности, нам не только известна их структура, но также и те условия, найденные экспериментально, при которых возникает турбулентность и которые должны учитываться теорией.
6. В диссипативных системах, отличных от вязкой жидкости, также могут наблюдаться как периодические, так и более сложные движения. С такими движениями встречаются при изучении некоторых систем, возникающих в химии.
§ 6. РЕДУКЦИЯ К РАЗМЕРНОСТИ ДВА
Определение (5.1). Пусть  — отображение класса
— отображение класса  имеющее неподвижную точку
имеющее неподвижную точку  , где
, где  — гильбертово пространство. Спектром отображения Ф в точке
— гильбертово пространство. Спектром отображения Ф в точке  назовем спектр индуцированного отображения
назовем спектр индуцированного отображения 
Пусть X — векторное поле класса  обращающееся в нуль в точке
обращающееся в нуль в точке  Тогда для каждого t интеграл векторного поля X за время t индуцирует отображение
Тогда для каждого t интеграл векторного поля X за время t индуцирует отображение  Пусть также
Пусть также  — такое непрерывное линейное отображение, определенное единственным образом, что
— такое непрерывное линейное отображение, определенное единственным образом, что 
Назовем спектром векторного поля X в точке  спектр отображения
спектр отображения  (заметим, что отображение
(заметим, что отображение  ) может быть также получено линеаризацией векторного поля X).
) может быть также получено линеаризацией векторного поля X).
Предложение (5.2). Пусть  — такое однопараметрическое семейство векторных полей класса С на гильбертовом пространстве
— такое однопараметрическое семейство векторных полей класса С на гильбертовом пространстве  , что отображение
, что отображение  . задаваемое равенством
. задаваемое равенством  также принадлежит классу С. Предположим, что
также принадлежит классу С. Предположим, что

(б) При  спектр векторного поля в нуле содержится в множестве
спектр векторного поля в нуле содержится в множестве 
(в) Для  (соответственно
(соответственно  спектр векторного поля
спектр векторного поля  в нуле имеет два изолированных собственных значения
в нуле имеет два изолированных собственных значения  с кратностью
с кратностью  (соответственно
(соответственно  ). Оставшаяся часть спектра содержится в множестве
). Оставшаяся часть спектра содержится в множестве 
Тогда существует такое (малое) трехмерное подмногообразие  класса
класса  лежащее в
лежащее в  и содержащее точку (0, 0), что
и содержащее точку (0, 0), что
1. Многообразие  локально инвариантно под действием интеграла векторного поля X (которое задается равенством
локально инвариантно под действием интеграла векторного поля X (которое задается равенством  ) локальная инвариантность означает, что существует такая окрестность U точки (0, 0), что
) локальная инвариантность означает, что существует такая окрестность U точки (0, 0), что  при
при 
2. Существует такая окрестность U точки (0,0), что для всякой рекуррентной точки  для которой
для которой  , имеем
, имеем 
3. Многообразие  касается в точке (0, 0) подпространства, натянутого на ось
касается в точке (0, 0) подпространства, натянутого на ось  и собственное подпространство, отвечающее собственным значениям
и собственное подпространство, отвечающее собственным значениям 
Доказательство. Имеем разложение  где подпространство
где подпространство  натянуто на ось
натянуто на ось  и собственное подпространство, отвечающее собственным значениям
и собственное подпространство, отвечающее собственным значениям  подпространство
подпространство  — собственное подпространство, отвечающее оставшейся (компактной) части спектра оператора
— собственное подпространство, отвечающее оставшейся (компактной) части спектра оператора  , Поскольку эта оставшаяся часть спектра компактна, она содержится в множестве
, Поскольку эта оставшаяся часть спектра компактна, она содержится в множестве  при некотором
при некотором  Мы можем теперь воспользоваться теоремой о центральном многообразии [5], доказательство которой переносится на случай гильбертовых пространств, и взять в качестве подмногообразия
Мы можем теперь воспользоваться теоремой о центральном многообразии [5], доказательство которой переносится на случай гильбертовых пространств, и взять в качестве подмногообразия  центральное многообразие отображения X в точке (0,0) [в силу предположения о том, что
центральное многообразие отображения X в точке (0,0) [в силу предположения о том, что  , подмногообразие
, подмногообразие  принадлежит классу
принадлежит классу  если мы предположим только, что для каждого
если мы предположим только, что для каждого  векторное поле
векторное поле  (а X лежит только в
(а X лежит только в  ), то многообразие
), то многообразие  будет класса
будет класса  но для каждого
но для каждого  многообразие
многообразие  будет класса
будет класса  . При положительных t отображение
. При положительных t отображение  является сжатием к подмногообразию
является сжатием к подмногообразию  (спектр в подпространстве
(спектр в подпространстве  содержится в множестве
содержится в множестве  ). Следовательно, существует такая окрестность U точки (0, 0), что
). Следовательно, существует такая окрестность U точки (0, 0), что

Предположим теперь, что  — рекуррентная точка и
— рекуррентная точка и  для всех t. Тогда для заданных
для всех t. Тогда для заданных  существует такое
существует такое  что расстояние между точками
что расстояние между точками  меньше е. Отсюда следует, что
меньше е. Отсюда следует, что  , если окрестность U выбрана достаточно малой. Это завершает доказательство требуемого утверждения.
, если окрестность U выбрана достаточно малой. Это завершает доказательство требуемого утверждения.
Замечание (5.3). Подобным образом доказывается аналогичное утверждение для однопараметрического семейства диффеоморфизмов,  Необходимые предположения в этом случае следующие:
Необходимые предположения в этом случае следующие:

(б) При  спектр отображения
спектр отображения  в нуле содержится в множестве
в нуле содержится в множестве 
(в) При  (соответственно
(соответственно  ) спектр отображения
) спектр отображения  в нуле имеет два изолированных собственных значения и
в нуле имеет два изолированных собственных значения и  с кратностями 1 и
с кратностями 1 и  (соответствен-но
(соответствен-но  ) Оставшаяся часть спектра, содержится в
) Оставшаяся часть спектра, содержится в
множестве  Теперь точно так же, как в предложении (5.2), строится центральное многообразие, которое содержит все локально рекуррентные точки.
Теперь точно так же, как в предложении (5.2), строится центральное многообразие, которое содержит все локально рекуррентные точки.
Замечание (5.4). Ограничение векторного поля X или диффеоморфизма Ф [определенного формулой  ] на трехмерное многообразие
] на трехмерное многообразие  удовлетворяет тем же предположениям (а), (б), (в) или (а), (б), (в) с той лишь разницей, что теперь гильбертово пространство Н имеет размерность 21), Таким образом, если мы хотим доказать свойство локальной рекуррентности точек для однопараметрического семейства векторных полей или диффеоморфизмов, удовлетворяющих условиям (а), (б), (в) или (а), (б) и (в), то достаточно доказать это в случае, когда
удовлетворяет тем же предположениям (а), (б), (в) или (а), (б), (в) с той лишь разницей, что теперь гильбертово пространство Н имеет размерность 21), Таким образом, если мы хотим доказать свойство локальной рекуррентности точек для однопараметрического семейства векторных полей или диффеоморфизмов, удовлетворяющих условиям (а), (б), (в) или (а), (б) и (в), то достаточно доказать это в случае, когда  .
.
Замечание (5.5). Все сказанное в настоящем параграфе остается справедливым, если заменить гильбертово пространство Я на банахово пространство с нормой класса  банахово пространство В снабжено нормой класса
банахово пространство В снабжено нормой класса  если отображение
если отображение  раз непрерывно дифференцируемо всюду, кроме нуля. Такая норма класса
раз непрерывно дифференцируемо всюду, кроме нуля. Такая норма класса  необходима для доказательства теоремы о центральном многообразии.
необходима для доказательства теоремы о центральном многообразии.
Замечание (5.6). Предложения (5.2) и (5.3) остаются верными, если
1. Мы опустим предположения о спектре векторного поля  (соответственно отображения
(соответственно отображения  ) для
) для 
2. Введем предположения о том, что в спектре векторного поля  (соответственно отображения
(соответственно отображения  ) содержится произвольное конечное число изолированных собственных значений, расположенных на вещественной оси (соответственно на единичной окружности). В этом случае размерность инвариантного многообразия Vе на единицу больше числа собственных значений.
) содержится произвольное конечное число изолированных собственных значений, расположенных на вещественной оси (соответственно на единичной окружности). В этом случае размерность инвариантного многообразия Vе на единицу больше числа собственных значений.
§ 6. БИФУРКАЦИЯ ХОПФА
Рассмотрим однопараметрическое семейство векторных полей  класса
класса  на плоскости
на плоскости  удовлетворяющих условиям предложения (5.2) (с
удовлетворяющих условиям предложения (5.2) (с  вместо Н);
вместо Н);  — собственные значения векторного поля
— собственные значения векторного поля  в точке (0,0). Заметим, что в подходящей системе координат векторное поле
в точке (0,0). Заметим, что в подходящей системе координат векторное поле
 можно представить в
можно представить в  члены более высокого порядка.
члены более высокого порядка.
Теорема (6.1) (Хопф [6]). Если  имеет положительную действительную часть и
имеет положительную действительную часть и  то существует однопараметрическое семейство замкнутых траекторий векторного поля
то существует однопараметрическое семейство замкнутых траекторий векторного поля  ) на
) на  лежащих вблизи точки (0, 0, 0) и имеющих период, близкий к
лежащих вблизи точки (0, 0, 0) и имеющих период, близкий к  существует такая окрестность U точки (0, 0, 0) в
существует такая окрестность U точки (0, 0, 0) в  что каждая замкнутая траектория векторного поля X, лежащая в U, принадлежит указанному выше семейству траекторий.
что каждая замкнутая траектория векторного поля X, лежащая в U, принадлежит указанному выше семейству траекторий.
Если точка (0,0) является «неопределенным аттрактором, (определение приводится ниже) для векторного поля  то это однопараметрическое семейство содержится в множестве
то это однопараметрическое семейство содержится в множестве  , а замкнутые траектории являются притягивающими.
, а замкнутые траектории являются притягивающими.
Доказательство. Докажем сначала лемму, оправдывающую переход к полярным координатам.
Лемма (6.2). Пусть X — векторное поле класса С на  и пусть
и пусть  . Введем полярные координаты при помощи отображения
. Введем полярные координаты при помощи отображения  Тогда существует такое единственное векторное поле Н класса
Тогда существует такое единственное векторное поле Н класса  на
на  , что
, что  (т. е. для любых
(т. е. для любых  ).
).
Доказательство леммы (6.2). Имеем 

Здесь  — «координатные векторные поля» по отношению к координатам
— «координатные векторные поля» по отношению к координатам  (Заметим, что
(Заметим, что  двузначны.)
двузначны.)
Рассмотрим теперь функции  . Они равны нулю при
. Они равны нулю при  это также верно для функций
это также верно для функций  . В силу теоремы о производной частного функции
. В силу теоремы о производной частного функции  принадлежат классам
принадлежат классам  соответственно. Мы можем теперь положить
соответственно. Мы можем теперь положить  единственность очевидна.
единственность очевидна.
Определение (6.3). Определим отображение Пуанкаре  связанное с векторным полем X, удовлетворяющим условиям теоремы (6.1):
связанное с векторным полем X, удовлетворяющим условиям теоремы (6.1):
это отображение задано на множестве  и переводит его в плоскость
и переводит его в плоскость  здесь число
здесь число  выбрано так, чтобы
выбрано так, чтобы  при
при  число
число  достаточно мало.
достаточно мало.
Отображение  сопоставляет точке
сопоставляет точке  первую точку пересечения кривой
первую точку пересечения кривой  с плоскостью
с плоскостью  удовлетворяющую дополнительному условию: проекции этой точки и точки
удовлетворяющую дополнительному условию: проекции этой точки и точки  на координатную ось
на координатную ось  имеют один и тот же знак.
имеют один и тот же знак.

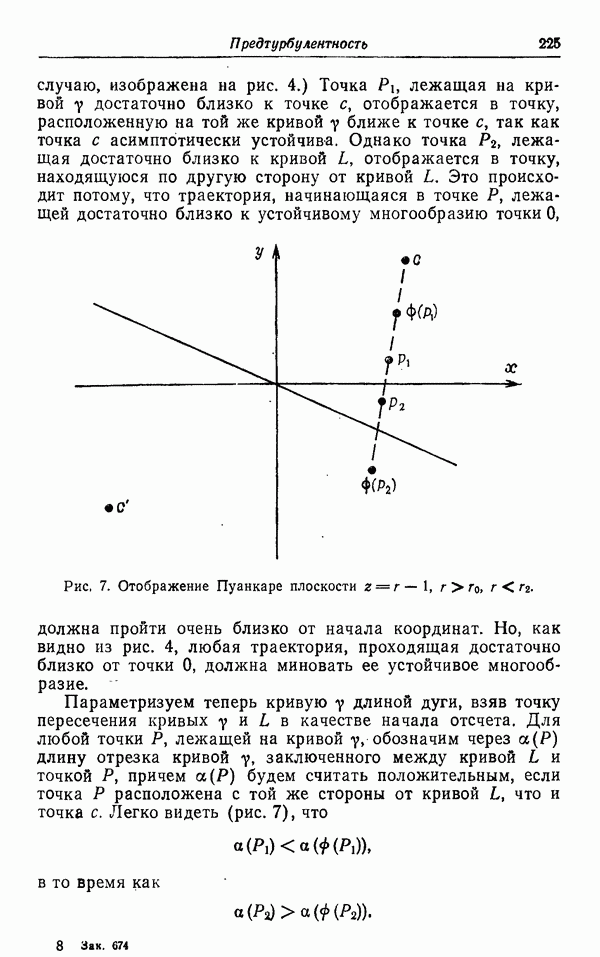
Рис. 6. Интегральная кривая X при  .
.
Замечание (6.4). Отображение  не меняет значения
не меняет значения  Характер этого отображения в плоскости
Характер этого отображения в плоскости  иллюстрируется на следующем рисунке. Условие
иллюстрируется на следующем рисунке. Условие  означает, что векторное поле X имеет «ненулевое вращение»; поэтому отображение
означает, что векторное поле X имеет «ненулевое вращение»; поэтому отображение  определено лишь для достаточно малых
определено лишь для достаточно малых  .
.
Замечание (6.5). Из леммы (6.2) легко следует, что отображение  принадлежит классу
принадлежит классу  Определим функцию смещения
Определим функцию смещения  по формуле
по формуле

Эта функция определена там же, где и отображение  принадлежит классу
принадлежит классу  и обладает следующими свойствами:
и обладает следующими свойствами:
(I) Функция V равна нулю на множестве  множество всех остальных нулей этой функции разбивается на пары (проекции входящих в пар точек на ось
множество всех остальных нулей этой функции разбивается на пары (проекции входящих в пар точек на ось  имеют противоположные
имеют противоположные
знаки), каждой паре соответствует замкнутая траектория векторного поля X. Если замкнутая траектория у векторного поля X содержится в достаточно малой окрестности точки (0, 0) и пересекает множество  только в двух точках, то функция V имеет соответствующую пару нулей (именно ими служат точки
только в двух точках, то функция V имеет соответствующую пару нулей (именно ими служат точки  (область определения
(область определения 
(II) При  имеем
имеем  при
при  и
и  имеем
имеем  и при
и при  имеем
имеем 
Эти свойства вытекают из предположений относительно  Поэтому, снова воспользовавшись теоремой о производной частного, получим, что функция
Поэтому, снова воспользовавшись теоремой о производной частного, получим, что функция  принадлежит классу
принадлежит классу  Имеем
Имеем  так что существует единственная
так что существует единственная  раза непрёрывно дифференцируемая кривая
раза непрёрывно дифференцируемая кривая  лежащая в некоторой окрестности точки (0,0), проходящая через эту точку и состоящая из нулей функции V. Локально множество нулей функции V является объединением кривой I и множества
лежащая в некоторой окрестности точки (0,0), проходящая через эту точку и состоящая из нулей функции V. Локально множество нулей функции V является объединением кривой I и множества  Кривая I индуцирует однопараметрическое семейство замкнутых траекторий векторного поля X.
Кривая I индуцирует однопараметрическое семейство замкнутых траекторий векторного поля X.
(III) Мы скажем, что точка (0,0) является «неопределенным аттрактором» векторного поля  если
если  (члены порядка
(члены порядка  ), где
), где  . Это означает, что благодаря членам третьего порядка точка (0,0) является притягивающей точкой потока, порожденного векторным полем
. Это означает, что благодаря членам третьего порядка точка (0,0) является притягивающей точкой потока, порожденного векторным полем  . В этом случае
. В этом случае  (члены высшего порядка), где
(члены высшего порядка), где  так что функция
так что функция  равна нулю только при
равна нулю только при  или
или  Это доказывает, что однопараметрическое семейство замкнутых траекторий содержится в множестве
Это доказывает, что однопараметрическое семейство замкнутых траекторий содержится в множестве 
(IV) Рассмотрим окрестность точки (0,0,0), в которой  Имеет место следующее утверждение: если
Имеет место следующее утверждение: если  то замкнутая траектория, которая проходит через область определения отображения
то замкнутая траектория, которая проходит через область определения отображения  в точке
в точке  является притягивающей траекторией векторного поля Это следует из двух фактов: во-первых, точка
является притягивающей траекторией векторного поля Это следует из двух фактов: во-первых, точка  — неподвижная точка отображения
— неподвижная точка отображения  и, во-вторых, производная в этой точке отображения
и, во-вторых, производная в этой точке отображения  рассматриваемого в плоскости
рассматриваемого в плоскости  при фиксированном значении параметра, равном
при фиксированном значении параметра, равном  меньше единицы (по абсолютной величине).
меньше единицы (по абсолютной величине).
Из свойств (III) и (IV) легко следует, что если точка (0,0) — неопределенный аттрактор, то любая замкнутая траектория, принадлежащая нашему однопараметрическому семейству траекторий и проходящая вблизи точки (0, 0), является притягивающей.
Наконец, мы можем утверждать существование такой окрестности U точки (0,0), что каждая замкнутая траектория векторного поля X, лежащая в окрестности U, принадлежит нашему семейству замкнутых траекторий. Прежде всего мы можем взять окрестность U столь малой, чтобы любая замкнутая траектория у поля X, лежащая в U, пересекала область определения отображения 
Пусть  — точка пересечения замкнутой траектории у с областью определения отображения
— точка пересечения замкнутой траектории у с областью определения отображения  Мы можем выбрать окрестность U столь малой, чтобы
Мы можем выбрать окрестность U столь малой, чтобы  (область определения
(область определения  (область определения
(область определения  ). Тогда точка
). Тогда точка  лежит в области определения отображения
лежит в области определения отображения  , так как
, так как  , то можно построить точку
, то можно построить точку  Продолжая рассуждения, построим точки
Продолжая рассуждения, построим точки  .
.
Отображение  рассмотренное на множестве
рассмотренное на множестве  является локальным диффеоморфизмом некоторого отрезка, лежащего на луче
является локальным диффеоморфизмом некоторого отрезка, лежащего на луче  или
или  в этот луч.
в этот луч.
Если первая координата точки  меньше (соответственно больше), чем
меньше (соответственно больше), чем  первая координата точки
первая координата точки  меньше (соответственно больше), чем первая координата точки
меньше (соответственно больше), чем первая координата точки  так что точка
так что точка  не лежит на замкнутой траектории. Поэтому первая координата точки
не лежит на замкнутой траектории. Поэтому первая координата точки  равна
равна  следовательно, точка
следовательно, точка  есть нуль функции V, так что в силу свойства (II) кривая у принадлежит нашему однопараметрическому семейству замкнутых траекторий.
есть нуль функции V, так что в силу свойства (II) кривая у принадлежит нашему однопараметрическому семейству замкнутых траекторий.
§ 7. БИФУРКАЦИЯ ХОПФА ДЛЯ ДИФФЕОМОРФИЗМОВ
Рассмотрим теперь однопараметрическое семейство диффеоморфизмов  удовлетворяющих условиям (а), (б) и (в) (см. замечание (5.3)) и таких, что
удовлетворяющих условиям (а), (б) и (в) (см. замечание (5.3)) и таких, что

Диффеоморфизмы такого рода встречаются, например, при изучении интеграла за единицу времени векторного поля, рассмотренного в § 2. Для этих диффеоморфизмов мы, конечно, не сможем отыскать все замкнутые траектории (эти траектории не образуют непрерывных семейств кривых в фазовом пространстве), но тем не менее мы сможем указать даже при еще более общих предположениях, относящихся к окрестности точки (0,0), и при достаточно малых  однопараметрическое семейство инвариантных окружностей.
однопараметрическое семейство инвариантных окружностей.
Приведем отображение  к более простому виду, сделав подходящую замену координат: сначала сделаем замену вдоль координаты
к более простому виду, сделав подходящую замену координат: сначала сделаем замену вдоль координаты  так, чтобы
так, чтобы

Далее сделаем замену координат в плоскости  (зависящую от
(зависящую от  ) так, чтобы в новых координатах
) так, чтобы в новых координатах  члены порядка
члены порядка  где
где  запись
запись  порядка
порядка  означает, что частные производные по
означает, что частные производные по  отображений
отображений  до порядка
до порядка  совпадают в точке (0, 0).
совпадают в точке (0, 0).
Мы введем теперь еще одно дополнительное условие на отображения Ф:

Предположение (7.1). Предположим, что отображения  удовлетворяют условиям
удовлетворяют условиям  и принадлежат классу
и принадлежат классу  Тогда для и, достаточно близких к 0, существует зависящая от и замена координат в
Тогда для и, достаточно близких к 0, существует зависящая от и замена координат в  приводящая
приводящая  к следующему виду:
к следующему виду:

 члены порядка
члены порядка 
Для каждого и замена координат в  принадлежит классу
принадлежит классу  индуцированная замена в
индуцированная замена в  принадлежит только классу
принадлежит только классу 
Доказательству этого утверждения посвящен следующий параграф. Наконец, введем еще одно предположение, касающееся отображения 
(e)  . Более того, мы предположим даже, что
. Более того, мы предположим даже, что  (это соответствует тому, что при
(это соответствует тому, что при  точка 0
точка 0
является неопределенным аттрактором, см. § 6). Случай  исследуется аналогично (достаточно рассмотреть и назовем это «упрощенной формой отображения
исследуется аналогично (достаточно рассмотреть и назовем это «упрощенной формой отображения 
Обозначение. Мы используем символ  для обозначения отображения
для обозначения отображения

и назовем это «упрощенной формой отображения 
Теорема (7.2). Предположим, что отображение  принадлежит по крайней мере классу
принадлежит по крайней мере классу  и удовлетворяет условиям (а), (б), (в), (г) и (д), а его нормальная форма
и удовлетворяет условиям (а), (б), (в), (г) и (д), а его нормальная форма  удовлетворяет условию (
удовлетворяет условию ( ). Тогда существует
). Тогда существует  и для каждого
и для каждого  непрерывно зависящая от
непрерывно зависящая от  инвариатная относительно Ф, притягивающая окружность (так что в целом мы имеем непрерывное однопараметрическое семейство инвариантных притягивающих окружностей).
инвариатная относительно Ф, притягивающая окружность (так что в целом мы имеем непрерывное однопараметрическое семейство инвариантных притягивающих окружностей).
Доказательство. Идея доказательства состоит в следующем: множество  лежащее в
лежащее в  -пространстве, инвариантно под действием упрощенной формы
-пространстве, инвариантно под действием упрощенной формы  Более того, отображение ЫФ «притягивает к этому множеству», так что 2 устойчиво в следующем смысле: последовательность многообразий
Более того, отображение ЫФ «притягивает к этому множеству», так что 2 устойчиво в следующем смысле: последовательность многообразий  сходится (при достаточно малых и) к инвариантному многообразию (это как раз то, что мы хотим доказать). Метод доказательства подобен тому, который использован в [4, 5].
сходится (при достаточно малых и) к инвариантному многообразию (это как раз то, что мы хотим доказать). Метод доказательства подобен тому, который использован в [4, 5].
Положим  и покажем, что
и покажем, что  а также
а также  Это вытекает из следующих соображений: если
Это вытекает из следующих соображений: если  - координата точки
- координата точки  , то
, то  -координата точки
-координата точки  равна
равна  и отображение
и отображение  переводит точку
переводит точку  во внутренность окрестности
во внутренность окрестности  Поскольку отображение Ф совпадает со своей упрощенной формой с точностью до членов порядка
Поскольку отображение Ф совпадает со своей упрощенной формой с точностью до членов порядка  то локально
то локально 
Отсюда следует, что при достаточно малом  и любом
и любом  где
где 
Для векторов, касательных к поверхности уровня  , лежащей в
, лежащей в  определим следующим образом угол наклона: если
определим следующим образом угол наклона: если  — касательный вектор к многообразию
— касательный вектор к многообразию  то угол наклона равен
то угол наклона равен  если
если  то угол наклона не определен.
то угол наклона не определен.
Прямыми вычислениями нетрудно показать, что если X — касательный вектор к многообразию  с углом наклона 1, а число
с углом наклона 1, а число  достаточно мало, то угол наклона вектора
достаточно мало, то угол наклона вектора  не превосходит
не превосходит  , где К — некоторое положительное число. Используя это обстоятельство и тот факт, что величина приблизительно постоянна в
, где К — некоторое положительное число. Используя это обстоятельство и тот факт, что величина приблизительно постоянна в  а отображения
а отображения  отличаются членами порядка
отличаются членами порядка  можно показать, что при достаточно малом
можно показать, что при достаточно малом  угол наклона вектора
угол наклона вектора  меньше 1, где X — касательный вектор к многообразию
меньше 1, где X — касательный вектор к многообразию  с углом наклона 1.
с углом наклона 1.
Отсюда следует, что при достаточно малом  и любом
и любом 

2. Угол наклона касательного вектора к многообразию  меньше 1.
меньше 1.
Это означает, что при любых 

где  — гладкая функция, удовлетворяющая условиям
— гладкая функция, удовлетворяющая условиям

Перечисленные выше условия определяют функцию  единственным образом. Мы теперь покажем, что при достаточно малом
единственным образом. Мы теперь покажем, что при достаточно малом  последовательность функции сходится. Фиксируем некоторое
последовательность функции сходится. Фиксируем некоторое  и положим
и положим

Снова воспользовавшись тем фактом, что величина  приблизительно постоянна (независимо от
приблизительно постоянна (независимо от  ), получим
), получим

и

где  — постоянные, не зависящие от
— постоянные, не зависящие от  Из определения функции
Из определения функции  следует, что
следует, что 
Оценим разность между  и
и
 . Поскольку
. Поскольку

то

Легко видеть также, что

Таким образом,

Выберем теперь  столь малым, чтобы
столь малым, чтобы  и положим
и положим 
Из сказанного выше следует, что

Это доказывает сходимость последовательности функций  и существование для каждого достаточно малого
и существование для каждого достаточно малого  инвариантной притягивающей окружности. Непрерывность построенного семейства окружностей вытекает из непрерывности по
инвариантной притягивающей окружности. Непрерывность построенного семейства окружностей вытекает из непрерывности по  предельной функции
предельной функции  что в свою очередь есть следствие равномерной сходимости последовательности функций
что в свою очередь есть следствие равномерной сходимости последовательности функций 
Замечание (7.3). При заданном  функция не только непрерывна, но даже удовлетворяет условию Липшица, поскольку она является пределом функций, производная каждой из которых
функция не только непрерывна, но даже удовлетворяет условию Липшица, поскольку она является пределом функций, производная каждой из которых
Поэтому можно воспользоваться результатами об инвариантных многообразиях, полученных в [4, 5], и доказать следующий факт:
Если отображение  принадлежит классу
принадлежит классу  при каждом
при каждом  то существует такое
то существует такое  что инвариантные окружности из построенного нами семейства окружностей, отвечающие значениям параметра
что инвариантные окружности из построенного нами семейства окружностей, отвечающие значениям параметра  принадлежат
принадлежат
классу  Это есть следствие того факта, что при
Это есть следствие того факта, что при  близких к 0, в окрестности
близких к 0, в окрестности  степень сжатия в направлении
степень сжатия в направлении  намного превосходит максимальную возможную степень сжатия в направлении
намного превосходит максимальную возможную степень сжатия в направлении 
§ 8. УПРОЩЕННЫЕ ФОРМЫ (ДОКАЗАТЕЛЬСТВО ПРЕДЛОЖЕНИЯ (7.1))
Сначала мы дадим некоторые определения. Пусть  — векторное пространство
— векторное пространство  -струй в нуле таких векторных полей на
-струй в нуле таких векторных полей на  у которых
у которых  -струя равна нулю (таким образом, элементы
-струя равна нулю (таким образом, элементы  могут быть единственным образом представлены векторными полями, координатные функции которых являются однородными многочленами степени
могут быть единственным образом представлены векторными полями, координатные функции которых являются однородными многочленами степени  ? Через V, обозначим множество
? Через V, обозначим множество  -струй диффеоморфизмов
-струй диффеоморфизмов  , у которых
, у которых  -струя есть «единица». Определим отображение
-струя есть «единица». Определим отображение  , положив для
, положив для  равным
равным  -струе диффеоморфизма, полученного из векторного поля а сдвигом на единицу времени.
-струе диффеоморфизма, полученного из векторного поля а сдвигом на единицу времени.
Замечание (8.1). Для  отображение
отображение  является диффеоморфизмом на и
является диффеоморфизмом на и  . Доказательство непосредственно следует из определений и предоставляется читателю
. Доказательство непосредственно следует из определений и предоставляется читателю 
Пусть теперь  линейное отображение. Индуцированное преобразование
линейное отображение. Индуцированное преобразование  определяется по формуле
определяется по формуле  или, что эквивалентно,
или, что эквивалентно, 
Замечание (8.2). Если  обозначает
обозначает  -струю диффеоморфизма
-струю диффеоморфизма  то для каждого а
то для каждого а  -струи
-струи  совпадают. Доказательство предоставляется читателю.
совпадают. Доказательство предоставляется читателю.
Пусть  — линейное отображение.
— линейное отображение.  -разложением называется разложение пространства
-разложением называется разложение пространства  в прямую сумму подпространств
в прямую сумму подпространств  удовлетворяющее условиям:
удовлетворяющее условиям:
1. Подпространства V и  инвариантны относительно
инвариантны относительно 
2. Единица не является собственным значением отображения 
Пример (8.3). Возьмем матрицу  с собственными значениями
с собственными значениями  , такими, что
, такими, что  или
или  , но
, но 
где  . Более того, матрицу А можно взять в виде
. Более того, матрицу А можно взять в виде

При  разложение пространства
разложение пространства  описывается следующим образом:
описывается следующим образом:
пространство V есть множество ( -струй) векторных полей, которые в полярных координатах записываются в виде
-струй) векторных полей, которые в полярных координатах записываются в виде  ; точнее,
; точнее,  порождается векторными полями
порождается векторными полями  (другие случаи приводят к векторным полям, которые не дифференцируемы в обычных координатах).
(другие случаи приводят к векторным полям, которые не дифференцируемы в обычных координатах).
Пространство V" есть множество ( -струй) векторных полей, записываемых в виде
-струй) векторных полей, записываемых в виде

где

Функции  должны быть линейными комбинациями функций
должны быть линейными комбинациями функций  где
где  ибо в противном случае соответствующие векторные поля не будут дифференцируемыми в обычных координатах (кроме того, не все такие линейные комбинации возможны).
ибо в противном случае соответствующие векторные поля не будут дифференцируемыми в обычных координатах (кроме того, не все такие линейные комбинации возможны).
Предложение (8.4). Для заданного диффеоморфизма  и заданного
и заданного  -разложения
-разложения  где и
где и  существует такое преобразование координат к:
существует такое преобразование координат к:  , что
, что
1.  тождественное отображение;
тождественное отображение;
2. для каждого  -струя диффеоморфизма
-струя диффеоморфизма  связана со своей
связана со своей  -струей следующим образом-.
-струей следующим образом-.  —полиномиальное отображение степени —1, имеющее подходящую
—полиномиальное отображение степени —1, имеющее подходящую  -струю. При этом
-струю. При этом  -струя диффеоморфизма Ф связана со своей
-струя диффеоморфизма Ф связана со своей  -струей, если существует такое
-струей, если существует такое  что диффеоморфизм
что диффеоморфизм  имеет ту же
имеет ту же  -струю, что и Ф.
-струю, что и Ф.
Доказательство. Воспользуемся индукцией. Предположим, что построено отображение k, удовлетворяющее условиям 1 и 2 при  Рассмотрим
Рассмотрим  -струю диффеоморфизма
-струю диффеоморфизма  Заменим отображение
Заменим отображение  на
на  для некоторого
для некоторого
 . Тогда диффеоморфизм
. Тогда диффеоморфизм  заменится на
заменится на  который, согласно замечанию (8.2), равен
который, согласно замечанию (8.2), равен 
Поскольку единица не является собственным значёнием отображения  то для каждого
то для каждого  существует единственное
существует единственное  такое, что замене отображения и на
такое, что замене отображения и на  и отвечает замена диффеоморфизма
и отвечает замена диффеоморфизма  на
на  . Отсюда легко следует, что существует единственное
. Отсюда легко следует, что существует единственное  такое, что отображение
такое, что отображение  удовлетворяет условию 2 при
удовлетворяет условию 2 при  Это доказывает требуемое утверждение.
Это доказывает требуемое утверждение.
Доказательство предложения (7.1). Для  близких к нулю, линейное отображение
близких к нулю, линейное отображение  имеет вид, описанный в примере (8.3). Поэтому указанное там разложение — это
имеет вид, описанный в примере (8.3). Поэтому указанное там разложение — это  -разложение пространства
-разложение пространства  где
где  близко к нулю. Проводя те же рассуждения, что и при доказательстве предложения (8.4), мы получим для каждого и преобразование координат
близко к нулю. Проводя те же рассуждения, что и при доказательстве предложения (8.4), мы получим для каждого и преобразование координат  которое приводит отображение
которое приводит отображение  к требуемому виду. При этом индуктивное рассуждение выглядит следующим образом: для заданного
к требуемому виду. При этом индуктивное рассуждение выглядит следующим образом: для заданного  и преобразования координат
и преобразования координат  удовлетворяющего условиям 1 и 2 при
удовлетворяющего условиям 1 и 2 при  существует единственное
существует единственное  такое, что отображение
такое, что отображение  удовлетворяет условиям 1 и 2 при
удовлетворяет условиям 1 и 2 при  Зависимость векторного поля
Зависимость векторного поля  от параметра
от параметра  будет класса
будет класса  если таковой будет зависимость
если таковой будет зависимость  -струи диффеоморфизма Ф от
-струи диффеоморфизма Ф от  по этой причине происходит уменьшение гладкости по параметру
по этой причине происходит уменьшение гладкости по параметру 
§ 9. НЕКОТОРЫЕ ПРИМЕРЫ
В этом параграфе мы покажем, как при помощи малого возмущения квазипериодического потока на торе можно получить потоки, имеющие странные аттракторы (предложение (9.2)), и даже потоки, не являющиеся системами Морса — Смейла (предложение (9.1)).
Предложение (9.1). Пусть  — постоянное векторное поле на торе
— постоянное векторное поле на торе  . В каждой достаточно малой в
. В каждой достаточно малой в  топологии окрестности векторного поля а существует открытое множество векторных полей, не являющихся системами Морса — Смейла.
топологии окрестности векторного поля а существует открытое множество векторных полей, не являющихся системами Морса — Смейла.
Мы рассмотрим сначала случай  . Положим
. Положим  можно считать, что
можно считать, что  . Для
. Для
заданного  можно выбрать такое постоянное векторное поле что
можно выбрать такое постоянное векторное поле что

где  — целые числа, а числа
— целые числа, а числа  не имеют общих делителей. Более того, мы можем взять числа
не имеют общих делителей. Более того, мы можем взять числа  достаточно большими и удовлетворяющими условию
достаточно большими и удовлетворяющими условию

Наконец, всем этим требованиям можно удовлетворить, выбрав числа  в виде
в виде 
Пусть  Зададим отображения
Зададим отображения  равенствами
равенствами

Имеем  и отображение g (соответственно h) обратимо на множестве точек
и отображение g (соответственно h) обратимо на множестве точек  (соответственно
(соответственно  ), где
), где 
Рассмотрим отображение f диска в себя (см. (11), § 1.5, рис. 7), введенное Смейлом для построения подковы Смейла. Вкладывая диск  в тор
в тор  так, чтобы
так, чтобы

мы можем добиться того, чтобы отображение f было отображением Пуанкаре некоторого потока на  Более точно, нетрудно задать векторное поле
Более точно, нетрудно задать векторное поле  на торе
на торе  так, чтобы для
так, чтобы для  мы имели
мы имели

где  — интеграл за единицу времени векторного поля X (рис. 7), и в окрестности множества
— интеграл за единицу времени векторного поля X (рис. 7), и в окрестности множества  это векторное поле равнялось бы (0, 1) (т. е.
это векторное поле равнялось бы (0, 1) (т. е.  ).
).
Для  определено отображение
определено отображение  . Зададим векторное поле У равенством
. Зададим векторное поле У равенством

где

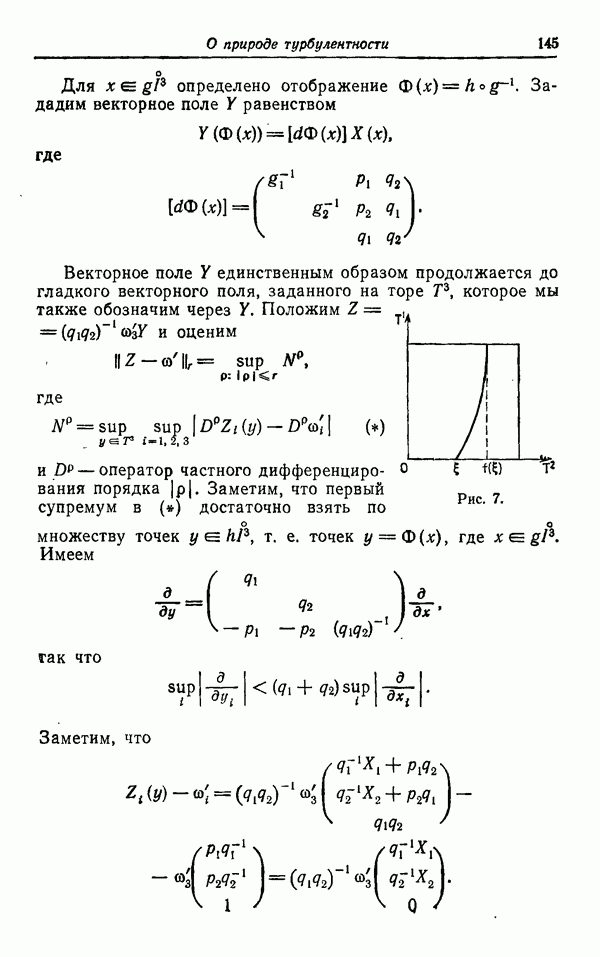
Векторное поле У единственным образом продолжается до гладкого векторного поля, заданного на торе  которое мы также обозначим через У. Положим
которое мы также обозначим через У. Положим  и оценим
и оценим

где

 — оператор частного дифференцирования порядка
— оператор частного дифференцирования порядка  Заметим, что первый супремум в
Заметим, что первый супремум в  достаточно взять по множеству точек
достаточно взять по множеству точек  , т. е. точек
, т. е. точек  , где
, где 

Рис. 7.
Имеем

так что

Заметим, что

Поэтому

Если выбрать  достаточно большими, то
достаточно большими, то

и поэтому

Рассмотрим отображение Пуанкаре  индуцированное потоком, задаваемым векторным полем Z на
индуцированное потоком, задаваемым векторным полем Z на  По построению неблуждающее множество для отображения Р содержит канторово множество, то же верно для любого векторного поля Z, достаточно близкого к
По построению неблуждающее множество для отображения Р содержит канторово множество, то же верно для любого векторного поля Z, достаточно близкого к  Это завершает доказательство для случая
Это завершает доказательство для случая 
В общем случае при 3 мы снова аппроксимируем постоянное векторное поле  постоянным векторным полем
постоянным векторным полем  компоненты которого являются рациональными числами и
компоненты которого являются рациональными числами и

причем целые числа  не имеют общих делителей. Более того, мы можем выбрать числа
не имеют общих делителей. Более того, мы можем выбрать числа  достаточно большими и такими, чтобы
достаточно большими и такими, чтобы

где С — постоянная, зависящая только от 
Остальная часть доказательства проводится так же, как в случае  с заменой диффеоморфизма, использованного при построении подковы Смейла, на подходящий диффеоморфизм класса
с заменой диффеоморфизма, использованного при построении подковы Смейла, на подходящий диффеоморфизм класса  . В частности, используя диффеоморфизм, схема действия которого изображена на рис. 2 (см. конец § 2), можно доказать следующий результат.
. В частности, используя диффеоморфизм, схема действия которого изображена на рис. 2 (см. конец § 2), можно доказать следующий результат.
Предложение (9.2). Пусть  постоянное векторное поле на торе
постоянное векторное поле на торе  . В каждой достаточно малой в
. В каждой достаточно малой в  -топологии векторного поля со существует открытое множество векторных полей, обладающих странными аттракторами.
-топологии векторного поля со существует открытое множество векторных полей, обладающих странными аттракторами.
ПРИЛОЖЕНИЕ. БИФУРКАЦИИ СТАЦИОНАРНЫХ РЕШЕНИЙ УРАВНЕНИЙ ГИДРОДИНАМИКИ
В этом приложении мы приведем теорему о бифуркациях неподвижных точек нелинейного отображения в банаховом пространстве. Наш результат отличается от известных исследованием вопроса дифференцируемой зависимости от бифуркационного параметра. Он может быть использован, например, для изучения бифуркации стационарных решений в задачах Тейлора и Бенара. Как показано у Бруновского (см. § 36)), обсуждаемые ниже бифуркации не типичны. Бифуркации стационарных решений в задачах Тейлора и Бенара также не типичны, поскольку они допускают группу преобразований.
Теорема. Пусть Н — банахово пространство, снабженное нормой класса  — дифферент цируемое отображение, такое, что
— дифферент цируемое отображение, такое, что  и отображение
и отображение  из пространства
из пространства  в R принадлежит классу
в R принадлежит классу  Пусть
Пусть

Предположим, что оператор имеет одно простое действительное изолированное собственное значение  непрерывно зависящее от
непрерывно зависящее от  причем
причем  предположим также, что оставшаяся часть спектра лежит в множестве
предположим также, что оставшаяся часть спектра лежит в множестве  Тогда
Тогда
а) В некоторой окрестности точки  существует однопараметрическое семейство неподвижных точек отображения
существует однопараметрическое семейство неподвижных точек отображения  (образующих кривую в классе
(образующих кривую в классе  ). Эти точки и точки
). Эти точки и точки  образуют в этой окрестности полный набор неподвижных точек отображения Ф.
образуют в этой окрестности полный набор неподвижных точек отображения Ф.
б) Пусть j (соответственно а — собственный вектор оператора  (соответственно сопряженного ему оператора
(соответственно сопряженного ему оператора  в сопряженном к Н пространстве Н с собственным значением 1, так что
в сопряженном к Н пространстве Н с собственным значением 1, так что  . Предположим, что для всех
. Предположим, что для всех

Тогда кривая I, построенная в (а), касается вектора  в точке (0, 0).
в точке (0, 0).
Из теоремы о центральном многообразии Хирша, Пью и Шуба следует, что существует двумерное многообразие  класса
класса  касающееся в точке
касающееся в точке  плоскости, натянутой на векторы
плоскости, натянутой на векторы  , и инвариантное относительно отображения Ф. Более того, существует такая окрестность U точки (0, 0), что каждая неподвижная точка отображения Ф, лежащая в U, принадлежит
, и инвариантное относительно отображения Ф. Более того, существует такая окрестность U точки (0, 0), что каждая неподвижная точка отображения Ф, лежащая в U, принадлежит 
Мы выберем координаты  на многообразии
на многообразии  так, чтобы
так, чтобы

причем  Неподвижные точки отображения Ф, лежащие в
Неподвижные точки отображения Ф, лежащие в  , ищутся из равенства
, ищутся из равенства  они состоят из точек
они состоят из точек  и решений уравнения
и решений уравнения

где  и в силу теоремы о производной частного функция
и в силу теоремы о производной частного функция  принадлежит классу
принадлежит классу  . Так как
. Так как  то утверждение (а) вытекает из теоремы о неявной функции.
то утверждение (а) вытекает из теоремы о неявной функции.
Пусть  . Представим вектор
. Представим вектор  в виде
в виде

где

Заметим, что

Поскольку выполнено условие (2):

то

где  обозначает члены порядка 2 и выше по
обозначает члены порядка 2 и выше по  Кривая I, состоящая из неподвижных точек отображения Ф и построенная в утверждении (а), задается равенством
Кривая I, состоящая из неподвижных точек отображения Ф и построенная в утверждении (а), задается равенством

и утверждение (б) следует из условий 
Замечание 1. Из условия (2) и инвариантности многообразия  вытекает, что
вытекает, что

поэтому

и равенство (5) можно записать более подробно

что позволяет вычислить коэффициент А при  в разложении
в разложении 

Рис. 8.
Тогда уравнение (6) с точностью до членов высшего порядка имеет вид

В зависимости от того, будет ли  или
или  кривая I лежит в области
кривая I лежит в области  или
или  и состоит из притягивающих или отталкивающих неподвижных точек. Это видно из рассмотрения знака функции
и состоит из притягивающих или отталкивающих неподвижных точек. Это видно из рассмотрения знака функции  (см. рис. 86, в); неподвижные
(см. рис. 86, в); неподвижные
точки  являются всегда притягивающими при
являются всегда притягивающими при  и отталкивающими при
и отталкивающими при  .
.
Замечание 2. Если кривая I, состоящая из неподвижных точек, не касается в точке (0, 0) вектора  , то точки этой кривой являются притягивающими при
, то точки этой кривой являются притягивающими при  и отталкивающими при
и отталкивающими при  (см. рис. 8, а).
(см. рис. 8, а).
Замечание 3. Если, так же как и в теореме, предположить, что оператор имеет одно простое изолированное собственное значение  , но оставшаяся часть спектра лежит в множестве
, но оставшаяся часть спектра лежит в множестве  , которое предпочтительнее множества
, которое предпочтительнее множества  , то теорема остается верной, неверными же являются приведенные выше результаты, дающие условия, при которых неподвижные точки будут притягивающими.
, то теорема остается верной, неверными же являются приведенные выше результаты, дающие условия, при которых неподвижные точки будут притягивающими.
СПИСОК ЛИТЕРАТУРЫ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- ПОПЫТКИ УСТАНОВИТЬ СООТНОШЕНИЕ МЕЖДУ УРАВНЕНИЯМИ НАВЬЕ-СТОКСА И ТУРБУЛЕНТНОСТЬЮ
- ПРИЛОЖЕНИЕ К СТАТЬЕ МАРСДЕНА БИФУРКАЦИИ, ПОЛУПОТОКИ И УРАВНЕНИЯ НАВЬЕ—СТОКСА
- ТЕОРИИ ТУРБУЛЕНТНОСТИ
- ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ РАСЧЕТА ТУРБУЛЕНТНЫХ СДВИГОВЫХ ТЕЧЕНИЙ
- ФРАКТАЛЫ И ТУРБУЛЕНТНОСТЬ: АТТРАКТОРЫ И РАЗБРОС
- СТРУКТУРА АТТРАКТОРОВ ЛОРЕНЦА
- ПРИЛОЖЕНИЕ К СТАТЬЕ Р. ВИЛЬЯМСА. «ИЗОБРАЖЕНИЕ АТТРАКТОРА ЛОРЕНЦА, ПОЛУЧЕННОЕ С ПОМОЩЬЮ КОМПЬЮТЕРА»
- ДВА ПОДХОДА К МОДЕЛИРОВАНИЮ ДВУМЕРНОЙ ТУРБУЛЕНТНОСТИ
- ДЕТЕРМИНИРОВАННОЕ НЕПЕРИОДИЧЕСКОЕ ТЕЧЕНИЕ
- О ПРИРОДЕ ТУРБУЛЕНТНОСТИ
- ДВУМЕРНОЕ ОТОБРАЖЕНИЕ СО СТРАННЫМ АТТРАКТОРОМ
- СИСТЕМА ДВУХДИСКОВОГО ДИНАМО РИКИТАКЕ
- МЕТАСТАБИЛЬНЫЙ ХАОС: ПЕРЕХОД К УСТОЙЧИВОМУ ХАОТИЧЕСКОМУ ПОВЕДЕНИЮ В МОДЕЛИ ЛОРЕНЦА
- ПРЕДТУРБУЛЕНТНОСТЬ: РЕЖИМ, НАБЛЮДАЕМЫЙ В ТЕЧЕНИИ ЖИДКОСТИ, ОПИСЫВАЕМОЙ МОДЕЛЬЮ ЛОРЕНЦА
- ТОПОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ АТТРАКТОРОВ ЛОРЕНЦА