| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ФРАКТАЛЫ И ТУРБУЛЕНТНОСТЬ: АТТРАКТОРЫ И РАЗБРОС
Б. Мандельброт
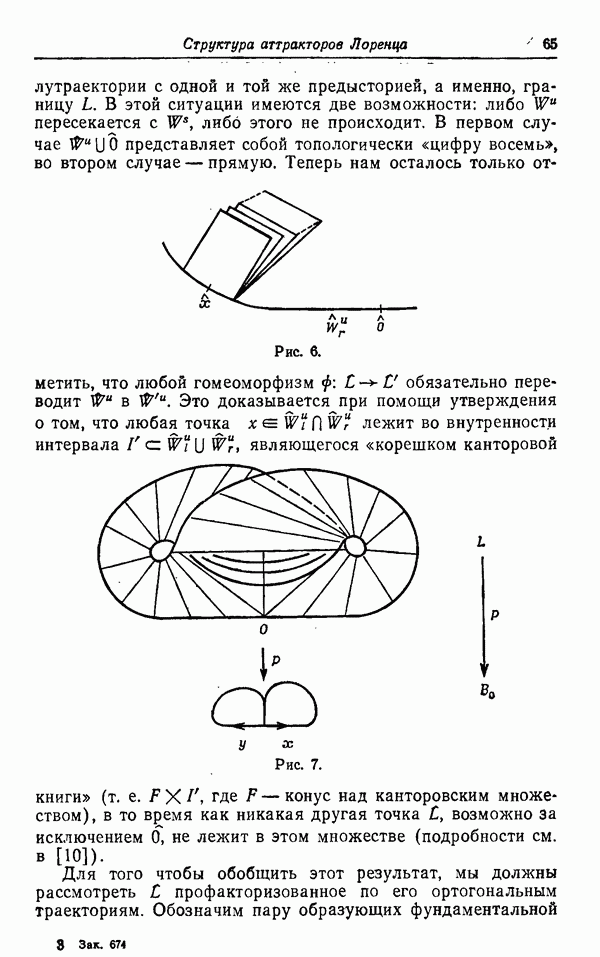
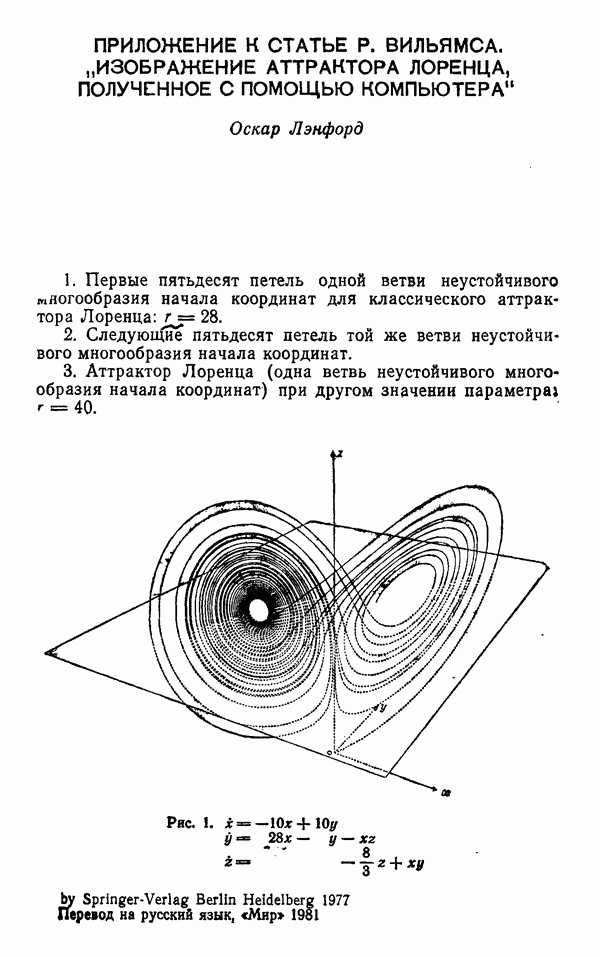
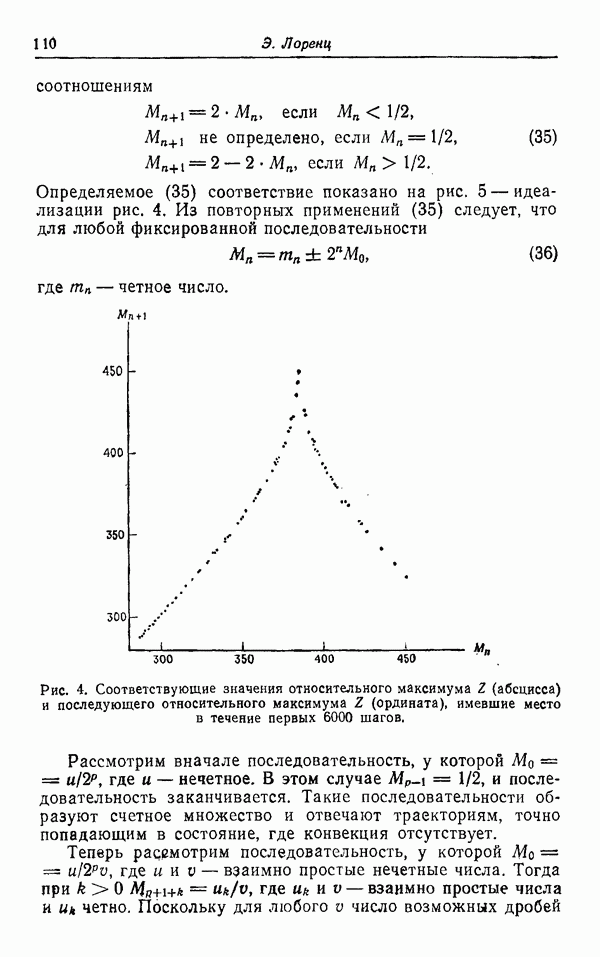
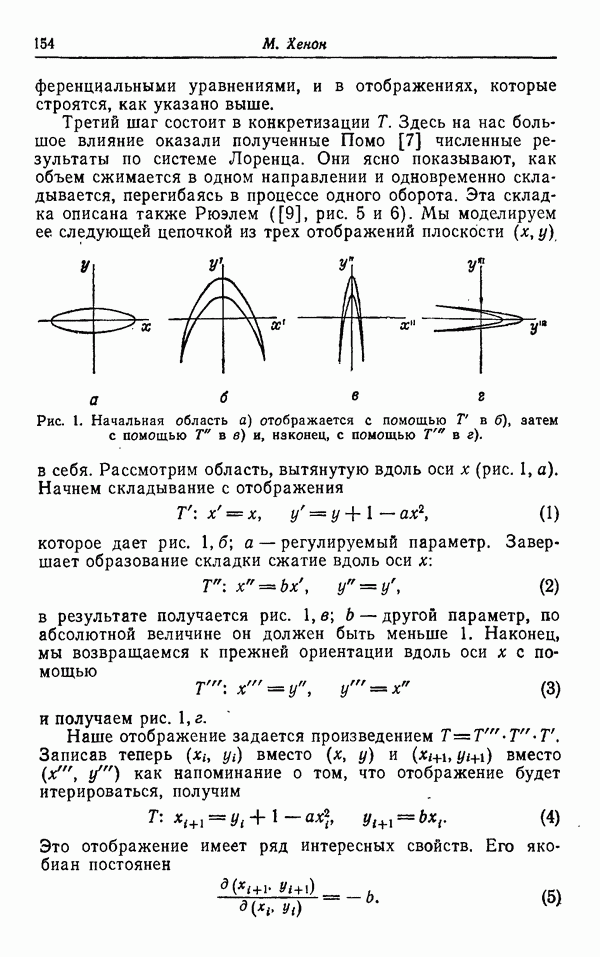
Возобновление интереса к математическим проблемам турбулентности связано с появлением ряда новых подходов, возникших почти одновременно и независимо друг от друга. Первый, связанный с теорией динамических систем, довольно полно представлен на этом семинаре и восходит к работам Лоренца [6] и Рюэля и Такенса [11]. Другой развит в работах Колмогорова [51, Бергера и Мандельброта [2] и Новикова и Стюарта [10]. Современное состояние вопроса изложено в работе Мандельброта [8] и в книге Мандельброта [9].
Оба подхода должны в конечном итоге привести к одним и тем же результатам, если, конечно, они относятся к одному и тому же явлению — а в этом нас убеждает работа У. Фриша — и если будет понята важная роль нестандартных множеств, которые я называю фракталами. В связи с исследованиями в этом направлении следует особо остановиться на понятии размерности Хаусдорфа — Безиковича D. Хотя это понятие является классическим, оно немногим известно, и поэтому ниже будет дано его определение. Однако уже сейчас было бы уместно сказать, что фрактальное множество это такое, для которого (см. цитированную выше книгу Мандельброта [9]) размерлость Хаусдорфа — Безиковича больше топологической размерности. Напротив, для стандартных множеств в евклидовом пространстве эти размерности совпадают. Понятие фрактальной структуры в широком смысле слова может служить синонимом структуры, связанной с размерностью D. Размерность D фрактального множества есть его фрактальная размерность.
Примером фрактального множества служит канторово множество, а также его произведение на интервал числовой оси. Этот последний пример рассмотрен в хорошо известной
работе Смейла [12] (см. также лекцию  ) и в статье Рюэля и Такенса [11]. Каждый шаг конструкции Смейла состоит в разбиении тора на
) и в статье Рюэля и Такенса [11]. Каждый шаг конструкции Смейла состоит в разбиении тора на  областей, причем обычно считают
областей, причем обычно считают  . В несколько ином виде разбиение на
. В несколько ином виде разбиение на  частей присутствует и в процедуре, предложеной Хилом, Новиковым и Стюартом, у которых фракталы фигурируют под именем «свертки». (Оба случая оторваны от имеющихся на сегодняшний день физических представлений.) В теории Новикова и Стюарта делается дополнительное (довольно слабо обоснованное) предположение, которое имеет свой аналог в теории Смейла, как об этом сказано в конце его лекции (но не в начале). Это предположение состоит в том, что на каждом шаге итерации множество (будь то свертка или пересечение области меридианом) разбивается на N подмножеств, которые подобны исходным с заданным коэффициентом
частей присутствует и в процедуре, предложеной Хилом, Новиковым и Стюартом, у которых фракталы фигурируют под именем «свертки». (Оба случая оторваны от имеющихся на сегодняшний день физических представлений.) В теории Новикова и Стюарта делается дополнительное (довольно слабо обоснованное) предположение, которое имеет свой аналог в теории Смейла, как об этом сказано в конце его лекции (но не в начале). Это предположение состоит в том, что на каждом шаге итерации множество (будь то свертка или пересечение области меридианом) разбивается на N подмножеств, которые подобны исходным с заданным коэффициентом 
Предположение относительно N является топологическим; напротив, предположение, касающееся  , носит метрический характер. Мы отметим одно метрическое свойство, состоящее в том, что в данном случае фрактальная размерность равна
, носит метрический характер. Мы отметим одно метрическое свойство, состоящее в том, что в данном случае фрактальная размерность равна  Существует много способов оценить размерность D по исходным данным (см. цитированную выше книгу «Фракталы»), и их практическая важность наводит на мысль, что подход, основанный на теории динамических систем, должен был бы развиваться, не касаясь топологии в той ее части, которая относится к теории фрактальных множеств. Аналогичное замечание применимо к исследованиям типа Лоренца [6]; нет сомнений (хотя факт остается недоказанным), что соответствующий «хуже, чем странный» аттрактор является фрактальным множеством; но его размерность мне не известна. Представляет существенный интерес вопрос о том, в какой степени реальная турбулентность моделируется простыми системами этого типа (например, моделью Хенона). Теория фрактальных множеств в этом случае могла бы оказать помощь скорее в количественном, чем в качественном отношении. (Значение размерности D может играть и в ряде случаев действительно играет роль показателя в спектральной плотности. Иногда кажется, что упрощенные динамические системы не могут приводить к колмогоровскому
Существует много способов оценить размерность D по исходным данным (см. цитированную выше книгу «Фракталы»), и их практическая важность наводит на мысль, что подход, основанный на теории динамических систем, должен был бы развиваться, не касаясь топологии в той ее части, которая относится к теории фрактальных множеств. Аналогичное замечание применимо к исследованиям типа Лоренца [6]; нет сомнений (хотя факт остается недоказанным), что соответствующий «хуже, чем странный» аттрактор является фрактальным множеством; но его размерность мне не известна. Представляет существенный интерес вопрос о том, в какой степени реальная турбулентность моделируется простыми системами этого типа (например, моделью Хенона). Теория фрактальных множеств в этом случае могла бы оказать помощь скорее в количественном, чем в качественном отношении. (Значение размерности D может играть и в ряде случаев действительно играет роль показателя в спектральной плотности. Иногда кажется, что упрощенные динамические системы не могут приводить к колмогоровскому  спектру, о качестве упрощенной системы судят именно по ее способности предсказывать показатель -5/3.)
спектру, о качестве упрощенной системы судят именно по ее способности предсказывать показатель -5/3.)
Возможно, понятие странного аттрактора, введенное в работе Рюэля и Такенса, [11] является жертвой самого успеха, связанного с общим подходом, и желательно определить это понятие более описательно. Можно ввести, например, понятие фрактального аттрактора. (Можно было бы утверждать даже большее, что первые два слова в заголовке этой статьи составляют предмет всего нашего симпозиума, однако я вовсе не стремлюсь пропагандировать этот взгляд.)
Два аспекта понятия размерности: мотивировка. Характерная математическая особенность, которая, как нам кажется, присуща как аттрактору Лоренца и другим «странным» аттракторам, так и фрактальным множествам, состоит в следующем: два разных определения понятия «размерности» приводят в обоих случаях к разным численным значениям.

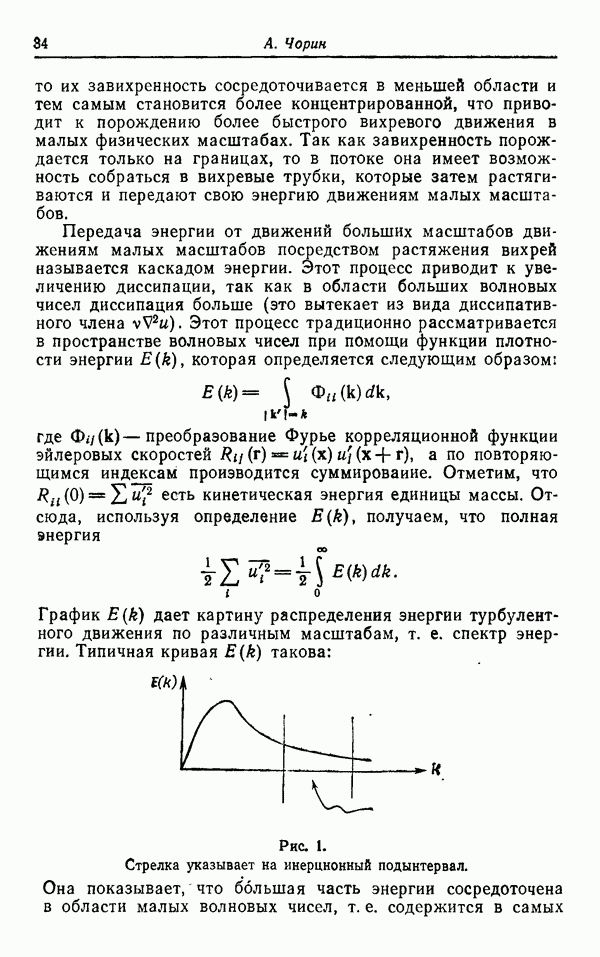
Рис. 1.
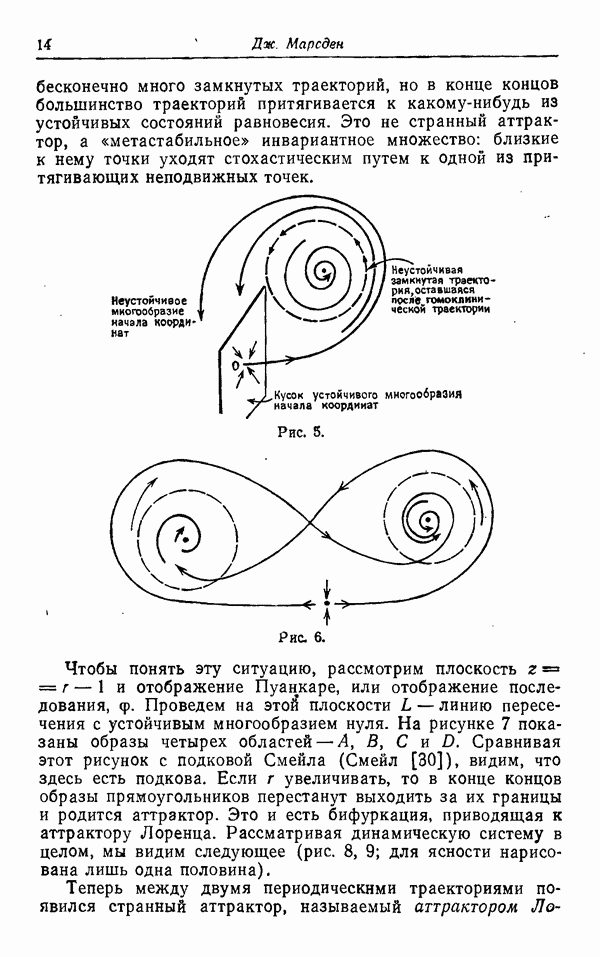
Это обстоятельство известно для фрактальных множеств и, вероятно, справедливо для странных аттракторов. Согласно первому определению, размерность множества — это его топологическая размерность DT. Согласно второму, — это размерность Хаусдорфа — Безиковича. Прежде чем привести это определение, полезно объяснить связанное с размерностью Хаусдорфа — Безиковича понятие размерности подобия, иллюстрируемое рис, 1. (Приведенная иллюстрация представляет
собой один из многочисленных примеров фрактального множества.) На рис. 1 представлена комбинация из двух многоугольников (полигонов) с очень большим числом сторон. Эти многоугольники можно было бы назвать терагонами. По гречески teras — это чудо, или чудовище, а в метрической системе tera означает  . Один из этих терагонов интенсивно искривляется вокруг себя, как это делается при построении кривой, заполняющей плоскость. Наоборот, вторая кривая может быть названа окаймляющей. Оба терагона получаются применением процедуры фон Коха, первый — из начального многоугольника и второй — из стандартного многоугольника. Первый шаг конструкции состоит в замене каждой стороны начального многоугольника на масштабно-преобразованный и сдвинутый многоугольник. На втором шаге эта конструкция повторяется применительно к полученному на первом шаге многоугольнику и так далее до бесконечности.
. Один из этих терагонов интенсивно искривляется вокруг себя, как это делается при построении кривой, заполняющей плоскость. Наоборот, вторая кривая может быть названа окаймляющей. Оба терагона получаются применением процедуры фон Коха, первый — из начального многоугольника и второй — из стандартного многоугольника. Первый шаг конструкции состоит в замене каждой стороны начального многоугольника на масштабно-преобразованный и сдвинутый многоугольник. На втором шаге эта конструкция повторяется применительно к полученному на первом шаге многоугольнику и так далее до бесконечности.

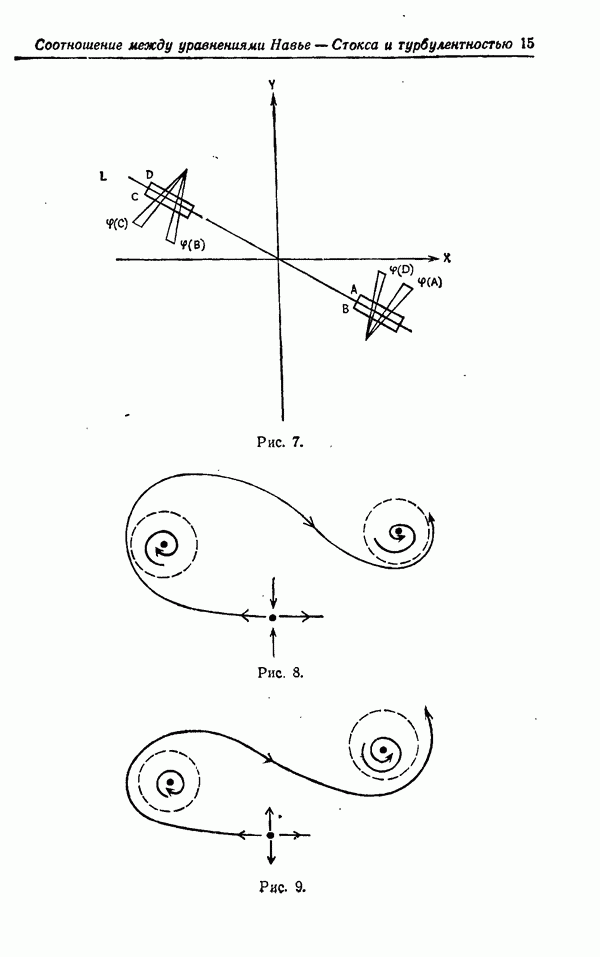
Рис. 2.
Первые шаги этой конструкции представлены на рис. 2. Начальным и стандартным многоугольниками служат соответственно единичный квадрат и открытый нерегулярный многоугольник с  сторонам
сторонам  (Его стороны проходят через каждую вершину некоторой решетки, содержащейся в единичном квадрате.) Далее, к каждой стороне этого
(Его стороны проходят через каждую вершину некоторой решетки, содержащейся в единичном квадрате.) Далее, к каждой стороне этого  -стороннего многоугольника пристраивается точно такой же полигон, но уменьшенный в отношении
-стороннего многоугольника пристраивается точно такой же полигон, но уменьшенный в отношении  Складываясь, они образуют многоугольник, граница которого может быть получена путем замены каждой стороны квадрата некоторой ломаной, составленной из
Складываясь, они образуют многоугольник, граница которого может быть получена путем замены каждой стороны квадрата некоторой ломаной, составленной из  звеньев длины
звеньев длины 
Напомним, что известная кривая Пеано и ее разновидности, появившиеся около 1900 г., также заполняют квадрат
или треугольник, однако современные варианты этих кривых, похожие на ту, которая описана выше, отличаются большим разнообразием в форме границ.
Так как на каждом шаге конструкции периметры обоих многоугольников умножаются на фиксированное число  то длины соответствующих предельных кривых равны бесконечности. Но степень заполнения плоскости вторым многоугольником больше, чем степень изогнутости первого. Более точно это обстоятельство формулируется на математическом языке с помощью понятия размерности подобия. Неформальное объяснение этого понятия основано на следующем факте: для каждого целого числа у «целый»
то длины соответствующих предельных кривых равны бесконечности. Но степень заполнения плоскости вторым многоугольником больше, чем степень изогнутости первого. Более точно это обстоятельство формулируется на математическом языке с помощью понятия размерности подобия. Неформальное объяснение этого понятия основано на следующем факте: для каждого целого числа у «целый»  -мерный параллелепипед можно замостить
-мерный параллелепипед можно замостить  «кусочками», каждый из которых является параллелепипедом, подобным данному с коэффициентом подобия
«кусочками», каждый из которых является параллелепипедом, подобным данному с коэффициентом подобия  . Следовательно,
. Следовательно,  Таким образом, определение размерности подобия как показателя самоподобия, формально применимо всякий раз, когда какой-либо целый объект может быть разбит на N частей, каждая из которых подобна исходному с коэффициентом подобия
Таким образом, определение размерности подобия как показателя самоподобия, формально применимо всякий раз, когда какой-либо целый объект может быть разбит на N частей, каждая из которых подобна исходному с коэффициентом подобия  (они получаются друг из друга с помощью сдвига или симметрии). В нашем случае можно определить размерность каждой из предельных кривых. Для окантовки
(они получаются друг из друга с помощью сдвига или симметрии). В нашем случае можно определить размерность каждой из предельных кривых. Для окантовки  и, следовательно,
и, следовательно,  Для кривой, заполняющей плоскость
Для кривой, заполняющей плоскость  следовательно,
следовательно,  Таким образом, утверждение о том, что заполнение происходит быстрее, чем окаймление, получает количественное подтверждение в виде неравенства между размерностями подобия. Тот факт, что вторая предельная кривая действительно заполняет плоскость, подтверждается тем, что ее размерность подобия равна 2.
Таким образом, утверждение о том, что заполнение происходит быстрее, чем окаймление, получает количественное подтверждение в виде неравенства между размерностями подобия. Тот факт, что вторая предельная кривая действительно заполняет плоскость, подтверждается тем, что ее размерность подобия равна 2.
Размерность Хаусдорфа — Безиковича и фракталы.
Первый шаг в общем определении размерности D состоит во введении хаусдорфовой  -меры. Для заданного множества S в метрическом пространстве и данного
-меры. Для заданного множества S в метрическом пространстве и данного  рассматривается покрытие S шарами радиусов
рассматривается покрытие S шарами радиусов  и образуется сумма
и образуется сумма  ; берется нижняя грань этих сумм по всем покрытиям, для которых
; берется нижняя грань этих сумм по всем покрытиям, для которых  , и далее ищется предел при
, и далее ищется предел при  таких нижних граней. Полученное в результате число
таких нижних граней. Полученное в результате число  называется хаусдорфовой
называется хаусдорфовой  -мерой множества S. Существует такое значение d, обозначаемое через D, что
-мерой множества S. Существует такое значение d, обозначаемое через D, что  для
для  для
для  Это число называется размерностью Хаусдорфа — Безиковича множества
Это число называется размерностью Хаусдорфа — Безиковича множества 
Очевидно, это понятие размерности является скорее метрическим, чем топологическим свойством; я рассматриваю размерность D как «фрактальное» свойство. Более точно, по теореме Шпильрайна (см. Гуревич и Веллмэн [4], стр. 107) топологическая размерность и введенная выше размерность D связаны между собой соотношением  . Это объясняет определение фрактальных множеств как таких, для которых
. Это объясняет определение фрактальных множеств как таких, для которых  Окаймляющая кривая, изображенная на рис. 1, имеет топологическую размерность, равную 1; следовательно, кривая, являющаяся пределом окаймляющих, будет фрактальной. Для триадического канторова множества
Окаймляющая кривая, изображенная на рис. 1, имеет топологическую размерность, равную 1; следовательно, кривая, являющаяся пределом окаймляющих, будет фрактальной. Для триадического канторова множества  в то время как
в то время как  следовательно, это множество фрактальное. Для канторова множества, рассмотренного Смейлом в лекции III,
следовательно, это множество фрактальное. Для канторова множества, рассмотренного Смейлом в лекции III,  . (Однако, взяв число N достаточно большим, можно получить по этой формуле любое значение размерности
. (Однако, взяв число N достаточно большим, можно получить по этой формуле любое значение размерности  Размерности изоповерхности скаляров в гауссовом приближении однородной колмогоровской турбулентности равны
Размерности изоповерхности скаляров в гауссовом приближении однородной колмогоровской турбулентности равны  следовательно, это фрактальная поверхность. (Хотя это значение размерности D постоянно использовалось в книге «Фракталы», полное формальное доказательство было получено намного позже, так что в библиографии к этой книге отсутствует соответствующая ссылка на работу Адлера [1].)
следовательно, это фрактальная поверхность. (Хотя это значение размерности D постоянно использовалось в книге «Фракталы», полное формальное доказательство было получено намного позже, так что в библиографии к этой книге отсутствует соответствующая ссылка на работу Адлера [1].)
Очень часто размерность D совпадает с размерностью подобия, рассмотренной в предыдущем параграфе.
Связь между фрактальной размерностью и метрической энтропией.
По теореме Безиковича и Эгглестона (см. Билингслей, [3]) фрактальная размерность при некоторых условиях совпадает с энтропийной характеристикой в теории информации б); в ряде случаев существует такое целое С и вероятности  что
что  .
.
Например, для канторова триадического множества  в то время как
в то время как  (следовательно,
(следовательно,  ); так что
); так что  Для сравнения топологическая
Для сравнения топологическая
энтропия равна  с неспецифическим для этого случая выбором основания логарифма. В случае метрической энтропии это основание равно
с неспецифическим для этого случая выбором основания логарифма. В случае метрической энтропии это основание равно 
Указанные соотношения между метрической энтропией и фрактальной размерностью могут помочь в установлении связи между динамическим и фрактальным аспектами турбулентности.
Разброс траектории жидкой частицы.
Задача фрактальнсго подхода заключается не в том, чтобы снабдить нас готовой теорией, а в том, чтобы помочь сформулировать эмпирические факты на геометрическом языке, провести дальнейшие эксперименты и поставить математические проблемы. В турбулентном случае рассмотрим явление дисперсии, когда вначале мы имеем гладкую кривую типа прямолинейного отрезка. Согласно одной из теорий, в случае однородной турбулентности длина этой кривой возрастает с течением времени экспоненциально. Легче представить себе наглядно, что будет при затухании одного «сгустка» турбулентной энергии. С точки зрения Ричардсона, рассматриваемый процесс является автомодельным и состоит из последовательных шагов, на каждом из которых длина кривой умножается на некоторое число, представляющее собой либо фиксированную постоянную, либо случайную величину с заданным распределением. Таким образом, это есть некоторый вариант процедуры Коха, изображенной на рисунках 1 и 2. Если бы этот процесс можно было продолжить до бесконечности (пренебрегая вязкостью и эффектами молекулярной диффузии), то мы пришли бы к некоторому предельному фрактальному множеству, и возник бы следующий вопрос: будет ли это предельное множество иметь размерность  и, следовательно, заполнять область в пространстве или же
и, следовательно, заполнять область в пространстве или же 
В сравнении с двумерной ситуацией случай  соответствует окаймляющей кривой, изображенной на рис. 1, в то время как случай
соответствует окаймляющей кривой, изображенной на рис. 1, в то время как случай  отвечает кривой, заполняющей плоскость. Исследуем первую возможность этой альтернативы. Можно представлять себе каждый
отвечает кривой, заполняющей плоскость. Исследуем первую возможность этой альтернативы. Можно представлять себе каждый  -сторонний полигон, фигурирующий в конструкции Коха, кривой, заполняющей плоскость, как небольшой вихрь (включая в это рассмотрение и перенос вещества). Отметим, что, начиная с двух разных начальных кривых, имеющих одинаковые длины, мы придем к двум областям с равными площадями. (В пространстве равным
-сторонний полигон, фигурирующий в конструкции Коха, кривой, заполняющей плоскость, как небольшой вихрь (включая в это рассмотрение и перенос вещества). Отметим, что, начиная с двух разных начальных кривых, имеющих одинаковые длины, мы придем к двум областям с равными площадями. (В пространстве равным
длинам соответствуют равные объемы.) Однако этот интересный факт перестает быть верным, если лежащая в основе процедуры Коха ломаная линия является окаймляющей кривой не квадрата, а границы некоторой области. Эта область может представлять собой целый квадрат, и первый шаг конструкции состоит в замене этого квадрата на 17 квадратиков; в совокупности они составляют некоторую область, граница которой может быть взята в качестве первого шага при построении окаймляющей кривой; далее процедура повторяется. Отметим, что наша кривая, опирающаяся на область, вкладывается в область, опирающуюся на область, и поэтому результат, полученный в первом случае, совпадает с результатом, полученным во втором. Любое другое начальное множество снова приводит к тому же результату, если оно содержится в квадрате и содержит его нижнюю сторону. Например, представим себе жидкость, находящуюся в трубе с диаметром 1/10 стороны начального квадрата, конец которой имеет форму, похожую на половину батона колбасы. Наша процедура преобразует эту область сначала в 17 меньших, потом в 172 меньших и т. д. Пределом будет вся внутренность, окаймленная кривой, изображенной на рис. 1. На каждом шаге конструкции отображение приклейки разрывно вдоль линий, где на предыдущих шагах были «вихри».
Перемешивание, (предположительно) имеющее место в турбулентных системах, связано, грубо говоря, с нестационарностыо. Это полностью отличает турбулентность от обычных стационарных отображений типа преобразования пекаря. Второе отличие: это «турбулентное» перемешивание допускает существование неподвижных точек, число которых экспоненциально увеличивается, в то время как перемешивающее преобразование пекаря имеет одну неподвижную точку. Третье отличие: есть основания ожидать, что последовательные шаги описанной выше процедуры применительно к турбулентности происходят с возрастающей скоростью, так что предельное положение достигается за конечное время. (Обозначая это время через t, получим, что длина будет расти как  с постоянным а.)
с постоянным а.)
Предыдущая модель легко обобщается. Предположим, что мы имеем дело с чисто ламинарными движениями. Получаемая при этом окончательная форма будет не столько «сферической», сколько иметь вид длинной узкой полоски; ее общие
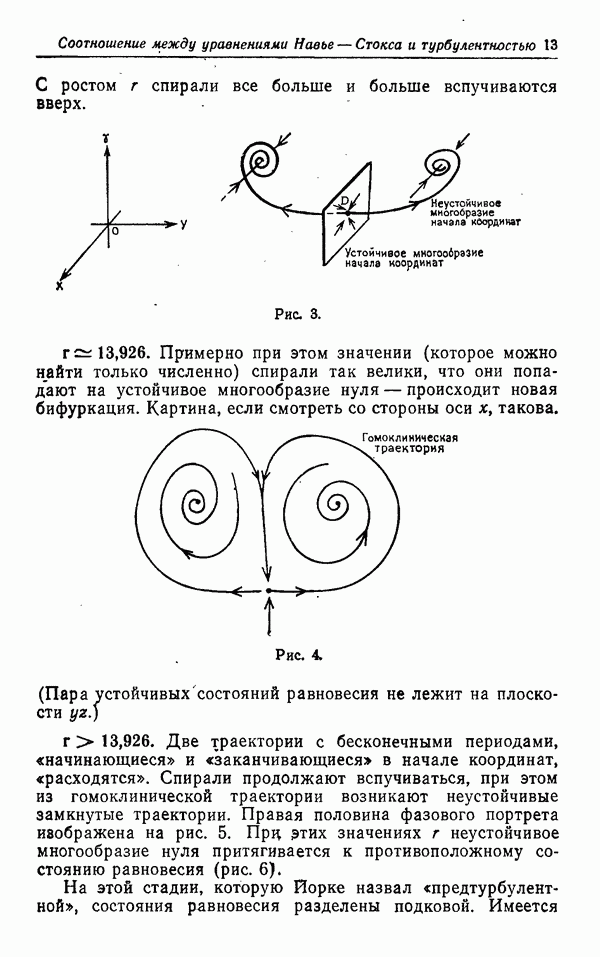
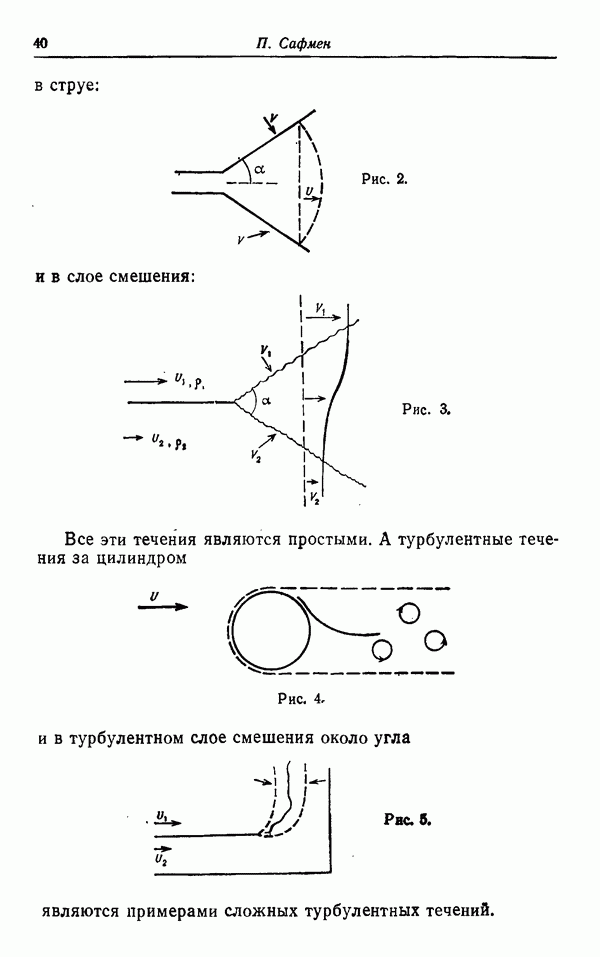
очертания вырисовываются как для турбулентного, так и для ламинарного потока, а детали структуры — только в турбулентном случае. Более того, получаемые вихри могут иметь различные размеры, как показано на рис. 3. В отличие
(см. скан)
Рис. 3.
от метода Коха применяемый здесь алгоритм оказывается более сложным в некоторых отношениях, на которых мы не будем подробно останавливаться. Грубо говоря, начальная форма (аналог «батона колбасы») имеет вид треугольника. Первые шаги конструкции явно видны (в уменьшенном масштабе) для восьми треугольников, расположенных в правом верхнем углу рисунка.
Иная точка зрения на турбулентность связывает ее с переходом от кривой, размерность которой  к фрактальной кривой, размерность которой
к фрактальной кривой, размерность которой  Легко видеть, что в плоском случае этому отвечает переход от кривой с
Легко видеть, что в плоском случае этому отвечает переход от кривой с  к кривой с
к кривой с  примером чему служит обертывающая кривая, приведенная в нижней четверти на рис. 1. Однако довольно трудно изобразить пространственный аналог этой кривой. Проще представить себе область в пространстве, ограниченную двумерной поверхностью, которая дисперсирует в область, ограниченную поверхностью с размерностью
примером чему служит обертывающая кривая, приведенная в нижней четверти на рис. 1. Однако довольно трудно изобразить пространственный аналог этой кривой. Проще представить себе область в пространстве, ограниченную двумерной поверхностью, которая дисперсирует в область, ограниченную поверхностью с размерностью  Например, см. книгу «Фракталы», стр. 52, где приведены (отчасти слабые) доводы в пользу того, что
Например, см. книгу «Фракталы», стр. 52, где приведены (отчасти слабые) доводы в пользу того, что  Подобным образом можно рассматривать струю жидкости, диаметр которой достаточно мал в единицах внешнего масштаба, но достаточно велик в единицах внутреннего масштаба, диктуемого вязкостью. Так как процесс развивается и образуется все больше вихрей со все меньшими диаметрами, эта струя должна вытягиваться и загибаться на себя. Предположение о том, что диаметры струи и вихрей пропорциональны, приводит снова к случаю
Подобным образом можно рассматривать струю жидкости, диаметр которой достаточно мал в единицах внешнего масштаба, но достаточно велик в единицах внутреннего масштаба, диктуемого вязкостью. Так как процесс развивается и образуется все больше вихрей со все меньшими диаметрами, эта струя должна вытягиваться и загибаться на себя. Предположение о том, что диаметры струи и вихрей пропорциональны, приводит снова к случаю  Для того чтобы получить
Для того чтобы получить  нужно предположить, что диаметры вихрей уменьшаются быстрее, чем диаметр струи. Такие вихри будут вытягивать струю до тех пор, пока ее диаметр не станет равным диаметру вихрей. После этого вихри будут оказывать влияние только на детали поверхности струи. Эффективная длина струи не будет изменяться.
нужно предположить, что диаметры вихрей уменьшаются быстрее, чем диаметр струи. Такие вихри будут вытягивать струю до тех пор, пока ее диаметр не станет равным диаметру вихрей. После этого вихри будут оказывать влияние только на детали поверхности струи. Эффективная длина струи не будет изменяться.
Конечно, в предыдущих построениях есть много свободных параметров, выбор которых вполне случаен, на что указывал Роберт Крейчнан. Однако в рамках указанной выше дихотомии между случаями  вероятность сколь-нибудь существенных отклонений от описанной картины мала. В первом случае она значительно меньше, чем во втором.
вероятность сколь-нибудь существенных отклонений от описанной картины мала. В первом случае она значительно меньше, чем во втором.
Перейдем теперь от рассмотрения отдельных сгустков турбулентной энергии к описанию однородной турбулентности, аппроксимируя процесс ее образования последовательностью сгустков. В случае  длина струи со временем будет расти экспоненциально по соображениям, указанным выше. Соответствующий ряд последовательных переходов должен быть ртационарньщ.
длина струи со временем будет расти экспоненциально по соображениям, указанным выше. Соответствующий ряд последовательных переходов должен быть ртационарньщ.
Прежде чем заниматься деталями модели турбулентности, желательно еще раз проанализировать более тщательно, чем это сделано мною в этой лекции, какой из упомянутых выше вариантов — а, может быть, это будет совсем другой вариант — лучше всего подходит для этого. Коль скоро один из этих вариантов положен в основу модели турбулентности, наши рассуждения, касающиеся итерационной процедуры, оказываются слишком общими, чтобы восприниматься всерьез, однако лежащие в их основе геометрические соображения, вероятно, будут полезны.
СПИООК ЛИТЕРАТУРЫ
1. Adler R. J. Hausdorff dimension and Gaussian fields. The Annals of Probability, Vol. 5, 145—151, 1977.
2. Berger J. М., Mandelbrot В. B. A new method model for the clustering of errors on telephone circuits. IBM Journal of Research and Development, Vol. 7, 224—236, 1963.
3. Billingsley P. Ergodic Theory and Information. New York: Wiley, 1967. (Русский перевод: Биллингслей П. Эргодическая теория и информация, Пер. с аигл. М.: Мир, 1969.)
4 Гуревич В., Волмэи Г. Теория размерности. Перев. с аигл. — М.: ИЛ, 1948.
5. Kolmogorov А. N. A refinement of previous hypothesis concerning the local structures of turbulence in a viscous incompressible fluid at high Reynolds number. Journal of Fluid Mechanics, Vol. 13, 82—85, 1962.
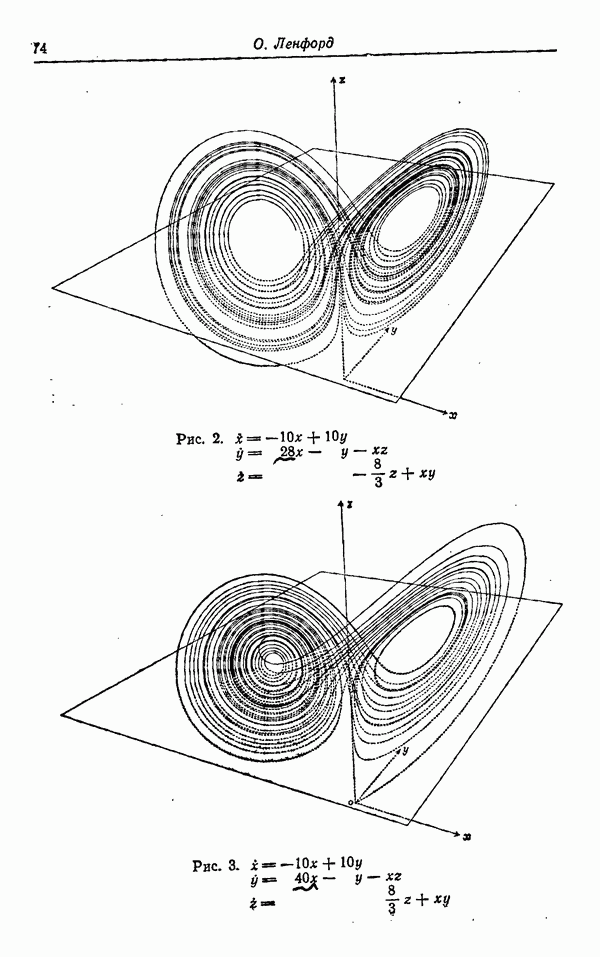
6. Lorenz E. N. Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, Vol. 20, 130—141, 1963 (см. наст, сб., стр. 88).
7. Mandelbrot В. В. Les objets fractals: forme, hasard et dimension. Paris and Montreal : Flammarion, 1975.
8. Mandelbrot В. B. Intermittent turbulence and fractal dimension: kurtosis and the spectral exponent 5/3 + B. In Turbulence and Navier Stokes
4 Equations, 121—145. Ed. R. Temam. Lecture Notes in Mathematics 565. ' New York, Springer, 1976.
9. Mandelbrot В. B. Fractals: form, chance, and dimension. San Francisco: W. H. Freeman and Company, 1977.
10. Новиков E. А., Стюарт P. Перемежаемость турбулентности и спектр флуктуаций функции энергии. Изи. АН СССР, Сер. геофиз., т. 3, 1964, с. 408—413.
!1. Ruelle D., Takens F. On the nature of turbulence. Communications on Mathematical Physics, Vol. 20, 167—192, Vol. 23, 343—344, 1971.
12. Смейл С. Дифференцируемые динамические системы, УМН, 25, № 1 (1970), 113—185.
13. Колмогоров А. Н. Асимптотические характеристики некоторых вполне ограниченных метрических пространств. Докл. АН СССР, т. 108, № 3, 1956, с. 585—589.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- ПОПЫТКИ УСТАНОВИТЬ СООТНОШЕНИЕ МЕЖДУ УРАВНЕНИЯМИ НАВЬЕ-СТОКСА И ТУРБУЛЕНТНОСТЬЮ
- ПРИЛОЖЕНИЕ К СТАТЬЕ МАРСДЕНА БИФУРКАЦИИ, ПОЛУПОТОКИ И УРАВНЕНИЯ НАВЬЕ—СТОКСА
- ТЕОРИИ ТУРБУЛЕНТНОСТИ
- ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ РАСЧЕТА ТУРБУЛЕНТНЫХ СДВИГОВЫХ ТЕЧЕНИЙ
- ФРАКТАЛЫ И ТУРБУЛЕНТНОСТЬ: АТТРАКТОРЫ И РАЗБРОС
- СТРУКТУРА АТТРАКТОРОВ ЛОРЕНЦА
- ПРИЛОЖЕНИЕ К СТАТЬЕ Р. ВИЛЬЯМСА. «ИЗОБРАЖЕНИЕ АТТРАКТОРА ЛОРЕНЦА, ПОЛУЧЕННОЕ С ПОМОЩЬЮ КОМПЬЮТЕРА»
- ДВА ПОДХОДА К МОДЕЛИРОВАНИЮ ДВУМЕРНОЙ ТУРБУЛЕНТНОСТИ
- ДЕТЕРМИНИРОВАННОЕ НЕПЕРИОДИЧЕСКОЕ ТЕЧЕНИЕ
- О ПРИРОДЕ ТУРБУЛЕНТНОСТИ
- ДВУМЕРНОЕ ОТОБРАЖЕНИЕ СО СТРАННЫМ АТТРАКТОРОМ
- СИСТЕМА ДВУХДИСКОВОГО ДИНАМО РИКИТАКЕ
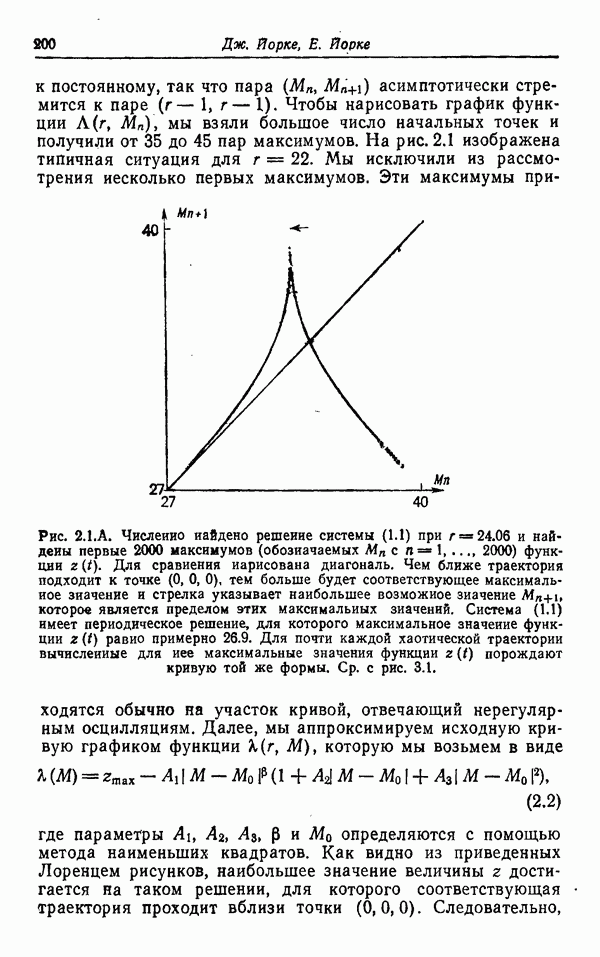
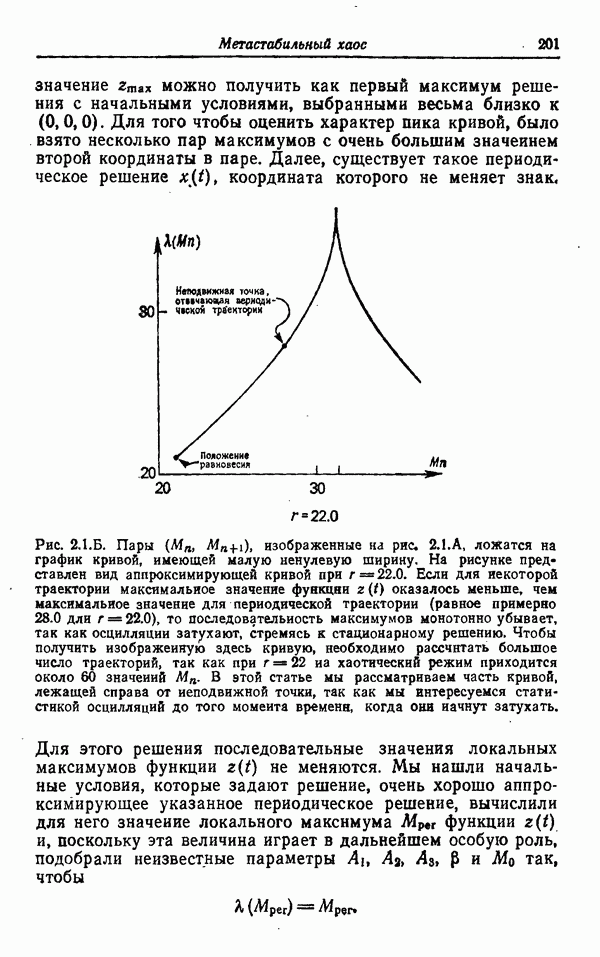
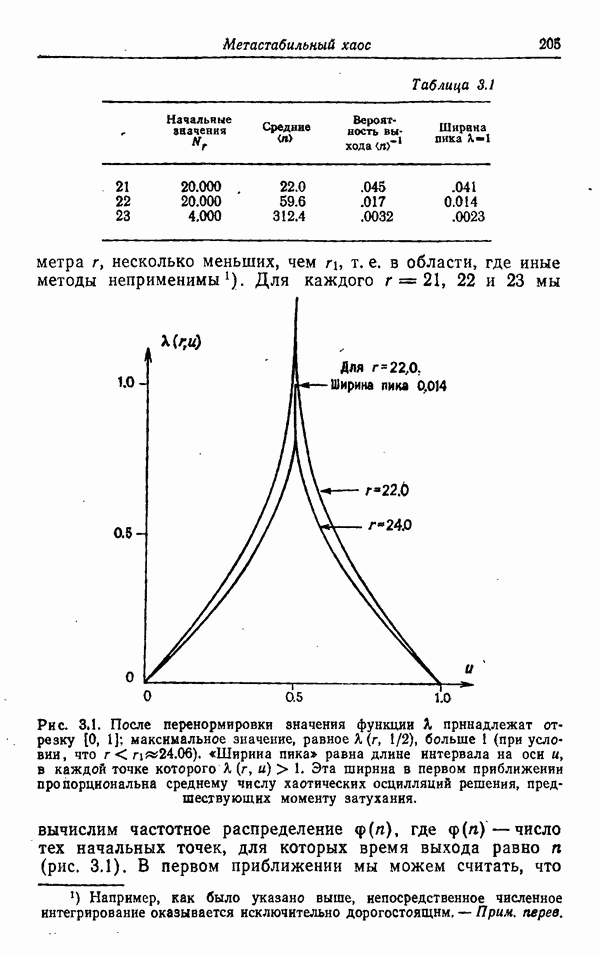
- МЕТАСТАБИЛЬНЫЙ ХАОС: ПЕРЕХОД К УСТОЙЧИВОМУ ХАОТИЧЕСКОМУ ПОВЕДЕНИЮ В МОДЕЛИ ЛОРЕНЦА
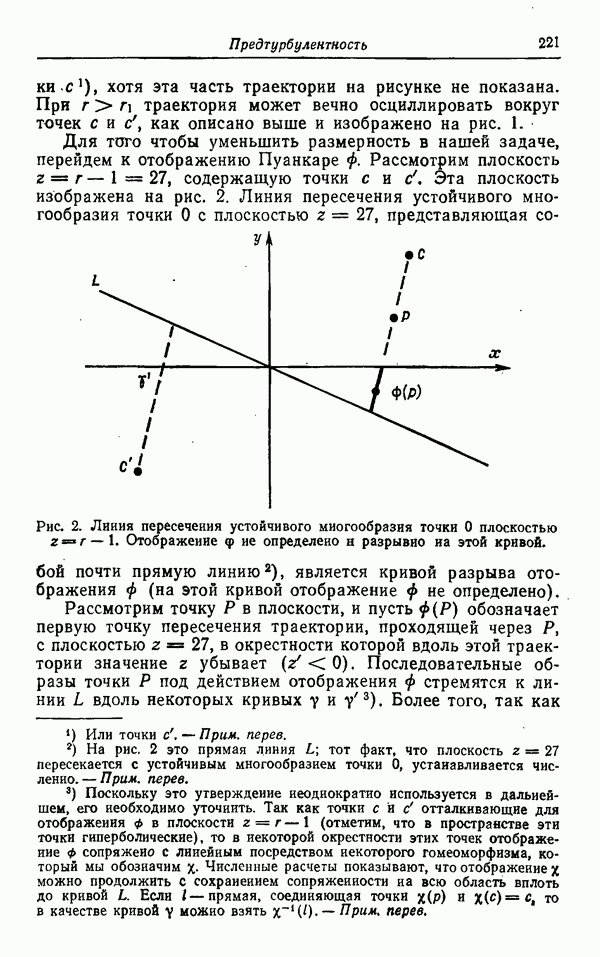
- ПРЕДТУРБУЛЕНТНОСТЬ: РЕЖИМ, НАБЛЮДАЕМЫЙ В ТЕЧЕНИИ ЖИДКОСТИ, ОПИСЫВАЕМОЙ МОДЕЛЬЮ ЛОРЕНЦА
- ТОПОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ АТТРАКТОРОВ ЛОРЕНЦА