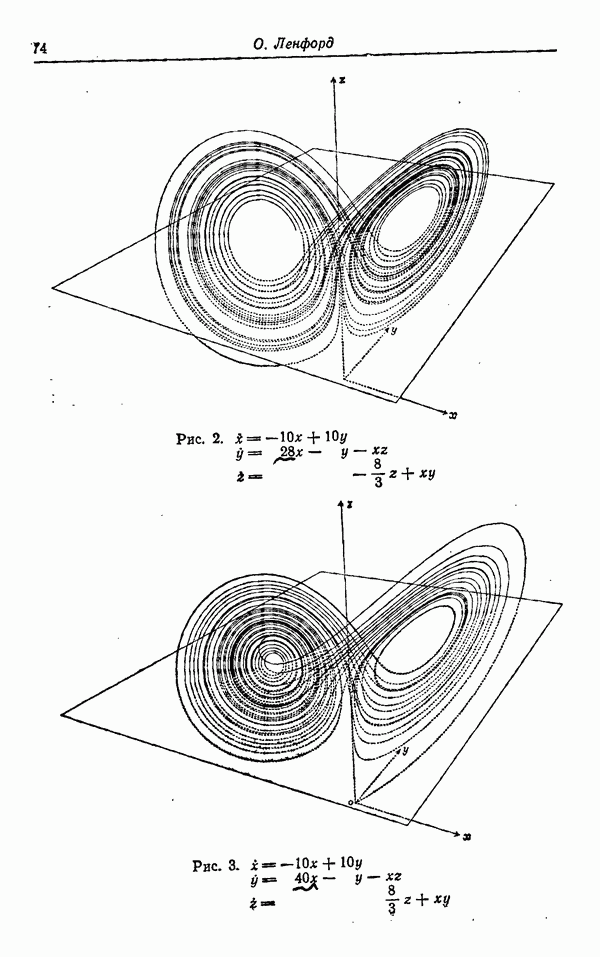
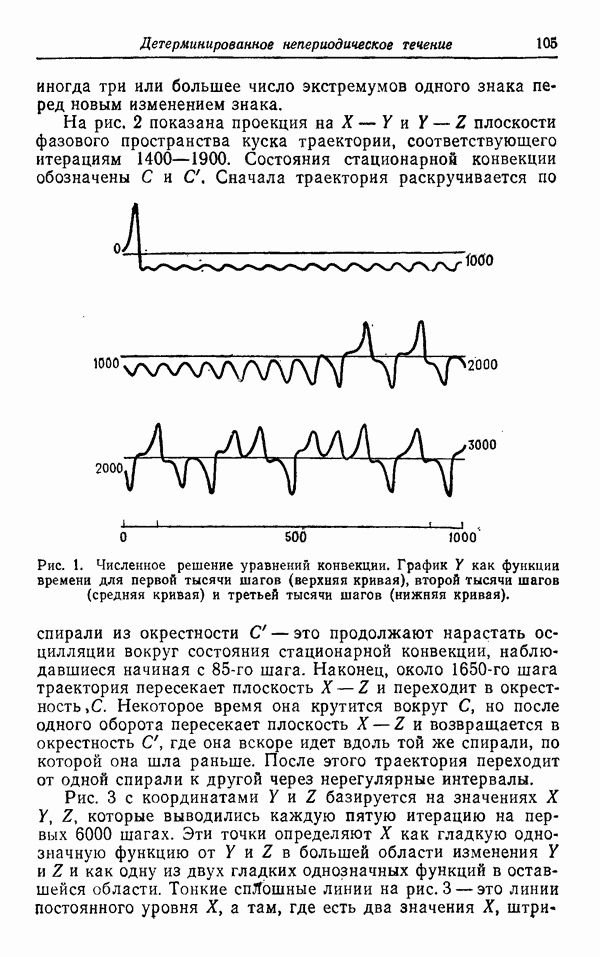
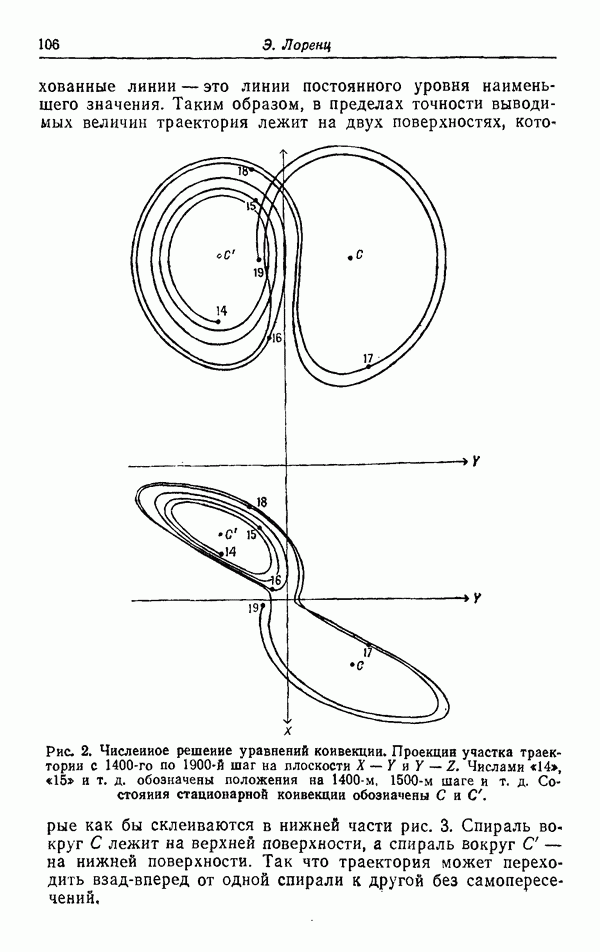
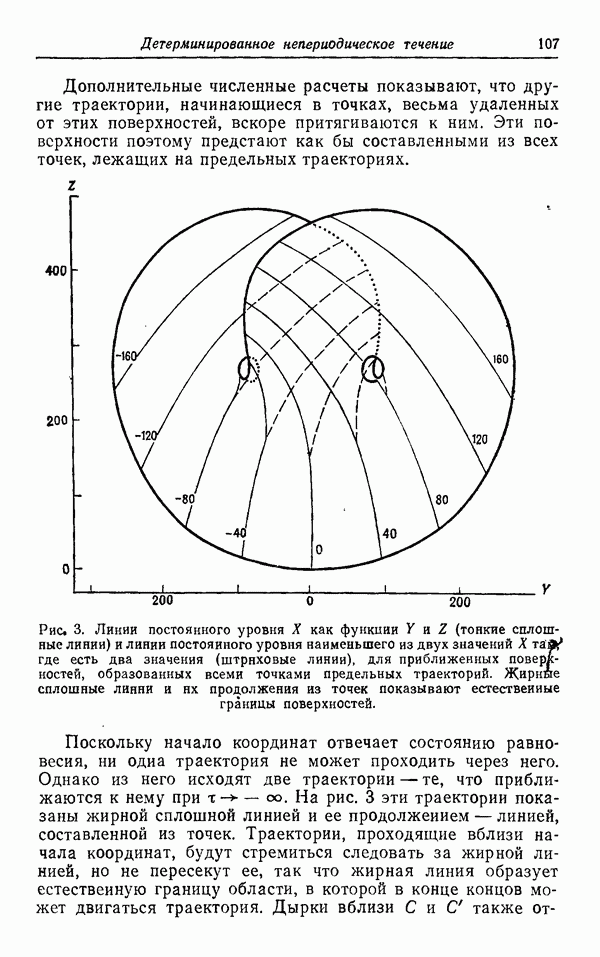
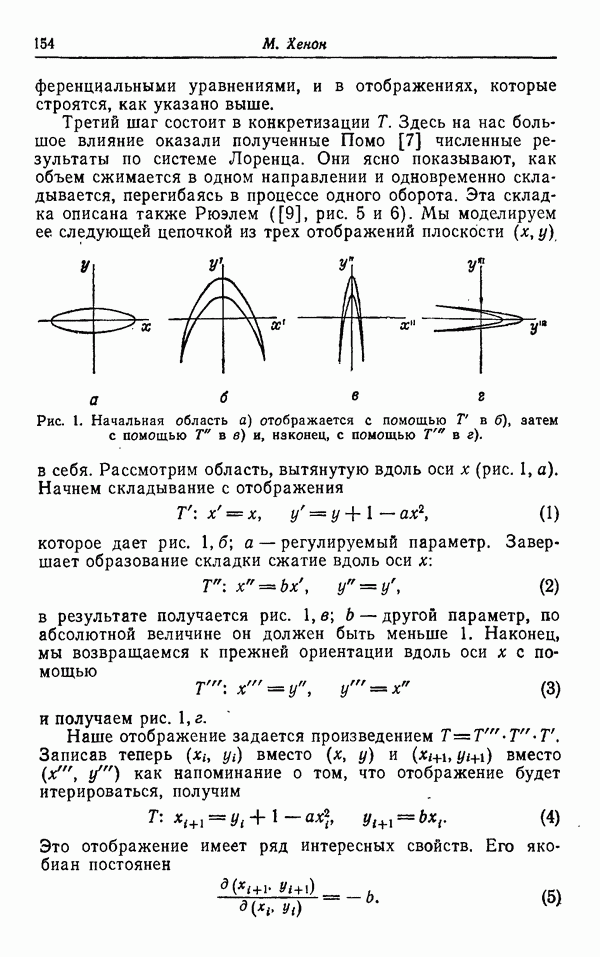
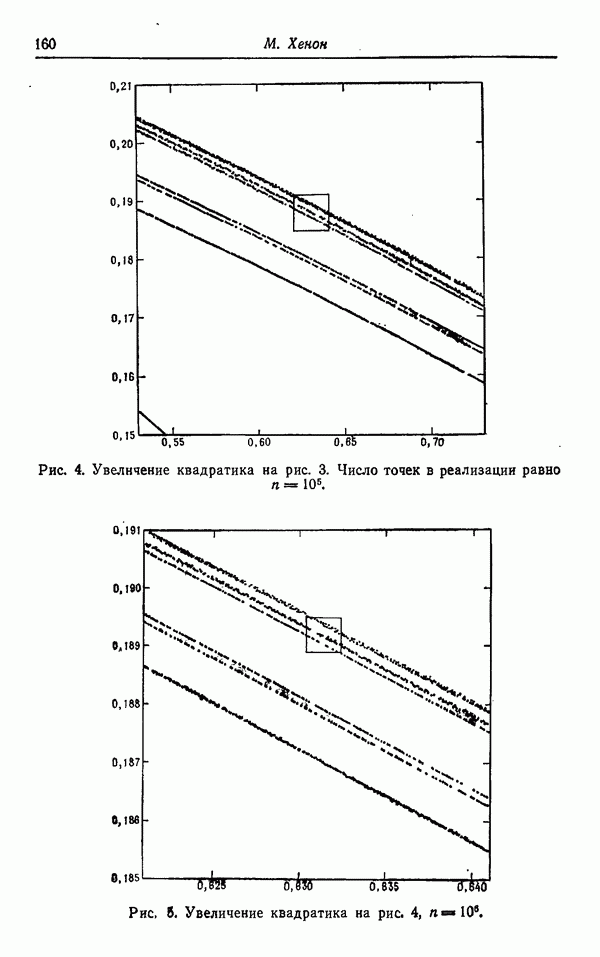
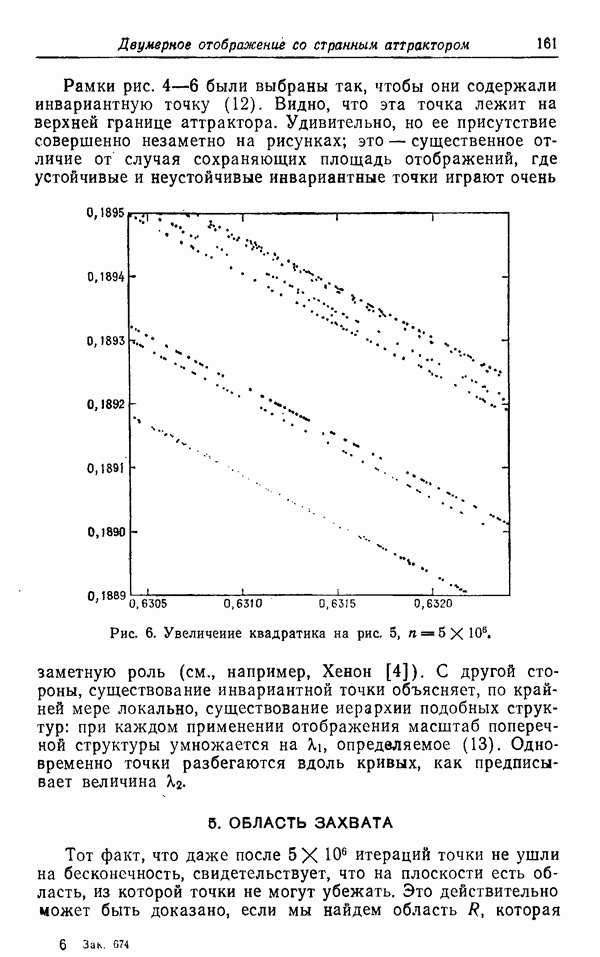
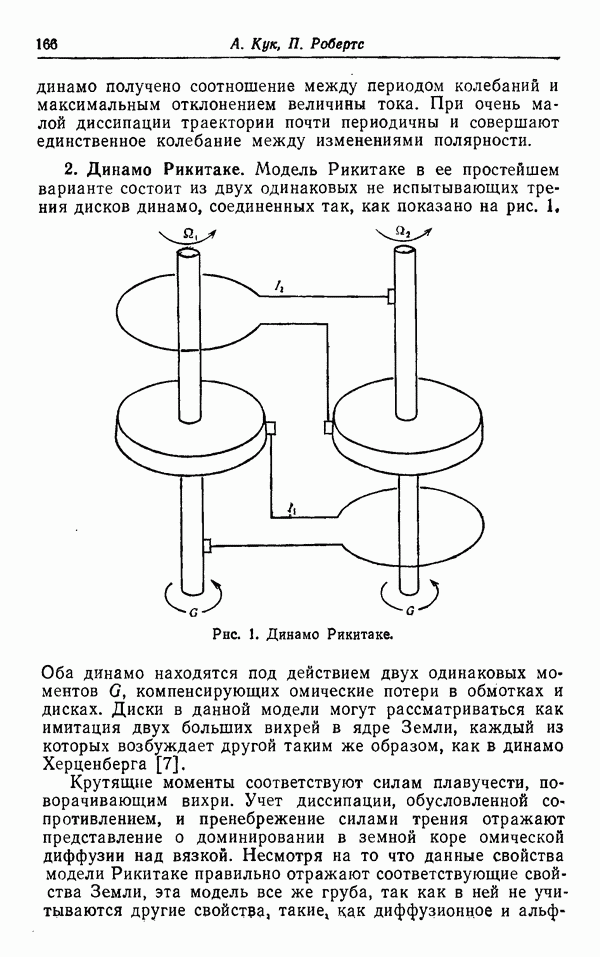
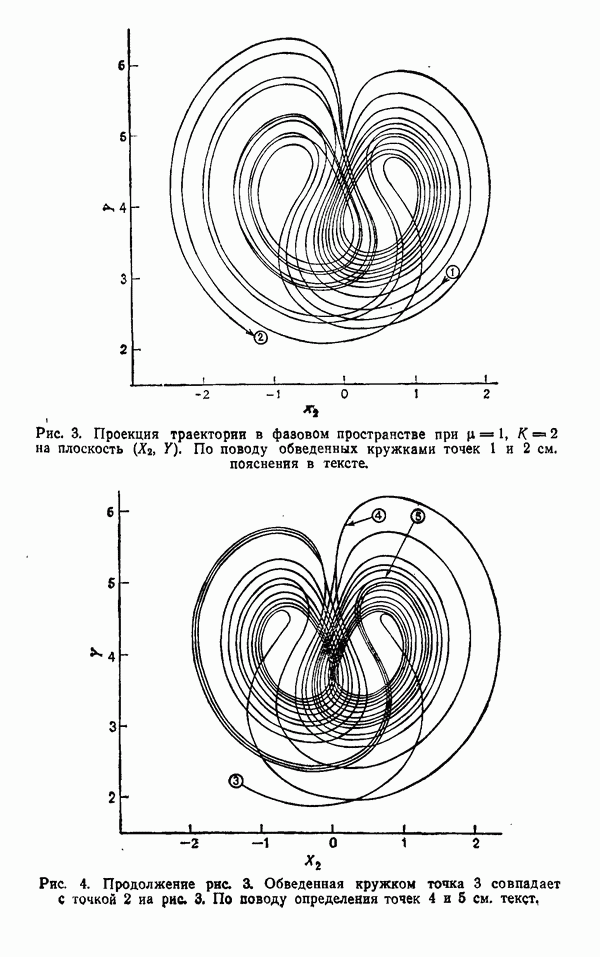
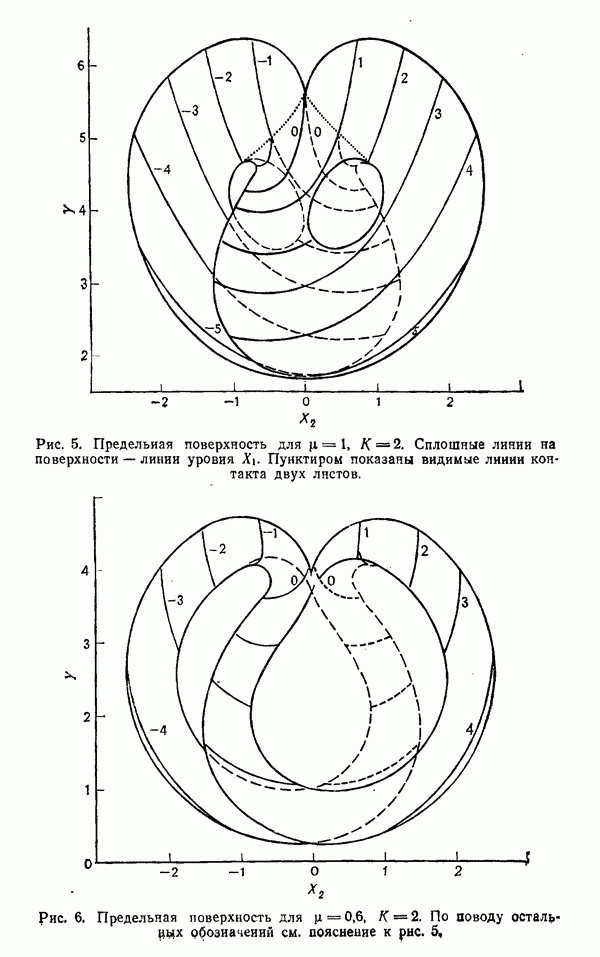
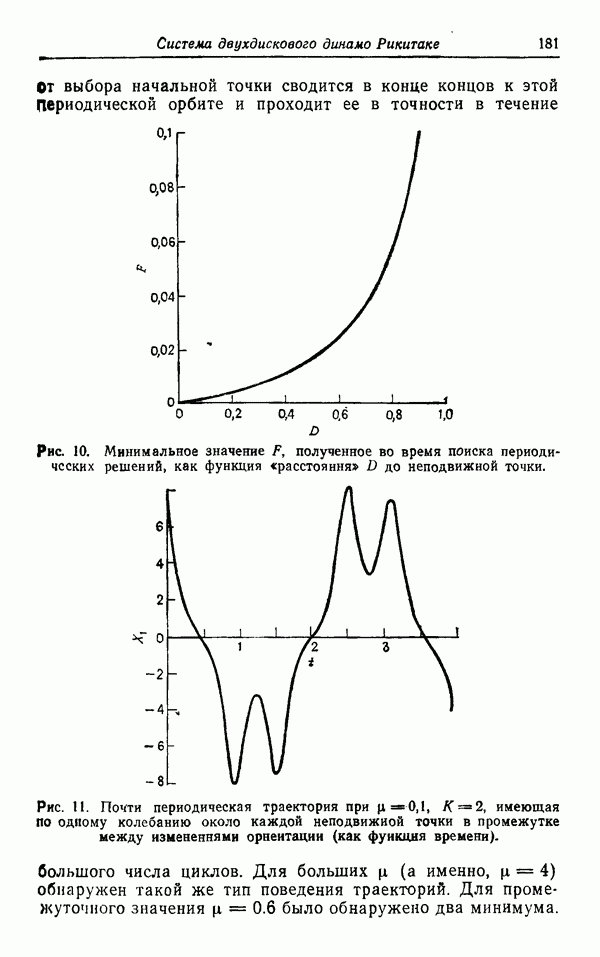
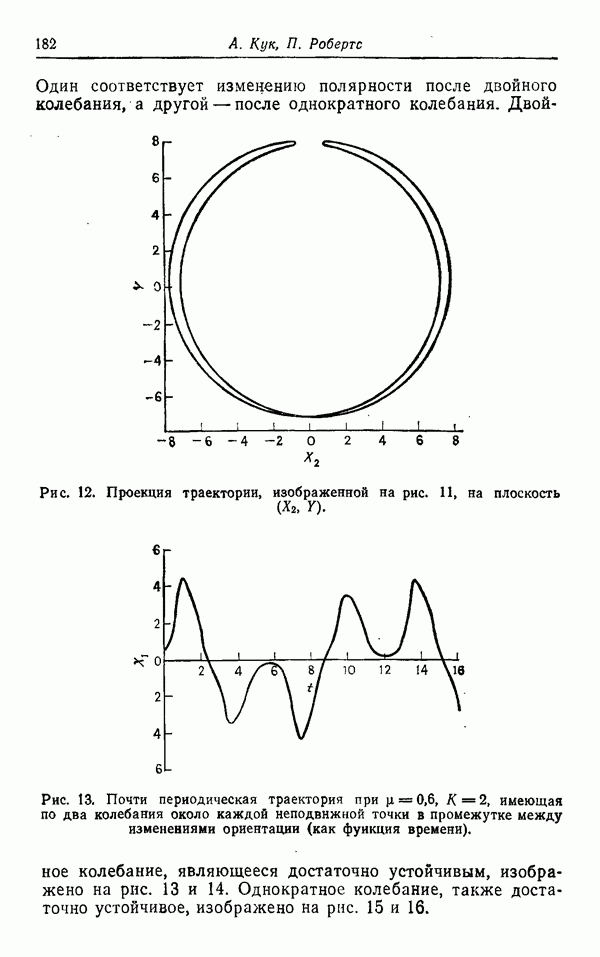
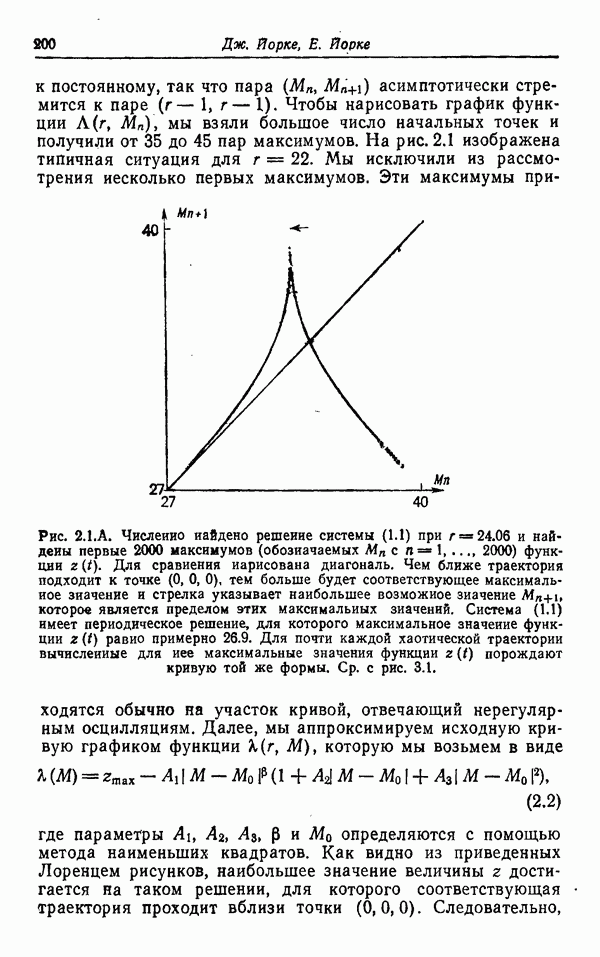
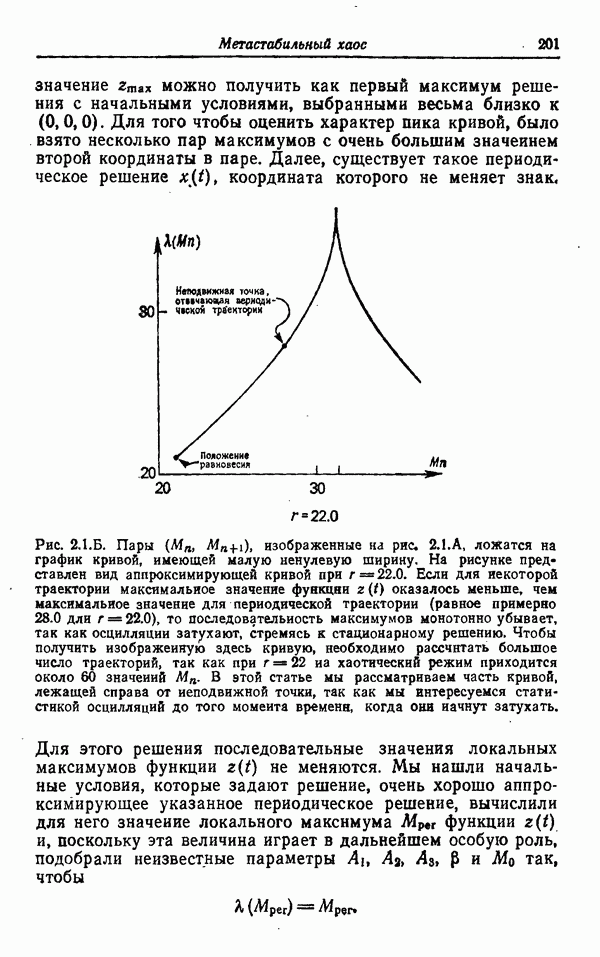
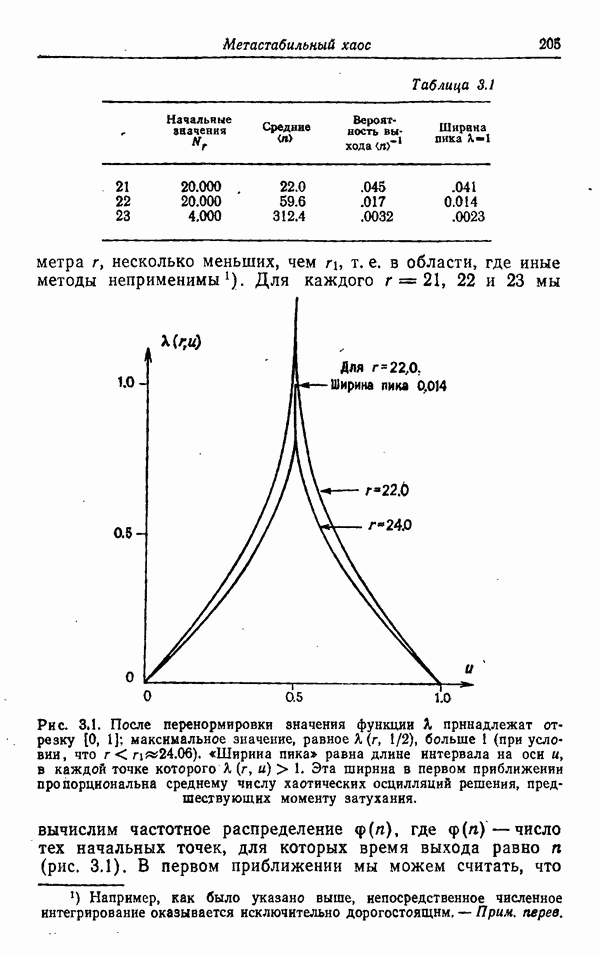
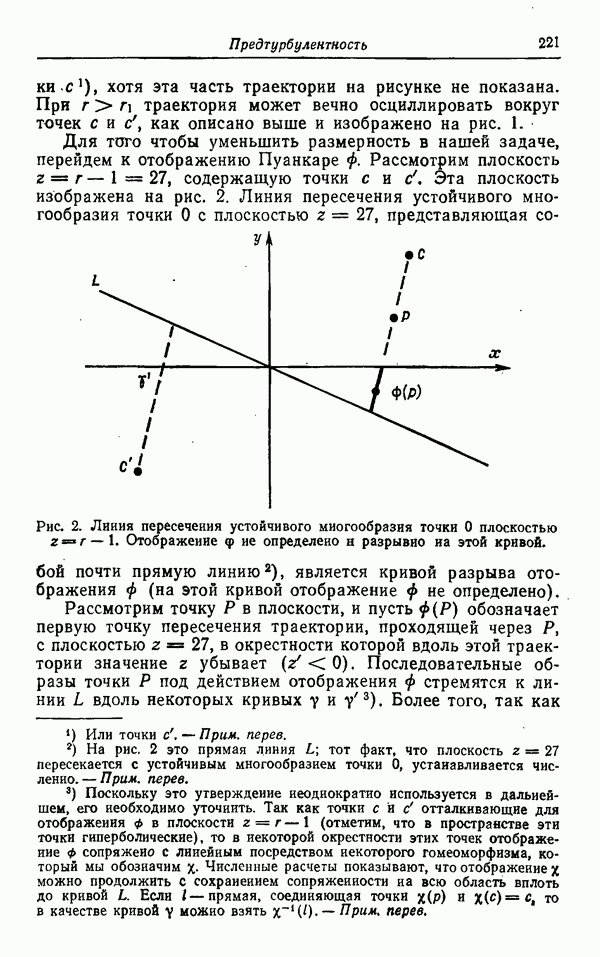
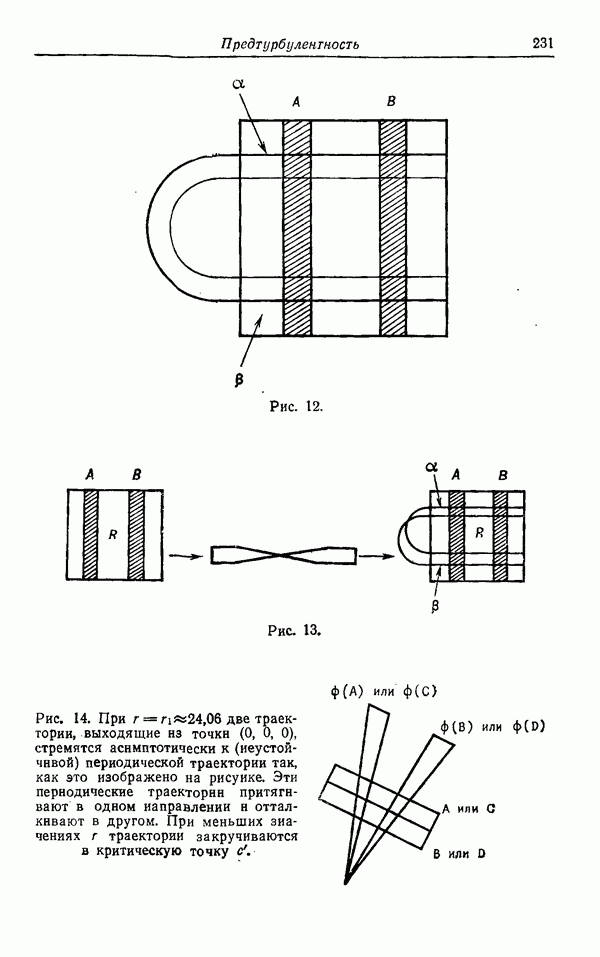
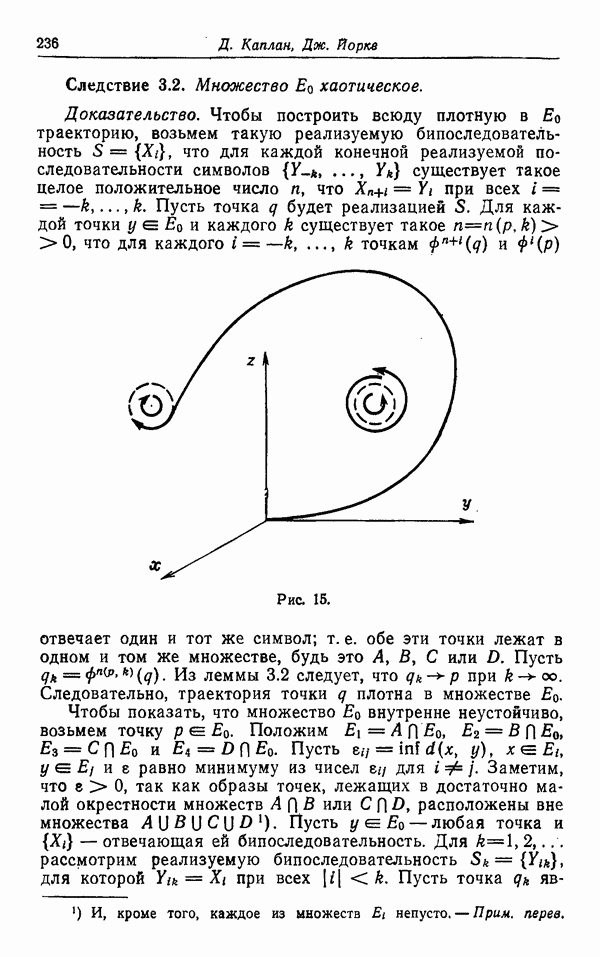
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ РАСЧЕТА ТУРБУЛЕНТНЫХ СДВИГОВЫХ ТЕЧЕНИЙ
П. Г. Сафмен
Предметом изучения в теории турбулентности можно считать исследование стохастических решений уравнений Навье — Стокса при определенных начальных и граничных условиях. Точное значение слова «стохастические» зависит от точки зрения произносящего это слово. Для математика «сто-хастичность» означает существование ансамбля возможных реализаций поля течения, для которого определено понятие среднего. Для инженера каждое турбулентное течение, с которым он сталкивается на практике, представляет собой единичную непрерывную реализацию поля течения, и «стохастический» на самом деле означает «непредсказуемый». Инженер надеется обнаружить предсказуемые свойства поля течения при помощи подходящего осреднения его по времени и/или по пространству.
Исторически сложилось так, что на самом деле исследовались два типа турбулентности: воображаемая турбулентность и реальная турбулентность. Воображаемая турбулентность представляет собой идеализированное турбулентное движение, однородное и изотропное, которое не встречается в природе. «Однородность» означает, что средние свойства течения одинаковы во всех точках пространства, а условие изотропии означает, что не существует преимущественной ориентации для осредненных характеристик турбулентных флюктуаций. Встречающиеся в природе турбулентные течения, которые могут быть названы «реальными», всегда неоднородны.
Турбулентность, которая приближенно является однородной и изотропной, существует реально. Она может быть создана
в лабораторной аэродинамической трубе за мелкой решеткой при прохождении через нее струи жидкости с достаточно большой скоростью. Экспериментально было обнаружено, что турбулентное движение жидкости достаточно далеко вниз по течению от решетки почти изотропно и в. системе координат, движущейся со средней скоростью течёния, почти однородно. Усредненные характеристики однородной и изотропной турбулентности могут со временем меняться, и поэтому скорость диссипации турбулентной кинетической энергии таких течений была объектом интенсивного исследования.
Теоретическое изучение однородной и изотропной турбулентности было начато Тейлором. Вначале считалось, что этот тип турбулентного движения более доступен математическому анализу, чем реальная турбулентность. К сожалению, математические трудности, возникающие при изучении воображаемой турбулентности оказались все же слишком велики, и понимание механизма такого движения остается весьма ограниченным. Кроме того, до сих пор неясно, может ли быть извлечена какая-либо польза из изучения этого вида турбулентности, так как для всех реальных турбулентных течений наличие сдвига оказывает нетривиальное воздействие на динамику турбулентного движения во всех масштабах.
Реальные турбулентные течения грубо могут быть разделены на два типа: «простые» и «сложные». Простыми турбулентными течениями являются такие, которые не испытывают влияния внешних, геометрических или феноменологических факторов. Турбулентное течение называется сложным, если оно не является простым. Например, сравним турбулентные течения в трубе:

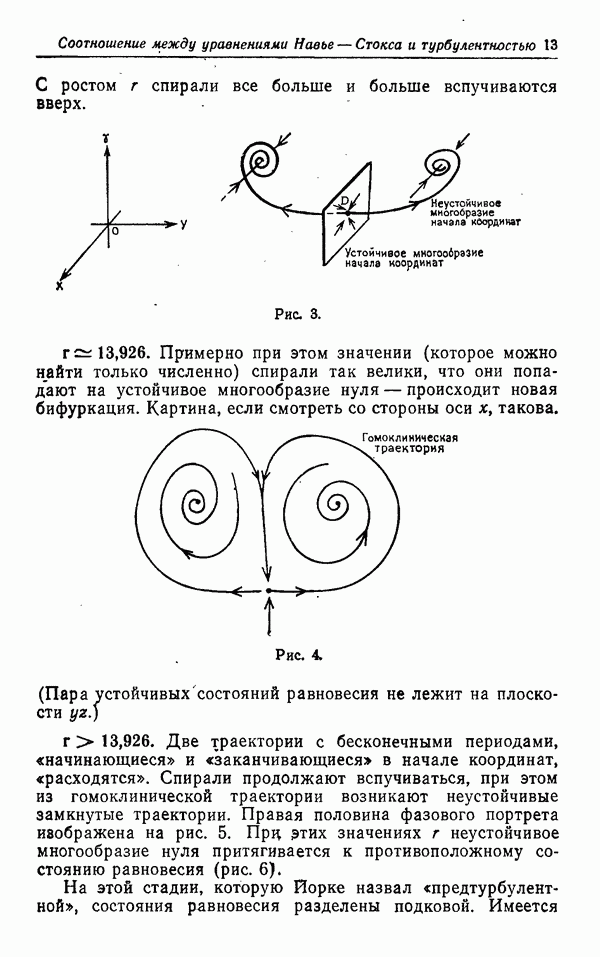
Рис. 1.
в струе:

Рис. 2.
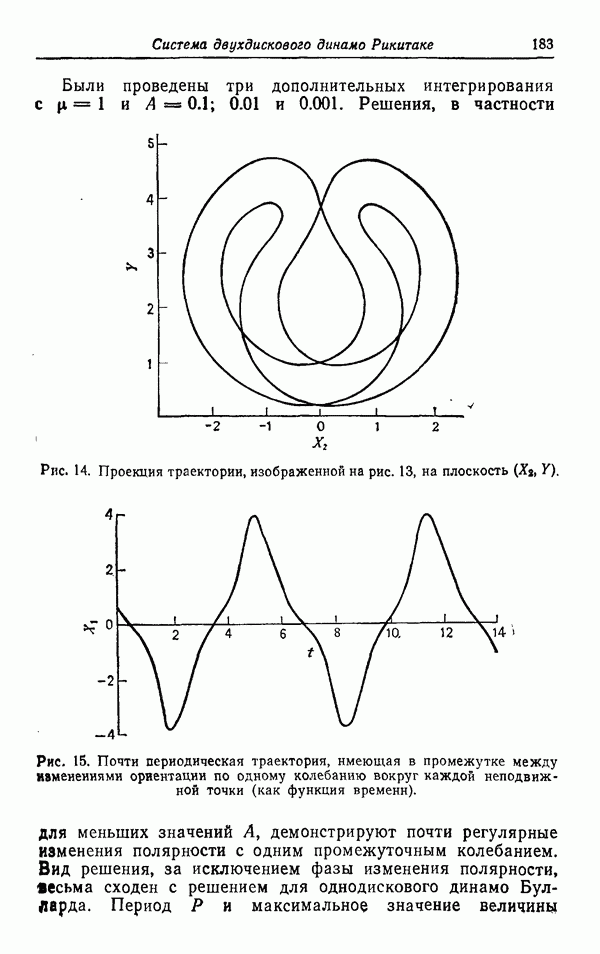
и в слое смешения:

Рис. 3.
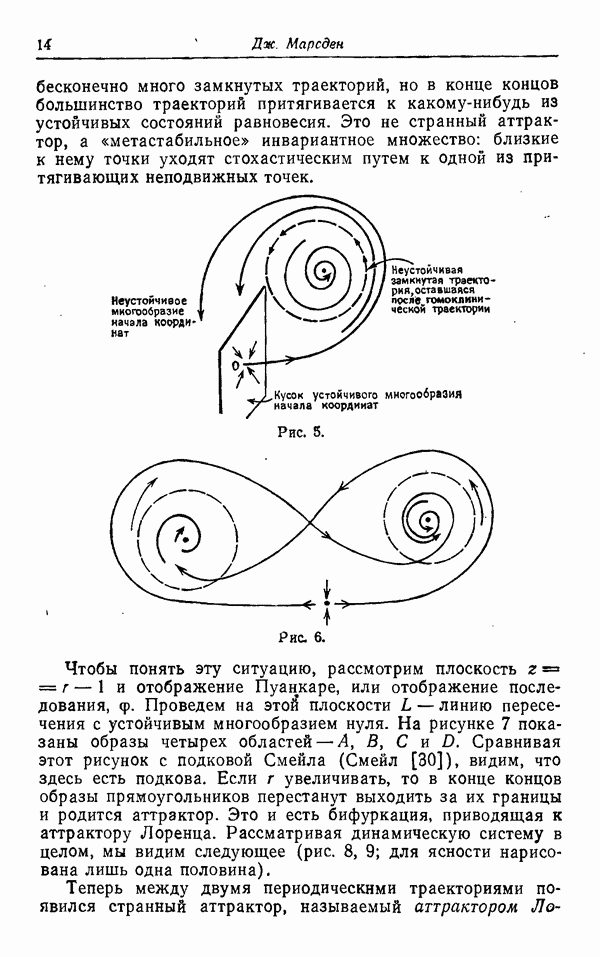
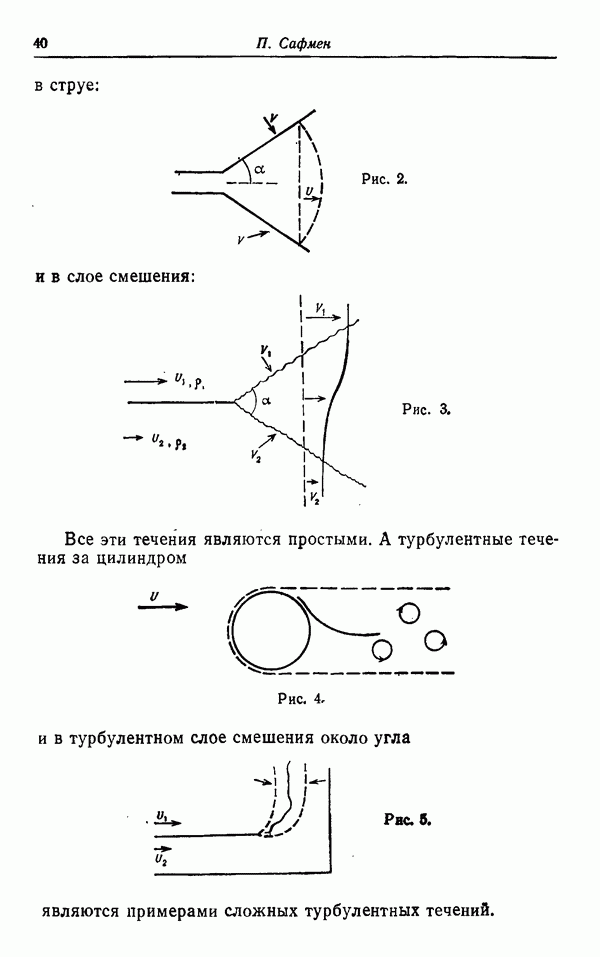
Все эти течения являются простыми. А турбулентные течения за цилиндром

Рис. 4.
и в турбулентном слое смешения около угла

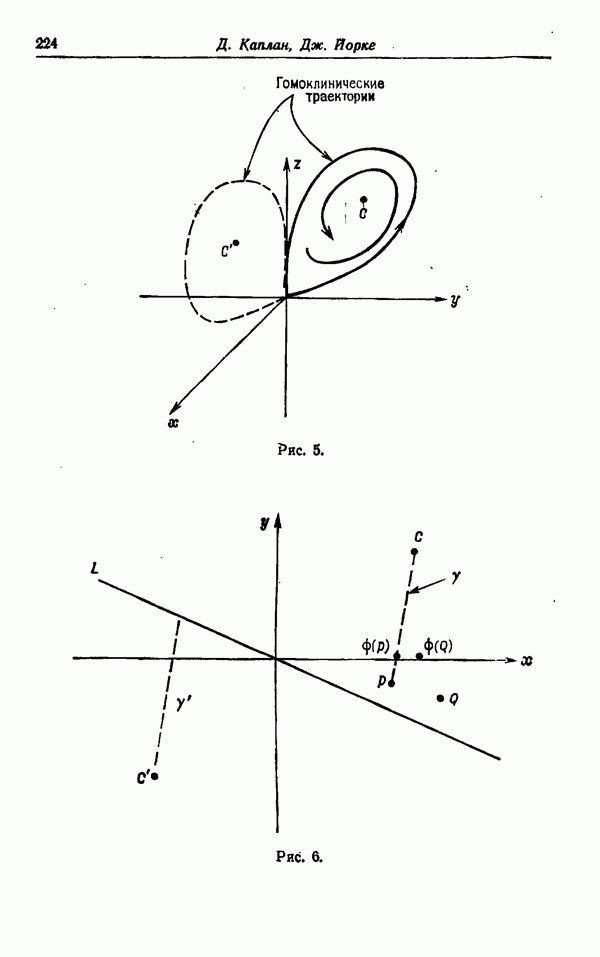
Рис. 5.
являются примерами сложных турбулентных течений.
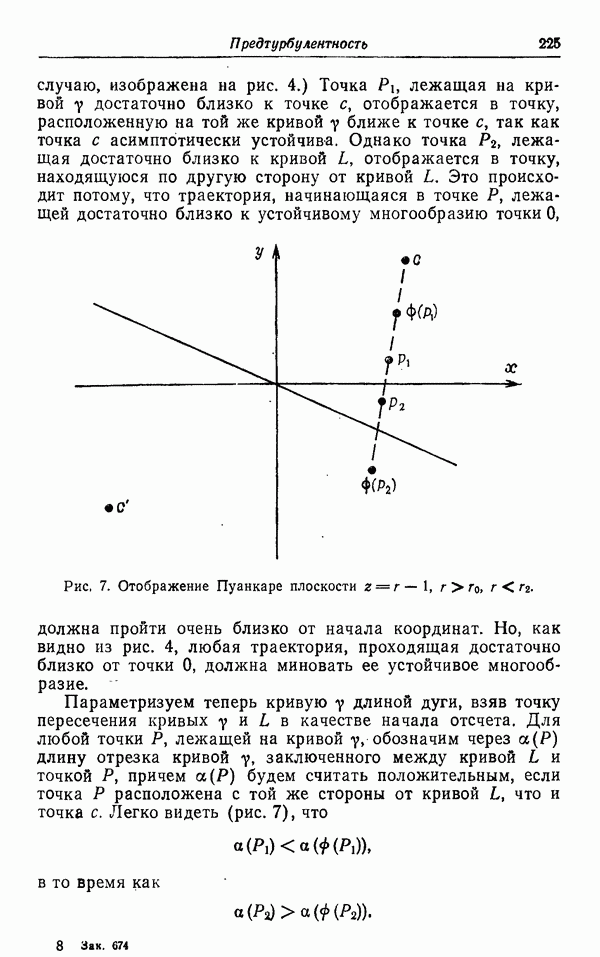
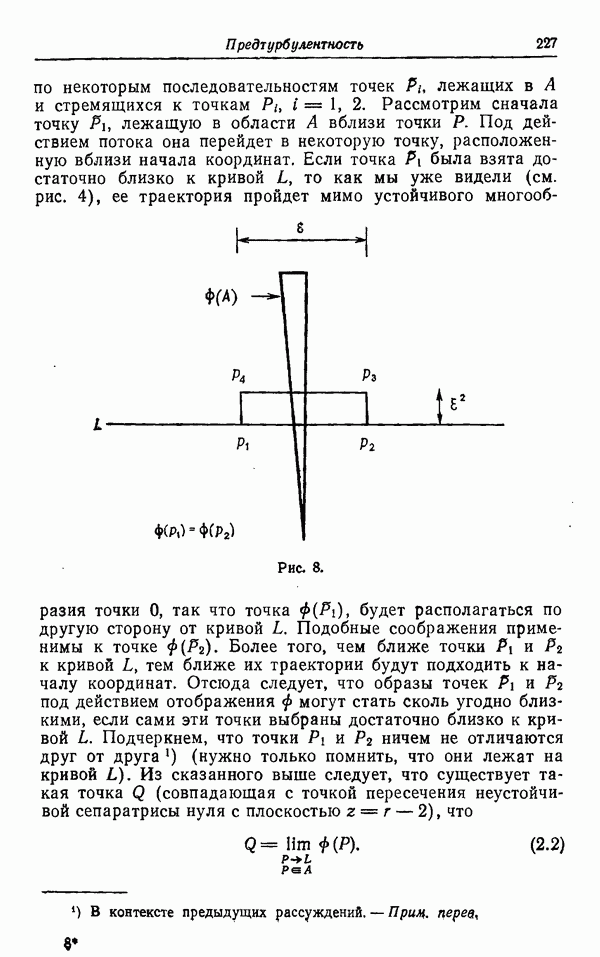
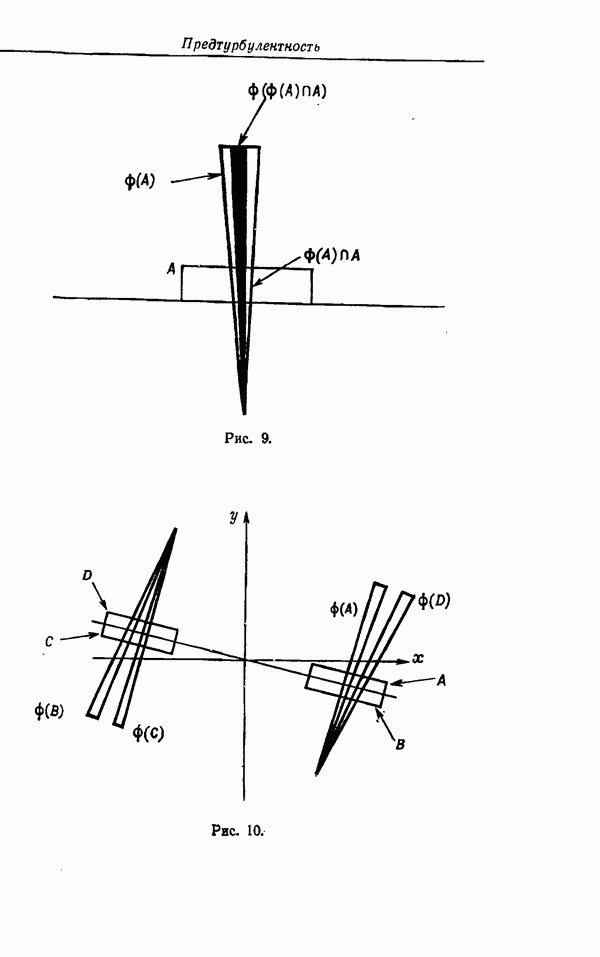
Для всех этих примеров, как простых, так и сложных, отсутствует удовлетворительное теоретическое объяснение. Рассмотрим турбулентное течение в трубе, изображенное на рис. 1. Было обнаружено, что для области  , где
, где  — кинематическая вязкость,
— кинематическая вязкость,  скорость трения,
скорость трения,  — напряжение сдвига на стенке, а величина а пропорциональна диаметру трубы, имеет место логарифмический закон для распределения средней скорости
— напряжение сдвига на стенке, а величина а пропорциональна диаметру трубы, имеет место логарифмический закон для распределения средней скорости

в любой трубе при достаточно больших числах Рейнольдса. Постоянная Кармана  постоянна для всех труб, а величина В зависит от шероховатости стенок трубы. Это соотношение, которое на самом деле имеет место для турбулентного течения в трубе с произвольным сечением, никогда не было выведено путем строгих теоретических рассуждений.
постоянна для всех труб, а величина В зависит от шероховатости стенок трубы. Это соотношение, которое на самом деле имеет место для турбулентного течения в трубе с произвольным сечением, никогда не было выведено путем строгих теоретических рассуждений.
Для турбулентного течения струи жидкости, вытекающей из отверстия, изображенного на рис. 2, хорошо было бы уметь предсказывать a priori величину угла расхождения струи а. Экспериментально для многих различных течений было обнаружено, что этот угол  Также важно уметь предсказывать скорость проникновения в струю жидкости, в которой струя распространяется, но в настоящее время нет такой теории турбулентности, которая позволила бы сделать это.
Также важно уметь предсказывать скорость проникновения в струю жидкости, в которой струя распространяется, но в настоящее время нет такой теории турбулентности, которая позволила бы сделать это.
Аналогично для слоя смешения, изображенного на рис. 3, хотелось бы уметь предсказывать величину угла расхождения и скорости проникновения 
Для турбулентного следа за цилиндром, изображенного на рис. 4, нужно уметь предсказывать характеристики примыкающего к цилиндру турбулентного пограничного слоя и находящейся непосредственно позади цилиндра области отрыва. Хотелось бы надеяться также, что теория турбулентности сможет предсказывать появления ряда больших вихрей, которые возникают вследствие течения попеременно выше и ниже цилиндра.
Ситуация, изображенная в примере сложного турбулентного потока на рис. 5, часто встречается на практике. В этом случае хотелось бы уметь предсказывать влияние присутствующего здесь угла на слой смешения, т. е. характер изгибания этого слоя и скорость проникновения в него жидкости из внешнего потока.
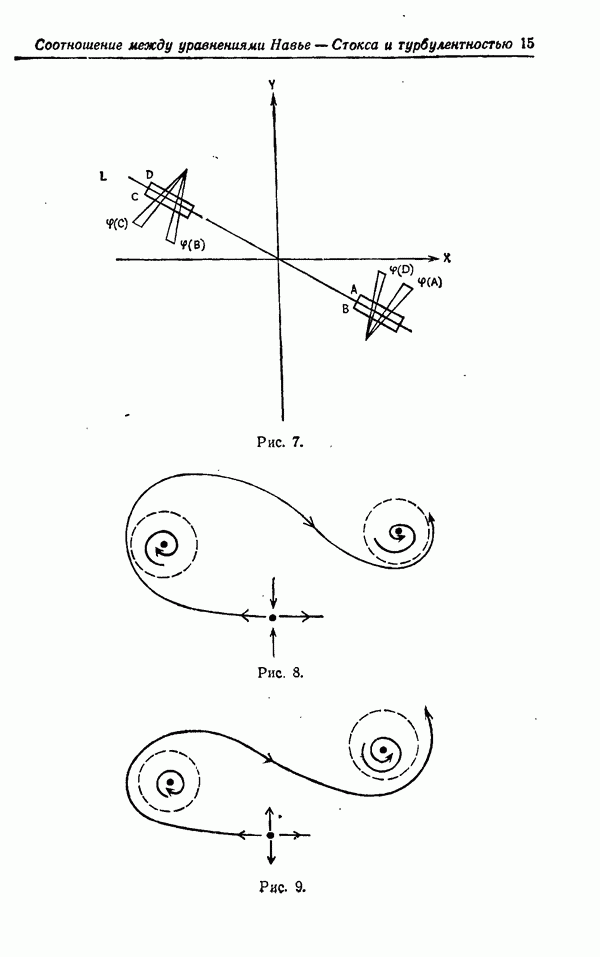
Мы должны признать, что простота течений, изображенных на первых трех рисунках, лишь видимая, а не подлинная.
Например, мгновенные фотографии течения в струе, сделанные Рошко, позволяют увидеть довольно сложную регулярную структуру, изображенную на рис. 6.
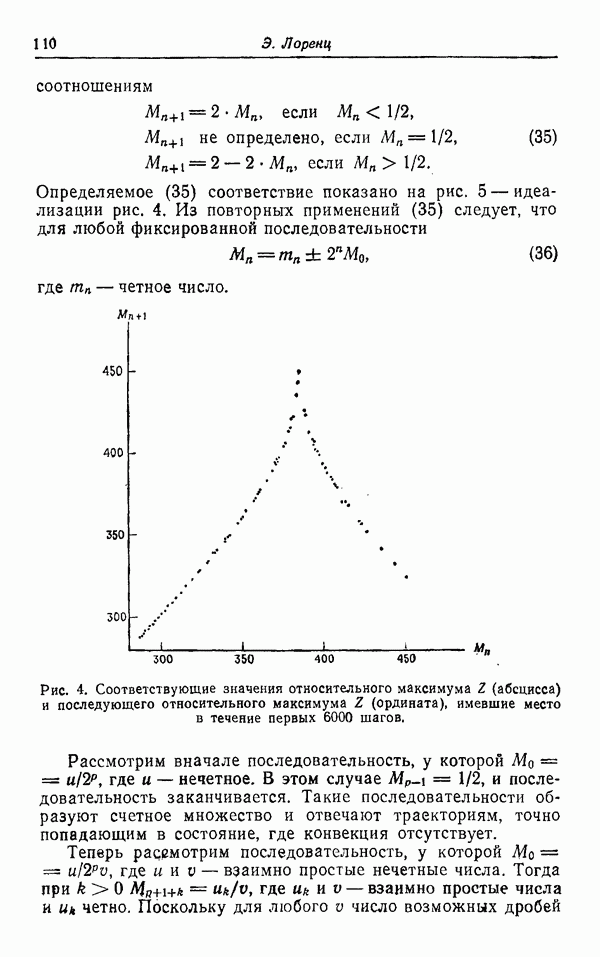
Представленные здесь вихри непрерывно взаимодействуют и искривляются исключительно сложным образом.

Рис. 6.
Теперь читателю должно быть уже предельно ясно, что в области турбулентности нет недостатка проблем, ожидающих решения. Попробуем выяснить, какой стратегии мы должны придерживаться, чтобы найти средства для решения хотя бы некоторых из них. Первый подход (и, возможно, наиболее разумный) состоит в отказе от каких бы то ни было попыток понять природу турбулентности. Много несостоявшихся научных карьер было посвящено безуспешным попыткам разгадать тайны турбулентности. Те горячие головы, которым нипочем эти предупреждения об опасности, могут пойти несколькими различными путями.
Первый из них — попытаться численно смоделировать турбулентные течения. Для этого уравнения Навье — Стокса точно решаются на машине для конечного числа начальных условий, а затем полученные результаты усредняются с тем, чтобы получить различные интересующие нас средние характеристики. Этот подход существенно ограничен числом узлов сетки, которое нужно использовать, чтобы решить конечноразностные аппроксимации уравнений Навье — Стокса при больших числах Рейнольдса. Число ячеек машины, которое для этого требуется, согласно оценкам,  что значительно превосходит мощность самых больших существующих в настоящее время ЭВМ.
что значительно превосходит мощность самых больших существующих в настоящее время ЭВМ.
Существует модификация этого подхода, называемая подсеточным моделированием. При этом вычисляют характеристики только крупномасштабного движения, используя сетку с большим шагом, и затем с помощью подходящих аппроксимаций пытаются оценить влияние мелкомасштабного (подсе-точного) движения на движения больших масштабов. К сожалению, математические трудности, возникающие при оценке влияния движения малых масштабов на крупномасштабное движение, почти идентичны трудностям, возникающим при аппроксимации напряжений Рейнольдса при попытке непосредственно решить уравнения для среднего поля скорости.
Другой подход к решению проблем, возникающих при исследовании турбулентных течений, — это метод моделирования напряжений Рейнольдса, активно разрабатываемый многими исследователями, наиболее видными из которых являются Лаундер из Великобритании и Ламли из Соединенных Штатов. Этот подход состоит в использовании замкнутой системы уравнений, задающих эволюцию рейнольдсовых напряжений, вместо того чтобы аппроксимировать их с помощью какой-либо модели диффузии вихрей, как это делали Буссинеск, Тейлор, Прандтль и фон Карман.
Путем преобразования уравнений Навье — Стокса можно вывести следующие уравнения для эволюции напряжений 

где

— член, описывающий генерацию 

— член, описывающий перераспределение между различными компонентами напряжения Рейнольдса;

— член, отвечающий за его диссипацию вследствие вязкости, и

описывает его диффузию под действием различных факторов.
Вычисление левой части уравнения (1) достаточно просто, но правая часть содержит члены, вычислить которые очень сложно. Данный метод моделирования уравнения для напряжений Рейнольдса состоит в отыскании такого представления величин  как функционалов от напряжений Рейнольдса, которое можно было бы строго обосновать. Не существует общепринятого представления о том,
как функционалов от напряжений Рейнольдса, которое можно было бы строго обосновать. Не существует общепринятого представления о том,
какой подход к построению таких аппроксимаций наиболее предпочтителен, и каждая группа исследователей придерживается в этом вопросе собственных вкусов. Пока еще рано делать выводы о том, насколько плодотворным окажется это направление.
На практике уравнения (1) дополняются еще одним эвристически выведенным уравнением для величины диссипативного члена  . Это уравнение описывает существующее феноменологическое представление об эволюции диссипации D. Таким образом, здесь используется тот же принцип, что и при предыдущем подходе к расчету турбулентных течений, т. е. феноменологическое моделирование.
. Это уравнение описывает существующее феноменологическое представление об эволюции диссипации D. Таким образом, здесь используется тот же принцип, что и при предыдущем подходе к расчету турбулентных течений, т. е. феноменологическое моделирование. 
Аппроксимация рейнольдсовых напряжений  с помощью модели диффузии вихря может рассматриваться как элементарный пример феноменологического моделирования. Сначала делается предположение о том, каким образом осуществляется турбулентный перенос импульса, а затем этот процесс моделируется при помощи подходящих для этого механизма масштабов скорости и длины. Например, если мы предполагаем, что в турбулентной струе перенос импульса осуществляется посредством хаотического движения вихрей, размер и скорость которых совпадают с соответствующими характеристиками струи, то можно считать, что
с помощью модели диффузии вихря может рассматриваться как элементарный пример феноменологического моделирования. Сначала делается предположение о том, каким образом осуществляется турбулентный перенос импульса, а затем этот процесс моделируется при помощи подходящих для этого механизма масштабов скорости и длины. Например, если мы предполагаем, что в турбулентной струе перенос импульса осуществляется посредством хаотического движения вихрей, размер и скорость которых совпадают с соответствующими характеристиками струи, то можно считать, что  где L — ширина струи,
где L — ширина струи,  — разность между максимальной скоростью и скоростью внешнего потока,
— разность между максимальной скоростью и скоростью внешнего потока,  эмпирически определяемая константа. Экспериментально показано, что выбор
эмпирически определяемая константа. Экспериментально показано, что выбор  дает прекрасные результаты.
дает прекрасные результаты.
При расчете турбулентных течений общего вида нужно быть готовым к использованию феноменологического моделирования значительно менее обоснованного типа, т. е. постулировать существование уравнений для эволюции характерного масштаба длины и/или времени и/или масштаба скорости турбулентного движения. Каждое из этих уравнений включает в себя известные особенности динамики поведения определенного масштаба. Для того чтобы связать эти уравнения с осредненными уравнениями Навье-Стокса, обычно постулируется существование связующих соотношений общего вида:

где  а Е — параметр, зависящий от масштаба, эволюция которого описывается модельным уравнением.
а Е — параметр, зависящий от масштаба, эволюция которого описывается модельным уравнением.
В 1942 году А. Н. Колмогоров в работе, лишь недавно «открытой» на Западе, предложил полную феноменологическую модель, в которой в соотношении (2) величина  , где А — константа,
, где А — константа,  турбулентная кинетическая энергия,
турбулентная кинетическая энергия,  масштаб, обратный времени, т. е. масштаб завихренности или масштаб частоты. Величины
масштаб, обратный времени, т. е. масштаб завихренности или масштаб частоты. Величины  и w должны определяться из модельных уравнений:
и w должны определяться из модельных уравнений:

Сафмен в 1970 г., не зная о работе Колмогорова, предложил удивительно похожий феноменологический подход. Этот подход также основан на соотношении (2). В его теории  где е — псевдоэнергия. Уравнения модели, описывающие эволюцию ей w, таковы:
где е — псевдоэнергия. Уравнения модели, описывающие эволюцию ей w, таковы:

Здесь  — универсальные постоянные, определяемые таким образом, чтобы решения системы уравнений (3) обладали рядом простых, эмпирически наблюдаемых свойств турбулентных течений. Например, известно, что энергия однородной турбулентности убывает со временем по степенному закону с показателем —6/5. Если уравнения (3) переписать для однородной турбулентности, то получится, что
— универсальные постоянные, определяемые таким образом, чтобы решения системы уравнений (3) обладали рядом простых, эмпирически наблюдаемых свойств турбулентных течений. Например, известно, что энергия однородной турбулентности убывает со временем по степенному закону с показателем —6/5. Если уравнения (3) переписать для однородной турбулентности, то получится, что  Поэтому мы должны положить
Поэтому мы должны положить  чтобы получить требуемый показатель убывания.
чтобы получить требуемый показатель убывания.
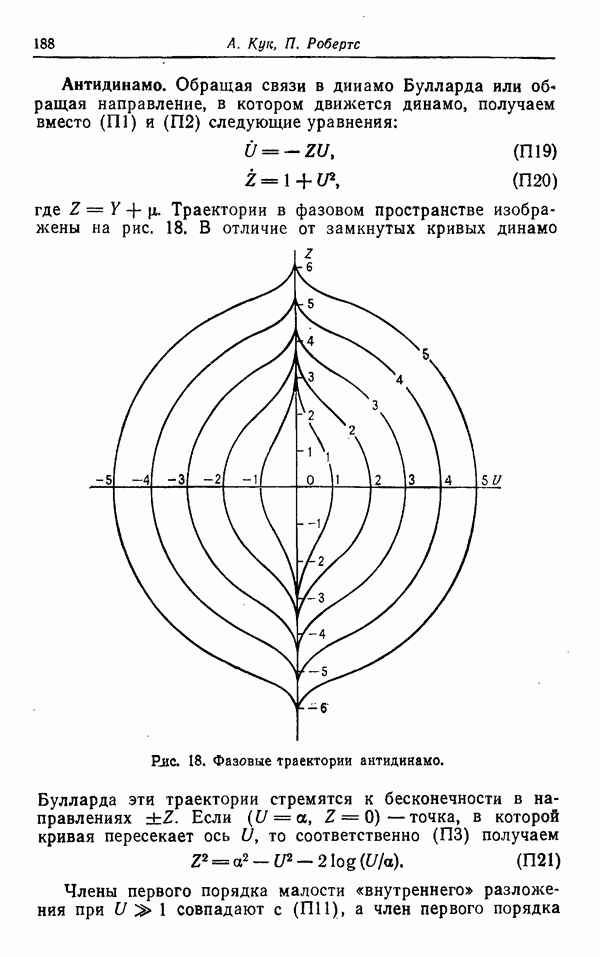
Другая интересная особенность уравнений (3) состоит в том, что они учитывают наличие поверхностей раздела между турбулентными и ламинарными областями, которые существуют во многих турбулентных течениях, например в струе. В турбулентной области  , а в ламинарной
, а в ламинарной  . Следует отметить, что диффузионный член в этих уравнениях стремится к нулю при
. Следует отметить, что диффузионный член в этих уравнениях стремится к нулю при  . Поскольку эти уравнения при отсутствии диффузионного члена допускают наличие разрывов,
. Поскольку эти уравнения при отсутствии диффузионного члена допускают наличие разрывов,
то возможно, что резкая граница, разделяющая ламинарный и турбулентный режимы течения, может быть ими описана.
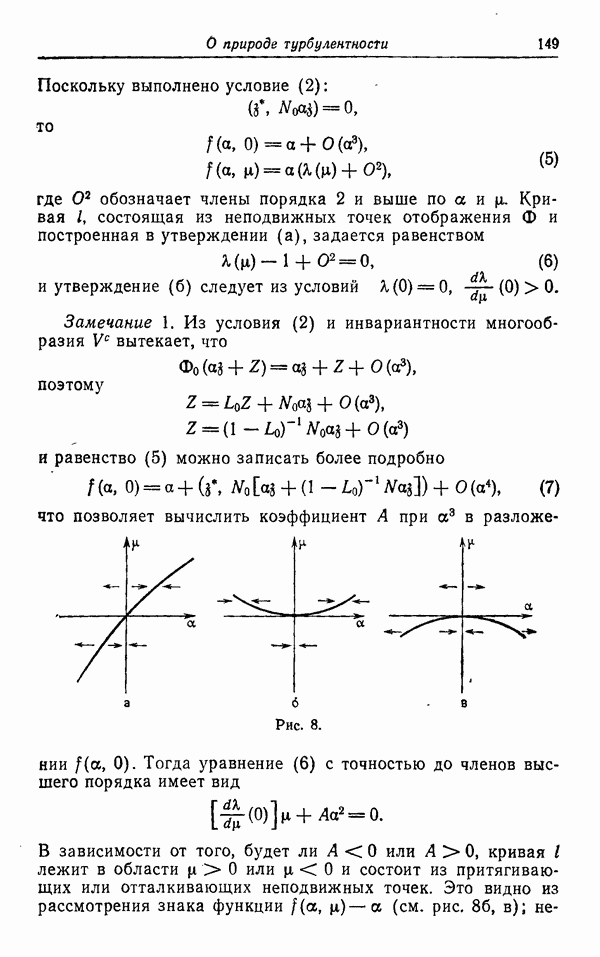
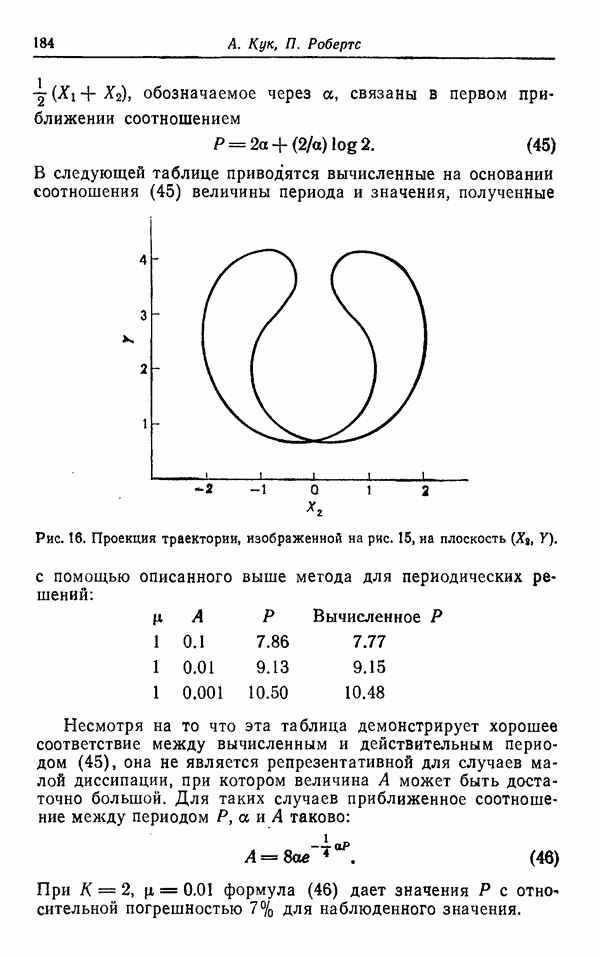
При применении системы (3) к расчету ряда различных турбулентных течений был достигнут определенный успех. Для простых автомодельных турбулентных течений, таких, как струя, слой смешения и след, для которых управляющие их динамикой уравнения в частных производных могут быть сведены к обыкновенным, эта феноменологическая теория точно воспроизвела известные об этих течениях эмпирические факты. При применении к турбулентному слою смешения жидкостей разной плотности и с разными числами Маха было полечено хорошее соответствие между этой теорией и экспериментом. Кроме того, удалось предсказать некоторый феномен для системы, до сих пор не исследовавшейся экспериментально. Было бы очень важно выяснить, является ли это предсказание правильным, так как по-настоящему хорошая теория турбулентности обязана давать правильные предсказания, а не только воспроизводить результаты, которые уже были получены экспериментально (т. е. не «постдикция», а предикция).
В заключение отметим, что феноменологический подход к расчету турбулентных течений привел к некоторым первоначальным достижениям, но должен быть в дальнейшем подвергнут значительно более серьезной проверке, т. е. применен к реальным сложным течениям. Только после этого можно сделать вывод: является ли он действительно хорошим или нет. Если эта модель будет продолжать работать и в дальнейшем, то нужно попытаться найти ее обоснование на основе уравнений Навье — Стокса.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- ПОПЫТКИ УСТАНОВИТЬ СООТНОШЕНИЕ МЕЖДУ УРАВНЕНИЯМИ НАВЬЕ-СТОКСА И ТУРБУЛЕНТНОСТЬЮ
- ПРИЛОЖЕНИЕ К СТАТЬЕ МАРСДЕНА БИФУРКАЦИИ, ПОЛУПОТОКИ И УРАВНЕНИЯ НАВЬЕ—СТОКСА
- ТЕОРИИ ТУРБУЛЕНТНОСТИ
- ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ РАСЧЕТА ТУРБУЛЕНТНЫХ СДВИГОВЫХ ТЕЧЕНИЙ
- ФРАКТАЛЫ И ТУРБУЛЕНТНОСТЬ: АТТРАКТОРЫ И РАЗБРОС
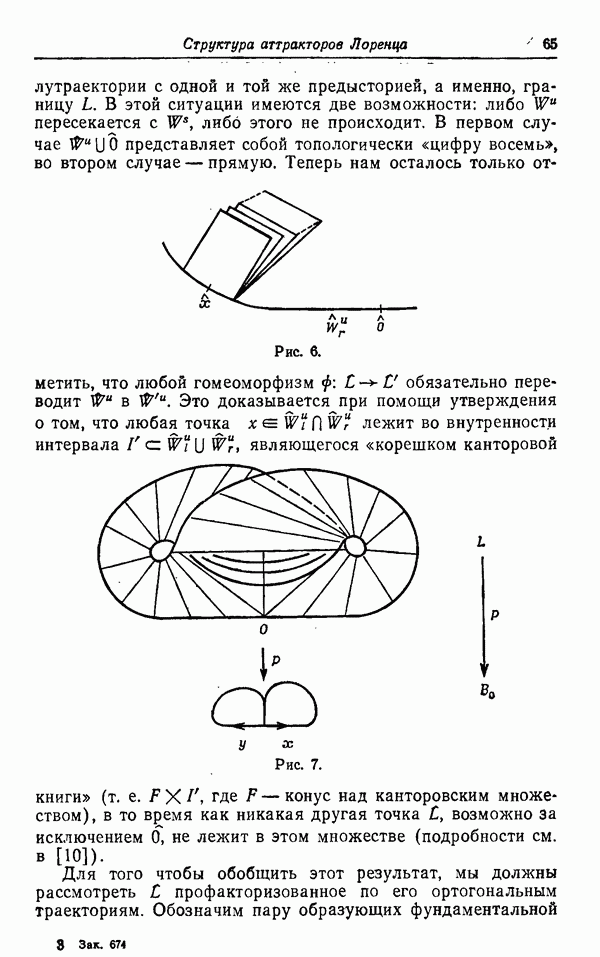
- СТРУКТУРА АТТРАКТОРОВ ЛОРЕНЦА
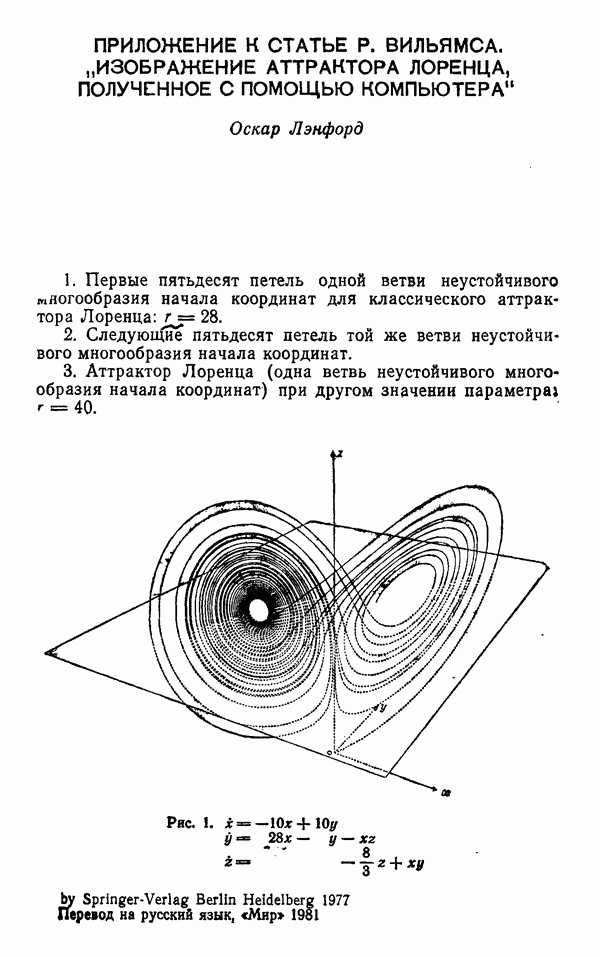
- ПРИЛОЖЕНИЕ К СТАТЬЕ Р. ВИЛЬЯМСА. «ИЗОБРАЖЕНИЕ АТТРАКТОРА ЛОРЕНЦА, ПОЛУЧЕННОЕ С ПОМОЩЬЮ КОМПЬЮТЕРА»
- ДВА ПОДХОДА К МОДЕЛИРОВАНИЮ ДВУМЕРНОЙ ТУРБУЛЕНТНОСТИ
- ДЕТЕРМИНИРОВАННОЕ НЕПЕРИОДИЧЕСКОЕ ТЕЧЕНИЕ
- О ПРИРОДЕ ТУРБУЛЕНТНОСТИ
- ДВУМЕРНОЕ ОТОБРАЖЕНИЕ СО СТРАННЫМ АТТРАКТОРОМ
- СИСТЕМА ДВУХДИСКОВОГО ДИНАМО РИКИТАКЕ
- МЕТАСТАБИЛЬНЫЙ ХАОС: ПЕРЕХОД К УСТОЙЧИВОМУ ХАОТИЧЕСКОМУ ПОВЕДЕНИЮ В МОДЕЛИ ЛОРЕНЦА
- ПРЕДТУРБУЛЕНТНОСТЬ: РЕЖИМ, НАБЛЮДАЕМЫЙ В ТЕЧЕНИИ ЖИДКОСТИ, ОПИСЫВАЕМОЙ МОДЕЛЬЮ ЛОРЕНЦА
- ТОПОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ АТТРАКТОРОВ ЛОРЕНЦА