| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРИЛОЖЕНИЕ К СТАТЬЕ МАРСДЕНА БИФУРКАЦИИ, ПОЛУПОТОКИ И УРАВНЕНИЯ НАВЬЕ—СТОКСА
Тюдор Рэтью
Как уже отмечалось в статье Дж. Марсдена, согласно предложенной Рюэлем и Такенсом картине турбулентности, движение жидкости само по себе стохастично-. Считается, что наблюдаемое при  течение (решение уравнений Стокса) с увеличением числа Рейнольдса
течение (решение уравнений Стокса) с увеличением числа Рейнольдса  в результате бифуркаций становится все более сложным и в конце концов притягивается к «странному» аттрактору, одной из главных черт которого является стохастичность. В этой лекции будет дай обзор математических результатов, имеющих отношение к такому подходу, и многие интересные идеи, представленные Марсденом, будут подкреплены точными формулировками теорем. Основным источником данной лекции является книга Марсдена и Мак-Кракена [7].
в результате бифуркаций становится все более сложным и в конце концов притягивается к «странному» аттрактору, одной из главных черт которого является стохастичность. В этой лекции будет дай обзор математических результатов, имеющих отношение к такому подходу, и многие интересные идеи, представленные Марсденом, будут подкреплены точными формулировками теорем. Основным источником данной лекции является книга Марсдена и Мак-Кракена [7].
Ведущая идея — это построение подходящей модели, следующей из уравнений Навье — Стокса для однородной несжимаемой вязкой жидкости:

с граничным условием: v задано на границе  возможно, в зависимости от v. Все происходит на компактном римановом многообразии М с гладкой границей
возможно, в зависимости от v. Все происходит на компактном римановом многообразии М с гладкой границей  — это поле скоростей жидкости, f — действующая на нее внешняя сила,
— это поле скоростей жидкости, f — действующая на нее внешняя сила,  — давление. Как уже отмечалось, уравнения Эйлера для идеальной жидкости получаются, если положить
— давление. Как уже отмечалось, уравнения Эйлера для идеальной жидкости получаются, если положить  в написанных выше уравнениях; существует теорема о том, что решения уравнений Эйлера получаются как сильный предел решений уравнений Навье — Стокса в Я-топологии при
в написанных выше уравнениях; существует теорема о том, что решения уравнений Эйлера получаются как сильный предел решений уравнений Навье — Стокса в Я-топологии при  (см. Эбии, Марсден [3]). Заметим также, что перейдя к уравнениям Эйлера, мы должны изменить
(см. Эбии, Марсден [3]). Заметим также, что перейдя к уравнениям Эйлера, мы должны изменить
граничные условия на  Интуитивно оно следует из отсутствия у идеальной жидкости трения на стенке; добавим, что тонкий формальный анализ описанного выше предельного перехода приводит к тому же результату, см. Эбин и Марсден [3].
Интуитивно оно следует из отсутствия у идеальной жидкости трения на стенке; добавим, что тонкий формальный анализ описанного выше предельного перехода приводит к тому же результату, см. Эбин и Марсден [3].
Теперь попытаемся записать наши уравнения Эйлера и Навье — Стокса в виде системы эволюционных уравнений

с начальным условием  где
где  — плотно определенный нелинейный оператор на пространстве функций, выбранный так, чтобы наши граничные условия и
— плотно определенный нелинейный оператор на пространстве функций, выбранный так, чтобы наши граничные условия и  удовлетворялись автоматически. Это поможет сделать теорема разложения Ходжа.
удовлетворялись автоматически. Это поможет сделать теорема разложения Ходжа.
Обозначим  замыкание нормированного векторного пространства векторнозначных функций класса
замыкание нормированного векторного пространства векторнозначных функций класса  на М с нормой
на М с нормой
Здесь  обозначает дифференциал
обозначает дифференциал  — это множество векторных полей класса
— это множество векторных полей класса  на М. Отметим, что функция принадлежи классу
на М. Отметим, что функция принадлежи классу  , если и только если все ее производные до
, если и только если все ее производные до  порядка включительно принадлежат классу
порядка включительно принадлежат классу 
Теорема разложения Ходжа. Пусть М — компактное риманово многообразие с границей и  Тогда X можно единственным образом разложить:
Тогда X можно единственным образом разложить:

где  и f принадлежит классу
и f принадлежит классу

Обозначим  Применяя теперь теорему Ходжа, получим отображение
Применяя теперь теорему Ходжа, получим отображение  через
через  . Теперь мы можем записать уравнения Эйлера следующим образом: пусть
. Теперь мы можем записать уравнения Эйлера следующим образом: пусть  требуется найти
требуется найти  где
где  такое, что
такое, что

(плюс начальные условия). Предположение, что  необходимо для того, чтобы произведение двух элементов из
необходимо для того, чтобы произведение двух элементов из
 также принадлежало
также принадлежало  Адамс [1], стр. 115). Таким образом, если
Адамс [1], стр. 115). Таким образом, если  то
то  и мы можем применить теорему Ходжа. Здесь мы молчаливо предполагаем, что внешняя сила потенциальна.
и мы можем применить теорему Ходжа. Здесь мы молчаливо предполагаем, что внешняя сила потенциальна.
Чтобы иметь возможность записать подобным образом уравнения Навье—Стокса, изменим пространство функций на  Тогда уравнения Навье — Стокса запишутся так: требуется найти
Тогда уравнения Навье — Стокса запишутся так: требуется найти  такое что
такое что

Следующая теорема доказана в гл. 9 книги Марсдена и 
Теорема. Уравнения Навье — Стокса в пространстве размерности 2 или 3 определяют гладкий локальный полипоток на  т. е. определено семейство отображений для
т. е. определено семейство отображений для  , удовлетворяющих условиям:
, удовлетворяющих условиям:
a)  определено на открытом подмножестве от
определено на открытом подмножестве от 

c)  раздельно, а следовательно, и совместно
раздельно, а следовательно, и совместно  непрерывно
непрерывно
d) для всех фиксированных  является отображением класса
является отображением класса  — гладкая полугруппа. Более того, наш полупоток удовлетворяет так называемому предположению о продолжаемости, а именно: если
— гладкая полугруппа. Более того, наш полупоток удовлетворяет так называемому предположению о продолжаемости, а именно: если  при каждом фиксированном
при каждом фиксированном  и при всех t, для которых
и при всех t, для которых  определено, лежит в ограниченном подмножестве
определено, лежит в ограниченном подмножестве  то
то  определено при всех
определено при всех  . Также
. Также  совместно гладко по
совместно гладко по  при
при  .
.
Этот результат, восходящий к работе Ладыженской [5], позволяет работать не с уравнениями Навье — Стокса в их классическом виде, а с порождаемыми ими эволюционными уравнениями на  и анализировать более подробно полупотоки, имеющие столь приятные свойства.
и анализировать более подробно полупотоки, имеющие столь приятные свойства.
Следуя представлениям о стохастической динамике, мы можем предположить, что турбулентность появляется в результате некоторой последовательности бифуркаций решений уравнений Навье — Стокса. Поэтому первый вопрос — насколько
классическая теория бифуркаций применима к полупотокам. Работы Марсдена показывают, что почти все применимо, если только наложить на полупотоки условия, обычно выполненные для векторных полей. Эти результаты будут описаны ниже.
Далее мы будем работать с системой эволюционных уравнений общего вида

 задано, X — нелинейный оператор, определенный на плотном подмножестве банахова пространства Е, обычно, как уже отмечалось, в пространстве функций;
задано, X — нелинейный оператор, определенный на плотном подмножестве банахова пространства Е, обычно, как уже отмечалось, в пространстве функций;  параметр. Предположим, что наша система определяет единственные локальные решения, порождающие полупоток F? при
параметр. Предположим, что наша система определяет единственные локальные решения, порождающие полупоток F? при  . На полупоток накладываются изложенные выше условия а), b), с) и d). Потребуем также, чтобы выполнялось сделанное выше предположение о продолжаемости. Может показаться, что мы налагаем на полупоток только те условия, которым удовлетворяет наша частная задача, В действительности все наоборот: сначала считается, что условия выполнены, а затем они проверяются для уравнений Навье — Стокса, а это сложная работа, требующая серьезной математической техники (см. гл. 9 книги Марсдена и Маккракена [7]). Предположение о продолжаемости не так сильно, как может показаться; оно только делает нашу теорему о локальном существовании «хорошей» настолько, чтобы траектория становилась неопределенной, только уйдя на бесконечность. Физически это означает, что решение уравнений Навье — Стокса, описывающих движение жидкости, перестает существовать только если оно взрывается. Другое замечание математического характера, оно касается производящего оператора полупотока это не гладкое отображение Е в Е, поэтому мы не можем ожидать гладкости
. На полупоток накладываются изложенные выше условия а), b), с) и d). Потребуем также, чтобы выполнялось сделанное выше предположение о продолжаемости. Может показаться, что мы налагаем на полупоток только те условия, которым удовлетворяет наша частная задача, В действительности все наоборот: сначала считается, что условия выполнены, а затем они проверяются для уравнений Навье — Стокса, а это сложная работа, требующая серьезной математической техники (см. гл. 9 книги Марсдена и Маккракена [7]). Предположение о продолжаемости не так сильно, как может показаться; оно только делает нашу теорему о локальном существовании «хорошей» настолько, чтобы траектория становилась неопределенной, только уйдя на бесконечность. Физически это означает, что решение уравнений Навье — Стокса, описывающих движение жидкости, перестает существовать только если оно взрывается. Другое замечание математического характера, оно касается производящего оператора полупотока это не гладкое отображение Е в Е, поэтому мы не можем ожидать гладкости  по t. Фактически, как можно видеть из изложенной выше теоремы о полупотоке Навье — Стокса, неприятности появляются только при
по t. Фактически, как можно видеть из изложенной выше теоремы о полупотоке Навье — Стокса, неприятности появляются только при  и именно производная при
и именно производная при  дает производящий оператор. Следующая группа предположений, необходимых для бифуркации, касается спектра линеаризованного полупотока.
дает производящий оператор. Следующая группа предположений, необходимых для бифуркации, касается спектра линеаризованного полупотока.
Предположения о спектре. Пусть  совместно непрерывна по
совместно непрерывна по  при
при  — точка, лежащая внутри интервала, содержащего
— точка, лежащая внутри интервала, содержащего  . Предположим также, что
. Предположим также, что
I) 0 — неподвижная точка 
II) при  спектр
спектр  содержится внутри единичного диска
содержится внутри единичного диска 
III) при  (соответственно
(соответственно  спектр G? в начале координат имеет два изолированных простых собственных значения
спектр G? в начале координат имеет два изолированных простых собственных значения  (соответственно
(соответственно  ), а остальная часть спектра лежит внутри D и остается отделенной от единичного круга;
), а остальная часть спектра лежит внутри D и остается отделенной от единичного круга;
IV)  т. е. собственные числа
т. е. собственные числа  равномерно движутся через единичную окружность;
равномерно движутся через единичную окружность;
V) при  начало координат асимптотически устойчиво.
начало координат асимптотически устойчиво.
Мы не будем объяснять здесь детали проверки этого последнего предположения, укажем только, что необходимо определить, имеет ли некая функция отклонения, получаемая из отображения Пуанкаре, строго отрицательную третью производную.
Иногда мы будем пользоваться этими же предположениями, но III) заменим на III):
III) при  (соответственно
(соответственно  спектр G? в начале координат имеет одно изолированное простое действительное Собственное значение
спектр G? в начале координат имеет одно изолированное простое действительное Собственное значение  (соответственно
(соответственно  а остальная часть спектра лежит в D и остается отделенной от единичного круга.
а остальная часть спектра лежит в D и остается отделенной от единичного круга.
Теорема о рождении периодического движения. Если выполняются сделанные выше предположения I) — V), то существует фиксированная окрестность V нуля в Е и  такие, что
такие, что  определено при всех
определено при всех  при
при  при -
при -  имеется единственное однопараметрическое семейство замкнутых траекторий, непрерывно зависящих от
имеется единственное однопараметрическое семейство замкнутых траекторий, непрерывно зависящих от  Они локально притягивающие и поэтому устойчивы. Близкие к ним решения определены при всех
Они локально притягивающие и поэтому устойчивы. Близкие к ним решения определены при всех  . Существует окрестность U начала координат, такая, что любая замкнутая траектория в U — это одна из описанных выше траекторий.
. Существует окрестность U начала координат, такая, что любая замкнутая траектория в U — это одна из описанных выше траекторий.
Теорема о рождении неподвижных точек.
Если выполняются те же условия, но с III) вместо III), то получится тот
же результат, только вместо одного семейства замкнутых траекторий будет существовать два семейства устойчивых состояний равновесия.
Мы не будем вникать в доказательство этих теорем, приведем только два лежащих в его основе факта. Первый — это теорема о центральном многообразии, второй — это теорема Чернова — Марсдена о сведении гладких полупотоков к потокам на конечномерных многообразиях. Если применить эти два результата, то всю задачу можно свести к теореме о рождении цикла в двумерном пространстве, которая относительно проста и восходит к работам Пуанкаре. Вот эти формулировки:
Теорема о центральном многообразии для полупотоков.
Пусть Z — банахово пространство с  -нормой всюду, кроме начала координат O), и пусть
-нормой всюду, кроме начала координат O), и пусть  непрерывный полупоток, определенный в окрестности 0 при
непрерывный полупоток, определенный в окрестности 0 при  . Пусть
. Пусть  и при
и при  совместно
совместно  - гладкого по t и
- гладкого по t и  Предположим, что спектр линейной полугруппы
Предположим, что спектр линейной полугруппы  имеет вид
имеет вид  где
где  лежит на единичной окружности (т. е.
лежит на единичной окружности (т. е.  лежит на мнимой оси), а
лежит на мнимой оси), а  лежит внутри единичной окружности на ненулевом расстоянии от нее при
лежит внутри единичной окружности на ненулевом расстоянии от нее при  в левой полуплоскости). Пусть У — обобщенное собственное подпространство, соответствующее спектру, лежащему на единичной окружности, и
в левой полуплоскости). Пусть У — обобщенное собственное подпространство, соответствующее спектру, лежащему на единичной окружности, и  Тогда существует окрестность 0 в Z и
Тогда существует окрестность 0 в Z и  — гладкое подмногообразие
— гладкое подмногообразие  размерности d, проходящее через 0 и касательное к Y в 0, такое, что для него выполняются следующие свойства: а) локальная инвариантность: если
размерности d, проходящее через 0 и касательное к Y в 0, такое, что для него выполняются следующие свойства: а) локальная инвариантность: если  то
то  локальная устойчивость, если при
локальная устойчивость, если при  определено и принадлежит V при всех
определено и принадлежит V при всех  при
при 
Чтобы применить эту теорему к  надо добавить
надо добавить  в качестве переменной, тогда получится полупоток
в качестве переменной, тогда получится полупоток  на прямом произведении фазового пространства и пространства параметра.
на прямом произведении фазового пространства и пространства параметра.
Хорошо известен вариант этой теоремы для  -гладких отображений; однако соответствующее утверждение для полупотоков, хотя оно и выглядит правдоподобно, не встречалось ранее в литературе, впервые оно появилось в гл. 2 книги Марсдена и Мак-Кракена [7]. Отметим, что все утверждения теоремы остаются справедливыми, даже если порождающий оператор полупотока X неограничен.
-гладких отображений; однако соответствующее утверждение для полупотоков, хотя оно и выглядит правдоподобно, не встречалось ранее в литературе, впервые оно появилось в гл. 2 книги Марсдена и Мак-Кракена [7]. Отметим, что все утверждения теоремы остаются справедливыми, даже если порождающий оператор полупотока X неограничен.
Теорема (Чернов — Марсден).
Пусть  локальный полупоток на банаховом многообразии N, совместно непрерывный и
локальный полупоток на банаховом многообразии N, совместно непрерывный и  -гладкий по
-гладкий по  Допустим, что имеется инвариантное относительно
Допустим, что имеется инвариантное относительно  конечномерное подмногообразие М N. Тогда на
конечномерное подмногообразие М N. Тогда на  локально обратимо, совместно
локально обратимо, совместно  -гладко по t и
-гладко по t и  и порождается гладким векторным полем на М.
и порождается гладким векторным полем на М.
Необходимо сделать несколько замечаний. Теорема о центральном многообразии является ключевым моментом в доказательстве теоремы о бифуркациях; но кроме этого она может оправдать некоторые конечно-модовые аппроксимации уравнений Навье — Стокса (см. замечание 8 в статье Марсдена). Отметим также, что в гл. 4а книги Марсдена и МакКракена [7] описывается алгоритм, позволяющий проверять устойчивость родившихся состояний равновесия и замкнутых траекторий (см. также замечание 4 статьи Марсдена.)
Следствием доказательства теоремы о бифуркациях является сведение рассматриваемой задачи к двумерному случаю. Получается, что вся сложность сосредоточена на плоскости, даже если мы начинаем с эволюционного уравнения в бесконечномерном пространстве функций. Эта ситуация характерна при работе с полупотоками: пытаясь доказать теорему о бифуркации, мы сводим все к конечномерному случаю, и это дает нам сразу два результата: саму теорему и сведение!
Двигаясь по этому пути, мы приходим к следующей бифуркации — рождению инвариантного тора. Здесь идея доказательства та же, что и была ранее, нужно только заменить ссылку на теорему о бифуркации в  ссылкой на аналогичную бифуркационную теорему для диффеоморфизмов. Вникать в технические детали мне бы не хотелось.
ссылкой на аналогичную бифуркационную теорему для диффеоморфизмов. Вникать в технические детали мне бы не хотелось.
Так в общих чертах решается задача о первых двух бифуркациях. Что будет дальше? Единственная плодотворная идея связана с отображением Пуанкаре и с тем фактом, что нечто инвариантное в отображении дает инвариантное многообразие в полупотоке размерности на единицу больше с сохранением свойства притяжения или отталкивания: неподвижная точка, притягивающая или отталкивающая, дает замкнутую траекторию, притягивающую или отталкивающую, цикл дает инвариантный тор и так далее.
Хочется отметить, что изложенные здесь геометрические методы, конечно, не единственные, с помощью которых можно попытаться решить проблему о бифуркациях решений уравнений Навье — Стокса. Прекрасным примером является книга Сэттинджера [9], в которой в 4—7 главах делается примерно то же самое, но используя методы задачи на собственные значения, энергетический метод и степень Лере — Шаудера. Я предпочитаю изложенный выше подход, поскольку он, как мне кажется, более отвечает геометрической интуиции.
В заключение сделаем следующее существенное замечание. Хотя кажется, что в задаче о первой бифуркации можно успешно продвинуться, если применить изложенные методы, возникающие сложности могут быть очень большими. Это связано с тем, что мы должны начинать с чего-либо известного, а именно с частного стационарного решения, рассматривая его как неподвижную точку полупотока, и проверить для него условия теоремы о бифуркациях.

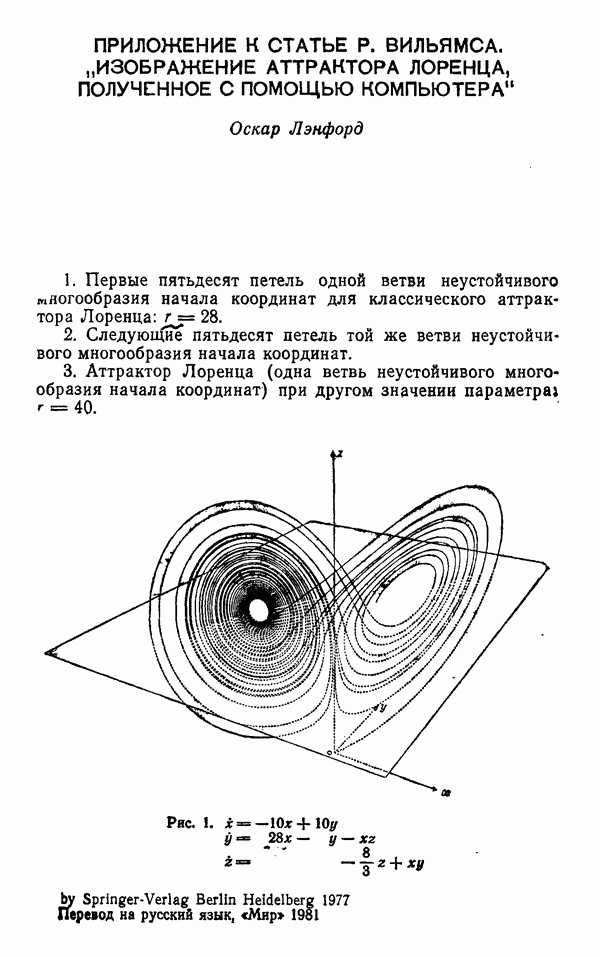
Рис. 1
Но во многих случаях нам известно даже стационарное решение! Именно в этом трудность предложенной в статье Марсдена задачи об обтекании цилиндра: точного решения  для двумерного или трехмерного обтекания нет, не говоря уже о более сложных ситуациях.
для двумерного или трехмерного обтекания нет, не говоря уже о более сложных ситуациях.
СПИСОК ЛИТЕРАТУРЫ
[1] Adams R. Sobolev Spaces, Academic Press, 1975, in series of Pure and Applied Mathematics, v. 65.
[2] Chernoff P., Marsden J. Properties of Infinite Dimensional Hamiltonian Systems, Lect. Notes in Math. 92, Springer-Verlag, 1974,
[31 Ebin D., Marsden J. Groups of Diffeomorphisms and the Motion of Incompressible Fluid, Ann. of Math. 92, n. 1, 1970, 102—163. (Русский перевод: сб. Математика, 17, № 5—6, 1973.)
[4] Hughes Т., Marsden J. A Short Course in Fluid Mechanics, Publish or Perish, 1976.
[5] Ладыженская О. А. Математическая теория вязкой несжимаемой жидкости. — М.: Наука, 1970.
[6] Marsden J., The Hopf Bifurcation for Nonlinear Semigroups, Bull, Amer. Math. Soc. 76, n. 3, 1973, 537—541.
[7] Marsden J., McCracken М., The Hopf Bifurcation, Appl. Math. Sci. 19, Springer-Verlag, 1976. (Русский перевод: Марсден Дж., Мак-Кракен М. Бифуркации рождения периодического движения и их применения.— Пер. с англ. М.: Мир, 1980.)
[8] Моггеу С. В. Multiple Integrals in the Calculus of Variations, Springer, 1966.
[9] Sattinger J. Topics in Stability and Bifurcation Theory, Lect. Notes in Math., 309, Springer-Verlag, 1973.
[10] Ruelle D., Takens F. On the Nature of Turbulence, Comm. Math. Phys, 20, 1971, 167—192. (Русский перевод в настоящем сборнике.)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- ПОПЫТКИ УСТАНОВИТЬ СООТНОШЕНИЕ МЕЖДУ УРАВНЕНИЯМИ НАВЬЕ-СТОКСА И ТУРБУЛЕНТНОСТЬЮ
- ПРИЛОЖЕНИЕ К СТАТЬЕ МАРСДЕНА БИФУРКАЦИИ, ПОЛУПОТОКИ И УРАВНЕНИЯ НАВЬЕ—СТОКСА
- ТЕОРИИ ТУРБУЛЕНТНОСТИ
- ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ РАСЧЕТА ТУРБУЛЕНТНЫХ СДВИГОВЫХ ТЕЧЕНИЙ
- ФРАКТАЛЫ И ТУРБУЛЕНТНОСТЬ: АТТРАКТОРЫ И РАЗБРОС
- СТРУКТУРА АТТРАКТОРОВ ЛОРЕНЦА
- ПРИЛОЖЕНИЕ К СТАТЬЕ Р. ВИЛЬЯМСА. «ИЗОБРАЖЕНИЕ АТТРАКТОРА ЛОРЕНЦА, ПОЛУЧЕННОЕ С ПОМОЩЬЮ КОМПЬЮТЕРА»
- ДВА ПОДХОДА К МОДЕЛИРОВАНИЮ ДВУМЕРНОЙ ТУРБУЛЕНТНОСТИ
- ДЕТЕРМИНИРОВАННОЕ НЕПЕРИОДИЧЕСКОЕ ТЕЧЕНИЕ
- О ПРИРОДЕ ТУРБУЛЕНТНОСТИ
- ДВУМЕРНОЕ ОТОБРАЖЕНИЕ СО СТРАННЫМ АТТРАКТОРОМ
- СИСТЕМА ДВУХДИСКОВОГО ДИНАМО РИКИТАКЕ
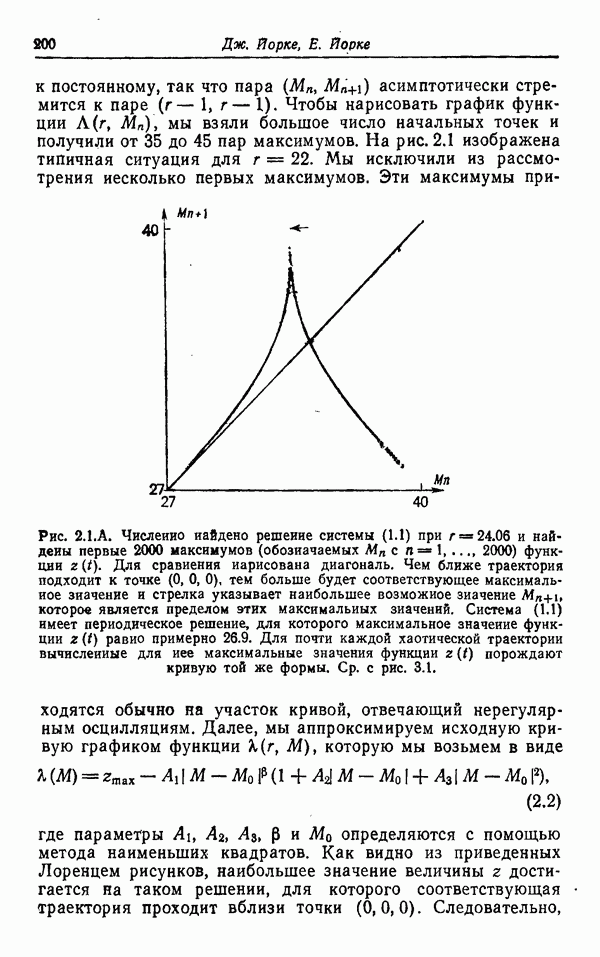
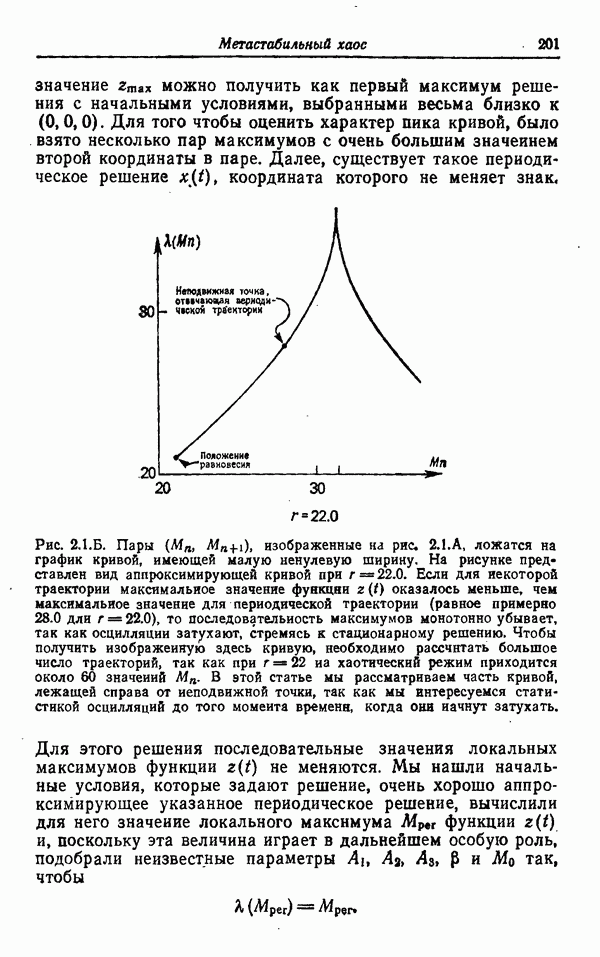
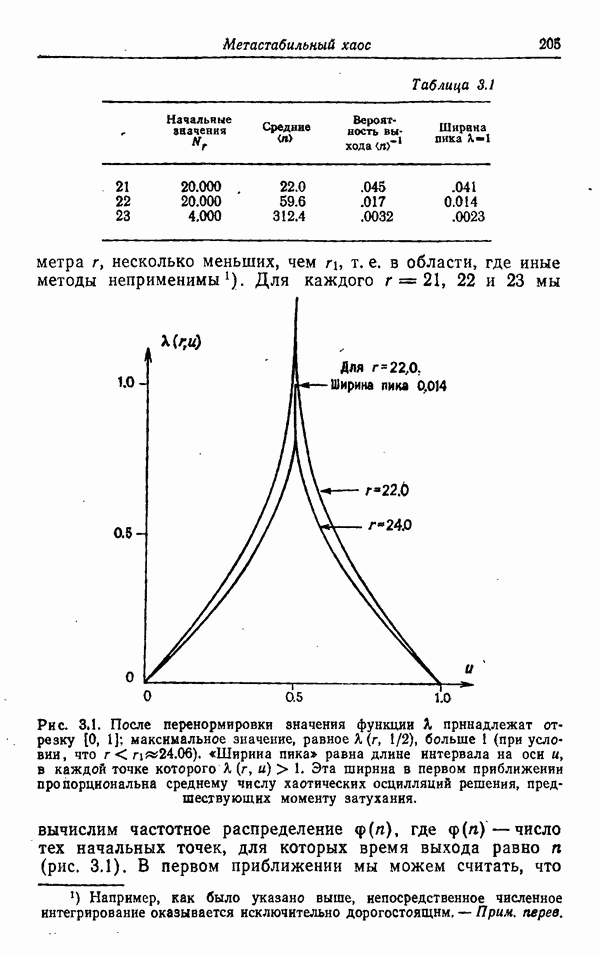
- МЕТАСТАБИЛЬНЫЙ ХАОС: ПЕРЕХОД К УСТОЙЧИВОМУ ХАОТИЧЕСКОМУ ПОВЕДЕНИЮ В МОДЕЛИ ЛОРЕНЦА
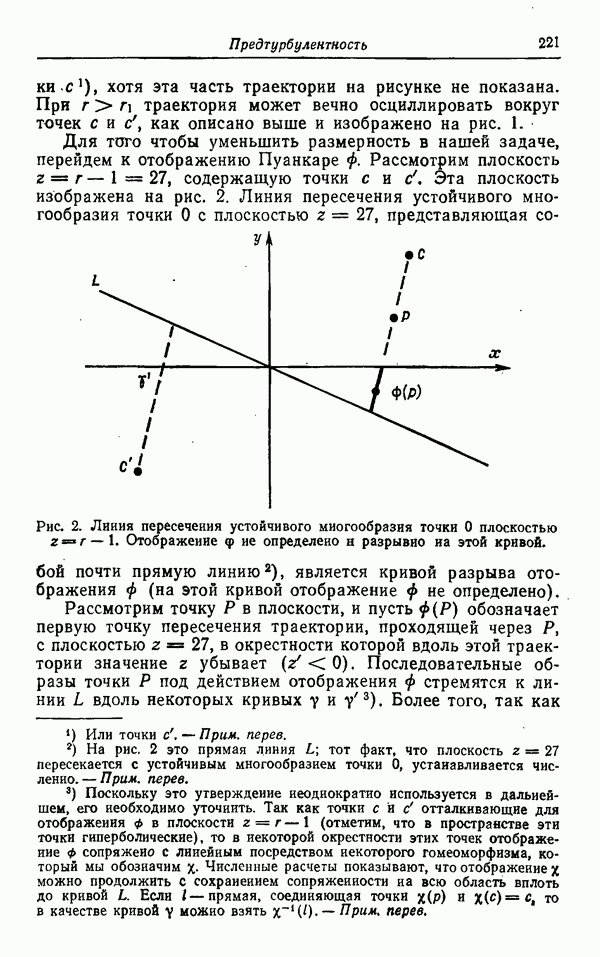
- ПРЕДТУРБУЛЕНТНОСТЬ: РЕЖИМ, НАБЛЮДАЕМЫЙ В ТЕЧЕНИИ ЖИДКОСТИ, ОПИСЫВАЕМОЙ МОДЕЛЬЮ ЛОРЕНЦА
- ТОПОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ АТТРАКТОРОВ ЛОРЕНЦА