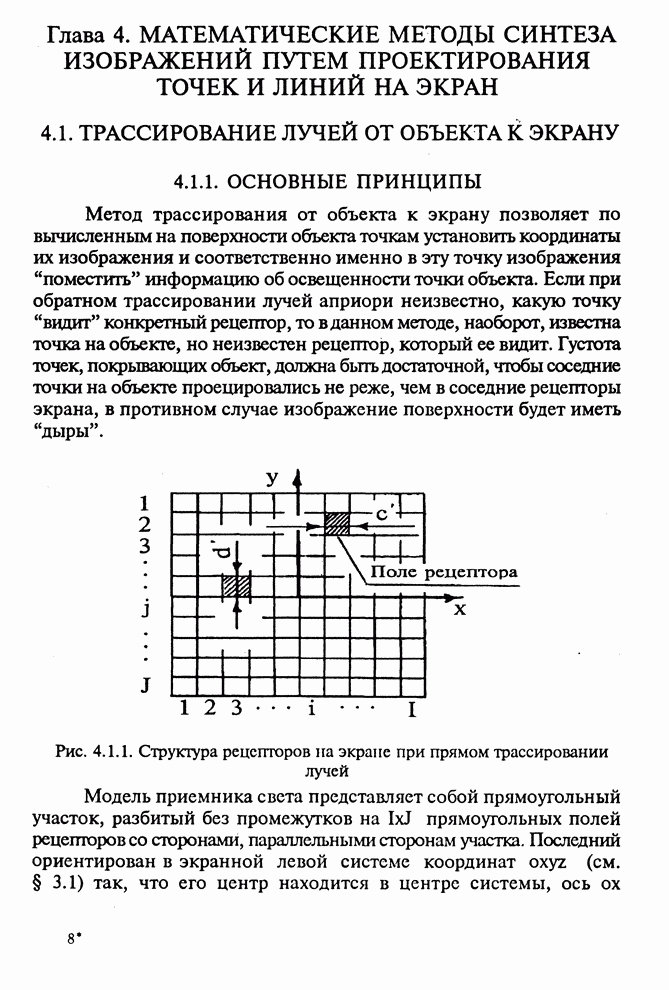
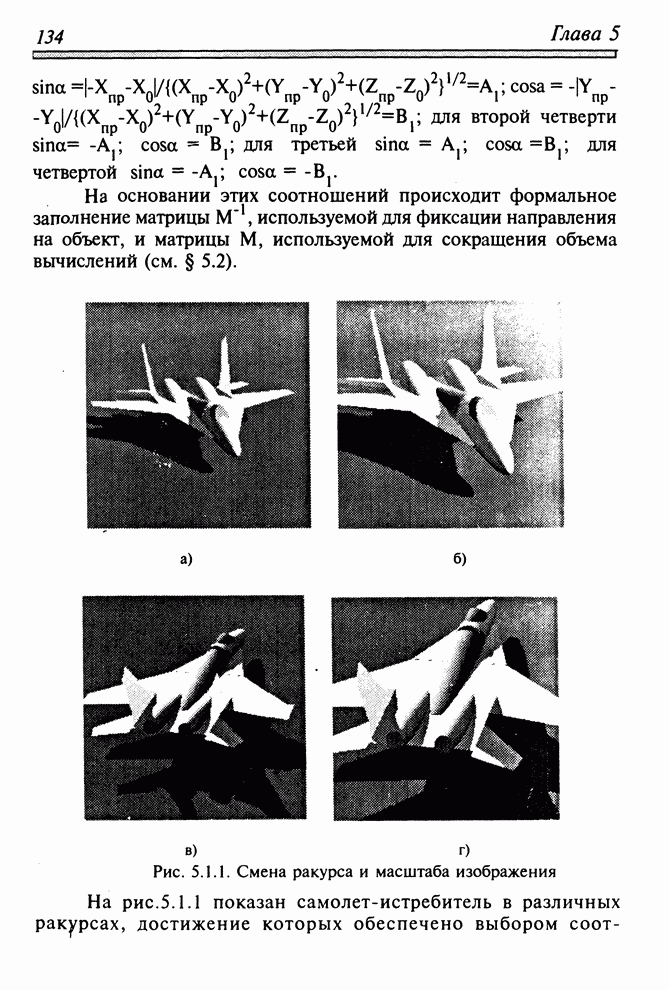
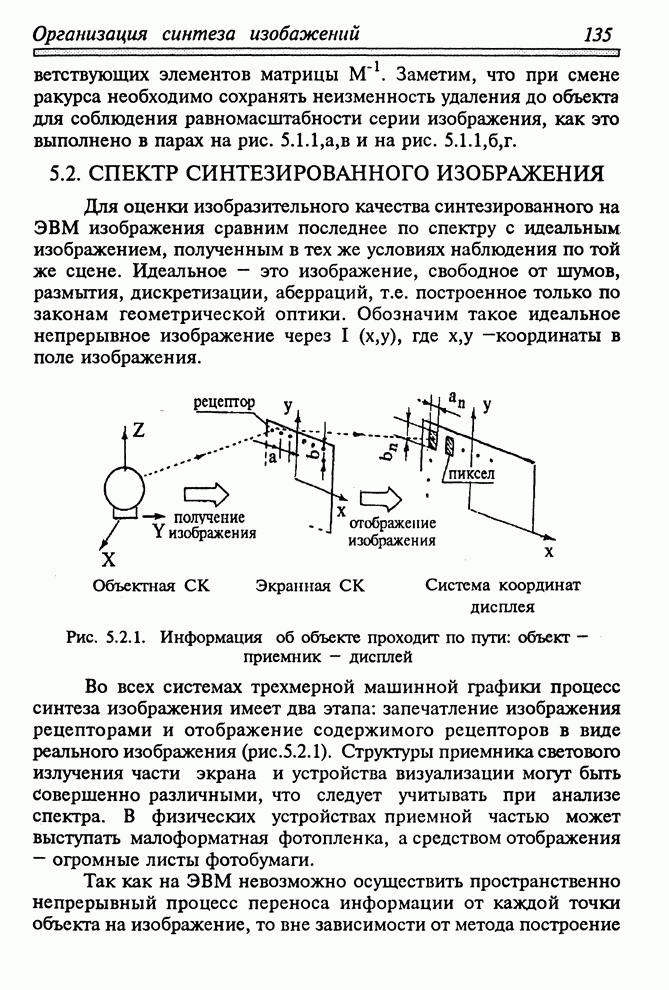
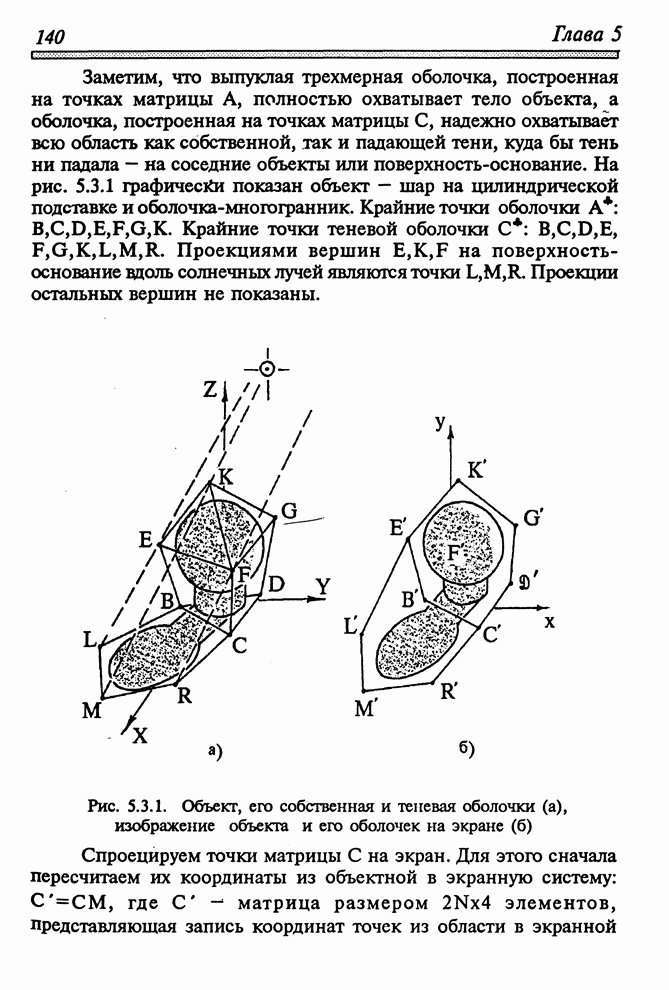
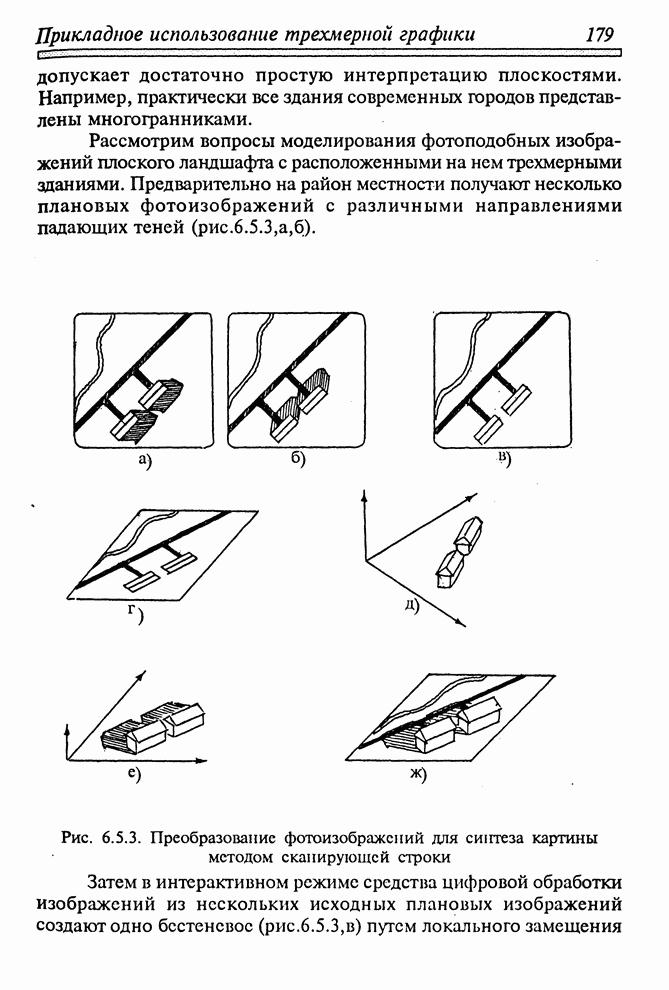
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
Поверхности
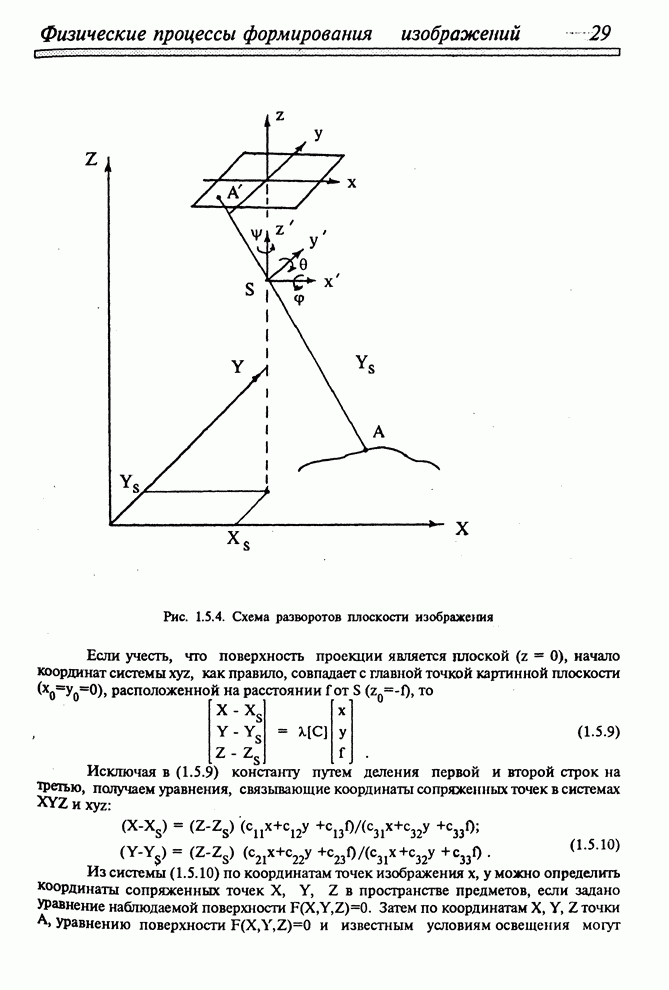
первого порядка. В системе координат ![]() объекта любой его отдельный плоский
участок лежит в плоскости, описываемой уравнением
объекта любой его отдельный плоский
участок лежит в плоскости, описываемой уравнением ![]() или в матричном виде
или в матричном виде ![]() , где
, где ![]() .
.
Изменив
компоненты матрицы ![]() , можно описать плоскость любой
ориентации и положения, однако каждый раз это будет описание бесконечно
простирающейся плоскости. Реальный плоский участок ограничен плоской кривой или
ломаной линией. Наиболее удобен для рассмотрения случай ограничения выпуклым
многоугольником. Все другие случаи, как криволинейного ограничения, так и
невыпуклой фигуры, могут быть сведены к указанному выше путем аппроксимации или
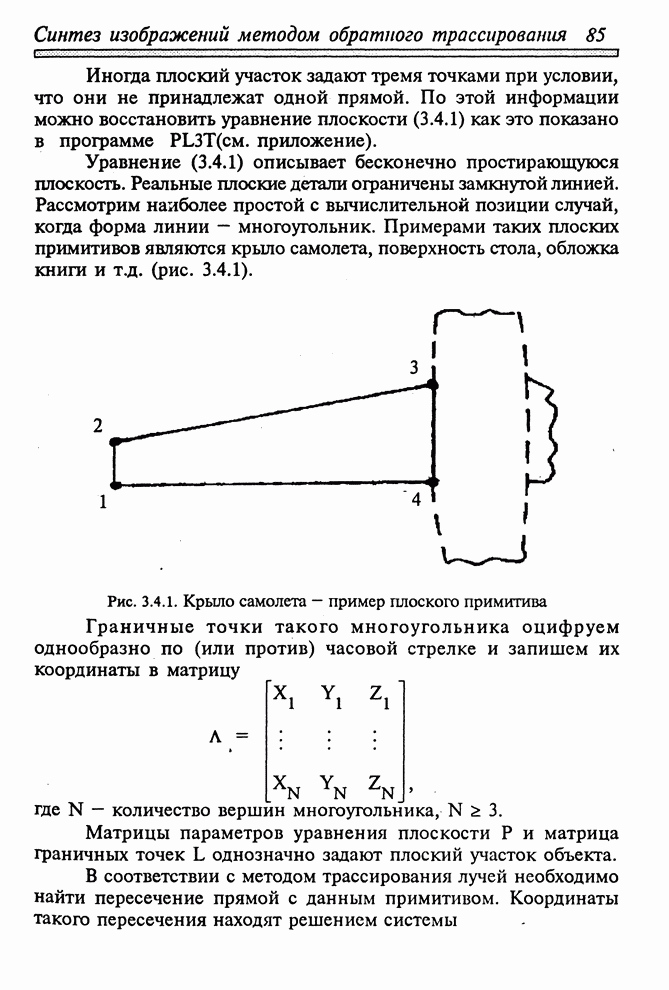
разбиения на выпуклые подфигуры. Примером плоского примитива является крыло
самолета. Граничные точки многоугольника однозначно (по или против часовой стрелки)
оцифровывают и записывают их координаты в матрицу
, можно описать плоскость любой
ориентации и положения, однако каждый раз это будет описание бесконечно
простирающейся плоскости. Реальный плоский участок ограничен плоской кривой или
ломаной линией. Наиболее удобен для рассмотрения случай ограничения выпуклым
многоугольником. Все другие случаи, как криволинейного ограничения, так и
невыпуклой фигуры, могут быть сведены к указанному выше путем аппроксимации или
разбиения на выпуклые подфигуры. Примером плоского примитива является крыло
самолета. Граничные точки многоугольника однозначно (по или против часовой стрелки)
оцифровывают и записывают их координаты в матрицу ![]() :
:
 ,
,
где
![]() – число
граничных точек,
– число
граничных точек, ![]() .
.
Уравнение
плоскости определяют на основании координат трех точек: ![]() ,
, ![]() ,
, ![]() , заведомо не лежащих на
одной прямой [11]:
, заведомо не лежащих на
одной прямой [11]:
 .
.
Программа PL3T (см. приложение) представляет реализацию этого решения на языке Турбо Паскаль.
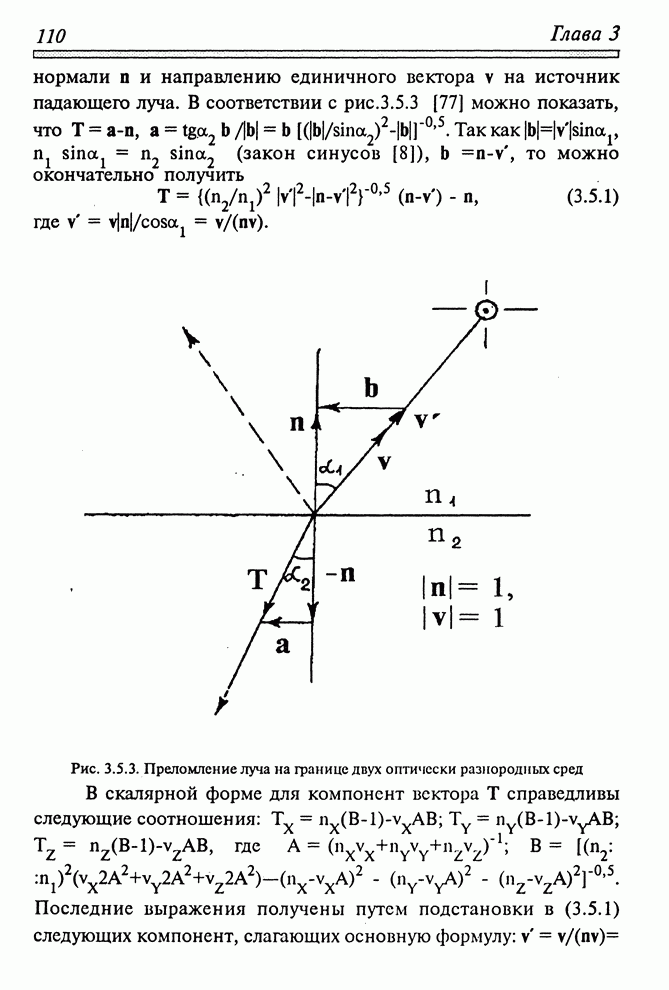
Нормальный
вектор ![]() плоскости
определяется следующим образом:
плоскости
определяется следующим образом: ![]() .
.
Направлен
этот вектор в сторону полупространства, где значения скалярного поля ![]() положительны. Из
поверхностей первого порядка можно составить описание поверхности объекта типа
полигонального поля [41,60]. Таким полем называют серию смежных
многоугольников, не имеющих разрывов между собой. Каждое ребро поля является
общим для смежных многоугольников. Таким образом, составная функция,
описывающая поверхность, обладает непрерывностью, а производная имеет разрывы в
местах стыка участков плоскостей. Простота обработки плоскостей заслуженно
привлекла внимание многих исследователей и разработчиков коммерческих
профессиональных программных продуктов. В [34,49,67,90] описаны алгоритмы
построения и изображения полигональных полей.
положительны. Из
поверхностей первого порядка можно составить описание поверхности объекта типа
полигонального поля [41,60]. Таким полем называют серию смежных
многоугольников, не имеющих разрывов между собой. Каждое ребро поля является
общим для смежных многоугольников. Таким образом, составная функция,
описывающая поверхность, обладает непрерывностью, а производная имеет разрывы в
местах стыка участков плоскостей. Простота обработки плоскостей заслуженно
привлекла внимание многих исследователей и разработчиков коммерческих
профессиональных программных продуктов. В [34,49,67,90] описаны алгоритмы
построения и изображения полигональных полей.
Поверхности второго порядка. Из аналитической геометрии [11,39] известно, что функция вида
![]() (2.2.1)
(2.2.1)
в
зависимости от выбора коэффициентов ![]() может описывать поверхности
эллипсоида, гиперболоида, конуса, параболоида, цилиндра или двух плоскостей.
Все поверхности второго порядка, за исключением эллипсоида, не локализованы в
пространстве и простираются в бесконечность. Поэтому только эллипсоид может
самостоятельно образовывать объемный примитив, все другие квадратичные формы
требуют пространственного ограничения линией или другими поверхностями.
может описывать поверхности
эллипсоида, гиперболоида, конуса, параболоида, цилиндра или двух плоскостей.
Все поверхности второго порядка, за исключением эллипсоида, не локализованы в
пространстве и простираются в бесконечность. Поэтому только эллипсоид может
самостоятельно образовывать объемный примитив, все другие квадратичные формы
требуют пространственного ограничения линией или другими поверхностями.
Наиболее удобно с вычислительной точки зрения представлять квадратичную функцию (2.2.1) в матричном виде:
![]() , (2.2.2)
, (2.2.2)
где
 . (2.2.3)
. (2.2.3)
Нормальный
вектор к квадратичной поверхности в точке ![]() определяется по правилу
определяется по правилу
![]() , (2.2.4)
, (2.2.4)
где
 ;
;
![]() ,
,
а
![]() – орты
осей
– орты
осей ![]() .
Направлен такой вектор по градиенту скалярного поля
.
Направлен такой вектор по градиенту скалярного поля ![]() , т. е. в ту сторону, где
наблюдается возрастание значений
, т. е. в ту сторону, где
наблюдается возрастание значений ![]() . Так как функция
. Так как функция ![]() является монотонной и
однократно знакопеременной, то нормаль
является монотонной и
однократно знакопеременной, то нормаль ![]() направлена в ту часть
подпространства, где значения функции положительны. Например, нормаль к
поверхности шара, заданного уравнением
направлена в ту часть
подпространства, где значения функции положительны. Например, нормаль к
поверхности шара, заданного уравнением ![]() , нацелена внутрь шара, а нормаль к
поверхности того же шара, но заданного в виде
, нацелена внутрь шара, а нормаль к
поверхности того же шара, но заданного в виде ![]() , уже направлена наружу шара.
, уже направлена наружу шара.
Явное
задание квадратичной поверхности применяют в машинной графике в методе
обратного трассирования лучей, при прямом трассировании используют
параметрическую форму типа ![]() ;
; ![]() ;
; ![]() . Каждая квадратичная поверхность
описывается своей системой уравнений. Приведем примеры для эллипсоида:
. Каждая квадратичная поверхность
описывается своей системой уравнений. Приведем примеры для эллипсоида: ![]() ;
; ![]() ;
; ![]() и эллиптического
параболоида:
и эллиптического
параболоида: ![]() ;
;
![]() ;
; ![]() , где
, где ![]() – размеры главных
полуосей эллипсоида;
– размеры главных
полуосей эллипсоида; ![]() – коэффициенты сжатия параболоида
вдоль осей
– коэффициенты сжатия параболоида
вдоль осей ![]() соответственно.
соответственно.
В
машинной графике часто используется операция пространственного переноса
предварительно заданной квадратичной поверхности. Известны [19] способы
определения коэффициентов уравнения квадратичной поверхности (2.2.2) при
изменении системы координат. Так, если в системе координат ![]() квадратичная поверхность
задается матрицей
квадратичная поверхность
задается матрицей ![]() , а для перевода некоторой точки
, а для перевода некоторой точки ![]() из этой системы в
другую –
из этой системы в
другую – ![]() необходимо
применить преобразование
необходимо
применить преобразование ![]() :
:
![]() ,
,
где
![]() –
матрица размера
–
матрица размера ![]() элемента
(см. §3.4.1 и [19]) , то новая матрица
элемента
(см. §3.4.1 и [19]) , то новая матрица ![]() квадратичной поверхности в новой
системе координат
квадратичной поверхности в новой
системе координат ![]() будет определяться по правилу
будет определяться по правилу
![]() . (2.2.5.)
. (2.2.5.)
Структура
матриц ![]() и
и
![]() приведена
в (2.2.3.). Подобным образом осуществляется переход в новую систему координат
параметрически заданной поверхности. Если в системе координат
приведена
в (2.2.3.). Подобным образом осуществляется переход в новую систему координат
параметрически заданной поверхности. Если в системе координат ![]() квадратичная
поверхность задается в виде
квадратичная
поверхность задается в виде ![]() ;
; ![]() ;
; ![]() , а новая система
, а новая система ![]() связана со старой
зависимостью
связана со старой
зависимостью ![]() ,
то новые параметрические описания
,
то новые параметрические описания ![]() ,
, ![]() ,
, ![]() могут быть получены следующей
операцией:
могут быть получены следующей
операцией:
![]() .
.
Приведем
пример преобразования функции шара ![]() из системы координат
из системы координат ![]() в систему
в систему ![]() , которая
образована путем сдвига
, которая
образована путем сдвига ![]() на пять единиц по каждой из
координатных осей.
на пять единиц по каждой из
координатных осей.
В матричном виде шар описывается формой
![]() ,
,
где
 .
.
В
соответствии с правилами построения матрицы преобразования координат ![]() (см. §3.4.1)
последняя имеет вид
(см. §3.4.1)
последняя имеет вид
 .
.
Новая
матрица ![]() ,
описывающая шар в системе
,
описывающая шар в системе ![]() , определяется правилом
, определяется правилом
 .
.
Проведя
операции умножения матриц, можно получить новую форму описания шара в системе ![]() в каноническом
виде:
в каноническом
виде:
![]() .
.
Заметим,
что при преобразовании координат по правилу (2.2.4) нормальный вектор сохраняет
свою исходную ориентацию, что важно при вычислении освещенности на поверхности
квадратичной функции. Например, если квадратичная функция задана в системе ![]() и нормальный
вектор из точки поверхности направлен в сторону выпуклости поверхности, то при
переносе и вращении поверхности по правилу (2.2.4) новый нормальный вектор из
этой точки также направлен в сторону выпуклости. Докажем этот факт.
и нормальный
вектор из точки поверхности направлен в сторону выпуклости поверхности, то при
переносе и вращении поверхности по правилу (2.2.4) новый нормальный вектор из
этой точки также направлен в сторону выпуклости. Докажем этот факт.
Действительно,
известно, что если ![]() – координаты точки
– координаты точки ![]() в системе
в системе ![]() , а системы
, а системы ![]() и
и ![]() связаны между
собой матрицей преобразования
связаны между
собой матрицей преобразования ![]() :
:
![]() ,
,
то
![]() .
.
Кроме
того, если квадратичная поверхность в системе ![]() описывается матрицей
описывается матрицей ![]() , а в системе
, а в системе ![]() – матрицей
– матрицей ![]() , то
, то ![]() . Тогда
справедливы следующие выражения:
. Тогда
справедливы следующие выражения:
 ,
,
где
![]() –
единичная матрица
–
единичная матрица ![]() элемента.
элемента.
Значение
функции в одной и той же точке пространства инвариантно к смене системы
координат, в которой эта функция задана. Пользуясь принципом относительности,
содержание этой фразы можно интерпретировать так: значение функции ![]() , описывающей
поверхность уравнением
, описывающей
поверхность уравнением ![]() в точке, перемещающейся по единому
закону с поверхностью, есть константа. Эти положения объясняют и инвариантность
ориентации нормали к поверхности при перемещении самой поверхности.
в точке, перемещающейся по единому
закону с поверхностью, есть константа. Эти положения объясняют и инвариантность
ориентации нормали к поверхности при перемещении самой поверхности.
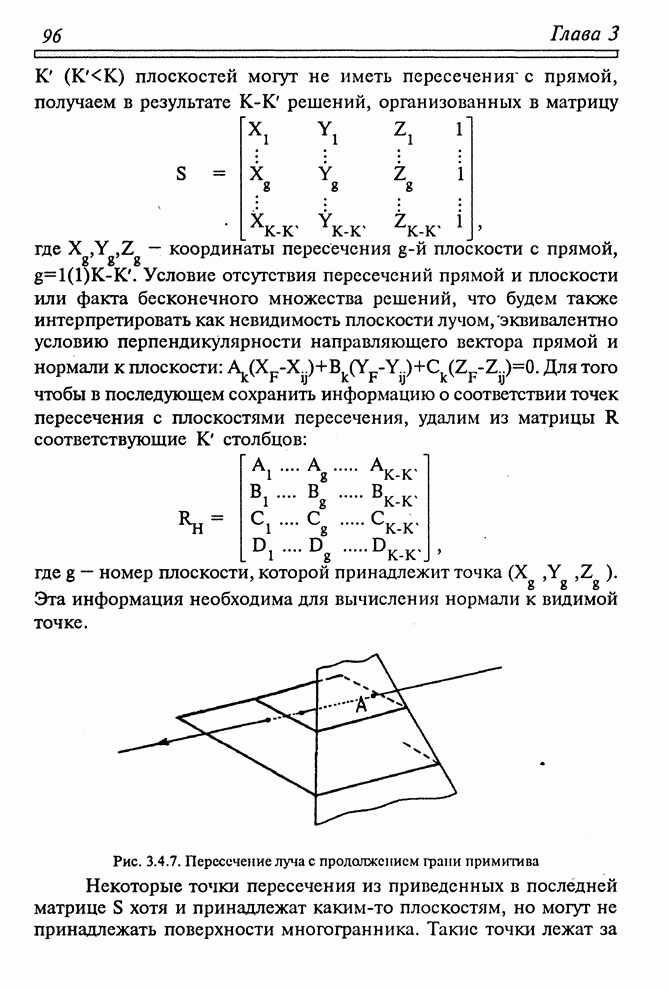
Поверхности типа экструзий. Название этих поверхностей происходит от английского слова extrusion, означающего выталкивание, выдавливание. С такими поверхностями встречаются довольно часто: это и металлические профили, выдавленные из расплава, и керамические пустотелые кирпичи, выдавленные из глины. К экструзиям относят и поверхности вращения, которые вырезаны резцом из заготовки.
Достаточно широкий класс машиностроительных деталей, предметов быта, архитектурных форм может быть представлен как результат вращения кривой или ломаной линии относительно некоторой оси. Обычно поверхности такого типа описывают в виде усеченных конусов, примыкающих друг к другу торцами (рис. 2.2.1,а,б).

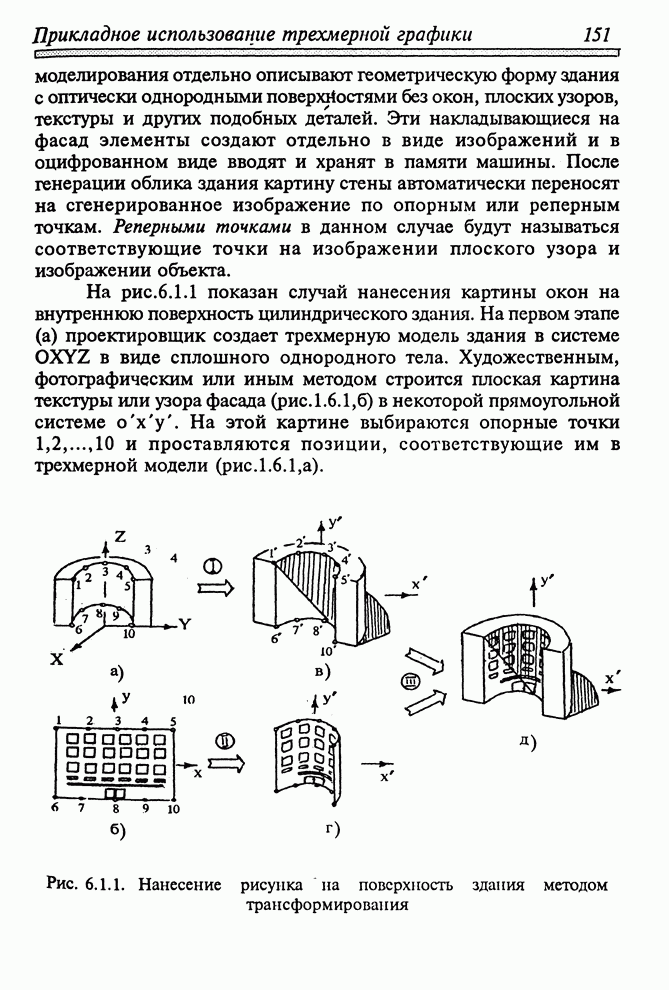
Рис. 2.2.1. Поверхности типа экструзий
Кривую линию, являющуюся линией вращения фигуры, аппроксимируют ломаной линией. Каждый отдельный участок последней становится образующей отдельного конуса. Таким образом, если кривая аппроксимируется ломаной из ста отрезков, то вся фигура представляется из ста попарно смежных конусов. Описание конуса может быть как неявным, так и параметрическим в зависимости от алгоритма синтеза изображения.
Другими представителями поверхностей-экструзий являются поверхности, образованные путем параллельного переноса кривой линии вдоль некоторой прямой. Как и в других случаях, кривую аппроксимируют ломаной линией, а всю поверхность фигуры представляют множеством смежных четырехугольников. Две стороны каждого четырехугольника параллельны направляющей прямой, а две остальные параллельны соответствующему отрезку ломаной (рис.2.2.1,в,г). Если в качестве направляющей используется кривая линия, то она, в свою очередь, также аппроксимируется ломаной. В пределах каждого отрезка направляющей ломаной линии поверхность представляется лентой смежных четырехугольников, которая сопрягается с соседней лентой, построенной в направлении следующего отрезка направляющей ломаной (рис.2.2.1,д,е).
Фрактальные поверхности. Естественные сцены часто не могут быть описаны на основе традиционных приемов, базирующихся на использовании непрерывных функций. Однако можно заметить, что большинство природных сцен статистически родственны. В [89] приводится анализ нерегулярности изображений береговой линии, полученных при съемке из космоса с высот 10; 3 км и, наконец, при наблюдении с уровня поверхности Земли. При этом установлено, что при любом уровне разрешения береговая линия может быть смоделирована и нарисована посредством объединения участков небольших прямолинейных сегментов. Причем при переходе на каждый следующий, более высокий уровень разрешения, который был предварительно аппроксимирован одним прямолинейным сегментом, этот сегмент теперь должен быть вероятностным образом разбит на последовательность линейных сегментов, и так далее и до бесконечности. На основании этого свойства – постоянства статистического закона порождения деталей природных образований при переходе от низких к более высоким уровням разрешения – построен метод использования фрактальных поверхностей.
В переводе с английского "фрактальный" означает состоящий из частиц, частей. Такими поверхностями называют класс нерегулярных геометрических форм, задаваемых вероятностным образом на основе исходного описания низкого разрешения. Случайный закон, с помощью которого исходная линия или поверхность дробится на несколько более мелких линий или поверхностей, подбирается опытным путем по критерию визуального согласования синтезированного изображения с реальной моделируемой сценой [43,80]. Наиболее часто фрактальные поверхности используются для моделирования горного ландшафта. Предварительно горный массив описывают очень приближенно полигональным полем из четырехугольников. Каждый четырехугольник разбивают с помощью случайной функции на четыре фигуры меньших размеров, причем эти фигуры вероятностным образом сдвигают относительно плоскости исходного четырехугольника, сохраняя для каждой фигуры по одной общей вершине с исходным четырехугольником. Каждую фигуру вновь делят, и так далее до достижения желаемого уровня изрезанности поверхности. Построение изображения осуществляется путем удаления скрытых поверхностей и закраски множества сгенерированных четырехугольников. Изображения, созданные на основе фрактальных поверхностей, только статистически идентичны реальным объектам, поэтому от них нельзя требовать идеальной точности.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА 1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ И ИХ МОДЕЛИРОВАНИЕ
- 1.1. МОДЕЛИ В МАШИННОЙ ГРАФИКЕ
- 1.2. ИСТОЧНИКИ ОСВЕЩЕНИЯ
- 1.2.1. ИСТОЧНИКИ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
- 1.2.2. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИСТОЧНИКОВ ПРОСТОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
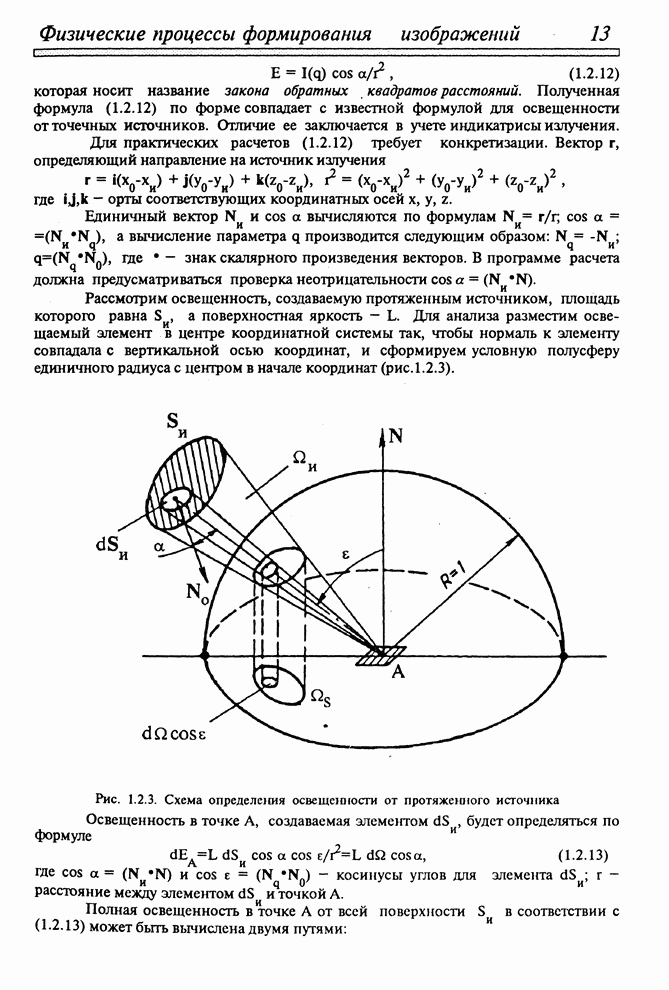
- 1.2.3. ОСВЕЩЕННОСТЬ, СОЗДАВАЕМАЯ ТОЧЕЧНЫМИ И ПРОТЯЖЕННЫМИ ИСТОЧНИКАМИ
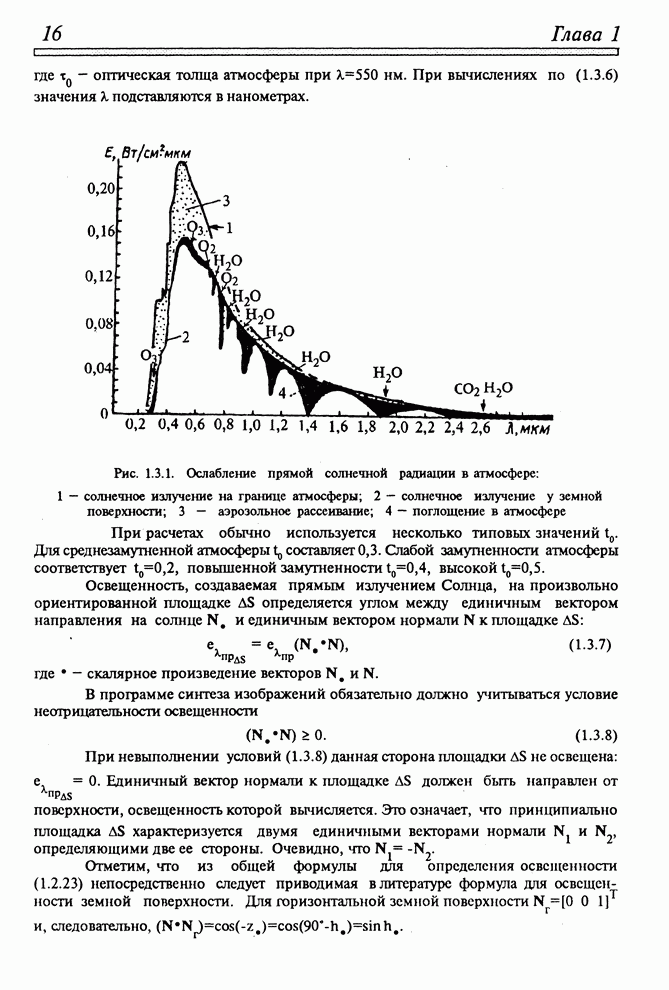
- 1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
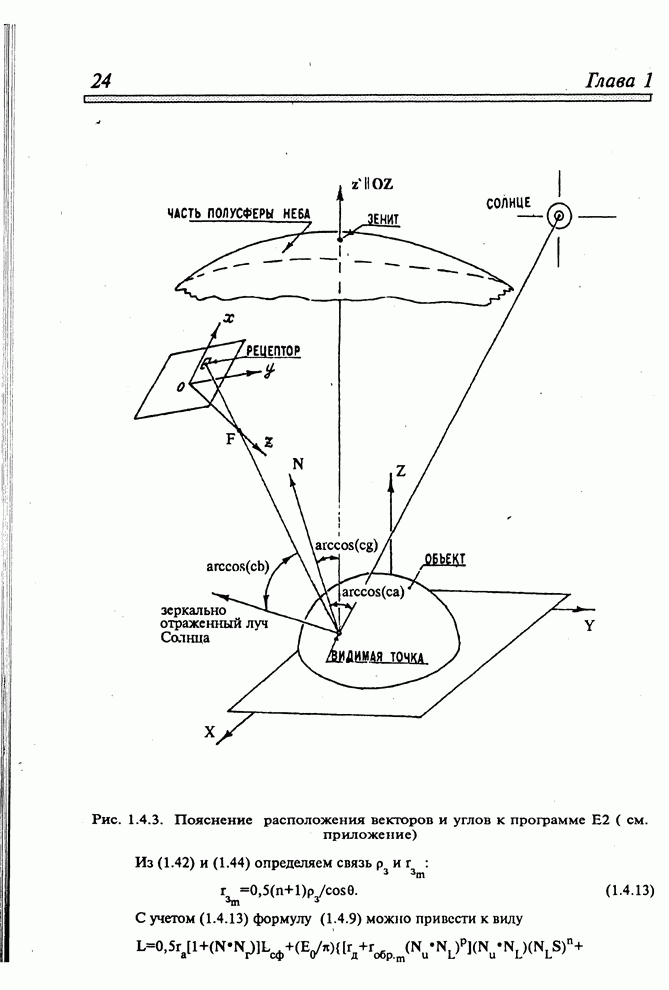
- 1.4. МОДЕЛИРОВАНИЕ ОТРАЖЕННОГО ИЗЛУЧЕНИЯ ОБЪЕКТОВ
- 1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
- 1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
- 1.5.2. ЦЕНТРАЛЬНАЯ (ПЕРСПЕКТИВНАЯ) ПРОЕКЦИЯ
- 1.5.3. ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ С ИСПОЛЬЗОВАНИЕМ ОДНОРОДНЫХ КООРДИНАТ
- 1.5.4. ПРОЕКЦИИ ПРИ РАЗЛИЧНЫХ ВИДАХ СЪЕМКИ
- 1.6. ТЕКСТУРА ИЗОБРАЖЕНИЯ
- 1.7. МОДЕЛИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.8. СИНТЕЗ ИЗОБРАЖЕНИЙ С УЧЕТОМ СПЕЦИФИКИ ИХ ФОРМИРОВАНИЯ В РЕАЛЬНЫХ УСЛОВИЯХ
- ГЛАВА 2. ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
- 2.1. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
- 2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
- 2.3. МОДЕЛИ ОБЪЕКТОВ И ИХ КЛАССИФИКАЦИЯ
- ГЛАВА 3. СИНТЕЗ ИЗОБРАЖЕНИЙ МЕТОДОМ ОБРАТНОГО ТРАССИРОВАНИЯ ЛУЧЕЙ
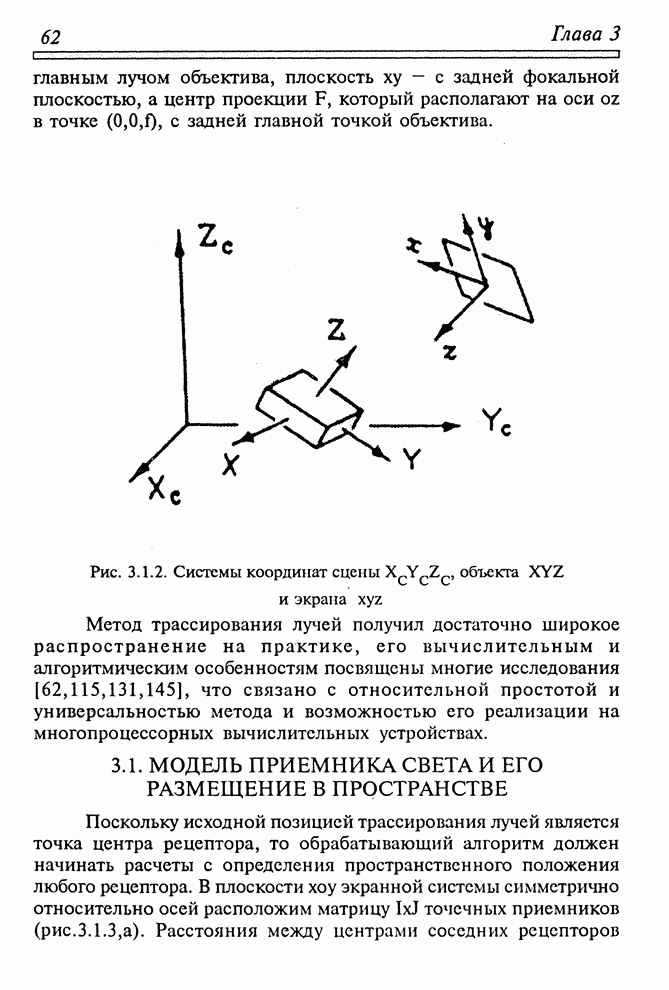
- 3.1. МОДЕЛЬ ПРИЕМНИКА СВЕТА И ЕГО РАЗМЕЩЕНИЕ В ПРОСТРАНСТВЕ
- 3.2. МОДЕЛЬ ОБЪЕКТА
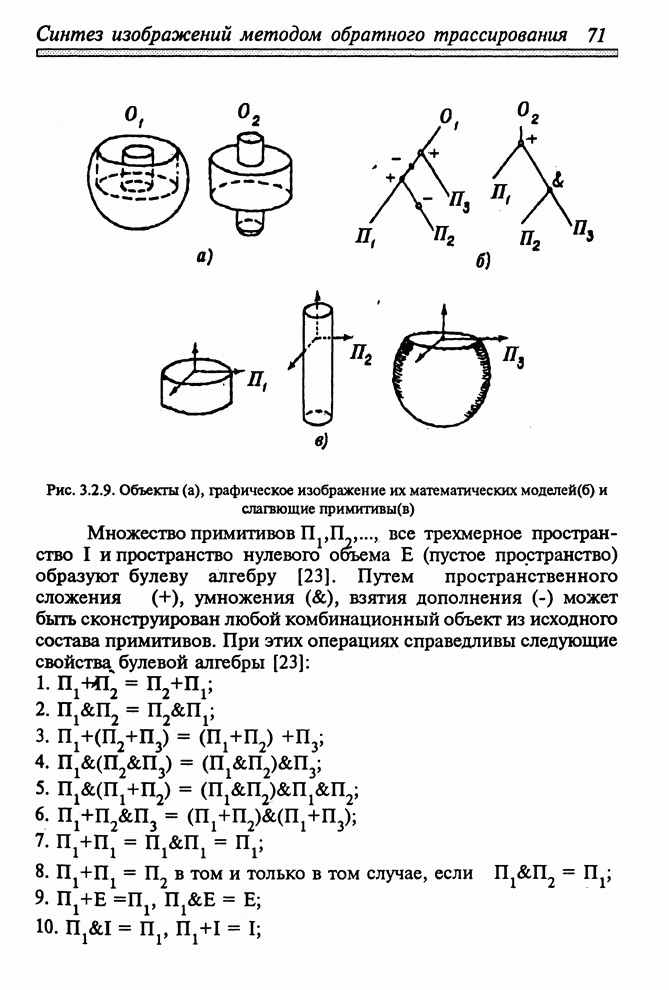
- 3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
- 3.2.2. ПРОСТРАНСТВЕННЫЕ КОМБИНАЦИИ ПРИМИТИВОВ
- 3.2.3. ФОРМАЛИЗОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
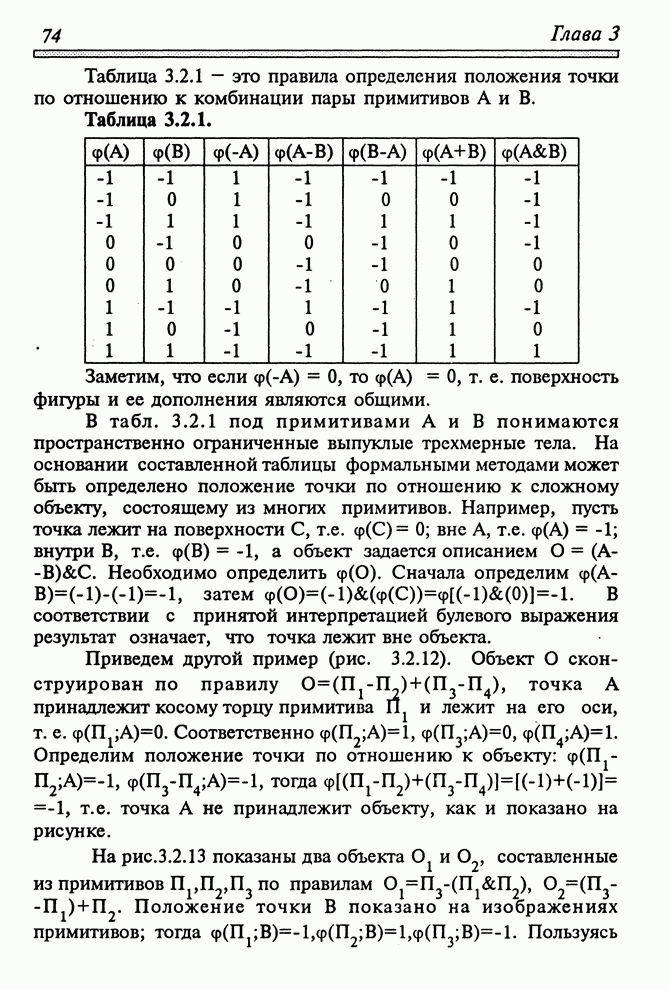
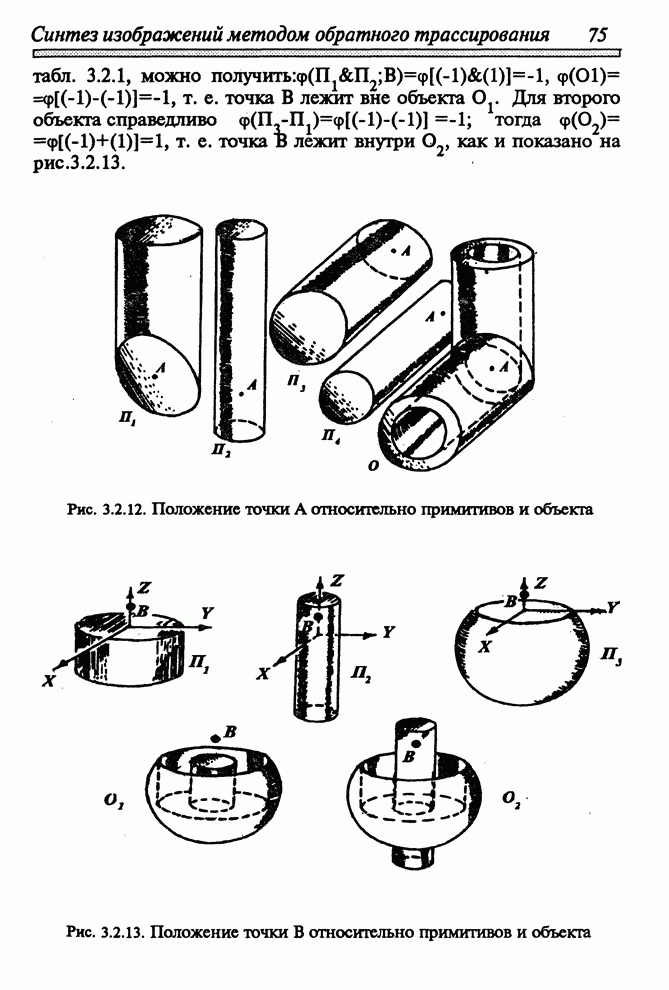
- 3.2.4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ОБЪЕКТА
- 3.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ И ЗАТЕНЕННЫХ ТОЧЕК
- 3.3.1. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С ПРИМИТИВОМ
- 3.3.2. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С КОМБИНАЦИЕЙ ПРИМИТИВОВ
- 3.3.3. ОПРЕДЕЛЕНИЕ ЗАТЕНЕННЫХ ТОЧЕК
- 3.4. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРИМИТИВОВ МЕТОДОМ ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.4.1. ПЛОСКИЕ МНОГОУГОЛЬНИКИ
- 3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
- 3.4.3. КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
- 3.4.4. БИКУБИЧЕСКИЕ ПОВЕРХНОСТИ
- 3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- 3.6. ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ ОСВЕЩЕННОСТИ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ИЗОБРАЖЕНИЙ ПУТЕМ ПРОЕКТИРОВАНИЯ ТОЧЕК И ЛИНИЙ НА ЭКРАН
- 4.1. ТРАССИРОВАНИЕ ЛУЧЕЙ ОТ ОБЪЕКТА К ЭКРАНУ
- 4.1.1. ОСНОВНЫЕ ПРИНЦИПЫ
- 4.1.2. МОДЕЛЬ ОБЪЕКТА
- 4.1.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ ТОЧЕК
- 4.1.4. ОПРЕДЕЛЕНИЕ ОСВЕЩЕННОСТИ
- 4.1.5. ИЗОБРАЖЕНИЕ ПОТОЧЕЧНО ОПИСАННЫХ ОБЪЕКТОВ
- 4.2. МЕТОД СКАНИРУЮЩЕЙ СТРОКИ
- 4.2.1. МОДЕЛЬ ОБЪЕКТА ИЗ МНОГОУГОЛЬНИКОВ
- 4.2.2. МОДЕЛЬ ПРИЕМНИКА
- 4.2.3. ИЗОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ НА ЭКРАНЕ
- 4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
- 4.3. АЛГОРИТМ РОБЕРТСА
- 4.3.1. МОДЕЛЬ ОБЪЕКТА
- 4.3.2. СИНТЕЗ ИЗОБРАЖЕНИЯ
- ГЛАВА 5. ОРГАНИЗАЦИЯ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.1. УПРАВЛЕНИЕ ПРОЦЕССОМ СИНТЕЗА
- 5.2. СПЕКТР СИНТЕЗИРОВАННОГО ИЗОБРАЖЕНИЯ
- 5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.3.1. МЕТОД ОБОЛОЧЕК
- 5.3.2. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ТРАНСПЬЮТЕРОВ В МАШИННОЙ ГРАФИКЕ
- ГЛАВА 6. ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКИ
- 6.1. АРХИТЕКТУРНОЕ ПРОЕКТИРОВАНИЕ
- 6.2. РАСПОЗНАВАНИЕ ВИДЕООБРАЗОВ
- 6.2.1. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИВНЫМ ЭТАЛОНАМ
- 6.2.2. РАСПОЗНАВАНИЕ ОБРАЗОВ В УСЛОВИЯХ НЕИЗВЕСТНОЙ ОРИЕНТАЦИИ ИХ КОРПУСОВ
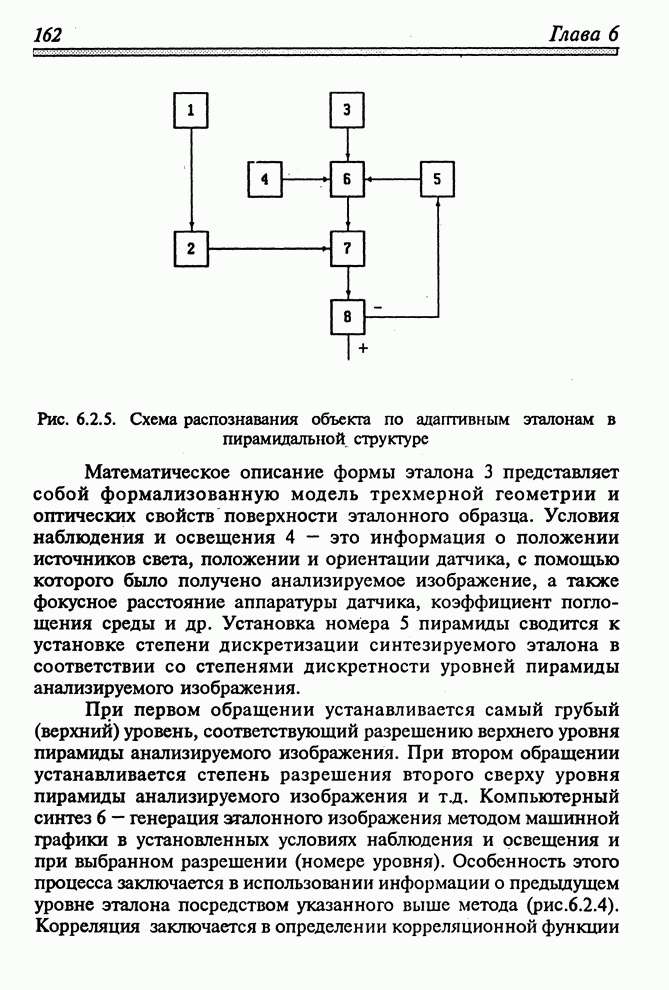
- 6.2.3. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИРОВАННЫМ ЭТАЛОНАМ В ПИРАМИДАЛЬНОЙ СТРУКТУРЕ
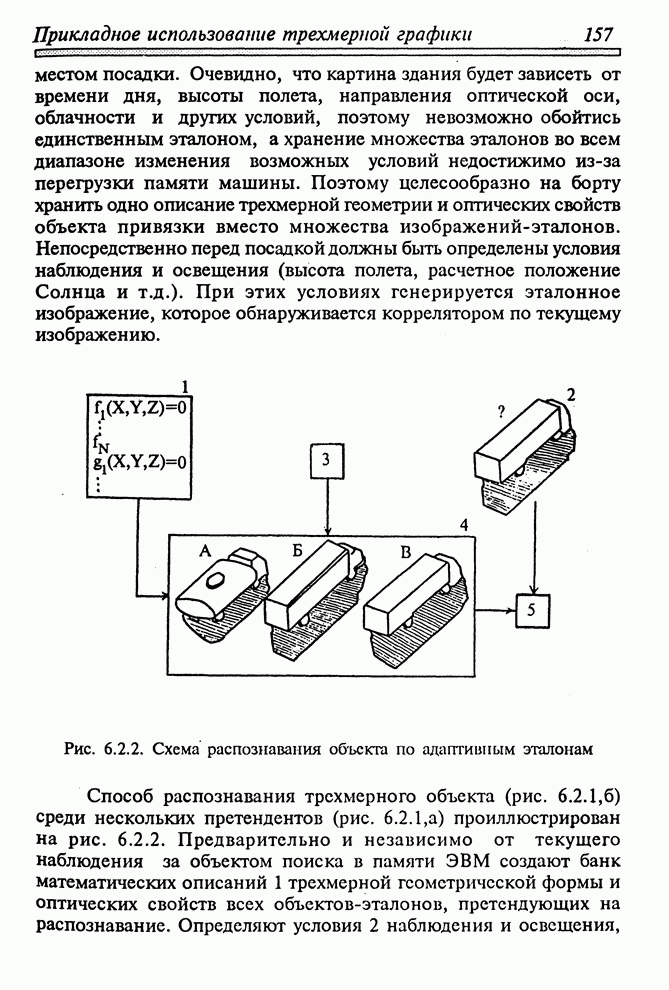
- 6.2.4. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО ЭТАЛОНАМ, АДАПТИРОВАННЫМ ПО УСЛОВИЯМ НАБЛЮДЕНИЯ И КАЧЕСТВУ
- 6.3. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ В МАШИНОСТРОЕНИИ
- 6.4. ВОССТАНОВЛЕНИЕ ФОРМЫ СКРЫТЫХ ОБЪЕКТОВ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ
- 6.5. ВИДЕОТРЕНАЖЕРЫ И ИМИТАТОРЫ СЛОЖНЫХ СЦЕН
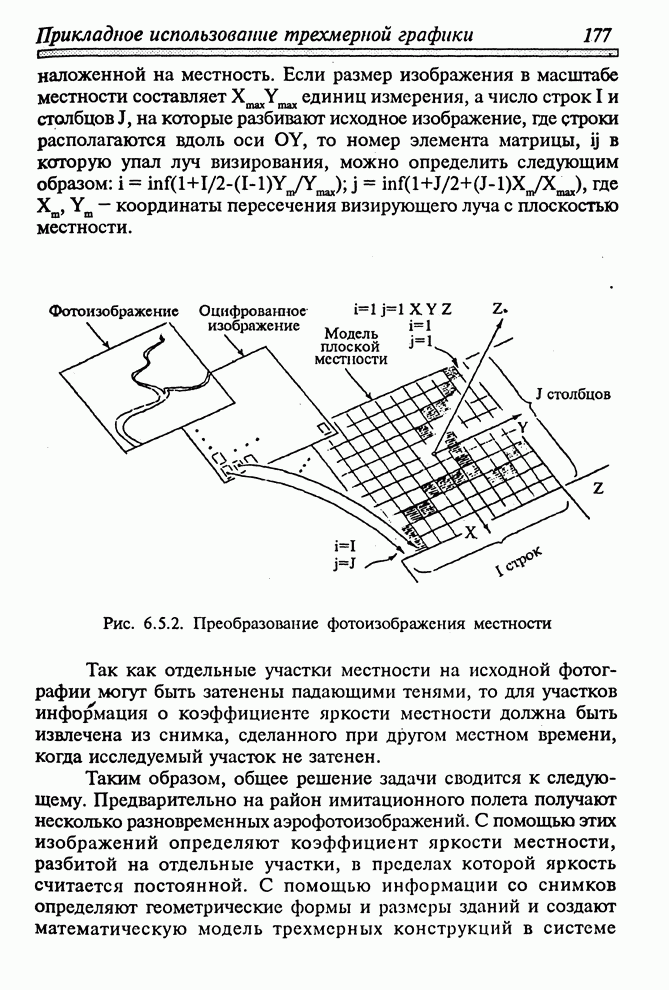
- 6.5.1. ТРЕНАЖЕР ДЛЯ ИМИТАЦИИ ПОЛЕТА НАД РЕАЛЬНОЙ МЕСТНОСТЬЮ
- 6.5.2. КОМПЬЮТЕРНЫЙ ИМИТАТОР ИЗОБРАЖЕНИЙ ОБЛАКОВ
- 6.6. РЕКЛАМА И МУЛЬТИПЛИКАЦИЯ
- ПРИЛОЖЕНИЕ. ОПИСАНИЕ ПРИКЛАДНЫХ ПОДПРОГРАММ
- СПИСОК ЛИТЕРАТУРЫ