| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
Пусть
объект представляет собой участок криволинейной поверхности типа ![]() ;
; ![]() ;
; ![]() . На основании
закона связи экранной
. На основании
закона связи экранной ![]() и объектной системы
и объектной системы ![]() преобразуем
описание поверхности в экранную систему:
преобразуем
описание поверхности в экранную систему: ![]() ;
; ![]() ;
; ![]() . Пересечем эту поверхность со
сканирующей плоскостью
. Пересечем эту поверхность со
сканирующей плоскостью ![]() , которая проходит через
, которая проходит через ![]() -ю сканирующую
строку и центр проекции
-ю сканирующую
строку и центр проекции ![]() . Для центральной проекции
. Для центральной проекции ![]() описывается
уравнением
описывается
уравнением
 ,
,
а
для ортогональной - параллельно оси ![]() , т.е. уравнение
, т.е. уравнение ![]() вырождается в форму
вырождается в форму ![]() .
.
Для определения пересечения решим систему из следующих уравнений:

результатом
которой является параметрическая кривая, которая, к сожалению, не всегда имеет
аналитическую форму и не всегда однозначна. Если же перебирать точки на
сканирующей строке от пиксела к пикселу, то численными методами удастся
определить параметры ![]() и
и ![]() в пересечениях световых лучей,
исходящих из пикселов и криволинейной поверхности. В случае ортогональной
проекции это означает, что для текущего пиксела под номером
в пересечениях световых лучей,
исходящих из пикселов и криволинейной поверхности. В случае ортогональной
проекции это означает, что для текущего пиксела под номером ![]()
![]() на
на ![]() -й сканирующей строке
необходимо найти решения
-й сканирующей строке
необходимо найти решения ![]() ;
; ![]() .
.
По
установленным параметрам ![]() для
для ![]() -гo пиксела вычисляется удаление до
пиксела. Подобные операции выполняются для всех поверхностей сцены. Наименьшее
удаление указывает на видимую поверхность, освещенность которой в данном
пикселе вычисляется по параметрам
-гo пиксела вычисляется удаление до
пиксела. Подобные операции выполняются для всех поверхностей сцены. Наименьшее
удаление указывает на видимую поверхность, освещенность которой в данном
пикселе вычисляется по параметрам ![]() . Конкретный алгоритм изображения
бикубической поверхности методом сканирующей строки описан в [71].
. Конкретный алгоритм изображения
бикубической поверхности методом сканирующей строки описан в [71].
Таким
образом, в общих чертах алгоритм сканирующей строки для криволинейных
поверхностей заключается в следующем. Предварительной сортировкой среди
множества поверхностей сцены выделяют такие, которые попадают в поле обзора.
Затем для каждой сканирующей строки ![]() ,
, ![]() , перебирают последовательно пикселы
строки
, перебирают последовательно пикселы
строки ![]() ,
,
![]() , и,
наконец, последовательно перебирают каждую поверхность. При этом решают
уравнения
, и,
наконец, последовательно перебирают каждую поверхность. При этом решают
уравнения ![]() ;
;
![]() и
вычисляют удаление от каждого
и
вычисляют удаление от каждого ![]() -гo пиксела до каждой поверхности.
Ближняя поверхность объявляется видимой, ее атрибуты и координаты
-гo пиксела до каждой поверхности.
Ближняя поверхность объявляется видимой, ее атрибуты и координаты ![]() используются для
расчета освещенности в текущем
используются для
расчета освещенности в текущем ![]() -м рецепторе.
-м рецепторе.
Изображение падающих теней для такого алгоритма затруднено, а собственные тени и блики на освещенной стороне имитируются достаточно просто.
Приведенный алгоритм имеет множество оригинальных модификаций, учитывающих, например, когерентность сканирующих строк [100] или ориентированных только на изображение сфер [124], что приводит к значительному повышению эффективности.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА 1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ И ИХ МОДЕЛИРОВАНИЕ
- 1.1. МОДЕЛИ В МАШИННОЙ ГРАФИКЕ
- 1.2. ИСТОЧНИКИ ОСВЕЩЕНИЯ
- 1.2.1. ИСТОЧНИКИ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
- 1.2.2. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИСТОЧНИКОВ ПРОСТОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
- 1.2.3. ОСВЕЩЕННОСТЬ, СОЗДАВАЕМАЯ ТОЧЕЧНЫМИ И ПРОТЯЖЕННЫМИ ИСТОЧНИКАМИ
- 1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
- 1.4. МОДЕЛИРОВАНИЕ ОТРАЖЕННОГО ИЗЛУЧЕНИЯ ОБЪЕКТОВ
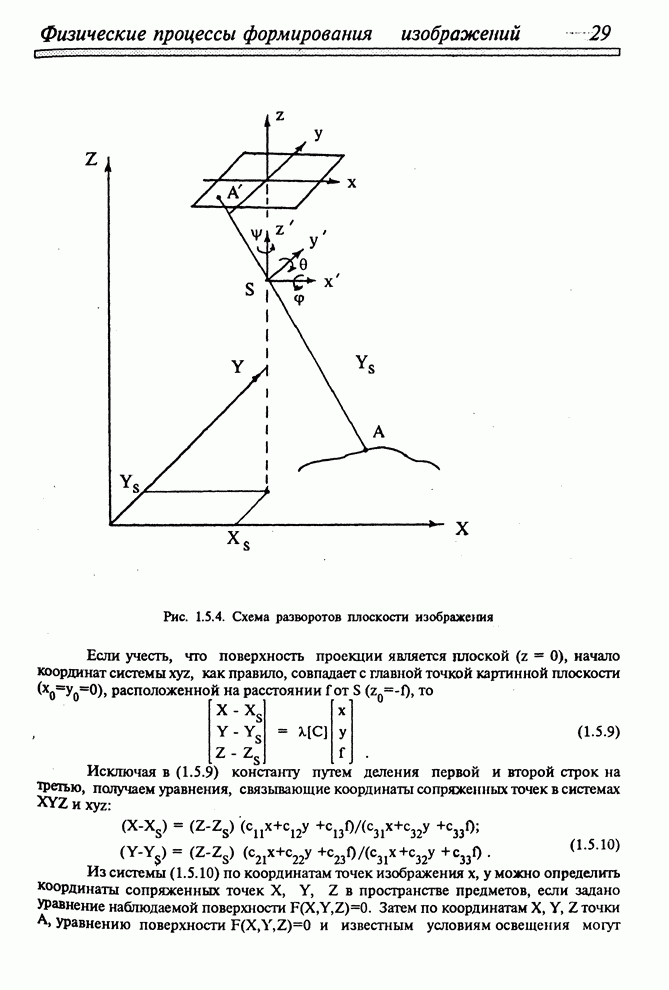
- 1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
- 1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
- 1.5.2. ЦЕНТРАЛЬНАЯ (ПЕРСПЕКТИВНАЯ) ПРОЕКЦИЯ
- 1.5.3. ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ С ИСПОЛЬЗОВАНИЕМ ОДНОРОДНЫХ КООРДИНАТ
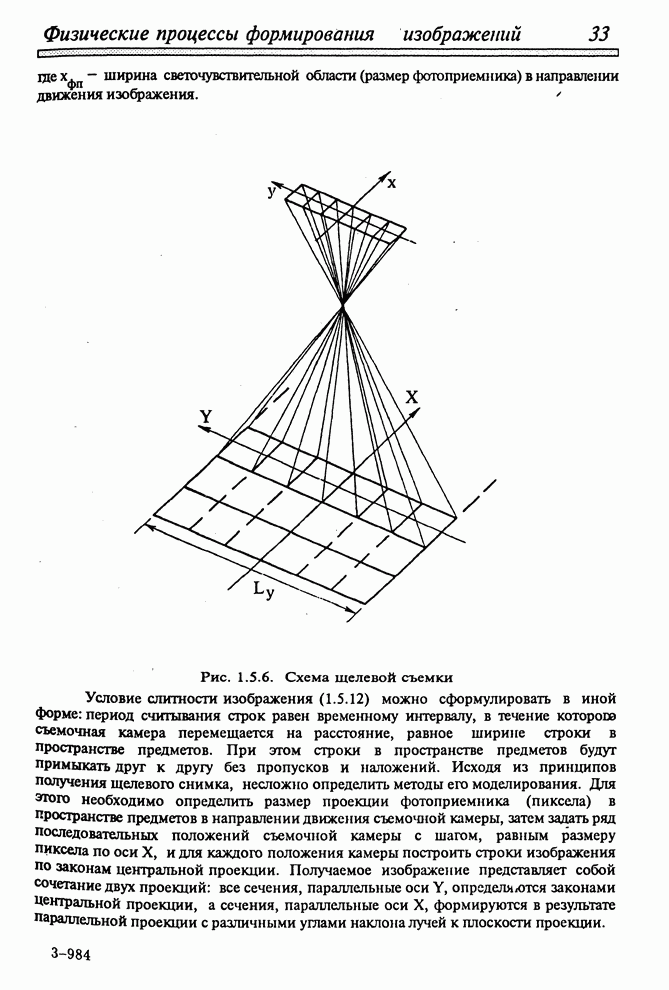
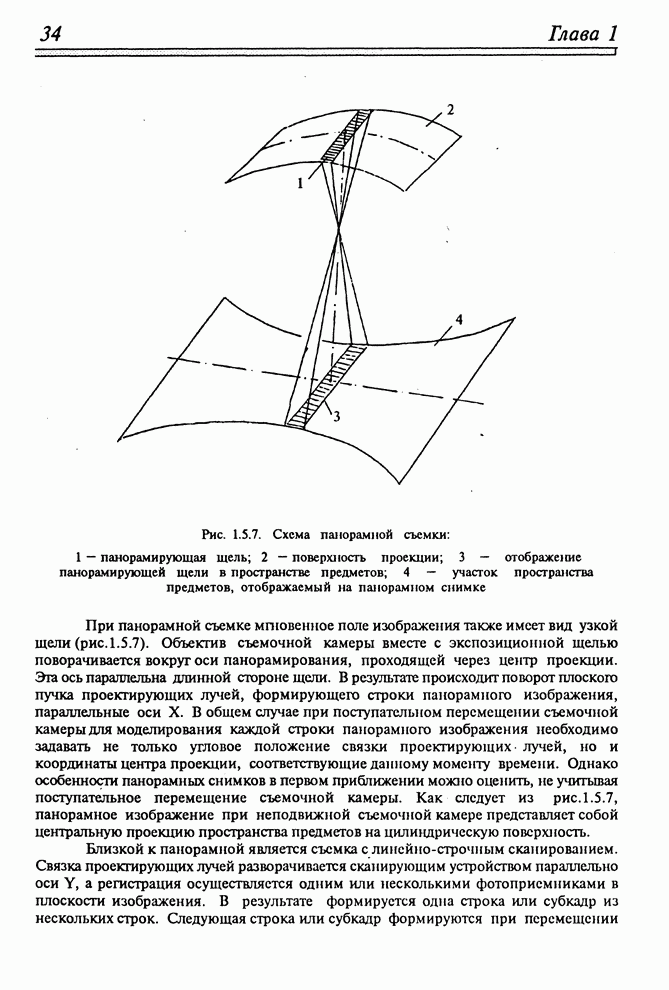
- 1.5.4. ПРОЕКЦИИ ПРИ РАЗЛИЧНЫХ ВИДАХ СЪЕМКИ
- 1.6. ТЕКСТУРА ИЗОБРАЖЕНИЯ
- 1.7. МОДЕЛИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.8. СИНТЕЗ ИЗОБРАЖЕНИЙ С УЧЕТОМ СПЕЦИФИКИ ИХ ФОРМИРОВАНИЯ В РЕАЛЬНЫХ УСЛОВИЯХ
- ГЛАВА 2. ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
- 2.1. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
- 2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
- 2.3. МОДЕЛИ ОБЪЕКТОВ И ИХ КЛАССИФИКАЦИЯ
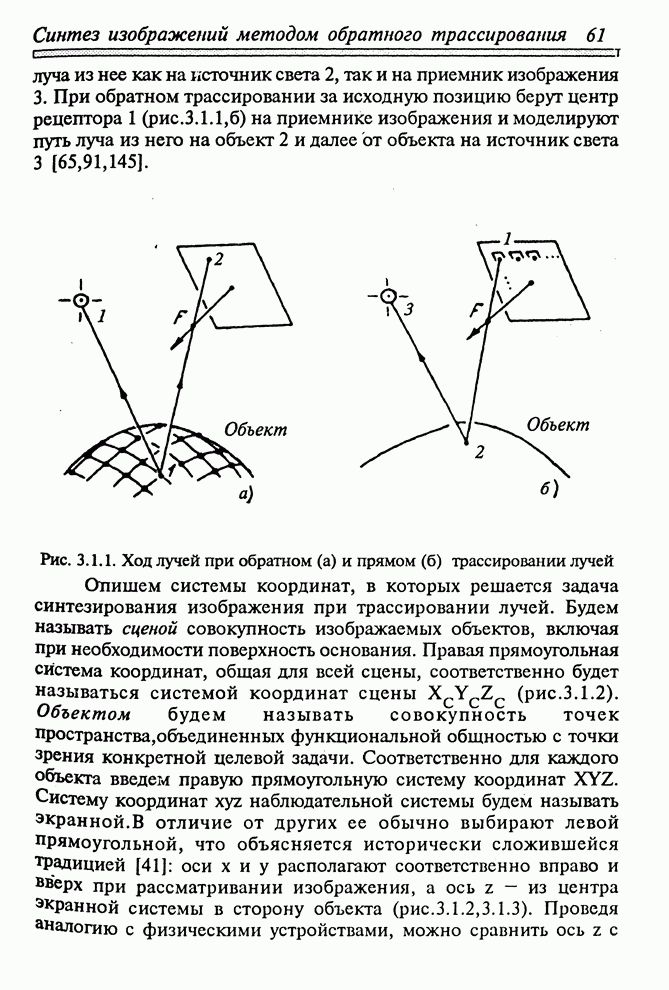
- ГЛАВА 3. СИНТЕЗ ИЗОБРАЖЕНИЙ МЕТОДОМ ОБРАТНОГО ТРАССИРОВАНИЯ ЛУЧЕЙ
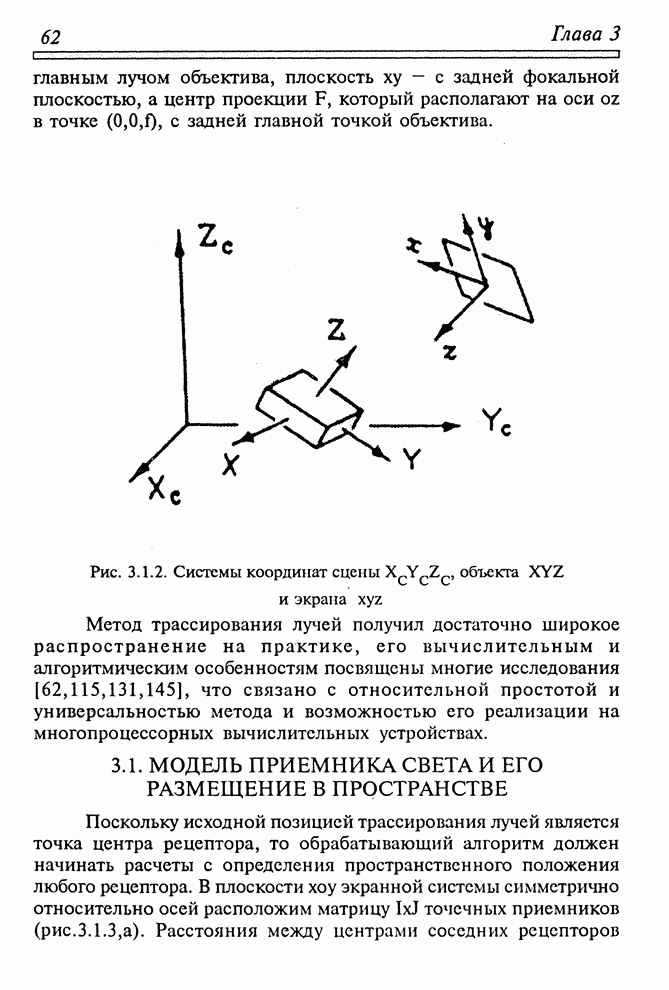
- 3.1. МОДЕЛЬ ПРИЕМНИКА СВЕТА И ЕГО РАЗМЕЩЕНИЕ В ПРОСТРАНСТВЕ
- 3.2. МОДЕЛЬ ОБЪЕКТА
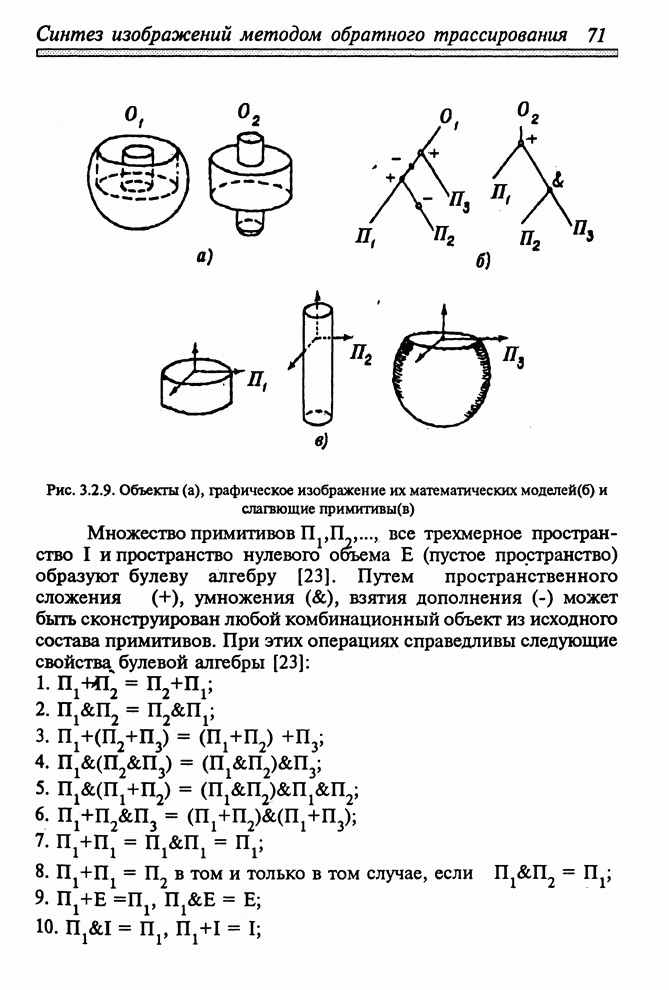
- 3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
- 3.2.2. ПРОСТРАНСТВЕННЫЕ КОМБИНАЦИИ ПРИМИТИВОВ
- 3.2.3. ФОРМАЛИЗОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
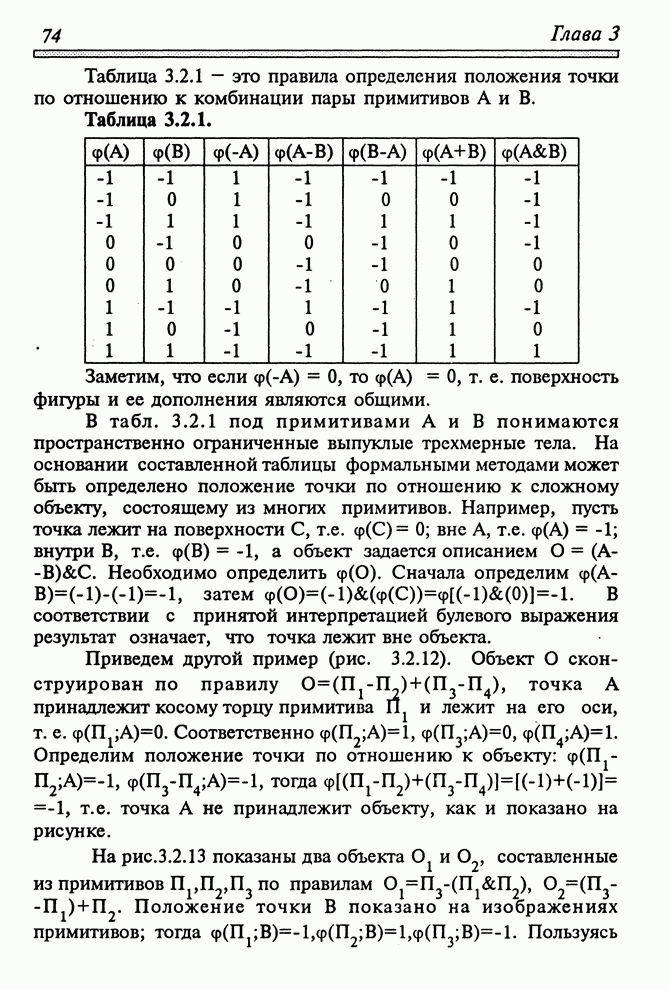
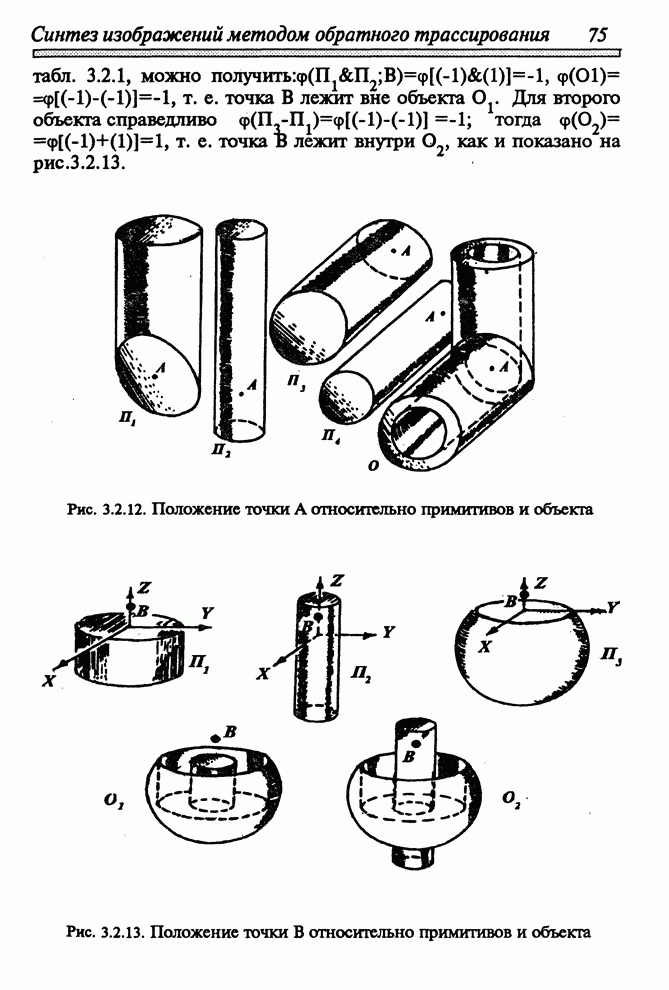
- 3.2.4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ОБЪЕКТА
- 3.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ И ЗАТЕНЕННЫХ ТОЧЕК
- 3.3.1. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С ПРИМИТИВОМ
- 3.3.2. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С КОМБИНАЦИЕЙ ПРИМИТИВОВ
- 3.3.3. ОПРЕДЕЛЕНИЕ ЗАТЕНЕННЫХ ТОЧЕК
- 3.4. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРИМИТИВОВ МЕТОДОМ ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.4.1. ПЛОСКИЕ МНОГОУГОЛЬНИКИ
- 3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
- 3.4.3. КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
- 3.4.4. БИКУБИЧЕСКИЕ ПОВЕРХНОСТИ
- 3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- 3.6. ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ ОСВЕЩЕННОСТИ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ИЗОБРАЖЕНИЙ ПУТЕМ ПРОЕКТИРОВАНИЯ ТОЧЕК И ЛИНИЙ НА ЭКРАН
- 4.1. ТРАССИРОВАНИЕ ЛУЧЕЙ ОТ ОБЪЕКТА К ЭКРАНУ
- 4.1.1. ОСНОВНЫЕ ПРИНЦИПЫ
- 4.1.2. МОДЕЛЬ ОБЪЕКТА
- 4.1.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ ТОЧЕК
- 4.1.4. ОПРЕДЕЛЕНИЕ ОСВЕЩЕННОСТИ
- 4.1.5. ИЗОБРАЖЕНИЕ ПОТОЧЕЧНО ОПИСАННЫХ ОБЪЕКТОВ
- 4.2. МЕТОД СКАНИРУЮЩЕЙ СТРОКИ
- 4.2.1. МОДЕЛЬ ОБЪЕКТА ИЗ МНОГОУГОЛЬНИКОВ
- 4.2.2. МОДЕЛЬ ПРИЕМНИКА
- 4.2.3. ИЗОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ НА ЭКРАНЕ
- 4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
- 4.3. АЛГОРИТМ РОБЕРТСА
- 4.3.1. МОДЕЛЬ ОБЪЕКТА
- 4.3.2. СИНТЕЗ ИЗОБРАЖЕНИЯ
- ГЛАВА 5. ОРГАНИЗАЦИЯ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.1. УПРАВЛЕНИЕ ПРОЦЕССОМ СИНТЕЗА
- 5.2. СПЕКТР СИНТЕЗИРОВАННОГО ИЗОБРАЖЕНИЯ
- 5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.3.1. МЕТОД ОБОЛОЧЕК
- 5.3.2. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ТРАНСПЬЮТЕРОВ В МАШИННОЙ ГРАФИКЕ
- ГЛАВА 6. ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКИ
- 6.1. АРХИТЕКТУРНОЕ ПРОЕКТИРОВАНИЕ
- 6.2. РАСПОЗНАВАНИЕ ВИДЕООБРАЗОВ
- 6.2.1. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИВНЫМ ЭТАЛОНАМ
- 6.2.2. РАСПОЗНАВАНИЕ ОБРАЗОВ В УСЛОВИЯХ НЕИЗВЕСТНОЙ ОРИЕНТАЦИИ ИХ КОРПУСОВ
- 6.2.3. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИРОВАННЫМ ЭТАЛОНАМ В ПИРАМИДАЛЬНОЙ СТРУКТУРЕ
- 6.2.4. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО ЭТАЛОНАМ, АДАПТИРОВАННЫМ ПО УСЛОВИЯМ НАБЛЮДЕНИЯ И КАЧЕСТВУ
- 6.3. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ В МАШИНОСТРОЕНИИ
- 6.4. ВОССТАНОВЛЕНИЕ ФОРМЫ СКРЫТЫХ ОБЪЕКТОВ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ
- 6.5. ВИДЕОТРЕНАЖЕРЫ И ИМИТАТОРЫ СЛОЖНЫХ СЦЕН
- 6.5.1. ТРЕНАЖЕР ДЛЯ ИМИТАЦИИ ПОЛЕТА НАД РЕАЛЬНОЙ МЕСТНОСТЬЮ
- 6.5.2. КОМПЬЮТЕРНЫЙ ИМИТАТОР ИЗОБРАЖЕНИЙ ОБЛАКОВ
- 6.6. РЕКЛАМА И МУЛЬТИПЛИКАЦИЯ
- ПРИЛОЖЕНИЕ. ОПИСАНИЕ ПРИКЛАДНЫХ ПОДПРОГРАММ
- СПИСОК ЛИТЕРАТУРЫ