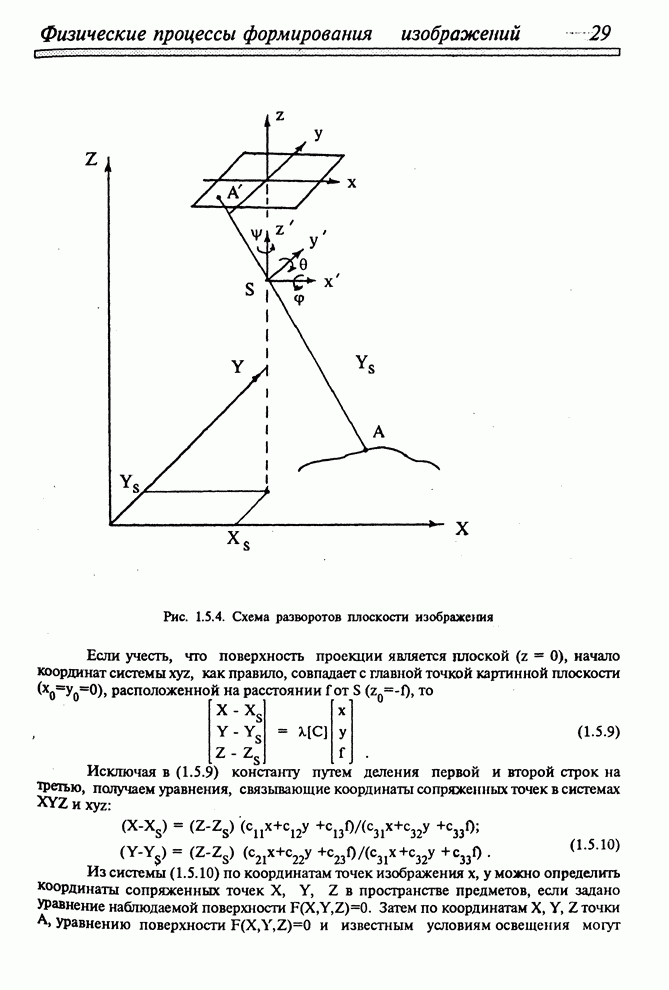
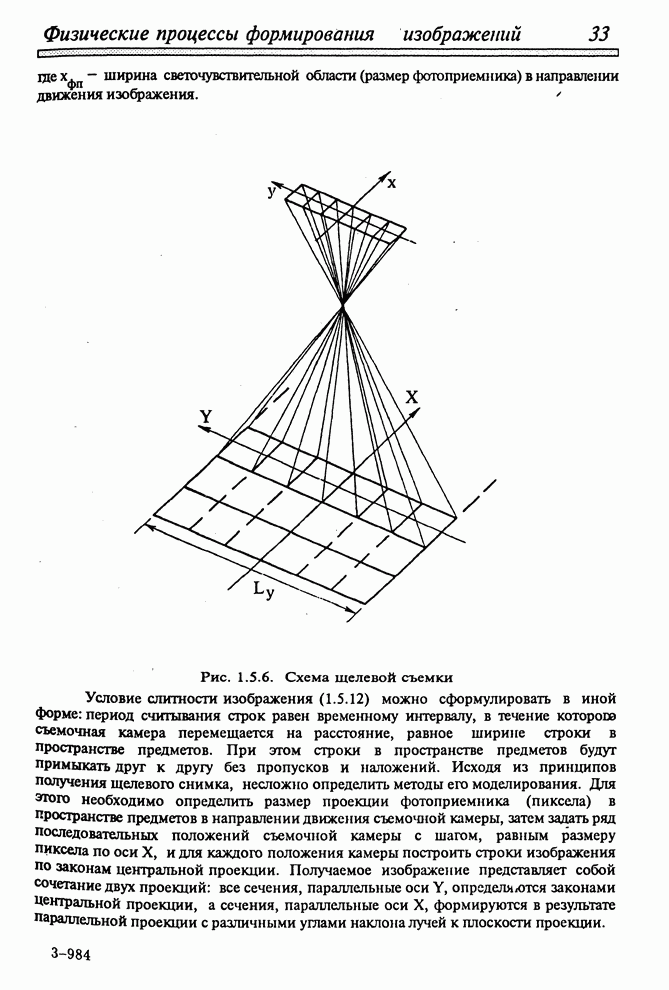
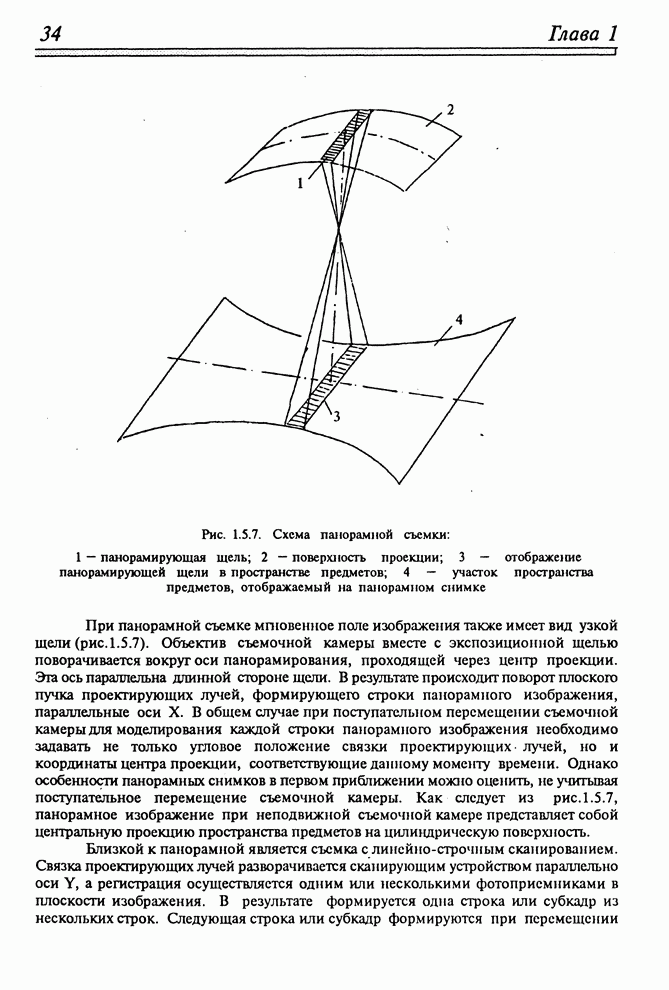
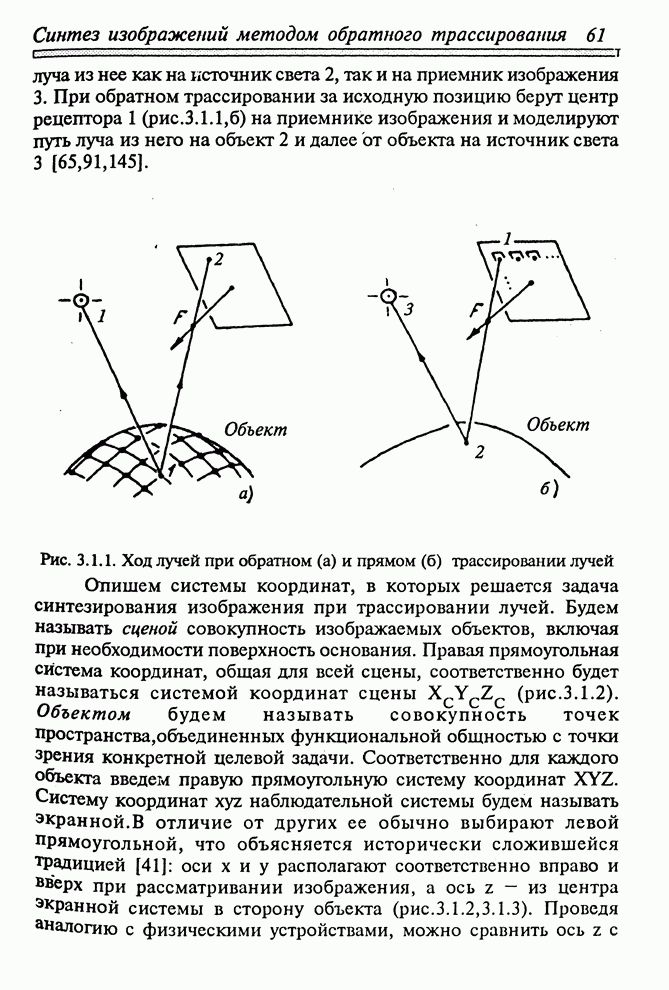
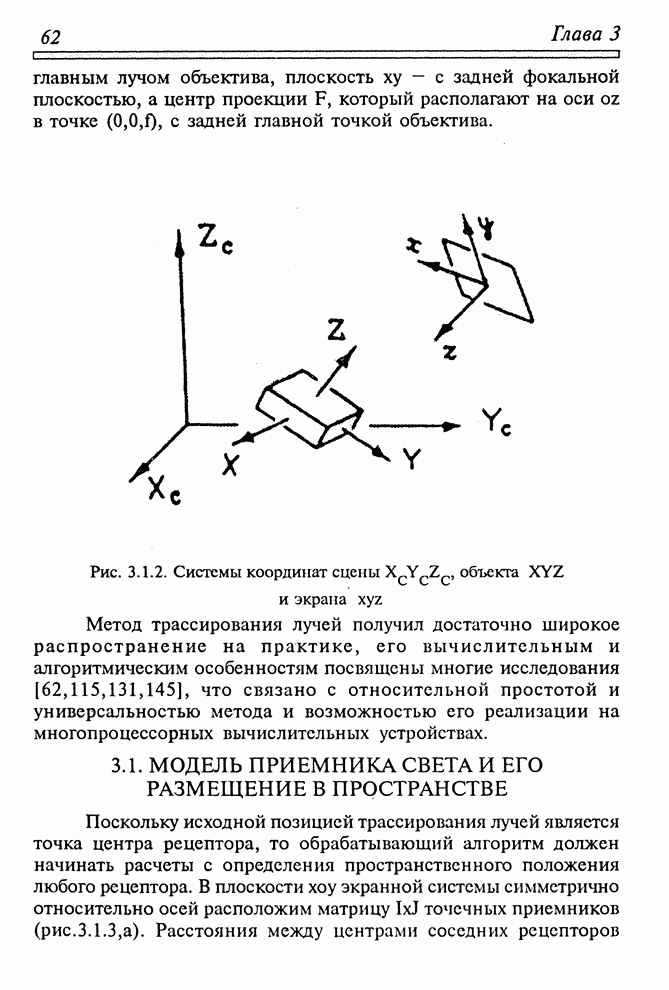
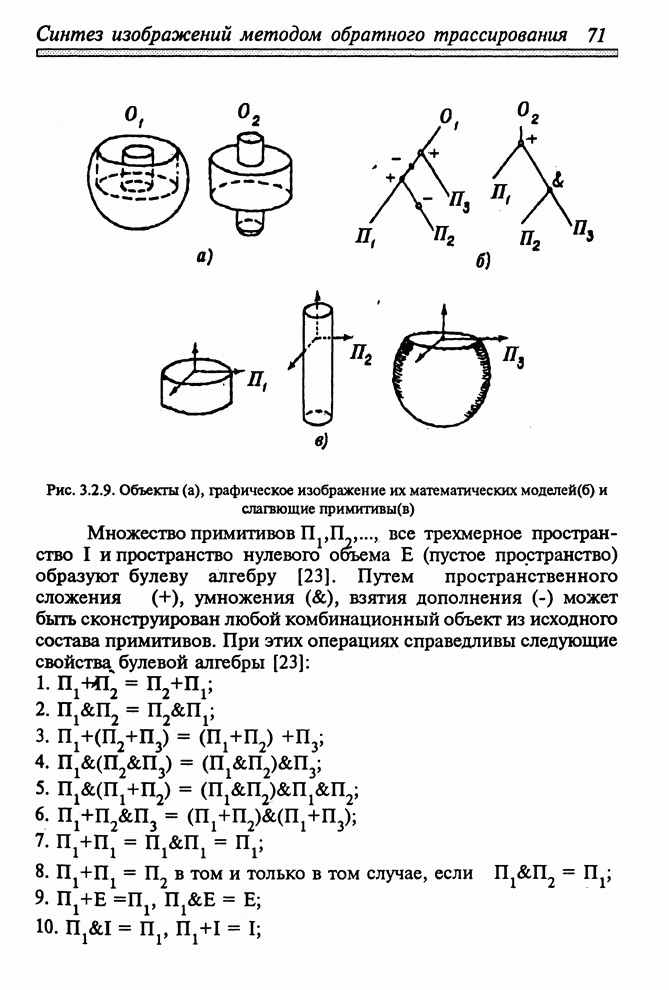
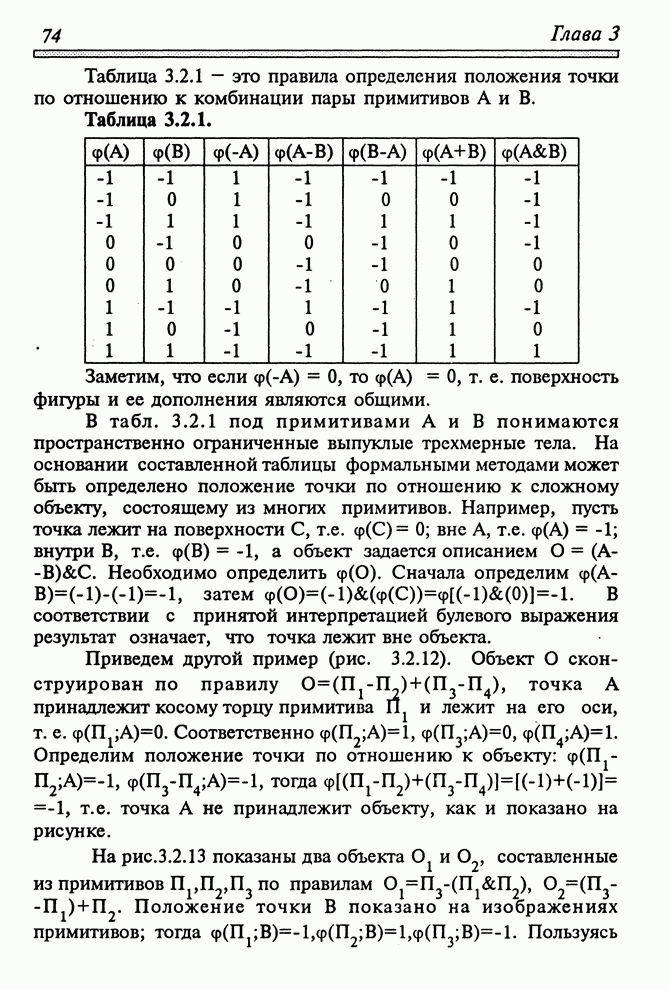
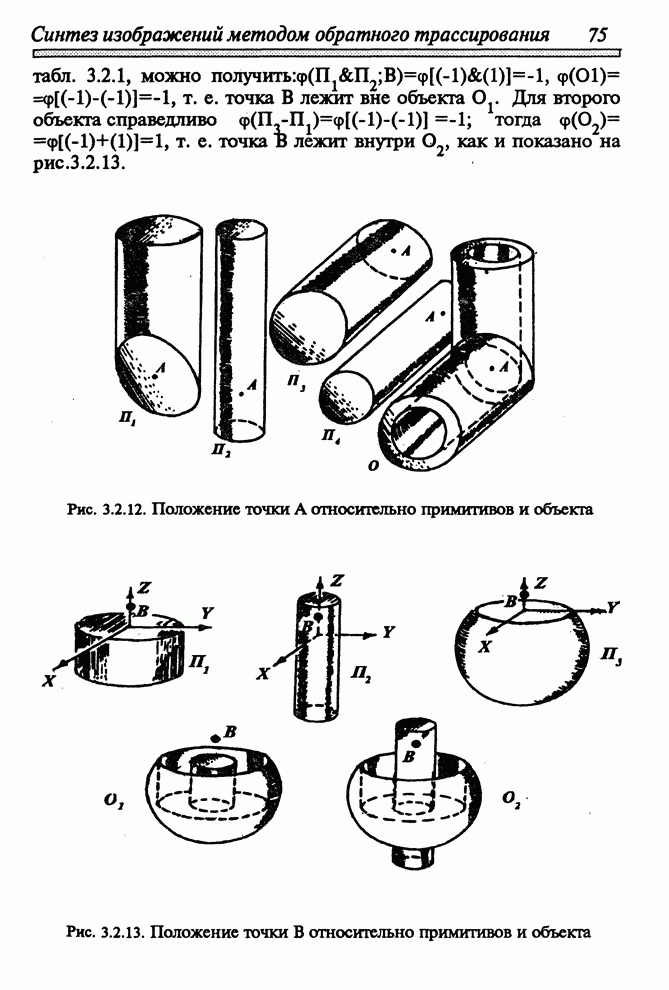
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
Выпуклые
многогранники часто используются в качестве примитивов в машинной графике.
Невыпуклые фигуры отдельно рассматриваться не будут, поскольку они всегда могут
быть разделены на несколько смежных выпуклых. Пусть в системе координат объекта
![]() многогранник
из
многогранник
из ![]() плоских
граней задан посредством матрицы
плоских
граней задан посредством матрицы
 ,
,
где
![]() –
коэффициент уравнения для
–
коэффициент уравнения для ![]() -й плоскости,
-й плоскости, ![]() ,
, ![]() .
.
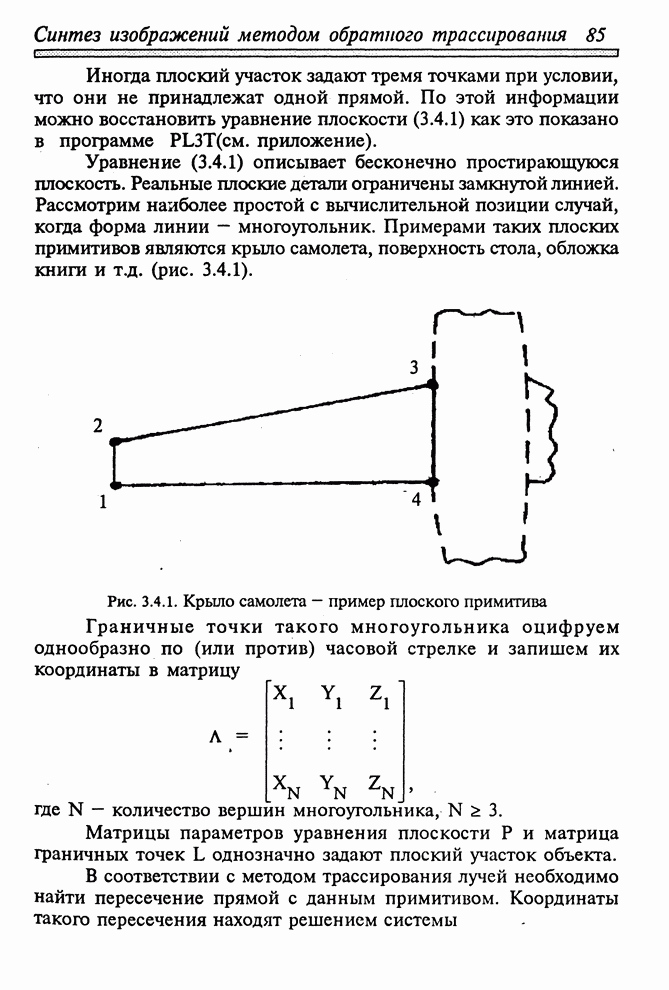
Плоскости,
описывающие грани, простираются в бесконечность (рис. 3.4.6). Для того чтобы
выделить из этого набора плоскостей центральное ядро-многогранник, зададим
последнему особые свойства по сравнению с наружным относительно него
полупространством. В соответствии с договоренностью о положительности
внутренней области многогранника выберем знак функции каждой плоскости ![]() таким, чтобы для
любой точки
таким, чтобы для
любой точки ![]() ,
лежащей на поверхности или внутри многогранника, значение этой функции было
неотрицательным:
,
лежащей на поверхности или внутри многогранника, значение этой функции было
неотрицательным: ![]() , где
, где ![]() . Тогда для каждой плоскости
положительное полупространство включает примитив, а отрицательное находится
снаружи примитива.
. Тогда для каждой плоскости
положительное полупространство включает примитив, а отрицательное находится
снаружи примитива.

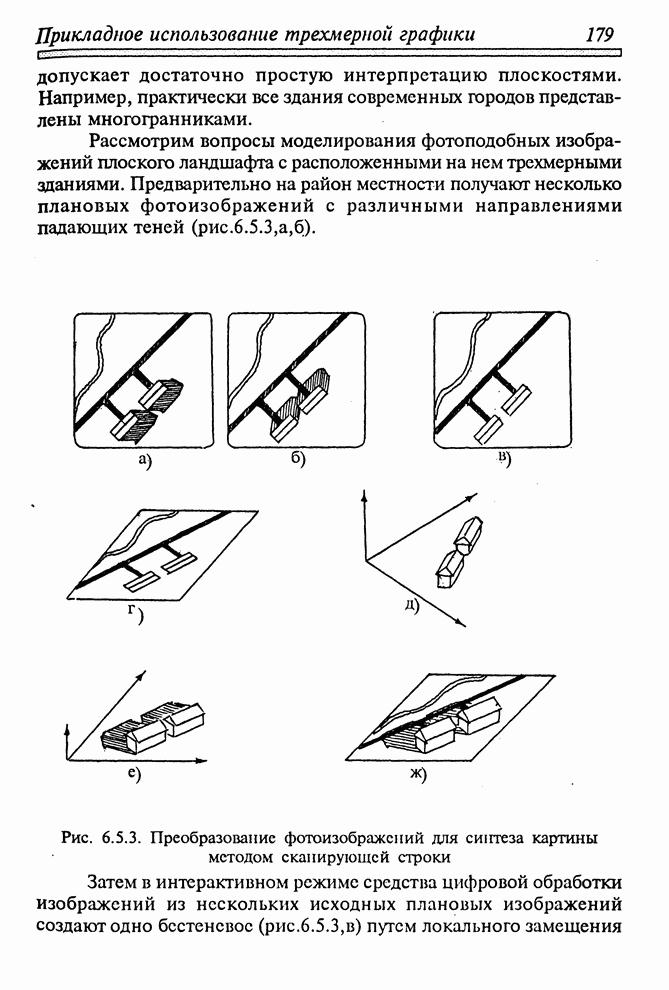
Рис. 3.4.6. Выпуклый многогранник и образующие его плоскости
В
соответствии с методом трассирования лучей необходимо найти координаты точек
пересечения светового луча, проходящего через точки ![]() – центр проекции и
– центр проекции и ![]() – центр
рецептора, с многогранником. Так как в общей случае прямая пересекает все
плоскости, то сначала найдем решение
– центр
рецептора, с многогранником. Так как в общей случае прямая пересекает все
плоскости, то сначала найдем решение ![]() систем вида
систем вида

Решение
каждой такой системы осуществляется в соответствии с методами, изложенными в
§3.4.1. С учетом того, что отдельные ![]()
![]() плоскостей могут не иметь
пересечения с прямой, получаем в результате
плоскостей могут не иметь
пересечения с прямой, получаем в результате ![]() решений, организованных в матрицу
решений, организованных в матрицу
 ,
,
где
![]() –
координаты пересечения
–
координаты пересечения ![]() -й плоскости с прямой,
-й плоскости с прямой, ![]() . Условие
отсутствия пересечений прямой и плоскости или факта бесконечного множества
решений, что будем также интерпретировать как невидимость плоскости лучом,
эквивалентно условию перпендикулярности направляющего вектора прямой и нормали
к плоскости:
. Условие
отсутствия пересечений прямой и плоскости или факта бесконечного множества
решений, что будем также интерпретировать как невидимость плоскости лучом,
эквивалентно условию перпендикулярности направляющего вектора прямой и нормали
к плоскости: ![]() .
Для того чтобы в последующем сохранить информацию о соответствии точек
пересечения с плоскостями пересечения, удалим из матрицы
.
Для того чтобы в последующем сохранить информацию о соответствии точек
пересечения с плоскостями пересечения, удалим из матрицы ![]() соответствующие
соответствующие ![]() столбцов:
столбцов:
 ,
,
где
![]() – номер
плоскости, которой принадлежит точка
– номер
плоскости, которой принадлежит точка ![]() . Эта информация необходима для
вычисления нормали к видимой точке.
. Эта информация необходима для
вычисления нормали к видимой точке.

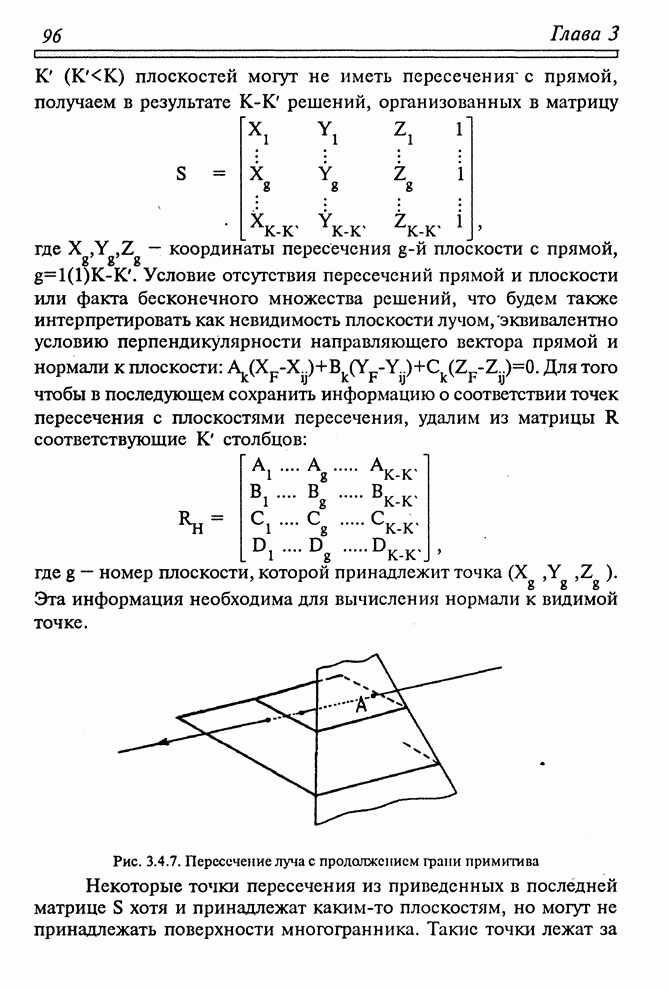
Рис. 3.4.7. Пересечение луча с продолжением грани примитива
Некоторые
точки пересечения из приведенных в последней матрице ![]() хотя и принадлежат
каким-то плоскостям, но могут не принадлежать поверхности многогранника. Такие
точки лежат за пределами примитива и следовательно должны быть устранены из
последующего анализа, как это необходимо сделать с точкой
хотя и принадлежат
каким-то плоскостям, но могут не принадлежать поверхности многогранника. Такие
точки лежат за пределами примитива и следовательно должны быть устранены из
последующего анализа, как это необходимо сделать с точкой ![]() на рис. 3.4.8. Осуществим
операцию оценки знака функций всех плоскостей последовательно для всех точек.
Введем матрицу
на рис. 3.4.8. Осуществим
операцию оценки знака функций всех плоскостей последовательно для всех точек.
Введем матрицу ![]() размера
размера
![]() . Если
выполняется условие
. Если
выполняется условие
 ,
,
то
в матрице ![]()
![]() -я точка
действительно принадлежит поверхности примитива. Если же найдется хотя бы одна
-я точка
действительно принадлежит поверхности примитива. Если же найдется хотя бы одна ![]() -я плоскость, для
которой
-я плоскость, для
которой ![]() ,
то
,
то ![]() -я
точка не принадлежит многограннику.
-я
точка не принадлежит многограннику.
При
увеличении числа граней принцип работы алгоритма не меняется. В результате
отсеивания всех возможных ![]() точек, лежащих вне тела примитива,
матрица
точек, лежащих вне тела примитива,
матрица ![]() сокращается
еще на
сокращается
еще на ![]() строк.
В последней матрице сосредоточились все действительные решения, которых в общем
случае может быть больше двух из-за возможного пересечения прямой с вершиной
многогранника. Устранив всех двойников одной и той же точки, получим в
результате только два решения:
строк.
В последней матрице сосредоточились все действительные решения, которых в общем
случае может быть больше двух из-за возможного пересечения прямой с вершиной
многогранника. Устранив всех двойников одной и той же точки, получим в
результате только два решения: ![]() и
и ![]() . Внешняя нормаль к поверхности
многогранника в этих точках имеет вид
. Внешняя нормаль к поверхности
многогранника в этих точках имеет вид ![]() ;
; ![]() , где
, где ![]() - номера плоскостей, которым и
принадлежат точки решения.
- номера плоскостей, которым и
принадлежат точки решения.
Эти
плоскости определяются путем одновременного удаления столбцов из матрицы ![]() под номерами,
равными номерам строк матрицы
под номерами,
равными номерам строк матрицы ![]() , удаляемыми как лежащие вне
примитива или как двойники действительных решений.
, удаляемыми как лежащие вне
примитива или как двойники действительных решений.
В
программах KOROB и SOME (см. приложение) приведены примеры решений пересечения
прямой и шестигранника. Подпрограмма KOROB определяет возможные переселения со
всеми шестью плоскостями и среди них выбирает ближайшее решение-точку к центру
проекции. Оценка расстояния между точками производится в объектной системе
координат по одной-единственной координате ![]() , что является частным случаем общего
алгоритма поиска ближайших точек. Выбор ближайшей точки осуществляется с
помощью подпрограммы SOME. Результат, полученный с помощью подпрограммы KOROB,
показан на рис. 3.2.4. Для изображения такого простого объекта нет
необходимости обязательно применять столь мощное средство как метод
трассирования лучей, однако как только сцена становится сложной: генерируются
тени, проявляются криволинейные и прозрачные поверхности и другие эффекты, -
применение этого метода становится оправданным. Если же сцена состоит только из
выпуклых многогранников, то целесообразно использовать метод сканирующей строки
или алгоритм Робертса (см. §4.2, 4.3).
, что является частным случаем общего
алгоритма поиска ближайших точек. Выбор ближайшей точки осуществляется с
помощью подпрограммы SOME. Результат, полученный с помощью подпрограммы KOROB,
показан на рис. 3.2.4. Для изображения такого простого объекта нет
необходимости обязательно применять столь мощное средство как метод
трассирования лучей, однако как только сцена становится сложной: генерируются
тени, проявляются криволинейные и прозрачные поверхности и другие эффекты, -
применение этого метода становится оправданным. Если же сцена состоит только из
выпуклых многогранников, то целесообразно использовать метод сканирующей строки
или алгоритм Робертса (см. §4.2, 4.3).
Важной
задачей в практике применения методов машинной графики является перемещение
многогранника в объектном пространстве. Пусть многогранник задан исходно в
правой прямоугольной системе координат ![]() матрицей
матрицей ![]() , тогда если новая система
координат
, тогда если новая система
координат ![]() связана
со старой
связана
со старой ![]() матрицей
преобразования
матрицей
преобразования ![]() :
:
![]() , то в
системе
, то в
системе ![]() новые
параметры плоскостей, сведенные в матрицу
новые
параметры плоскостей, сведенные в матрицу
 ,
,
можно
вычислить по правилу ![]() . Этот вывод вытекает из обобщения
формулы для случая системы плоскостей.
. Этот вывод вытекает из обобщения
формулы для случая системы плоскостей.
Как
на этапе определения яркости теневой точки, так и для определения
принадлежности некоторой точки поверхности многогранника необходимо соблюдение
правила ориентации нормалей по всем граням внутри фигуры. При переносе
многогранника в объектном пространстве, что эквивалентно выбору новой системы
координат, меняются значения коэффициентов плоскостей, а это может нарушить
ориентацию нормали. Однако этого не происходит в силу сохранения знаков
полупространства для каждой из плоскостей, образующих многогранник. Так, если в
некоторой системе координат ![]() внутренняя область многогранника,
который описан матрицей
внутренняя область многогранника,
который описан матрицей ![]() , положительна относительно каждой
грани, т.е. для каждой точки
, положительна относительно каждой
грани, т.е. для каждой точки ![]() , заведомо лежащей внутри фигуры,
справедливо
, заведомо лежащей внутри фигуры,
справедливо ![]() ,
где
,
где ![]() -
положительное число,
-
положительное число, ![]() , то положительность внутренней
области сохраняется при любом изменении системы координат.
, то положительность внутренней
области сохраняется при любом изменении системы координат.
Действительно,
известно, что ![]() ;
;
![]() ;
; ![]() , тогда можно получить
, тогда можно получить
![]() .
.
Многогранник можно перемещать и вращать относительно его исходного положения с помощью преобразования координат, не опасаясь нарушения общего алгоритма.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА 1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ И ИХ МОДЕЛИРОВАНИЕ
- 1.1. МОДЕЛИ В МАШИННОЙ ГРАФИКЕ
- 1.2. ИСТОЧНИКИ ОСВЕЩЕНИЯ
- 1.2.1. ИСТОЧНИКИ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
- 1.2.2. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИСТОЧНИКОВ ПРОСТОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
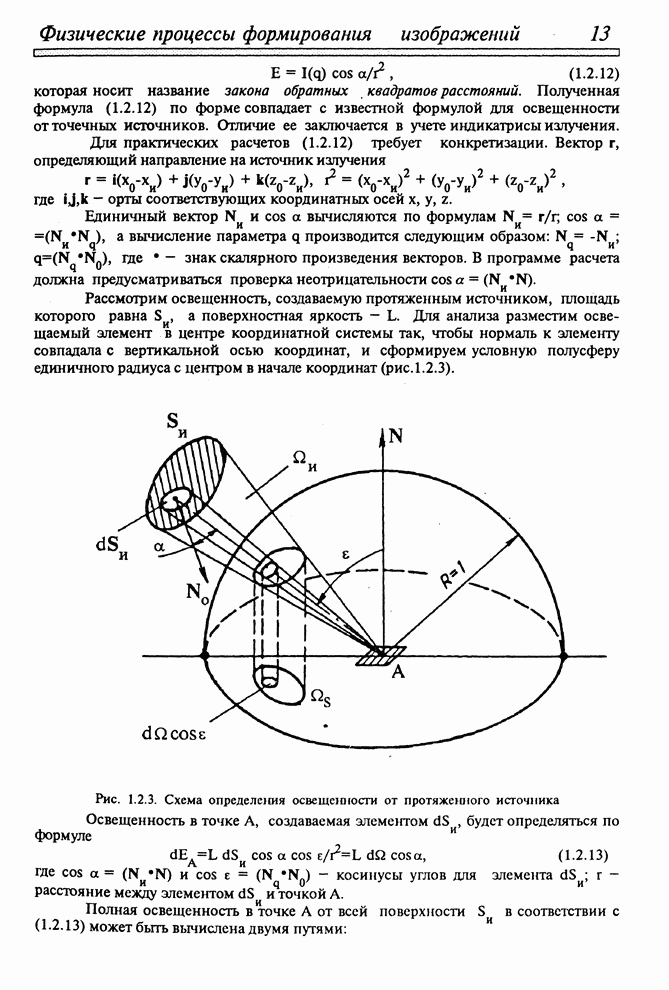
- 1.2.3. ОСВЕЩЕННОСТЬ, СОЗДАВАЕМАЯ ТОЧЕЧНЫМИ И ПРОТЯЖЕННЫМИ ИСТОЧНИКАМИ
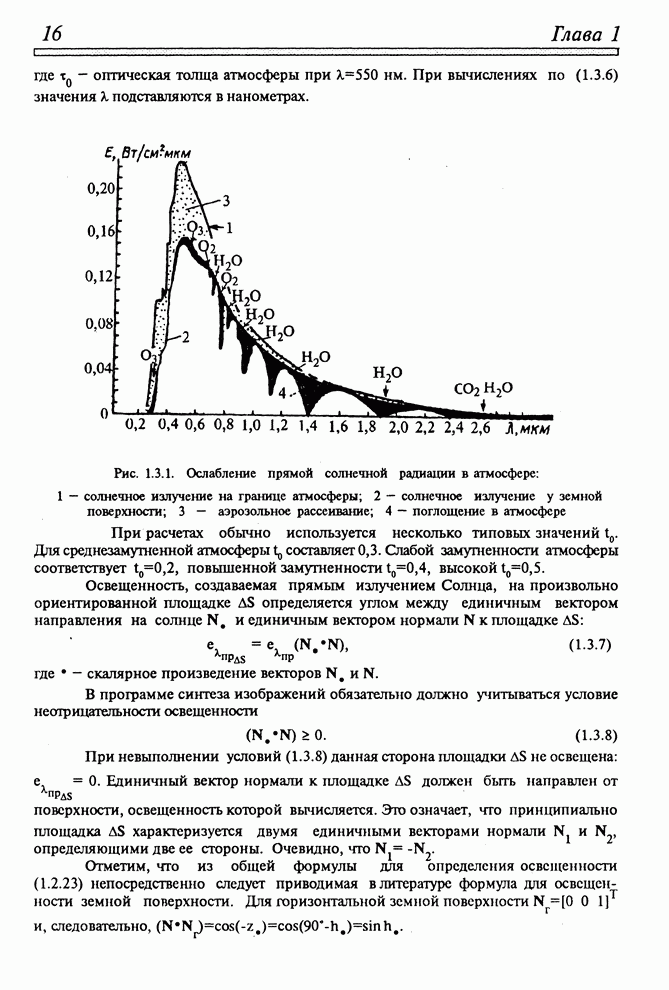
- 1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
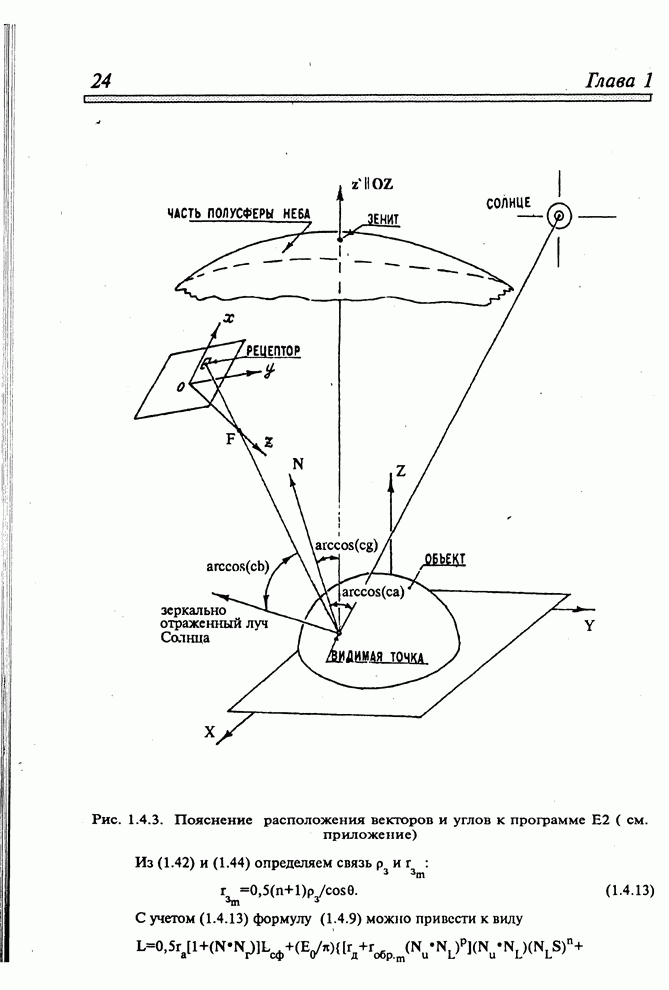
- 1.4. МОДЕЛИРОВАНИЕ ОТРАЖЕННОГО ИЗЛУЧЕНИЯ ОБЪЕКТОВ
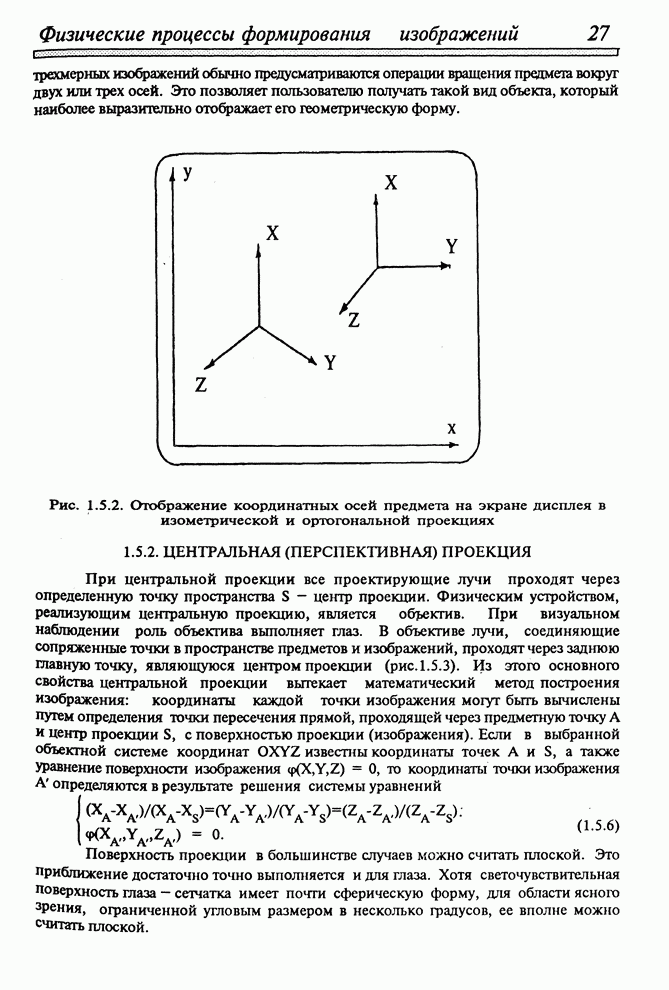
- 1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
- 1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
- 1.5.2. ЦЕНТРАЛЬНАЯ (ПЕРСПЕКТИВНАЯ) ПРОЕКЦИЯ
- 1.5.3. ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ С ИСПОЛЬЗОВАНИЕМ ОДНОРОДНЫХ КООРДИНАТ
- 1.5.4. ПРОЕКЦИИ ПРИ РАЗЛИЧНЫХ ВИДАХ СЪЕМКИ
- 1.6. ТЕКСТУРА ИЗОБРАЖЕНИЯ
- 1.7. МОДЕЛИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.8. СИНТЕЗ ИЗОБРАЖЕНИЙ С УЧЕТОМ СПЕЦИФИКИ ИХ ФОРМИРОВАНИЯ В РЕАЛЬНЫХ УСЛОВИЯХ
- ГЛАВА 2. ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
- 2.1. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
- 2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
- 2.3. МОДЕЛИ ОБЪЕКТОВ И ИХ КЛАССИФИКАЦИЯ
- ГЛАВА 3. СИНТЕЗ ИЗОБРАЖЕНИЙ МЕТОДОМ ОБРАТНОГО ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.1. МОДЕЛЬ ПРИЕМНИКА СВЕТА И ЕГО РАЗМЕЩЕНИЕ В ПРОСТРАНСТВЕ
- 3.2. МОДЕЛЬ ОБЪЕКТА
- 3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
- 3.2.2. ПРОСТРАНСТВЕННЫЕ КОМБИНАЦИИ ПРИМИТИВОВ
- 3.2.3. ФОРМАЛИЗОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
- 3.2.4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ОБЪЕКТА
- 3.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ И ЗАТЕНЕННЫХ ТОЧЕК
- 3.3.1. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С ПРИМИТИВОМ
- 3.3.2. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С КОМБИНАЦИЕЙ ПРИМИТИВОВ
- 3.3.3. ОПРЕДЕЛЕНИЕ ЗАТЕНЕННЫХ ТОЧЕК
- 3.4. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРИМИТИВОВ МЕТОДОМ ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.4.1. ПЛОСКИЕ МНОГОУГОЛЬНИКИ
- 3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
- 3.4.3. КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
- 3.4.4. БИКУБИЧЕСКИЕ ПОВЕРХНОСТИ
- 3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- 3.6. ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ ОСВЕЩЕННОСТИ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ИЗОБРАЖЕНИЙ ПУТЕМ ПРОЕКТИРОВАНИЯ ТОЧЕК И ЛИНИЙ НА ЭКРАН
- 4.1. ТРАССИРОВАНИЕ ЛУЧЕЙ ОТ ОБЪЕКТА К ЭКРАНУ
- 4.1.1. ОСНОВНЫЕ ПРИНЦИПЫ
- 4.1.2. МОДЕЛЬ ОБЪЕКТА
- 4.1.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ ТОЧЕК
- 4.1.4. ОПРЕДЕЛЕНИЕ ОСВЕЩЕННОСТИ
- 4.1.5. ИЗОБРАЖЕНИЕ ПОТОЧЕЧНО ОПИСАННЫХ ОБЪЕКТОВ
- 4.2. МЕТОД СКАНИРУЮЩЕЙ СТРОКИ
- 4.2.1. МОДЕЛЬ ОБЪЕКТА ИЗ МНОГОУГОЛЬНИКОВ
- 4.2.2. МОДЕЛЬ ПРИЕМНИКА
- 4.2.3. ИЗОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ НА ЭКРАНЕ
- 4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
- 4.3. АЛГОРИТМ РОБЕРТСА
- 4.3.1. МОДЕЛЬ ОБЪЕКТА
- 4.3.2. СИНТЕЗ ИЗОБРАЖЕНИЯ
- ГЛАВА 5. ОРГАНИЗАЦИЯ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.1. УПРАВЛЕНИЕ ПРОЦЕССОМ СИНТЕЗА
- 5.2. СПЕКТР СИНТЕЗИРОВАННОГО ИЗОБРАЖЕНИЯ
- 5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.3.1. МЕТОД ОБОЛОЧЕК
- 5.3.2. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ТРАНСПЬЮТЕРОВ В МАШИННОЙ ГРАФИКЕ
- ГЛАВА 6. ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКИ
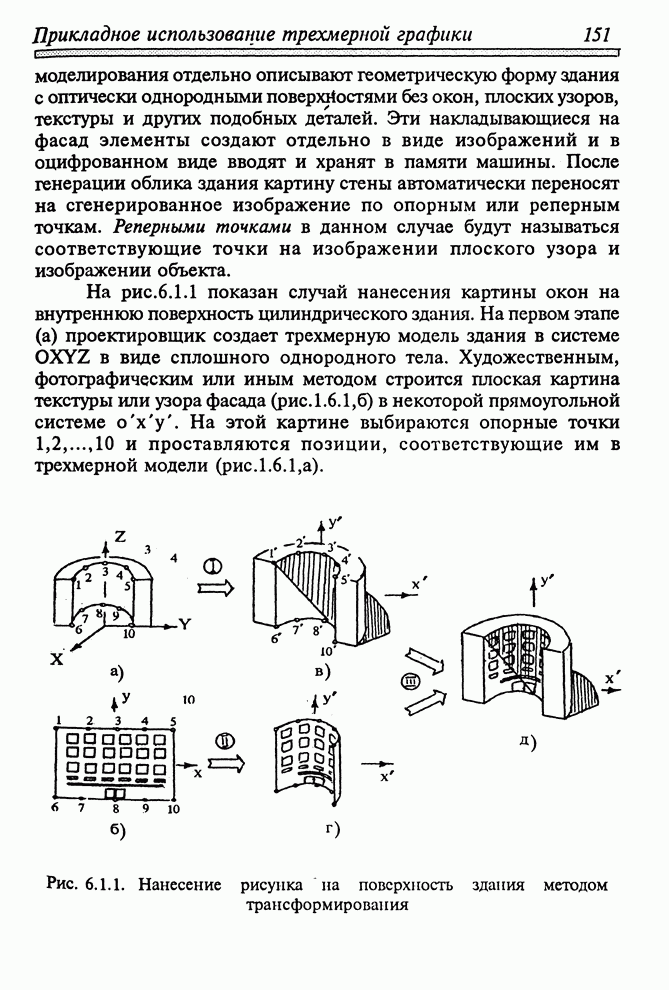
- 6.1. АРХИТЕКТУРНОЕ ПРОЕКТИРОВАНИЕ
- 6.2. РАСПОЗНАВАНИЕ ВИДЕООБРАЗОВ
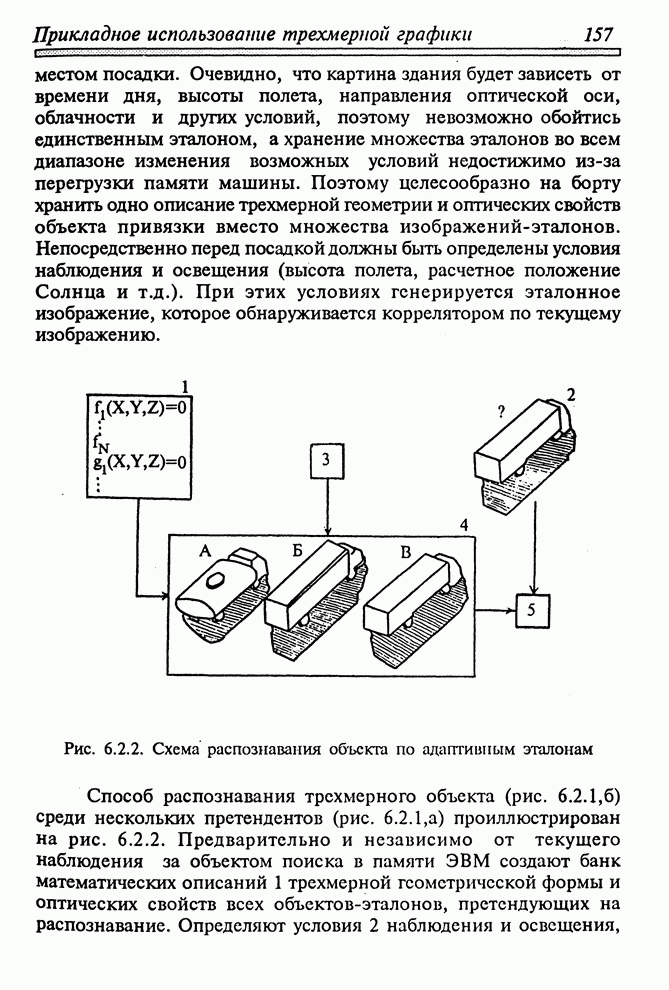
- 6.2.1. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИВНЫМ ЭТАЛОНАМ
- 6.2.2. РАСПОЗНАВАНИЕ ОБРАЗОВ В УСЛОВИЯХ НЕИЗВЕСТНОЙ ОРИЕНТАЦИИ ИХ КОРПУСОВ
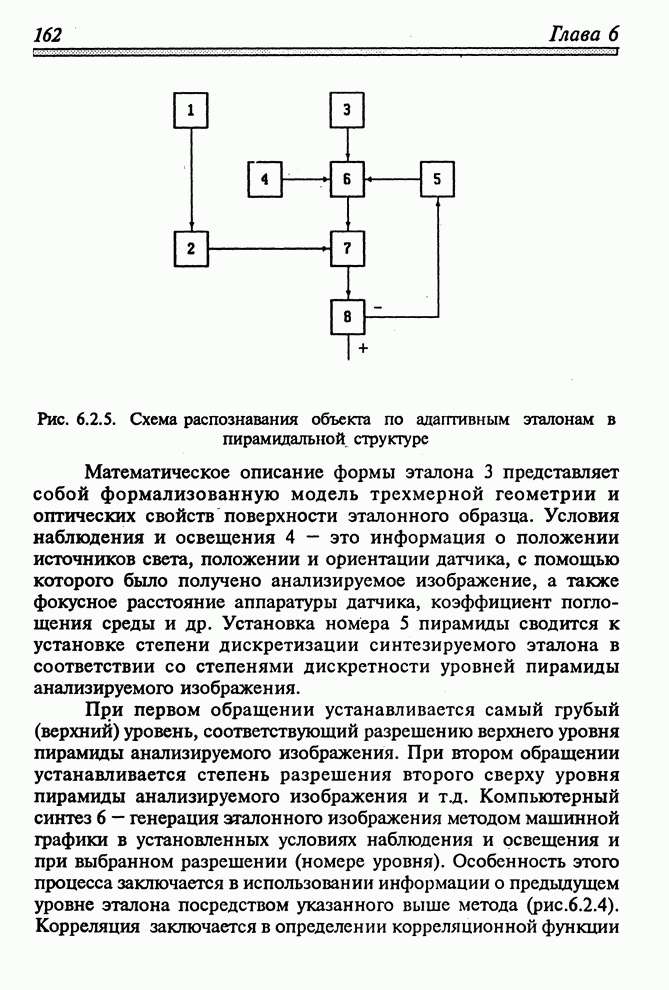
- 6.2.3. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИРОВАННЫМ ЭТАЛОНАМ В ПИРАМИДАЛЬНОЙ СТРУКТУРЕ
- 6.2.4. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО ЭТАЛОНАМ, АДАПТИРОВАННЫМ ПО УСЛОВИЯМ НАБЛЮДЕНИЯ И КАЧЕСТВУ
- 6.3. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ В МАШИНОСТРОЕНИИ
- 6.4. ВОССТАНОВЛЕНИЕ ФОРМЫ СКРЫТЫХ ОБЪЕКТОВ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ
- 6.5. ВИДЕОТРЕНАЖЕРЫ И ИМИТАТОРЫ СЛОЖНЫХ СЦЕН
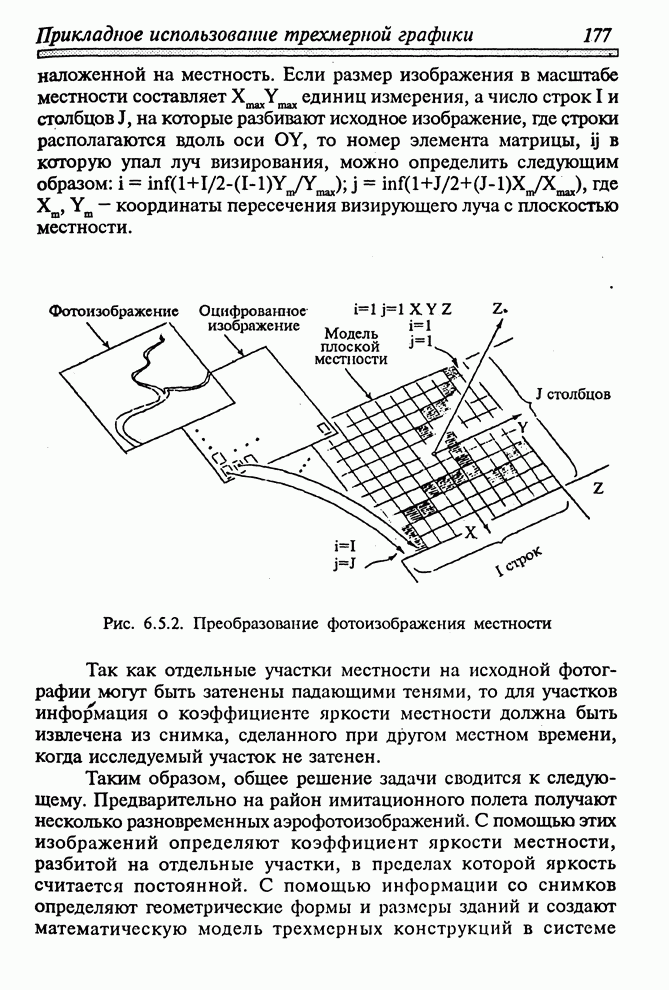
- 6.5.1. ТРЕНАЖЕР ДЛЯ ИМИТАЦИИ ПОЛЕТА НАД РЕАЛЬНОЙ МЕСТНОСТЬЮ
- 6.5.2. КОМПЬЮТЕРНЫЙ ИМИТАТОР ИЗОБРАЖЕНИЙ ОБЛАКОВ
- 6.6. РЕКЛАМА И МУЛЬТИПЛИКАЦИЯ
- ПРИЛОЖЕНИЕ. ОПИСАНИЕ ПРИКЛАДНЫХ ПОДПРОГРАММ
- СПИСОК ЛИТЕРАТУРЫ