| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
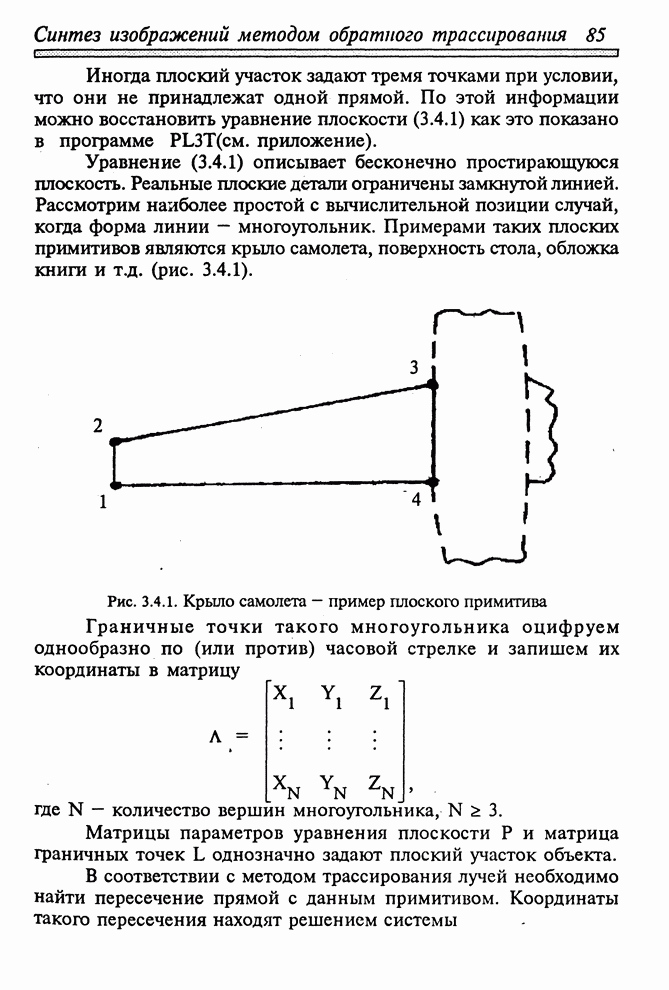
1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
Все виды проекций, используемые в инженерной графике, а также реализуемые в системах формирования изображений, представляют собой комбинации двух главных типов проекций: параллельной и перспективной (центральной).
1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
В
инженерной графике и начертательной геометрии преимущественно используется
параллельная проекция. Точки предмета проецируются на поверхность пучком лучей,
параллельных заданному направлению ![]() (рис.1.5.1).
(рис.1.5.1).

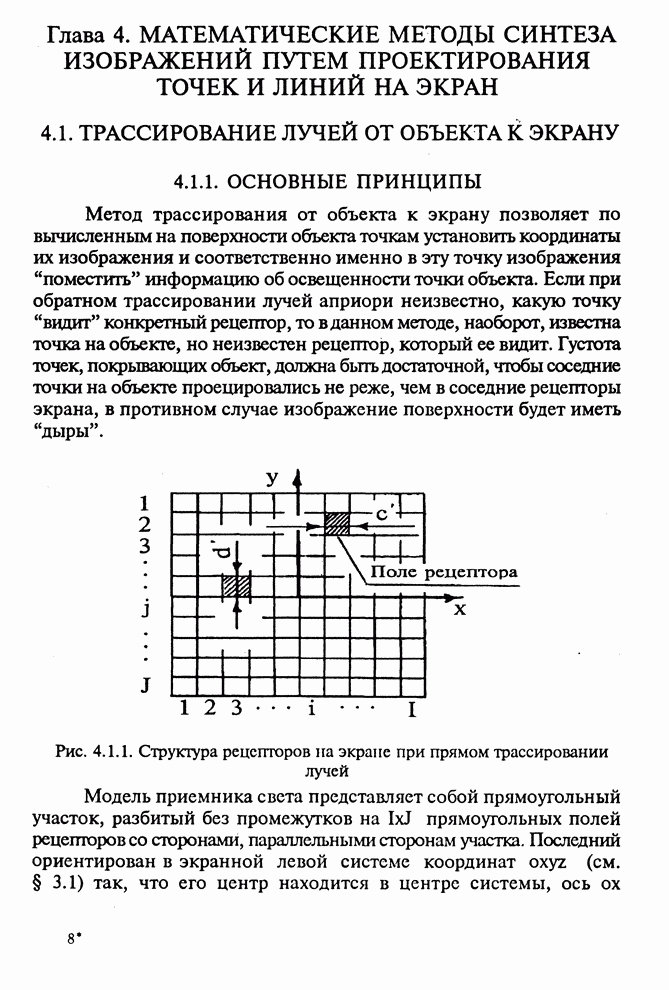
Рис. 1.5.1. Параллельная проекция
Координаты
точек изображения при параллельной проекции определяются путем совместного
решения уравнения прямой, проходящей через предметную точку ![]() параллельно единичному
вектору, и уравнения поверхности проекции:
параллельно единичному
вектору, и уравнения поверхности проекции:
 (1.5.1)
(1.5.1)
где
![]() –
координаты точки предмета;
–
координаты точки предмета; ![]() – координаты точки изображения;
– координаты точки изображения; ![]() – уравнение
поверхности проекции.
– уравнение
поверхности проекции.
Если
проецирование осуществляется на плоскость и проектирующие лучи перпендикулярны
к ней, то проекция называется ортогональной или перпендикулярной. Этот вид
проекции широко используется в техническом черчении. Если оси ![]() лежат в плоскости
проекции, a
лежат в плоскости
проекции, a ![]() перпендикулярна
ей, то при представлении предмета в координатном базисе плоскости проекции,
координаты точек изображения можно определить по координатам точек предмета с
помощью простого соотношения
перпендикулярна
ей, то при представлении предмета в координатном базисе плоскости проекции,
координаты точек изображения можно определить по координатам точек предмета с
помощью простого соотношения
![]() , (1.5.2)
, (1.5.2)
где
![]() – координата
плоскости проекции по оси
– координата
плоскости проекции по оси ![]() .
.
Как
следует из (1.5.2), для получения ортогональной проекции принципиально
достаточно определить координаты ![]() и
и ![]() предмета. Однако этим не
ограничивается процедура построения трехмерной модели на экране дисплея.
Предмет обычно задается в своей объектной системе координат
предмета. Однако этим не
ограничивается процедура построения трехмерной модели на экране дисплея.
Предмет обычно задается в своей объектной системе координат ![]() , оси которой в исходном
состоянии параллельны экранной системе дисплея
, оси которой в исходном
состоянии параллельны экранной системе дисплея ![]() . Изображение предмета отображается на
экране дисплея с некоторым масштабным коэффициентом
. Изображение предмета отображается на
экране дисплея с некоторым масштабным коэффициентом ![]() , а начало объектной системы
координат располагается в точке
, а начало объектной системы
координат располагается в точке ![]() экрана. Для этого более общего случая
можно записать
экрана. Для этого более общего случая
можно записать
 . (1.5.3)
. (1.5.3)
Выбором
значения ![]() можно
осуществлять масштабирование изображения объекта.
можно
осуществлять масштабирование изображения объекта.
Чтобы обеспечить наиболее наглядное отображение объемности предмета, обычно выбирается положение предмета относительно плоскости проекции. В техническом черчении положение предмета определяется типом аксонометрической проекции. Чтобы получить аксонометрическую проекцию, предмет вместе со связанной системой координат разворачивается таким образом, что проекции координатных осей получают определенную ориентацию друг относительно друга, а отрезки, взятые по координатным осям, отображаются на проекции с определенным соотношением масштабных коэффициентов.
Чтобы
в машинной графике воспроизвести предмет в заданной проекции, необходимо
определить матрицу преобразования координат. Основой для этого являются
принципы построения изображения в данной проекции. В частности, в
изометрической проекции координатные оси предмета ![]() отображаются на плоскости экрана
дисплея под углом 120°, а масштабные коэффициенты по всем трем осям одинаковы
(рис. 1.5.2). С учетом этих свойств изометрической проекции получим
отображаются на плоскости экрана
дисплея под углом 120°, а масштабные коэффициенты по всем трем осям одинаковы
(рис. 1.5.2). С учетом этих свойств изометрической проекции получим
 . (1.5.4)
. (1.5.4)

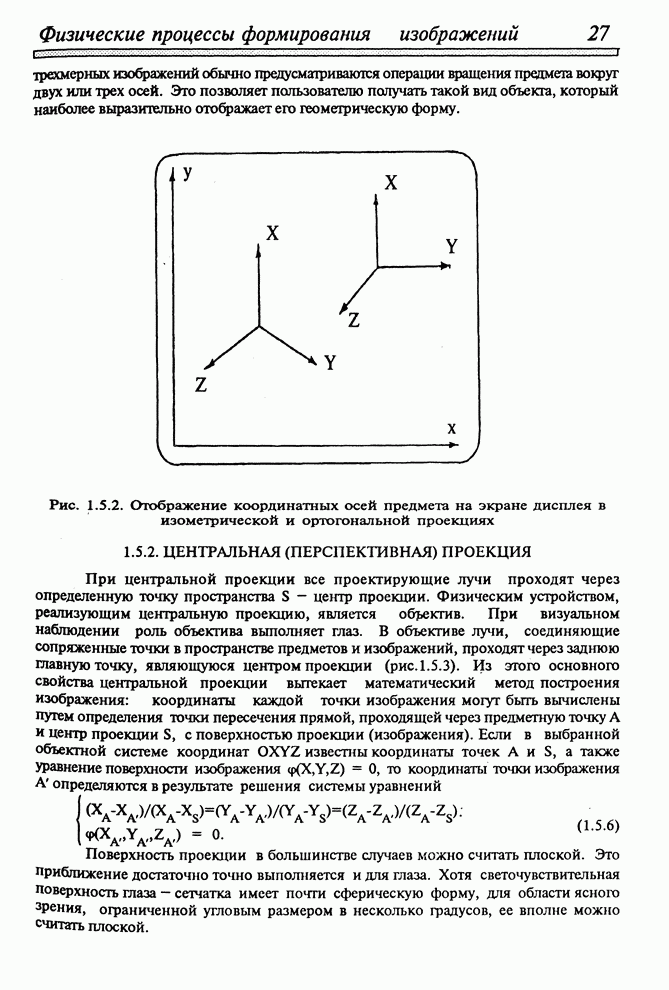
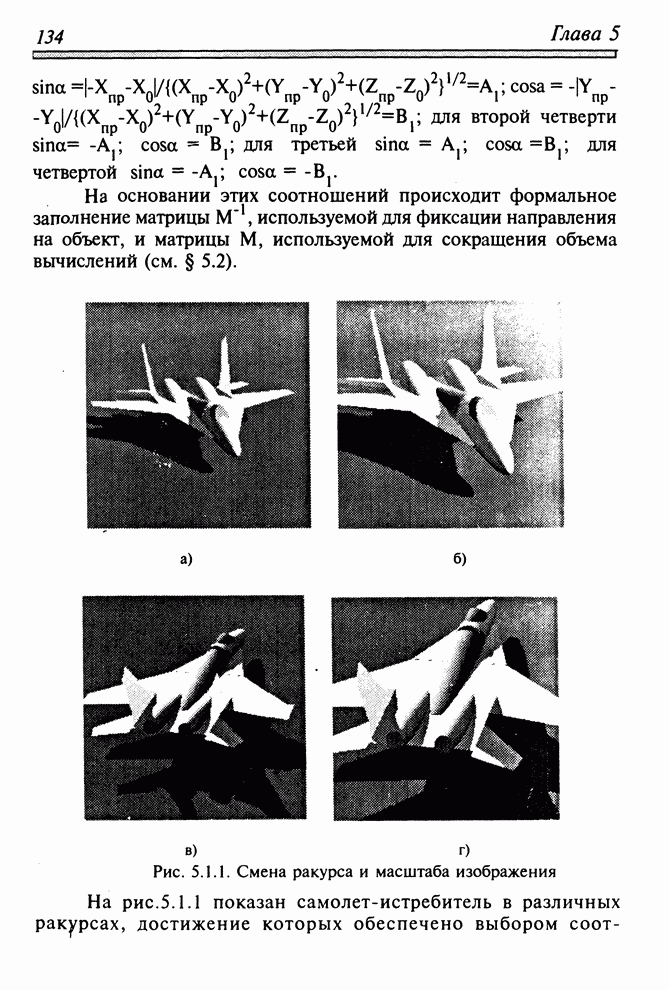
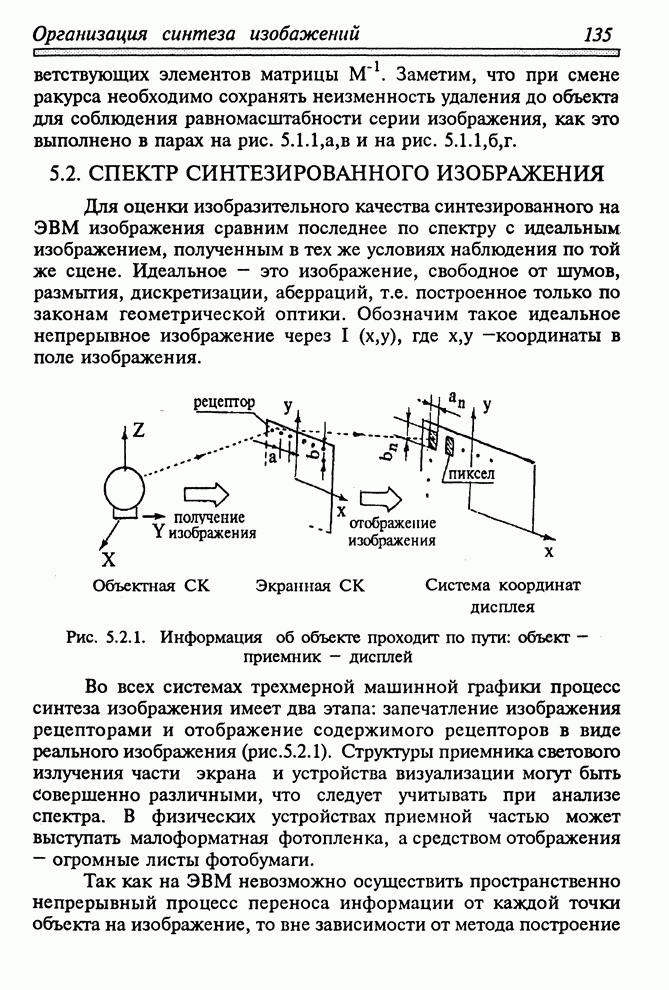
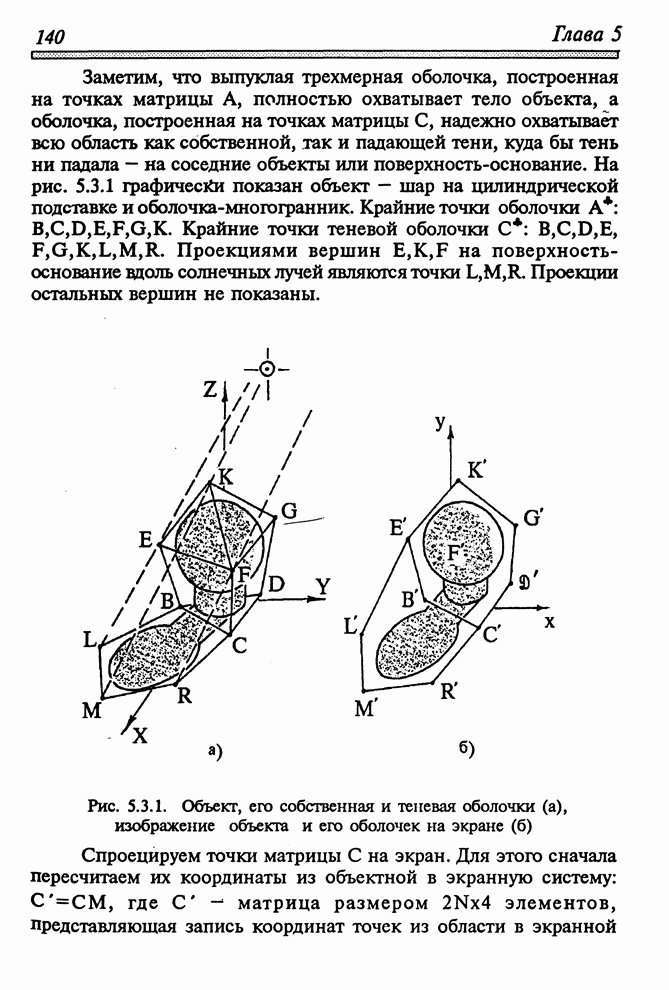
Рис. 1.5.2. Отображение координатных осей предмета на экране дисплея в изометрической и ортогональной проекциях
Аналогично
можно получить формулу преобразования для фронтальной проекции, при которой оси
![]() проецируются
параллельно осям
проецируются
параллельно осям ![]() дисплея,
а проекция оси
дисплея,
а проекция оси ![]() совпадает
с биссектрисой угла между осями
совпадает
с биссектрисой угла между осями ![]() и
и ![]() (рис. 1.5.2). В этом случае
преобразование координат выполняется следующим образом:
(рис. 1.5.2). В этом случае
преобразование координат выполняется следующим образом:
 . (l.5.5)
. (l.5.5)
Можно отметить, что фронтальная проекция не является линейным преобразованием пространства предметов.
Формулы преобразования (1.5.4) и (1.5.5) принципиально позволяют обеспечить вычерчивание на дисплее изображений в изометрической или фронтальной проекции, если задано математическое описание предмета. Однако такой узкопрактический подход не позволяет в полной мере использовать возможности машинной графики. В системах трехмерной машинной графики нет необходимости фиксировать какие-либо конкретные виды проекций. В программах формирования трехмерных изображений обычно предусматриваются операции вращения предмета вокруг двух или трех осей. Это позволяет пользователю получать такой вид объекта, который наиболее выразительно отображает его геометрическую форму.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА 1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ И ИХ МОДЕЛИРОВАНИЕ
- 1.1. МОДЕЛИ В МАШИННОЙ ГРАФИКЕ
- 1.2. ИСТОЧНИКИ ОСВЕЩЕНИЯ
- 1.2.1. ИСТОЧНИКИ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
- 1.2.2. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИСТОЧНИКОВ ПРОСТОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
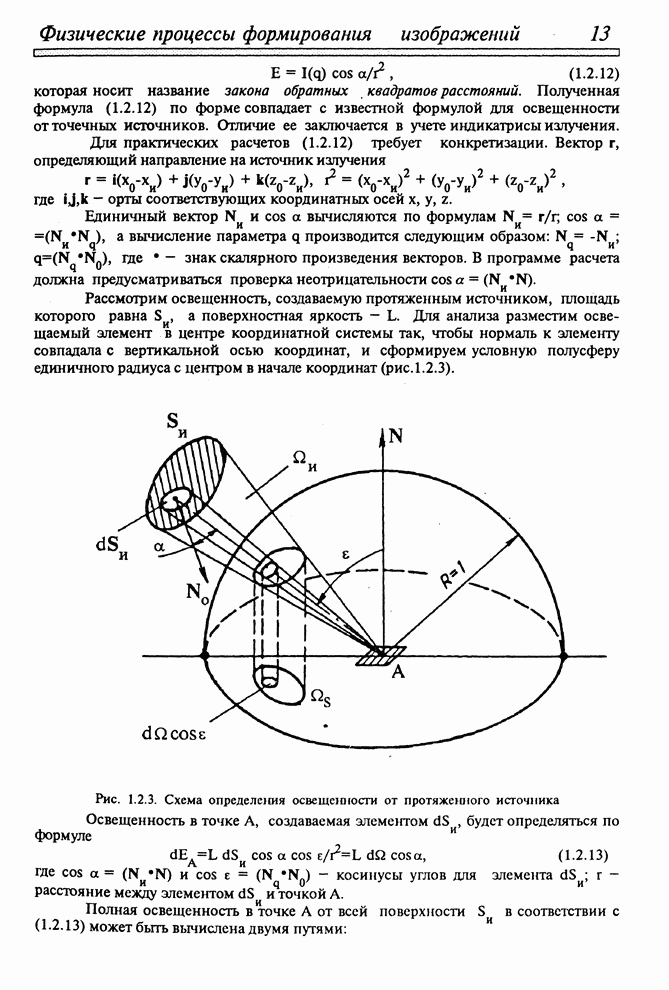
- 1.2.3. ОСВЕЩЕННОСТЬ, СОЗДАВАЕМАЯ ТОЧЕЧНЫМИ И ПРОТЯЖЕННЫМИ ИСТОЧНИКАМИ
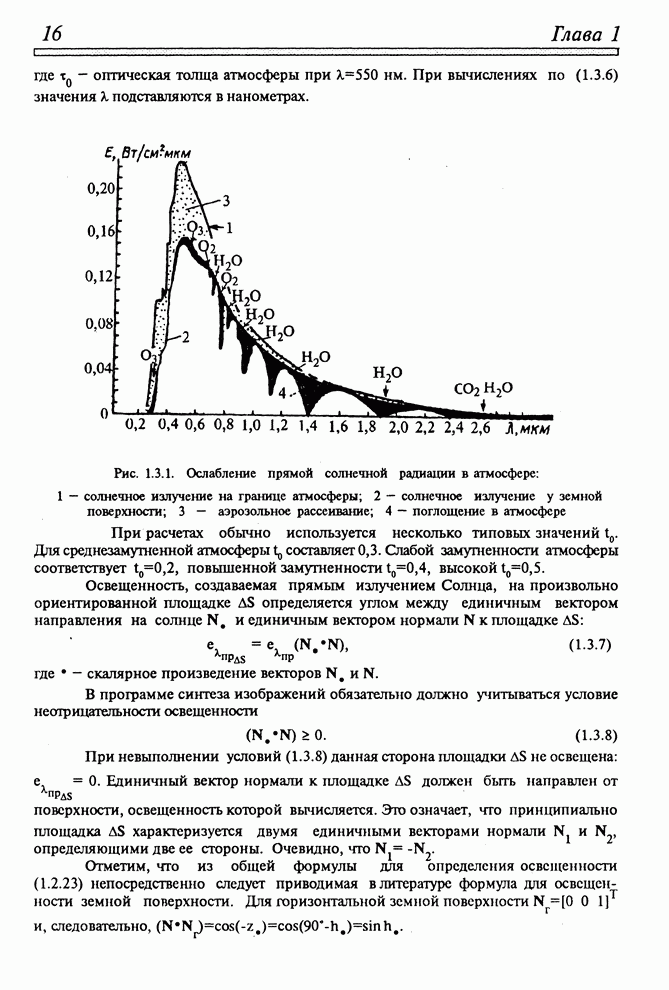
- 1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
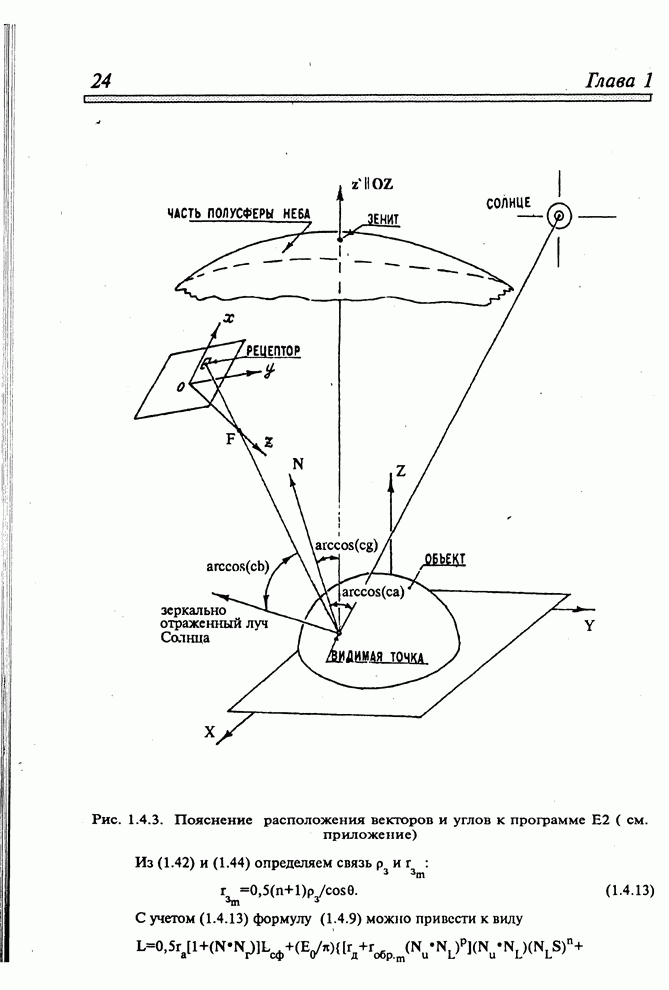
- 1.4. МОДЕЛИРОВАНИЕ ОТРАЖЕННОГО ИЗЛУЧЕНИЯ ОБЪЕКТОВ
- 1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
- 1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
- 1.5.2. ЦЕНТРАЛЬНАЯ (ПЕРСПЕКТИВНАЯ) ПРОЕКЦИЯ
- 1.5.3. ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ С ИСПОЛЬЗОВАНИЕМ ОДНОРОДНЫХ КООРДИНАТ
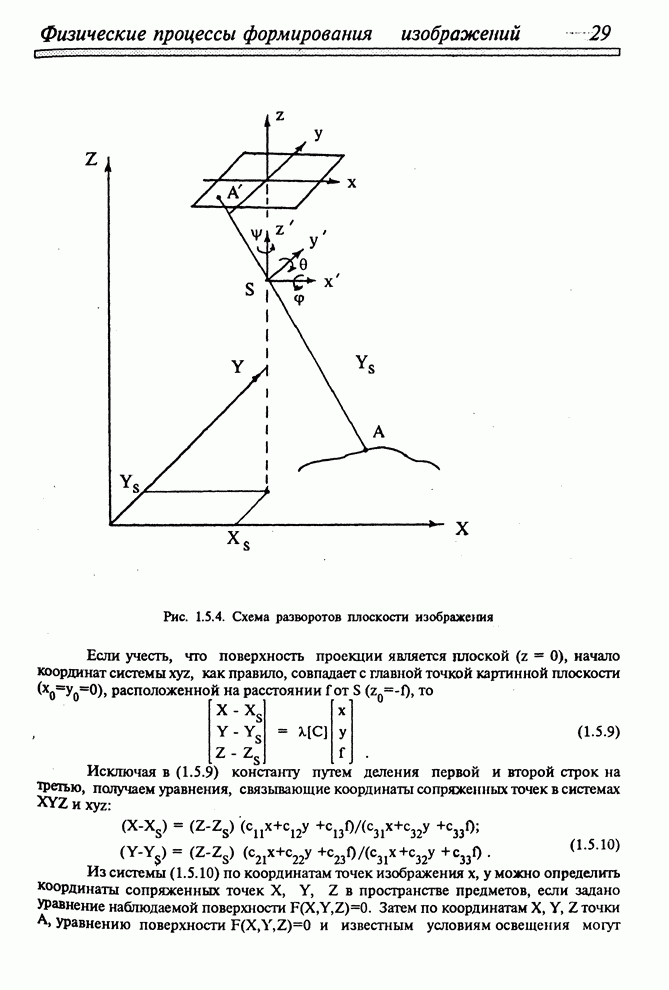
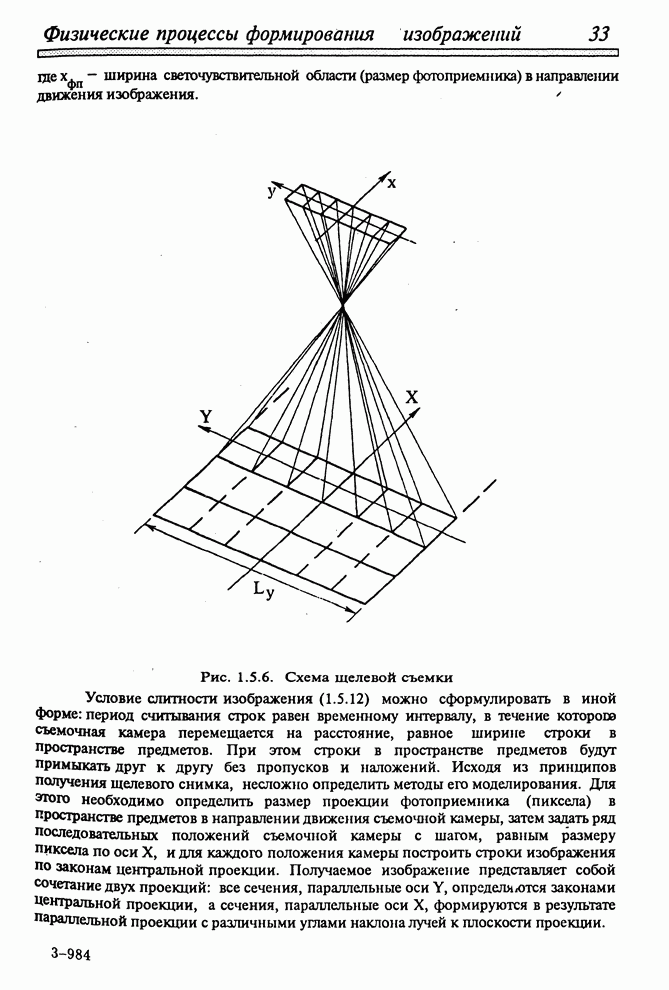
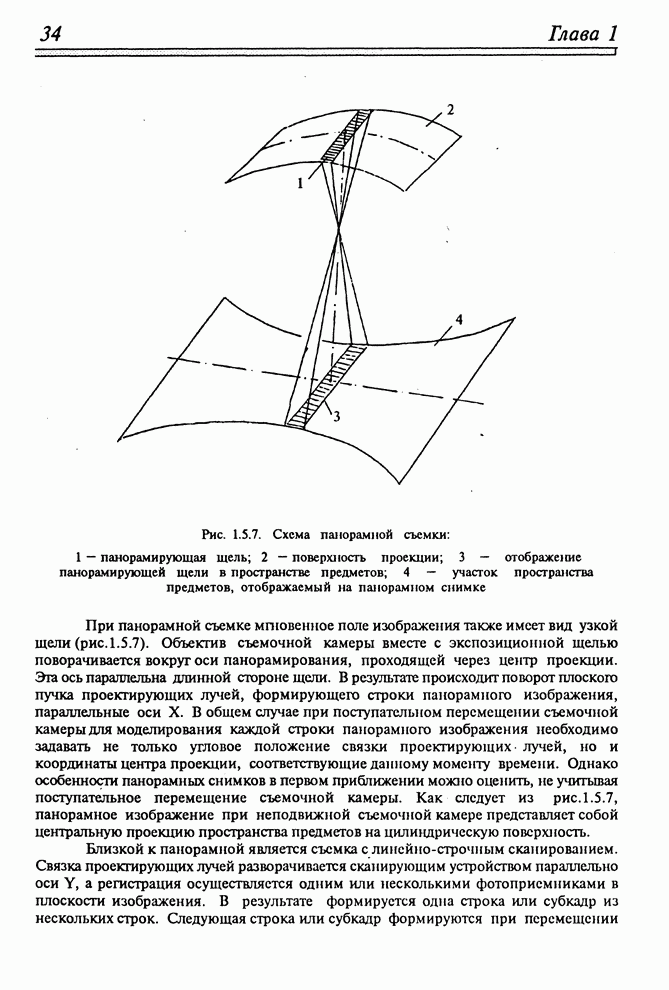
- 1.5.4. ПРОЕКЦИИ ПРИ РАЗЛИЧНЫХ ВИДАХ СЪЕМКИ
- 1.6. ТЕКСТУРА ИЗОБРАЖЕНИЯ
- 1.7. МОДЕЛИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.8. СИНТЕЗ ИЗОБРАЖЕНИЙ С УЧЕТОМ СПЕЦИФИКИ ИХ ФОРМИРОВАНИЯ В РЕАЛЬНЫХ УСЛОВИЯХ
- ГЛАВА 2. ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
- 2.1. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
- 2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
- 2.3. МОДЕЛИ ОБЪЕКТОВ И ИХ КЛАССИФИКАЦИЯ
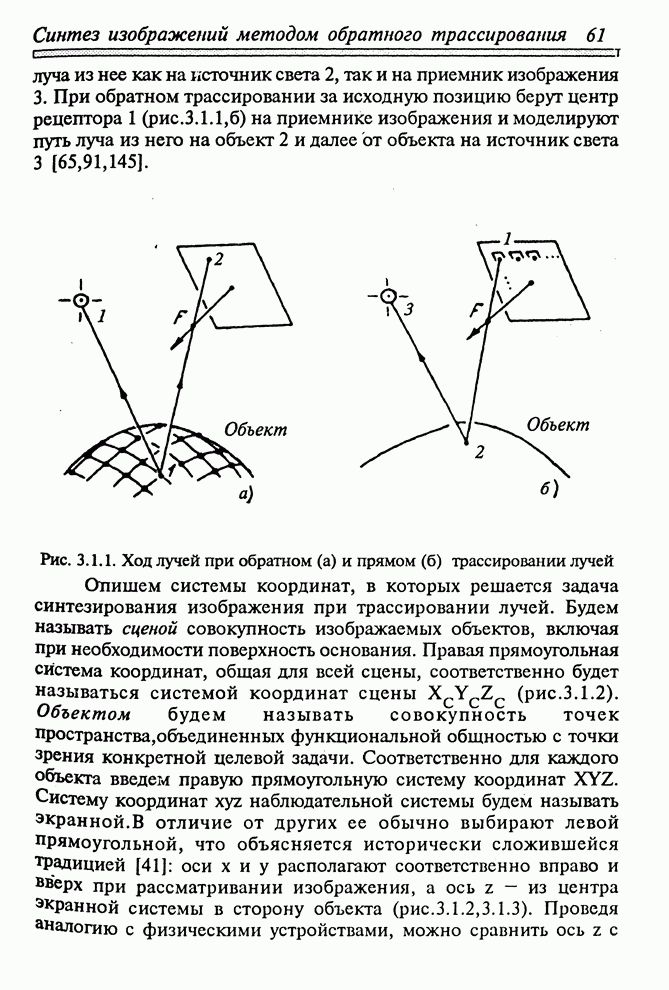
- ГЛАВА 3. СИНТЕЗ ИЗОБРАЖЕНИЙ МЕТОДОМ ОБРАТНОГО ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.1. МОДЕЛЬ ПРИЕМНИКА СВЕТА И ЕГО РАЗМЕЩЕНИЕ В ПРОСТРАНСТВЕ
- 3.2. МОДЕЛЬ ОБЪЕКТА
- 3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
- 3.2.2. ПРОСТРАНСТВЕННЫЕ КОМБИНАЦИИ ПРИМИТИВОВ
- 3.2.3. ФОРМАЛИЗОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
- 3.2.4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ОБЪЕКТА
- 3.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ И ЗАТЕНЕННЫХ ТОЧЕК
- 3.3.1. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С ПРИМИТИВОМ
- 3.3.2. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С КОМБИНАЦИЕЙ ПРИМИТИВОВ
- 3.3.3. ОПРЕДЕЛЕНИЕ ЗАТЕНЕННЫХ ТОЧЕК
- 3.4. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРИМИТИВОВ МЕТОДОМ ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.4.1. ПЛОСКИЕ МНОГОУГОЛЬНИКИ
- 3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
- 3.4.3. КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
- 3.4.4. БИКУБИЧЕСКИЕ ПОВЕРХНОСТИ
- 3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- 3.6. ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ ОСВЕЩЕННОСТИ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ИЗОБРАЖЕНИЙ ПУТЕМ ПРОЕКТИРОВАНИЯ ТОЧЕК И ЛИНИЙ НА ЭКРАН
- 4.1. ТРАССИРОВАНИЕ ЛУЧЕЙ ОТ ОБЪЕКТА К ЭКРАНУ
- 4.1.1. ОСНОВНЫЕ ПРИНЦИПЫ
- 4.1.2. МОДЕЛЬ ОБЪЕКТА
- 4.1.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ ТОЧЕК
- 4.1.4. ОПРЕДЕЛЕНИЕ ОСВЕЩЕННОСТИ
- 4.1.5. ИЗОБРАЖЕНИЕ ПОТОЧЕЧНО ОПИСАННЫХ ОБЪЕКТОВ
- 4.2. МЕТОД СКАНИРУЮЩЕЙ СТРОКИ
- 4.2.1. МОДЕЛЬ ОБЪЕКТА ИЗ МНОГОУГОЛЬНИКОВ
- 4.2.2. МОДЕЛЬ ПРИЕМНИКА
- 4.2.3. ИЗОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ НА ЭКРАНЕ
- 4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
- 4.3. АЛГОРИТМ РОБЕРТСА
- 4.3.1. МОДЕЛЬ ОБЪЕКТА
- 4.3.2. СИНТЕЗ ИЗОБРАЖЕНИЯ
- ГЛАВА 5. ОРГАНИЗАЦИЯ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.1. УПРАВЛЕНИЕ ПРОЦЕССОМ СИНТЕЗА
- 5.2. СПЕКТР СИНТЕЗИРОВАННОГО ИЗОБРАЖЕНИЯ
- 5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.3.1. МЕТОД ОБОЛОЧЕК
- 5.3.2. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ТРАНСПЬЮТЕРОВ В МАШИННОЙ ГРАФИКЕ
- ГЛАВА 6. ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКИ
- 6.1. АРХИТЕКТУРНОЕ ПРОЕКТИРОВАНИЕ
- 6.2. РАСПОЗНАВАНИЕ ВИДЕООБРАЗОВ
- 6.2.1. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИВНЫМ ЭТАЛОНАМ
- 6.2.2. РАСПОЗНАВАНИЕ ОБРАЗОВ В УСЛОВИЯХ НЕИЗВЕСТНОЙ ОРИЕНТАЦИИ ИХ КОРПУСОВ
- 6.2.3. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИРОВАННЫМ ЭТАЛОНАМ В ПИРАМИДАЛЬНОЙ СТРУКТУРЕ
- 6.2.4. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО ЭТАЛОНАМ, АДАПТИРОВАННЫМ ПО УСЛОВИЯМ НАБЛЮДЕНИЯ И КАЧЕСТВУ
- 6.3. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ В МАШИНОСТРОЕНИИ
- 6.4. ВОССТАНОВЛЕНИЕ ФОРМЫ СКРЫТЫХ ОБЪЕКТОВ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ
- 6.5. ВИДЕОТРЕНАЖЕРЫ И ИМИТАТОРЫ СЛОЖНЫХ СЦЕН
- 6.5.1. ТРЕНАЖЕР ДЛЯ ИМИТАЦИИ ПОЛЕТА НАД РЕАЛЬНОЙ МЕСТНОСТЬЮ
- 6.5.2. КОМПЬЮТЕРНЫЙ ИМИТАТОР ИЗОБРАЖЕНИЙ ОБЛАКОВ
- 6.6. РЕКЛАМА И МУЛЬТИПЛИКАЦИЯ
- ПРИЛОЖЕНИЕ. ОПИСАНИЕ ПРИКЛАДНЫХ ПОДПРОГРАММ
- СПИСОК ЛИТЕРАТУРЫ