| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
Основным
источником, определяющим естественную освещенность, является Солнце.
Спектральный состав солнечного излучения на границе атмосферы принято
аппроксимировать излучением черного тела с температурой ![]() К. Истинное распределение
энергии в спектре солнечного излучения несколько отличается от распределения
для черного тела с
К. Истинное распределение
энергии в спектре солнечного излучения несколько отличается от распределения
для черного тела с ![]() К: в области 0,4...0,75 мкм Солнце
излучает больше энергии, чем черный излучатель при
К: в области 0,4...0,75 мкм Солнце
излучает больше энергии, чем черный излучатель при ![]() К, в ультрафиолетовой
области – меньше, а в инфракрасной области отличия несущественны. Солнце как
излучатель представляет собой шар и теоретически излучает расходящийся поток
лучей, однако из-за большого удаления Солнца его излучение на земной
поверхности практически представляет поток параллельных лучей. Энергетическая
освещенность, которую создают солнечные лучи на перпендикулярной к ним плоскости
вне земной атмосферы на среднем расстоянии от Земли до Солнца, характеризуется
солнечной постоянной
К, в ультрафиолетовой
области – меньше, а в инфракрасной области отличия несущественны. Солнце как
излучатель представляет собой шар и теоретически излучает расходящийся поток
лучей, однако из-за большого удаления Солнца его излучение на земной
поверхности практически представляет поток параллельных лучей. Энергетическая
освещенность, которую создают солнечные лучи на перпендикулярной к ним плоскости
вне земной атмосферы на среднем расстоянии от Земли до Солнца, характеризуется
солнечной постоянной ![]() .
.
Освещенность
естественных ландшафтов определяется высотой Солнца над горизонтом ![]() и влиянием
атмосферы. Высота Солнца
и влиянием
атмосферы. Высота Солнца ![]() для района с геодезической широтой
для района с геодезической широтой ![]() и долготой
и долготой ![]() определяется по
следующей расчетной формуле:
определяется по
следующей расчетной формуле:
![]() , (1.3.1)
, (1.3.1)
где
![]() –
склонение Солнца на дату наблюдения;
–
склонение Солнца на дату наблюдения; ![]() – разность долгот Солнца
– разность долгот Солнца ![]() и наблюдателя
(часовой угол).
и наблюдателя
(часовой угол).
Разность
долгот ![]() (градус)
связана с местным временем
(градус)
связана с местным временем ![]() соотношением
соотношением ![]() , где
, где ![]() – время в часах и его
долях.
– время в часах и его
долях.
На
заданный момент московского времени ![]() величина
величина ![]() определяется следующими равенствами
для зимнего и летнего времени соответственно:
определяется следующими равенствами
для зимнего и летнего времени соответственно:
![]() ;
;
![]() , (1.3.2)
, (1.3.2)
где
![]() –
уравнение времени (поправка по времени) в долях часа.
–
уравнение времени (поправка по времени) в долях часа.
Склонение
Солнца ![]() задается
таблично, но с достаточной для моделирования точностью может быть определено
аналитически:
задается
таблично, но с достаточной для моделирования точностью может быть определено
аналитически: ![]() ,
где
,
где ![]() –
время в сутках от дневного равноденствия (22 марта) до даты съемки. Значения
определяются
–
время в сутках от дневного равноденствия (22 марта) до даты съемки. Значения
определяются ![]() по
номограмме или по таблицам.
по
номограмме или по таблицам.
Для
моделирования реалистичных изображений при естественном освещении необходимо
определить также азимут Солнца ![]() , для вычисления которого используются
, для вычисления которого используются
![]() ,
, ![]() и
и ![]() :
:
![]() ;
;
![]() . (1.3.3)
. (1.3.3)
В
процедурах синтеза изображений целесообразно использовать единичный вектор ![]() , указывающий
направление на Солнце. Если использовать правую топоцентрическую систему
координат, в которой ось
, указывающий
направление на Солнце. Если использовать правую топоцентрическую систему
координат, в которой ось ![]() направлена на север, а ось
направлена на север, а ось ![]() перпендикулярна
поверхности Земли и направлена в зенит, то составляющие вектора
перпендикулярна
поверхности Земли и направлена в зенит, то составляющие вектора ![]() по осям
по осям ![]() будут определяться
следующими соотношениями:
будут определяться
следующими соотношениями:
 (1.3.4)
(1.3.4)
Отметим,
что для характеристик положения Солнца наряду с высотой ![]() используется зенитное
расстояние
используется зенитное
расстояние ![]() .
.
Воздействие
атмосферы проявляется в ослаблении прямого солнечною излучения и его
рассеивании. В соответствии с этим освещенность земной поверхности определяется
двумя световыми потоками: ослабленной прямой радиацией ![]() и рассеянной радиацией
солнечного излучения
и рассеянной радиацией
солнечного излучения ![]() , идущей к Земле.
, идущей к Земле.
Существенная нестабильность свойств атмосферы, значительное число факторов, обусловливающих ее изменчивость, не позволяют давать точный прогноз освещенности. Обычно используются приближенные модели с ограниченным числом параметров, характеризующих оптические свойства атмосферы. Для расчетов широко используется модель средней стандартной атмосферы. Спектральная освещенность, создаваемая Солнцем у поверхности Земли на площадке, перпендикулярной солнечным лучам, при безоблачном небе и стандартной атмосфере определяется формулой
![]() , (1.3.5)
, (1.3.5)
где
![]() - спектральная
освещенность, создаваемая солнечным излучением на границе атмосферы;
- спектральная
освещенность, создаваемая солнечным излучением на границе атмосферы; ![]() – оптическая толща
атмосферы.
– оптическая толща
атмосферы.
Обобщенным
параметром ![]() практически
можно пользоваться в диапазоне
практически
можно пользоваться в диапазоне ![]() , в пределах которого ослабление
прямой солнечной радиации обусловлено в основном молекулярным и аэрозольным
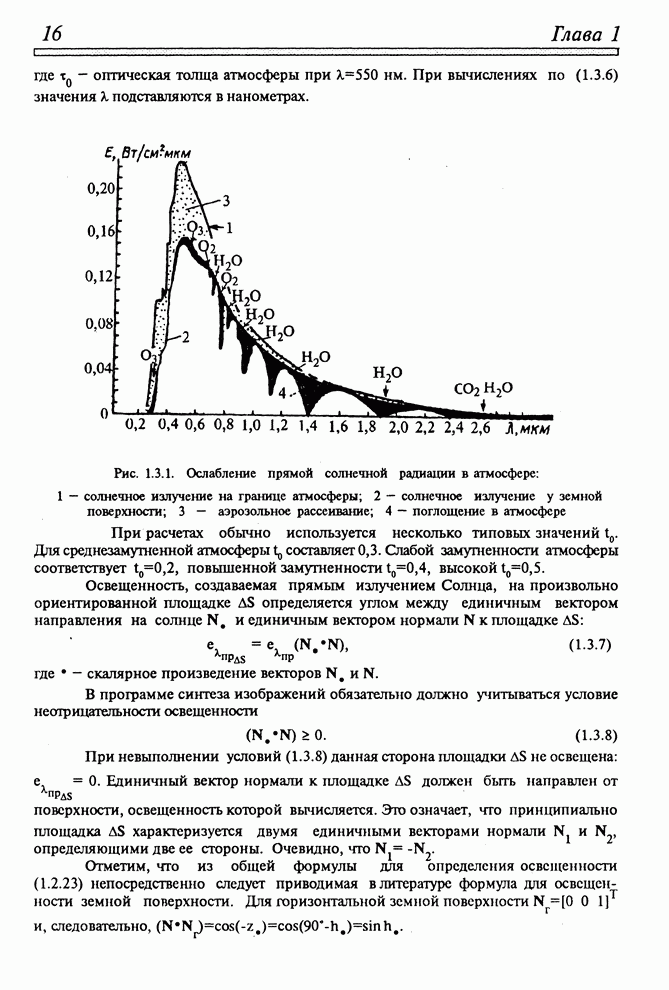
рассеиванием (рис. 1.3.1).
, в пределах которого ослабление
прямой солнечной радиации обусловлено в основном молекулярным и аэрозольным
рассеиванием (рис. 1.3.1).

Рис. 1.3.1. Ослабление прямой солнечной радиации в атмосфере:
1 – солнечное излучение на границе атмосферы; 2 – солнечное излучение у земной поверхности; 3 – аэрозольное рассеивание; 4 – поглощение в атмосфере
Для
этого диапазона зависимость ![]() от длины волны для стандартной
атмосферы описывается эмпирической формулой
от длины волны для стандартной
атмосферы описывается эмпирической формулой
![]() , (1.3.6)
, (1.3.6)
где
![]() –
оптическая толща атмосферы при
–
оптическая толща атмосферы при ![]() нм. При вычислениях по (1.3.6)
значения
нм. При вычислениях по (1.3.6)
значения ![]() подставляются
в нанометрах.
подставляются
в нанометрах.
При
расчетах обычно используется несколько типовых значений ![]() . Для среднезамутненной
атмосферы
. Для среднезамутненной
атмосферы ![]() составляет
0,3. Слабой замутненности атмосферы соответствует
составляет
0,3. Слабой замутненности атмосферы соответствует ![]() , повышенной замутненности
, повышенной замутненности ![]() , высокой
, высокой ![]() .
.
Освещенность,
создаваемая прямым излучением Солнца, на произвольно ориентированной площадке ![]() определяется углом
между единичным вектором направления на солнце
определяется углом
между единичным вектором направления на солнце ![]() и единичным вектором нормали
и единичным вектором нормали ![]() к площадке
к площадке ![]() :
:
![]() , (1.3.7)
, (1.3.7)
где
![]() –
скалярное произведение векторов
–
скалярное произведение векторов ![]() и
и ![]() .
.
В программе синтеза изображений обязательно должно учитываться условие неотрицательности освещенности
![]() . (1.3.8)
. (1.3.8)
При
невыполнении условий (1.3.8) данная сторона площадки ![]() не освещена:
не освещена: ![]() . Единичный вектор
нормали к площадке
. Единичный вектор
нормали к площадке ![]() должен быть направлен от поверхности,
освещенность которой вычисляется. Это означает, что принципиально площадка
должен быть направлен от поверхности,
освещенность которой вычисляется. Это означает, что принципиально площадка ![]() характеризуется
двумя единичными векторами нормали
характеризуется
двумя единичными векторами нормали ![]() и
и ![]() , определяющими две ее стороны.
Очевидно, что
, определяющими две ее стороны.
Очевидно, что ![]() .
.
Отметим,
что из общей формулы для определения освещенности (1.2.23) непосредственно
следует приводимая в литературе формула для освещенности земной поверхности.
Для горизонтальной земной поверхности ![]() и, следовательно,
и, следовательно, ![]() .
.
Освещенность, создаваемая рассеянной радиацией, определяется яркостью неба. Важность учета рассеянной радиации обусловлена тем, что она определяет освещенность участков сцены, находящихся в тени.
Яркость
произвольной точки небосвода ![]() представляет собой функцию четырех
основных параметров [13]: высоты Солнца
представляет собой функцию четырех
основных параметров [13]: высоты Солнца ![]() , пропускания атмосферы
, пропускания атмосферы ![]() , зенитного
расстояния
, зенитного
расстояния ![]() точки
небосвода и угла
точки
небосвода и угла ![]() между
направлением на Солнце и в заданную точку небосвода.
между
направлением на Солнце и в заданную точку небосвода.
Расчет освещенности произвольно ориентированной площадки с учетом истинного распределения яркости небосвода требует выполнения численного интегрирования с использованием таблично заданных функций. Это весьма серьезно усложняет процедуру вычисления освещенности точек картинной плоскости. Процедуру вычислений можно существенно упростить, если яркость всех точек небосвода принять одинаковой и равной некоторой усредненной величине. Среднюю яркость небосвода можно аппроксимировать зависимостью вида [6]
![]() . (1.3.9)
. (1.3.9)
Величина
![]() сравнительно
слабо зависит от
сравнительно
слабо зависит от ![]() и
и
![]() . В ряде
случаев ее полагают постоянной. Более точное приближение можно получить, если
полагать
. В ряде
случаев ее полагают постоянной. Более точное приближение можно получить, если
полагать ![]() .
При этом различия в результатах, полученных на основе более точных моделей и изложенной
выше, невелики. Максимальные различия достигают 20 % лишь при значительной
высоте Солнца (
.
При этом различия в результатах, полученных на основе более точных моделей и изложенной
выше, невелики. Максимальные различия достигают 20 % лишь при значительной
высоте Солнца (![]() ).
).
Для
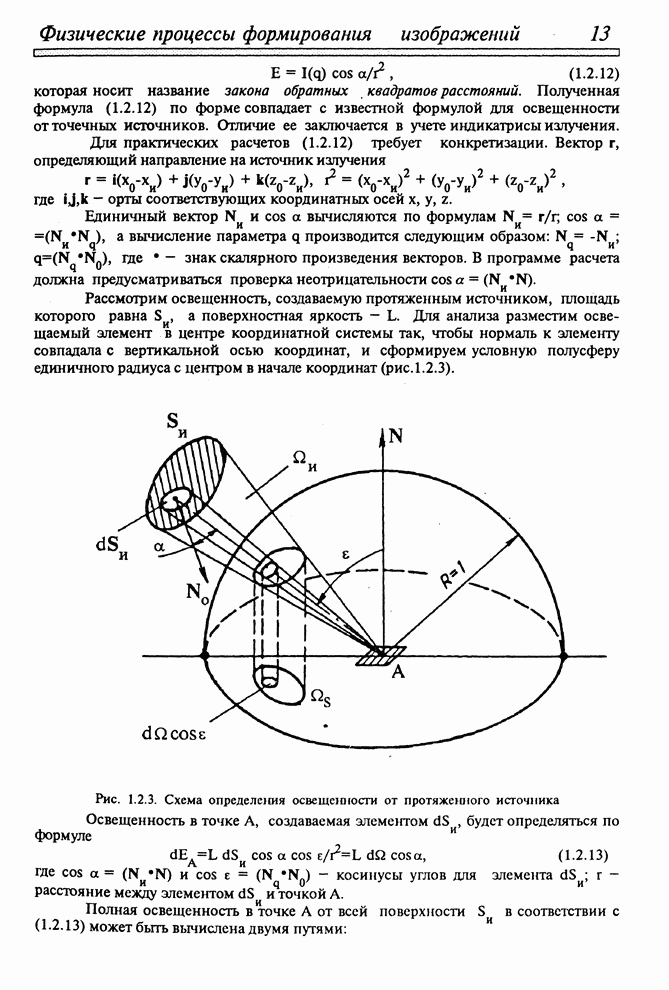
определения освещенности от небосвода произвольно ориентированной площадки ![]() рассмотрим общую
схему определения освещенности, создаваемой протяженным источником (рис.
1.3.2).
рассмотрим общую
схему определения освещенности, создаваемой протяженным источником (рис.
1.3.2).

Рис. 1.3.2. Определение освещенности произвольно ориентированной площадки небосводом
В
соответствии с (1.2.16) освещенность от небосвода площадки ![]() определяется следующим
образом:
определяется следующим
образом: ![]() ,
где
,
где ![]() –
проекция на освещаемую плоскость
–
проекция на освещаемую плоскость ![]() , в которой лежит площадка
, в которой лежит площадка ![]() , видимой части
небесной сферы.
, видимой части
небесной сферы.
Если
поверхность ![]() наклонена
на угол
наклонена
на угол ![]() относительно
горизонта, то проекция
относительно
горизонта, то проекция ![]() телесного угла видимой части
небосвода
телесного угла видимой части
небосвода ![]() на
плоскость
на
плоскость ![]() определяется
простым соотношением
определяется
простым соотношением ![]() .
.
В
результате освещенность ![]() произвольно ориентированной площадки,
обусловленная рассеянной радиацией, составляет
произвольно ориентированной площадки,
обусловленная рассеянной радиацией, составляет
![]() . (1.3.10)
. (1.3.10)
Полная
освещенность в спектральном диапазоне от ![]() до
до ![]() для произвольных поверхностей, не
закрытых тенью, в энергетической системе единиц может быть определена
интегрированием:
для произвольных поверхностей, не
закрытых тенью, в энергетической системе единиц может быть определена
интегрированием:
 (1.3.11)
(1.3.11)
Для
систем, работающих в видимом диапазоне, освещенность наблюдаемого пространства
принято указывать в светотехнической системе единиц. Переход к светотехнической
системе может быть осуществлен путем учета относительной видности
монохроматических излучений ![]() :
:
 . (1.3.12)
. (1.3.12)
Интегрирование
в соотношении (1.3.12) выполняется в пределах от ![]() до
до ![]() . За пределами этого диапазона
значения
. За пределами этого диапазона
значения ![]() практически
являются нулевыми.
практически
являются нулевыми.
Хотя переход от энергетической системы к светотехнической не вызывает принципиальных затруднений, однако для систем видимого диапазона удобнее пользоваться расчетными формулами, выражающими освещенность непосредственно в светотехнической системе. Для таких расчетов может быть использовано соотношение, базирующееся на известном в [6], но дополненное учетом наклона освещаемой площадки:
![]() , (1.3.13)
, (1.3.13)
где
![]() –
освещенность плоскости, перпендикулярной к лучам Солнца на границе атмосферы в
светотехнической системе единиц;
–
освещенность плоскости, перпендикулярной к лучам Солнца на границе атмосферы в
светотехнической системе единиц; ![]() – коэффициенты, характеризующие
прозрачность и рассеивание в атмосфере.
– коэффициенты, характеризующие
прозрачность и рассеивание в атмосфере.
Для
средних параметров стандартной атмосферы ![]() ;
; ![]() . В соответствии с (1.2.29)
максимальная освещенность горизонтальной площадки на земной поверхности для
стандартных условий составляет 106000 лк (при
. В соответствии с (1.2.29)
максимальная освещенность горизонтальной площадки на земной поверхности для
стандартных условий составляет 106000 лк (при ![]() ).
).
На
величину естественной освещенности большое влияние оказывает характер
облачности. Наличие облачности вызывает значительное увеличение рассеянного
излучения. При разорванной облачности освещенность "на Солнце"
оказывается на 10...30 % выше, чем при безоблачной погоде, а освещенность в
тени может возрастать до двукратной величины. Это обстоятельство является
причиной значительного разброса в экспериментальных данных по освещенности в
тени и оправдывает применение в машинной графике относительно простых моделей
расчета освещенности, использование поправочных коэффициентов, увеличивающих
значение освещенности в тени по сравнению с расчетными при углах Солнца ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА 1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ И ИХ МОДЕЛИРОВАНИЕ
- 1.1. МОДЕЛИ В МАШИННОЙ ГРАФИКЕ
- 1.2. ИСТОЧНИКИ ОСВЕЩЕНИЯ
- 1.2.1. ИСТОЧНИКИ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
- 1.2.2. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИСТОЧНИКОВ ПРОСТОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
- 1.2.3. ОСВЕЩЕННОСТЬ, СОЗДАВАЕМАЯ ТОЧЕЧНЫМИ И ПРОТЯЖЕННЫМИ ИСТОЧНИКАМИ
- 1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
- 1.4. МОДЕЛИРОВАНИЕ ОТРАЖЕННОГО ИЗЛУЧЕНИЯ ОБЪЕКТОВ
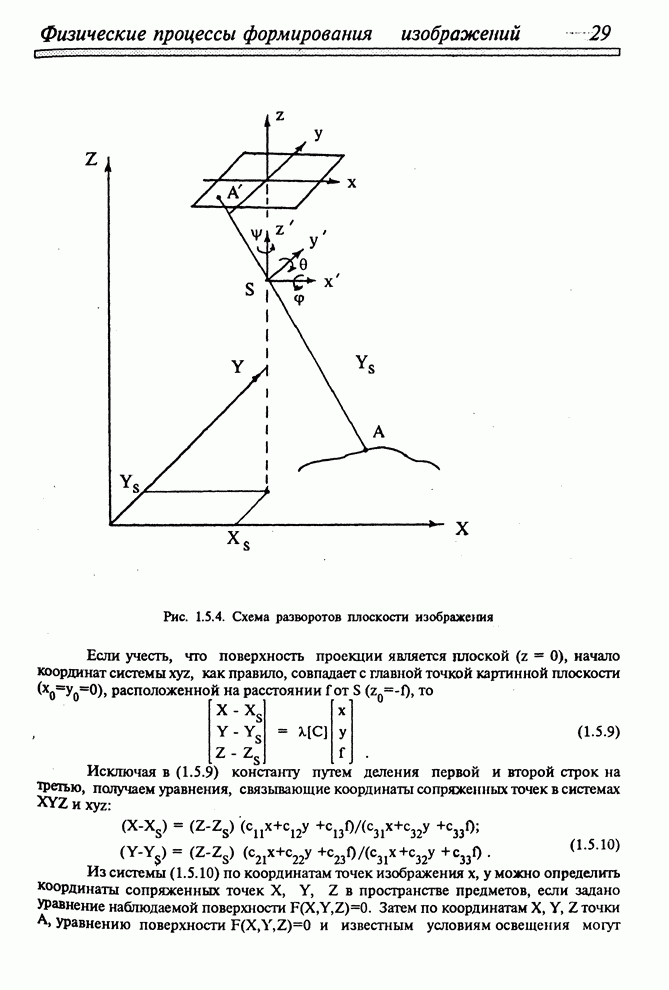
- 1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
- 1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
- 1.5.2. ЦЕНТРАЛЬНАЯ (ПЕРСПЕКТИВНАЯ) ПРОЕКЦИЯ
- 1.5.3. ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ С ИСПОЛЬЗОВАНИЕМ ОДНОРОДНЫХ КООРДИНАТ
- 1.5.4. ПРОЕКЦИИ ПРИ РАЗЛИЧНЫХ ВИДАХ СЪЕМКИ
- 1.6. ТЕКСТУРА ИЗОБРАЖЕНИЯ
- 1.7. МОДЕЛИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.8. СИНТЕЗ ИЗОБРАЖЕНИЙ С УЧЕТОМ СПЕЦИФИКИ ИХ ФОРМИРОВАНИЯ В РЕАЛЬНЫХ УСЛОВИЯХ
- ГЛАВА 2. ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
- 2.1. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
- 2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
- 2.3. МОДЕЛИ ОБЪЕКТОВ И ИХ КЛАССИФИКАЦИЯ
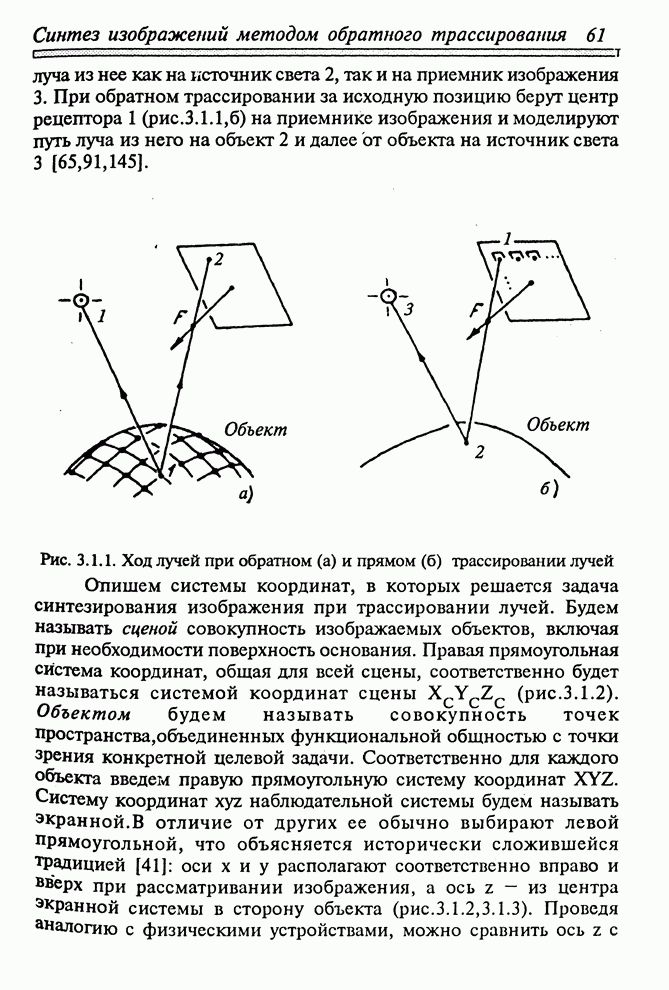
- ГЛАВА 3. СИНТЕЗ ИЗОБРАЖЕНИЙ МЕТОДОМ ОБРАТНОГО ТРАССИРОВАНИЯ ЛУЧЕЙ
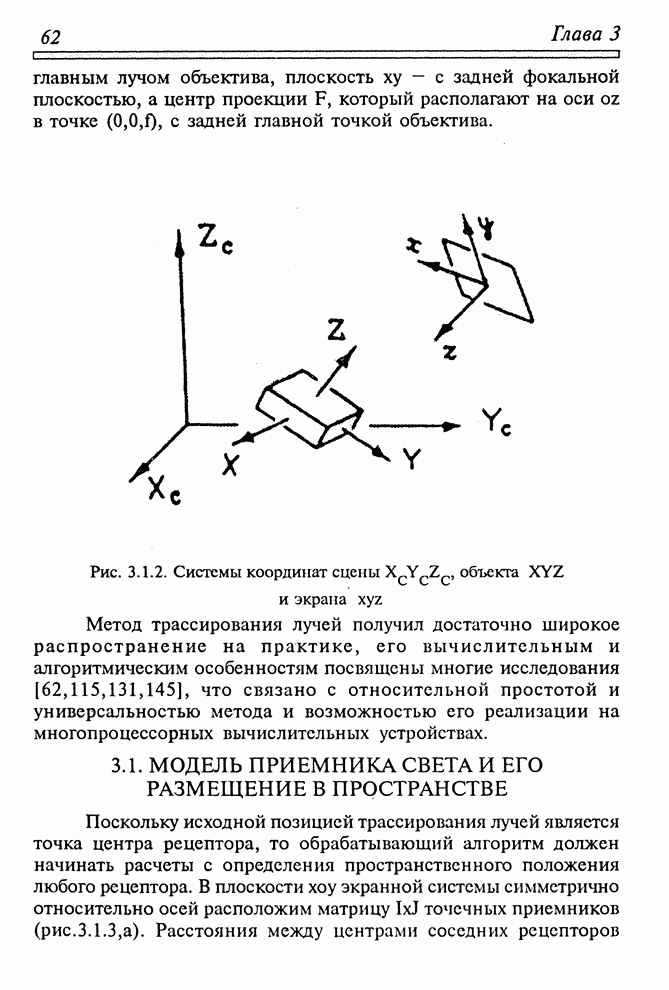
- 3.1. МОДЕЛЬ ПРИЕМНИКА СВЕТА И ЕГО РАЗМЕЩЕНИЕ В ПРОСТРАНСТВЕ
- 3.2. МОДЕЛЬ ОБЪЕКТА
- 3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
- 3.2.2. ПРОСТРАНСТВЕННЫЕ КОМБИНАЦИИ ПРИМИТИВОВ
- 3.2.3. ФОРМАЛИЗОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
- 3.2.4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ОБЪЕКТА
- 3.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ И ЗАТЕНЕННЫХ ТОЧЕК
- 3.3.1. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С ПРИМИТИВОМ
- 3.3.2. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С КОМБИНАЦИЕЙ ПРИМИТИВОВ
- 3.3.3. ОПРЕДЕЛЕНИЕ ЗАТЕНЕННЫХ ТОЧЕК
- 3.4. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРИМИТИВОВ МЕТОДОМ ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.4.1. ПЛОСКИЕ МНОГОУГОЛЬНИКИ
- 3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
- 3.4.3. КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
- 3.4.4. БИКУБИЧЕСКИЕ ПОВЕРХНОСТИ
- 3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- 3.6. ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ ОСВЕЩЕННОСТИ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ИЗОБРАЖЕНИЙ ПУТЕМ ПРОЕКТИРОВАНИЯ ТОЧЕК И ЛИНИЙ НА ЭКРАН
- 4.1. ТРАССИРОВАНИЕ ЛУЧЕЙ ОТ ОБЪЕКТА К ЭКРАНУ
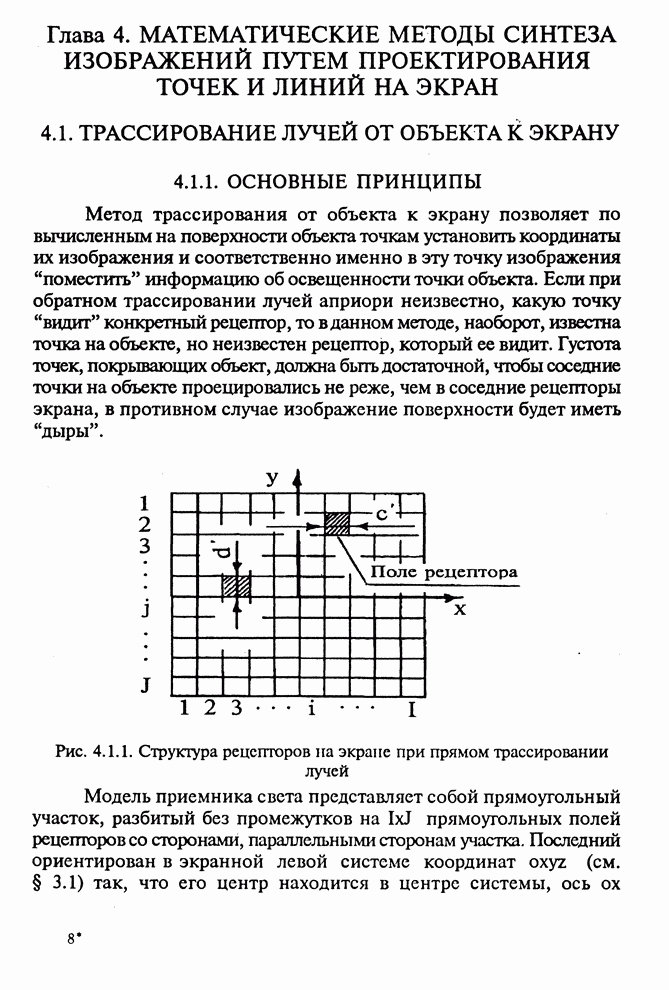
- 4.1.1. ОСНОВНЫЕ ПРИНЦИПЫ
- 4.1.2. МОДЕЛЬ ОБЪЕКТА
- 4.1.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ ТОЧЕК
- 4.1.4. ОПРЕДЕЛЕНИЕ ОСВЕЩЕННОСТИ
- 4.1.5. ИЗОБРАЖЕНИЕ ПОТОЧЕЧНО ОПИСАННЫХ ОБЪЕКТОВ
- 4.2. МЕТОД СКАНИРУЮЩЕЙ СТРОКИ
- 4.2.1. МОДЕЛЬ ОБЪЕКТА ИЗ МНОГОУГОЛЬНИКОВ
- 4.2.2. МОДЕЛЬ ПРИЕМНИКА
- 4.2.3. ИЗОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ НА ЭКРАНЕ
- 4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
- 4.3. АЛГОРИТМ РОБЕРТСА
- 4.3.1. МОДЕЛЬ ОБЪЕКТА
- 4.3.2. СИНТЕЗ ИЗОБРАЖЕНИЯ
- ГЛАВА 5. ОРГАНИЗАЦИЯ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.1. УПРАВЛЕНИЕ ПРОЦЕССОМ СИНТЕЗА
- 5.2. СПЕКТР СИНТЕЗИРОВАННОГО ИЗОБРАЖЕНИЯ
- 5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.3.1. МЕТОД ОБОЛОЧЕК
- 5.3.2. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ТРАНСПЬЮТЕРОВ В МАШИННОЙ ГРАФИКЕ
- ГЛАВА 6. ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКИ
- 6.1. АРХИТЕКТУРНОЕ ПРОЕКТИРОВАНИЕ
- 6.2. РАСПОЗНАВАНИЕ ВИДЕООБРАЗОВ
- 6.2.1. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИВНЫМ ЭТАЛОНАМ
- 6.2.2. РАСПОЗНАВАНИЕ ОБРАЗОВ В УСЛОВИЯХ НЕИЗВЕСТНОЙ ОРИЕНТАЦИИ ИХ КОРПУСОВ
- 6.2.3. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИРОВАННЫМ ЭТАЛОНАМ В ПИРАМИДАЛЬНОЙ СТРУКТУРЕ
- 6.2.4. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО ЭТАЛОНАМ, АДАПТИРОВАННЫМ ПО УСЛОВИЯМ НАБЛЮДЕНИЯ И КАЧЕСТВУ
- 6.3. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ В МАШИНОСТРОЕНИИ
- 6.4. ВОССТАНОВЛЕНИЕ ФОРМЫ СКРЫТЫХ ОБЪЕКТОВ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ
- 6.5. ВИДЕОТРЕНАЖЕРЫ И ИМИТАТОРЫ СЛОЖНЫХ СЦЕН
- 6.5.1. ТРЕНАЖЕР ДЛЯ ИМИТАЦИИ ПОЛЕТА НАД РЕАЛЬНОЙ МЕСТНОСТЬЮ
- 6.5.2. КОМПЬЮТЕРНЫЙ ИМИТАТОР ИЗОБРАЖЕНИЙ ОБЛАКОВ
- 6.6. РЕКЛАМА И МУЛЬТИПЛИКАЦИЯ
- ПРИЛОЖЕНИЕ. ОПИСАНИЕ ПРИКЛАДНЫХ ПОДПРОГРАММ
- СПИСОК ЛИТЕРАТУРЫ