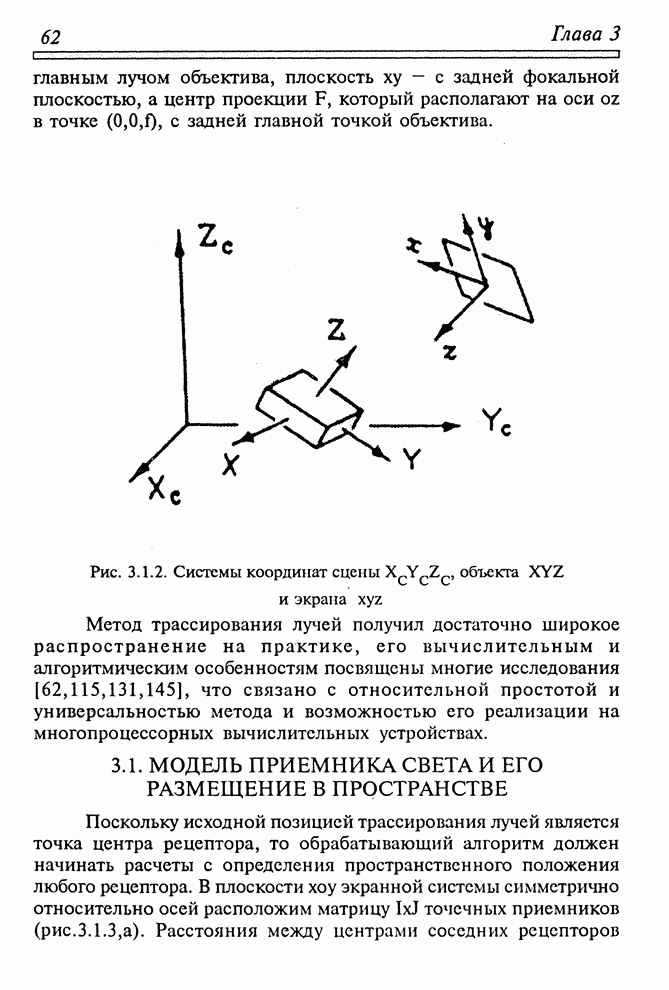
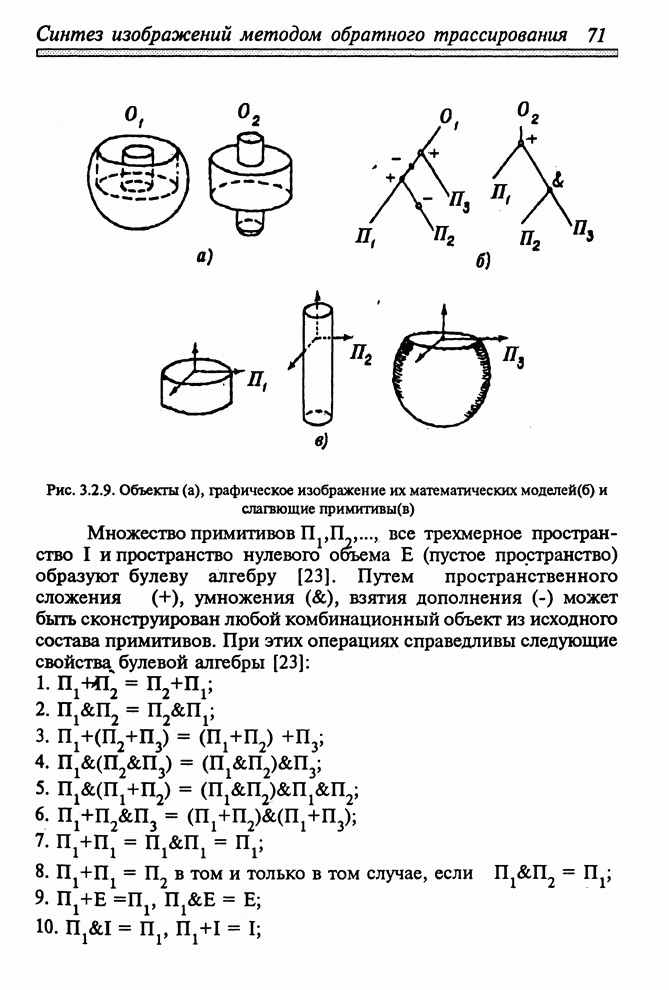
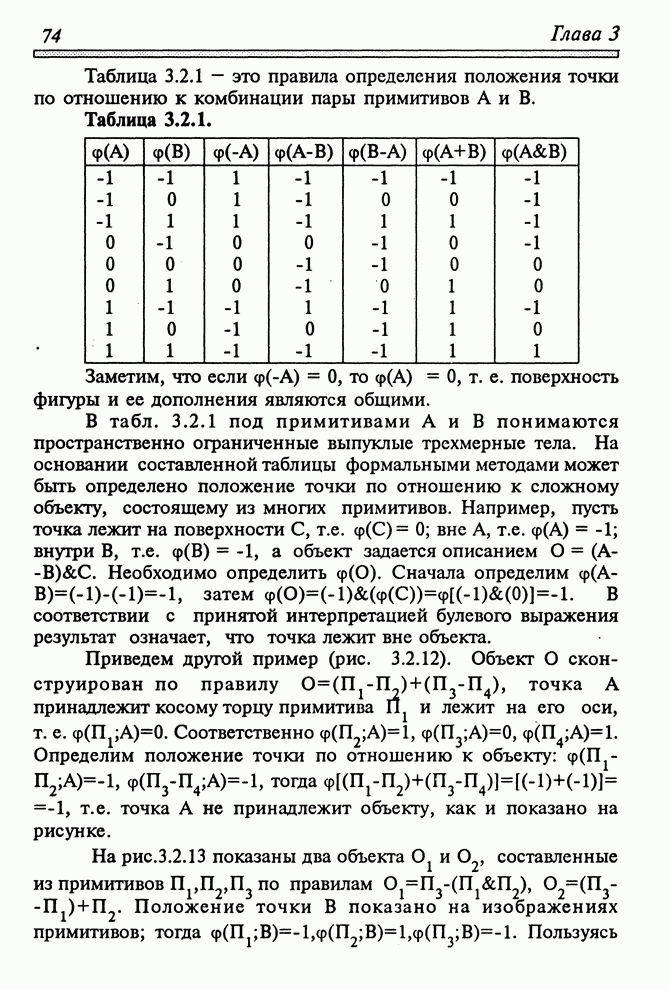
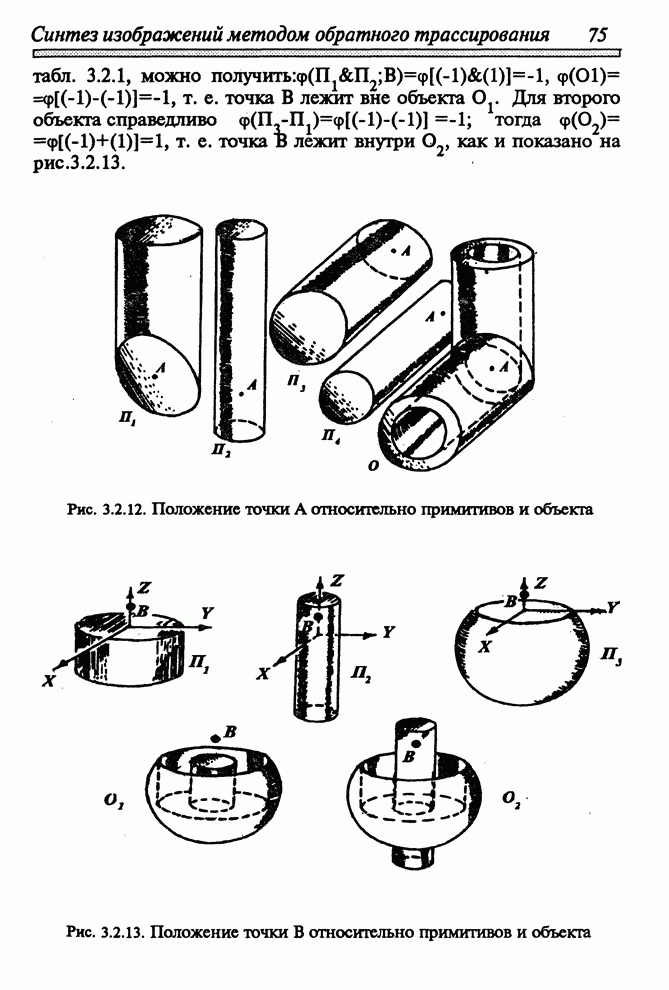
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
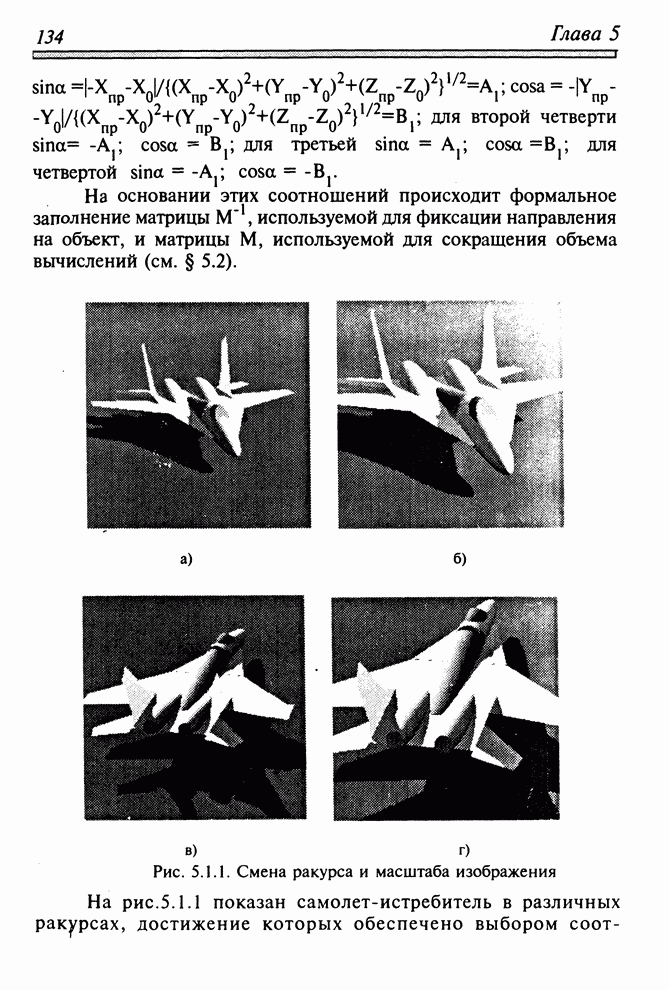
4.3. АЛГОРИТМ РОБЕРТСА
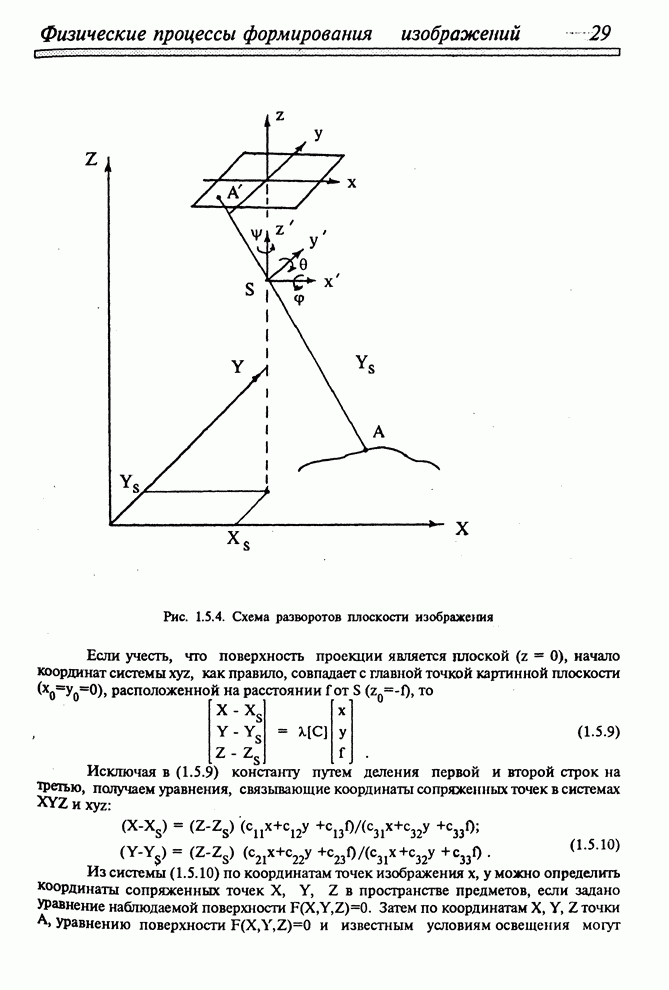
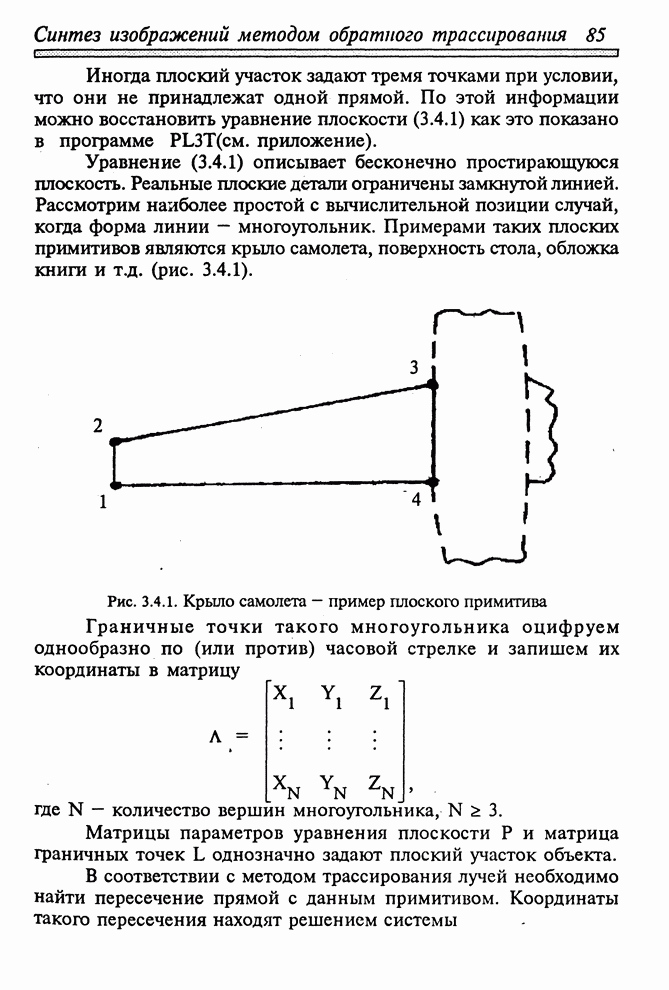
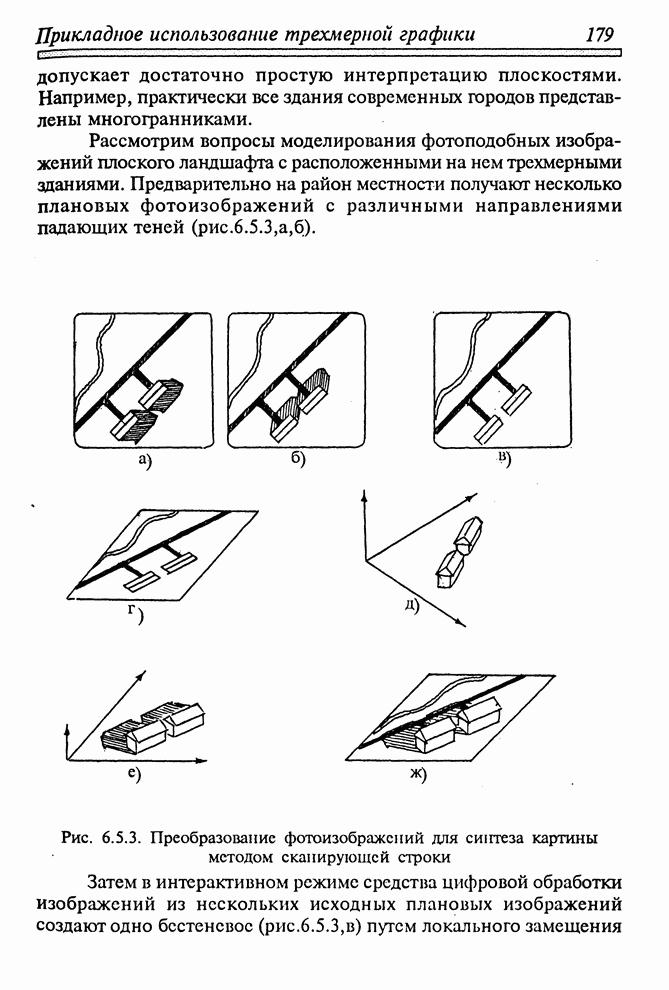
Алгоритм получения изображений одиночных выпуклых объектов, составленных из плоских граней, был впервые разработан Робертсом. В переводной литературе метод описан в [41] и наиболее подробно - в [49]. Алгоритм Робертса может быть с успехом применен для изображения множества выпуклых многогранников на одной сцене в виде проволочной модели с удаленными невидимыми линиями. Метод не пригоден непосредственно для передачи падающих теней и других сложных визуальных эффектов. Рассмотрим основные идеи метода на примере одиночного выпуклого многогранника.
4.3.1. МОДЕЛЬ ОБЪЕКТА
Объект
- многогранник, состоящий из ![]() граней, описывается матрицей
граней, описывается матрицей ![]() размера
размера ![]() , каждый
, каждый ![]() -й столбец которой
содержит описание
-й столбец которой
содержит описание ![]() -й
-й ![]() плоскости
плоскости ![]() в объектной системе
координат
в объектной системе
координат ![]() :
:
 .
.
Минимальное
число граней ![]() наблюдается
у тетраэдра.
наблюдается
у тетраэдра.
Важное
требование к модели объекта в алгоритме Робертса заключается в достижении такой
формы (знака) в функции каждой плоскости ![]() , при которой справедливо
, при которой справедливо ![]() для любой точки
для любой точки ![]() , заведомо принадлежащей
телу многогранника. Достижение этого условия осуществляется путем опытной
проверки знака функции относительно внутренней точки, в качестве которой может
выступать точка со средним геометрическим положением относительно всех вершин
многогранника. Формально правило формирования "положительной" грани
может быть представлено в виде
, заведомо принадлежащей
телу многогранника. Достижение этого условия осуществляется путем опытной
проверки знака функции относительно внутренней точки, в качестве которой может
выступать точка со средним геометрическим положением относительно всех вершин
многогранника. Формально правило формирования "положительной" грани
может быть представлено в виде ![]() , где
, где ![]() - функция, описывающая
- функция, описывающая ![]() -ю грань с априори
неизвестным знаком относительно внутренней точки;
-ю грань с априори
неизвестным знаком относительно внутренней точки; ![]() - та же функция, но с положительным
значением. При достижении "положительности" всех граней автоматически
достигается ориентация нормали
- та же функция, но с положительным
значением. При достижении "положительности" всех граней автоматически
достигается ориентация нормали ![]() к любой из граней внутрь фигуры.
к любой из граней внутрь фигуры.
Кроме
параметров уравнений граней необходимо знать координаты вершин каждой грани.
Вершины могут быть заданы или вычислены из матрицы ![]() путем определения общих
решений каждой плоскости со всеми остальными. В любом случае для каждой
путем определения общих
решений каждой плоскости со всеми остальными. В любом случае для каждой ![]() -й грани должна
быть составлена матрица
-й грани должна
быть составлена матрица ![]() - числа вершин:
- числа вершин:
 .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- ГЛАВА 1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ И ИХ МОДЕЛИРОВАНИЕ
- 1.1. МОДЕЛИ В МАШИННОЙ ГРАФИКЕ
- 1.2. ИСТОЧНИКИ ОСВЕЩЕНИЯ
- 1.2.1. ИСТОЧНИКИ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
- 1.2.2. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИСТОЧНИКОВ ПРОСТОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
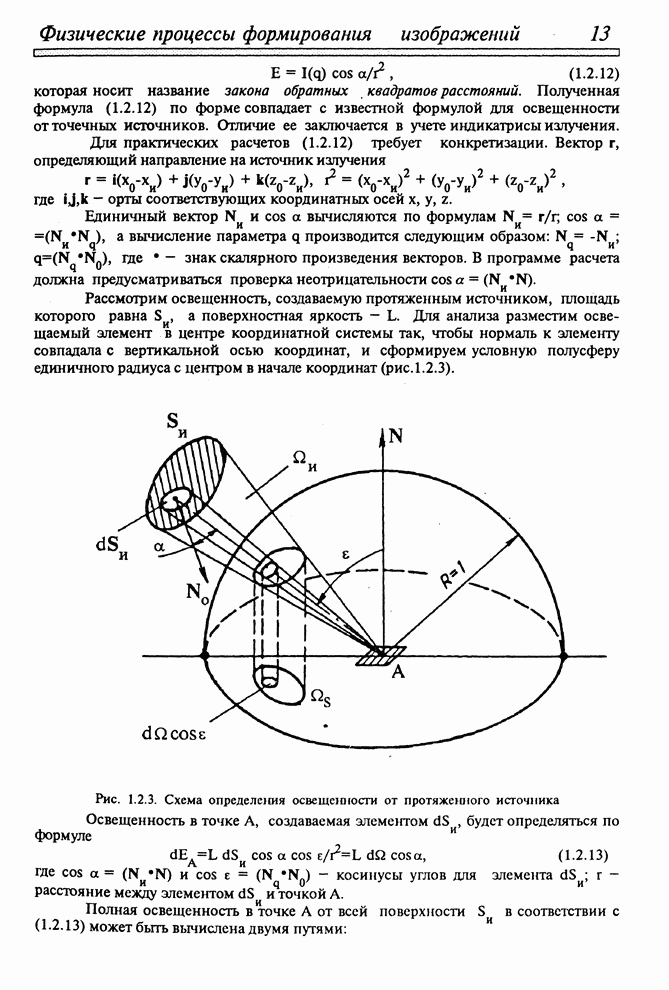
- 1.2.3. ОСВЕЩЕННОСТЬ, СОЗДАВАЕМАЯ ТОЧЕЧНЫМИ И ПРОТЯЖЕННЫМИ ИСТОЧНИКАМИ
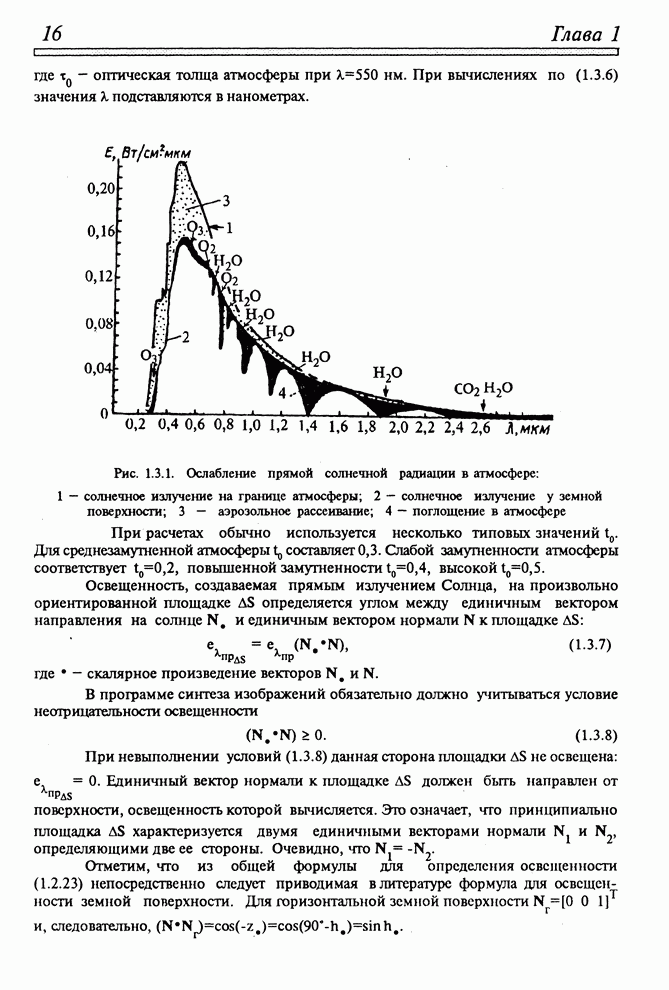
- 1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
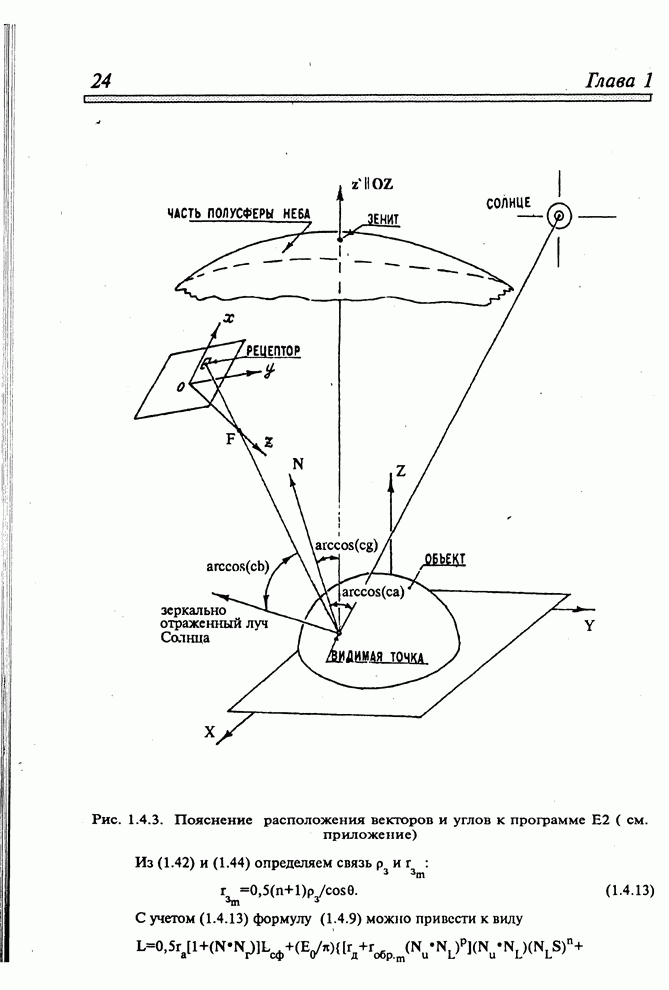
- 1.4. МОДЕЛИРОВАНИЕ ОТРАЖЕННОГО ИЗЛУЧЕНИЯ ОБЪЕКТОВ
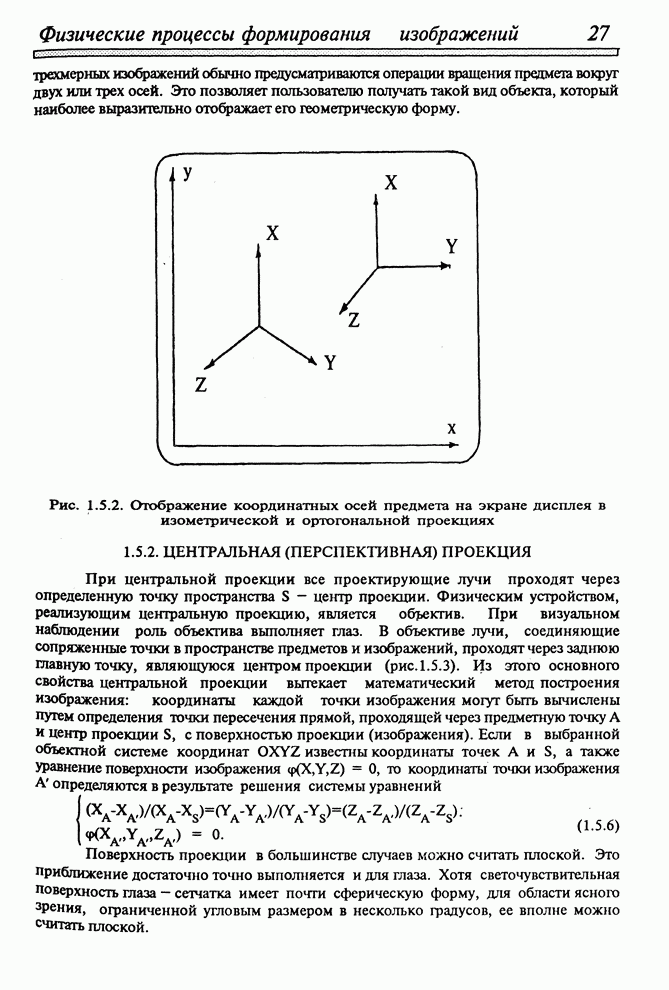
- 1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
- 1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
- 1.5.2. ЦЕНТРАЛЬНАЯ (ПЕРСПЕКТИВНАЯ) ПРОЕКЦИЯ
- 1.5.3. ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ С ИСПОЛЬЗОВАНИЕМ ОДНОРОДНЫХ КООРДИНАТ
- 1.5.4. ПРОЕКЦИИ ПРИ РАЗЛИЧНЫХ ВИДАХ СЪЕМКИ
- 1.6. ТЕКСТУРА ИЗОБРАЖЕНИЯ
- 1.7. МОДЕЛИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.8. СИНТЕЗ ИЗОБРАЖЕНИЙ С УЧЕТОМ СПЕЦИФИКИ ИХ ФОРМИРОВАНИЯ В РЕАЛЬНЫХ УСЛОВИЯХ
- ГЛАВА 2. ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
- 2.1. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
- 2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
- 2.3. МОДЕЛИ ОБЪЕКТОВ И ИХ КЛАССИФИКАЦИЯ
- ГЛАВА 3. СИНТЕЗ ИЗОБРАЖЕНИЙ МЕТОДОМ ОБРАТНОГО ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.1. МОДЕЛЬ ПРИЕМНИКА СВЕТА И ЕГО РАЗМЕЩЕНИЕ В ПРОСТРАНСТВЕ
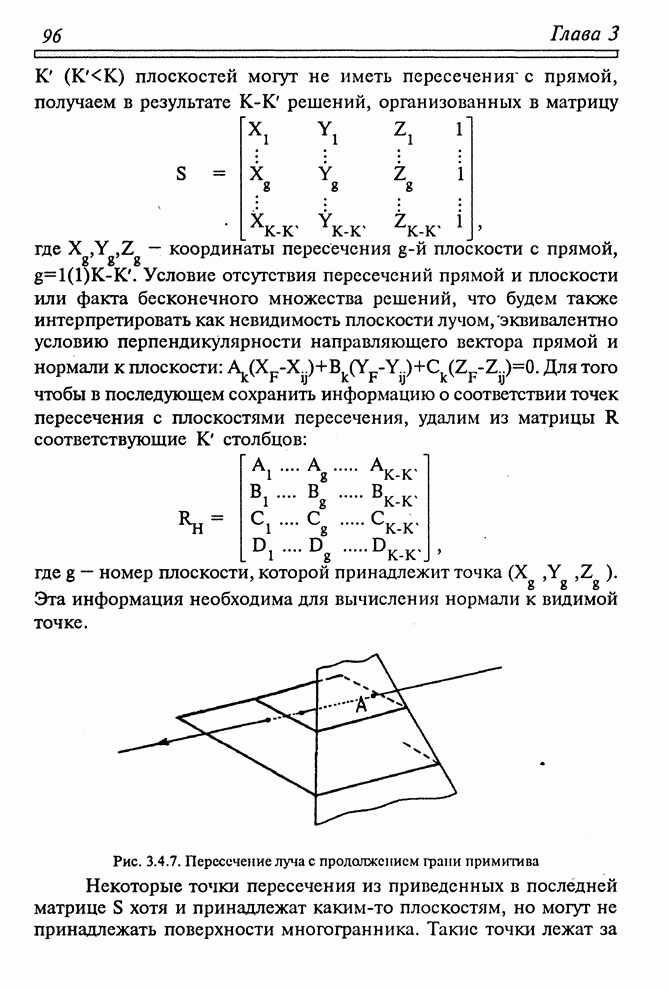
- 3.2. МОДЕЛЬ ОБЪЕКТА
- 3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
- 3.2.2. ПРОСТРАНСТВЕННЫЕ КОМБИНАЦИИ ПРИМИТИВОВ
- 3.2.3. ФОРМАЛИЗОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
- 3.2.4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ОБЪЕКТА
- 3.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ И ЗАТЕНЕННЫХ ТОЧЕК
- 3.3.1. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С ПРИМИТИВОМ
- 3.3.2. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С КОМБИНАЦИЕЙ ПРИМИТИВОВ
- 3.3.3. ОПРЕДЕЛЕНИЕ ЗАТЕНЕННЫХ ТОЧЕК
- 3.4. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРИМИТИВОВ МЕТОДОМ ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.4.1. ПЛОСКИЕ МНОГОУГОЛЬНИКИ
- 3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
- 3.4.3. КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
- 3.4.4. БИКУБИЧЕСКИЕ ПОВЕРХНОСТИ
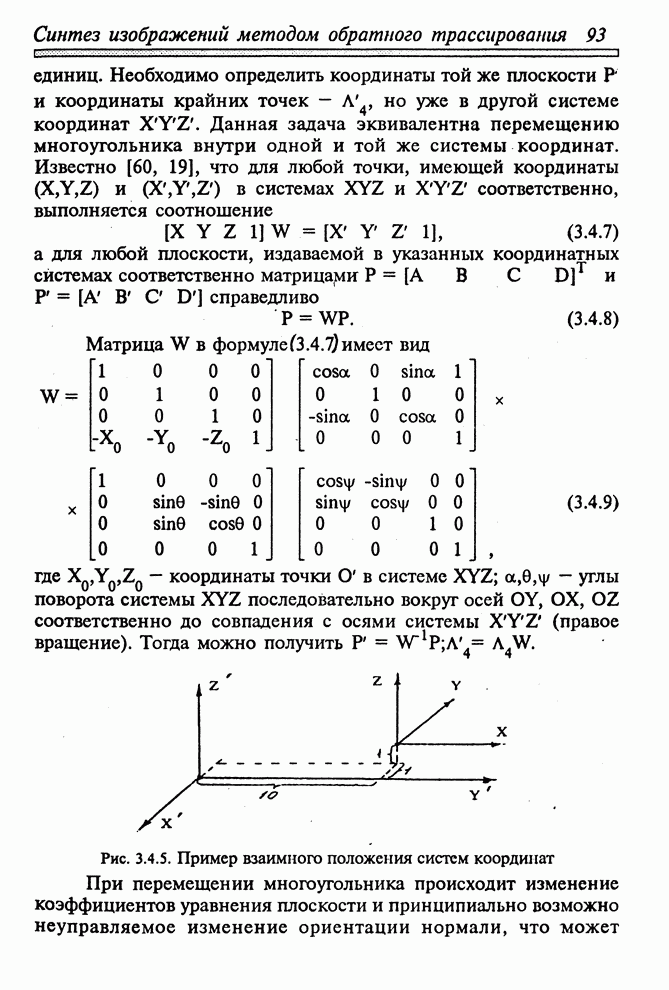
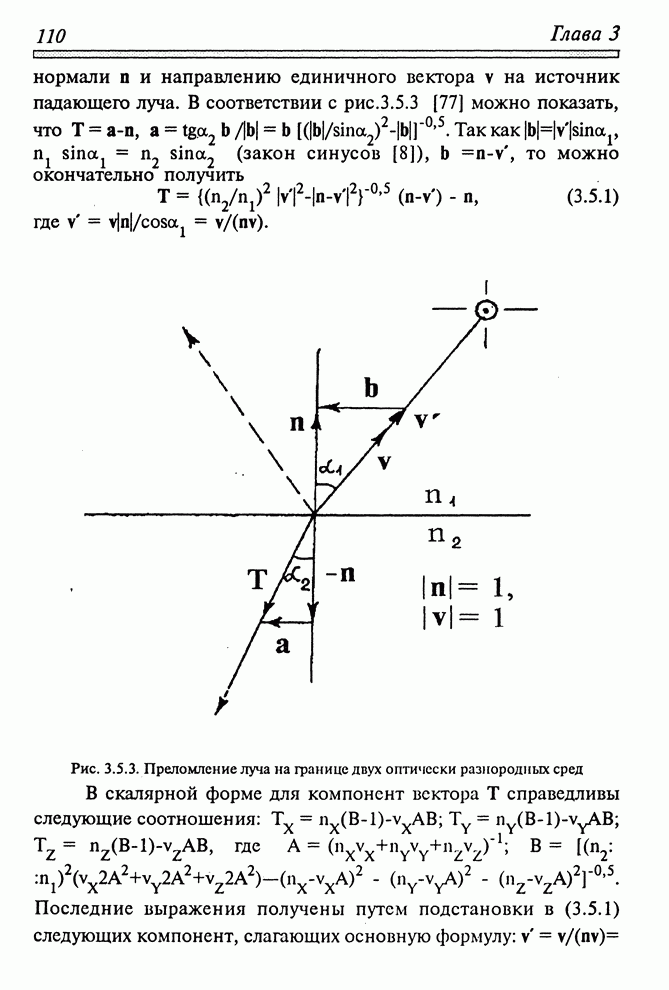
- 3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- 3.6. ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ ОСВЕЩЕННОСТИ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ИЗОБРАЖЕНИЙ ПУТЕМ ПРОЕКТИРОВАНИЯ ТОЧЕК И ЛИНИЙ НА ЭКРАН
- 4.1. ТРАССИРОВАНИЕ ЛУЧЕЙ ОТ ОБЪЕКТА К ЭКРАНУ
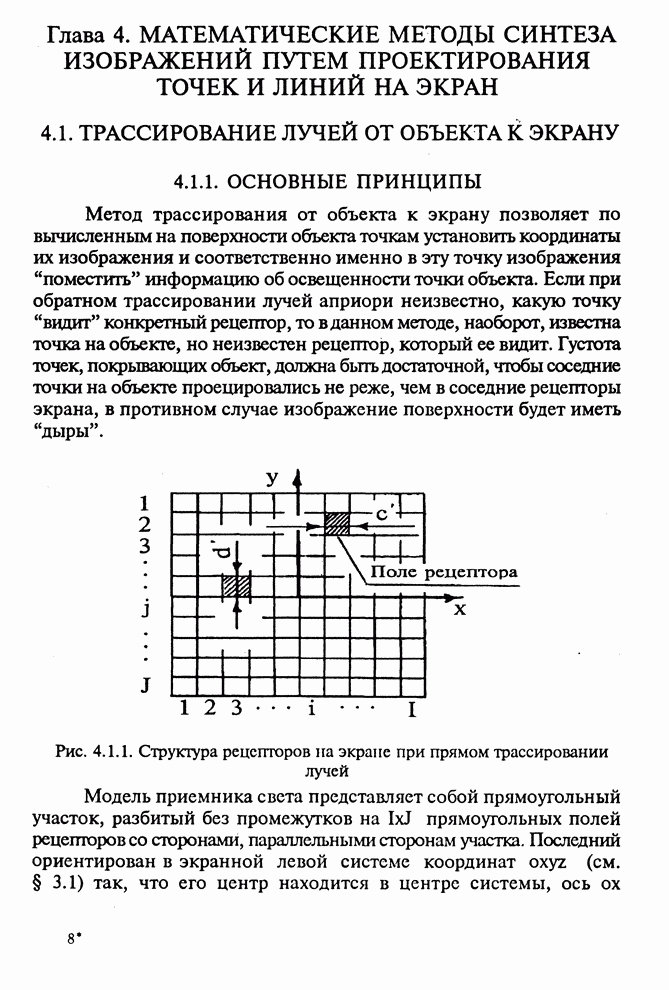
- 4.1.1. ОСНОВНЫЕ ПРИНЦИПЫ
- 4.1.2. МОДЕЛЬ ОБЪЕКТА
- 4.1.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ ТОЧЕК
- 4.1.4. ОПРЕДЕЛЕНИЕ ОСВЕЩЕННОСТИ
- 4.1.5. ИЗОБРАЖЕНИЕ ПОТОЧЕЧНО ОПИСАННЫХ ОБЪЕКТОВ
- 4.2. МЕТОД СКАНИРУЮЩЕЙ СТРОКИ
- 4.2.1. МОДЕЛЬ ОБЪЕКТА ИЗ МНОГОУГОЛЬНИКОВ
- 4.2.2. МОДЕЛЬ ПРИЕМНИКА
- 4.2.3. ИЗОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ НА ЭКРАНЕ
- 4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
- 4.3. АЛГОРИТМ РОБЕРТСА
- 4.3.1. МОДЕЛЬ ОБЪЕКТА
- 4.3.2. СИНТЕЗ ИЗОБРАЖЕНИЯ
- ГЛАВА 5. ОРГАНИЗАЦИЯ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.1. УПРАВЛЕНИЕ ПРОЦЕССОМ СИНТЕЗА
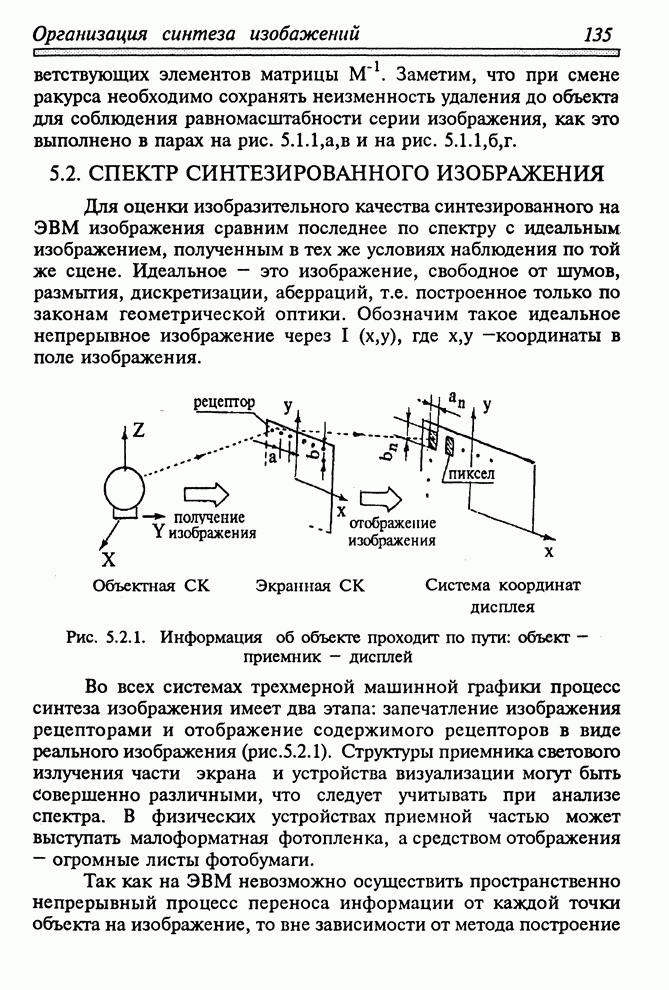
- 5.2. СПЕКТР СИНТЕЗИРОВАННОГО ИЗОБРАЖЕНИЯ
- 5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
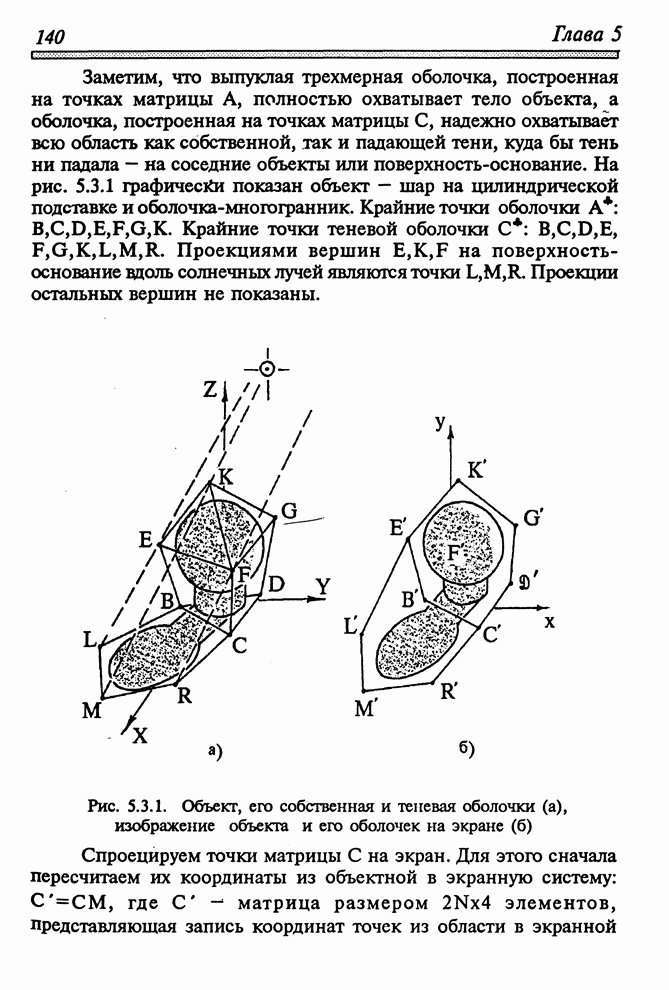
- 5.3.1. МЕТОД ОБОЛОЧЕК
- 5.3.2. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ТРАНСПЬЮТЕРОВ В МАШИННОЙ ГРАФИКЕ
- ГЛАВА 6. ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКИ
- 6.1. АРХИТЕКТУРНОЕ ПРОЕКТИРОВАНИЕ
- 6.2. РАСПОЗНАВАНИЕ ВИДЕООБРАЗОВ
- 6.2.1. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИВНЫМ ЭТАЛОНАМ
- 6.2.2. РАСПОЗНАВАНИЕ ОБРАЗОВ В УСЛОВИЯХ НЕИЗВЕСТНОЙ ОРИЕНТАЦИИ ИХ КОРПУСОВ
- 6.2.3. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИРОВАННЫМ ЭТАЛОНАМ В ПИРАМИДАЛЬНОЙ СТРУКТУРЕ
- 6.2.4. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО ЭТАЛОНАМ, АДАПТИРОВАННЫМ ПО УСЛОВИЯМ НАБЛЮДЕНИЯ И КАЧЕСТВУ
- 6.3. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ В МАШИНОСТРОЕНИИ
- 6.4. ВОССТАНОВЛЕНИЕ ФОРМЫ СКРЫТЫХ ОБЪЕКТОВ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ
- 6.5. ВИДЕОТРЕНАЖЕРЫ И ИМИТАТОРЫ СЛОЖНЫХ СЦЕН
- 6.5.1. ТРЕНАЖЕР ДЛЯ ИМИТАЦИИ ПОЛЕТА НАД РЕАЛЬНОЙ МЕСТНОСТЬЮ
- 6.5.2. КОМПЬЮТЕРНЫЙ ИМИТАТОР ИЗОБРАЖЕНИЙ ОБЛАКОВ
- 6.6. РЕКЛАМА И МУЛЬТИПЛИКАЦИЯ
- ПРИЛОЖЕНИЕ. ОПИСАНИЕ ПРИКЛАДНЫХ ПОДПРОГРАММ
- СПИСОК ЛИТЕРАТУРЫ