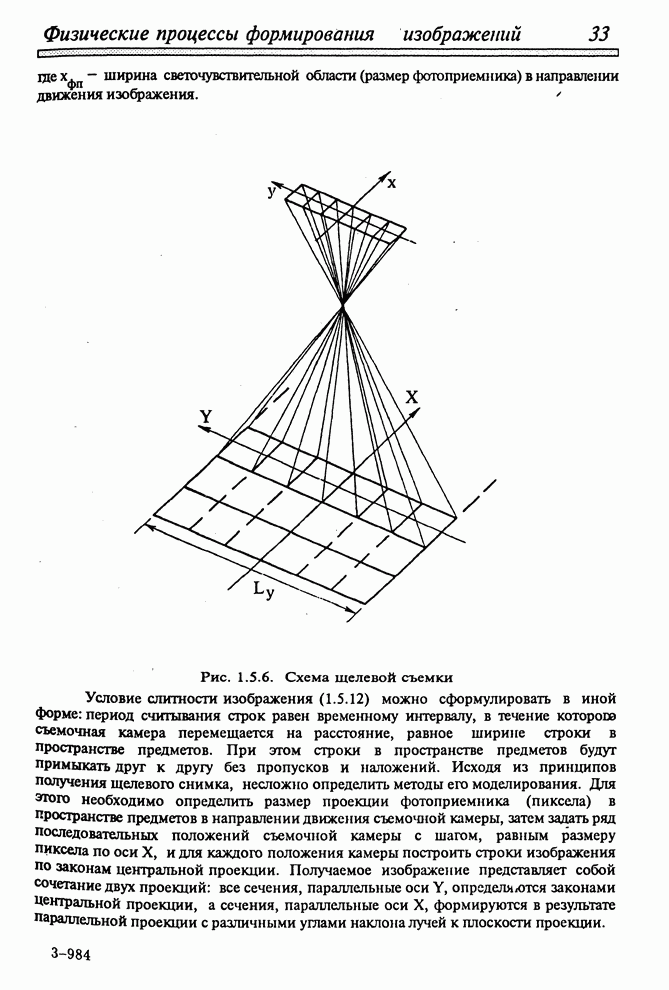
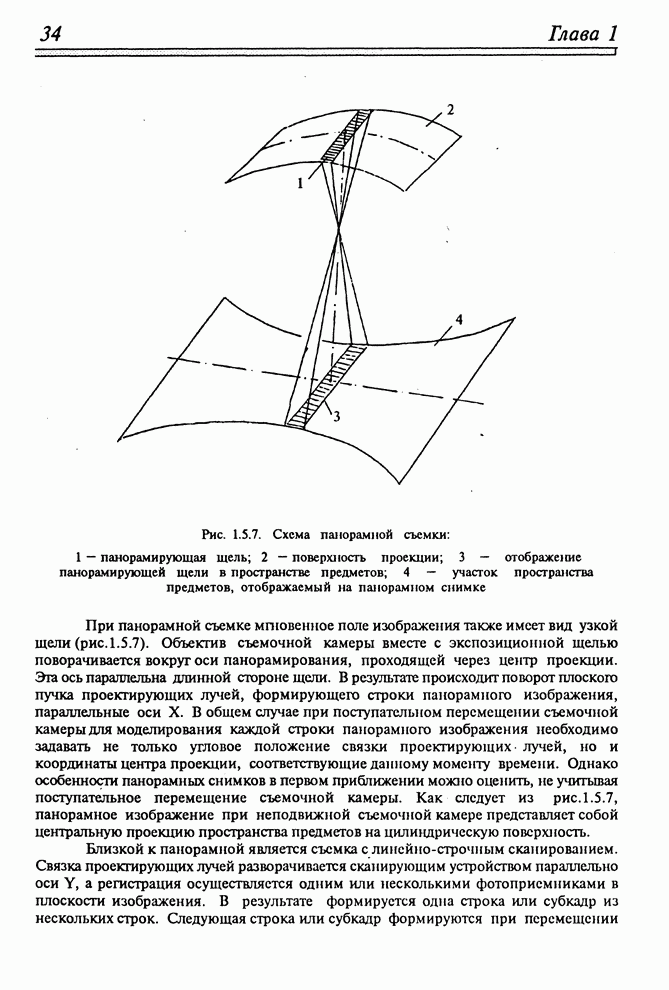
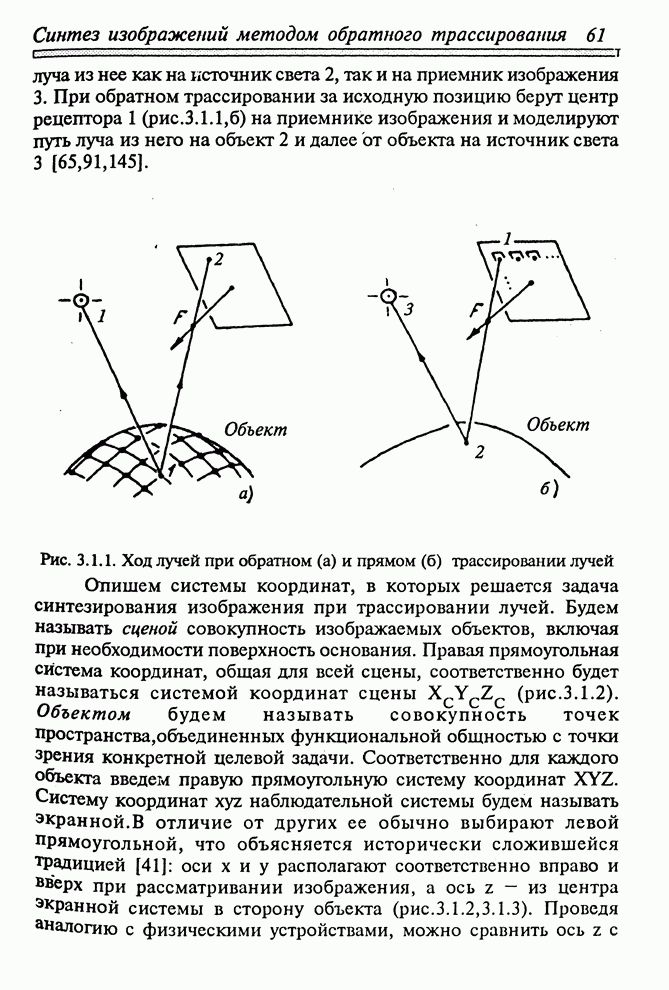
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
Трассирование
лучей является единственным пригодным инструментом изображения зеркальных и
преломляющих поверхностей, что связано с высокой степенью адекватности модели
реальным оптическим процессам. В оптике луч ![]() (рис.3.5.1), исходящий из источника
света и падающий на некоторую поверхность 1, расщепляется на преломленный 1п,
отраженный 1з и множество диффузных 1д. Каждый из этих дочерних лучей при
встрече с очередной поверхностью вновь дробится на новые вторичные лучи,
например, преломленный луч 1п дробится на 2з, 2п и серию лучей 2д. В рецептор
наблюдательной системы попадает лишь малая часть циркулирующих в сцене лучей,
которые также являются преломленными, отраженными и диффузно рассеянными от
участка поверхности, видимого рецептором.
(рис.3.5.1), исходящий из источника
света и падающий на некоторую поверхность 1, расщепляется на преломленный 1п,
отраженный 1з и множество диффузных 1д. Каждый из этих дочерних лучей при
встрече с очередной поверхностью вновь дробится на новые вторичные лучи,
например, преломленный луч 1п дробится на 2з, 2п и серию лучей 2д. В рецептор
наблюдательной системы попадает лишь малая часть циркулирующих в сцене лучей,
которые также являются преломленными, отраженными и диффузно рассеянными от
участка поверхности, видимого рецептором.

Рис. 3.5.1. Расщепление луча, излучаемого источником света
Метод трассирования лучей повторяет природу, но в обратном направлении распространения света – от рецептора к объекту, что вполне корректно из-за известного принципа обратимости хода светового луча [8]. Для изображения поверхностей, обладающих одновременно диффузными, зеркальными и преломляющими свойствами, в модели отслеживаются пути светового луча по направлению рецептор – центр проекции – ближайшая поверхность, вторичные лучи – очередная ближайшая поверхность – очередные вторичные лучи и т.д. К сожалению, диффузное отражение приводит к появлению бесконечного числа лучей [8], оттрассировать которые невозможно. Поэтому диффузное отражение не учитывают вовсе или учитывают только для первой к рецептору поверхности. В последнем случае освещенность рассеянного света вычисляют по закону Ламберта. Вторичные лучи, состоящие из зеркальных и преломленных, вновь пересекаются с ближайшими к нам поверхностями, и каждый вновь расщепляется на два (рис.3.5.2). Таким образом, путь луча представляется ветвящимся деревом, "загущенность кроны" которого пропорциональна числу объектов в сцене. Каждый отщепившийся луч ни в природе, ни в модели не отслеживается бесконечно долго: дальнейшее ветвление трассы луча прекращается, когда луч выходит за пределы сцены, или встречается с непрозрачным диффузно рассеивающим телом, или попадает в источник света либо когда интенсивность луча падает ниже порога чувствительности или, наконец, когда число пересечений луча становится слишком большим как для памяти машины, так и для счета.

Рис. 3.5.2. Расщепление луча по пути от рецептора к источнику света
Многократно зеркально отражающиеся и преломляющиеся лучи на каждом очередном шаге ветвления процесса требуют определения своего пространственного положения. Ниже приводятся правила определения направления преломленного луча и угла зеркальности.
Определение
вектора преломленного луча. Для определения трассы луча после прохождения
границы двух сред с разными показателями преломления ![]() и
и ![]() (рис.3.5.3) необходимо
определить вектор
(рис.3.5.3) необходимо
определить вектор ![]() по известному единичному вектору
внешней нормали
по известному единичному вектору
внешней нормали ![]() и
направлению единичного вектора
и
направлению единичного вектора ![]() на источник падающего луча. В
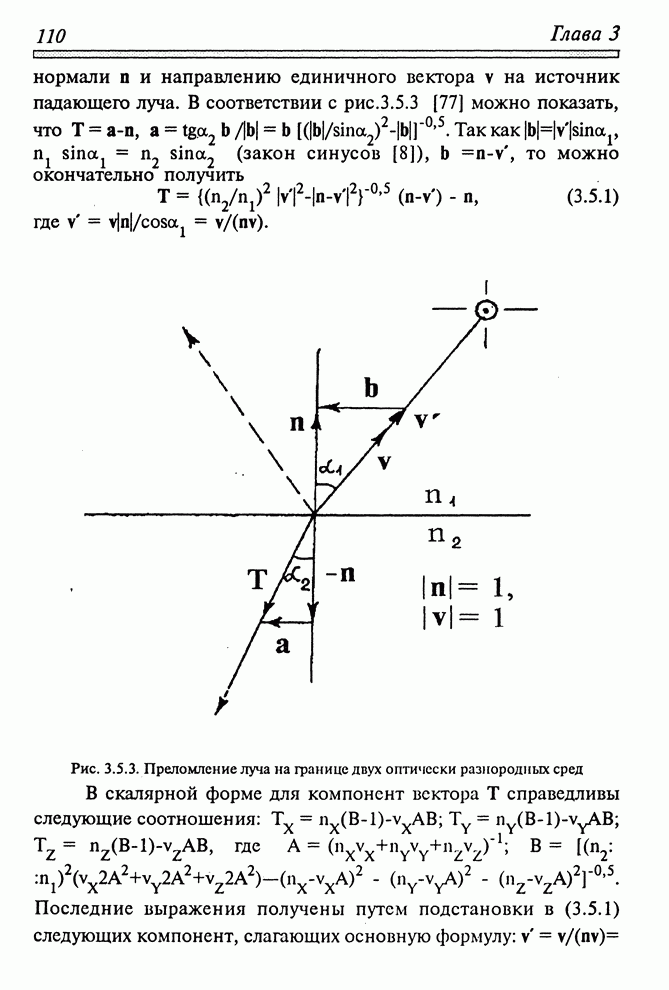
соответствии с рис.3.5.3 [77] можно показать, что
на источник падающего луча. В
соответствии с рис.3.5.3 [77] можно показать, что ![]() ,
, ![]() . Так как
. Так как ![]() ,
, ![]() (закон синусов [8]),
(закон синусов [8]), ![]() , то можно
окончательно получить
, то можно
окончательно получить
![]() , (3.5.1)
, (3.5.1)
где
![]() .
.

Рис. 3.5.3. Преломление луча на границе двух оптически разнородных сред
В
скалярной форме для компонент вектора ![]() справедливы следующие соотношения:
справедливы следующие соотношения: ![]() ;
; ![]() ;
; ![]() , где
, где
![]() ;
;
![]() . Последние выражения
получены путем подстановки в (3.5.1) следующих компонент, слагающих основную
формулу:
. Последние выражения
получены путем подстановки в (3.5.1) следующих компонент, слагающих основную
формулу:

![]() ,
,
тогда
![]() ,
,
![]() .
.
Окончательно получаем, вводя обозначение:

тогда
![]() ;
;
![]() ;
; ![]() .
.
Вычисление
вектора и угла зеркальности. Углом зеркальности ![]() будем называть угол между текущим
лучом визирования и направлением распространения зеркально отраженного луча.
Угол зеркальности показывает, на сколько в угловой мере отклонен
светочувствительный приемник от положения зеркального луча наибольшей мощности.
Световая энергия убывает с увеличением
будем называть угол между текущим
лучом визирования и направлением распространения зеркально отраженного луча.
Угол зеркальности показывает, на сколько в угловой мере отклонен
светочувствительный приемник от положения зеркального луча наибольшей мощности.
Световая энергия убывает с увеличением ![]() по закону, близкому к зависимости
по закону, близкому к зависимости ![]()
![]() .
.
В
машинной графике определение освещенности рецепторов от зеркально отражающих
поверхностей производится посредством вычисления значения ![]() . Существует несколько
способов такого расчета [77,63]. Приведем один из вычислительно простых.
Обозначим:
. Существует несколько
способов такого расчета [77,63]. Приведем один из вычислительно простых.
Обозначим: ![]() –
центр рецептора в объектной СК;
–
центр рецептора в объектной СК; ![]() – точка, видимая из этого рецептора
на поверхности;
– точка, видимая из этого рецептора
на поверхности; ![]() – внешняя нормаль к поверхности в
видимой точке;
– внешняя нормаль к поверхности в
видимой точке; ![]() –
положение источника света. Введем векторы:
–
положение источника света. Введем векторы: ![]() ,
, ![]() . На рис. 3.5.4 показаны данные
векторы в плоскости, проходящей через падающий луч
. На рис. 3.5.4 показаны данные
векторы в плоскости, проходящей через падающий луч ![]() и нормаль
и нормаль ![]() . Из законов
геометрической оптики известно, что отраженный луч
. Из законов
геометрической оптики известно, что отраженный луч ![]() также лежит в этой
плоскости и может быть вычислен по правилу [61]:
также лежит в этой
плоскости и может быть вычислен по правилу [61]: ![]() . Раскрывая векторную форму, можно
получить
. Раскрывая векторную форму, можно
получить

где ![]() .
.

Рис. 3.5.4. Положение векторов при зеркальном отражении
Угол
![]() между
зеркально отраженным лучом
между
зеркально отраженным лучом ![]() и направлением на текущий рецептор
и направлением на текущий рецептор ![]() определяется по
формуле
определяется по
формуле ![]() или
в скалярной форме
или
в скалярной форме

где
![]() .
.
В программе BETTA (см. приложение) приведены реализация алгоритма вычисления косинуса зеркального угла по известным направлениям: нормали, на источник и на приемник света.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА 1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ И ИХ МОДЕЛИРОВАНИЕ
- 1.1. МОДЕЛИ В МАШИННОЙ ГРАФИКЕ
- 1.2. ИСТОЧНИКИ ОСВЕЩЕНИЯ
- 1.2.1. ИСТОЧНИКИ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
- 1.2.2. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИСТОЧНИКОВ ПРОСТОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
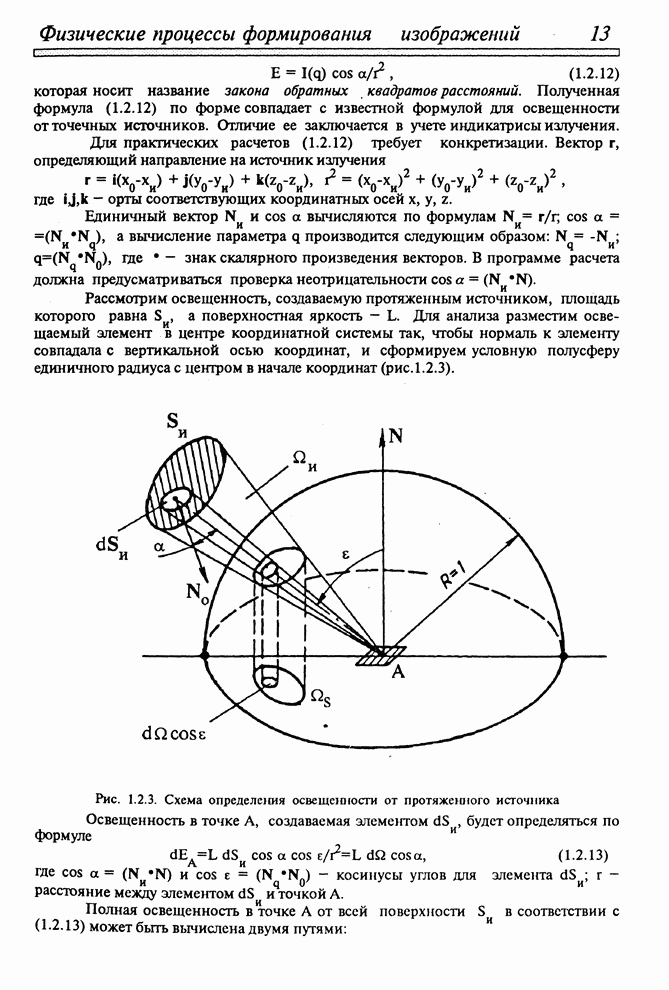
- 1.2.3. ОСВЕЩЕННОСТЬ, СОЗДАВАЕМАЯ ТОЧЕЧНЫМИ И ПРОТЯЖЕННЫМИ ИСТОЧНИКАМИ
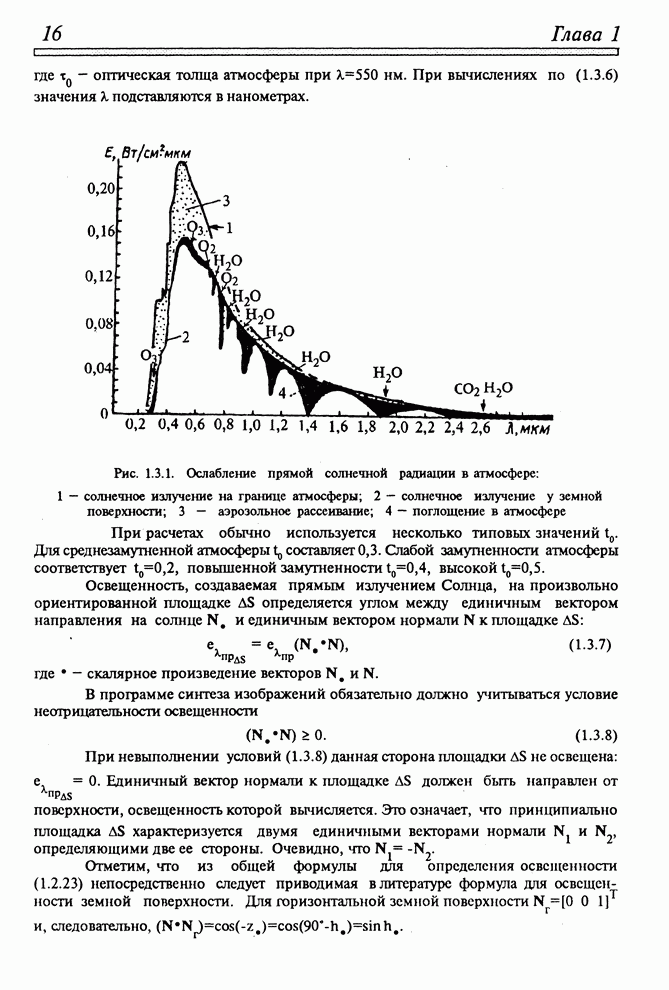
- 1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
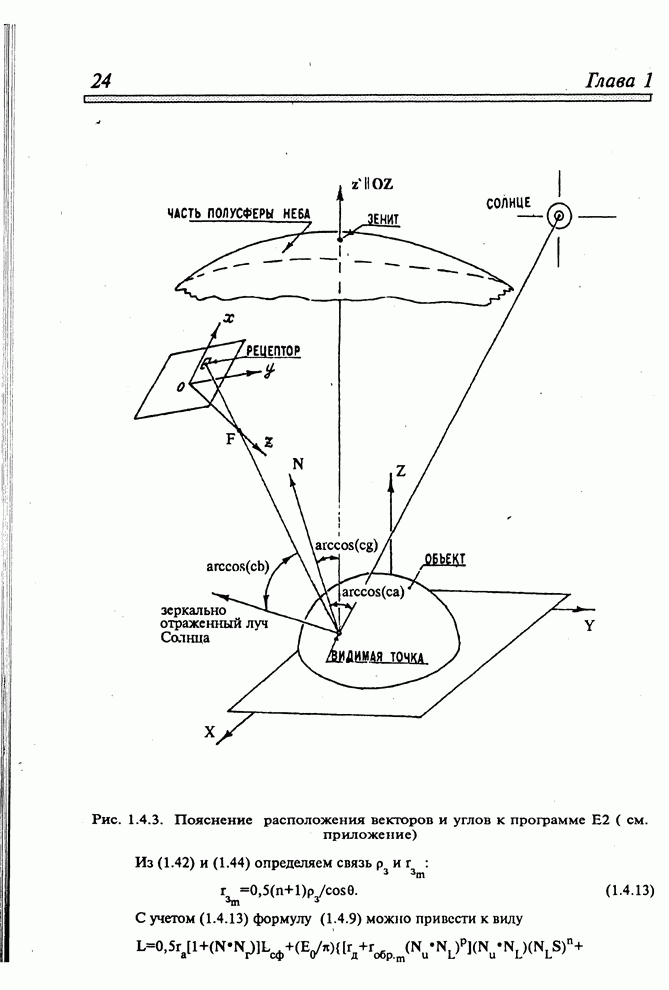
- 1.4. МОДЕЛИРОВАНИЕ ОТРАЖЕННОГО ИЗЛУЧЕНИЯ ОБЪЕКТОВ
- 1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
- 1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
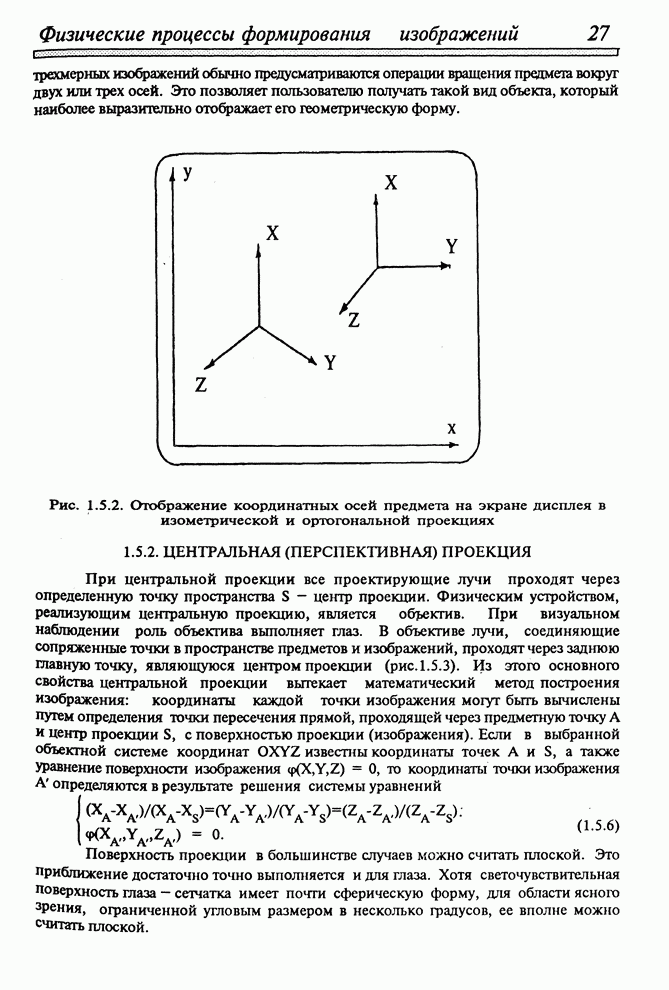
- 1.5.2. ЦЕНТРАЛЬНАЯ (ПЕРСПЕКТИВНАЯ) ПРОЕКЦИЯ
- 1.5.3. ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ С ИСПОЛЬЗОВАНИЕМ ОДНОРОДНЫХ КООРДИНАТ
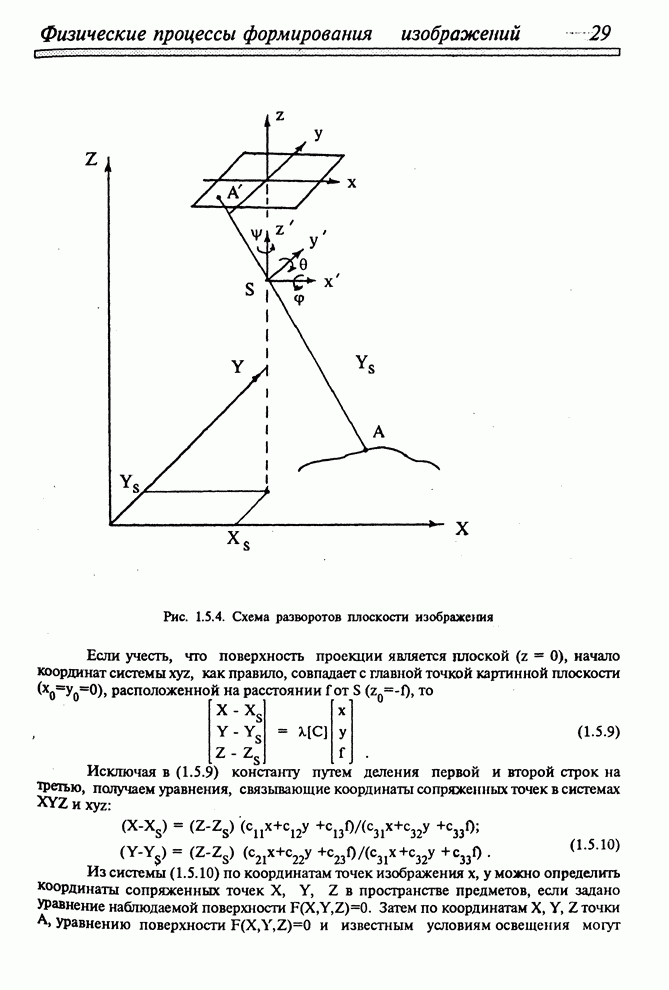
- 1.5.4. ПРОЕКЦИИ ПРИ РАЗЛИЧНЫХ ВИДАХ СЪЕМКИ
- 1.6. ТЕКСТУРА ИЗОБРАЖЕНИЯ
- 1.7. МОДЕЛИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.8. СИНТЕЗ ИЗОБРАЖЕНИЙ С УЧЕТОМ СПЕЦИФИКИ ИХ ФОРМИРОВАНИЯ В РЕАЛЬНЫХ УСЛОВИЯХ
- ГЛАВА 2. ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
- 2.1. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
- 2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
- 2.3. МОДЕЛИ ОБЪЕКТОВ И ИХ КЛАССИФИКАЦИЯ
- ГЛАВА 3. СИНТЕЗ ИЗОБРАЖЕНИЙ МЕТОДОМ ОБРАТНОГО ТРАССИРОВАНИЯ ЛУЧЕЙ
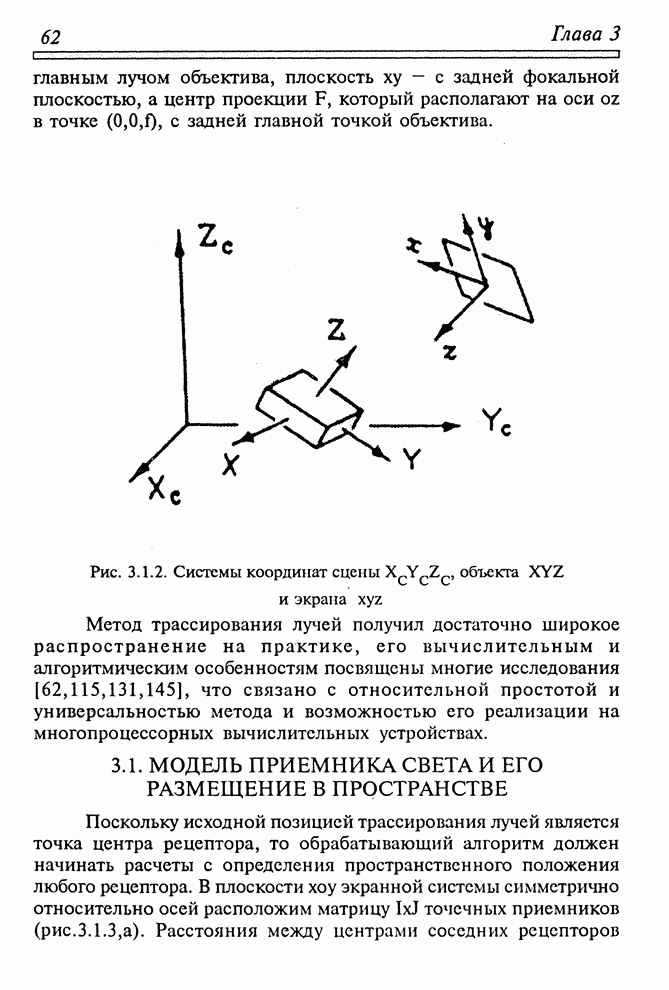
- 3.1. МОДЕЛЬ ПРИЕМНИКА СВЕТА И ЕГО РАЗМЕЩЕНИЕ В ПРОСТРАНСТВЕ
- 3.2. МОДЕЛЬ ОБЪЕКТА
- 3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
- 3.2.2. ПРОСТРАНСТВЕННЫЕ КОМБИНАЦИИ ПРИМИТИВОВ
- 3.2.3. ФОРМАЛИЗОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
- 3.2.4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ОБЪЕКТА
- 3.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ И ЗАТЕНЕННЫХ ТОЧЕК
- 3.3.1. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С ПРИМИТИВОМ
- 3.3.2. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С КОМБИНАЦИЕЙ ПРИМИТИВОВ
- 3.3.3. ОПРЕДЕЛЕНИЕ ЗАТЕНЕННЫХ ТОЧЕК
- 3.4. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРИМИТИВОВ МЕТОДОМ ТРАССИРОВАНИЯ ЛУЧЕЙ
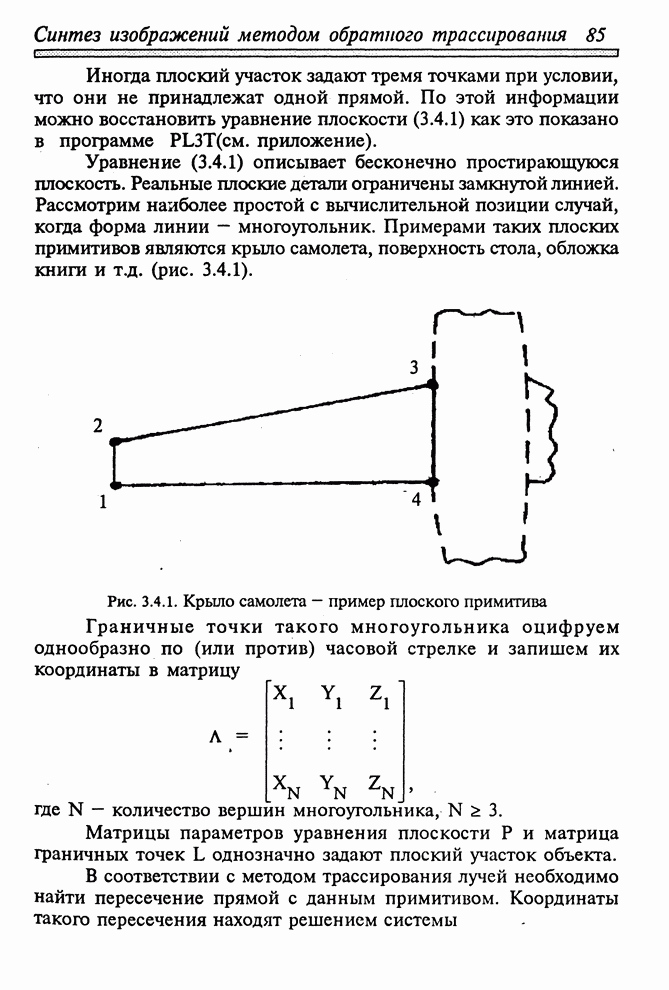
- 3.4.1. ПЛОСКИЕ МНОГОУГОЛЬНИКИ
- 3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
- 3.4.3. КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
- 3.4.4. БИКУБИЧЕСКИЕ ПОВЕРХНОСТИ
- 3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- 3.6. ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ ОСВЕЩЕННОСТИ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ИЗОБРАЖЕНИЙ ПУТЕМ ПРОЕКТИРОВАНИЯ ТОЧЕК И ЛИНИЙ НА ЭКРАН
- 4.1. ТРАССИРОВАНИЕ ЛУЧЕЙ ОТ ОБЪЕКТА К ЭКРАНУ
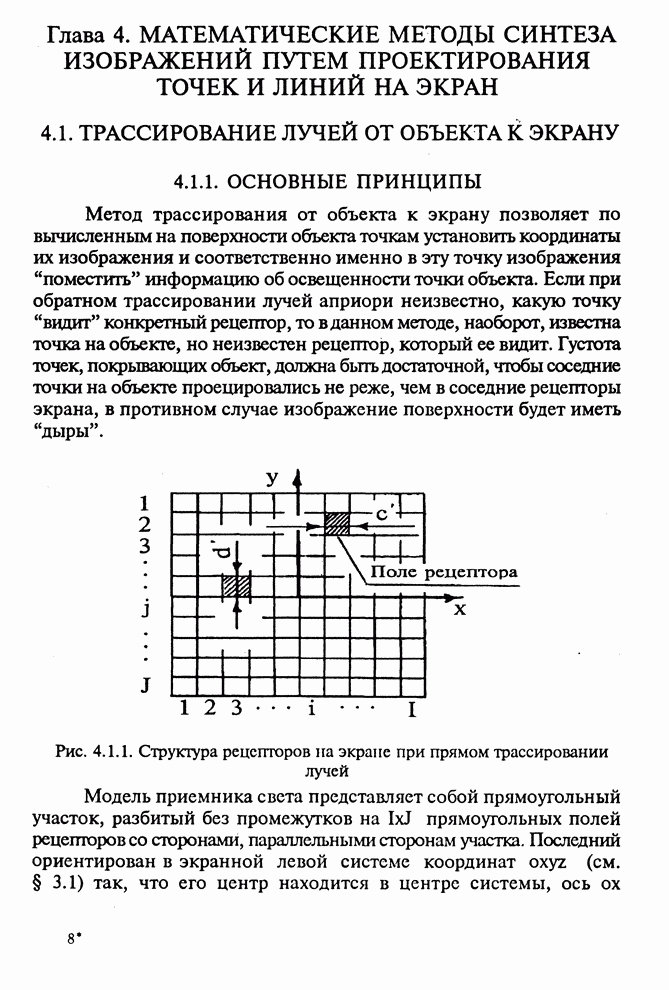
- 4.1.1. ОСНОВНЫЕ ПРИНЦИПЫ
- 4.1.2. МОДЕЛЬ ОБЪЕКТА
- 4.1.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ ТОЧЕК
- 4.1.4. ОПРЕДЕЛЕНИЕ ОСВЕЩЕННОСТИ
- 4.1.5. ИЗОБРАЖЕНИЕ ПОТОЧЕЧНО ОПИСАННЫХ ОБЪЕКТОВ
- 4.2. МЕТОД СКАНИРУЮЩЕЙ СТРОКИ
- 4.2.1. МОДЕЛЬ ОБЪЕКТА ИЗ МНОГОУГОЛЬНИКОВ
- 4.2.2. МОДЕЛЬ ПРИЕМНИКА
- 4.2.3. ИЗОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ НА ЭКРАНЕ
- 4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
- 4.3. АЛГОРИТМ РОБЕРТСА
- 4.3.1. МОДЕЛЬ ОБЪЕКТА
- 4.3.2. СИНТЕЗ ИЗОБРАЖЕНИЯ
- ГЛАВА 5. ОРГАНИЗАЦИЯ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.1. УПРАВЛЕНИЕ ПРОЦЕССОМ СИНТЕЗА
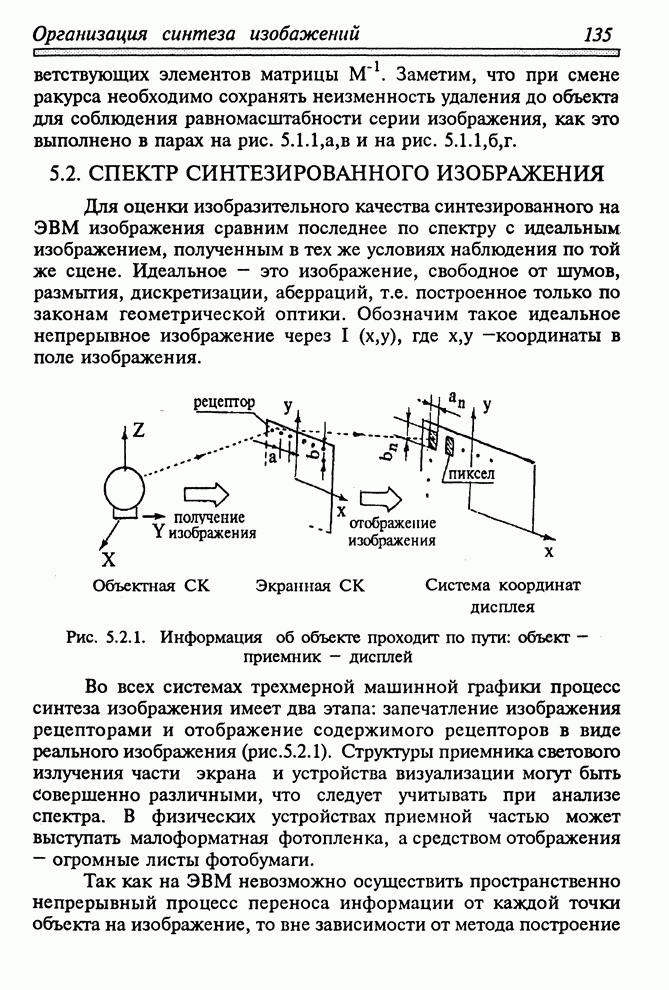
- 5.2. СПЕКТР СИНТЕЗИРОВАННОГО ИЗОБРАЖЕНИЯ
- 5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
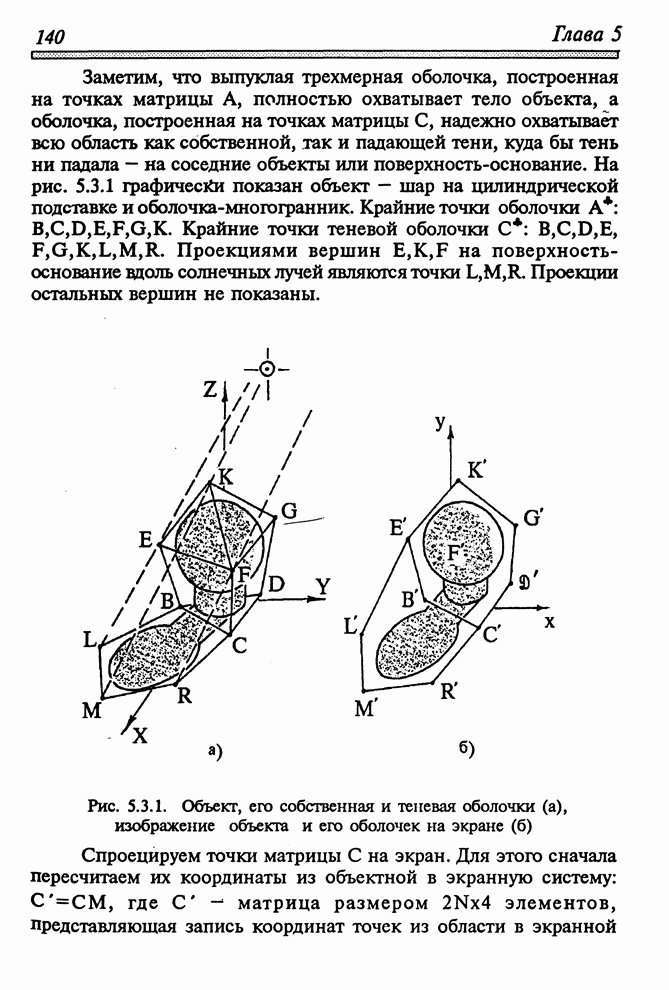
- 5.3.1. МЕТОД ОБОЛОЧЕК
- 5.3.2. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ТРАНСПЬЮТЕРОВ В МАШИННОЙ ГРАФИКЕ
- ГЛАВА 6. ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКИ
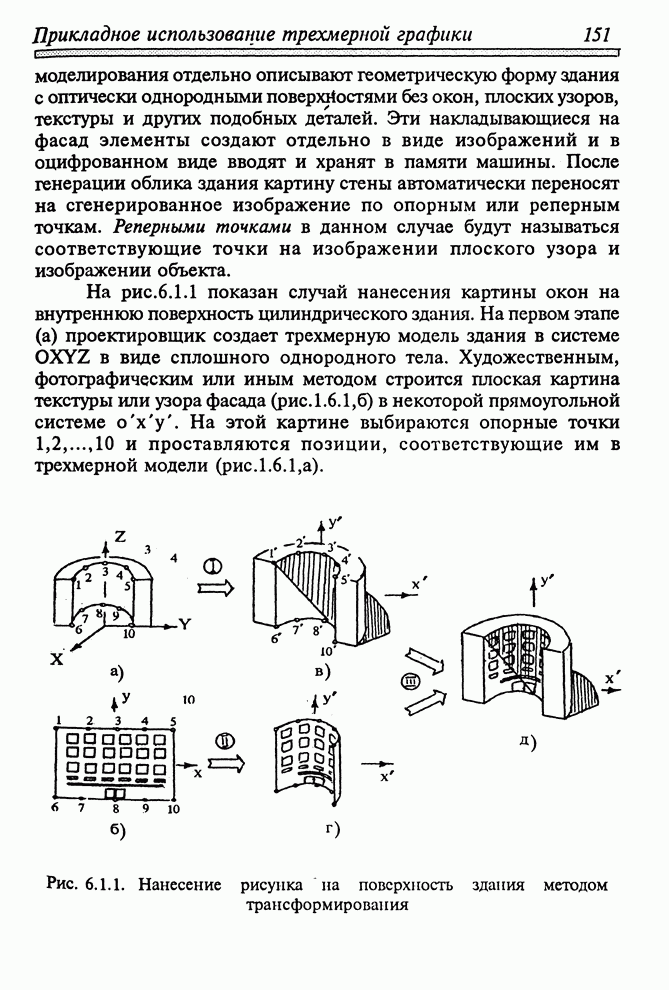
- 6.1. АРХИТЕКТУРНОЕ ПРОЕКТИРОВАНИЕ
- 6.2. РАСПОЗНАВАНИЕ ВИДЕООБРАЗОВ
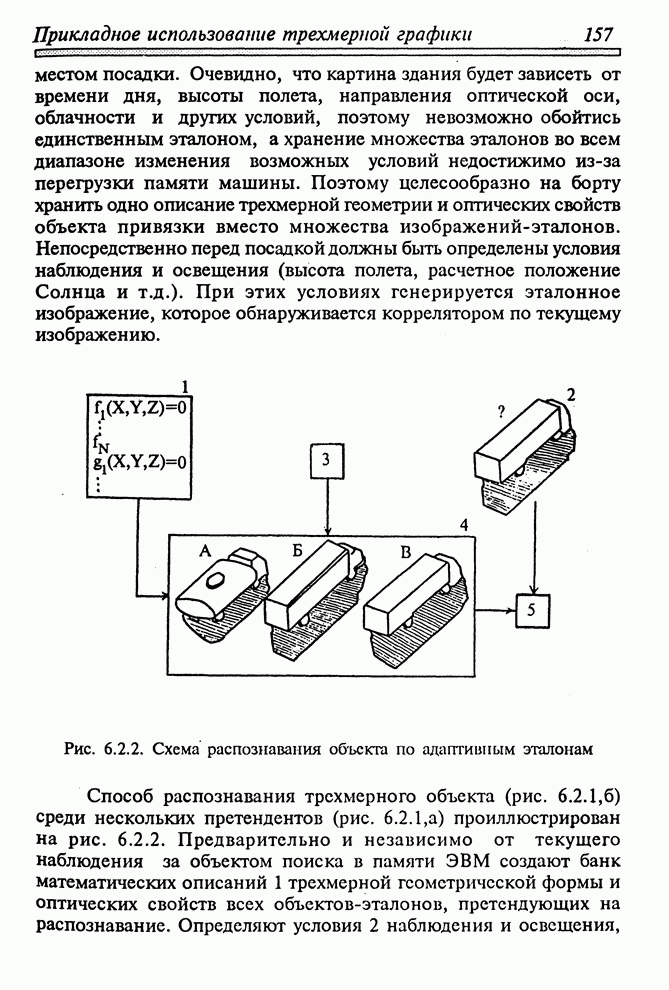
- 6.2.1. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИВНЫМ ЭТАЛОНАМ
- 6.2.2. РАСПОЗНАВАНИЕ ОБРАЗОВ В УСЛОВИЯХ НЕИЗВЕСТНОЙ ОРИЕНТАЦИИ ИХ КОРПУСОВ
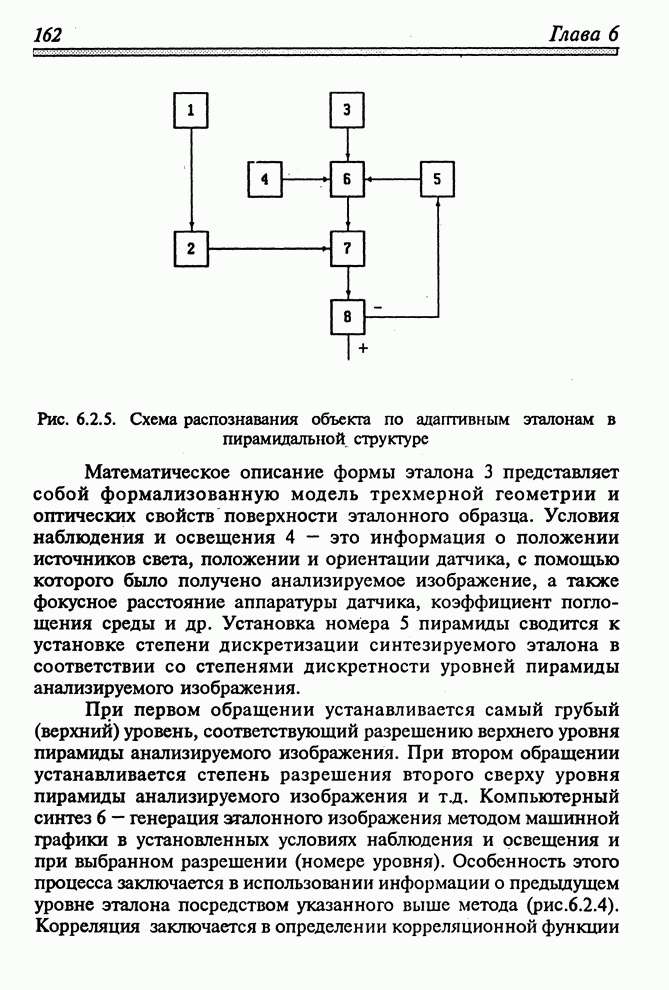
- 6.2.3. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИРОВАННЫМ ЭТАЛОНАМ В ПИРАМИДАЛЬНОЙ СТРУКТУРЕ
- 6.2.4. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО ЭТАЛОНАМ, АДАПТИРОВАННЫМ ПО УСЛОВИЯМ НАБЛЮДЕНИЯ И КАЧЕСТВУ
- 6.3. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ В МАШИНОСТРОЕНИИ
- 6.4. ВОССТАНОВЛЕНИЕ ФОРМЫ СКРЫТЫХ ОБЪЕКТОВ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ
- 6.5. ВИДЕОТРЕНАЖЕРЫ И ИМИТАТОРЫ СЛОЖНЫХ СЦЕН
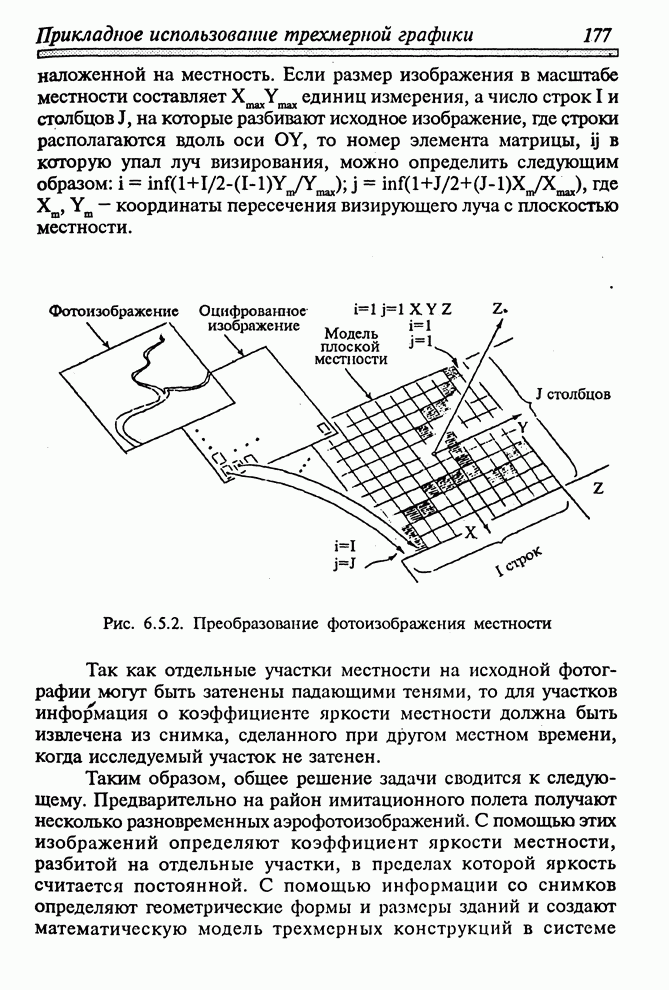
- 6.5.1. ТРЕНАЖЕР ДЛЯ ИМИТАЦИИ ПОЛЕТА НАД РЕАЛЬНОЙ МЕСТНОСТЬЮ
- 6.5.2. КОМПЬЮТЕРНЫЙ ИМИТАТОР ИЗОБРАЖЕНИЙ ОБЛАКОВ
- 6.6. РЕКЛАМА И МУЛЬТИПЛИКАЦИЯ
- ПРИЛОЖЕНИЕ. ОПИСАНИЕ ПРИКЛАДНЫХ ПОДПРОГРАММ
- СПИСОК ЛИТЕРАТУРЫ