| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
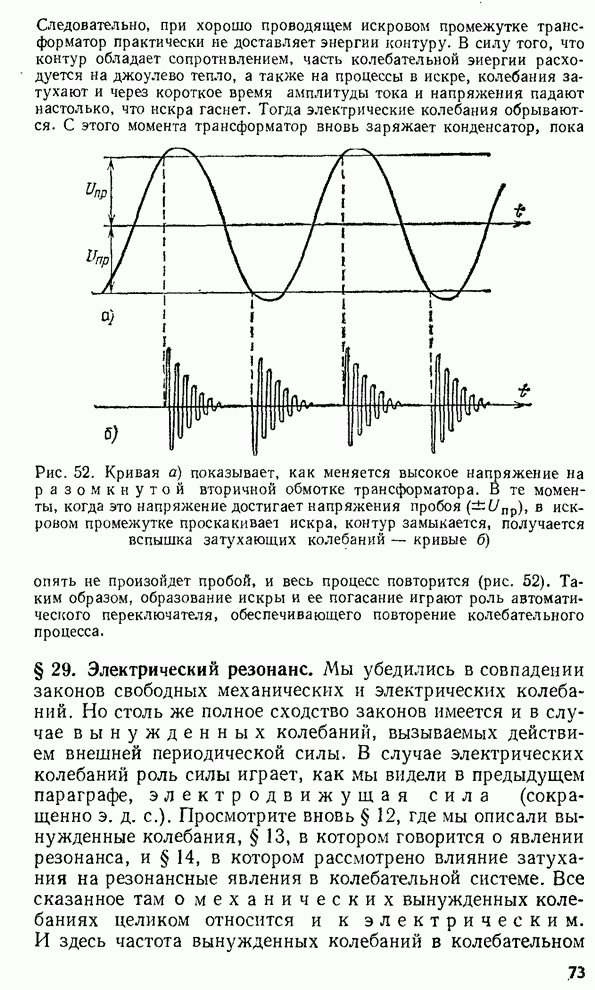
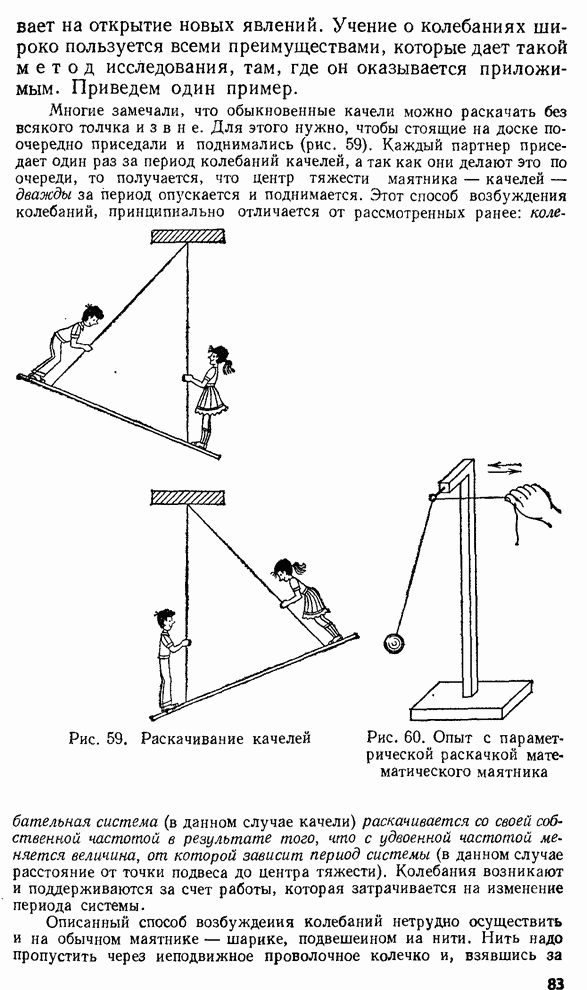
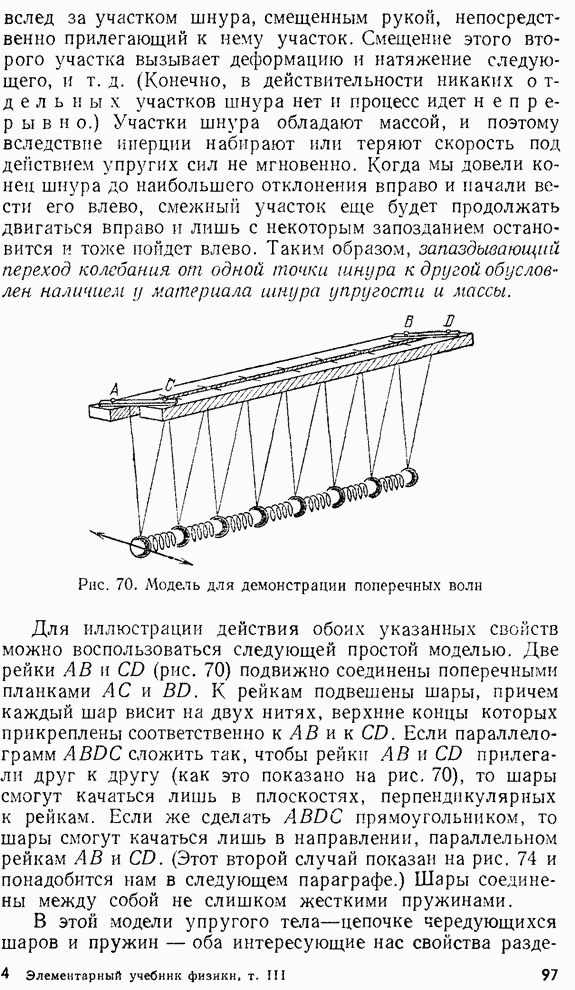
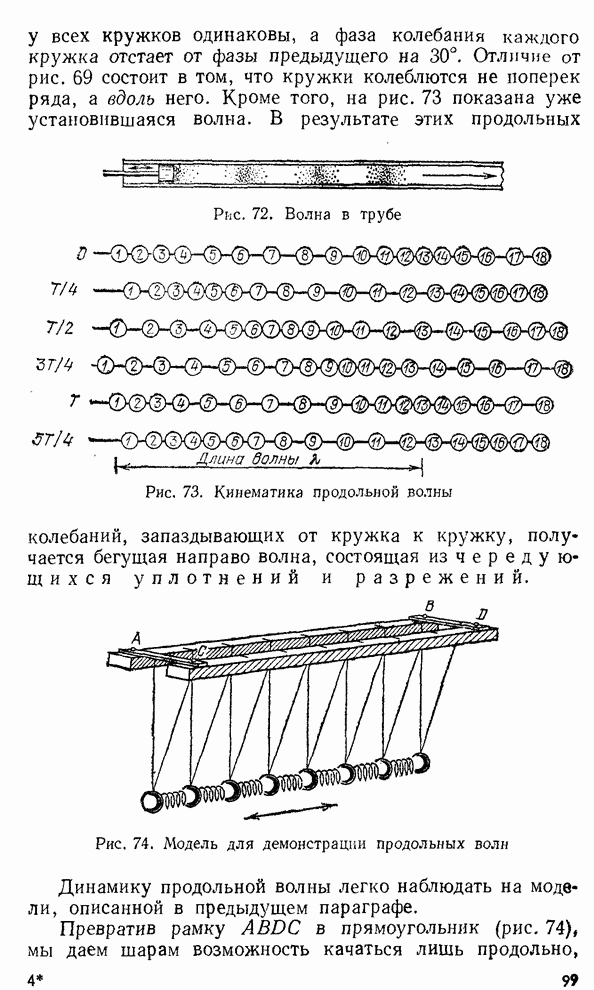
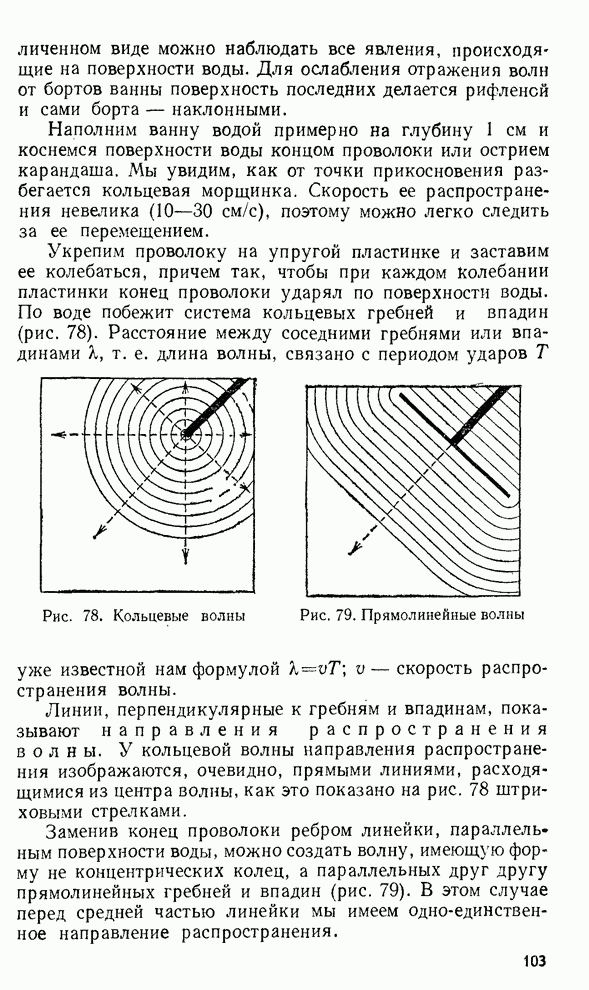
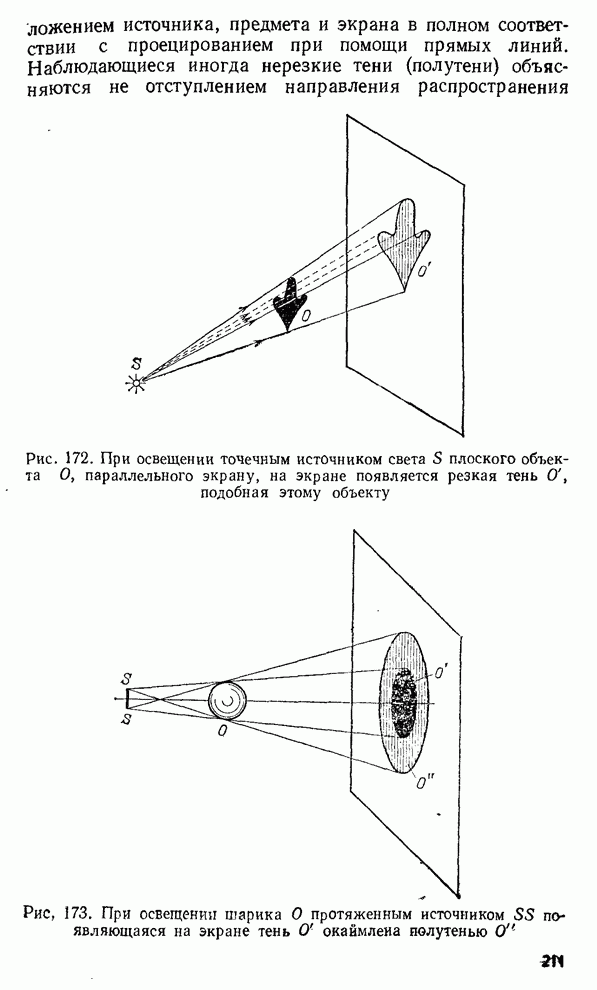
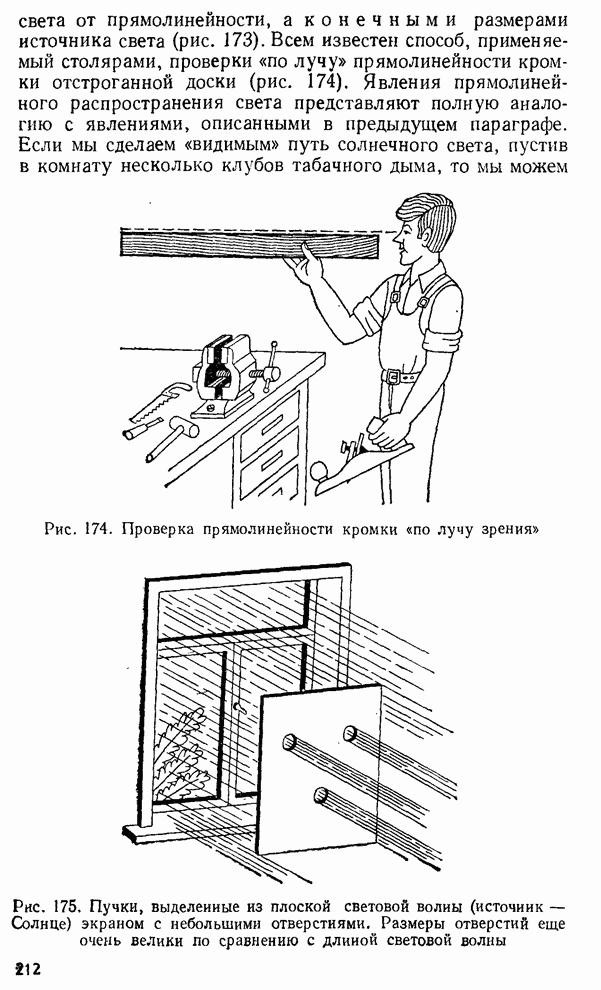
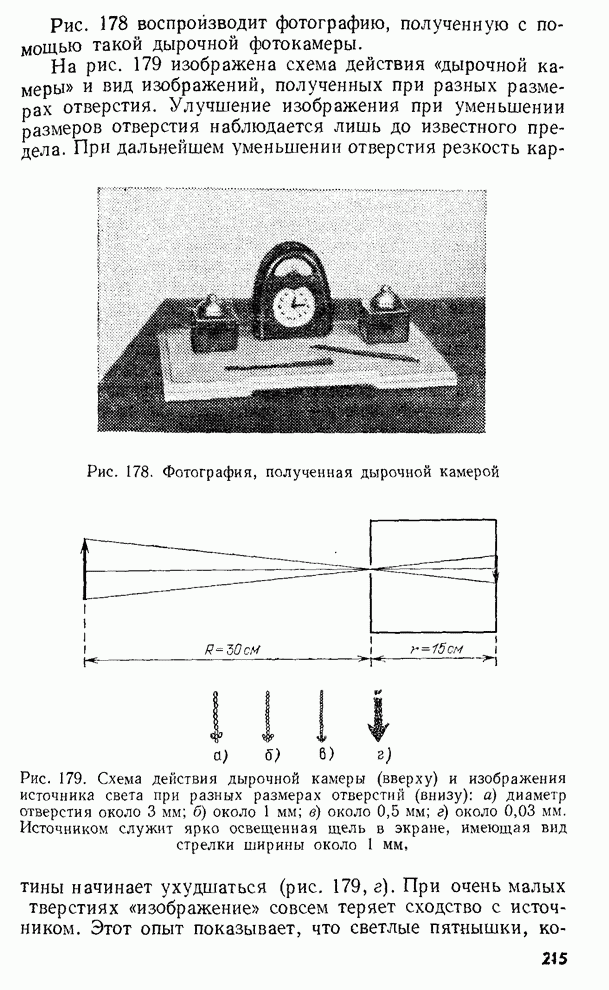
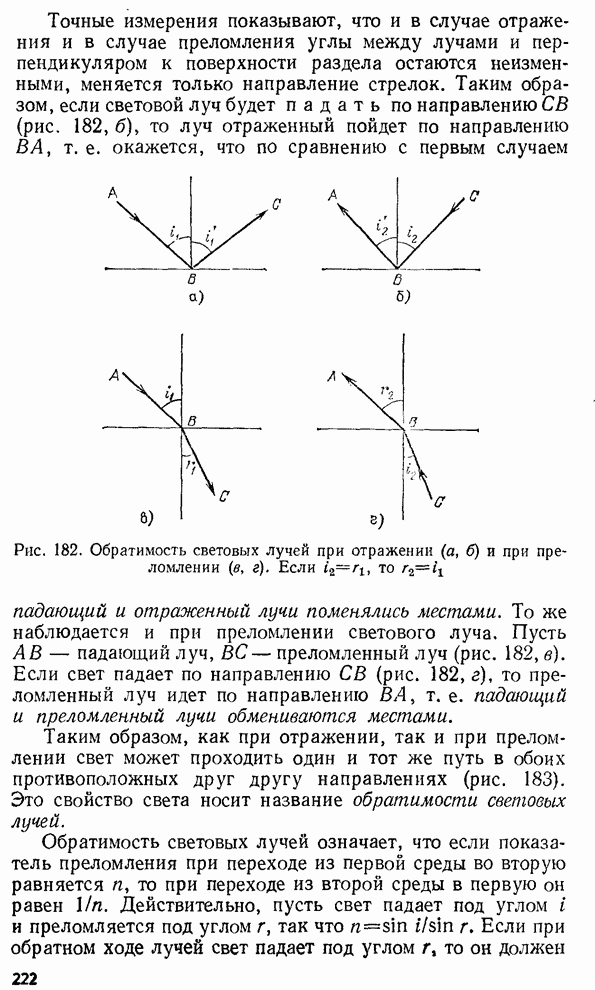
§ 11. Влияние трения. Затухание
Рассматривая свободные колебания маятника, шарика с пружинами, диска и т.д., мы отвлекались до сих пор от явления, которое неизбежно имеет место в каждом из описанных выше опытов и вследствие которого колебания не являются строго периодическими, а именно: амплитуда колебаний с каждым размахом делается все меньше и меньше, так что рано или поздно колебания прекращаются. Это явление называется затуханием колебаний.
Причина затухания заключается в том, что во всякой колебательной системе, кроме возвращающей силы, всегда действуют разного рода силы трения, сопротивление воздуха и т. п., которые тормозят движение. При каждом размахе часть полной колебательной энергии (потенциальной и кинетической) расходуется на работу против сил трения. В конечном счете на эту работу уходит весь запас энергии, сообщенный колебательной системе первоначально (см. том I, §§ 102—104).
Затрата энергии на работу против сил трения может иметь весьма разнообразный характер. Возможно трение между твердыми поверхностями, например трение призмы коромысла весов об опору. Энергия может затрачиваться на преодоление сопротивления среды (воздух, вода) (см. том 1, § 64, 65). Кроме того, колеблющиеся тела приводят в движение окружающую среду, отдавая на это при каждом колебании часть своей энергии (см. том 1, § 67). Наконец, сами деформации пружин, пластинок, проволок и т. д. тоже происходят с некоторой потерей энергии на внутреннее трение в материале, из которого эти тела сделаны (см. том I, § 202).
Незатухающие свободные колебания, которые происходили бы в колебательной системе в отсутствие трения, называются собственными колебаниями системы.
Отвлекаясь до сих пор от сил трения, мы рассматривали, таким образом, именно эти идеальные, строго периодические собственные колебания, чем сознательно упрощали себе изучение колебаний за счет несколько неточного их описания. Такое упрощение является, однако, возможным и пригодным только потому, что у многих колебательных систем трение и вызываемое им затухание действительно малы: система успевает совершить очень большое число колебаний, прежде чем их амплитуда уменьшится заметным образом. При изучении таких систем с достаточно малым затуханием можно для очень многих вопросов совсем не учитывать этого затухания и считать свободные колебания системы строго периодическими, т. е. рассматривать собственные колебания, как это мы и делали выше.
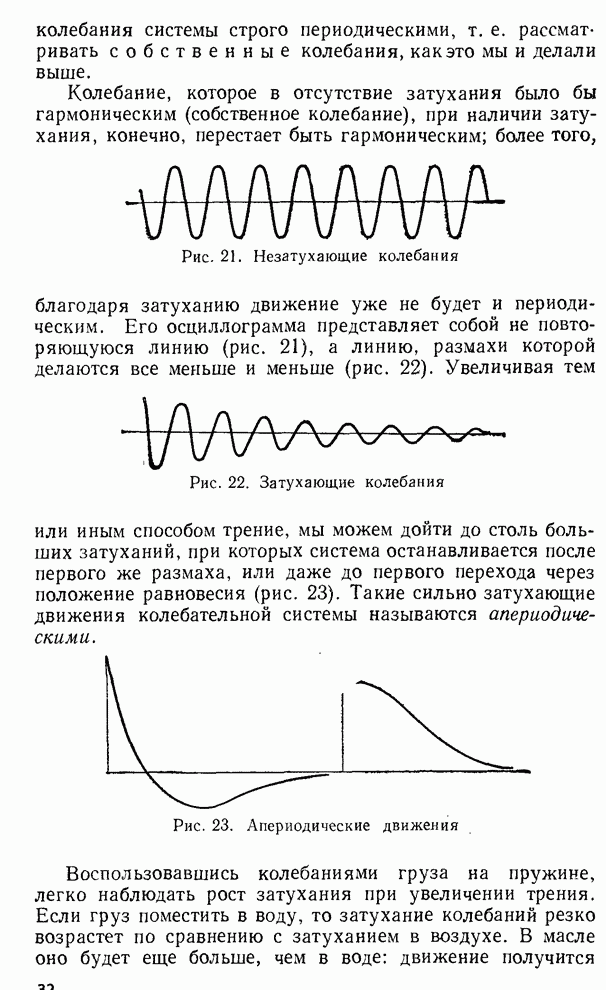
Колебание, которое в отсутствие затухания было бы гармоническим (собственное колебание), при наличии затухания, конечно, перестает быть гармоническим; более того, благодаря затуханию движение уже не будет и периодическим. Его осциллограмма представляет собой не повторяющуюся линию (рис. 21), а линию, размахи которой делаются все меньше и меньше (рис. 22). Увеличивая тем или иным способом трение, мы можем дойти до столь больших затуханий, при которых система останавливается после первого же размаха, или даже до первого перехода через положение равновесия (рис. 23). Такие сильно затухающие движения колебательной системы называются апериодическими.

Рис. 21. Незатухающие колебания

Рис. 22. Затухающие колебания

Рис. 23. Апериодические движения
Воспользовавшись колебаниями груза на пружине, легко наблюдать рост затухания при увеличении трения. Если груз поместить в воду, то затухание колебаний резко возрастет по сравнению с затуханием в воздухе. В масле оно будет еще больше, чем в воде: движение получится апериодическим или близким к апериодическому. Чем менее обтекаемой является форма груза (при той же массе), тем больше затухание, так как тем больше энергии отдается на приведение в движение окружающей среды (см. том I, § 190).
На практике встречается надобность как в уменьшении, так и в увеличении затухания. Например, ось балансира часов кончается остриями, которые упираются в хорошо отполированные конические подпятники из твердого камня (агата, рубина). Это делается для того, чтобы балансир имел малое затухание. Наоборот, во многих измерительных приборах желательно, чтобы подвижная часть устройства устанавливалась при измерениях быстро, не совершая большого числа колебаний, или даже апериодически. С этой целью применяются различные демпферы – устройства, увеличивающие трение и вообще потерю энергии. Используются пластинки, прикрепленные к подвижной части прибора и погруженные в масло; применяются электромагнитные демпферы (рис. 24), основанные на торможении, которое испытывает движущаяся между полюсами электромагнита металлическая пластинка благодаря вихревым электрическим токам (см. II, § 143) и т.д.

Рис. 24. Маятник, демпфированный вихревым электрическим током.
Трение влияет не только на амплитуду колебаний (затухание), но и на продолжительность размахов. Мы не можем называть эту продолжительность периодом, так как затухающее колебание — движение непериодическое. Однако если затухание невелико, то условно можно говорить о периоде, понимая под этим время между двумя прохождениями в одном и том же направлении через положение равновесия. С увеличением трения период удлиняется.
Характерной чертой колебательных систем является то, что влияние небольшого трения на период колебаний гораздо меньше, чем на амплитуду. Это обстоятельство сыграло огромную роль в усовершенствовании часов. Еще Галилей высказал мысль об использовании в часах маятника, т. е. колебательной системы.
Первые часы с маятником построил голландский физик и математик Христиан Гюйгенс (1629—1695) в 1673г. Этот год можно считать датой рождения современных часов, вытеснивших затем все предшествующие часовые устройства. Произошло это в большой мере потому, что ход часов с маятником очень мало чувствителен к изменениям такого зависящего от многих обстоятельств фактора, как трение. У прежних же безмаятниковых часов (например, водяных — см. том I, §8) скорость хода зависела от трения очень сильно.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к первому изданию
- Раздел первый. Колебания и волны
- Глава I. Основные понятия. Механические колебания
- § 1. Периодические движения. Период
- § 2. Колебательные системы
- § 3. Маятник; кинематика его колебаний
- § 4. Колебания камертона
- § 5. Гармоническое колебание. Частота
- § 6. Сдвиг фаз
- § 7. Динамика колебаний маятника
- § 8. Формула периода математического маятника
- § 9. Упругие колебания
- § 10. Крутильные колебания
- § 11. Влияние трения. Затухание
- § 12. Вынужденные колебания
- § 13. Резонанс
- § 14. Влияние трения на резонансные явления
- § 15. Примеры резонансных явлений
- § 16. Резонансные явления при действии негармонической периодической силы
- § 17. Форма периодических колебаний и ее связь с гармоническим составом этих колебаний
- Глава II. Звуковые колебания
- § 18. Звуковые колебания
- § 19. Предмет акустики
- § 20. Музыкальный тон. Громкость и высота тона
- § 21. Тембр
- § 22. Акустический резонанс
- § 23. Запись и воспроизведение звука
- § 24. Анализ и синтез звука
- § 25. Шумы
- Глава III. Электрические колебания
- § 26. Электрические колебания. Методы их наблюдения
- § 27. Колебательный контур
- § 28. Аналогия с механическими колебаниями. Формула Томсона
- § 29. Электрический резонанс
- § 30. Незатухающие колебания. Автоколебательные системы
- § 31. Ламповый генератор электрических колебаний
- Глава IV. Волновые явления
- § 32. Учение о колебаниях
- § 33. Волновые явления
- § 34. Скорость распространения волн
- § 35. Радиолокация, гидроакустическая локация и звукометрия
- § 36. Поперечные волны в шнуре
- § 37. Продольные волны в столбе воздуха
- § 38. Волны на поверхности жидкости
- § 39. Перенос энергии волнами
- § 40. Отражение волн
- § 41. Дифракция
- § 42. Направленное излучение
- Глава V. Интерференция волн
- § 43. Наложение волн
- § 44. Интерференция волн
- § 45. Условия образования максимумов и минимумов
- § 46. Интерференция звуковых волн
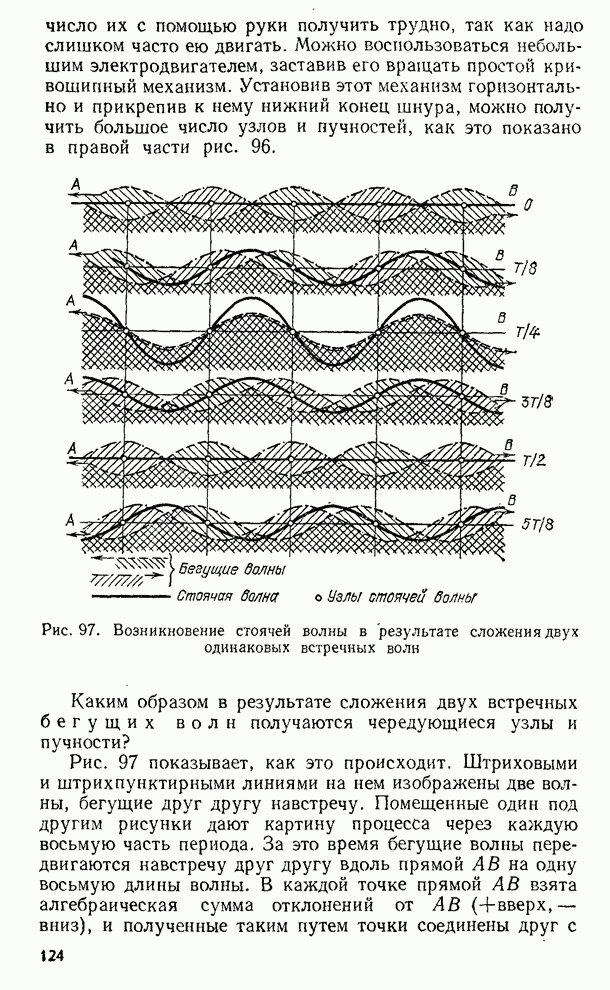
- § 47. Стоячие волны
- § 48. Колебания упругих тел как стоячие волны
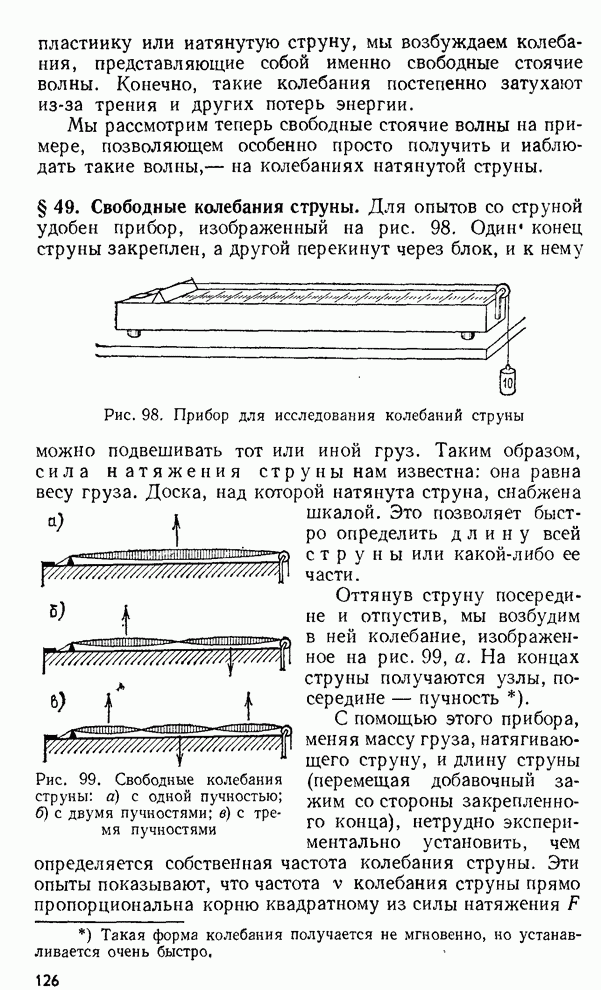
- § 49. Свободные колебания струны
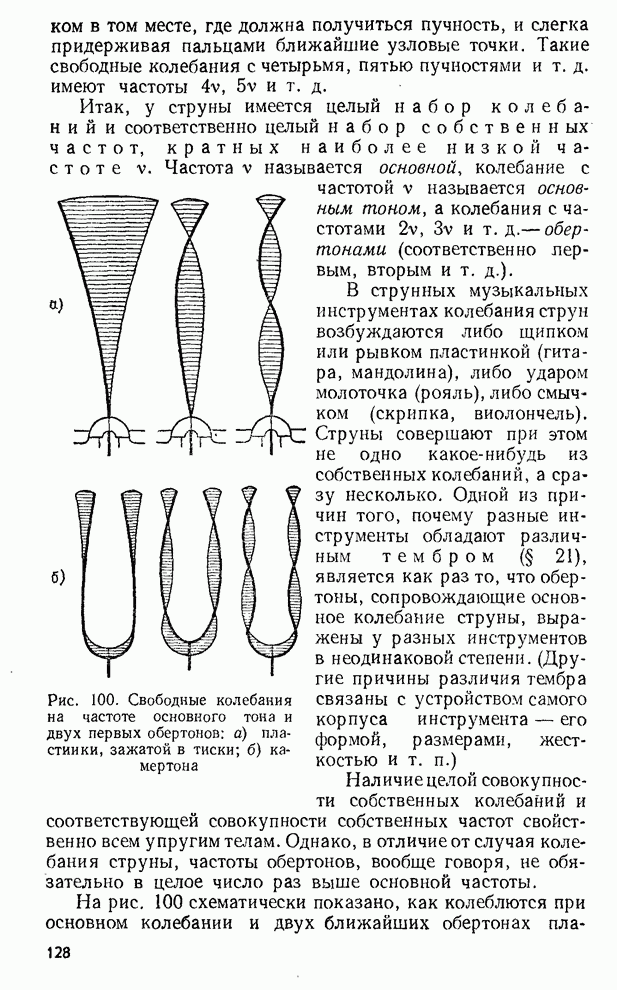
- § 50. Стоячие волны в пластинках и других протяженных телах
- § 51. Резонанс при наличии многих собственных частот
- § 52. Условия хорошего излучения звука
- § 53. Бинауральный эффект. Звукопеленгация
- Глава VI. Электромагнитные волны
- § 54. Электромагнитные волны
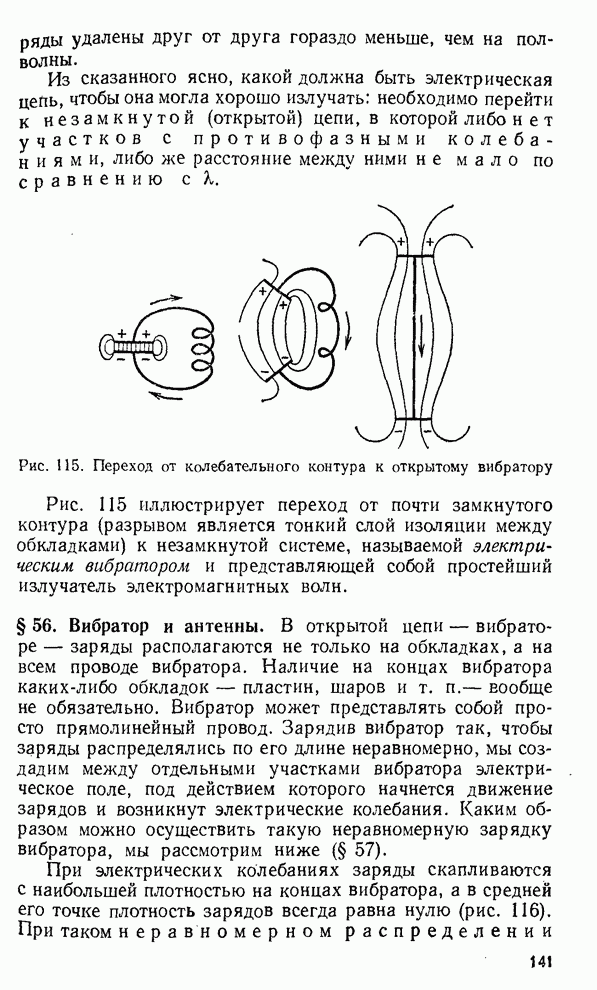
- § 55. Условия хорошего излучения электромагнитных волн
- § 56. Вибратор и антенны
- § 57. Опыты Герца по получению и исследованию электромагнитных волн. Опыты Лебедева
- § 58. Электромагнитная теория света. Шкала электромагнитных волн
- § 59 Опыты с электромагнитными волнами
- § 60. Изобретение радио Поповым
- § 61. Современная радиосвязь
- § 62. Другие применения радио
- § 63. Распространение радиоволн
- § 64. Заключительные замечания
- Раздел второй. Геометрическая оптика
- Глава VII. Общая характеристика световых явлений
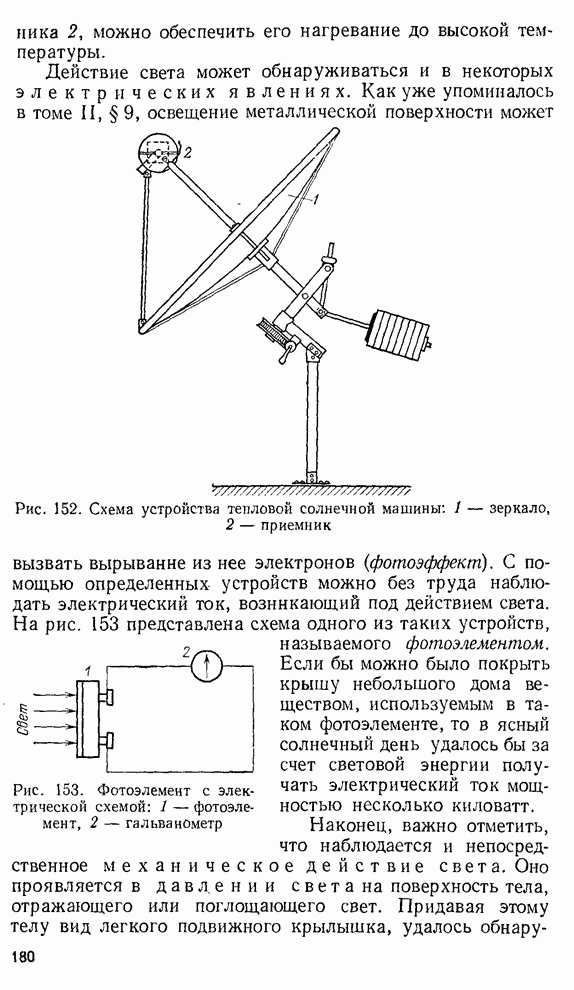
- § 65. Разнообразные действия света
- § 66. Интерференция света. Цвета тонких пленок
- § 67. Краткие сведения из истории оптики
- Глава VIII. Фотометрия и светотехника
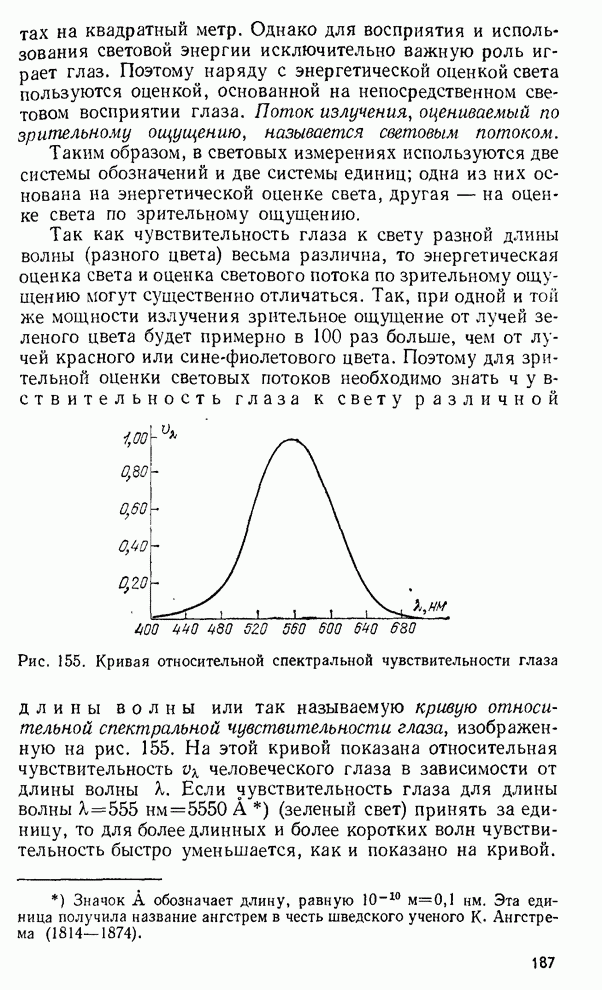
- § 68. Энергия излучения. Световой поток
- § 69. Точечные источники света
- § 70. Сила света и освещенность
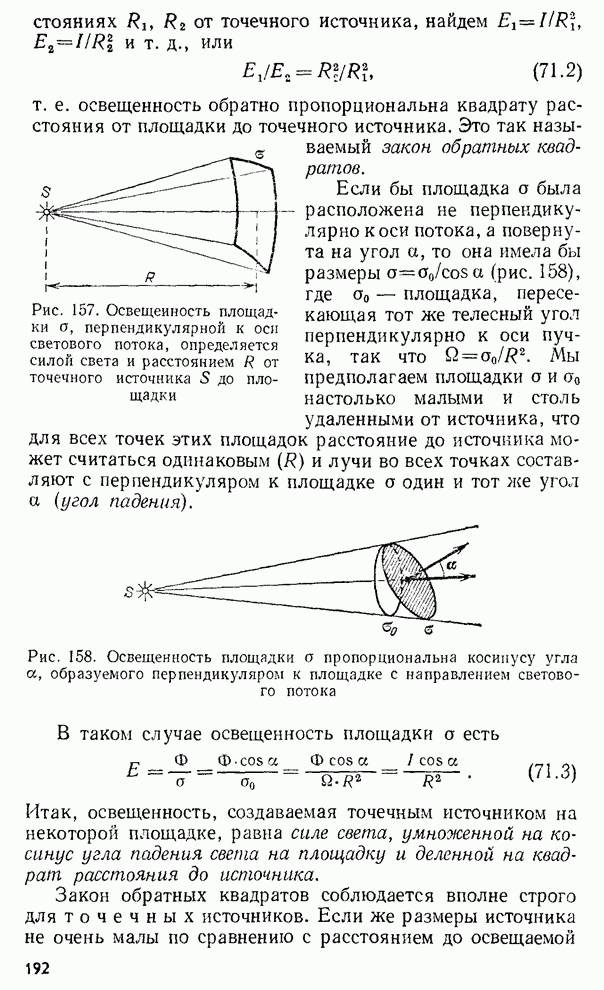
- § 71. Законы освещенности
- § 72. Единицы световых величин
- § 73. Яркость источников
- § 74. Задачи светотехники
- § 75. Приспособления для концентрации светового потока
- § 76. Отражающие и рассеивающие тела
- § 77. Яркость освещенных поверхностей
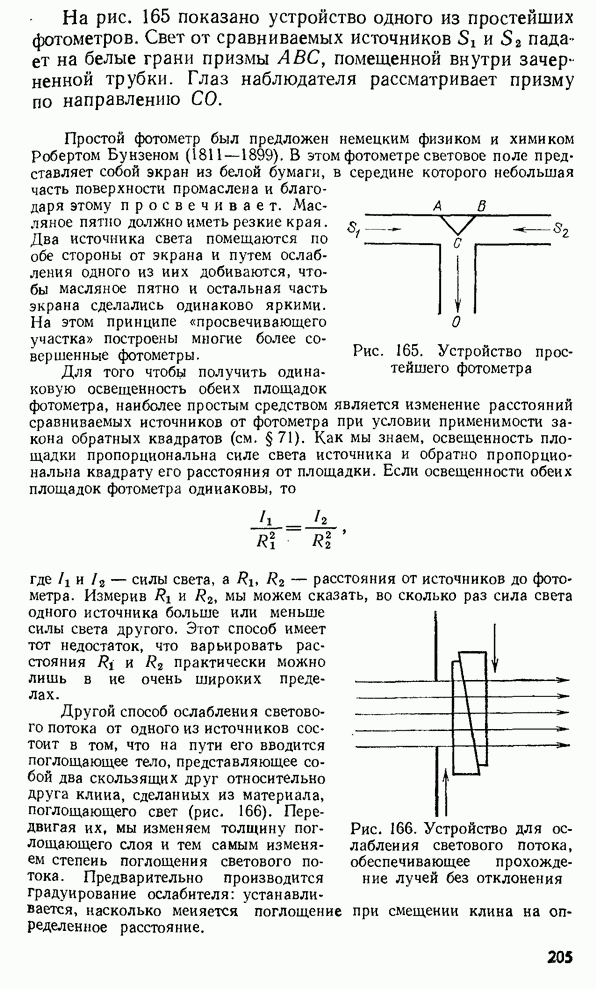
- § 78. Световые измерения и измерительные приборы
- Глава IX. Основные законы геометрической оптики
- § 79. Прямолинейное распространение волн
- § 80. Прямолинейное распространение света и световые лучи
- § 81. Законы отражения и преломления света
- § 82. Обратимость световых лучей
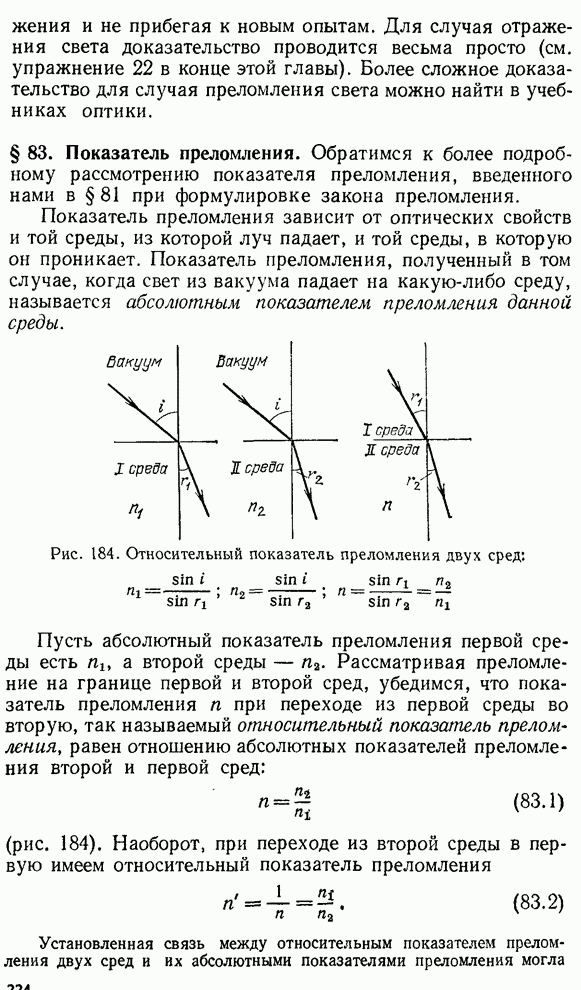
- § 83. Показатель преломления
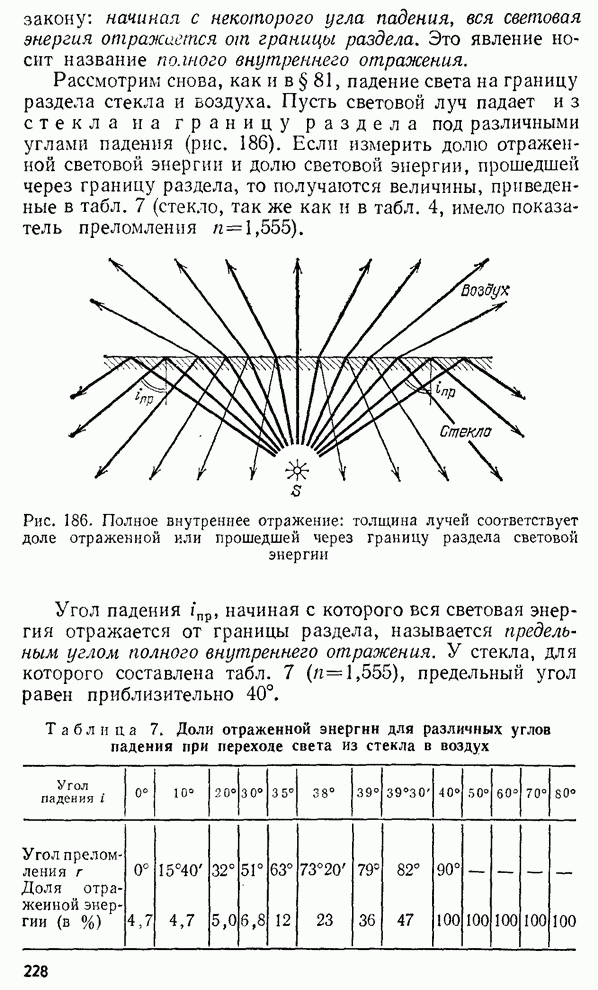
- § 84. Полное внутреннее отражение
- § 85. Преломление в плоскопараллельной пластинке
- § 86. Преломление в призме
- Глава X. Применение отражения и преломления света для получения изображений
- § 87. Источник света и его изображение
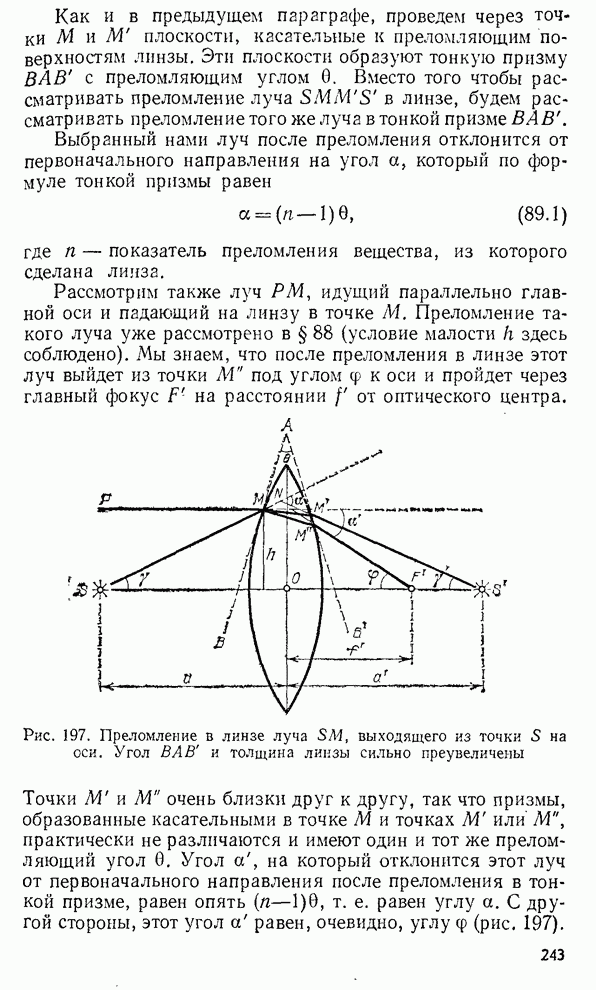
- § 88. Преломление в линзе
- § 89. Изображение в линзе точек, лежащих на главной оптической оси. Формула линзы.
- § 90. Применения формулы тонкой линзы. Действительные и мнимые изображения.
- § 91. Изображение точечного источника и протяженного объекта в плоском зеркале. Изображение точечного источника в сферическом зеркале
- § 92. Фокус и фокусное расстояние сферического зеркала
- § 93. Связь между положениями источника и его изображения на главной оси сферического зеркала
- § 94. Способы изготовления линз и зеркал
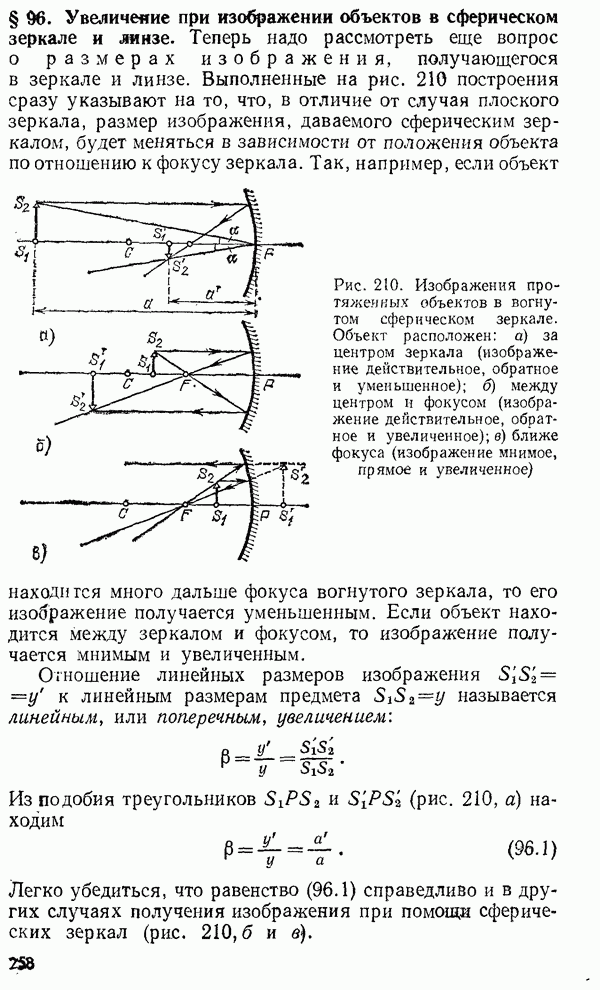
- § 95. Изображение протяженных объектов в сферическом зеркале и линзе
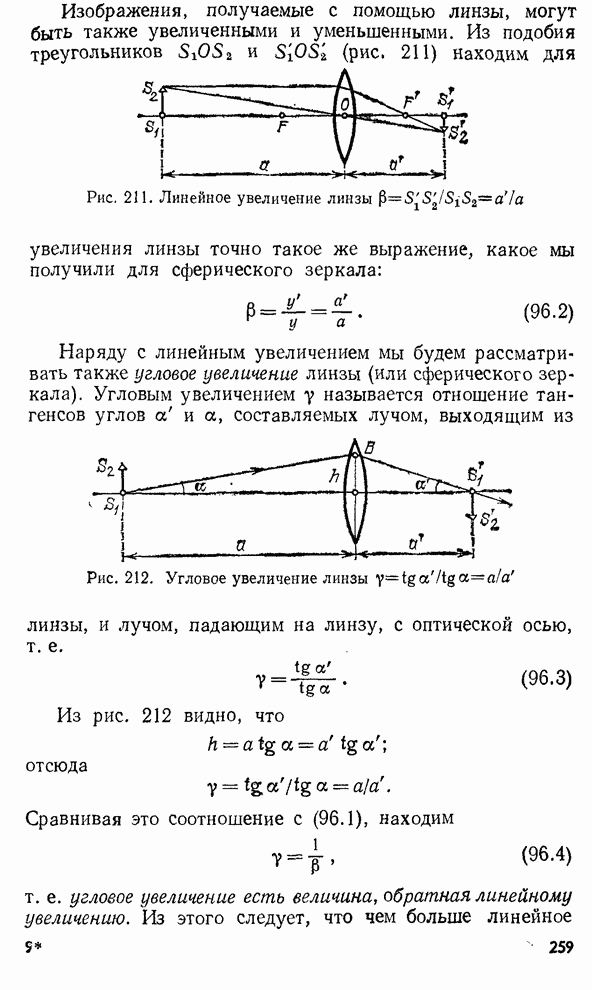
- § 96. Увеличение при изображении объектов в сферическом зеркале и линзе
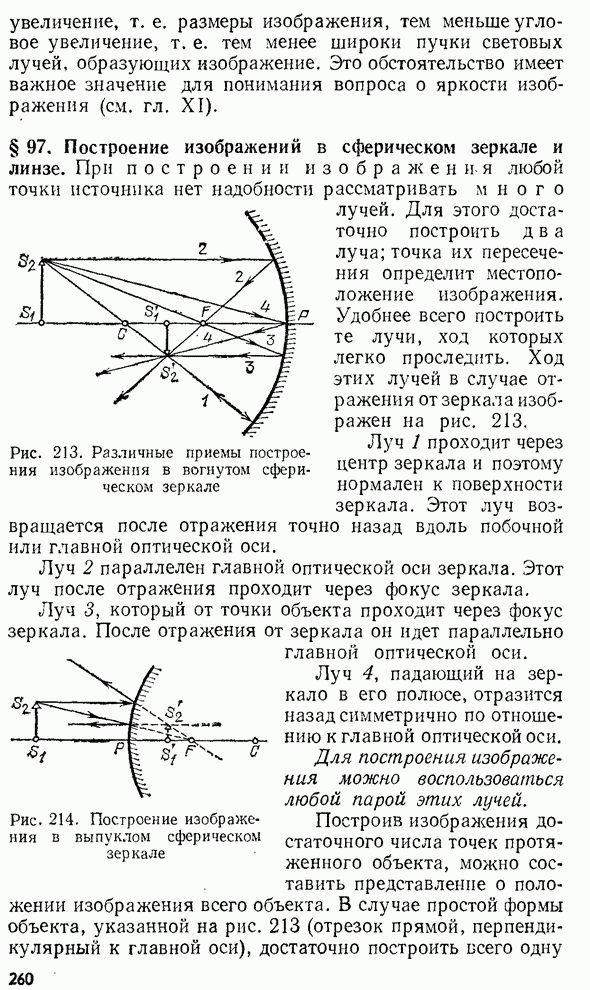
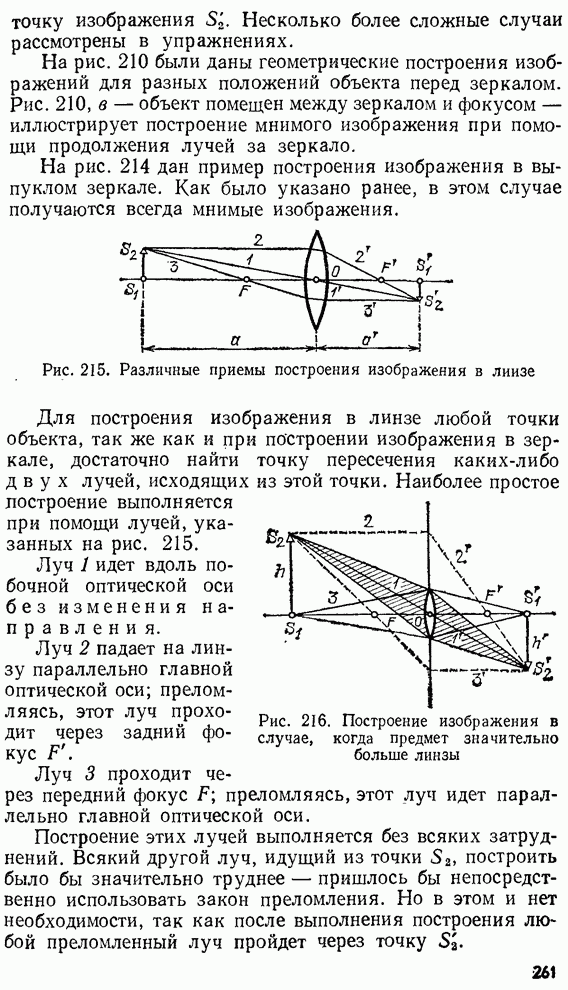
- § 97. Построение изображений в сферическом зеркале и линзе
- § 98. Оптическая сила линз
- Глава XI. Оптические системы и их погрешности
- § 99. Оптическая система
- § 100. Главные плоскости и главные точки системы
- § 101. Построение изображений в системе
- § 102. Увеличение системы
- § 103. Недостатки оптических систем
- § 104. Сферическая аберрация
- § 105. Астигматизм
- § 106. Хроматическая аберрация
- § 107. Ограничение пучков в оптических системах
- § 108. Светосила линзы
- § 109. Яркость изображения
- Глава XII. Оптические приборы
- § 110. Проекционные оптические приборы
- § 111. Фотографический аппарат
- § 112. Глаз как оптическая система
- § 113. Оптические приборы, вооружающие глаз
- § 114. Лупа
- § 115. Микроскоп
- § 116. Разрешающая способность микроскопа
- § 117. Зрительные трубы
- § 118. Увеличение зрительной трубы
- § 119. Телескопы
- § 120. Яркость изображения для протяженных и точечных источников
- § 121. «Ночезрительная труба» Ломоносова
- § 122. Зрение двумя глазами и восприятие глубины пространства. Стереоскоп.
- Раздел третий. Физическая оптика
- Глава XIII. Интерференция света
- § 123. Геометрическая и физическая оптика
- § 124. Опытное осуществление интерференции света
- § 125. Объяснение цветов тонких пленок
- § 126. Кольца Ньютона
- § 127. Определение длины световой волны с помощью колец Ньютона
- Глава XIV. Дифракция света
- § 128. Пучки лучей и форма волновой поверхности
- § 129. Принцип Гюйгенса
- § 130. Законы отражения и преломления света на основе принципа Гюйгенса
- § 131. Принцип Гюйгенса в толковании Френеля
- § 132. Простейшие дифракционные явления
- § 133. Объяснение дифракции по методу Френеля
- § 134. Разрешающая сила оптических инструментов
- § 135. Дифракционные решетки
- § 136. Дифракционная решетка как спектральный прибор
- § 137. Изготовление дифракционных решеток
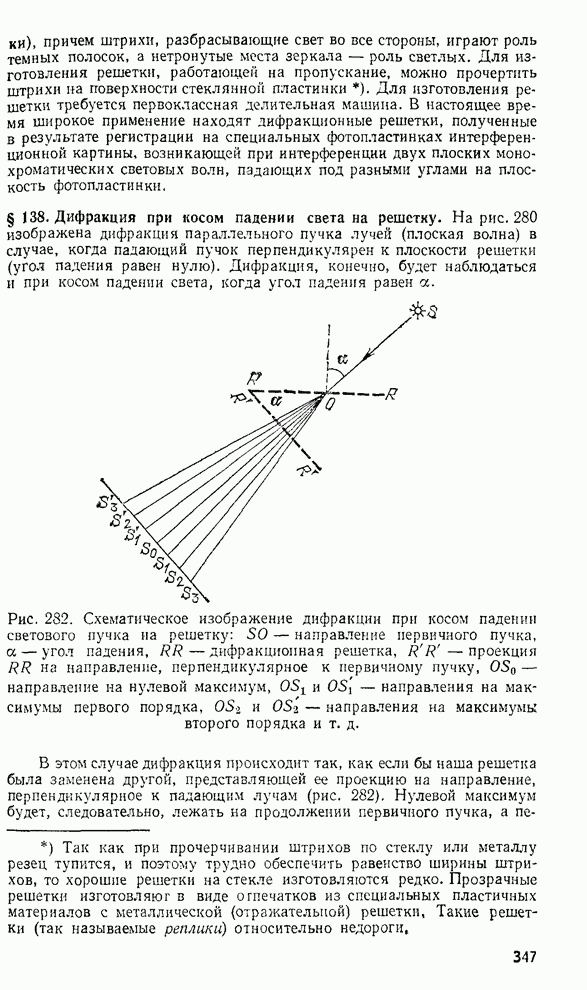
- § 138. Дифракция при косом падении света на решетку
- Глава XV. Физические принципы оптической голографии
- § 139. Фотография и голография
- § 140. Запись голограммы с помощью плоской опорной волны
- § 141. Получение оптических изображений по методу восстановления волнового фронта
- § 142. Голографирование по методу встречных световых пучков
- § 143. Использование голографии в оптической интерферометрии
- Глава XVI. Поляризация света и поперечность световых волн
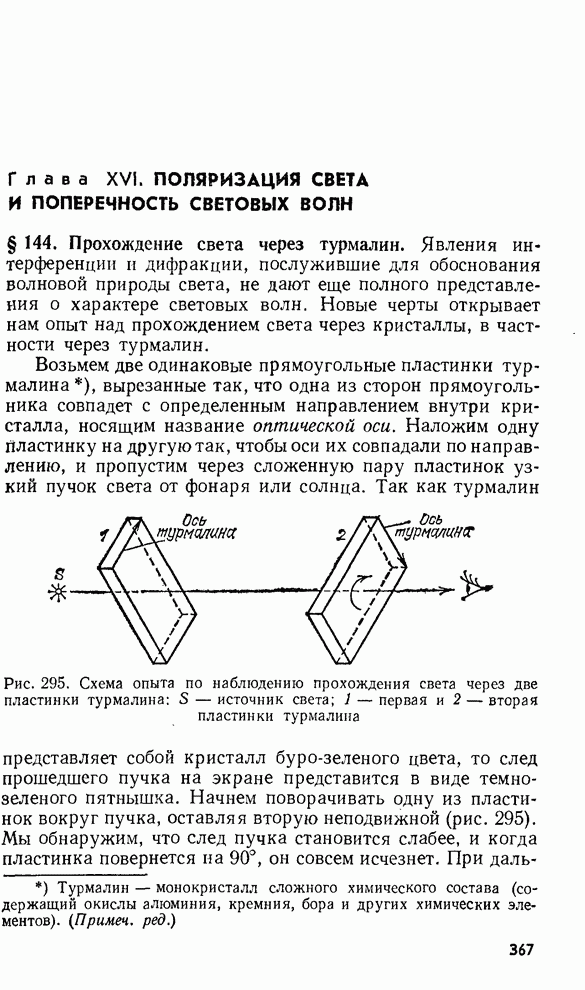
- § 144. Прохождение света через турмалин
- § 145. Гипотезы, объясняющие наблюдаемые явления. Понятие о поляризованном свете
- § 146. Механическая модель явлений поляризации
- § 147. Поляроиды
- § 148. Поперечность световых волн и электромагнитная теория света
- Глава XVII. Шкала электромагнитных волн
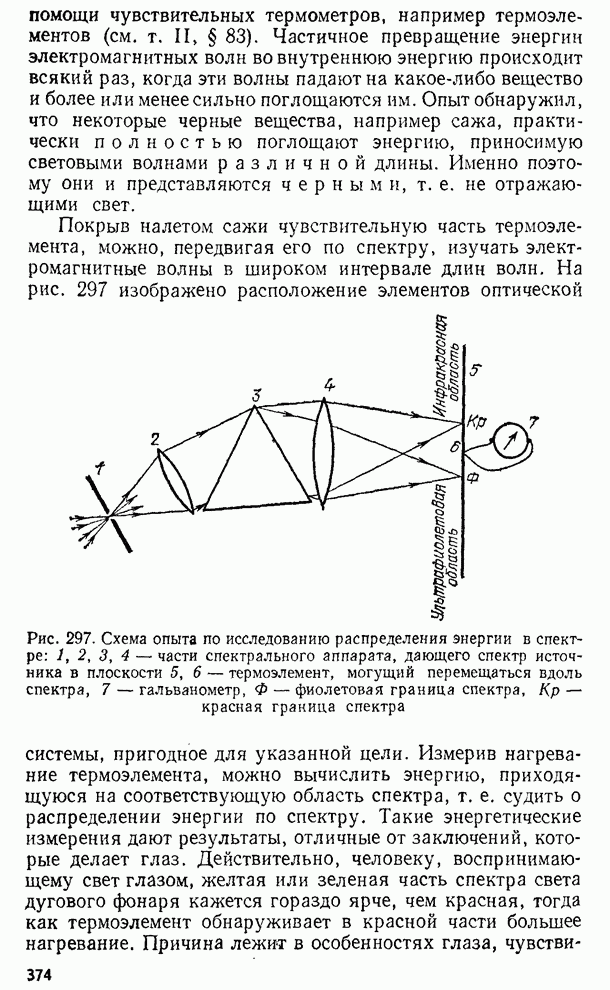
- § 149. Способы исследования электромагнитных волн различной длины
- § 150. Инфракрасное и ультрафиолетовое излучение
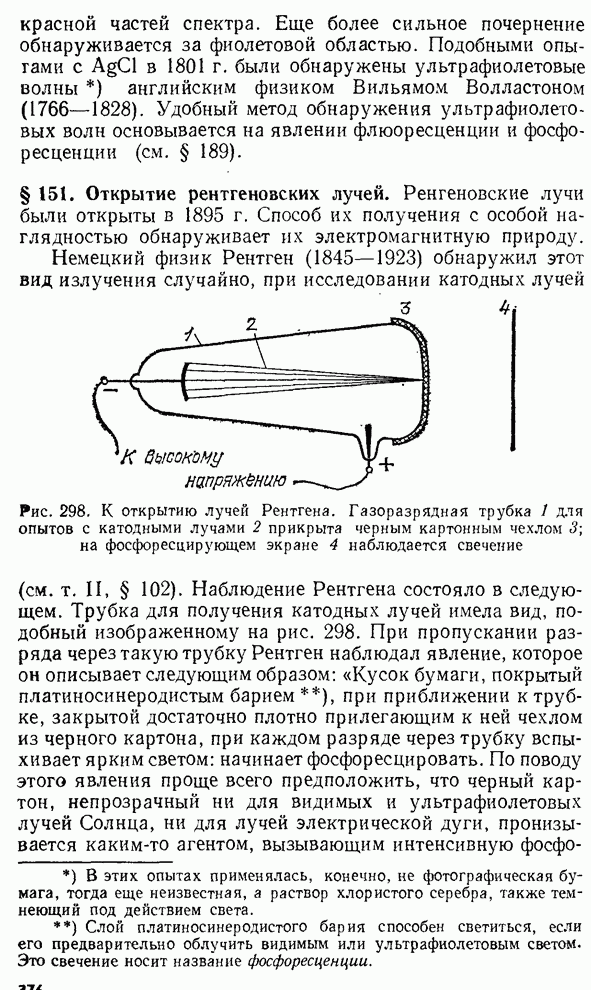
- § 151. Открытие рентгеновских лучей
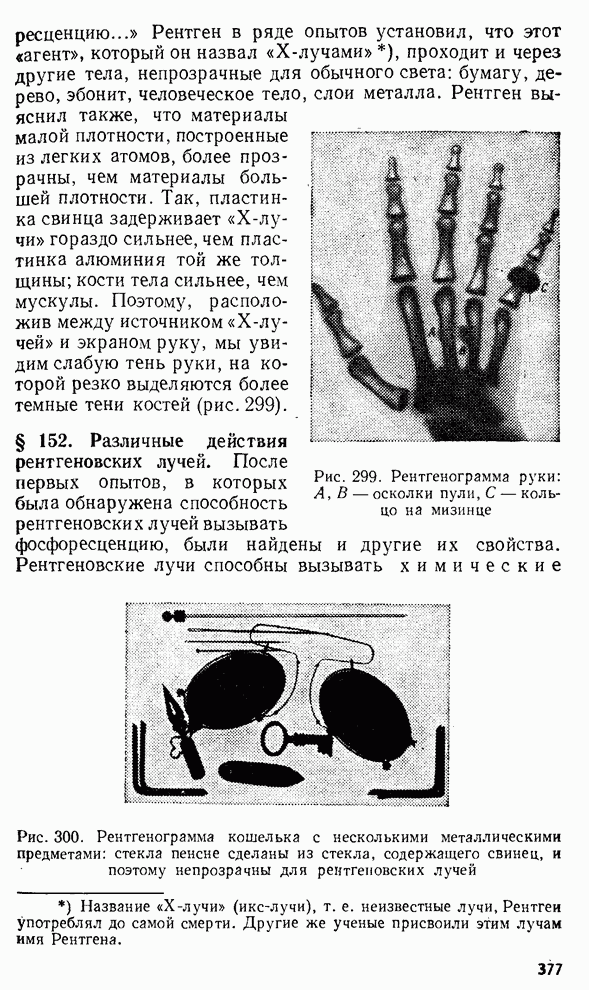
- § 152. Различные действия рентгеновских лучей
- § 153. Устройство рентгеновской трубки
- § 154. Происхождение и природа рентгеновских лучей
- § 155. Шкала электромагнитных волн
- Глава XVIII. Скорость света
- § 156. Первые попытки определения скорости света
- § 157. Определение скорости света Рёмером
- § 158. Определение скорости света по методу вращающегося зеркала
- Глава XIX. Дисперсия света и цвета тел
- § 159. Состояние вопроса о цвете тел до исследований Ньютона
- § 160. Основное открытие Ньютона в оптике
- § 161. Истолкование наблюдений Ньютона
- § 162. Дисперсия показателя преломления различных материалов
- § 163. Дополнительные цвета
- § 164. Спектральный состав света различных источников
- § 165. Свет и цвета тел
- § 166. Коэффициенты поглощения, отражения и пропускания
- § 167. Цветные тела, освещенные белым светом
- § 168. Цветные тела, освещенные цветным светом
- § 169. Маскировка и демаскировка
- § 170. Насыщенность цветов
- § 171. Цвет неба и зорь
- Глава XX. Спектры и спектральные закономерности
- § 172. Спектральные аппараты
- § 173. Типы спектров испускания
- § 174. Происхождение спектров различных типов
- § 175. Спектральные закономерности
- § 176. Спектральный анализ по спектрам испускания
- § 177. Спектры поглощения жидких и твердых тел
- § 178. Спектры поглощения атомов. Линии Фраунгофера
- § 179. Излучение накаленных тел. Абсолютно черное тело
- § 180. Зависимость излучения накаленных тел от температуры. Лампы накаливания
- § 181. Оптическая пирометрия
- XXI. Действия света
- § 182. Действия света на вещество. Фотоэлектрический эффект
- § 183. Законы фотоэлектрического эффекта
- § 184. Понятие о световых квантах
- § 185. Применение фотоэлектрических явлений
- § 186. Фотолюминесценция. Правило Стокса
- § 187. Физический смысл правила Стока
- § 188. Люминесцентный анализ
- § 189. Фотохимические действия света
- § 190. Роль длины волны в фотохимических процессах
- § 191. Фотография
- § 192. Фотохимическая теория зрения
- § 193. Длительность зрительного ощущения
- Раздел четвертый. Атомная и ядерная физика
- Глава XXII. Строение атома
- § 194. Представление об атомах
- § 195. Постоянная Авогадро. Размеры и массы атомов
- § 196. Элементарный электрический заряд
- § 197. Единицы заряда, массы и энергии в атомной физике
- § 198. Измерение массы заряженных частиц. Масс-спектрограф
- § 199. Масса электрона. Зависимость массы от скорости
- § 200. Закон Эйнштейна
- § 201. Массы атомов; изотопы
- § 202. Разделение изотопов. Тяжелая вода
- § 203. Ядерная модель атома
- § 204. Энергетические уровни атомов
- § 205. Вынужденное излучение света. Квантовые генераторы
- § 206. Атом водорода. Своеобразие законов движения электрона в атоме
- § 207. Многоэлектронные атомы. Происхождение оптических и рентгеновских спектров атомов
- § 208. Периодическая система элементов Менделеева
- § 209. Квантовые и волновые свойства фотонов
- § 210. Понятие о квантовой (волновой) механике
- Глава XXIII. Радиоактивность
- § 211. Открытие радиоактивности. Радиоактивные элементы
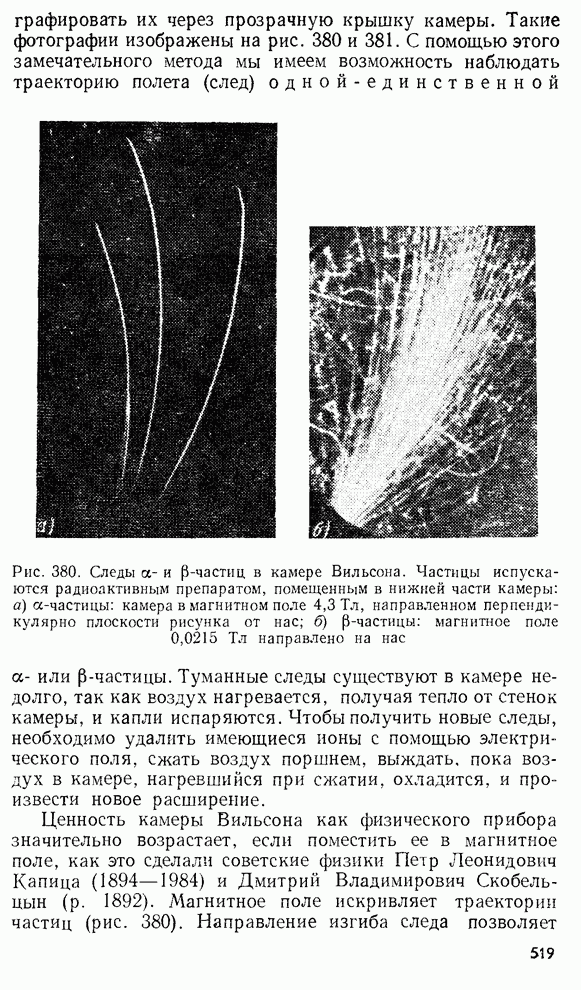
- § 212. L-, B-, Г- излучение. Камера Вильсона
- § 213. Способы регистрации заряженных частиц
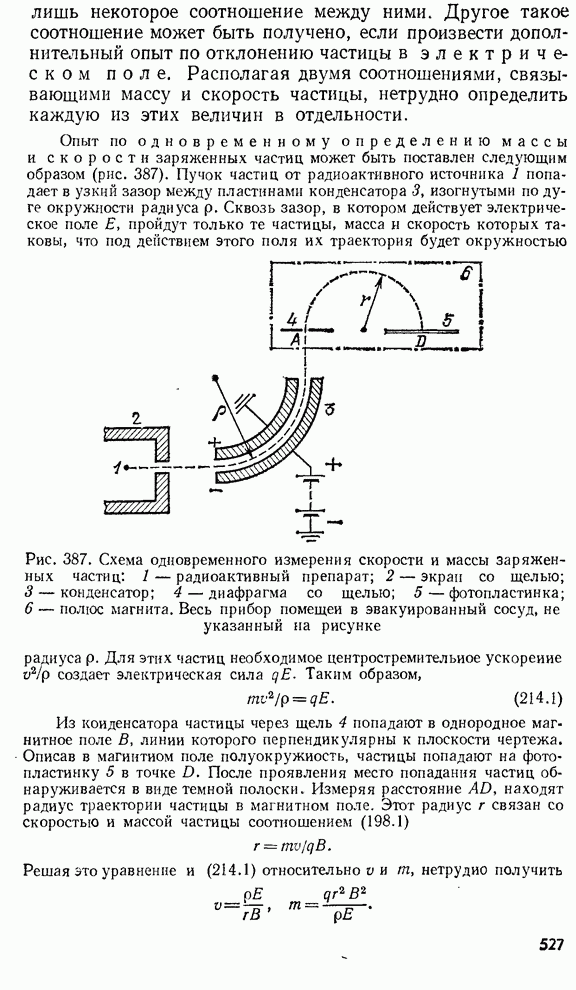
- § 214. Природа радиоактивного излучения
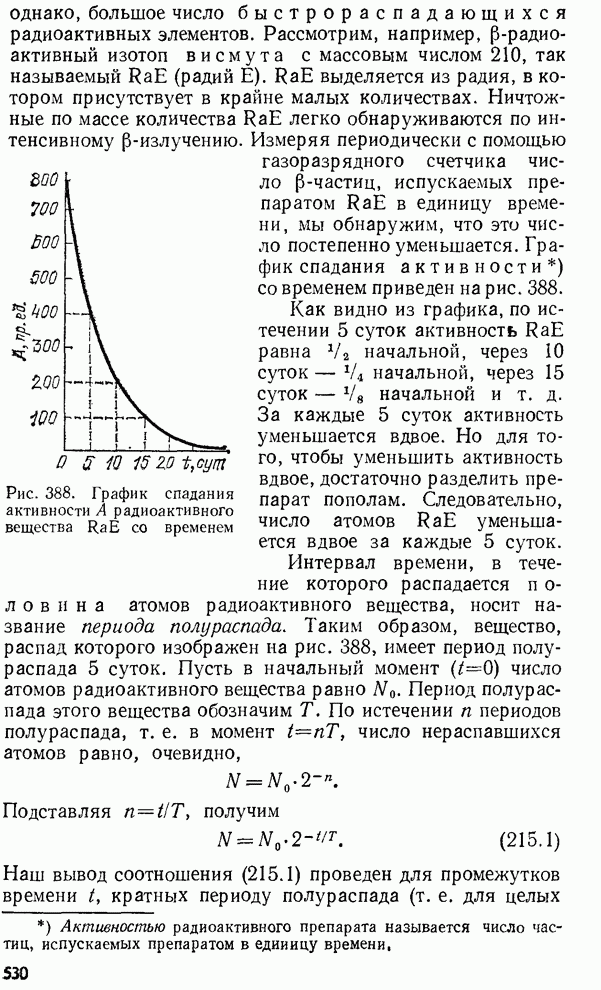
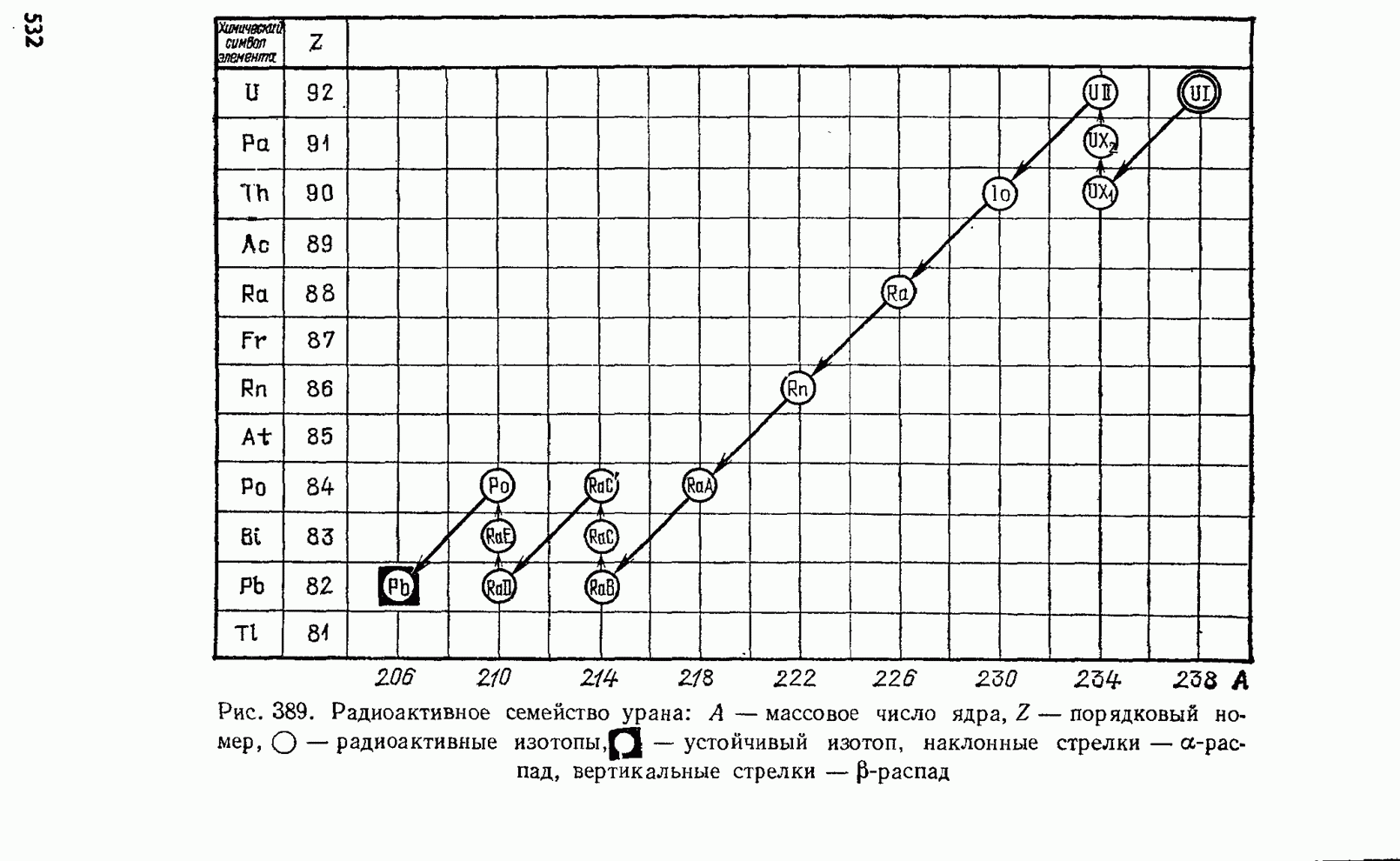
- § 215. Радиоактивный распад и радиоактивные превращения
- § 216. Применения радиоактивности
- § 217. Ускорители
- Глава XXIV. Атомные ядра и ядерная энергия
- § 218. Понятие о ядерных реакциях
- § 219. Ядерные реакции и превращение элементов
- § 220. Свойства нейтронов
- § 221. Ядерные реакции под действием нейтронов
- § 222. Искусственная радиоактивность
- § 223. Позитрон
- § 224. Применение закона Эйнштейна к процессам аннигиляции и образования пар
- § 225. Строение атомного ядра
- § 226. Ядерная энергия. Источник энергии звезд.
- § 227. Деление урана
- § 228. Применения незатухающей цепной реакции деления. Атомная и водородная бомбы
- § 229. Ядерные реакторы и их применения
- Глава XXV. Элементарные частицы
- § 230. Общие замечания
- § 231. Нейтрино
- § 232. Ядерные силы. Мезоны
- § 233. Частицы и античастицы
- § 234. Частицы и взаимодействия
- § 235. Детекторы элементарных частиц
- § 236. Парадокс часов
- § 237. Космическое излучение (космические лучи)
- Глава XXVI. Новые достижения в физике элементарных частиц
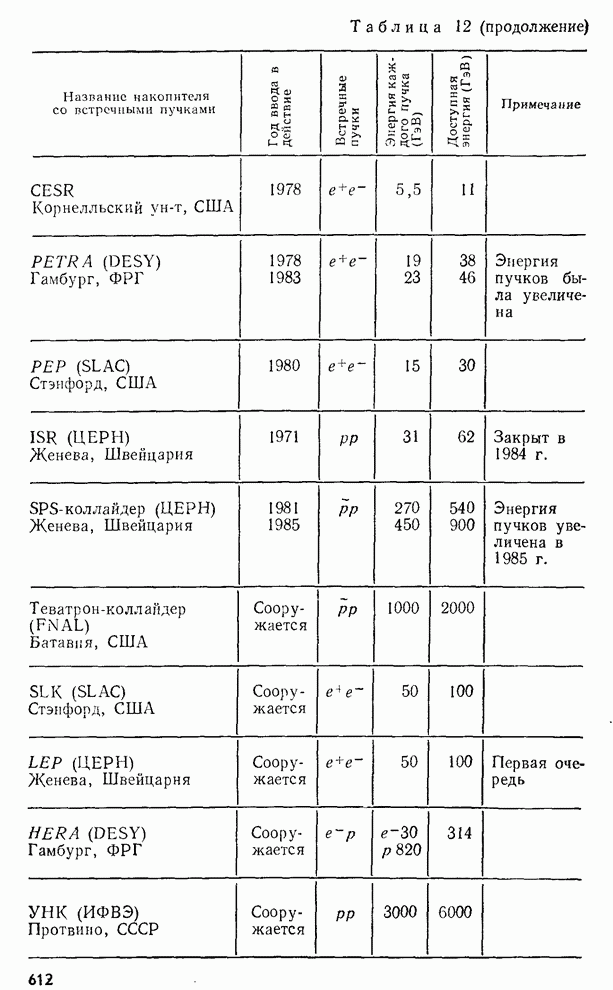
- § 238. Ускорители и экспериментальная техника
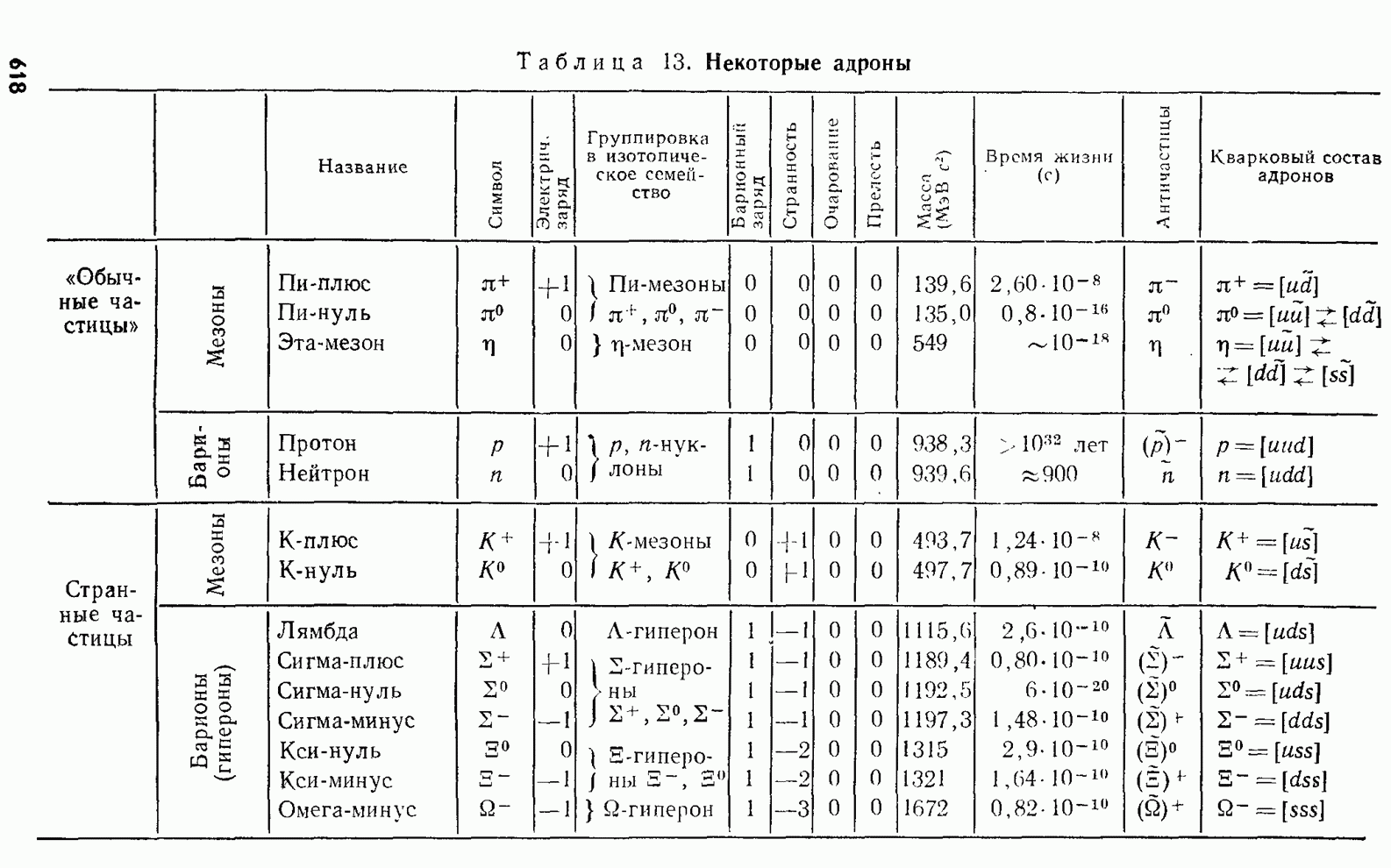
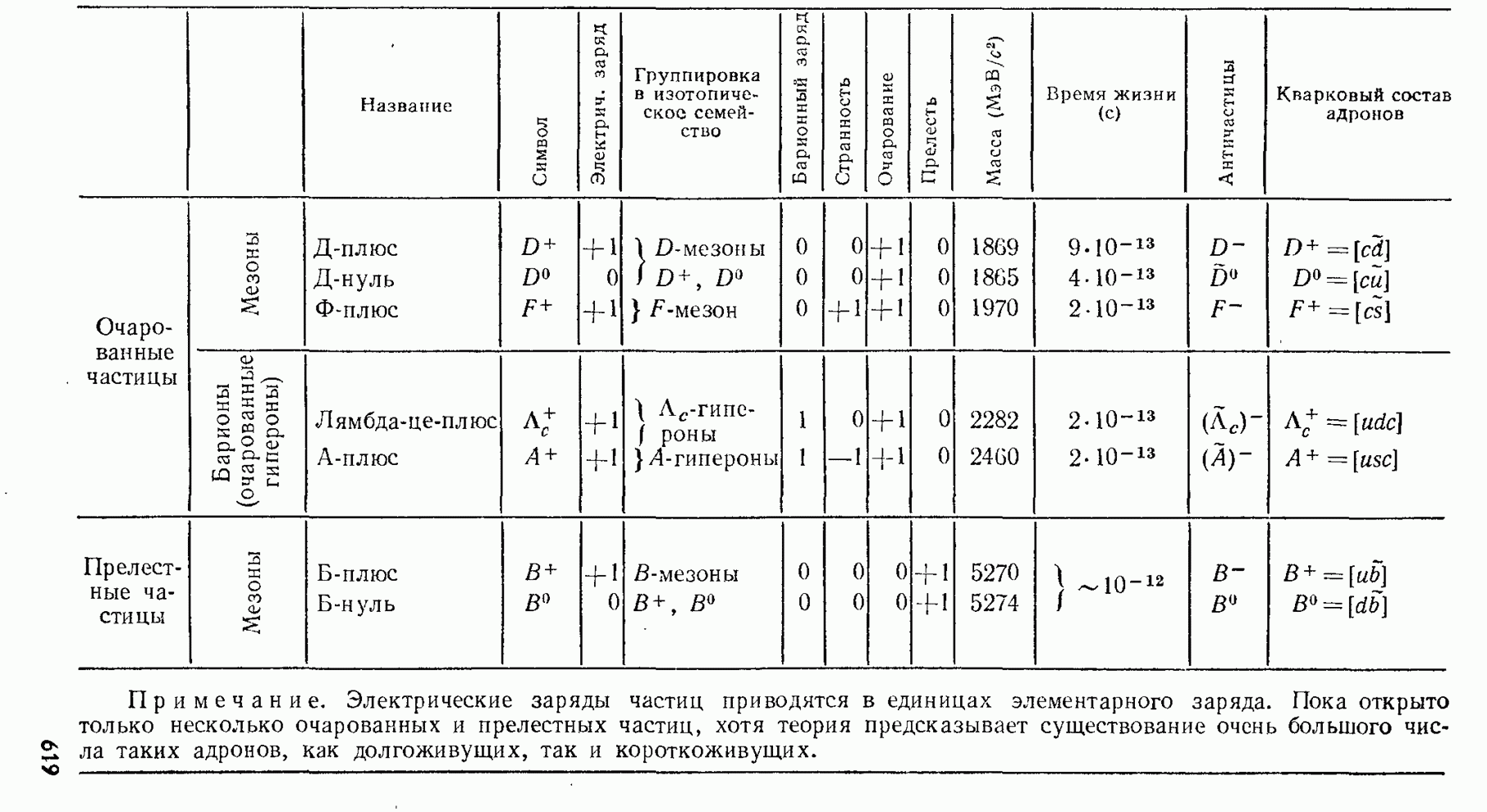
- § 239. Адроны и кварки
- § 240. Кварковая структура андронов
- § 241. Кварковая модель и процессы образования и распада адронов
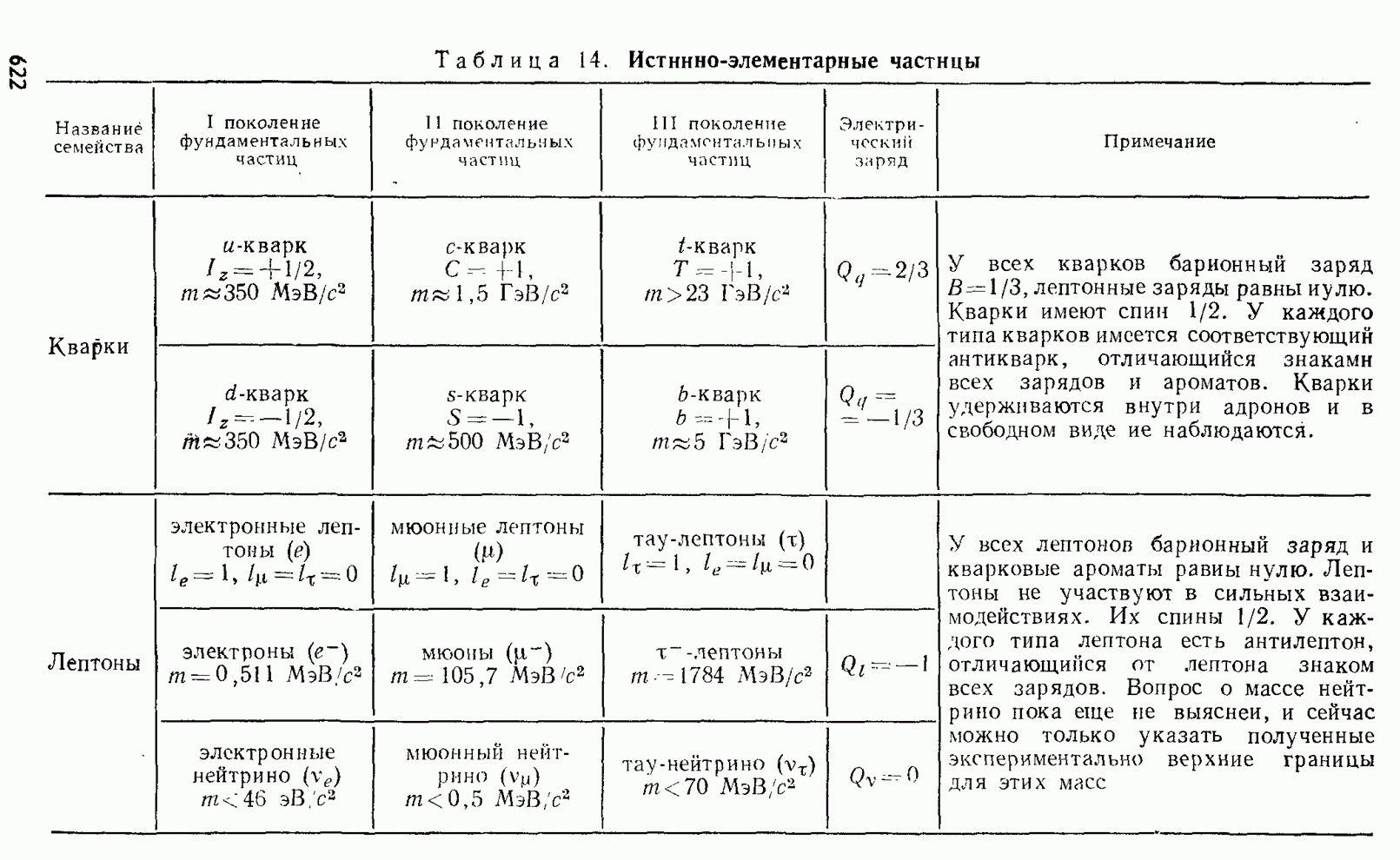
- § 242. Лептоны. Промежуточные бозоны. Единство всех взаимодействий
- Заключение