| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
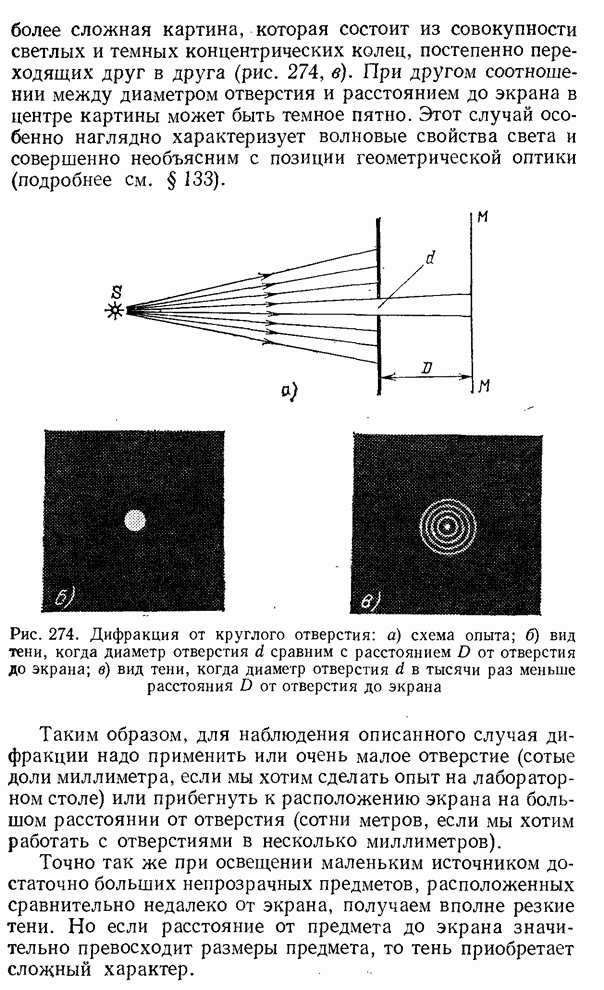
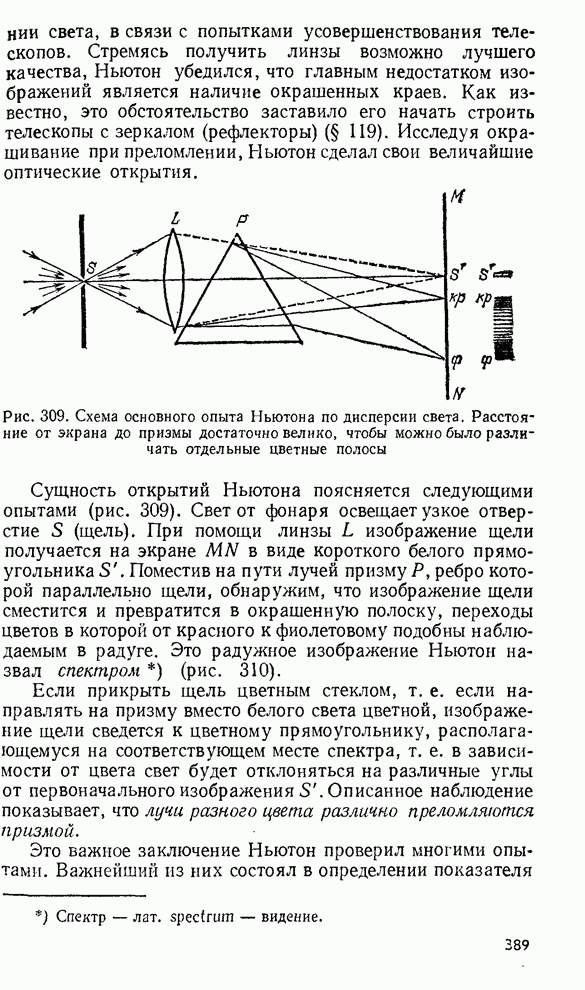
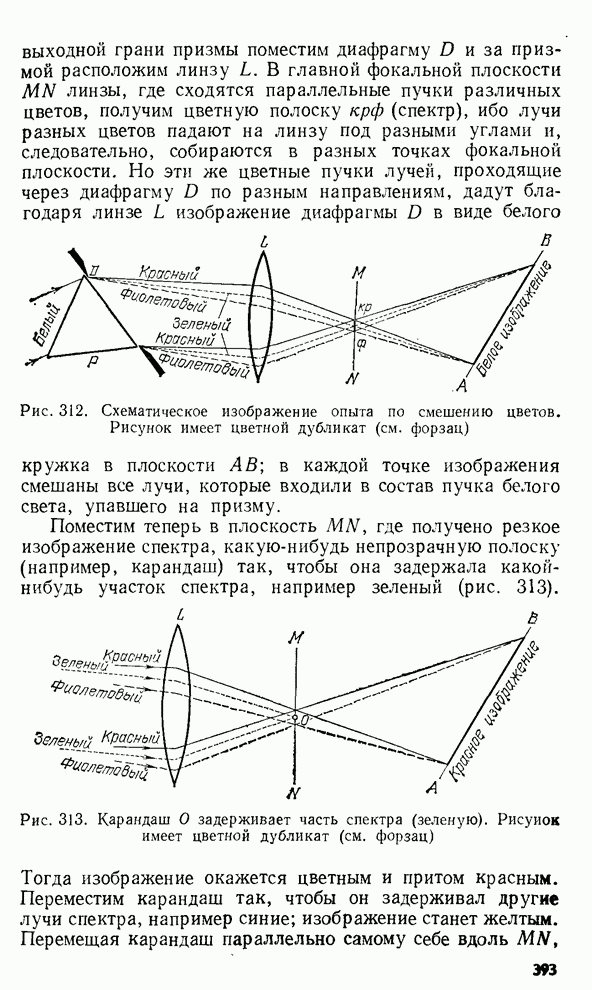
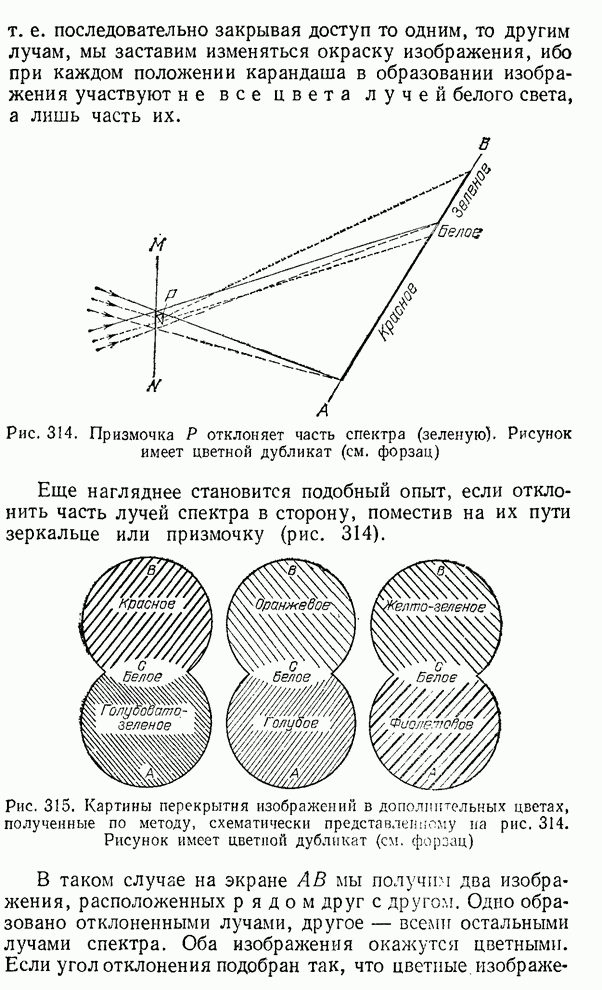
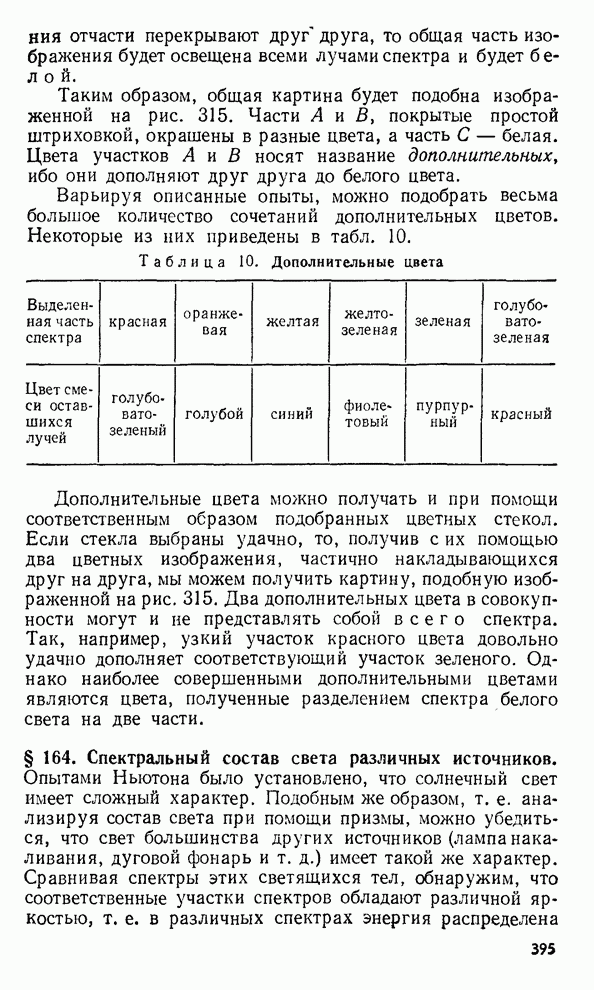
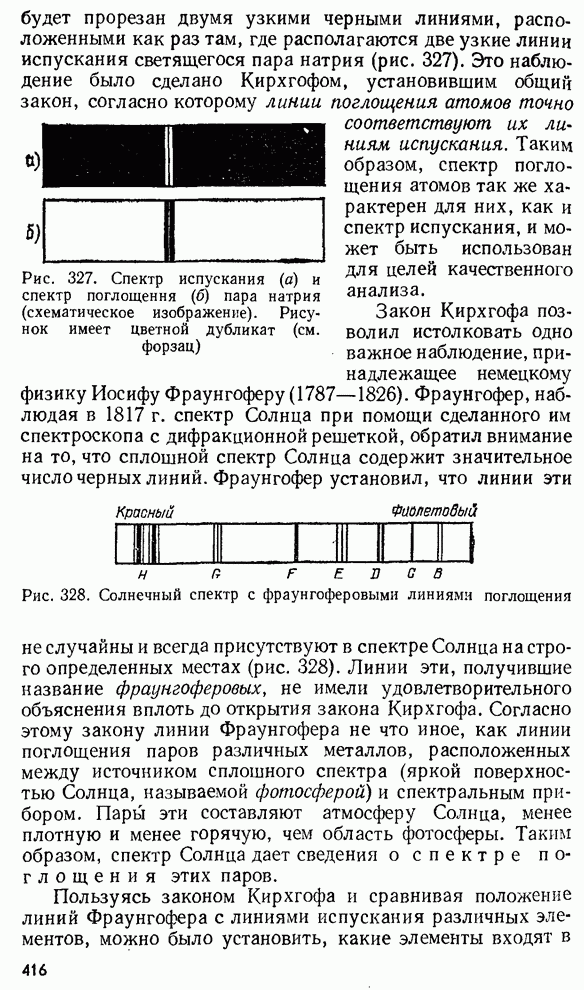
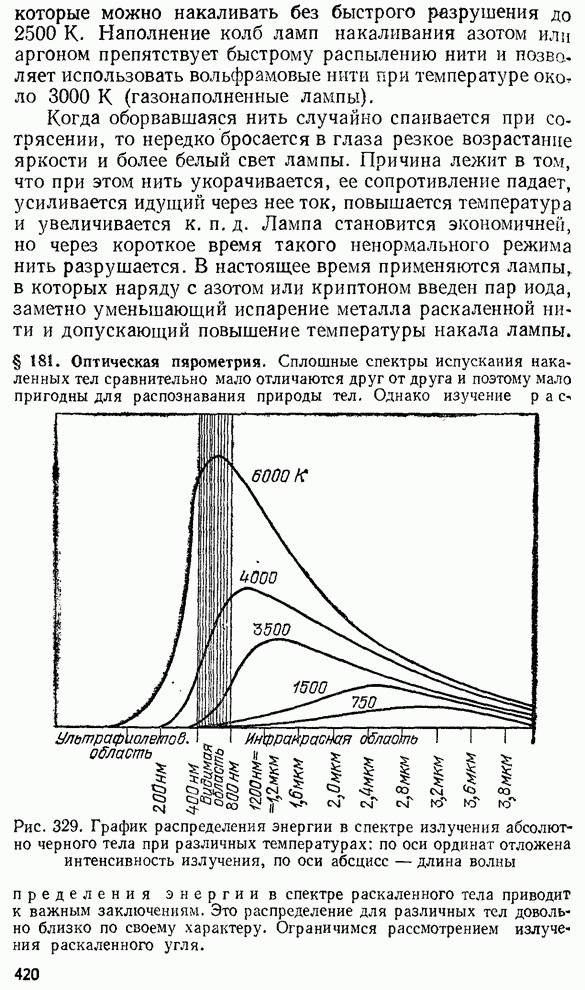
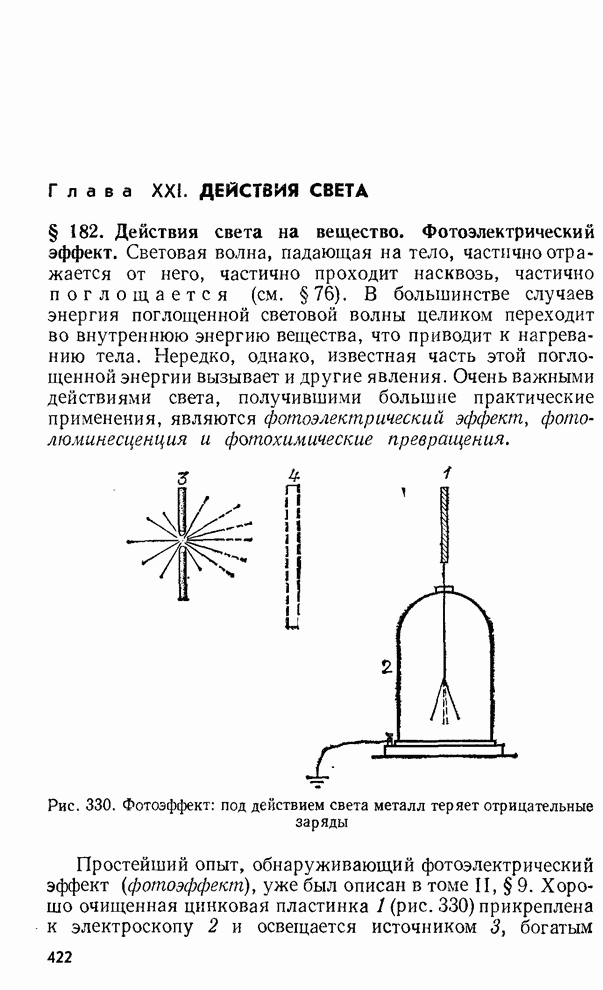
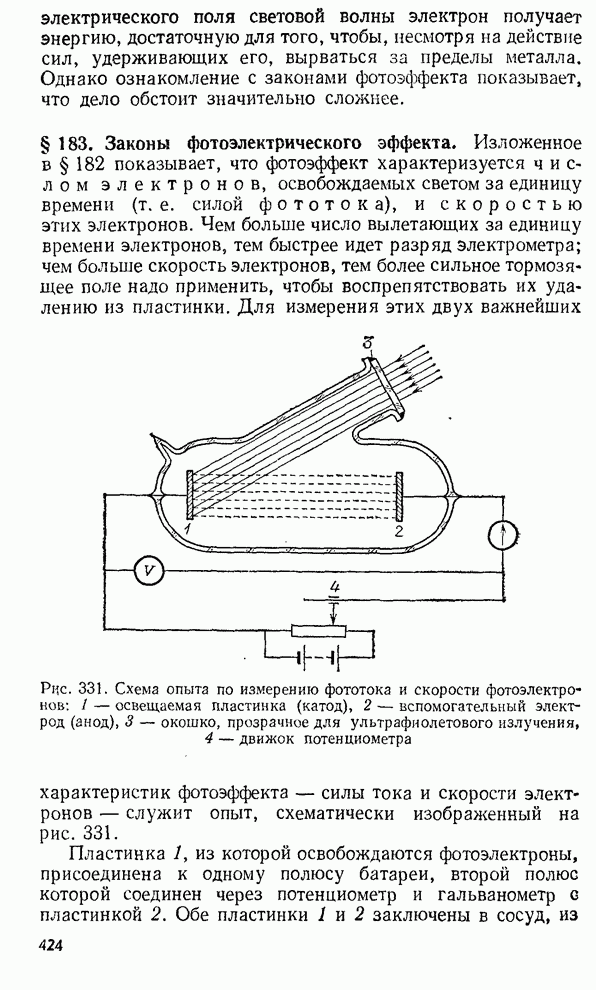
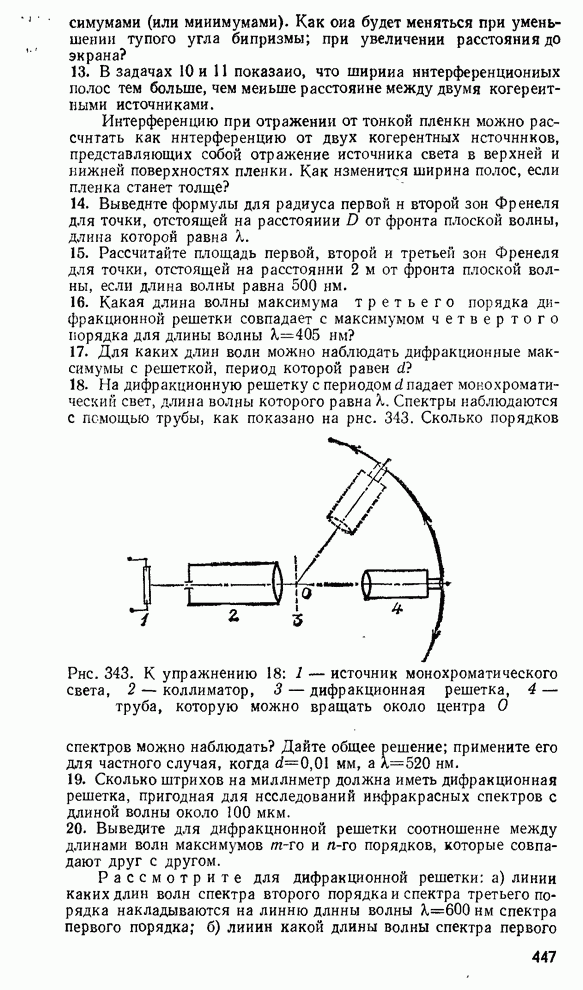
§ 127. Определение длины световой волны с помощью колец Ньютона
Для того чтобы использовать интерференционные явления, в частности кольца Ньютона для измерения длины волны, надо подробнее рассмотреть условия образования максимумов и минимумов света.
При
падении света на пленку или тонкую часть света проходит сквозь нее, а часть отражается. Предположим, что монохроматический
свет длины волны ![]() падает на пластинку перпендикулярно
к его поверхности. Будем рассматривать малый участок пластинки, считая его
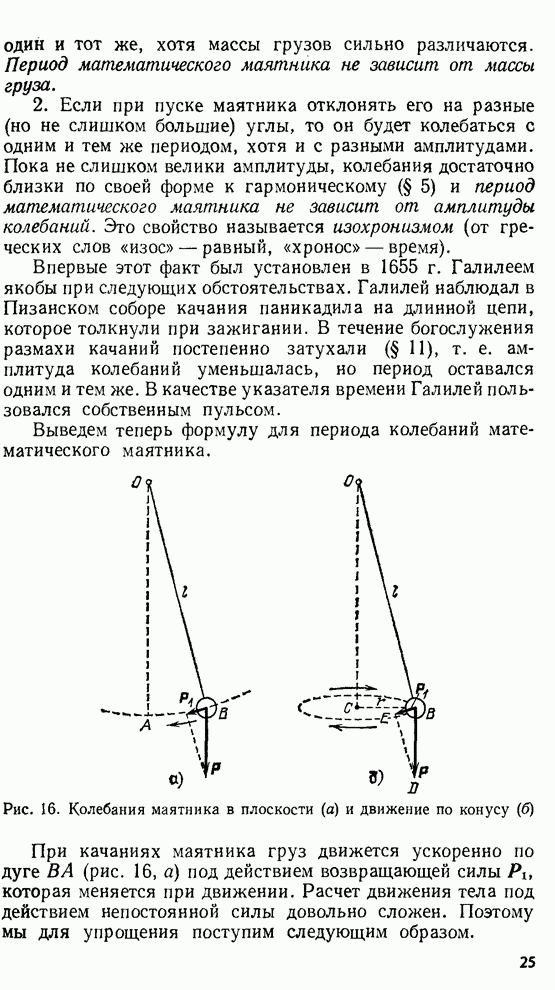
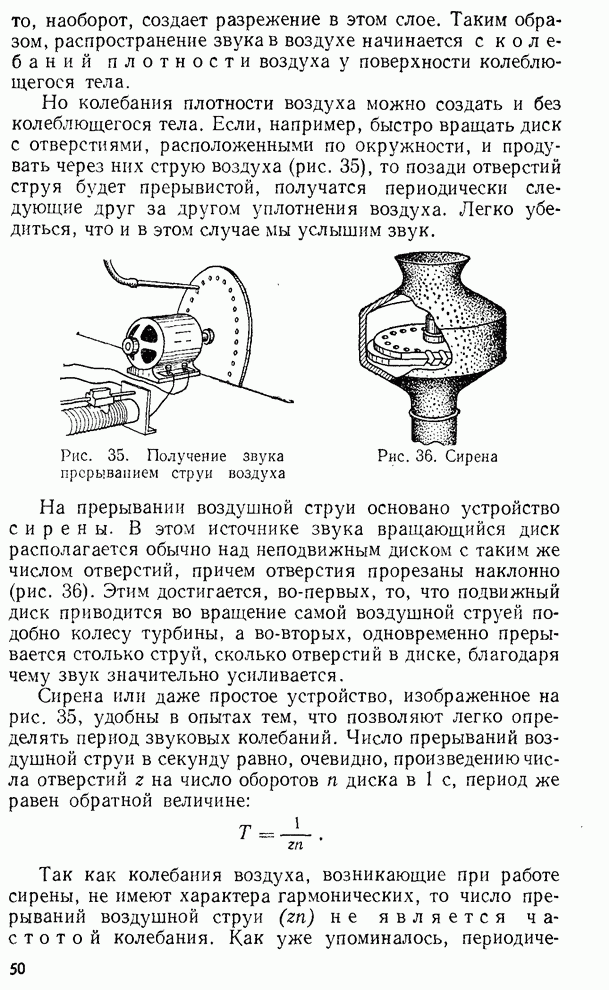
плоскопараллельным. На рис. 268 изображен ход лучей в пластинке, причем для
наглядности изображены не вполне перпендикулярными к ней. В отраженном свете
имеем луч 1, отраженный от верхней поверхности пластинки и луч 2, отраженный от
нижней поверхности. В проходящем — луч
падает на пластинку перпендикулярно
к его поверхности. Будем рассматривать малый участок пластинки, считая его
плоскопараллельным. На рис. 268 изображен ход лучей в пластинке, причем для
наглядности изображены не вполне перпендикулярными к ней. В отраженном свете
имеем луч 1, отраженный от верхней поверхности пластинки и луч 2, отраженный от
нижней поверхности. В проходящем — луч ![]() , прямо прошедший через пластинку и
луч
, прямо прошедший через пластинку и
луч ![]() , отразившийся
по одному разу от нижней и от верхней поверхностей.
, отразившийся
по одному разу от нижней и от верхней поверхностей.

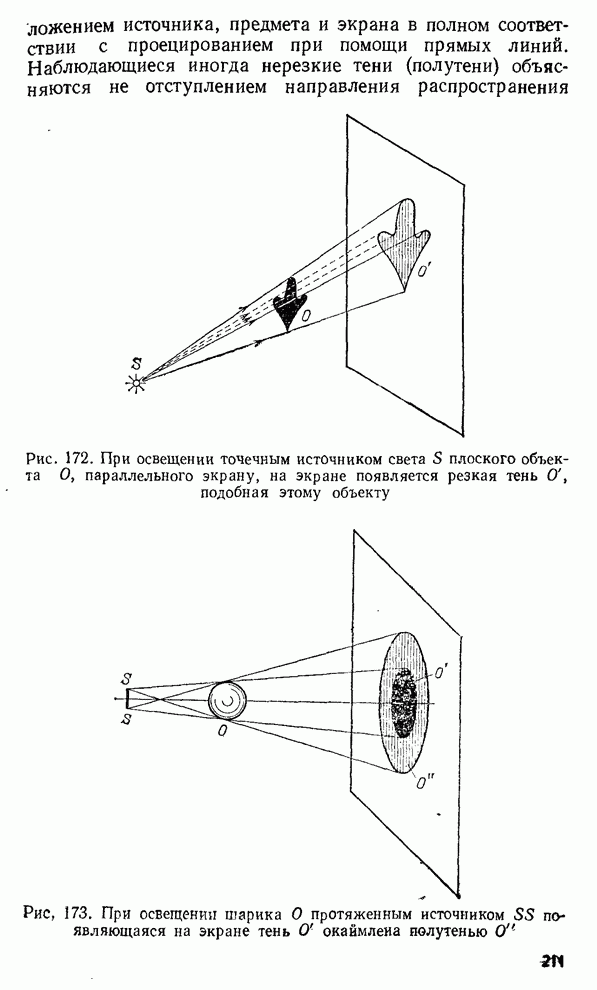
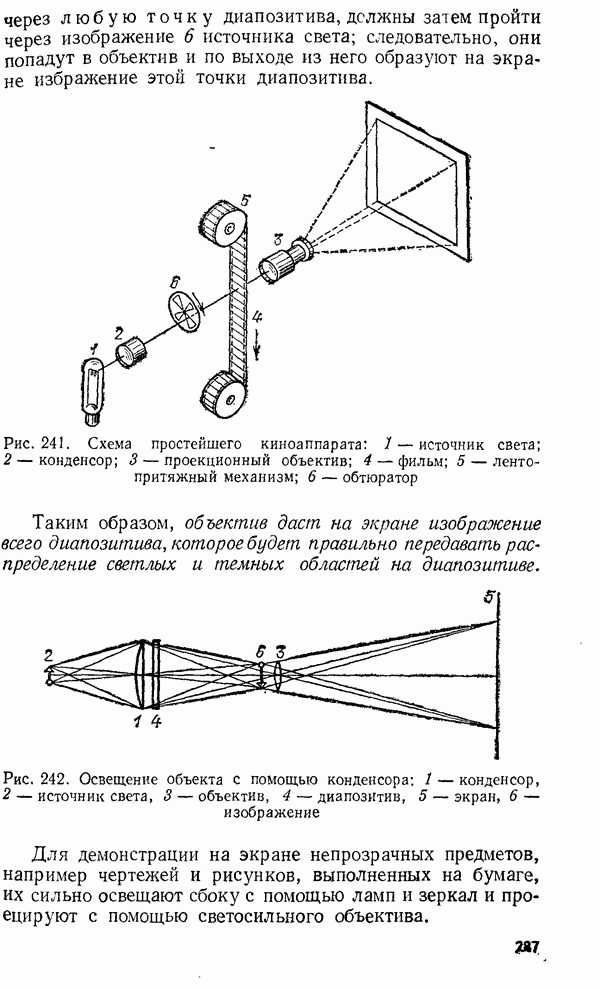
Рис. 268. Ход отраженных и проходящих лучей при двукратном отражении в пленке
Рассмотрим
сначала проходящие лучи. Лучи ![]() и
и ![]() обладают разностью хода, так как
первый прошел через нашу пленку один раз, а второй — три раза. Образовавшаяся
разность хода при нормальном падении света есть
обладают разностью хода, так как
первый прошел через нашу пленку один раз, а второй — три раза. Образовавшаяся
разность хода при нормальном падении света есть ![]() , где
, где ![]() — толщина пластинки. Если эта
разность хода равна целому числу волн, т. е. четному числу полуволн, то лучи
усиливают друг друга; если же разность хода равна нечетному числу полуволн, то
лучи взаимно ослабляются. Итак, максимумы и минимумы получаются в тех местах
пластинки, толщина которых
— толщина пластинки. Если эта
разность хода равна целому числу волн, т. е. четному числу полуволн, то лучи
усиливают друг друга; если же разность хода равна нечетному числу полуволн, то
лучи взаимно ослабляются. Итак, максимумы и минимумы получаются в тех местах
пластинки, толщина которых ![]() удовлетворяет условию
удовлетворяет условию
![]()
причем
минимумы соответствуют нечетному значению ![]() , максимумы соответствуют четному
значению
, максимумы соответствуют четному
значению ![]() .
Таковы выводы для проходящего света.
.
Таковы выводы для проходящего света.
В
отраженном свете разность хода между лучами 1 и 2 при нормальном падении света
есть ![]() , т.
е. такая же, как и для проходящего света. Можно было бы думать, что и в
отраженном свете максимумы и минимумы будут на тех же местах пластинки, что и в
проходящем свете. Однако это означало бы, что места пластинки, которые меньше
всего отражают света, меньше всего и пропускают его. В частности, если бы вся
пластинка имела одну и ту же толщину и притом такую, что
, т.
е. такая же, как и для проходящего света. Можно было бы думать, что и в
отраженном свете максимумы и минимумы будут на тех же местах пластинки, что и в
проходящем свете. Однако это означало бы, что места пластинки, которые меньше
всего отражают света, меньше всего и пропускают его. В частности, если бы вся
пластинка имела одну и ту же толщину и притом такую, что ![]() равно нечетному числу
полуволн, то такая пластинка давала бы и минимальное отражение, и минимальное
пропускание. Но так как мы предполагаем, что пластинка не поглощает света, то
одновременное ослабление и отраженного, и пропущенного света невозможно. Само
собой разумеется, что в непоглощающей пластинке свет отраженный должен
дополнять свет прошедший, так что темные места в проходящем свете соответствуют
светлым в отраженном и наоборот, И действительно, опыт подтверждает это
заключение.
равно нечетному числу
полуволн, то такая пластинка давала бы и минимальное отражение, и минимальное
пропускание. Но так как мы предполагаем, что пластинка не поглощает света, то
одновременное ослабление и отраженного, и пропущенного света невозможно. Само
собой разумеется, что в непоглощающей пластинке свет отраженный должен
дополнять свет прошедший, так что темные места в проходящем свете соответствуют
светлым в отраженном и наоборот, И действительно, опыт подтверждает это
заключение.
В чем же
ошибочность нашего расчета интерференции отраженных световых волн? Дело в том,
что мы не учли различия в условиях отражения. Некоторые из отражений имеют место
на границах воздух — стекло, а другие на границах стекло — воздух (если речь
идет о тонкой стеклянной пластинке в воздухе). Это различие приводит к возникновению
дополнительной разности фаз, которая соответствует дополнительной разности
хода, равной ![]() .
Поэтому полная разность хода для лучей, отраженных от верхней и нижней
поверхностей пластинки толщиной
.
Поэтому полная разность хода для лучей, отраженных от верхней и нижней
поверхностей пластинки толщиной ![]() равняется
равняется ![]() . Места минимумов соответствуют
условию
. Места минимумов соответствуют
условию
![]() ,
,
где ![]() - нечетное число;
места максимумов — четным значениям
- нечетное число;
места максимумов — четным значениям ![]() .
.
Следовательно,
максимумы и минимумы получаются в тех местах пластинки, толщина которых ![]() удовлетворяет
условию
удовлетворяет
условию
![]()
причем ![]() обозначено через
обозначено через
![]() . Минимумы
соответствуют четным значениям
. Минимумы
соответствуют четным значениям ![]() , максимумы соответствуют нечетным
значениям
, максимумы соответствуют нечетным
значениям ![]() .
.
Сопоставим
результаты, полученные для определения положения максимумов и минимумов в проходящем и отраженном свете.
Положения максимумов и минимумов соответствуют толщине пленки, определяемой из
условия: ![]() ,
причем:
,
причем:
|
|
В проходящем свете |
В отраженном свете |
|
При При |
максимум минимум |
минимум максимум |
Таким образом, области максимумов в проходящем свете соответствуют областям минимумов в отраженном и наоборот – в согласии с опытом и с высказанными выше соображениями.
Применительно
к кольцам Ньютона, которые обычно наблюдаются в отраженном свете (§ 126),
получаем, что места максимумов соответствуют нечетным значениям ![]() , а места
минимумов — четным
, а места
минимумов — четным ![]() . Центральный (нулевой
. Центральный (нулевой ![]() ) минимум имеет
вид темного кружка, следующее первое темное кольцо соответствует
) минимум имеет
вид темного кружка, следующее первое темное кольцо соответствует ![]() , второе
, второе ![]() и т.д. Вообще
номер
и т.д. Вообще
номер ![]() темного
кольца связан с числом
темного
кольца связан с числом ![]() соотношением
соотношением ![]() .
.
Вместо
определения толщины ![]() того места воздушной прослойки,
которое соответствует кольцу номера
того места воздушной прослойки,
которое соответствует кольцу номера ![]() , удобнее измерять диаметр или
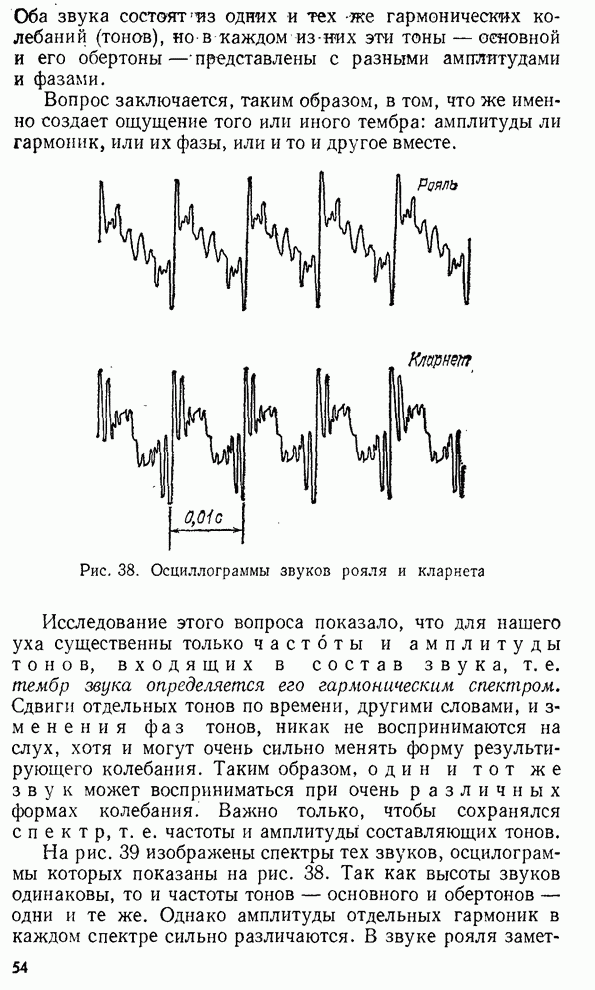
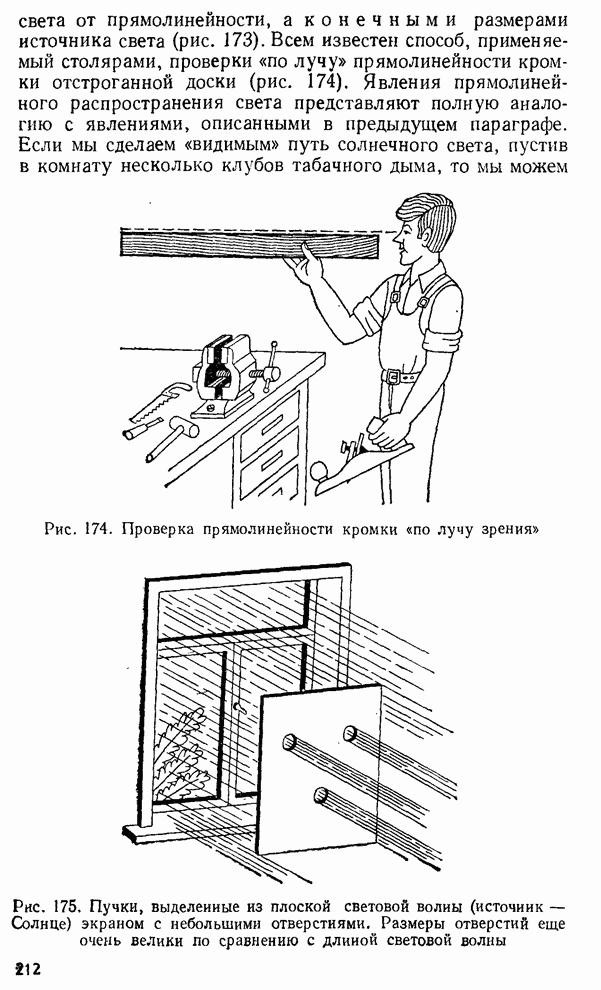
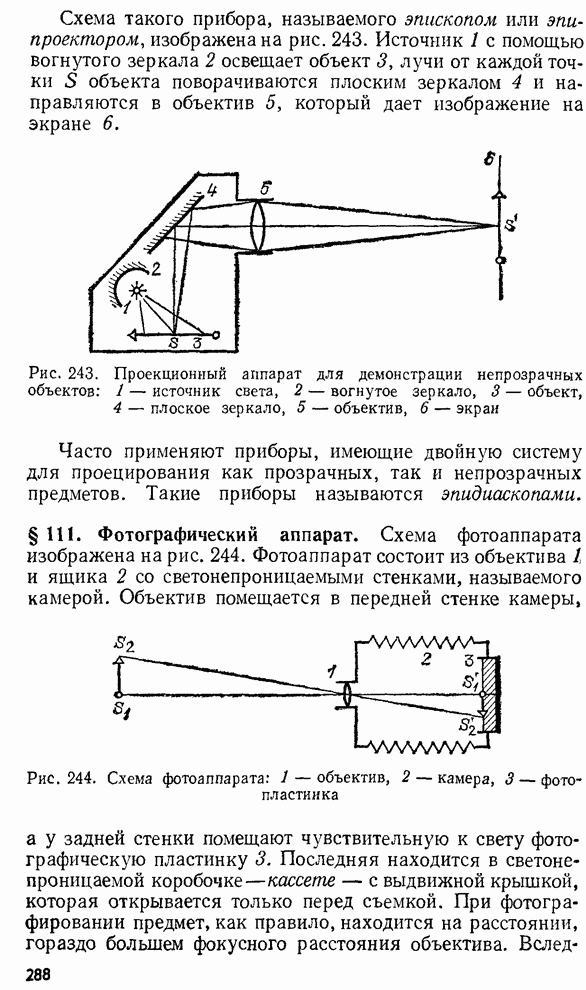
радиус соответствующего кольца. Из рис. 269 следует:
, удобнее измерять диаметр или
радиус соответствующего кольца. Из рис. 269 следует: ![]() и, следовательно, толщина
прослойки
и, следовательно, толщина
прослойки ![]() связана
с радиусом кольца
связана
с радиусом кольца ![]() и радиусом линзы
и радиусом линзы ![]() соотношением
соотношением
![]() .
.

Рис. 269. К расчету радиусов колец Ньютона
Для
опытов с кольцами Ньютона пользуются линзами с очень большим радиусом ![]() (несколько
метров). Поэтому можно пренебречь величиной
(несколько
метров). Поэтому можно пренебречь величиной ![]() по сравнению с
по сравнению с ![]() и упростить последнее
соотношение, записав:
и упростить последнее
соотношение, записав:
![]() ,
или
,
или ![]() .
.
Итак, для определения длины волны ![]() с помощью колец
Ньютона имеем
с помощью колец
Ньютона имеем
![]() .
.
Если
измерять радиусы темных колец, то номер кольца ![]() . В таком случае длина волны
выразится формулой
. В таком случае длина волны
выразится формулой
![]() ,
,
где ![]() есть радиус
есть радиус ![]() темного кольца.
темного кольца.
Проводя измерения радиусов светлых колец, мы
должны иметь в виду, что ![]() . В соответствии с этим получаем
соотношение
. В соответствии с этим получаем
соотношение
 ,
,
где ![]() есть радиус
есть радиус ![]() светлого кольца.
светлого кольца.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к первому изданию
- Раздел первый. Колебания и волны
- Глава I. Основные понятия. Механические колебания
- § 1. Периодические движения. Период
- § 2. Колебательные системы
- § 3. Маятник; кинематика его колебаний
- § 4. Колебания камертона
- § 5. Гармоническое колебание. Частота
- § 6. Сдвиг фаз
- § 7. Динамика колебаний маятника
- § 8. Формула периода математического маятника
- § 9. Упругие колебания
- § 10. Крутильные колебания
- § 11. Влияние трения. Затухание
- § 12. Вынужденные колебания
- § 13. Резонанс
- § 14. Влияние трения на резонансные явления
- § 15. Примеры резонансных явлений
- § 16. Резонансные явления при действии негармонической периодической силы
- § 17. Форма периодических колебаний и ее связь с гармоническим составом этих колебаний
- Глава II. Звуковые колебания
- § 18. Звуковые колебания
- § 19. Предмет акустики
- § 20. Музыкальный тон. Громкость и высота тона
- § 21. Тембр
- § 22. Акустический резонанс
- § 23. Запись и воспроизведение звука
- § 24. Анализ и синтез звука
- § 25. Шумы
- Глава III. Электрические колебания
- § 26. Электрические колебания. Методы их наблюдения
- § 27. Колебательный контур
- § 28. Аналогия с механическими колебаниями. Формула Томсона
- § 29. Электрический резонанс
- § 30. Незатухающие колебания. Автоколебательные системы
- § 31. Ламповый генератор электрических колебаний
- Глава IV. Волновые явления
- § 32. Учение о колебаниях
- § 33. Волновые явления
- § 34. Скорость распространения волн
- § 35. Радиолокация, гидроакустическая локация и звукометрия
- § 36. Поперечные волны в шнуре
- § 37. Продольные волны в столбе воздуха
- § 38. Волны на поверхности жидкости
- § 39. Перенос энергии волнами
- § 40. Отражение волн
- § 41. Дифракция
- § 42. Направленное излучение
- Глава V. Интерференция волн
- § 43. Наложение волн
- § 44. Интерференция волн
- § 45. Условия образования максимумов и минимумов
- § 46. Интерференция звуковых волн
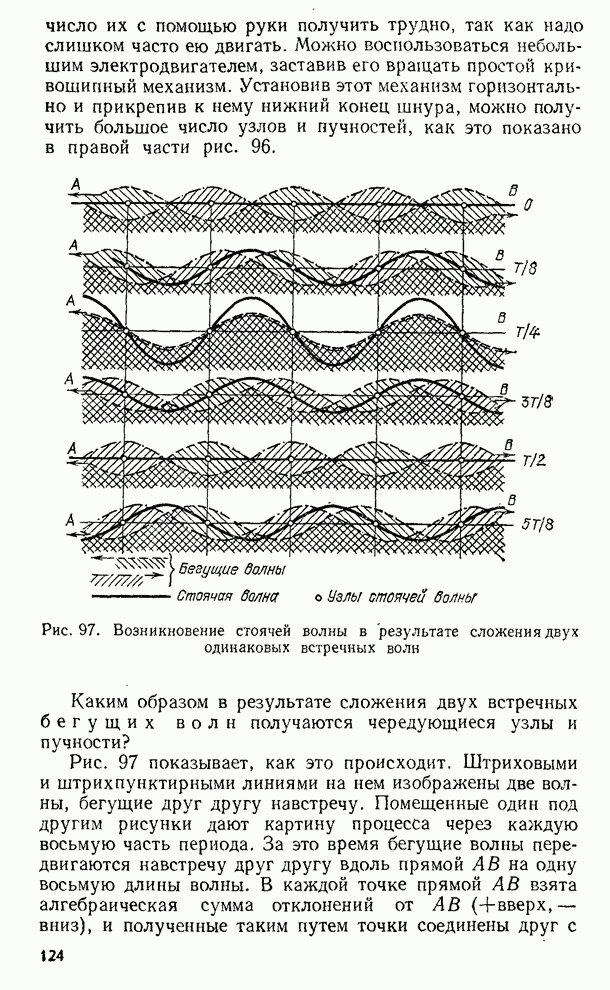
- § 47. Стоячие волны
- § 48. Колебания упругих тел как стоячие волны
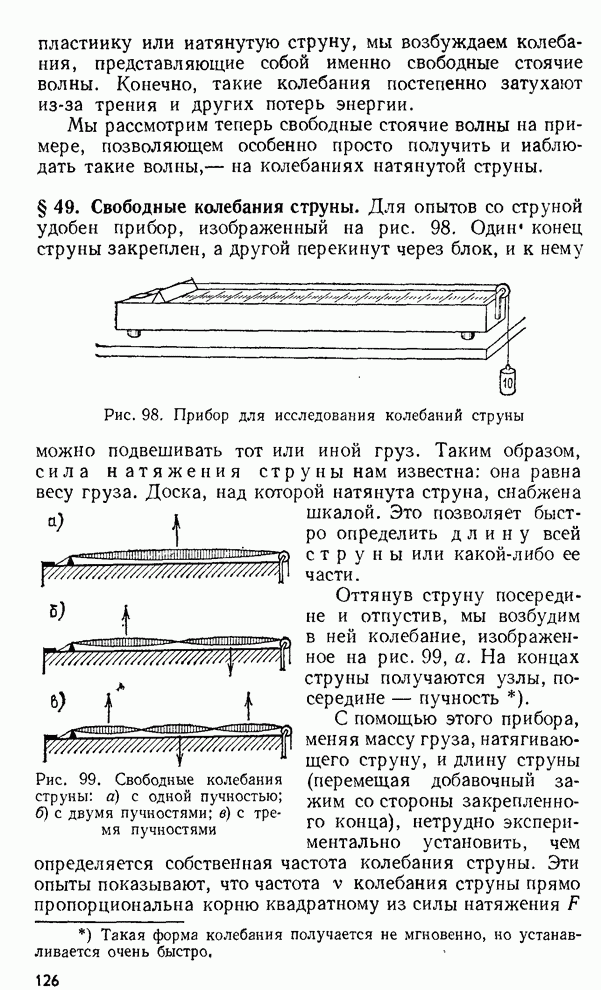
- § 49. Свободные колебания струны
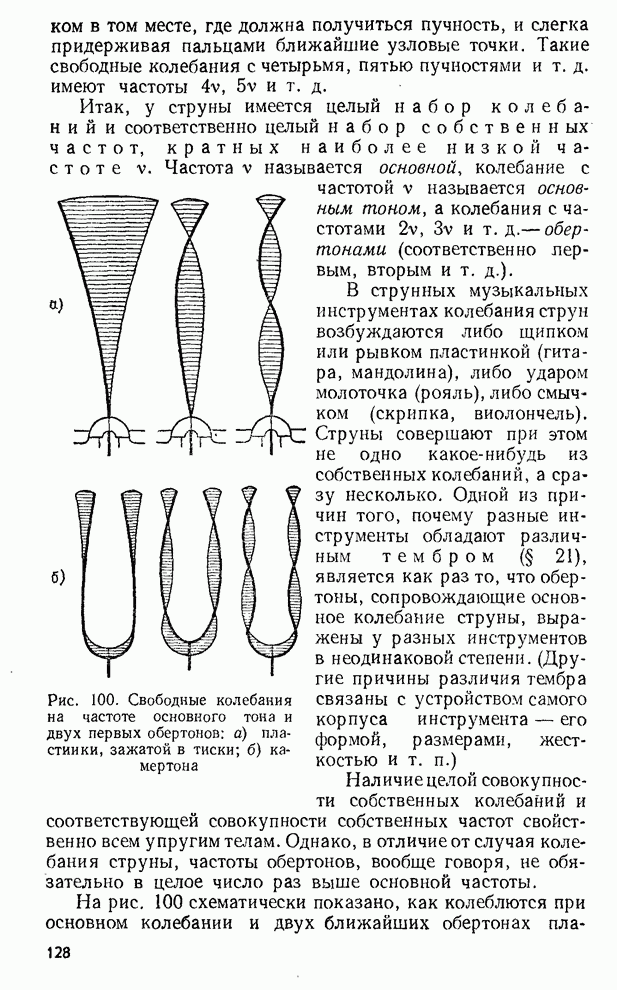
- § 50. Стоячие волны в пластинках и других протяженных телах
- § 51. Резонанс при наличии многих собственных частот
- § 52. Условия хорошего излучения звука
- § 53. Бинауральный эффект. Звукопеленгация
- Глава VI. Электромагнитные волны
- § 54. Электромагнитные волны
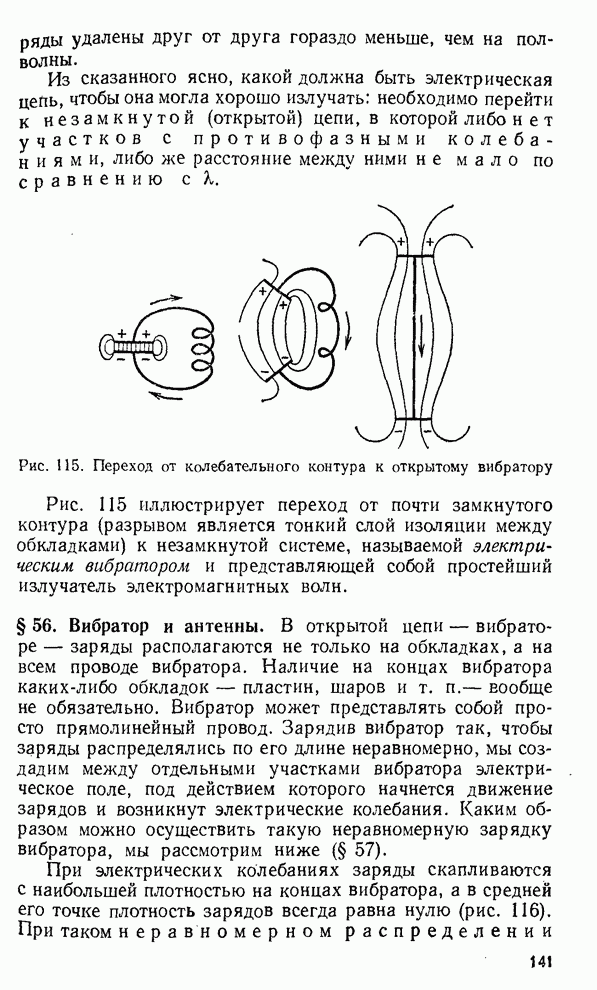
- § 55. Условия хорошего излучения электромагнитных волн
- § 56. Вибратор и антенны
- § 57. Опыты Герца по получению и исследованию электромагнитных волн. Опыты Лебедева
- § 58. Электромагнитная теория света. Шкала электромагнитных волн
- § 59 Опыты с электромагнитными волнами
- § 60. Изобретение радио Поповым
- § 61. Современная радиосвязь
- § 62. Другие применения радио
- § 63. Распространение радиоволн
- § 64. Заключительные замечания
- Раздел второй. Геометрическая оптика
- Глава VII. Общая характеристика световых явлений
- § 65. Разнообразные действия света
- § 66. Интерференция света. Цвета тонких пленок
- § 67. Краткие сведения из истории оптики
- Глава VIII. Фотометрия и светотехника
- § 68. Энергия излучения. Световой поток
- § 69. Точечные источники света
- § 70. Сила света и освещенность
- § 71. Законы освещенности
- § 72. Единицы световых величин
- § 73. Яркость источников
- § 74. Задачи светотехники
- § 75. Приспособления для концентрации светового потока
- § 76. Отражающие и рассеивающие тела
- § 77. Яркость освещенных поверхностей
- § 78. Световые измерения и измерительные приборы
- Глава IX. Основные законы геометрической оптики
- § 79. Прямолинейное распространение волн
- § 80. Прямолинейное распространение света и световые лучи
- § 81. Законы отражения и преломления света
- § 82. Обратимость световых лучей
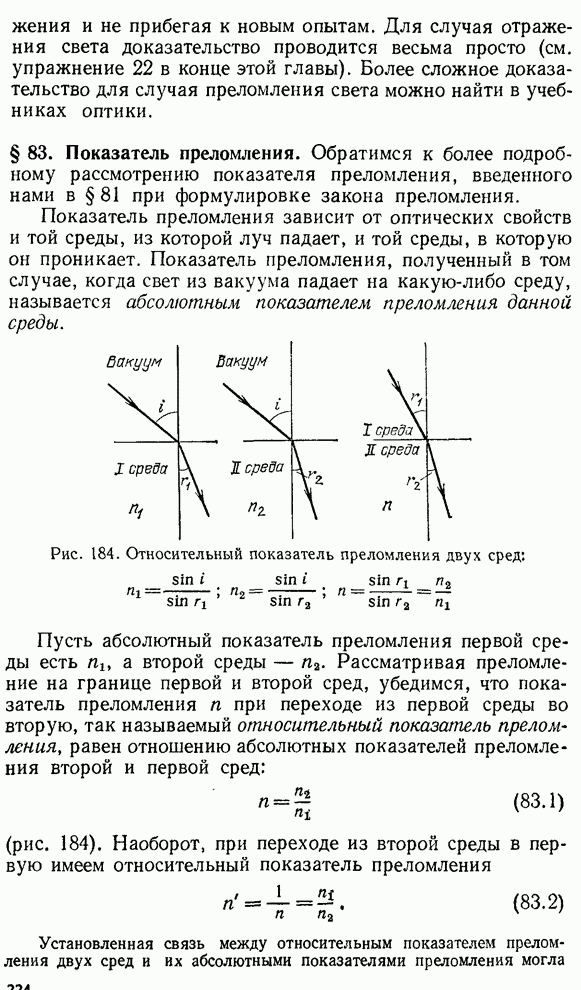
- § 83. Показатель преломления
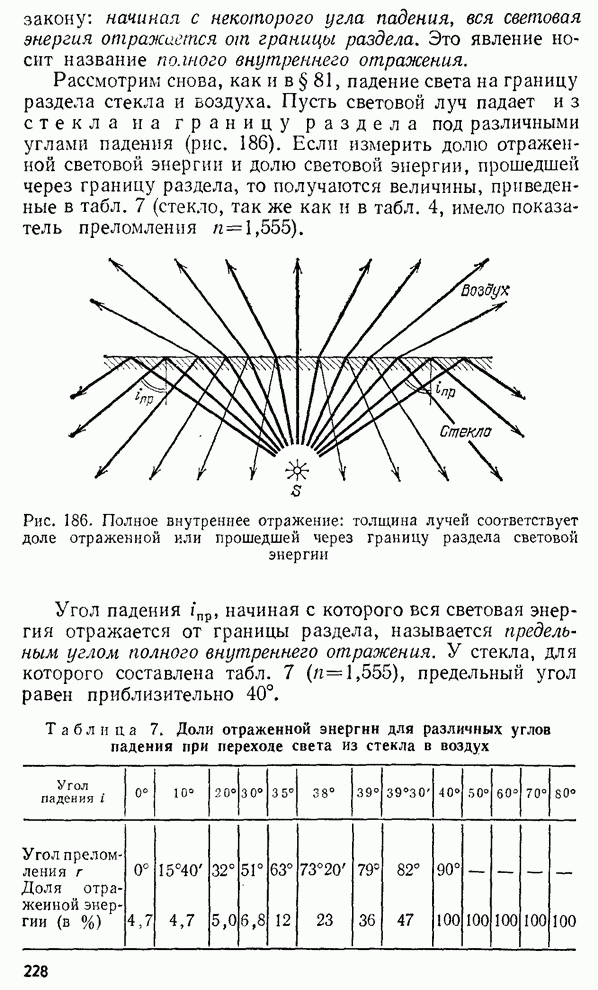
- § 84. Полное внутреннее отражение
- § 85. Преломление в плоскопараллельной пластинке
- § 86. Преломление в призме
- Глава X. Применение отражения и преломления света для получения изображений
- § 87. Источник света и его изображение
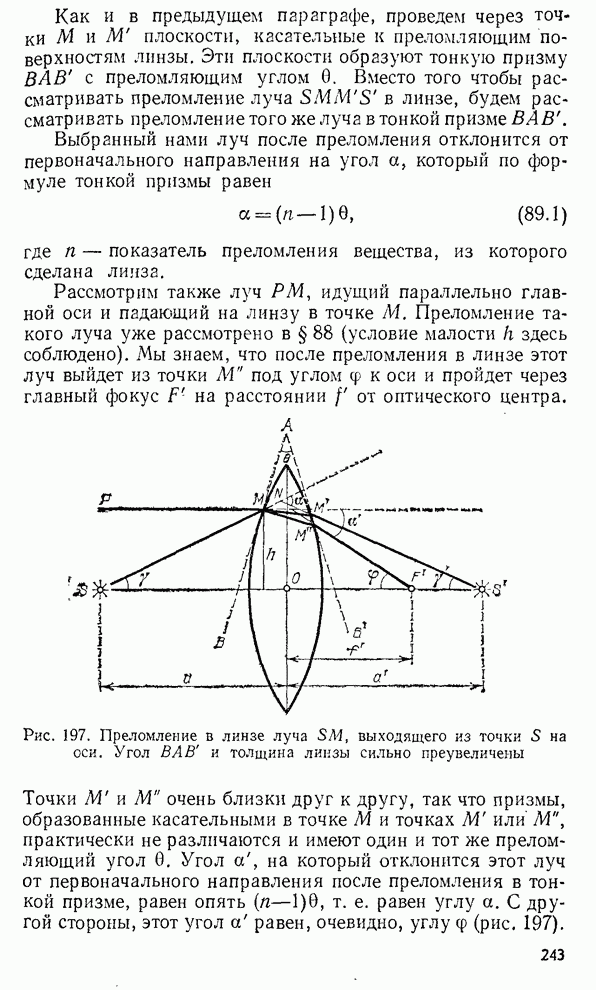
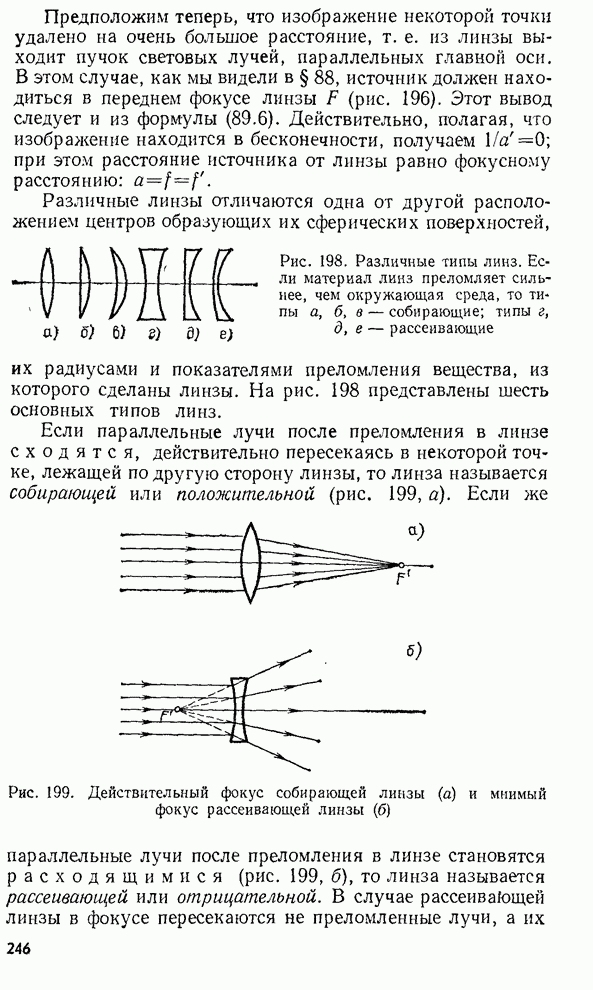
- § 88. Преломление в линзе
- § 89. Изображение в линзе точек, лежащих на главной оптической оси. Формула линзы.
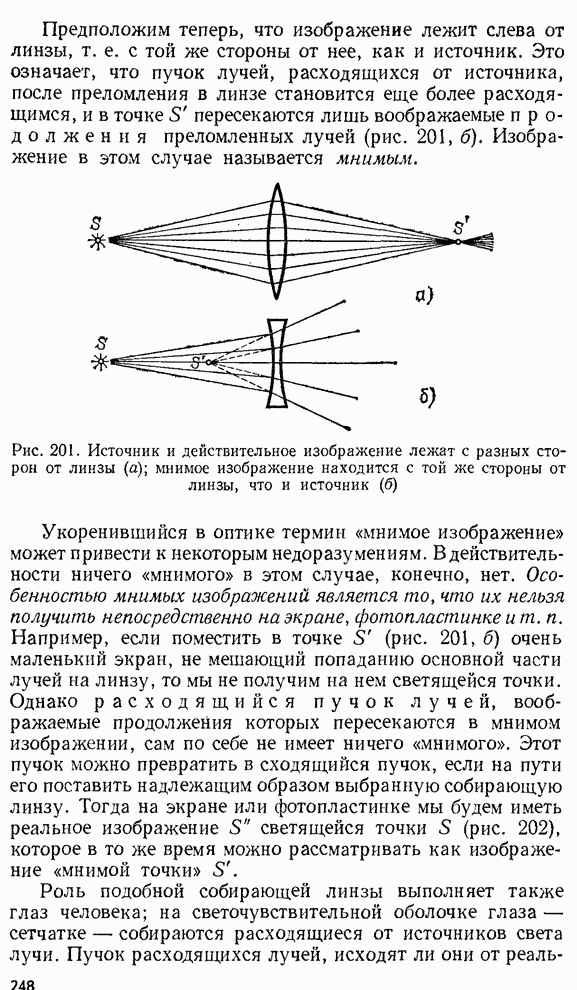
- § 90. Применения формулы тонкой линзы. Действительные и мнимые изображения.
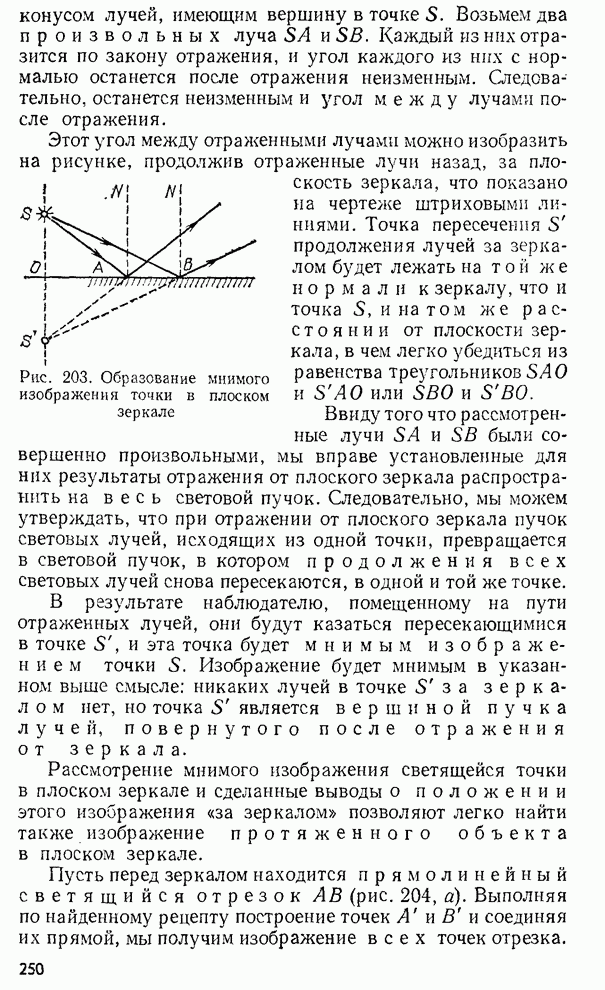
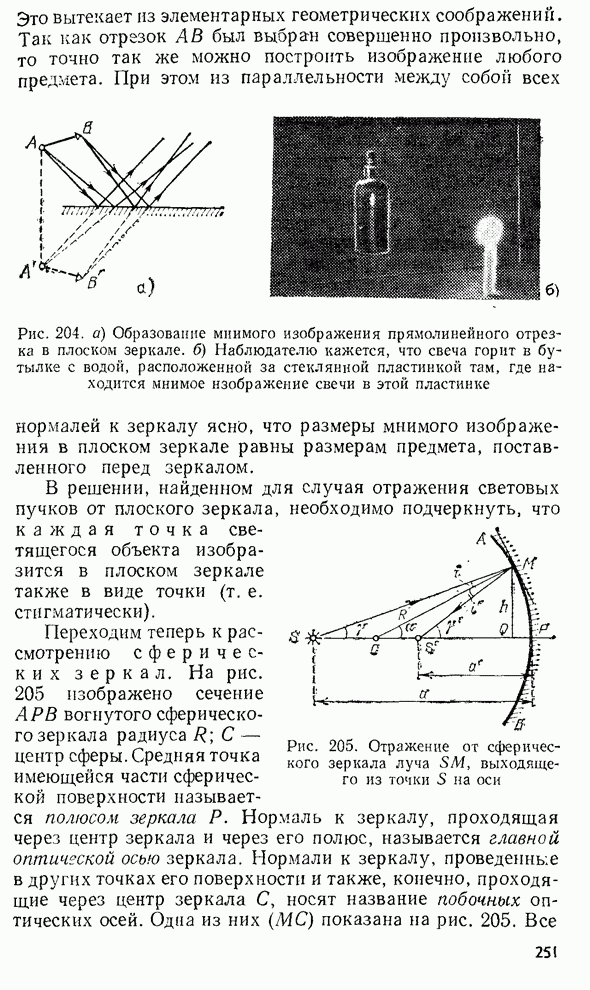
- § 91. Изображение точечного источника и протяженного объекта в плоском зеркале. Изображение точечного источника в сферическом зеркале
- § 92. Фокус и фокусное расстояние сферического зеркала
- § 93. Связь между положениями источника и его изображения на главной оси сферического зеркала
- § 94. Способы изготовления линз и зеркал
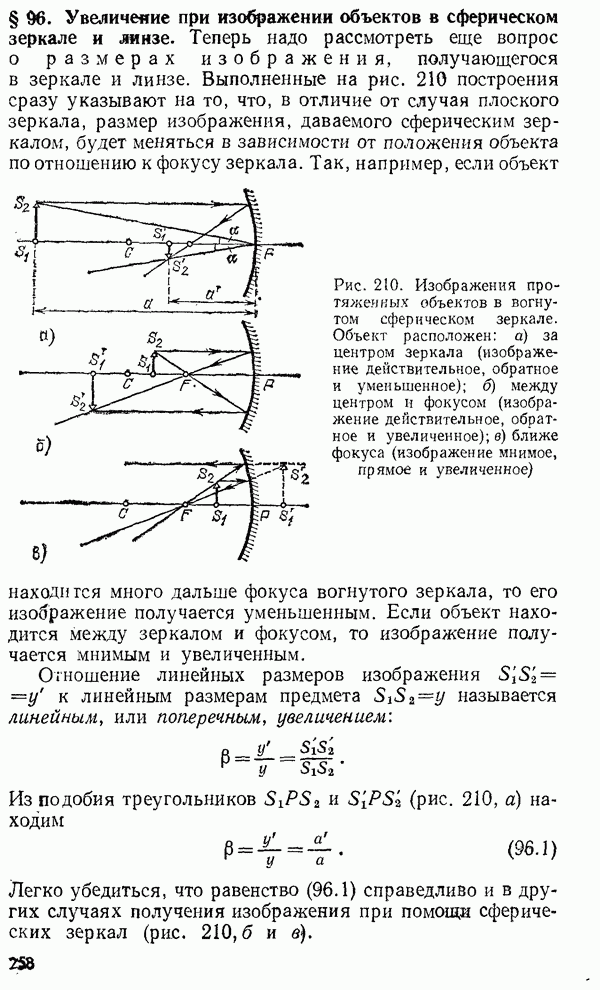
- § 95. Изображение протяженных объектов в сферическом зеркале и линзе
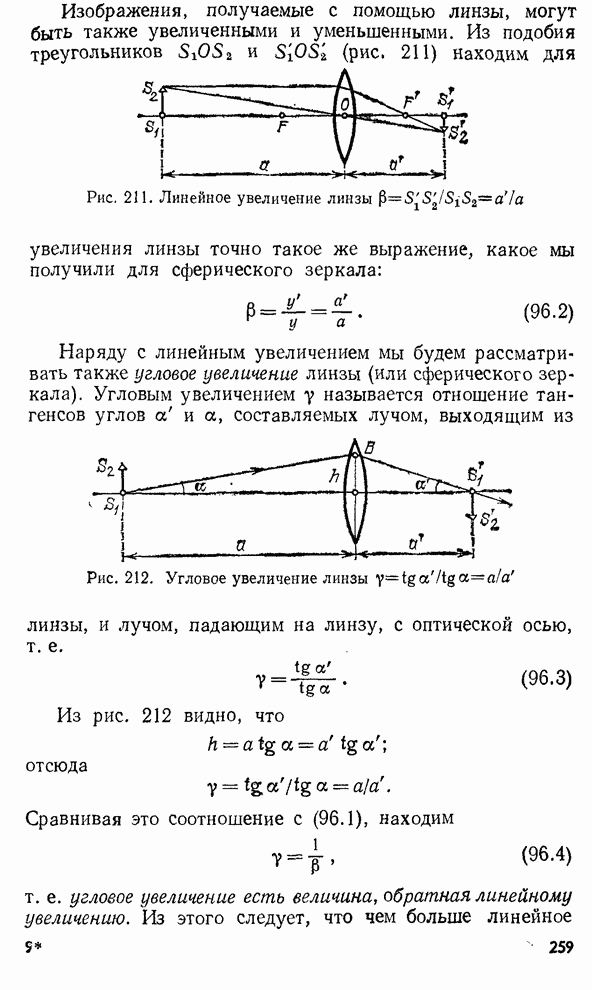
- § 96. Увеличение при изображении объектов в сферическом зеркале и линзе
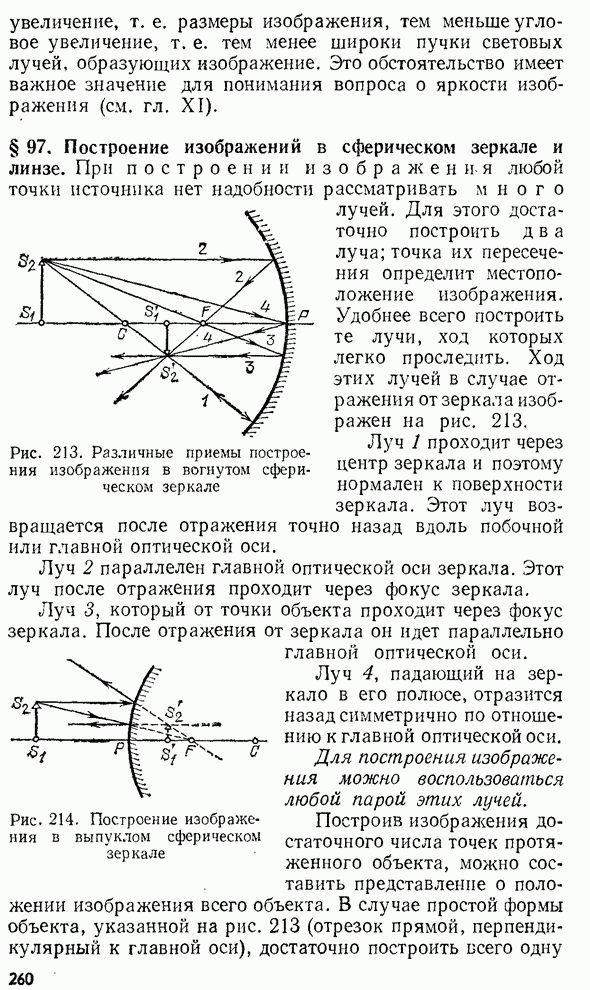
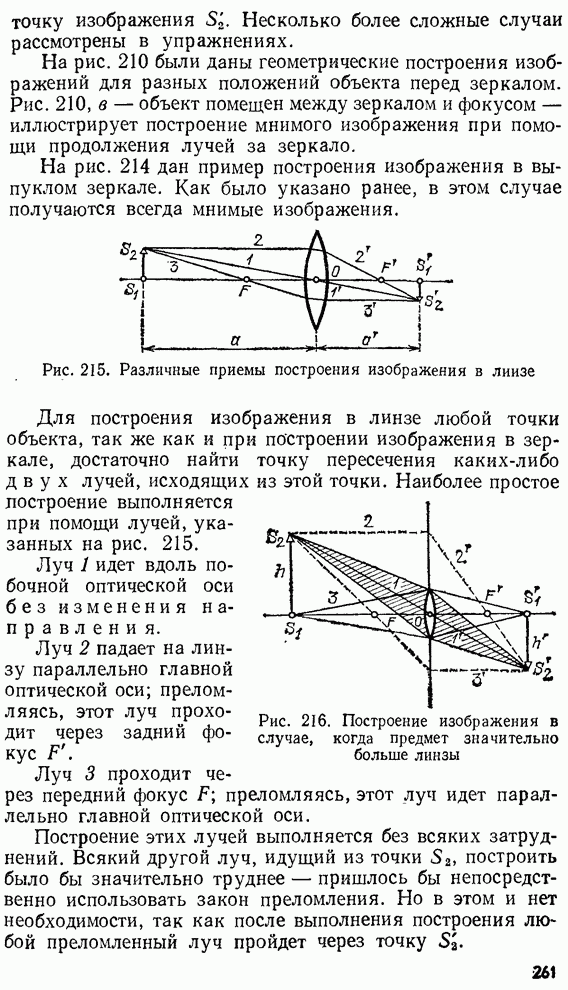
- § 97. Построение изображений в сферическом зеркале и линзе
- § 98. Оптическая сила линз
- Глава XI. Оптические системы и их погрешности
- § 99. Оптическая система
- § 100. Главные плоскости и главные точки системы
- § 101. Построение изображений в системе
- § 102. Увеличение системы
- § 103. Недостатки оптических систем
- § 104. Сферическая аберрация
- § 105. Астигматизм
- § 106. Хроматическая аберрация
- § 107. Ограничение пучков в оптических системах
- § 108. Светосила линзы
- § 109. Яркость изображения
- Глава XII. Оптические приборы
- § 110. Проекционные оптические приборы
- § 111. Фотографический аппарат
- § 112. Глаз как оптическая система
- § 113. Оптические приборы, вооружающие глаз
- § 114. Лупа
- § 115. Микроскоп
- § 116. Разрешающая способность микроскопа
- § 117. Зрительные трубы
- § 118. Увеличение зрительной трубы
- § 119. Телескопы
- § 120. Яркость изображения для протяженных и точечных источников
- § 121. «Ночезрительная труба» Ломоносова
- § 122. Зрение двумя глазами и восприятие глубины пространства. Стереоскоп.
- Раздел третий. Физическая оптика
- Глава XIII. Интерференция света
- § 123. Геометрическая и физическая оптика
- § 124. Опытное осуществление интерференции света
- § 125. Объяснение цветов тонких пленок
- § 126. Кольца Ньютона
- § 127. Определение длины световой волны с помощью колец Ньютона
- Глава XIV. Дифракция света
- § 128. Пучки лучей и форма волновой поверхности
- § 129. Принцип Гюйгенса
- § 130. Законы отражения и преломления света на основе принципа Гюйгенса
- § 131. Принцип Гюйгенса в толковании Френеля
- § 132. Простейшие дифракционные явления
- § 133. Объяснение дифракции по методу Френеля
- § 134. Разрешающая сила оптических инструментов
- § 135. Дифракционные решетки
- § 136. Дифракционная решетка как спектральный прибор
- § 137. Изготовление дифракционных решеток
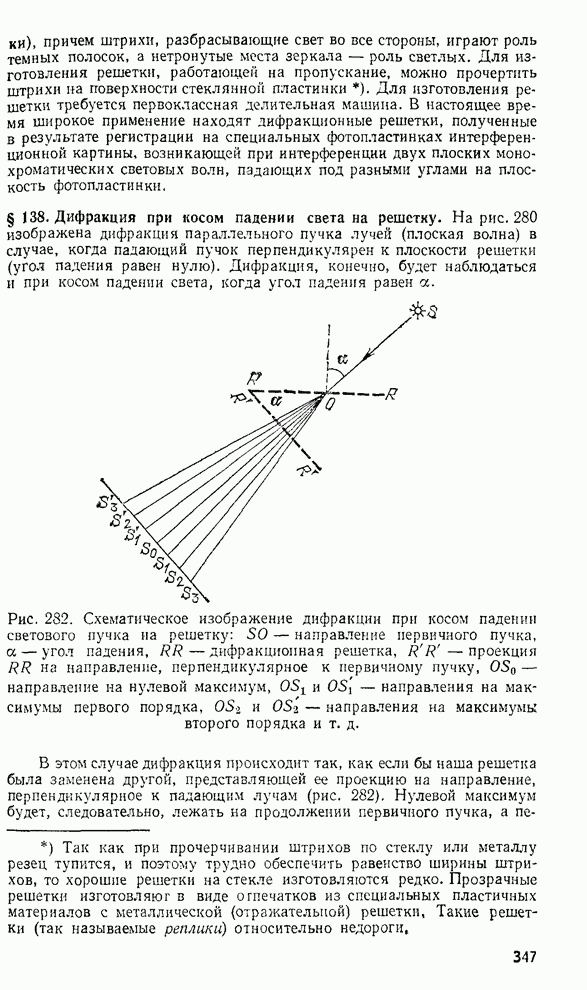
- § 138. Дифракция при косом падении света на решетку
- Глава XV. Физические принципы оптической голографии
- § 139. Фотография и голография
- § 140. Запись голограммы с помощью плоской опорной волны
- § 141. Получение оптических изображений по методу восстановления волнового фронта
- § 142. Голографирование по методу встречных световых пучков
- § 143. Использование голографии в оптической интерферометрии
- Глава XVI. Поляризация света и поперечность световых волн
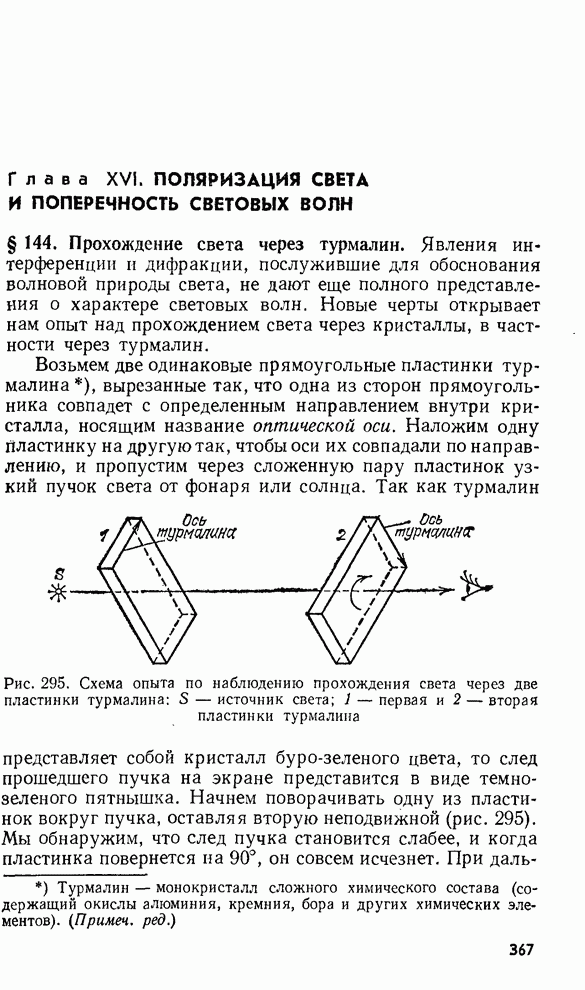
- § 144. Прохождение света через турмалин
- § 145. Гипотезы, объясняющие наблюдаемые явления. Понятие о поляризованном свете
- § 146. Механическая модель явлений поляризации
- § 147. Поляроиды
- § 148. Поперечность световых волн и электромагнитная теория света
- Глава XVII. Шкала электромагнитных волн
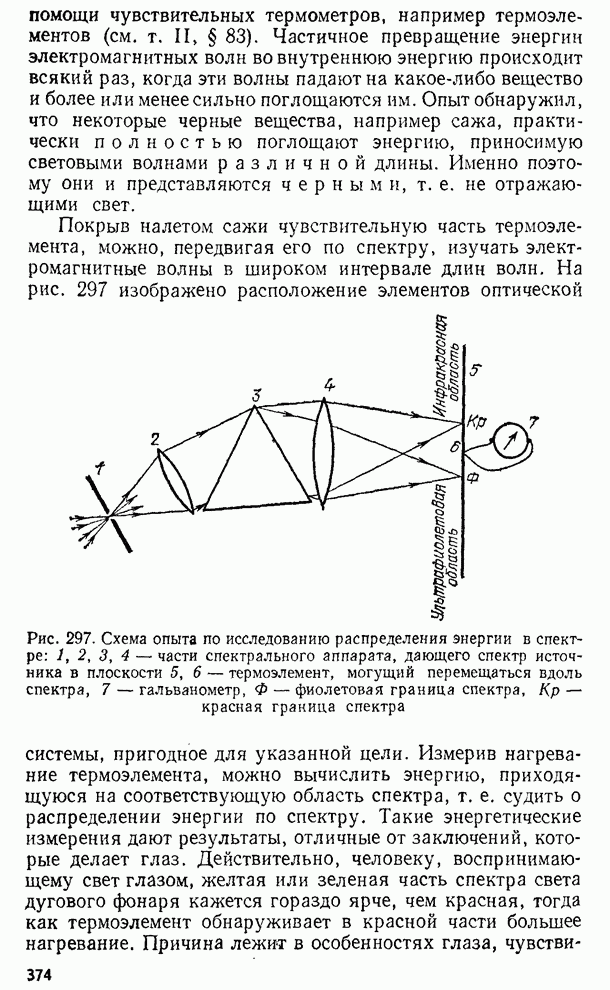
- § 149. Способы исследования электромагнитных волн различной длины
- § 150. Инфракрасное и ультрафиолетовое излучение
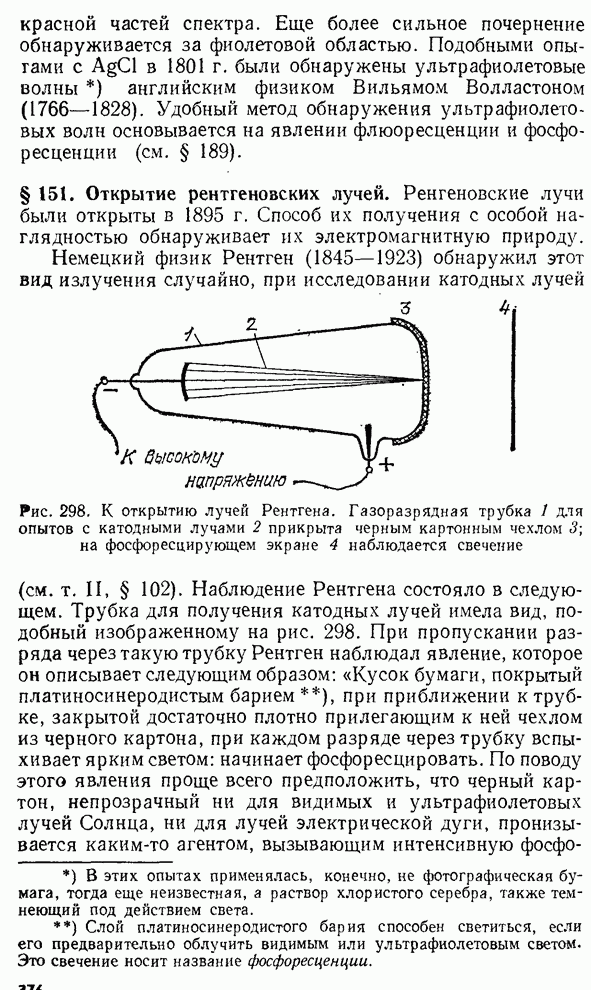
- § 151. Открытие рентгеновских лучей
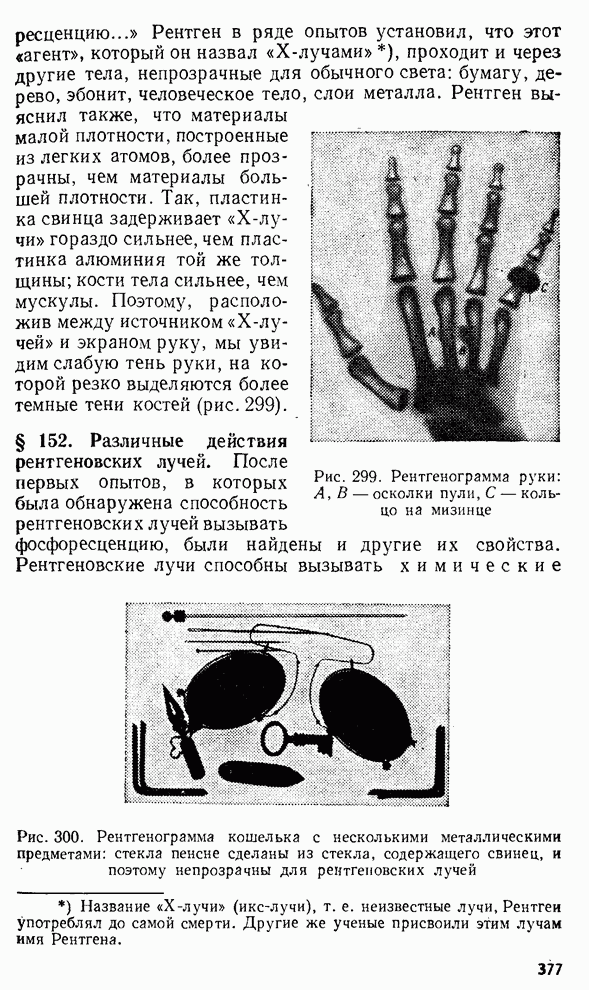
- § 152. Различные действия рентгеновских лучей
- § 153. Устройство рентгеновской трубки
- § 154. Происхождение и природа рентгеновских лучей
- § 155. Шкала электромагнитных волн
- Глава XVIII. Скорость света
- § 156. Первые попытки определения скорости света
- § 157. Определение скорости света Рёмером
- § 158. Определение скорости света по методу вращающегося зеркала
- Глава XIX. Дисперсия света и цвета тел
- § 159. Состояние вопроса о цвете тел до исследований Ньютона
- § 160. Основное открытие Ньютона в оптике
- § 161. Истолкование наблюдений Ньютона
- § 162. Дисперсия показателя преломления различных материалов
- § 163. Дополнительные цвета
- § 164. Спектральный состав света различных источников
- § 165. Свет и цвета тел
- § 166. Коэффициенты поглощения, отражения и пропускания
- § 167. Цветные тела, освещенные белым светом
- § 168. Цветные тела, освещенные цветным светом
- § 169. Маскировка и демаскировка
- § 170. Насыщенность цветов
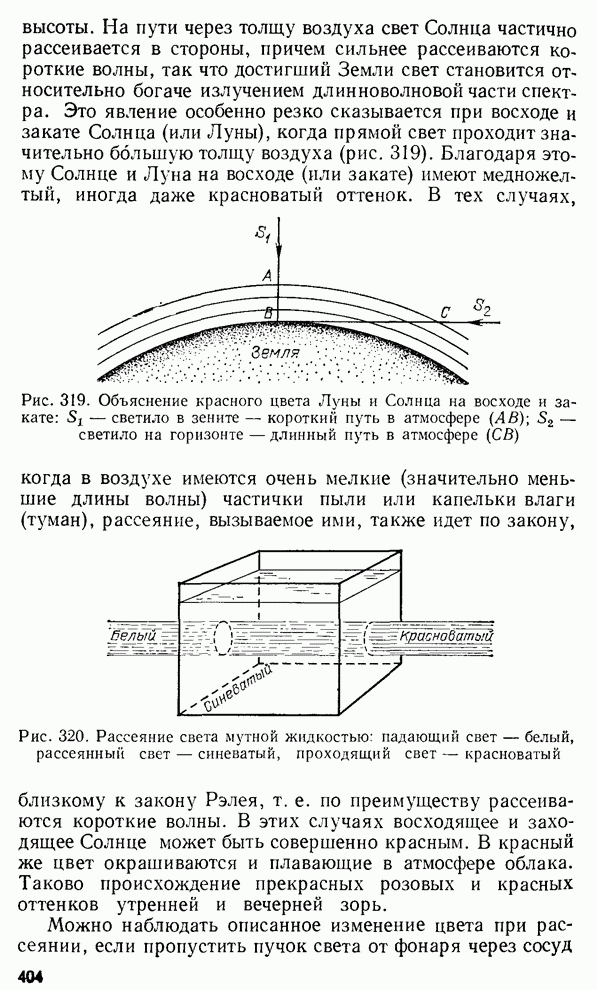
- § 171. Цвет неба и зорь
- Глава XX. Спектры и спектральные закономерности
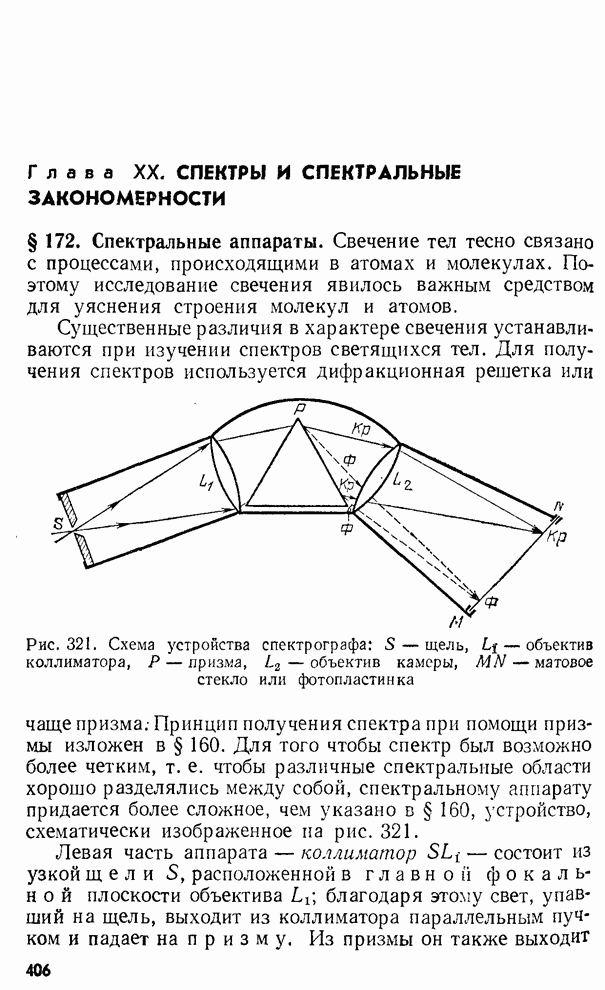
- § 172. Спектральные аппараты
- § 173. Типы спектров испускания
- § 174. Происхождение спектров различных типов
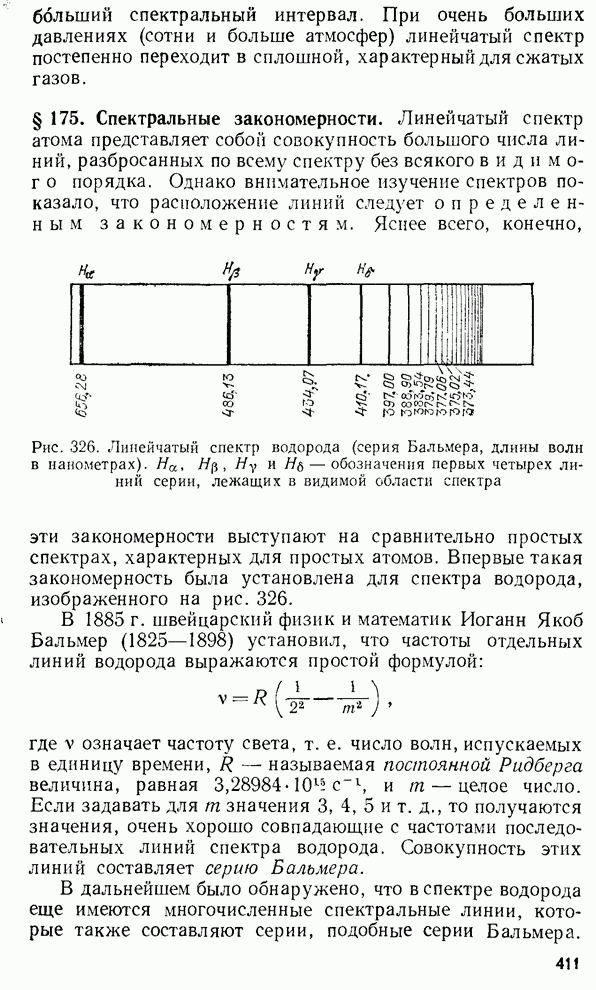
- § 175. Спектральные закономерности
- § 176. Спектральный анализ по спектрам испускания
- § 177. Спектры поглощения жидких и твердых тел
- § 178. Спектры поглощения атомов. Линии Фраунгофера
- § 179. Излучение накаленных тел. Абсолютно черное тело
- § 180. Зависимость излучения накаленных тел от температуры. Лампы накаливания
- § 181. Оптическая пирометрия
- XXI. Действия света
- § 182. Действия света на вещество. Фотоэлектрический эффект
- § 183. Законы фотоэлектрического эффекта
- § 184. Понятие о световых квантах
- § 185. Применение фотоэлектрических явлений
- § 186. Фотолюминесценция. Правило Стокса
- § 187. Физический смысл правила Стока
- § 188. Люминесцентный анализ
- § 189. Фотохимические действия света
- § 190. Роль длины волны в фотохимических процессах
- § 191. Фотография
- § 192. Фотохимическая теория зрения
- § 193. Длительность зрительного ощущения
- Раздел четвертый. Атомная и ядерная физика
- Глава XXII. Строение атома
- § 194. Представление об атомах
- § 195. Постоянная Авогадро. Размеры и массы атомов
- § 196. Элементарный электрический заряд
- § 197. Единицы заряда, массы и энергии в атомной физике
- § 198. Измерение массы заряженных частиц. Масс-спектрограф
- § 199. Масса электрона. Зависимость массы от скорости
- § 200. Закон Эйнштейна
- § 201. Массы атомов; изотопы
- § 202. Разделение изотопов. Тяжелая вода
- § 203. Ядерная модель атома
- § 204. Энергетические уровни атомов
- § 205. Вынужденное излучение света. Квантовые генераторы
- § 206. Атом водорода. Своеобразие законов движения электрона в атоме
- § 207. Многоэлектронные атомы. Происхождение оптических и рентгеновских спектров атомов
- § 208. Периодическая система элементов Менделеева
- § 209. Квантовые и волновые свойства фотонов
- § 210. Понятие о квантовой (волновой) механике
- Глава XXIII. Радиоактивность
- § 211. Открытие радиоактивности. Радиоактивные элементы
- § 212. L-, B-, Г- излучение. Камера Вильсона
- § 213. Способы регистрации заряженных частиц
- § 214. Природа радиоактивного излучения
- § 215. Радиоактивный распад и радиоактивные превращения
- § 216. Применения радиоактивности
- § 217. Ускорители
- Глава XXIV. Атомные ядра и ядерная энергия
- § 218. Понятие о ядерных реакциях
- § 219. Ядерные реакции и превращение элементов
- § 220. Свойства нейтронов
- § 221. Ядерные реакции под действием нейтронов
- § 222. Искусственная радиоактивность
- § 223. Позитрон
- § 224. Применение закона Эйнштейна к процессам аннигиляции и образования пар
- § 225. Строение атомного ядра
- § 226. Ядерная энергия. Источник энергии звезд.
- § 227. Деление урана
- § 228. Применения незатухающей цепной реакции деления. Атомная и водородная бомбы
- § 229. Ядерные реакторы и их применения
- Глава XXV. Элементарные частицы
- § 230. Общие замечания
- § 231. Нейтрино
- § 232. Ядерные силы. Мезоны
- § 233. Частицы и античастицы
- § 234. Частицы и взаимодействия
- § 235. Детекторы элементарных частиц
- § 236. Парадокс часов
- § 237. Космическое излучение (космические лучи)
- Глава XXVI. Новые достижения в физике элементарных частиц
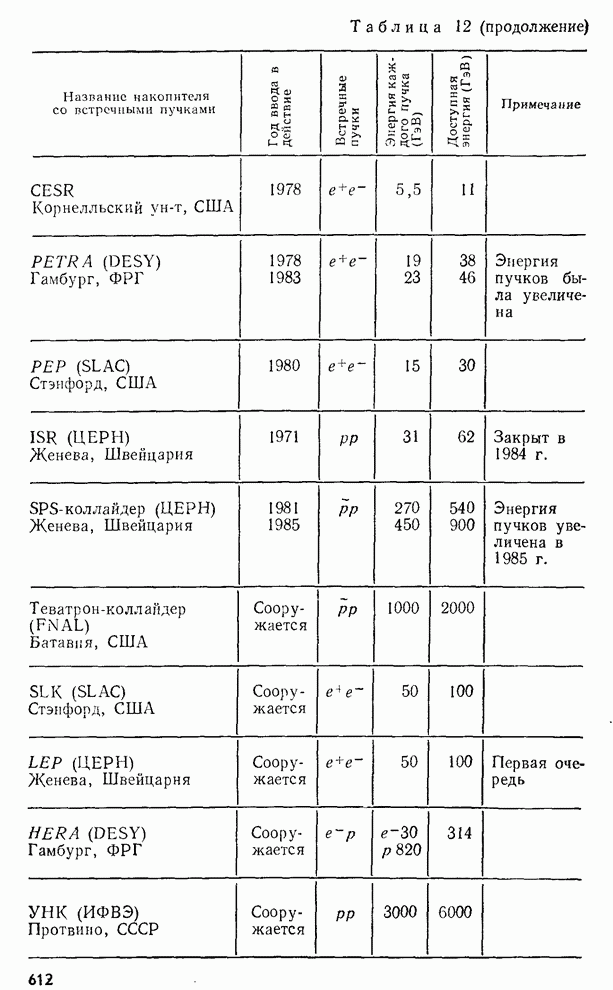
- § 238. Ускорители и экспериментальная техника
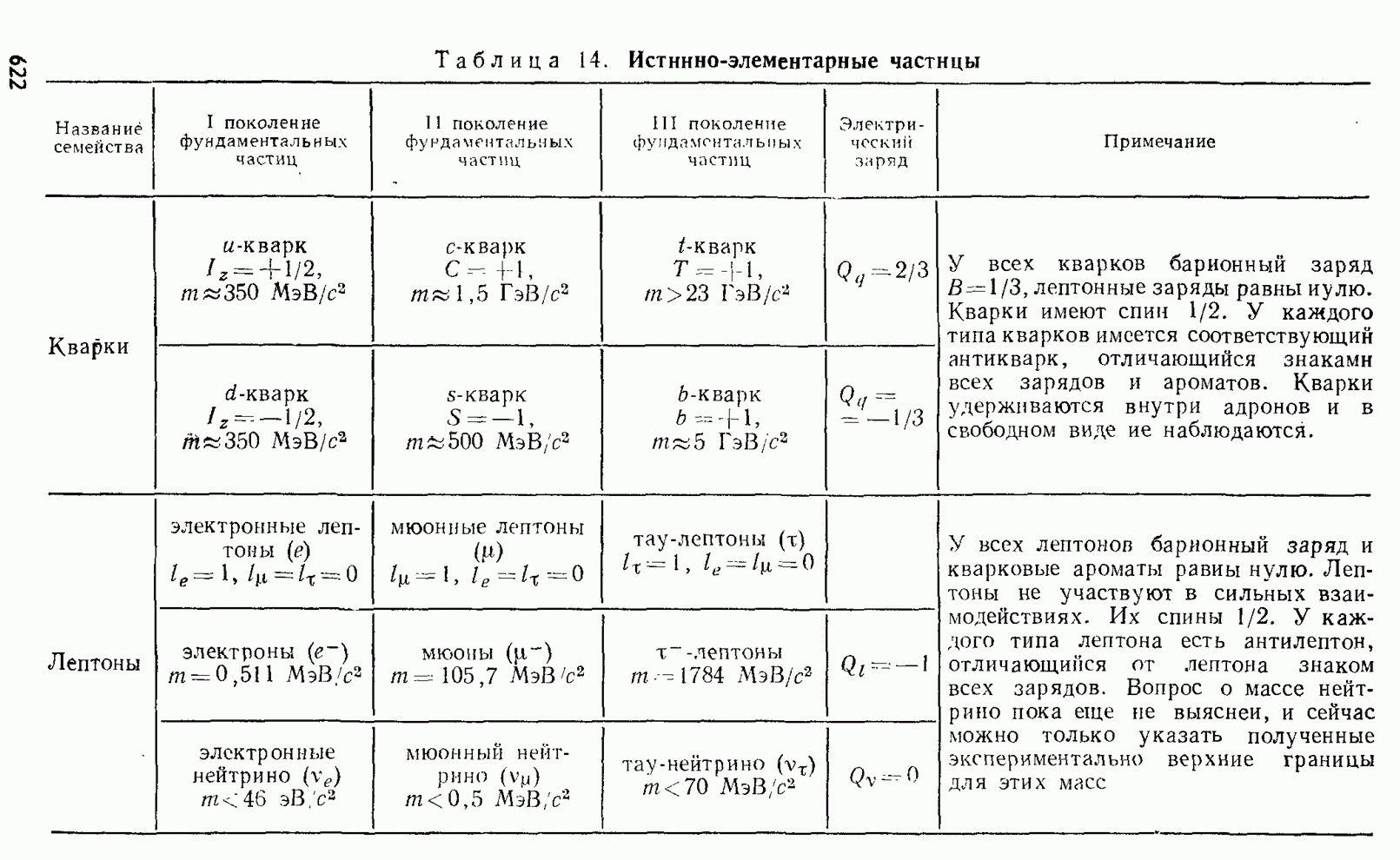
- § 239. Адроны и кварки
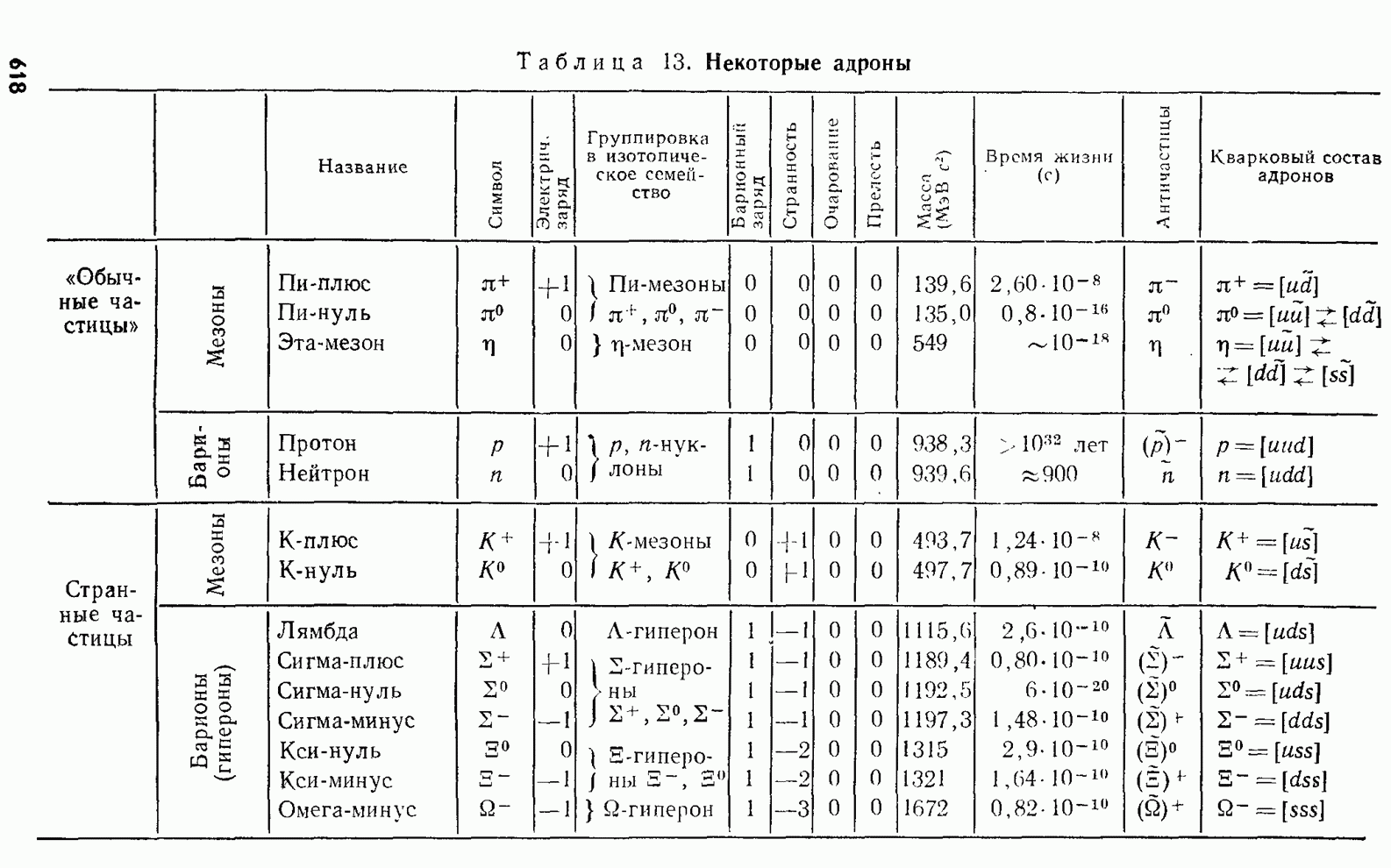
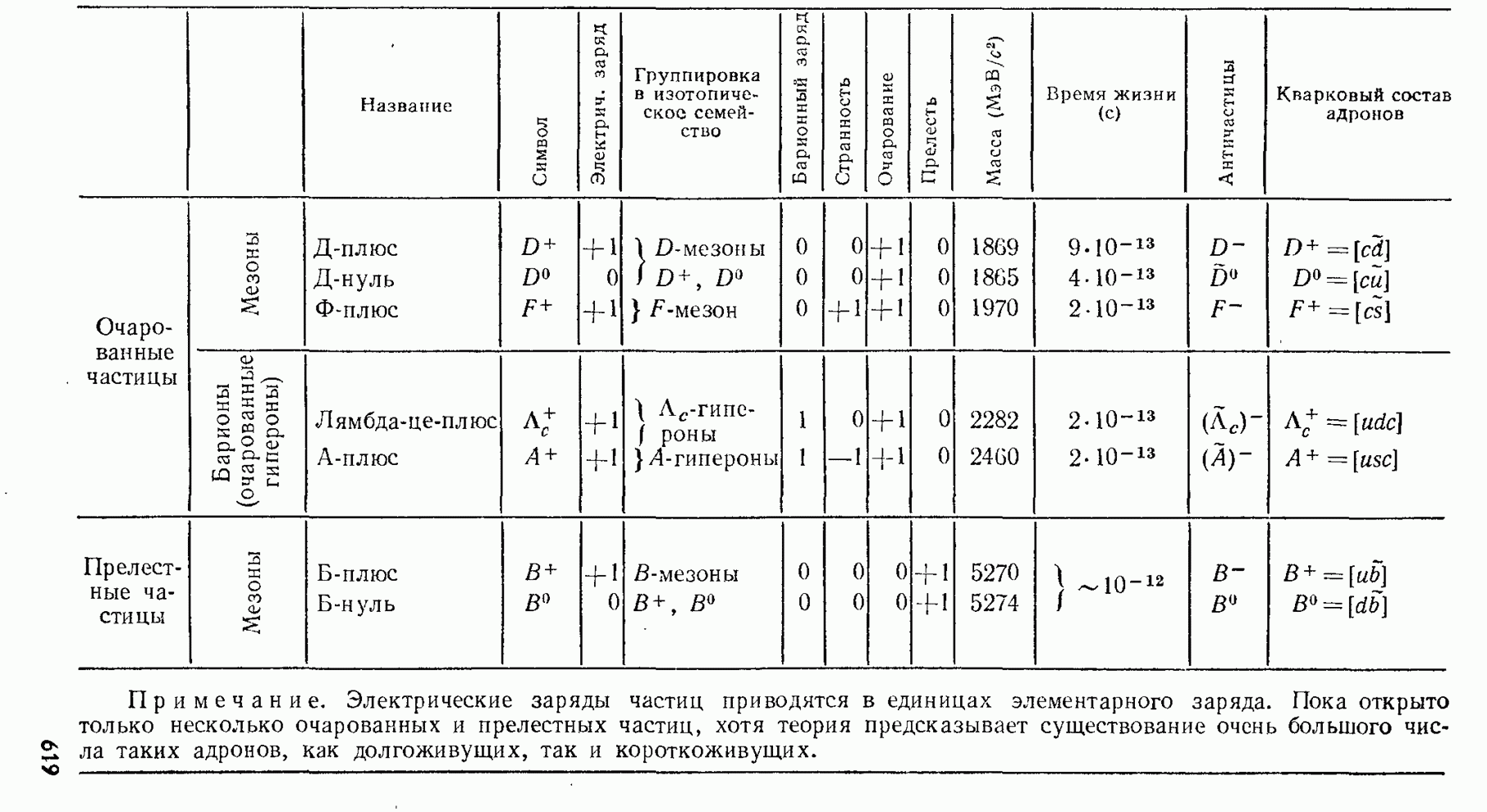
- § 240. Кварковая структура андронов
- § 241. Кварковая модель и процессы образования и распада адронов
- § 242. Лептоны. Промежуточные бозоны. Единство всех взаимодействий
- Заключение