3.3. Система с ожиданием при простейшем потоке вызовов

Система распределения информации называется системой с ожиданием, если заявка, заставшая все каналы занятыми, становится в очередь и ждет, пока не освободится какая-либо линия связи.

Если время ожидания ничем не ограничено, то система называется «чистой системой с ожиданием». Если оно ограничено какими-либо условиями, то система называется «системой смешанного типа».

Заявки, стоящие в очереди, могут быть обслужены тремя способами: первым пришел – первым обслужен (упорядоченное обслуживание), обслуживание в случайном порядке и обслуживание по заданным приоритетам.

Рассмотрим «чистую систему с ожиданием» с упорядоченным типом обслуживания заявок в очереди и простейшим входным потоком вызовов. Будем также полагать, что величина нагрузки входного потока  меньше числа каналов связи . В этом случае средняя длина очереди заявок . При этом «чистая система с ожиданием»  будет иметь бесконечное, но счетное число состояний:

 - ни один канал связи не занят,
 - занят ровно один канал связи,
…
 - занято ровно  каналов связи,

…
 - заняты все  каналов связи,
 - заняты все  каналов связи и одна заявка находится в очереди,
…
 - заняты все  каналов связи и  заявок находится в очереди,
…

Число заявок , стоящих в очереди, может быть сколько угодно большим. При этом очевидно, что первые  дифференциальных уравнений ничем не будут отличаться от ранее рассмотренных уравнений Эрланга:

Отличие новых уравнений Эрланга начнется при . Действительно, в состояние  система с ожиданием может перейти не только из , но и из состояния .

Составим дифференциальное уравнение для . Зафиксируем момент времени  и найдем  - вероятность того, что система в момент времени  будет в состоянии . Это может произойти в трех случаях:

 - в момент времени  система находилась в состоянии  и за промежуток времени  не пришел ни один вызов и ни один канал связи не освободился;
 - в момент времени  система находилась в состоянии  и за промежуток времени  пришел один вызов;
 - в момент времени  система находилась в состоянии  и за промежуток времени  освободился один канал связи.

Учитывая, что интенсивность входного потока заявок , а выходного  с показательным временем обслуживания, вероятность

и после перехода к пределу при , получаем

.

Вычислим вероятности  того, что в момент времени  в очереди находится ровно  заявок. Очевидно, что система может перейти в это состояние при выполнении одного из трех событий:

 - в момент времени  система находилась в состоянии  и за время  не пришла ни одна заявка и ни один канал не освободился;
 - в момент времени  система находилась в состоянии  и за время  пришла одна заявка;
 - в момент времени  система находилась в состоянии  и за время  освободился один канал.

В результате получим следующие вероятности данных событий:

Так как события ,  и  несовместны, то вероятность

и переходя к пределу при , получаем

.

В результате получаем следующую систему дифференциальных уравнений:

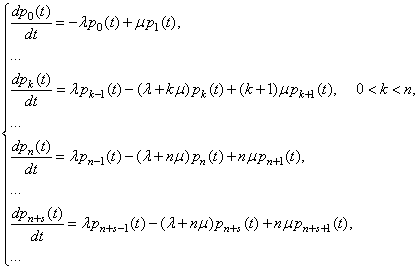
Полученные дифференциальные уравнения являются естественным обобщением уравнений Эрланга на случай системы с ожиданием. При интегрировании полученной системы уравнений нужно учитывать, что хотя теоретически число возможных состояний системы бесконечно, но на практике вероятности  при возрастании  становятся пренебрежимо малыми, и соответствующие уравнения могут быть отброшены.

Система дифференциальных уравнений Эрланга переходит в систему линейных уравнений при установившемся режиме работы, т.е. при . В этом случае вероятности  стремятся к своим предельным значениям , а производные равны нулю:

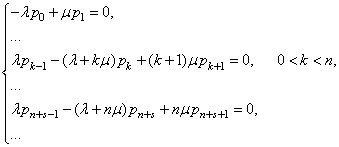
Для решения полученной системы уравнений необходимо добавить условие

.                                                        (3.7)

Очевидно, что вероятности  будут определяться полученным ранее выражением (3.3). При  путем последовательных подстановок получим

.

Учитывая условие (3.7), выразим вероятность  через  и :

,

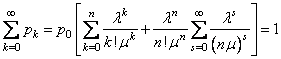т.к. величина  меньше единицы, то ряд 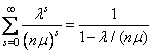 образует геометрическую прогрессию и искомое выражение равно

.

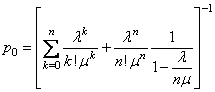Учитывая, что величина  соответствует входной нагрузке, получаем формулу для расчета вероятностей :

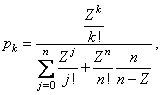 при ,                   (3.8)

 при .                         (3.9)

Выражения (3.8) и (3.9) представляют собой распределение Эрланга для систем с ожиданием. Математическое описание таких систем определяется не только вероятностями , но и вероятностью  того, что время ожидания  окажется больше заданной величины . Данная вероятность будет зависеть от одновременного совершения двух событий:  - существование очереди и  - время ожидания в очереди больше величины :

                   (3.10)

Очевидно, что вероятность  складывается из вероятностей , , ,…, ,…, т.е. вероятностей занятости всех каналов связи и вероятностей нахождения в очереди одной и более заявок:

.

Подставляя вместо величин  выражение (3.9), получим

.

Данное выражение получило название второй формулы Эрланга. Вычислим вероятность второго события . Допустим, что в очереди стоит одна заявка. Она будет находиться там до тех пор, пока один из  каналов связи не освободится. Вероятность того, что канал связи в течение времени  будет обрабатывать запрос, определяется величиной . Учитывая, что общее число каналов связи равно  и все они должны быть заняты в промежуток времени , искомая вероятность нахождения одной заявки в очереди равна . Однако, в общем случае, очередь может состоять из произвольного числа вызовов. Очевидно, что, например, для второй заявки в очереди, вероятность  изменится пропорционально уменьшению числа каналов связи на единицу. Действительно, в случае освобождения одного из  каналов связи на его вход тут же поступает заявка, стоящая первой в очереди, а вторая встает на место первой. Следовательно, вероятность того, что вторая заявка простоит в очереди время , равна . В общем случае сложно определить на каком месте в очереди будет стоять та или иная заявка, но, зная величину нагрузки входного потока , можно определить среднюю длину очереди как . Тогда вероятность нахождения заявки в очереди время  запишется в виде

.

После подстановки выражений для  и  в формулу (3.10), получим

.

Величина  позволяет определить качество работы системы распределения информации с ожиданием. Так, при  система имеет повышенное качество, а при  - пониженное.