6.5. Моделирование самоподобных случайных процессов

Исследования реальных трафиков в цифровых сетях связи (Internet, Ethernet, Telnet и др.) показали, что они лучше всего описываются самоподобными случайными процессами. В данном параграфе рассмотрим некоторые из наиболее распространенных распределений, используемых при моделировании пульсирующих источников.

Одним из первых неэкспоненциальных распределений, которые были применены при моделировании сетевого трафика, является логнормальное распределение. Определение логнормального распределения основывается на нормальном распределении в виде функциональной зависимости

,

где  - нормально распределенная СВ с нулевым средним;  - СВ распределенная по логнормальному закону, который имеет вид

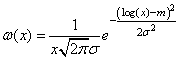, при ,

где  - среднеквадратическое отклонение СВ ;  - математическое ожидание. Эти параметры можно определить на основе экспериментальных данных по следующим формулам:

; .

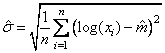На основе известных значений  и  нормально распределенной СВ  можно определить математическое ожидание и дисперсию для логнормально распределенной СВ :

; .

Генерировать логнормальные СВ  можно путем следующего функционального преобразования:

,

где  - нормально распределенная СВ с нулевым МО и единичной дисперсией.

Для моделирования размеров передаваемых файлов, типовых сообщений, Web-страниц часто используется распределение Парето, которое имеет следующий вид

; ; ; ,

где  - параметр формы;  - параметр, определяющий нижнюю границу для случайной величины.

Известно, что ЭВМ позволяет генерировать равномерно распределенные СВ  в диапазоне от 0 до 1. Для того, чтобы смоделировать СВ с ПРВ Парето необходимо найти функциональное преобразование . Это можно сделать на основе выражения

,

откуда

, при .

Таким образом, получаем следующее выражение для моделирования СВ с ПРВ Парето:

,

где  - случайное число, генерируемое на ЭВМ в диапазоне от 0 до 1. Параметр  связан с показателем Херста выражением

.

Параметр  обычно вычисляется на основе метода максимального правдоподобия [6] по известным результатам измерения интенсивности реального трафика :

,

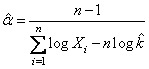где .

Пример сгенерированной случайной последовательности с параметрами  и , представлен на рис. 6.5.

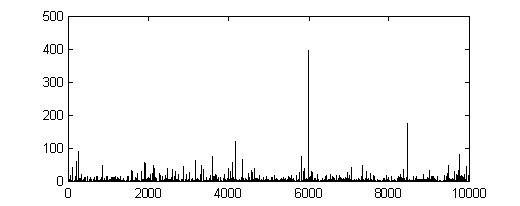
Рис. 6.5. Пример фрактальной случайной последовательности с ПРВ Парето

Другим примером ПРВ для генерирования самоподобных трафиков является распределение Вейбулла, которое имеет следующий вид:

,

где  и  - некоторые параметры, влияющие на форму ПРВ. Для моделирования СВ  с ПРВ Вейбулла используется функциональное преобразование вида:

.

Существуют разные способы подбора распределения Вейбулла: метод наименьших квадратов, метод моментов, оценка максимального правдоподобия и др [6,7]. Однако наиболее простым и надежным способом является метод максимального правдоподобия, при котором оценка параметра  определяется последовательным вычислением:

.

В свою очередь, оценка параметра  находится как

.

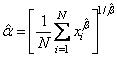На основе вычисленных значений трафика  можно путем моделирования определить средний объем использованного буфера при передаче данных по каналу связи с заданной пропускной способностью  (в условных единицах измерения). Алгоритм моделирования заключается в следующем. Если значение передаваемого трафика , то в буфере передачи запоминается объем данных равный , в противном случае . В следующий момент времени  объем передаваемых данных составит величину . Если данное значение больше пропускной способности канала передачи , то в буфере запоминается объем данных . И так далее, до тех пор, пока все данные не будут переданы по каналу связи. Таким образом, получаем набор значений , которые будут характеризовать размер данных, находящихся в буфере в моменты времени . Следовательно, средний размер использования буфера можно найти по формуле

.

Следует заметить, что если размер буфера резко возрастает при уменьшении , то канал с такой пропускной способностью «не справляется» с требуемым объемом передаваемых данных, и, следовательно, значение  нужно увеличивать.

Зная средний объем использования буфера, по формуле Литтла можно определить среднее время нахождения единицы данных (байт, пакет, и т.д.) в буфере:

,

где  - средняя интенсивность входного потока, которая определяется как

,

где  - используемая ПРВ при моделировании входного потока.