5.3. Анализ цифровых сетей с простейшим входным потоком и ограниченным объемом буфера

В реальных системах входной буфер имеет ограничения на объем хранимых данных. Следовательно, при поступлении большого числа пакетов на вход такой системы может возникнуть блокировка, т.е. отказ в обслуживании поступившего пакета, который в результате оказывается потерянным. Очевидно, что при проектировании систем связи необходимо уметь вычислять вероятность возникновения такой ситуации.

Вначале рассмотрим цифровую систему, состоящую из буфера с ограниченным объемом и одного сервера (рис. 5.5).

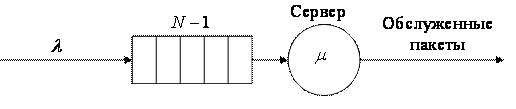
Рис. 5.5. Система с ограниченной длиной очереди и одним сервером

Допустим, что максимальное число заявок в системе может быть равно  (включая и ту, которая находится на сервере). Поступивший  пакет получает отказ в обслуживании и считается потерянным. Также будем полагать, что интервалы времени между поступлениями пакетов распределены по пуассоновскому закону с параметром , а время обслуживания подчинено показательному закону с параметром . Тогда, используя формулу Эрланга для систем с ограничением по длине очереди, можно вычислить вероятность нахождения  пакетов в системе

,                                             (5.2)

где ;  - число серверов;  - число пакетов в очереди. Так как в данном случае , то формула (5.2) упрощается

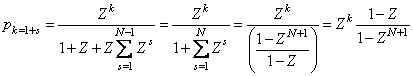, при

и

, при .

Полученное выражение для  можно использовать при вычислении вероятности блокировки. Очевидно, что блокировки возникают при одновременном совершении двух событий: когда в системе находится  пакетов и когда на ее вход поступает  пакет. Вероятность первого события

,

вероятность второго

и вероятность потери пакета

.

Например, при  и размере буфера  пакетов, вероятность блокировки примерно равна .

Среднее число пакетов в системе может быть найдено как математическое ожидание по формуле

,

а среднее время пребывания пакетов в системе

.

Определим пропускную способность системы как число пакетов, обслуживаемых системой за единицу времени, т.е. необходимо определить среднюю интенсивность выходного потока. Очевидно, что при возможности потерь части поступающих пакетов, интенсивность выходного потока  будет отличаться от интенсивности входного . Однако, зная интенсивность обслуживания одного пакета  и вероятность занятости сервера , средняя интенсивность выходного потока может быть определена по формуле

.

В качестве реального примера рассмотрим концентратор сети с коммутацией пакетов, который обрабатывает пакеты со средней длиной 1200 битов со скоростью  пакета/с (выходной поток из концентратора имеет скорость 2400 бит/с). Если входной поток имеет интенсивность  пакет/с, то  и можно рассчитать, что при  пакетов в системе вероятность блокировки составит примерно 0,001. Для того чтобы получить вероятность блокировки , необходимо использовать буфер не менее 18 пакетов () по 1200 бит каждый, т.е. 2700 байт.