3.4. Система с ожиданием при примитивном потоке вызовов

Допустим, что поток заявок формируется ограниченным числом пользователей  и является примитивным с параметром , где  - интенсивность потока заявок от одного абонента. Время обслуживания заявок будем считать подчиненным показательному закону распределения с параметром . Требуется определить вероятность  того, что заявка, заставшая все  каналов связи занятыми, простоит в очереди дольше заданного времени . Данная вероятность также определяется выражением . Найдем величины  и .

Так как входной поток заявок является примитивным, то вероятность того, что в системе связи будет находиться  вызовов, можно определить по формуле Энгеста

.                                                (3.11)

Так как в системе распределения информации имеется  каналов связи, то вероятность  - существования очереди - определяется выражением

.

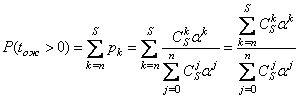Найдем вероятность  при условии, что все  каналов заняты. Вероятность занятости одного ОП в течение времени  определяется выражением . Если заявка стоит первой в очереди, то . В общем случае для произвольной -й заявки в очереди имеем . Так как номер заявки, стоящей в очереди, неизвестен, то значение  необходимо положить равным средней длины очереди , где  - средняя интенсивность входного потока:

.

Подставляя вместо  выражение , а вместо  формулу (3.11), получаем

.

Таким образом, получаем искомое выражение для вероятности :

,

а вероятность  определяется как

.