4.3. Метод расчета потерь для многозвенных схем

Рассмотрим трехзвенную коммутационную схему, в которой каждый выход коммутатора первого звена связан с одним входом коммутатора второго звена, а каждый выход коммутатора второго звена связан со входом коммутатора третьего звена (рис. 4.6).

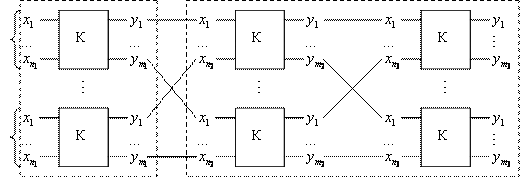
Рис. 4.6. Трехзвенная коммутационная схема связанного типа

При расчете потерь условно разделим данную схему на две: однозвенную, состоящую из коммутаторов первого звена и двухзвенную, состоящую из коммутаторов второго и третьего звеньев. Потери на первом звене обозначим через , а на втором и третьем – через . Величина  показывает вероятность того, что поступивший вызов не может быть соединен ни с одним из  выходов коммутатора первого звена, а потери  вероятность того, что вход коммутатора второго звена не может обеспечить соединение ни с одним из выходов схемы. Общие потери  будут складываться из потерь для каждой условной схемы. Учитывая, что вероятности  и  описывают совместные события, получаем следующую формулу для расчета потерь:

.                             (4.7)

Если на вход системы поступает простейший поток вызовов при числе входов , то потери на первом звене можно найти по формуле Эрланга:

,

где  - величина нагрузки на входе коммутатора первого звена.

В другом случае, когда число входов  не намного больше числа выходов , вероятность потерь  определяется по формуле Энгеста:

,

где  - нагрузка, поступающая от одного абонента.

В третьем случае, когда  потери , т.к. соединение с одним из  выходов всегда возможно.

При расчете потерь  второй условной схемы полагают, что на ее вход поступает примитивный поток вызовов, подчиненный закону Бернулли, а на вход коммутаторов третьего звена простейший поток заявок [1].

Если число входов  коммутаторов второго звена равно числу выходов , то потери из-за невозможности соединения входа коммутатора с одним из его выходов равны нулю и общие потери  будут определяться по формуле (4.2). Причем вероятность

,

где  - величина нагрузки, приходящая на  выходов коммутатора второго звена, а вероятность

,

где  - средняя интенсивность нагрузки, приходящая на одну промежуточную линию между коммутаторами второго и третьего звеньев. Таким образом, общие потери определяются по формуле

.                          (4.8)

Если число входов , то возникают дополнительные потери . В этом случае, с учетом выражений (4.6) и (4.8), получаем

,

где  - средняя интенсивность потока обслуженных заявок одним входом коммутатора второго звена.

Аналогично можно вычислить потери  для разных режимов работы второй условной схемы и затем путем подстановки найденных значений  и  вычислять общие потери по формуле (4.7).