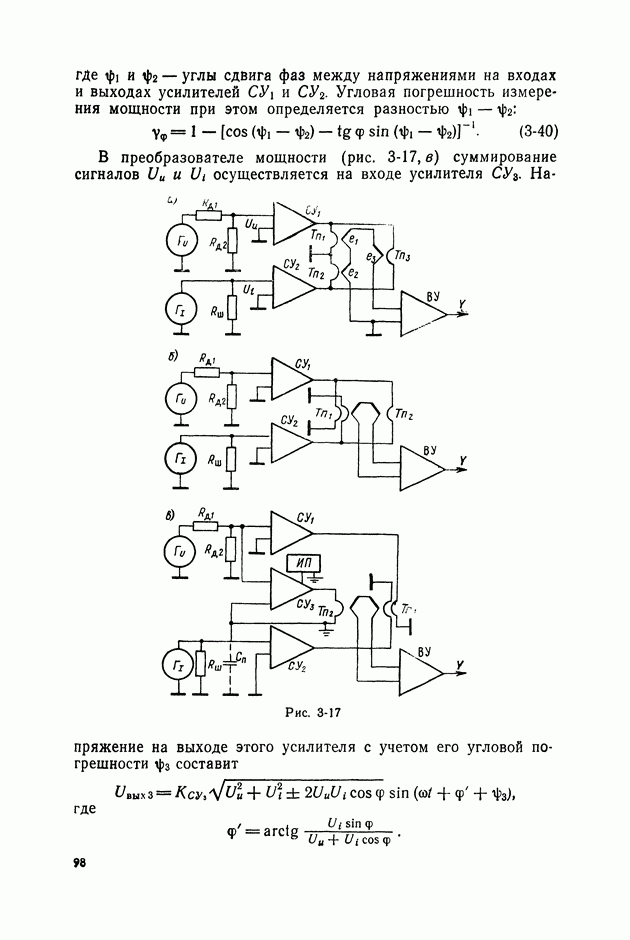
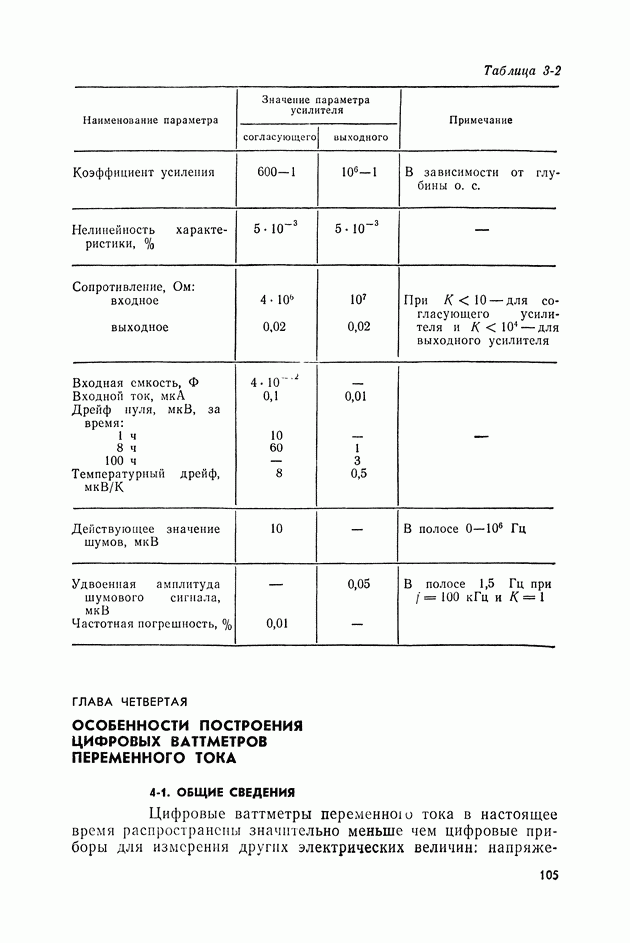
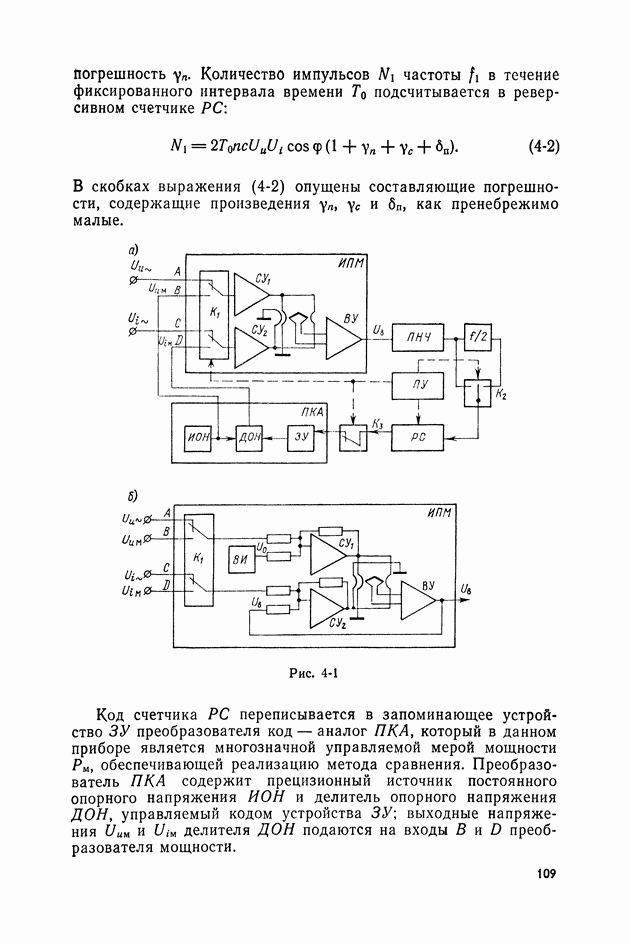
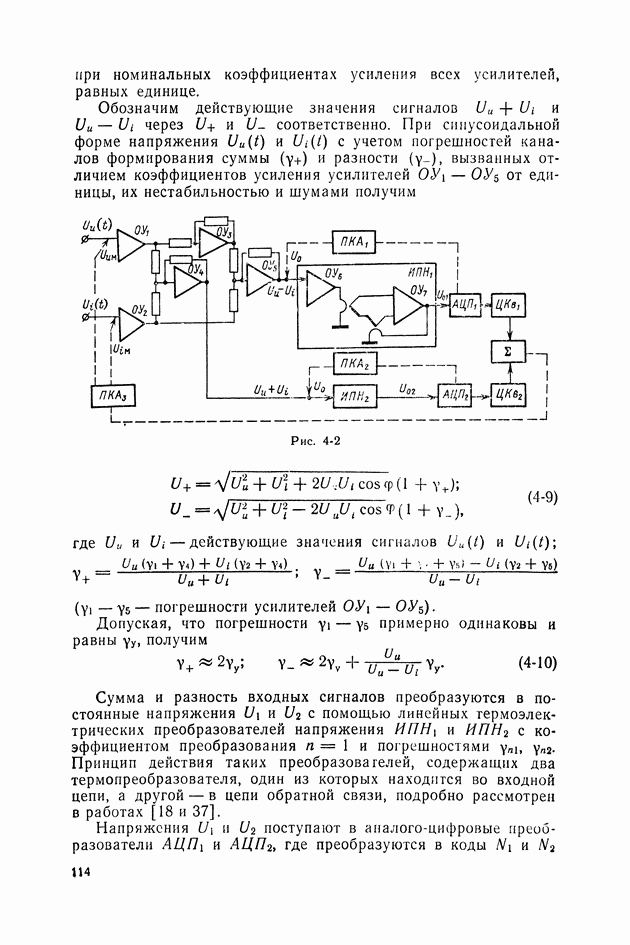
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА ТРЕТЬЯ. ПРИБОРЫ СРАВНЕНИЯ ДЛЯ ИЗМЕРЕНИЙ ЭЛЕКТРИЧЕСКОЙ МОЩНОСТИ
3-1. ВИДЫ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ МОЩНОСТИ ДЛЯ РЕАЛИЗАЦИИ МЕТОДА СРАВНЕНИЯ
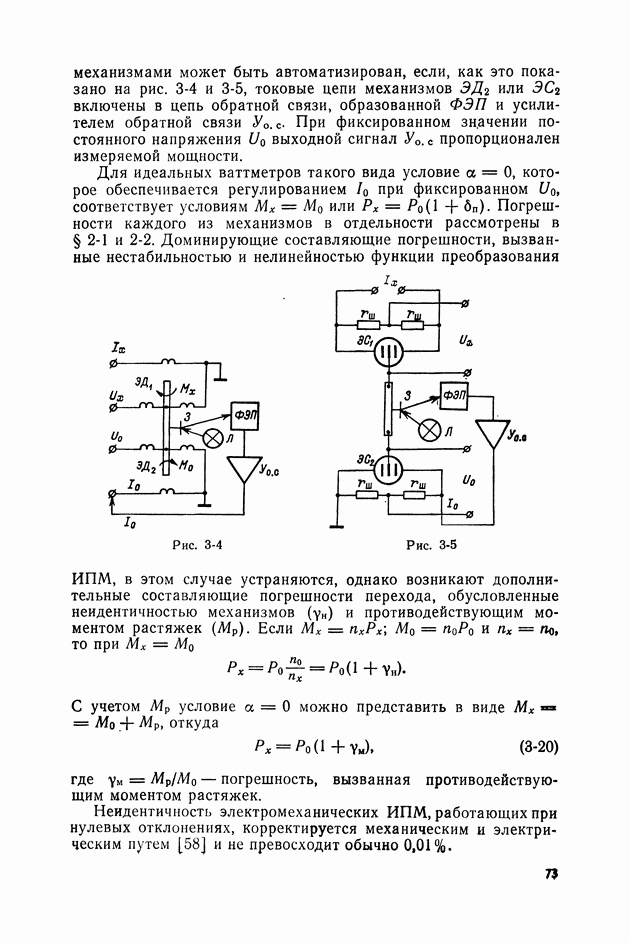
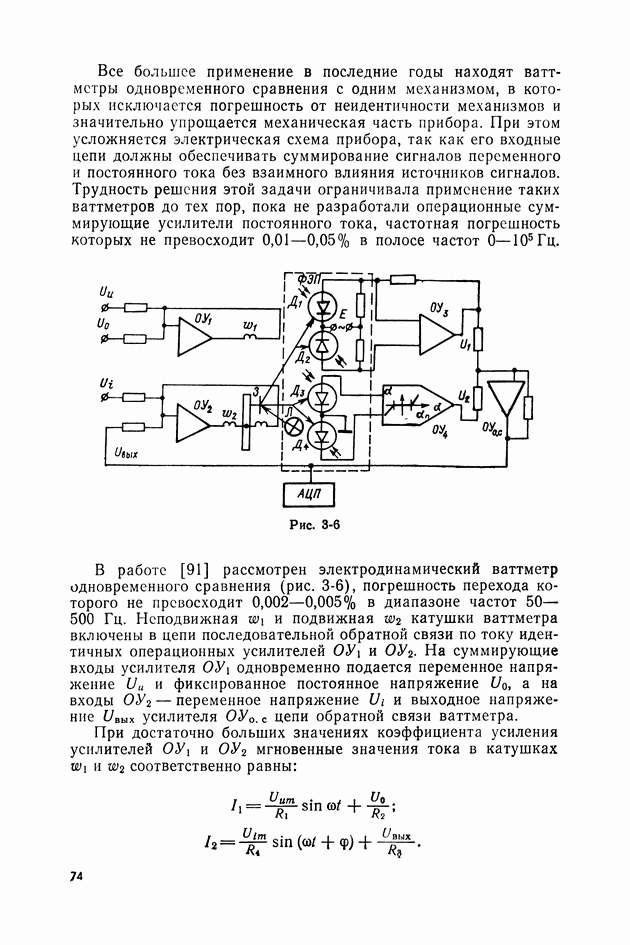
Измерение активной мощности  методом сравнения в большинстве случаев производится путем сравнения ее с известной мощностью постоянного тока
методом сравнения в большинстве случаев производится путем сравнения ее с известной мощностью постоянного тока  Для этой цели может быть использован любой из рассмотренных выше ваттметров или измерительных преобразователей мощности (ИПМ) и в любом случае будет достигнуто повышение точности за счет уменьшения погрешности, вызванной неопределенностью и нестабильностью функции преобразования ИПМ. Однако максимальная эффективность метода сравнения достигается в том случае, если выбранный вид ИПМ обладает наименьшей, по сравнению с другими, погрешностью перехода
Для этой цели может быть использован любой из рассмотренных выше ваттметров или измерительных преобразователей мощности (ИПМ) и в любом случае будет достигнуто повышение точности за счет уменьшения погрешности, вызванной неопределенностью и нестабильностью функции преобразования ИПМ. Однако максимальная эффективность метода сравнения достигается в том случае, если выбранный вид ИПМ обладает наименьшей, по сравнению с другими, погрешностью перехода  Особое место среди составляющих
Особое место среди составляющих  [см. выражение (1-50)] занимает погрешность неоднозначности [см. уравнение (1-48)], характерная только для средств измерений мощности (СИМ). Если частотная и угловая погрешности ограничивают применение СИМ определенной областью частот и
[см. выражение (1-50)] занимает погрешность неоднозначности [см. уравнение (1-48)], характерная только для средств измерений мощности (СИМ). Если частотная и угловая погрешности ограничивают применение СИМ определенной областью частот и  то погрешность
то погрешность  проявляется на любых частотах, включая
проявляется на любых частотах, включая  и именно в области низких частот, где
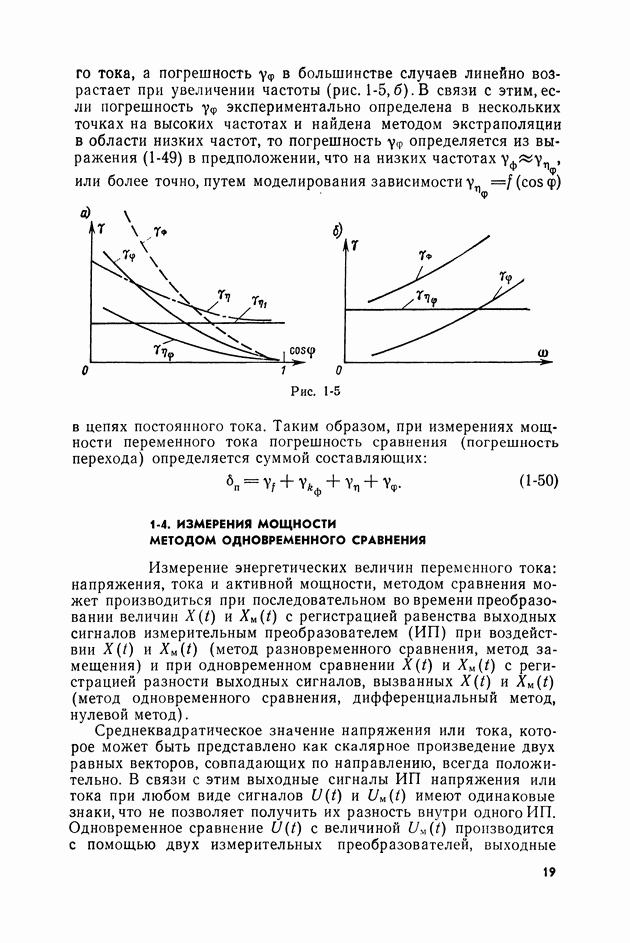
и именно в области низких частот, где  незначительны, является доминирующей.
незначительны, является доминирующей.
Как уже отмечалось в § 1-3, обусловлена отклонением функции преобразования реального ИПМ от идеальной функции произведения. Это отклонение условно можно представить как следствие нелинейных искажений электрических сигналов в преобразователе на одной из стадий их преобразования.
В зависимости от того, на какой стадии преобразования сигналы в преобразователе мощности подвергаются нелинейным
искажениям, преобразователи, имеющие одинаковые отклонения функции преобразования от идеальной, обладают различной  Покажем это путем исследования математических моделей реальных измерительных преобразователей мощности: ИПМ с линейным преобразованием входных сигналов и ИПМ с нелинейным преобразованием входных сигналов вида
Покажем это путем исследования математических моделей реальных измерительных преобразователей мощности: ИПМ с линейным преобразованием входных сигналов и ИПМ с нелинейным преобразованием входных сигналов вида  .
.
Преобразователи, обладающие неидеальной (нелинейной) характеристикой, могут быть представлены двумя структурными схемами (рис. 3-1, а и б), которые содержат функциональный преобразователь  идеально реализующий функцию вида
идеально реализующий функцию вида  интегратор И и нелинейный преобразователь
интегратор И и нелинейный преобразователь  моделирующий в данных схемах нелинейность характеристики реального ИПМ. Расположение
моделирующий в данных схемах нелинейность характеристики реального ИПМ. Расположение  в схеме относительно интегратора определяется тем, происходит ли в реальном ИПМ искажение мгновенных значений произведения входных величин (рис. 3-1, а) или нелинейным искажениям подвергается среднее значение этого произведения (рис. 3-1,б).
в схеме относительно интегратора определяется тем, происходит ли в реальном ИПМ искажение мгновенных значений произведения входных величин (рис. 3-1, а) или нелинейным искажениям подвергается среднее значение этого произведения (рис. 3-1,б).

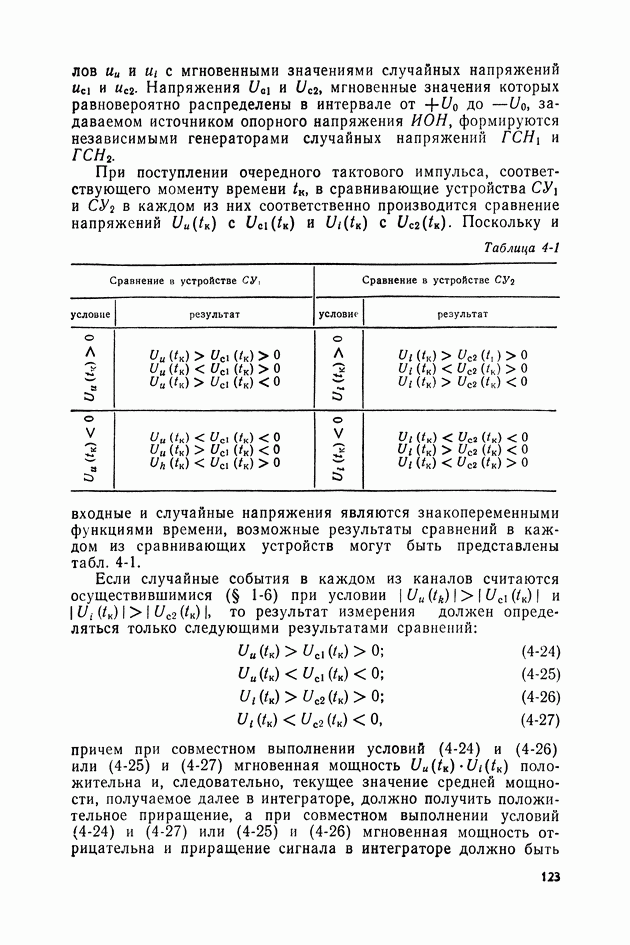
Рис. 3-1
Характеристики преобразователей мощности обоих видов при воздействии на их входы сигналов постоянного тока  одинаковы:
одинаковы:

где  — коэффициенты полинома, аппроксимирующего нелинейную характеристику преобразователя.
— коэффициенты полинома, аппроксимирующего нелинейную характеристику преобразователя.
При работе на переменном же токе математические выражения характеристик ИПМ обеих схем будут различны:

Если допустить, что значения мощностей переменного и постоянного токов, поступающих на вход преобразователя, равны  то погрешность для каждой из схем составит:
то погрешность для каждой из схем составит:

При синусоидальных входных сигналах:  мгновенное значение мощности имеет вид:
мгновенное значение мощности имеет вид:

Согласно формулам (3-2) и (3-5)

Представив  в виде биномиального ряда, получим
в виде биномиального ряда, получим

здесь  — биномиальный коэффициент.
— биномиальный коэффициент.
При  , согласно уравнениям (3-4) и (3-7),
, согласно уравнениям (3-4) и (3-7),

Отметим, что значение  при
при  растет с увеличением
растет с увеличением  что соответствует выражению (1-47).
что соответствует выражению (1-47).
Значение  из сопоставления выражений (3-1) и (3-3), при
из сопоставления выражений (3-1) и (3-3), при 

Из выражений (3-8) и (3-9) следует, что если в ИПМ с линейным преобразованием входных сигналов нелинейным искажениям подвергается сигнал, пропорциональный мгновенной мощности, то при сравнении возникает погрешность  если же нелинейным искажениям подвергается сигнал, пропорциональный средней мощности, погрешность отсутствует.
если же нелинейным искажениям подвергается сигнал, пропорциональный средней мощности, погрешность отсутствует.
Проведенный анализ показывает, что для решения вопроса о применимости ИПМ с линейным преобразованием входных сигналов для сравнения  необходимо установить характер нелинейности. Покажем это на примере сравнения двух широко распространенных типов измерительных преобразователей мощности: ИПМ, основанного на эффекте Холла, и электродинамического ИПМ.
необходимо установить характер нелинейности. Покажем это на примере сравнения двух широко распространенных типов измерительных преобразователей мощности: ИПМ, основанного на эффекте Холла, и электродинамического ИПМ.
В преобразователе Холла в силу нелинейности магнитной системы, выпрямительного эффекта в контактах токовой цепи, неэквипотенциальности выходных контактов и т. д. э. д. с.  пропорциональная мгновенной мощности
пропорциональная мгновенной мощности  нелинейно связана с произведением мгновенных значений
нелинейно связана с произведением мгновенных значений  . Средняя мощность в преобразователе Холла получается путем интегрирования
. Средняя мощность в преобразователе Холла получается путем интегрирования  с помощью внешних активных или пассивных интеграторов. По структуре преобразователь Холла относится к ИПМ, схема которого приведена на рис. 3-1, а, и ему присуща погрешность
с помощью внешних активных или пассивных интеграторов. По структуре преобразователь Холла относится к ИПМ, схема которого приведена на рис. 3-1, а, и ему присуща погрешность  , которая может рассматриваться как инструментальная.
, которая может рассматриваться как инструментальная.
Вращающий момент электродинамического механизма в общем случае также нелинейно связан с произведением токов в контурах [см. формулу (2-2)]. Если допустить, что инерционность механизма мала и что а изменяется в течение периода переменного тока, то выражение для мгновенного значения вращающего момента имеет вид:

Среднее значение вращающего момента при этом определяется как

что соответствует характеристике ИПМ [см. выражение (3-2)], которому присуща погрешность  .
.
Практически инерционность подвижной части такова, что изменения а в течение одного периода тока не происходит, т. е.  зависит только от среднего значения произведения входных величин. Среднее значение вращающего момента в этом случае
зависит только от среднего значения произведения входных величин. Среднее значение вращающего момента в этом случае

что соответствует характеристике ИПМ согласно выражению (3-3).
Погрешность сравнения  этим преобразователем, вызванная нелинейностью зависимости
этим преобразователем, вызванная нелинейностью зависимости  будет практически отсутствовать.
будет практически отсутствовать.
Измерительные преобразователи мощности, реализующие сумма-разностный метод, также могут быть представлены двумя видами структурных схем (рис. 3-2, а и б), где  сумматоры мгновенных значений входных сигналов;
сумматоры мгновенных значений входных сигналов;  квадраторы с идеальной характеристикой;
квадраторы с идеальной характеристикой;  нелинейные преобразователи, имитирующие неквадратичность характеристик реальных квадраторов;
нелинейные преобразователи, имитирующие неквадратичность характеристик реальных квадраторов;  — интеграторы;
— интеграторы;  -сумматор выходных сигналов
-сумматор выходных сигналов  .
.
В цепи постоянного гока функция преобразования мощности  обоих видов преобразователей будет одинакова:
обоих видов преобразователей будет одинакова:

Выражение для У может быть найдено путем аппроксимации характеристики реального квадратора, обладающего, как правило, характеристикой, симметричной относительно оси ординат, степенным рядом с четными степенями аргумента. При этом, обозначив сигналы на выходах и  через и
через и  -соответственно, определим сигналы на выходах реальных квадраторов
-соответственно, определим сигналы на выходах реальных квадраторов 

откуда

Для определения характеристик  и
и  обеих схем на переменном токе введем обозначения:
обеих схем на переменном токе введем обозначения:


Рис. 3-2
Сигналы на входах интеграторов  :
:

что, по аналогии с выражением (3-7), после интегрирования дает:

Переходя к действующим значениям и к суммированию в степенном ряду от  , а в биномиальном от
, а в биномиальном от  , получим:
, получим:

Поскольку значения интегралов в выражениях (3-13) не зависят от 

где  — значение определенного интеграла от суммы членов ряда.
— значение определенного интеграла от суммы членов ряда.
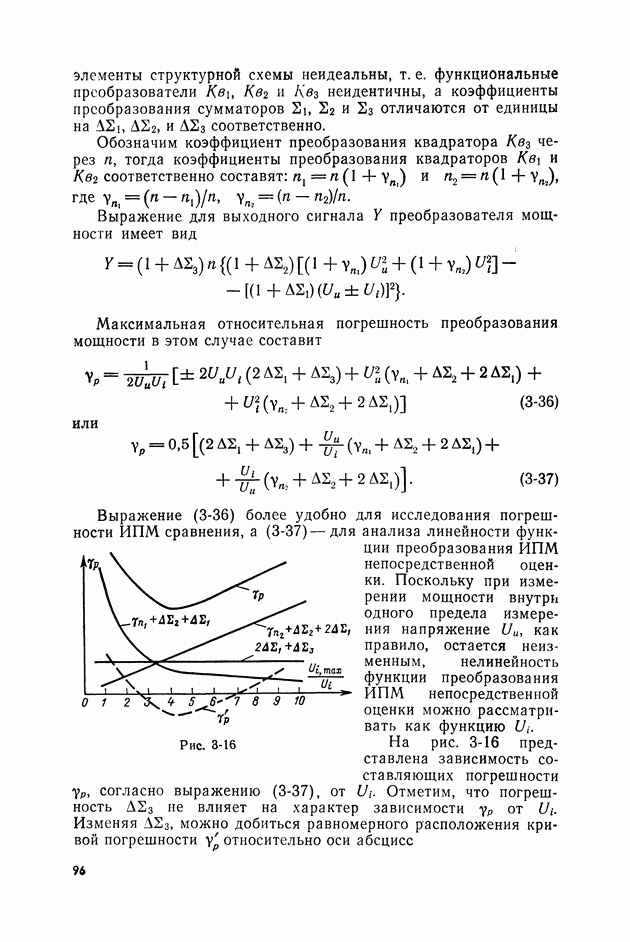
В соответствии с выражениями (3-11) и (3-14) погрешность для преобразователя (рис. 3-2, а) будет

Для преобразователя, соответствующего схеме рис. 3-2, б,

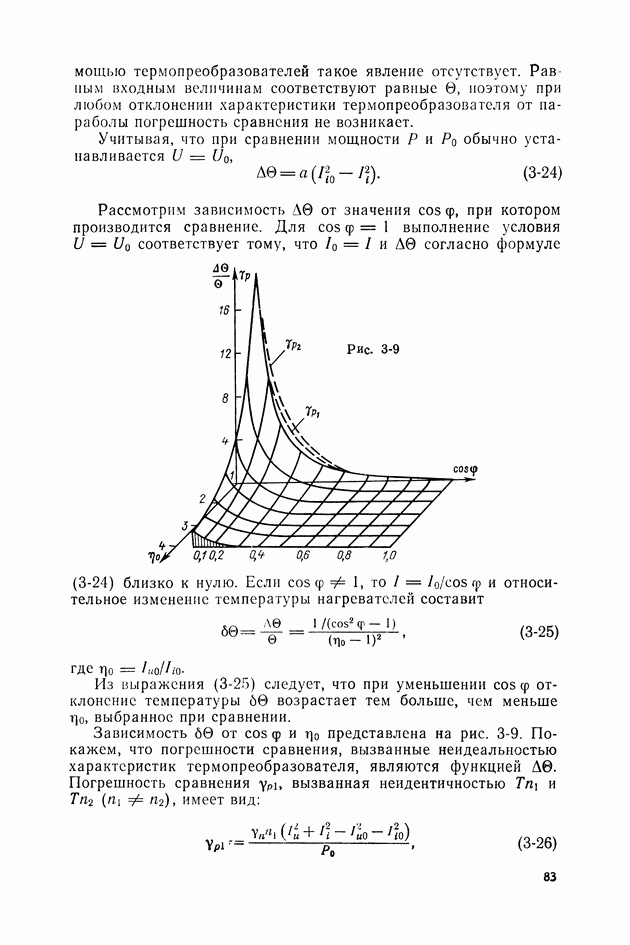
Неидеальность характеристик квадраторов обоих видов преобразователей приводит к возникновению составляющей погрешности перехода  . Однако, как следует из выражения (3-16), для преобразователя, составленного по схеме рис. 3-2,б, эта погрешность обращается в нуль при условии, что
. Однако, как следует из выражения (3-16), для преобразователя, составленного по схеме рис. 3-2,б, эта погрешность обращается в нуль при условии, что

т. е. может быть устранена при выполнении условий:

Возможны и другие пути устранения  они рассмотрены ниже.
они рассмотрены ниже.
Погрешность же  преобразователя (рис. 3-1, а) может быть уменьшена при тех же условиях только до некоторого минимального значения:
преобразователя (рис. 3-1, а) может быть уменьшена при тех же условиях только до некоторого минимального значения:

Как и в предыдущем случае, погрешность  может быть устранена, если нелинейным искажениям подвергается среднеквадратическое значение сигнала на выходе квадраторов
может быть устранена, если нелинейным искажениям подвергается среднеквадратическое значение сигнала на выходе квадраторов  если же искажены мгновенные значения:
если же искажены мгновенные значения:  погрешность у не устраняется и может быть уменьшена только путем совершенствования параметров квадраторов.
погрешность у не устраняется и может быть уменьшена только путем совершенствования параметров квадраторов.
Сопоставим на основе полученных данных ИПМ с диодными квадраторами и ИПМ с электростатическими квадраторами. В первом случае неидеальность характеристики функционального преобразователя определяется погрешностью аппроксимации. При этом мгновенные значения сигнала  на выходе этого преобразователя нелинейно связаны с квадратом мгновенных
на выходе этого преобразователя нелинейно связаны с квадратом мгновенных
значений входного сигнала:

Среднее значение сигнала на выходе функционального преобразователя выделяется с помощью активного или пассивного интегратора, обладающего пренебрежимо малой нелинейностью характеристики:

Отсюда следует, что использование рассматриваемого функционального преобразователя, входящего в ИПМ, который соответствует схсме рис. 3-2, б, приведет к возникновению  . К аналогичным выводам приводит исследование причин неквадратичности функциональных преобразователей, использующих нелинейности вольт-амперных характеристик, преобразователей с коэффициентом передачи, линейно зависящим от входного сигнала преобразователя, использующих продольный гальваномагнитный эффект, и функциональных преобразователей, выполненных на многосеточных лампах.
. К аналогичным выводам приводит исследование причин неквадратичности функциональных преобразователей, использующих нелинейности вольт-амперных характеристик, преобразователей с коэффициентом передачи, линейно зависящим от входного сигнала преобразователя, использующих продольный гальваномагнитный эффект, и функциональных преобразователей, выполненных на многосеточных лампах.
Вращающий момент М электростатического механизма также не является идеальной функцией квадрата напряжения. В области инфразвуковых частот, где  его среднее значение определяется интегралом:
его среднее значение определяется интегралом:

соответствующим по виду интегралам выражения (3-12), т.е. в этой области частот ИПМ с электростатическим квадратором соответствует рис. 3-2, б.
В области звуковых частот а практически не изменяется в течение периода переменного тока. При этом

и ИПМ с электростатическим механизмом можно рассматривать как ИПМ, соответствующий схеме рис. 3-2, б, и считать, что этот преобразователь обладает устранимой погрешностью 
Аналогичные результаты дает рассмотрение причин неквадратичности функциональных преобразователей, использующих электротепловой эффект (см. § 3-3).
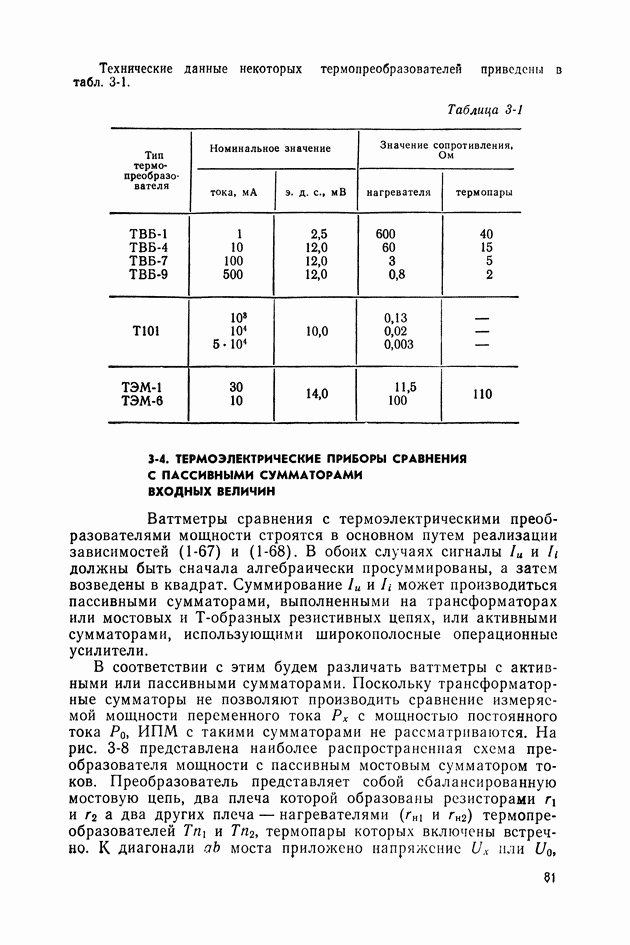
Анализ составляющей погрешности перехода, вызванной неидеальностью функционального преобразователя, позволяет выделить некоторые общие характеристики, присущие измерительным
преобразователям, приведенным на рис. 3-1, а и б и 3-2, а и б. ИПМ (рис. 3-1, а и 3-2, а) обладают систематической погрешностью перехода  , имеющей характер инструментальной погрешности; ИПМ (рис. 3-1,б и 3-2,б) либо вообще не обладают погрешностью перехода
, имеющей характер инструментальной погрешности; ИПМ (рис. 3-1,б и 3-2,б) либо вообще не обладают погрешностью перехода  , либо она носит характер методической погрешности и при определенных условиях может быть устранена. ИПМ, собранные по схемам рис. 3-1, а и 3-2, а, являются преобразователями мгновенного значения мощности. Среднее значение мощности может быть получено с их помощью путем подключения к выходу преобразователя внешнего интегратора. ИПМ, собранные по схемам рис. 3-1,б и 3-2,б, принципиально являются преобразователями среднего значения мощности. Общим для них является наличие внутреннего интегратора, физически совмещенного с функциональным преобразователем. Наличие внутреннего интегратора обеспечивает неизменность параметров функционального преобразователя в течение одного периода переменного тока, что является необходимым условием отсутствия погрешности
, либо она носит характер методической погрешности и при определенных условиях может быть устранена. ИПМ, собранные по схемам рис. 3-1, а и 3-2, а, являются преобразователями мгновенного значения мощности. Среднее значение мощности может быть получено с их помощью путем подключения к выходу преобразователя внешнего интегратора. ИПМ, собранные по схемам рис. 3-1,б и 3-2,б, принципиально являются преобразователями среднего значения мощности. Общим для них является наличие внутреннего интегратора, физически совмещенного с функциональным преобразователем. Наличие внутреннего интегратора обеспечивает неизменность параметров функционального преобразователя в течение одного периода переменного тока, что является необходимым условием отсутствия погрешности  .
.
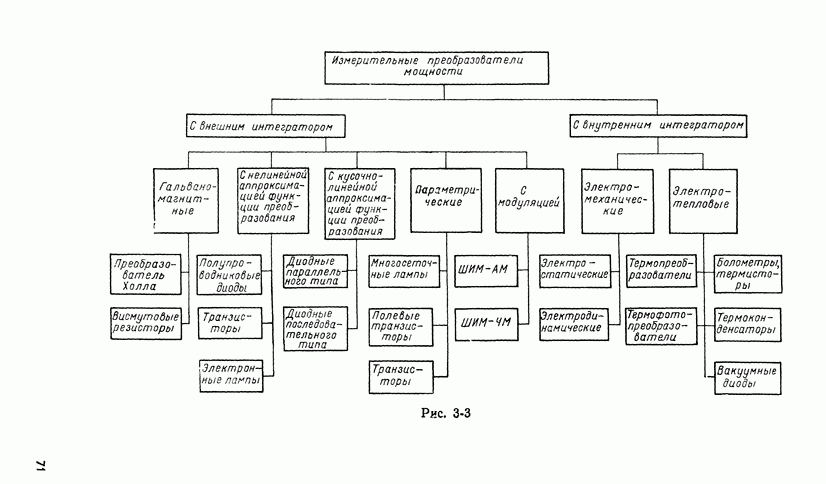
Указанные обобщенные характеристики ИПМ позволяют предложить для преобразователей, используемых для реализации метода сравнения, классификационную схему, приведенную на рис. 3-3.
В качестве основного классификационного признака, отраженного во второй строке схемы, принято наличие в ИПМ внутреннего или внешнего интегратора. Третья строка отражает физические явления, лежащие в основе принципа действия ИПМ, или искусственные методы создания заданной функции преобразования. В столбцах четвертой строки даны элементы, реализующие эти физические явления, или искусственные методы. Характерной особенностью предложенной классификации является то, что под основным классификационным признаком объединены ИПМ, реализующие различные виды математических зависимостей, основанные на различных физических явлениях, обладающие существенными конструктивными различиями, но однотипные с точки зрения влияния неидеальности их характеристик на точность сравнения сигналов переменного и постоянного токов. Такая классификация в некоторой степени является условной в силу неидеальности интеграторов, используемых в ИПМ.
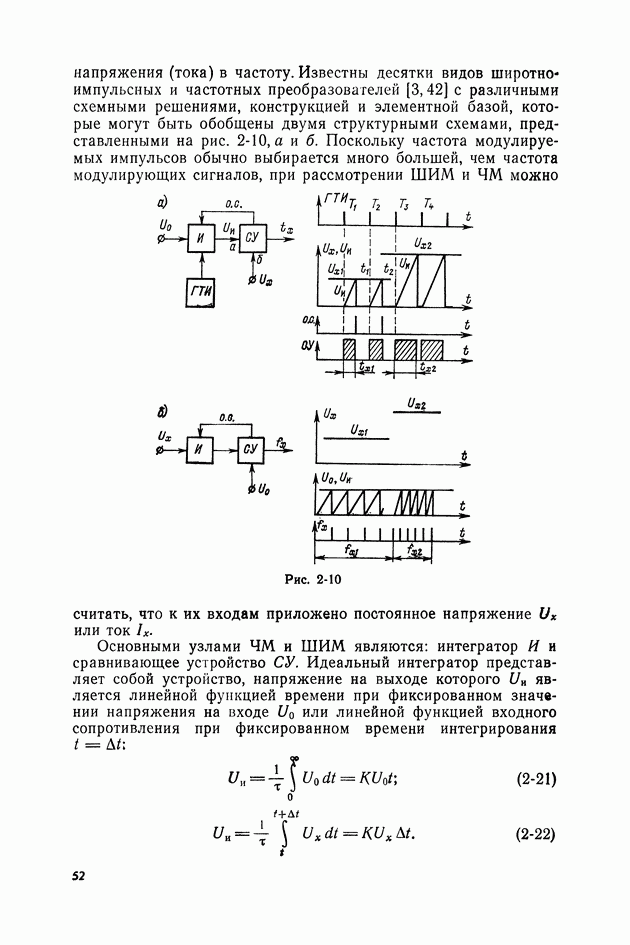
В реальных ИПМ функцию интегратора выполняет инерционное звено, обладающее приближенно передаточной функцией вида

где К — статический коэффициент передачи интегратора;  — тепловая или механическая постоянная времени.
— тепловая или механическая постоянная времени.
В области частот входного сигнала:  эффективность внутреннего интегратора падает с уменьшением частоты,
эффективность внутреннего интегратора падает с уменьшением частоты,

(кликните для просмотра скана)
что не позволяет выделить ИПМ с внутренним интегратором в отдельный подкласс.
В области звуковых и высоких частот обычно  .
.
В этом случае использование предложенной классификации представляется обоснованным.
Из приведенного выше анализа влияния неидеальности характеристик ИПМ на результат сравнения мощностей постоянного и переменного токов следует, что для создания аппаратуры высокой точности желательно использовать ИПМ с внутренним интегратором. Минимальное значение ул в этой группе без применения каких-либо методических приемов для ее уменьшения достигается применением ИПМ с линейным преобразованием входных величин (рис. 3-1,б). Практическая реализация таких ИПМ возможна в настоящее время только на базе электродинамического измерительного механизма.
Наименьшим значением  среди ИПМ с функциональным преобразованием входных величин обладают преобразователи, использующие электростатические и электротепловые функциональные преобразователи.
среди ИПМ с функциональным преобразованием входных величин обладают преобразователи, использующие электростатические и электротепловые функциональные преобразователи.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ВОПРОСЫ ТЕОРИИ ИЗМЕРЕНИИ ЭЛЕКТРИЧЕСКОЙ МОЩНОСТИ
- 1-1. МОЩНОСТЬ В ЦЕПЯХ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА
- 1-2. ПРЯМЫЕ И КОСВЕННЫЕ ИЗМЕРЕНИЯ МОЩНОСТИ
- Методы прямых измерений мощности.
- Методические погрешности измерений мощности.
- 1-3. МЕТОД НЕПОСРЕДСТВЕННОЙ ОЦЕНКИ И МЕТОД СРАВНЕНИЯ ПРИ ИЗМЕРЕНИЯХ МОЩНОСТИ
- Особенности измерений мощности постоянного тока методом сравнения.
- Особенности измерений мощности переменного тока методом сравнения.
- 1-4. ИЗМЕРЕНИЯ МОЩНОСТИ МЕТОДОМ ОДНОВРЕМЕННОГО СРАВНЕНИЯ
- 1-5. МЕТОДЫ СРАВНЕНИЯ РАВНЫХ И НЕРАВНЫХ ЗНАЧЕНИЙ
- 1-6. МЕТОДЫ ПОСТРОЕНИЯ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ МОЩНОСТИ
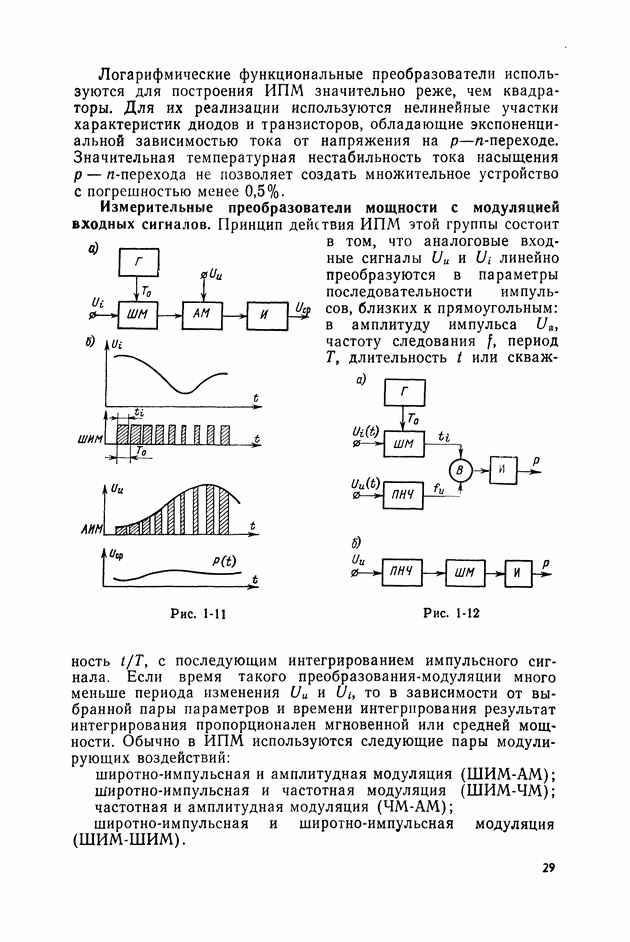
- Измерительные преобразователи мощности с фукциональным преобразованием входных величин.
- Измерительные преобразователи мощности с модуляцией входных сигналов.
- ГЛАВА ВТОРАЯ. ПРИБОРЫ НЕПОСРЕДСТВЕННОЙ ОЦЕНКИ ДЛЯ ИЗМЕРЕНИИ АКТИВНОЙ МОЩНОСТИ
- 2-1. ЭЛЕКТРОДИНАМИЧЕСКИЕ И ФЕРРОДИНАМИЧЕСКИЕ ВАТТМЕТРЫ
- Погрешности, вызванные реактивностью цепей прибора.
- Погрешности, вызванные вихревыми токами.
- Погрешность от взаимной индуктивности.
- Температурная погрешность.
- Погрешности от влияния внешних магнитных полей.
- Основные методы компенсации погрешностей ваттметров.
- Ваттметры с электронными усилителями во входных цепях.
- 2-2. ЭЛЕКТРОСТАТИЧЕСКИЕ ВАТТМЕТРЫ
- 2-3. ВАТТМЕТРЫ С ПРЕОБРАЗОВАТЕЛЯМИ ХОЛЛА
- 2-4. ВАТТМЕТРЫ С МОДУЛЯЦИОННЫМИ ИЗМЕРИТЕЛЬНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ МОЩНОСТИ
- ГЛАВА ТРЕТЬЯ. ПРИБОРЫ СРАВНЕНИЯ ДЛЯ ИЗМЕРЕНИЙ ЭЛЕКТРИЧЕСКОЙ МОЩНОСТИ
- 3-1. ВИДЫ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ МОЩНОСТИ ДЛЯ РЕАЛИЗАЦИИ МЕТОДА СРАВНЕНИЯ
- 3-2. ПРИБОРЫ СРАВНЕНИЯ С ЭЛЕКТРОМЕХАНИЧЕСКИМИ ИЗМЕРИТЕЛЬНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ МОЩНОСТИ
- 3-3. ЭЛЕКТРОТЕПЛОВЫЕ ПРЕОБРАЗОВАТЕЛИ ДЛЯ ПРИБОРОВ СРАВНЕНИЯ
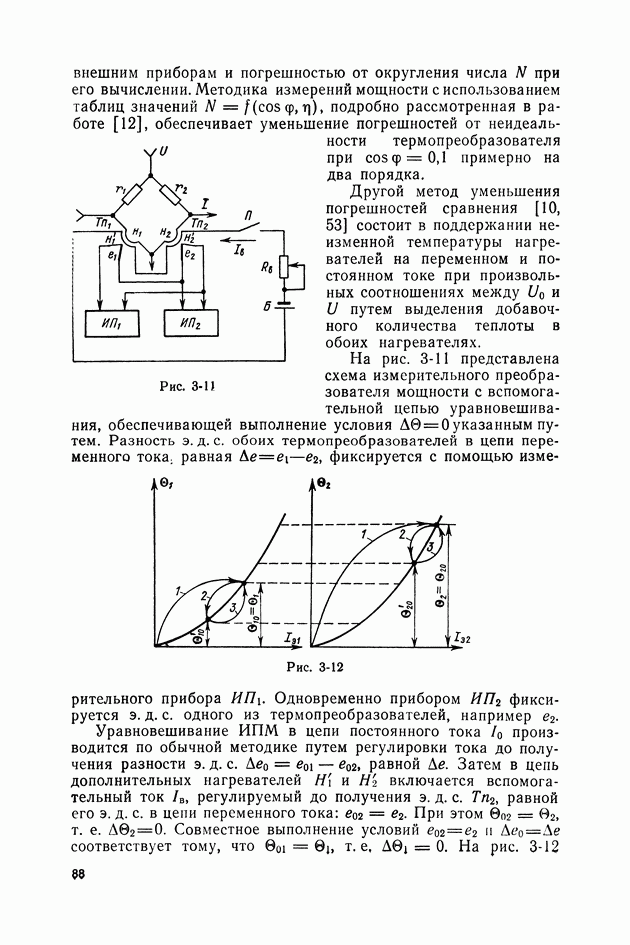
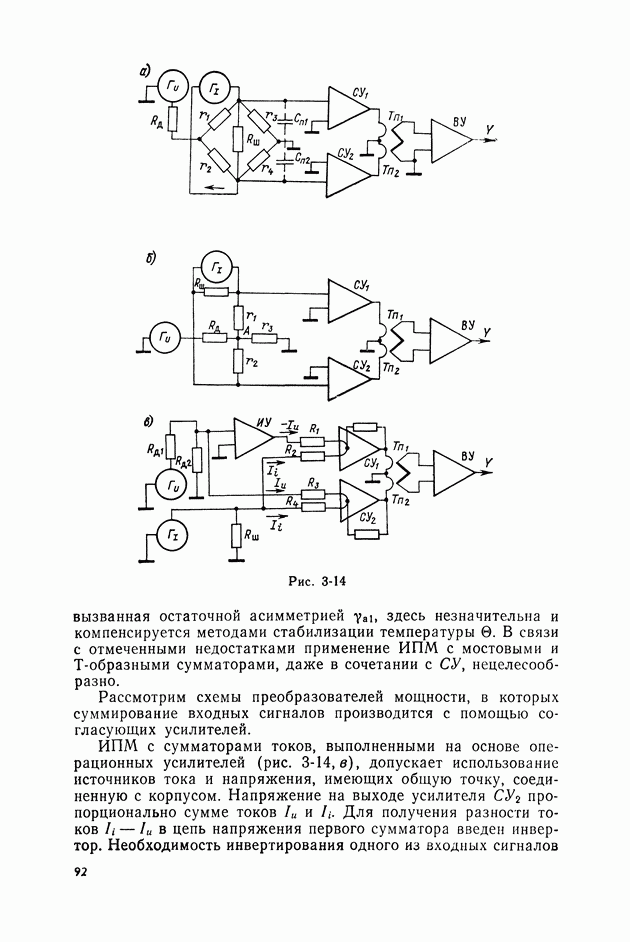
- 3-4. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ СРАВНЕНИЯ С ПАССИВНЫМИ СУММАТОРАМИ ВХОДНЫХ ВЕЛИЧИН
- Погрешности сравнения, вызванные неидеальностью сумматоров.
- Методы уменьшения погрешностей, вызванных неидеальностью термопреобразователей и сумматоров входных величин.
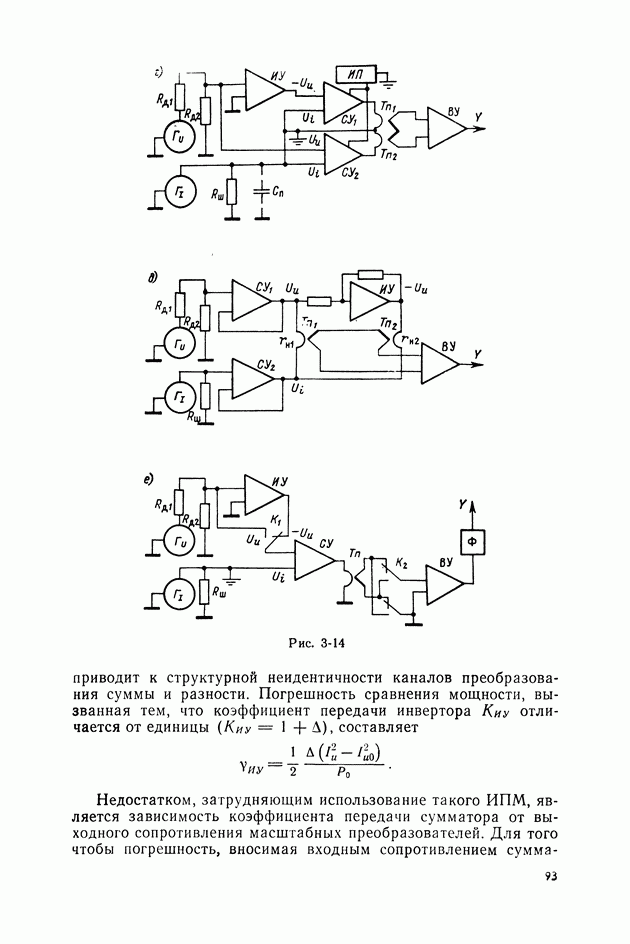
- 3-5. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ СРАВНЕНИЙ С АКТИВНЫМИ СУММАТОРАМИ ВХОДНЫХ ВЕЛИЧИН
- Термоэлектрические измерительные преобразователи мощности с тремя квадраторами.
- Одновременное сравнение мощностей термоэлектрическим измерительным преобразователем мощности.
- Погрешности измерительных преобразователей мощности с усилителями во входных и выходных цепях.
- ГЛАВА ЧЕТВЕРТАЯ. ОСОБЕННОСТИ ПОСТРОЕНИЯ ЦИФРОВЫХ ВАТТМЕТРОВ ПЕРЕМЕННОГО ТОКА
- 4-2. ЦИФРОВЫЕ ВАТТМЕТРЫ С АВТОМАТИЧЕСКОЙ КОРРЕКЦИЕЙ ПОГРЕШНОСТЕЙ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ МОЩНОСТИ
- 4-3. ЦИФРОВЫЕ ВАТТМЕТРЫ С НЕПОЛНЫМ АНАЛОГОВЫМ ПРЕОБРАЗОВАНИЕМ ВХОДНЫХ ВЕЛИЧИН
- 4-4. ЦИФРОВОЙ МИКРОВАТТМЕТР С АДДИТИВНОЙ КОРРЕКЦИЕЙ МЕТОДИЧЕСКОЙ ПОГРЕШНОСТИ
- 4-5. ЦИФРОВОЙ ВАТТМЕТР, ОСНОВАННЫЙ НА МЕТОДЕ СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ
- 4-6. ЦИФРОВЫЕ ВАТТМЕТРЫ С ПРЕОБРАЗОВАНИЕМ МОЩНОСТИ В ИНТЕРВАЛ ВРЕМЕНИ ИЛИ ЧАСТОТУ
- Цифровой ваттметр с терморезонансными преобразователями.
- ГЛАВА ПЯТАЯ. ПЕРВИЧНЫЕ ПРЕОБРАЗОВАТЕЛИ НАПРЯЖЕНИЯ И ТОКА
- 5-1. ВИДЫ ПЕРВИЧНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 5-2. РЕЗИСТИВНЫЕ ПЕРВИЧНЫЕ ПРЕОБРАЗОВАТЕЛИ НАПРЯЖЕНИЯ
- 5-3. РЕДИСТИВНЫЕ ПЕРВИЧНЫЕ ПРЕОБРАЗОВАТЕЛИ ТОКА
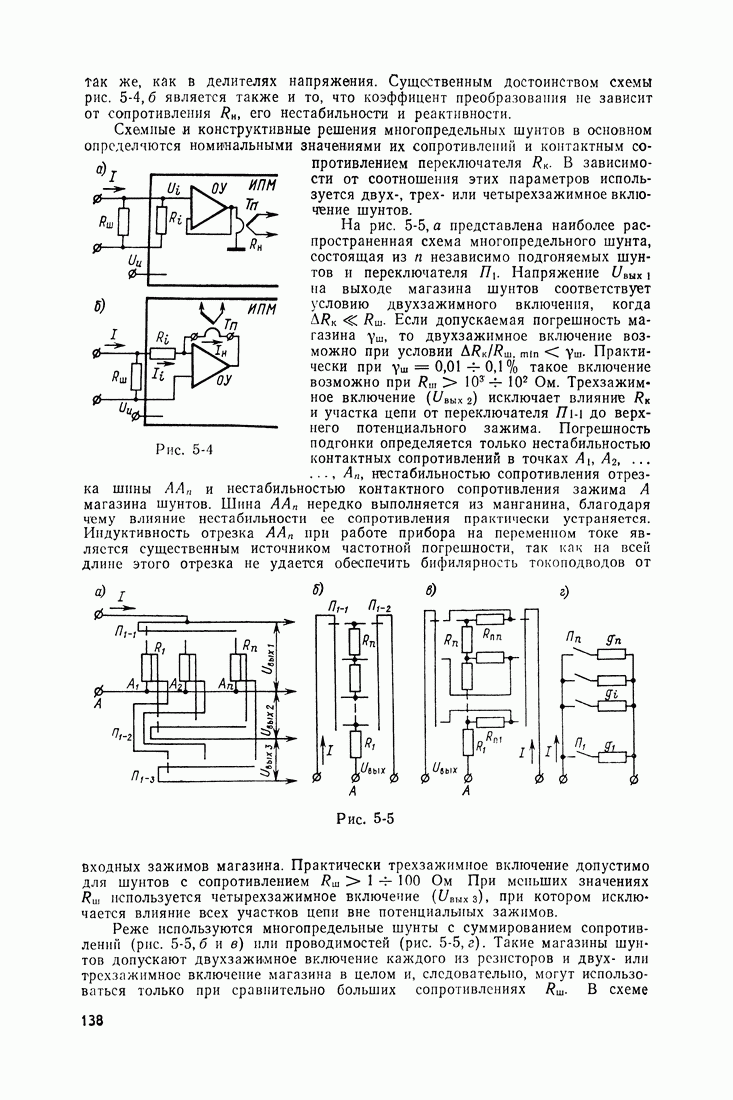
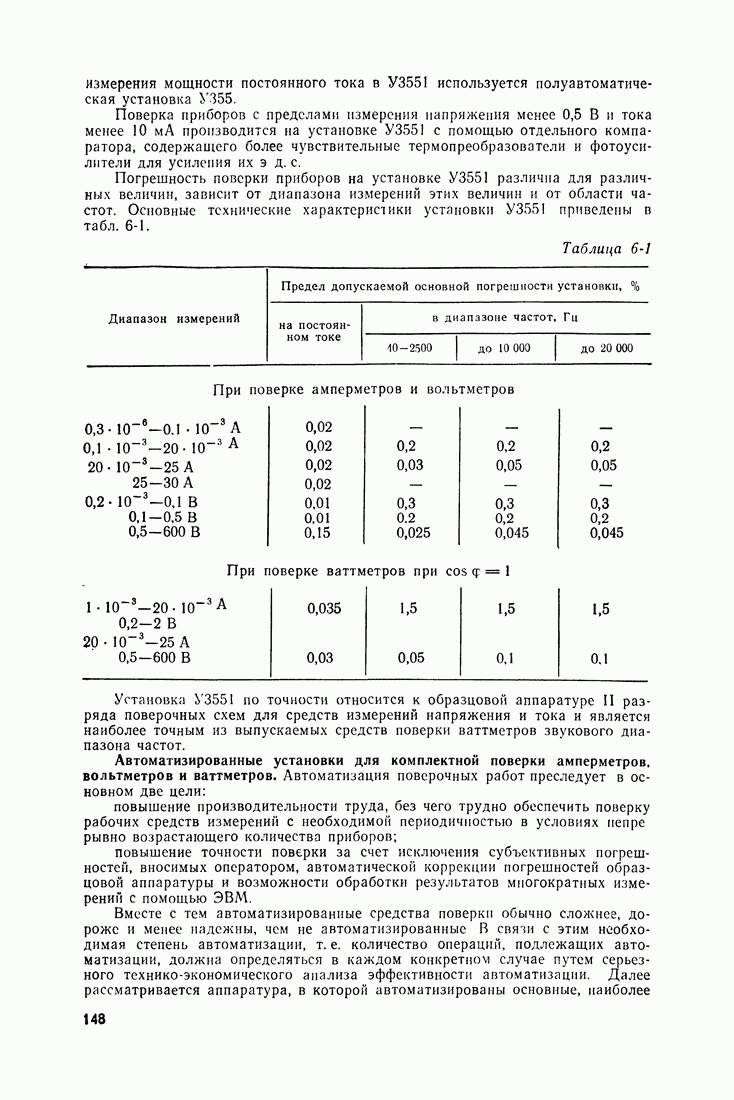
- 5-4. РЕЗИСТОРЫ ПЕРВИЧНЫХ ПРЕОБРАЗОВАТЕЛЕЙ НАПРЯЖЕНИЯ И ТОКА
- Реактивность проволочных резисторов.
- ГЛАВА ШЕСТАЯ. ПОВЕРКА СРЕДСТВ ИЗМЕРЕНИЙ МОЩНОСТИ
- 6-1. ОСОБЕННОСТИ ПОВЕРКИ СРЕДСТВ ИЗМЕРЕНИЙ МОЩНОСТИ
- 6-2. КОМПЛЕКТНАЯ ПОВЕРКА СРЕДСТВ ИЗМЕРЕНИЙ МОЩНОСТИ
- Установки для комплектной поверки СИМ.
- Автоматизированные установки для комплектной поверки амперметров, вольтметров и ваттметров.
- Структуры установок для автоматического определения погрешностей.
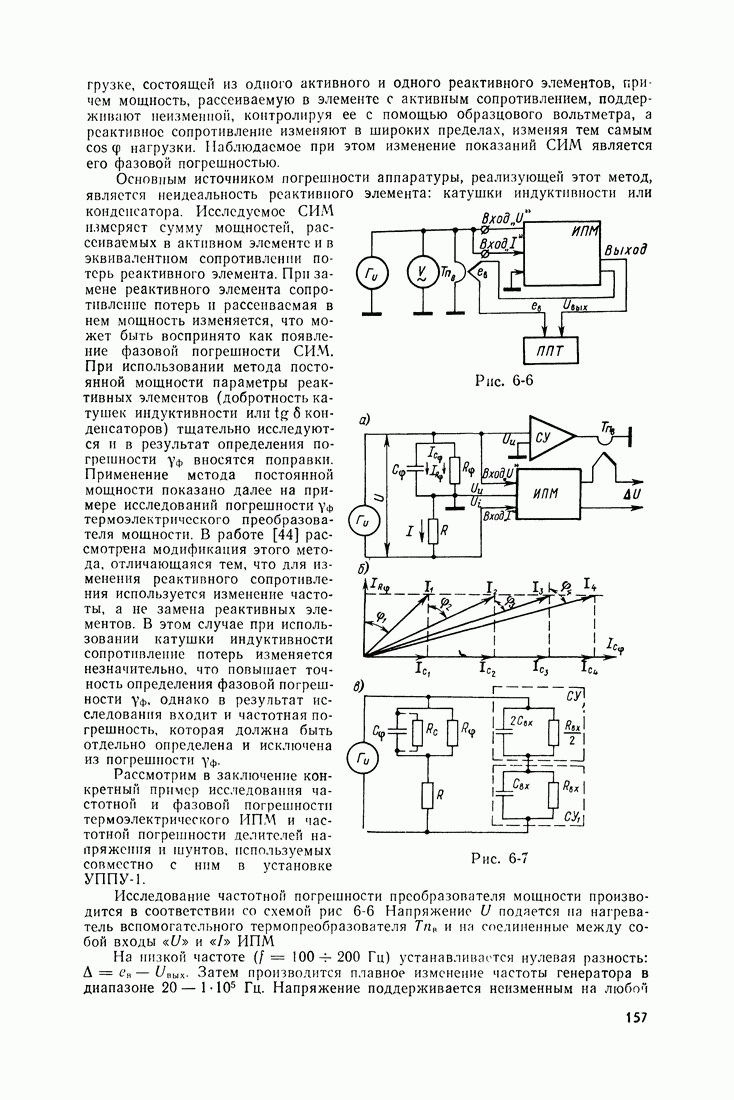
- Установка поверочная полуавтоматическая универсальная УППУ-1.
- 6-3. ЭКСПЕРИМЕНТАЛЬНО-РАСЧЕТНЫЕ МЕТОДЫ ПОВЕРКИ СРЕДСТВ ИЗМЕРЕНИЙ МОЩНОСТИ
- Определение погрешности перехода от постоянного тока к переменному.
- СПИСОК ЛИТЕРАТУРЫ