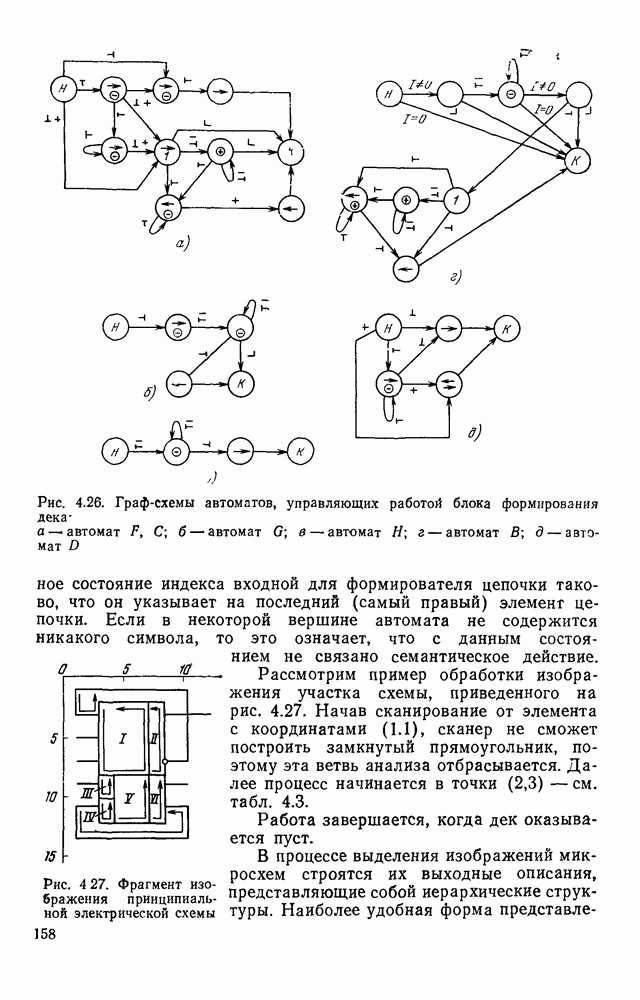
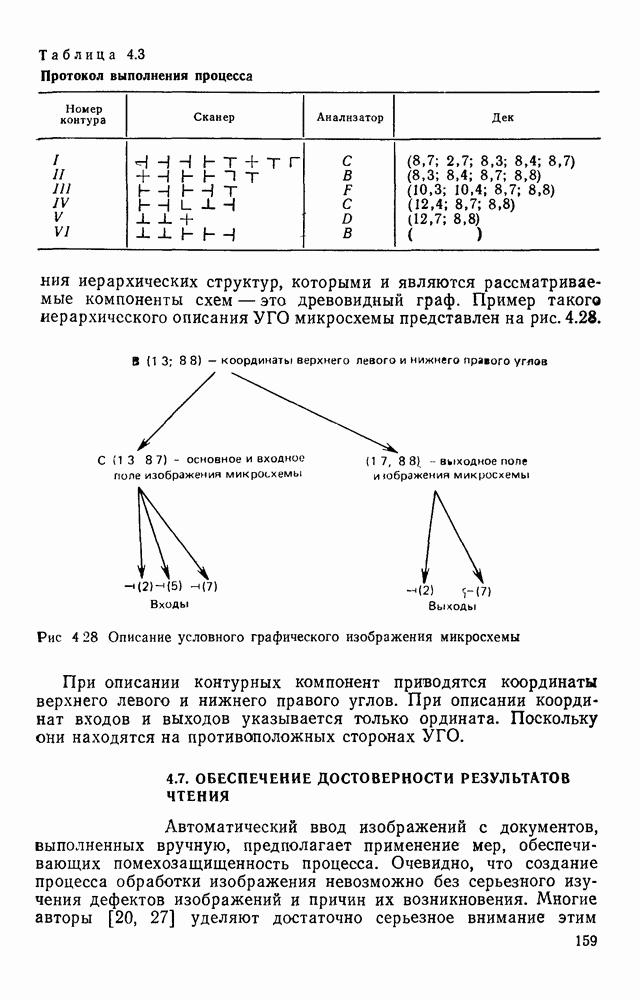
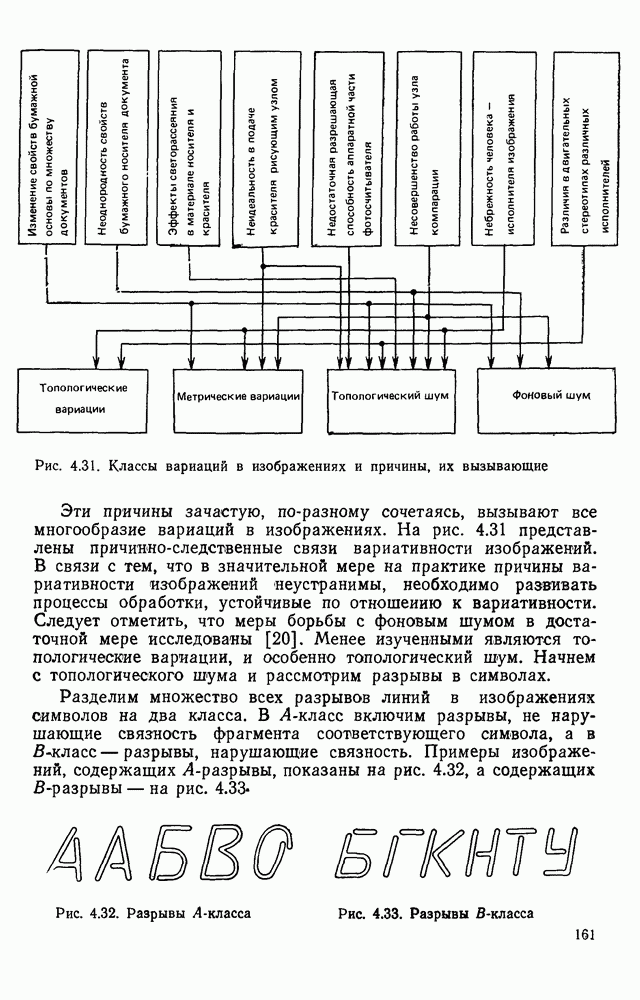
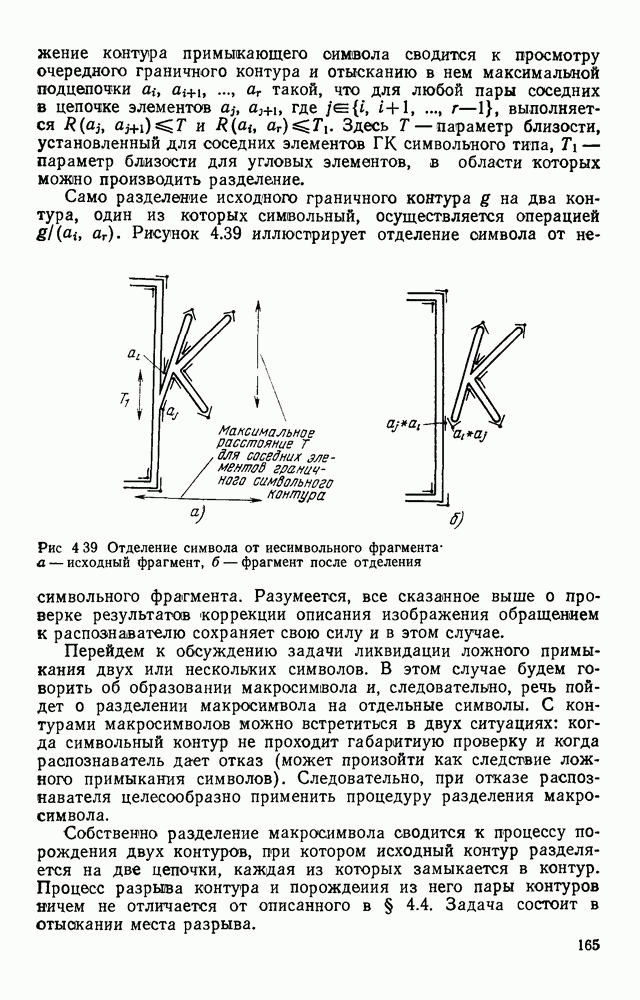
5.6. ОПТИМАЛЬНОЕ РАСПОЛОЖЕНИЕ КОНТРОЛЬНЫХ ЛОСТОВ В ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССАХ

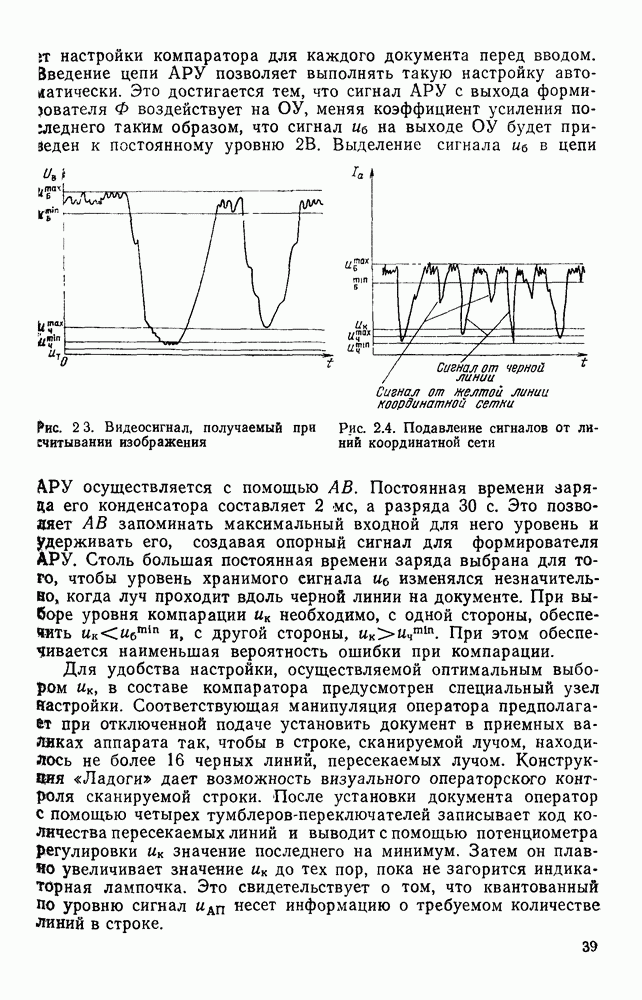
Усложнение изделий электронной техники приводит к необходимости использовать дорогостоящее контрольное оборудование. В частности, стоимость автоматических систем контроля внешнего вида печатного монтажа может достигать нескольких десятков тысяч рублей. Этот факт ставит задачу оптимальною использования дорогостоящих контролирующих устройств, т. е. оптимального размещения контрольных операций в технологических процессах. Контроль внешнего вида печатных плат и микросборок мажет производиться после ряда технологических операций. Дефекты, допущенные на ранних этапах изготовления изделий и контролируемые по их внешнему виду, в принципе могут быть обнаружены при контроле последующих операций. Однако при этом дефектные изделия не будут во время изъяты из технологического процесса и ряд операций будет выполняться впустую, увеличивая тем самым среднюю себестоимость одного годного изделия.

Если предположить, что итоговый контроль внешнего вида позволяет выявить все дефекты, то возможны две крайние стратегии контроля. В первой из них минимизируются затраты на контроль: оставляется только итоговый контроль, а промежуточные технологические операции не контролируются. При этом суммарные затраты на технологические операции будут максимальны. Другая крайняя стратегия минимизирует затраты на технологические операции: посты контроля располагаются после каждой допускающей контроль технологической операции и дефектные изделия своевременно изымаются из технологического процесса. Однако в этом случае затраты на контроль будут максимальны. Естественно попытаться найти такое размещение контролирующих устройств, при котором минимизируется средняя стоимость одного годного изделия. Решение этой задачи сводится к перебору и сравнению различных допустимых вариантов.

Ниже излагается несколько теорем, позволяющих сократить такой перебор, и приводятся алгоритмы решения этой задачи, основанные на сокращенном переборе. Для простоты считается, что контроль каждой технологической операции позволяет безошибочно обнаружить все дефекты предыдущих операций, а также не учитывается возможность ремонта (устранения дефекта). Эти ограничения в принципе могут быть сняты. Однако при этом

выражения, отражающие стоимость изделий, становятся более громоздкими. Соответствующие результаты можно найти в [53].

Модель технологического процесса.

Технологический процесс изготовления схем будем называть просто технологическим процессом, а заготовку, поступающую на вход технологического процесса или прошедшую несколько операций, — изделием (строго говоря, изделием она становится лишь по окончании технологического процесса).

Совокупность рабочих операций разбивается на укрупненных технологических операций, после каждой из которых возможно установить контрольный пост. В дальнейшем каждую укрупненную технологическую операцию будем называть просто операцией. Каждый контрольный пост определяет степень соответствия изделия заданным требованиям. Изделия, содержащие дефекты, считаются негодными и на следующую операцию не поступают. Каждая операция, технологическая или контрольная, может характеризоваться различными затратами—материальными, временными и т. д. В общем случае будем называть этот параметр стоимостью.

В результате анализа технологического процесса определяются для всех операций следующие его параметры: — вероятность события, при котором операция будет выполнена без дефектов; а, — стоимость укрупненной технологической операции в пересчете на одно изделие; — стоимость контроля одного изделия после i-й операции.

Исследуемый технологический процесс всегда можно разбить на укрупненных технологических операций таким образом, что после любой i-й операции будет возможно обнаружить большую часть дефектов, возникших после выполнения предыдущих операций. Готовые изделия через пост ОТК поступают в сборочный цех. Поэтому в отношении контрольных операций сделаны следующие допущения: контроль после i-й операции обнаруживает все дефекты изделия, которые появились при выполнении любой из предыдущих операций; итоговый контроль (после операции) обязателен.

Вводится в рассмотрение двоичный вектор компонента которого принимает единичное значение, если после i-й операции установлен контрольный пост; в противном случае равна нулю. Вектор X однозначно определяет план размещения постов контроля, поэтому будем называть его вектором-планом размещения постов контроля или просто планом. Схематически модель технологического процесса представлена на рис. 5.33.

Введем характеристики потока изделий, участвующего в технологическом процессе. Пусть на вход технологического процесса поступает N изделий. В процессе обработки дефектные изделия при прохождении через контрольные посты из общего потока изымаются и на вход i-й операции поступает изделий (здесь и далее во всех .формулах пределы изменения индекса i от 1 до ).

Назовем относительным потоком изделий, поступающих на вход i-й операции. Если , то определяется следующим образом:

Будем называть номером единичной компоненты, предшествующей . Дополним поразрядный вектор X компонентной . Будем считать поток на входе технологического процесса полностью проконтролированным, т. е. Если , то . Если , то .

Рис. 5.33. Модель процесса, отражающая последовательность технологических и контрольных операций

Если операционный контроль полностью достоверен (безошибочен), насыщенность потока годными изделиями на выходе i-й операции составляет в соответствии с (5.19)

Поскольку итоговый контроль обязателен, на выходе технологического процесса получается годных изделий: Для иллюстрации введенных выше характеристик рассмотрим следующий пример. Пусть технологический процесс состоит из четырех операций, причем после первой и четвертой установлены контрольные посты. В табл. 5.3 представлены параметры потока изделий для каждой операции.

Средняя стоимость готового изделия на выходе технологического процесса равна

Таблица 5.3. Пример технологического процесса

В (5.21) для любого значения вектора-плана X знаменатель (относительный поток годных изделий на выходе технологического процесса) есть величина постоянная, поэтому при нахождении минимальной средней стоимости годного изделия можно ограничиться получением минимального значения числителя.

Выбор оптимального плана размещения точек контроля сводится к решению следующей задачи. Требуется найти оптимальный вектор-план доставляющий минимум функции при следующих условиях: и ограничениях

Решение задачи оптимального размещения постов контроля сводится к перебору возможных вариантов для выбора наилучшего. При поиске решения приходится вычислять значений функционала стоимости. Некоторое упрощение счета может быть достигнуто, если предусмотреть лексико графическое упорядочение вычислений при обходе дерева перебора вариантов Экономия достигается за счет того, что общие части нескольких функционалов вычисляются один раз. Однако и с учетом этого трудоемкость вычислений для больших делает эту задачу практически неразрешимой. Ниже предложены два подхода, позволяющие существенно сократить число рассматриваемых вариантов.

Сокращение числа рассматриваемых вариантов на основе выделения частичных планов.

Пусть Назовем частичными векторами-планами размещения постов контроля или просто частичными планами. Частичные планы однозначно определяют размещение постов контроля на участках технологического процесса, включающих операции с первой по по соответственно. Частичные планы полностью определяют план X. Этот факт будем обозначать (следующим образом:

Под функционалами будем понимать затраты на обработку на соответствующих участках технологического процесса. Очевидно, Для операции с некоторым фиксированным номерам с обозначим множество планов X, в которых параметры сохраняют свои значения и равны соответственно символом

Теорема 5.1. В классе планов план является оптимальным, тогда и только тогда, когда частичные планы доставляют минимум функционалам соответственно.

Доказательство теоремы здесь не приводится. Оно строится исходя из следующих соображений. Если во всех планах

множества (5.22) на вход операции поступает один и тот же поток , равный и при этом насыщенность потока годными изделиями остается постоянной, равной v, то любой план можно рассматривать как два независимых Задача сводится к отысканию минимальных значений и соответствуюших им частичных планов.

Следствие 5.1. Для рассматриваемой модели в классе планов, для которых , план является оптимальным, если и только если в этом классе частичные планы доставляют минимум частичным функционалам соответственно.

Алгоритм 5.1. 1. . Первым компонентам -мерных векторов присвоить значения нуль и единица соответственно»

2. компонентам векторов с номерами от до присвоить единичные значения и вычислить частичные суммы функционалов

3. Из вычисленных по п. 2 частичных сумм выбрать наименьшую и соответствующие ей значения компонент вектора присвоить вектору. Если перейти к п. 2.

4. компонентам векторов от до присвоить нулевые значения и вычислить частичные суммы, функционалов Присвоить и перейти к п. 2.

5. Отпечатать вектор X и соответствующее ему значение Прекратить вычисления.

При реализации алгоритма рассматриваются возможные переходы на дереве поиска из вершин первого яруса последовательно в вершины второго, затем третьего и т. д. до яруса. Начиная со второго, на каждом ярусе исключаются из дальнейшего рассмотрения путей переходов через единичные вершины рассматриваемого яруса. На каждом ярусе подсчитывается частичных сумм, что дает существенный выигрыш в быстродействии по сравнению с алгоритмом полного перебора, по которому приходится подсчитывать 2 частичных сумм. При подсчете частичных сумм алгоритма) на ярусе используются вычисленные ранее частичные суммы При спуске на ярус получается значений функционала стоимости из которых выбирают соответствующее

Алгоритм иллюстрирует рис. 5.34. Пусть технологический процесс состоит из четырех операций. Предположим, что при переходе в единичные вершины

На дереве поиска решений из некоторых вершин второго и третьего яруса отсутствуют пути переходов в вершины четвертого яруса — согласно алгоритму соответствующие планы размещения

исключаются из рассмотрения как заведомо неоптимальные. В итоге найдено четыре варианта плана, из которых надо выбирать оптимальный.

Дальнейшее сокращение числа рассматриваемых вариантов может быть достигнуто с помощью критериев, позволяющих в случае их выполнения определить оптимальные значения некоторых компонент вектора X на основе анализа соотношений характеристик контрольных и технологических операций на ограниченном участке технологического процесса. Назовем такие критерии локальными.

Рис. 5.34. Сокращенное дерево перебора вариантов расположения постов контроля

Локальные критерии оптимизации.

Будем считать, что контроль i-й операции целесообразен (нецелесообразен), если существуют варианты планов с компонентой при которых функция стоимости принимает минимальное значение.

Теорема 5.2. Если

то контроль i-й операции целесообразен независимо от распределения постов контроля на других технологических операциях.

Условие (5.23) соответствует ситуации, при которой затраты на обработку дефектных изделий технологической операции превышают затраты на контроль после i-й операции. Доказательство теоремы основано на том, что затраты на контроль окупаются уже на операции за счет того, что здесь не будут обрабатываться изделия, при изготовлении которых операция выполнена с дефектом.

Теорема 5.2 естественно допускает обобщение на случай, когда затраты на контроль сравниваются со стоимостью не одной операции, а с суммарной стоимостью нескольких соседних технологических и контрольных операций, благодаря чему получены менее «жесткие», чем локальные критерии. Ниже приводятся лишь те критерии, которые в результате многократного их использования при решении различных задач оказались наиболее эффективными.

По аналогии с теоремой 5.2 можно доказать теоремы обобщив условие (5.23) на несколько соседних операций. Введем переменную которая может принимать значения из множества Если одна или несколько следующих за i-й технологических операций не контролируются, их можно считать одной обобщенной технологической операцией со стоимостью, равной сумме стоимостей неконтролируемых операций. Стоимость обработки потока из изделий на обобщенной операции составляет

С учетом (6.24) минимальные и максимальные затраты на обработку дефектных изделий, которые могут быть отбракованы после i-й технологической операции, на участке технологического процесса с до операции составляют соответственно»

Теорема 5.3. Если и выполняется условие

то контроль i-й операции целесообразен независимо от распределения постов контроля на других технологических операциях.

Следствие 5.3 а. Если а компоненты с номерами определены и имеют нулевые значения, то контроль i-й операции целесообразен при выполнении условия

Следствие 5.36. Если компоненте предшествуюг нулевые компоненты с номерами то условия (5.25) и (5.26) можно записать в виде (5.27) и (5.28) соответственно:

Очевидно, условие (5.25) выполняется с большей вероятностью, чем (5.23). Существенной задержки при вычислении минимального, значения переменной не происходит, если определять компоненты, начиная с в порядке убывания их номеров. Например, выбирается из двух элементов — минимальное значение также из двух элементов — и т. д. Отметим следующий частный случай: если между компонентами одна или несколько «омпонент определены и имеют нулевые значения, то из множества значении переменной исключаются соответствующие элементы. Например, если . Рассмотрим условия, позволяющие присвоить компонентам вектора X нулевые значения.

Теорема 5.4. Если и выполняется условие

то контроль i-й операции нецелесообразен независимо от распределения постов контроля на других технологических операциях.

Следствие 5.4 а. Если компоненты с номерами определены и имеют нулевые значения, то контроль i-й операции нецелесообразен при выполнении условия

Следствие 5.46. Если и между компонентами с номерами s и i нет ни одной единичной, то условия (5.29) и ) можнозаписать в виде и (5.32) соответственно:

На основе использования локальных критериев (5.25) — (5.32) и следствия из теоремы о частичных планах можно (построить следующий алгоритм решения поставленной задачи.

Алгоритм 5.2.

1. (-размерному вектору X присвоить значение

2. если то перейти к п. 14.

3. Если перейти к п. 2), иначе, если то перейти к п. 2).

4. ; если то перейти к п. 12.

5. Если то перейти к п. 7), иначе, если то

6. Перейти к п. 4.

7. ; если то перейти к п. 2).

8. Если то перейти к п. 7, иначе, если где нулевых компонент, то перейти к п. 7).

9. ; если то перейти к п. 12.

10. Если то перейти к п. 9.

11. Если то перейти к п. 12), иначе, если то перейти к п. 9).

12. С помощью метода частичных планов вычислить значения неопределенных компонент на участке т.

13. ; перейти к п. 7.

14. Отпечатать результаты.

15. Конец.

Программы оптимизации системы контроля технологического процесса.

Для автоматизации решения задачи на алгоритмическом языке ФОРТРАН-IV созданы три программы: программа 1, реализующая метод полного перебора; программа 2, реализующая метод частичных планов (алгоритмы 5.1); программа 3, реализующая метой локальных критериев в совокупности с методом частичных планов (алгоритм 5.2). Время счета программы 3 зависит от числа

компонент вектора X, значения которых определяются с помощью локальных критериев оптимизации. Для определения характеристик программы 3 на ЭВМ ЕС-1020 проведены ее статистические испытания для Время счета измерено путем усреднения экспериментальных данных, полученных при решении различных примеров, и составило время реализации программ 1 и 2 — соответственно 25 и 10 с. Среднее число определяемых с помощью локальных критериев компонент вектора X при решении одной задачи составляет 55% общего числа компонент, что подтверждает целесообразность использования локальных критериев оптимизации.

Время решения задачи выбора оптимального плана размещения постов контроля в технологическом процессе [31] с помощью программы 3 составило 50 с. Для сравнения та же задача была решена с использованием программ 2 и 1. Время счета составило 90 с и 200 мин соответственно.

Таким образом, изложенные в этом параграфе результаты существенно сокращают трудоемкость выбора оптимального плана размещения постов контроля. С помощью программы 3 эта задача была решена для нескольких технологических процессов производства микросхем и печатных плат. При этом оказалось, что автоматизация оптического контроля не только облегчает труд человека, но и во многих случаях приводит к снижению себестоимости изделий.