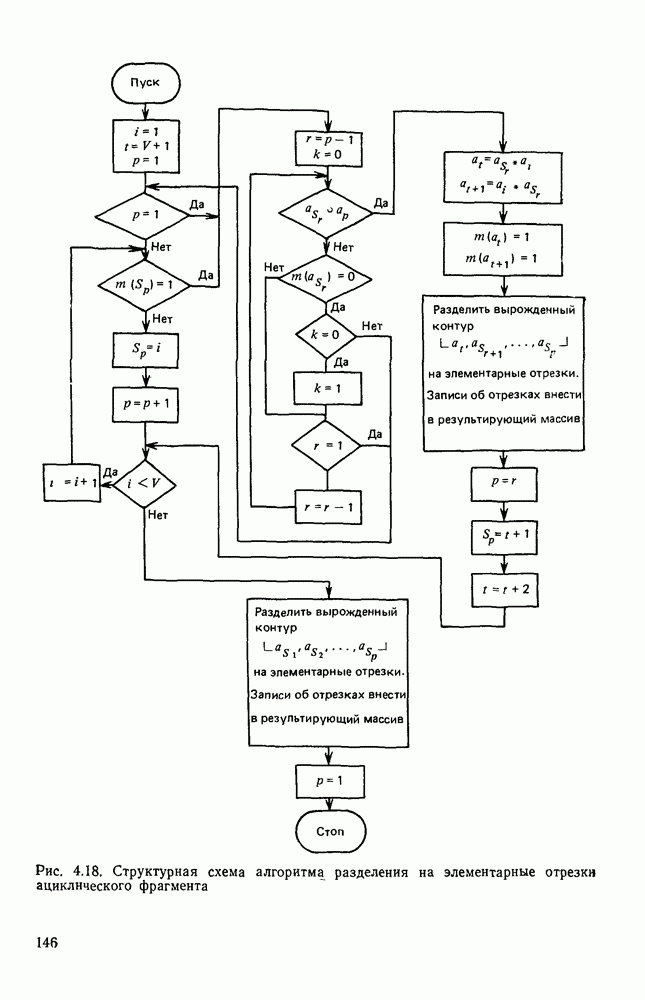
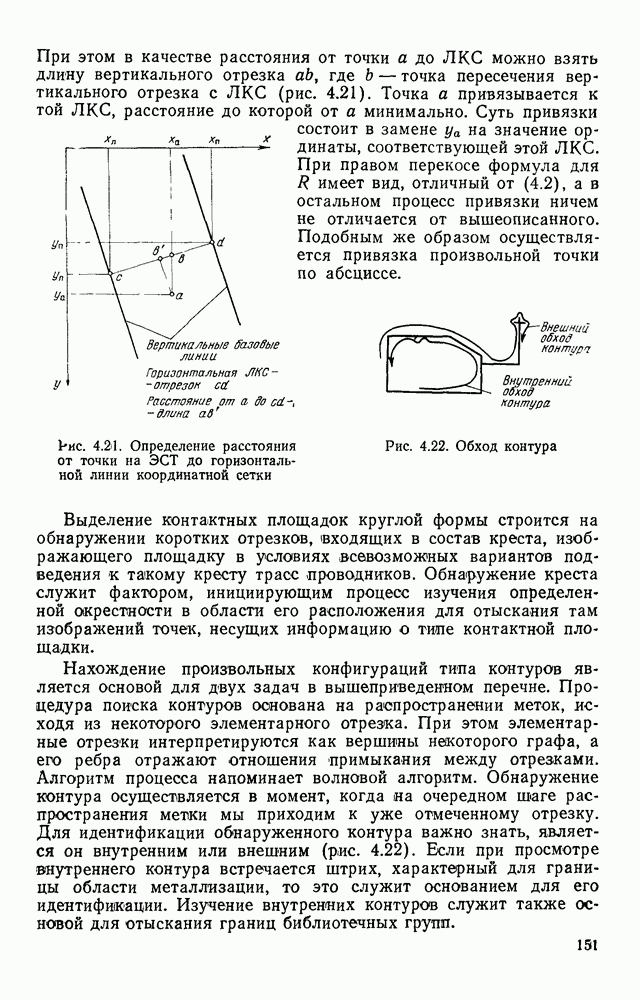
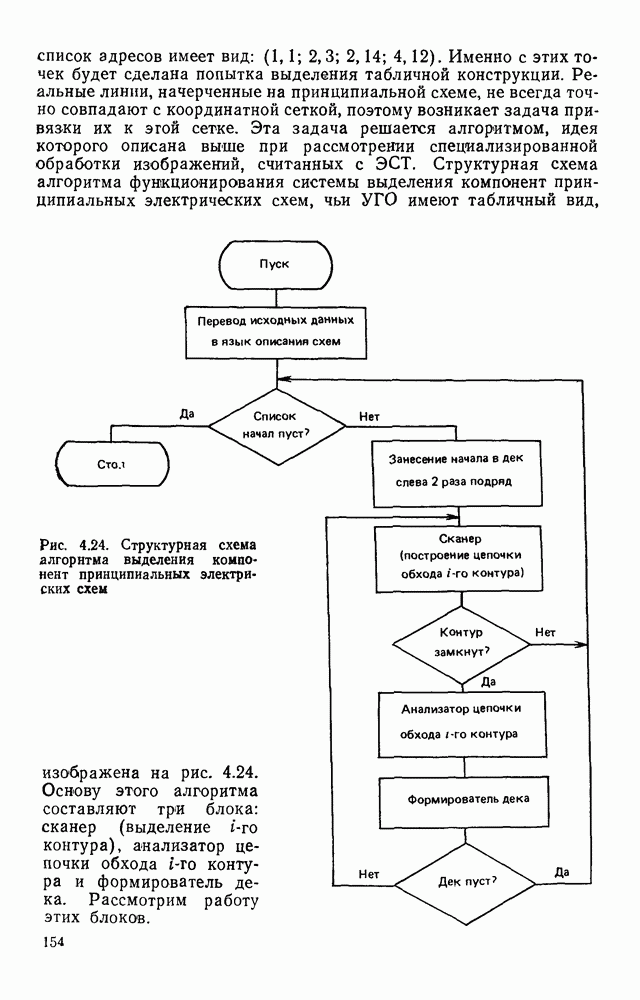
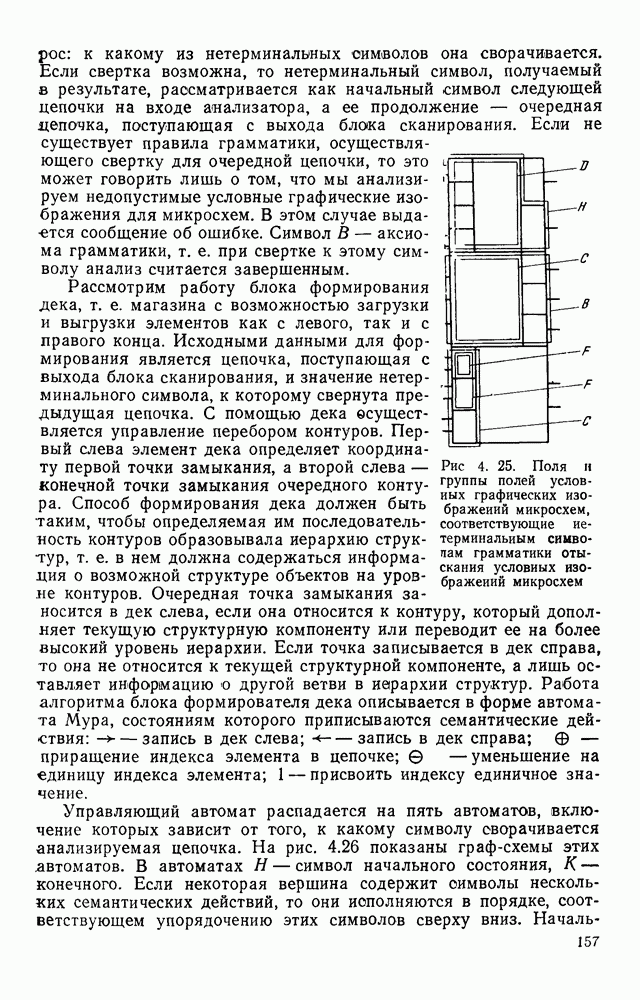
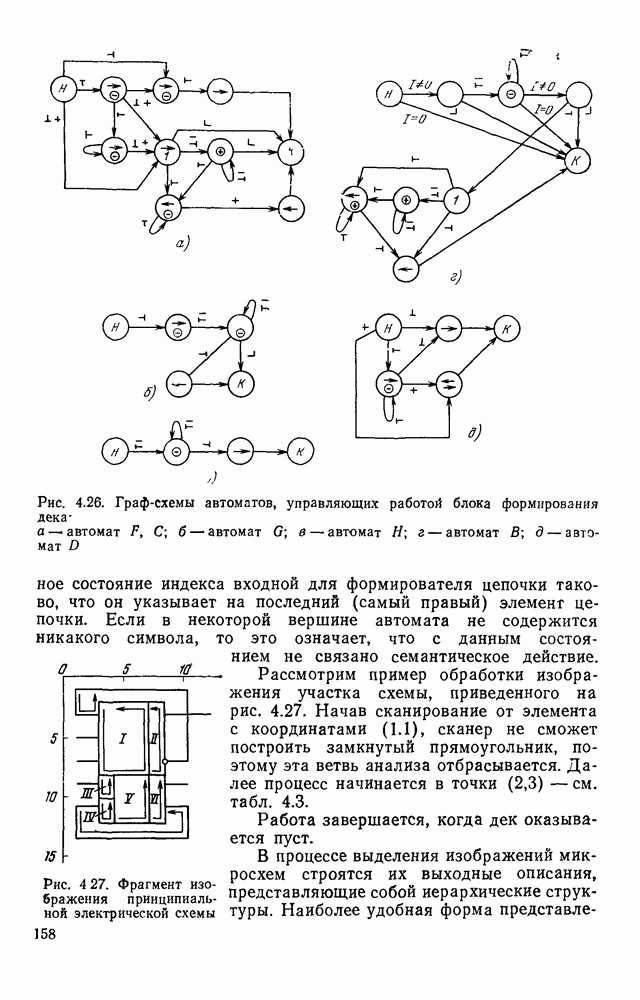
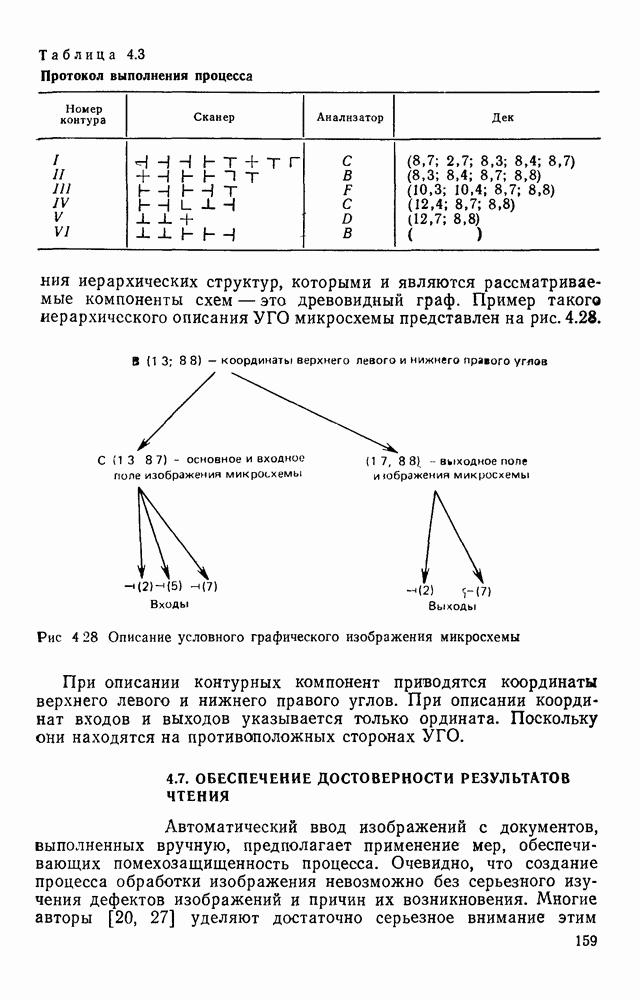
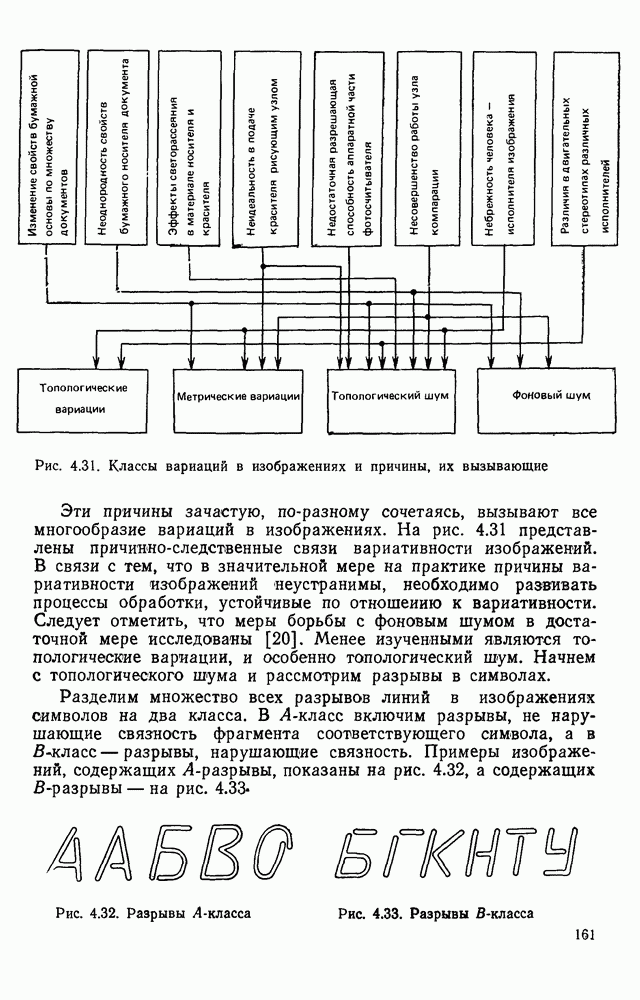
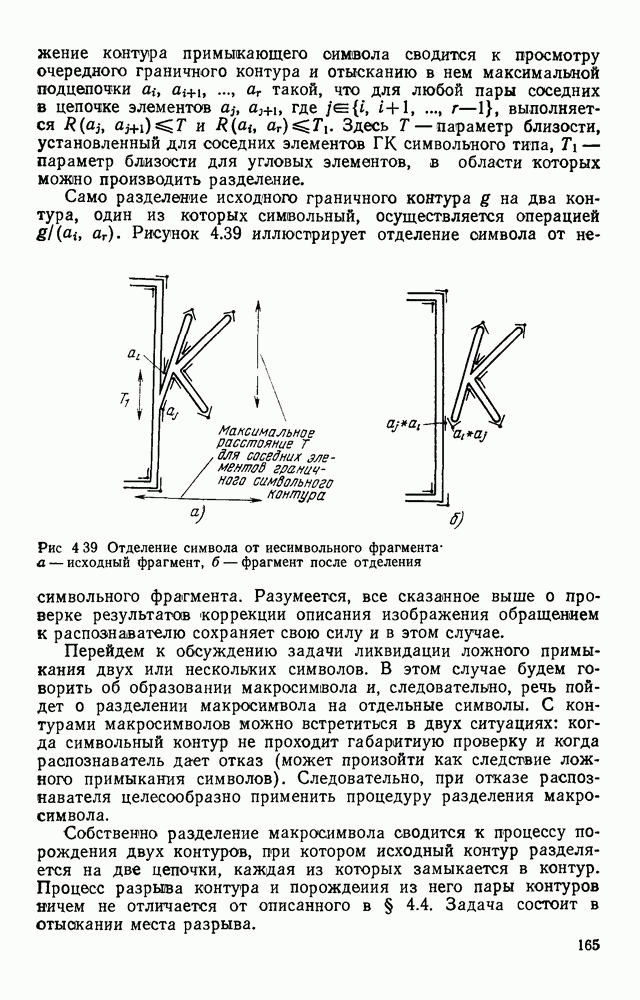
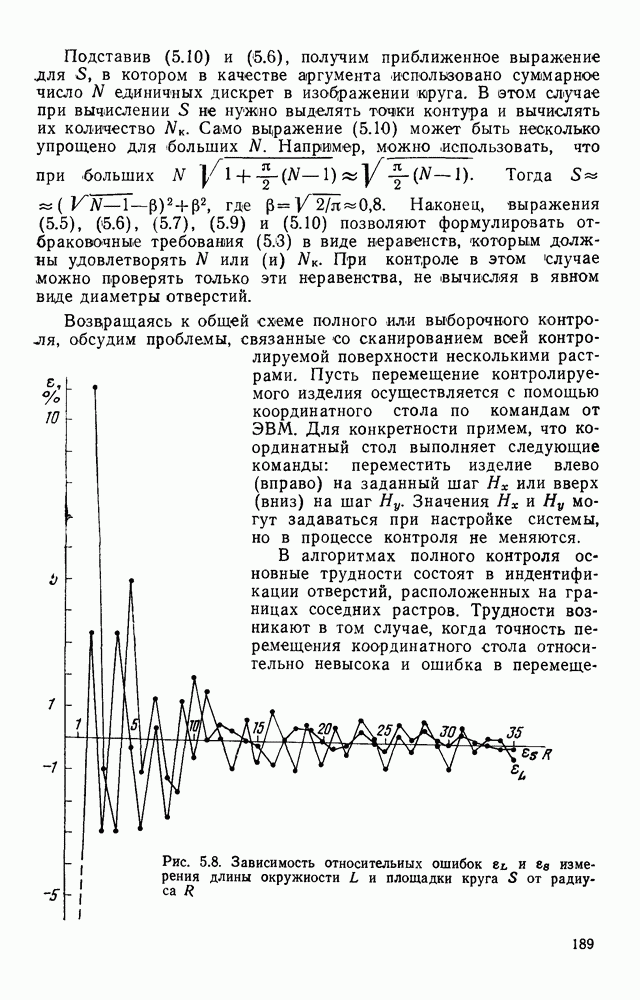
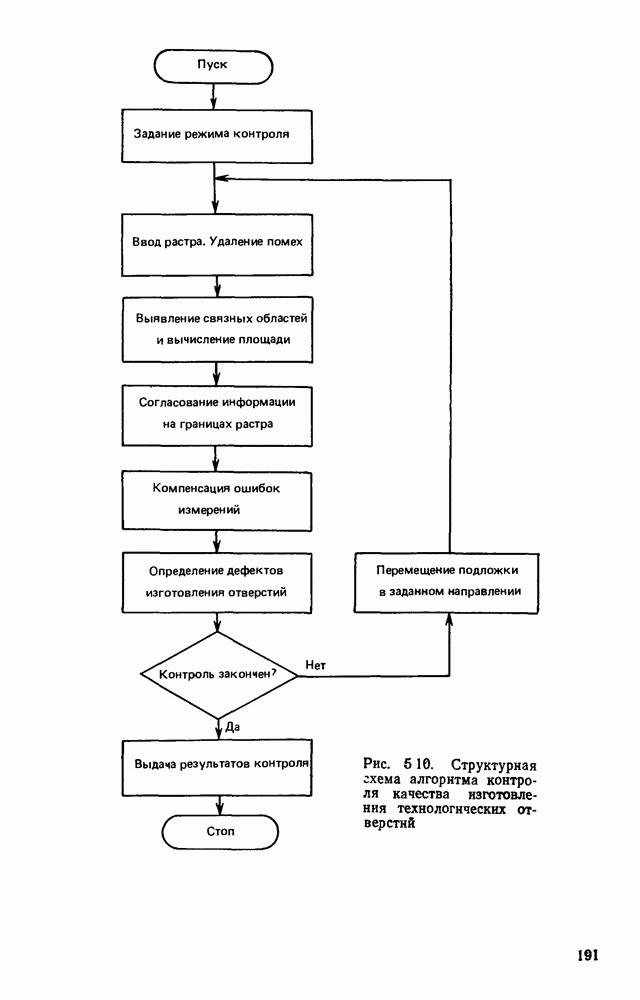
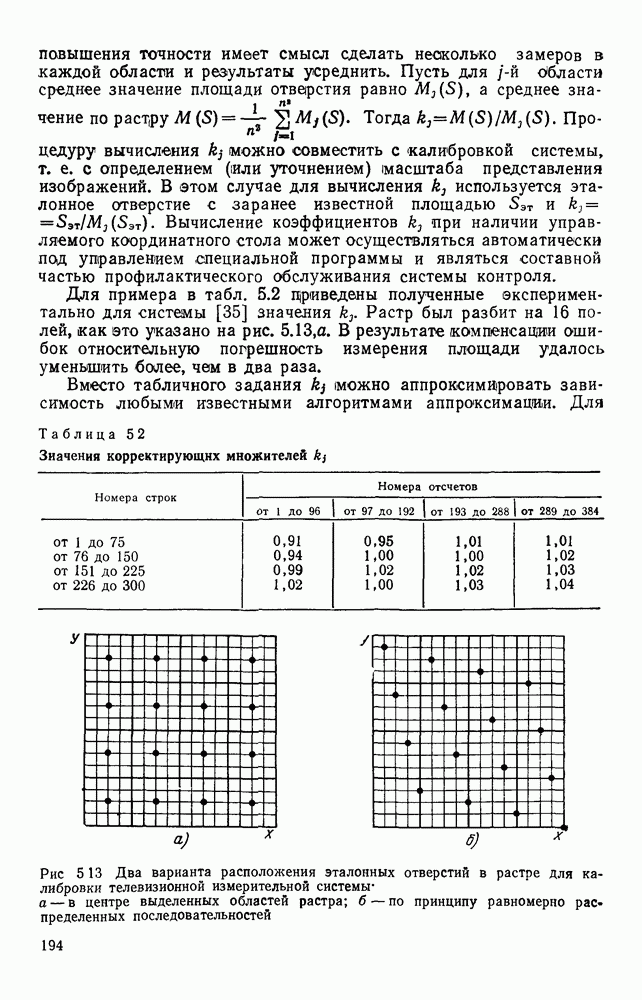
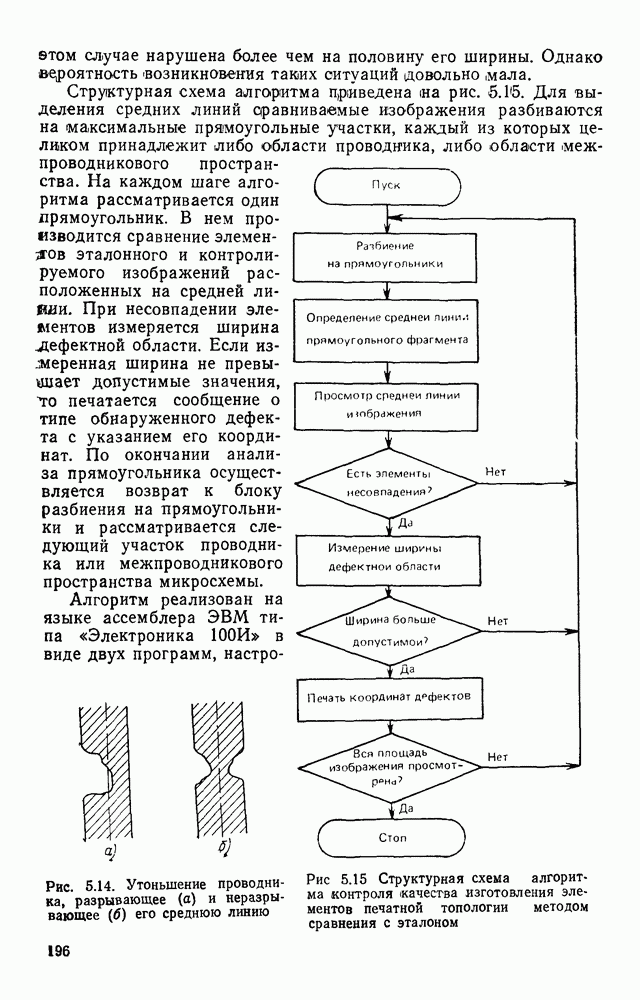
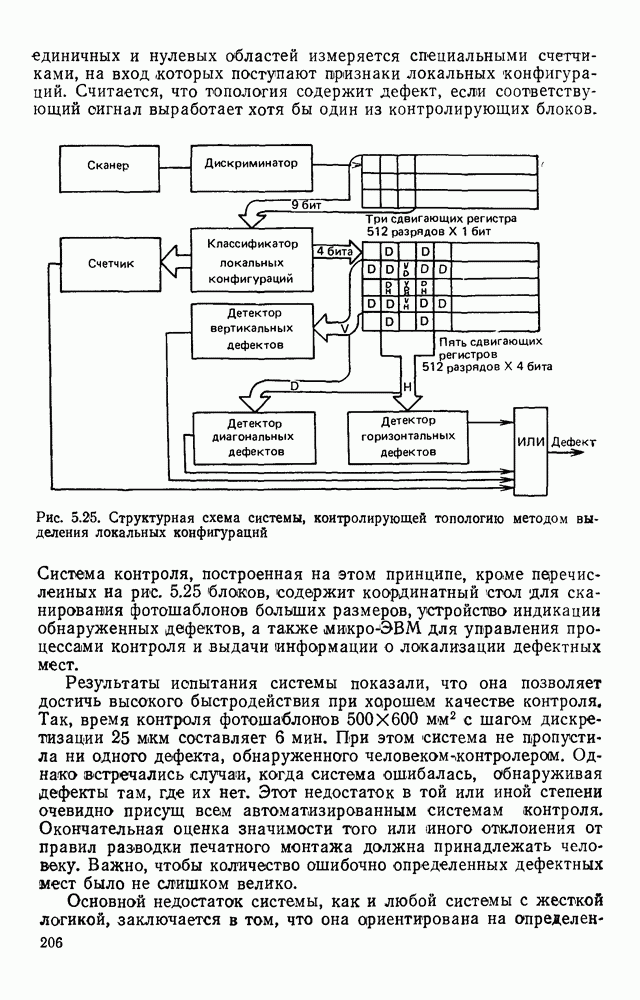
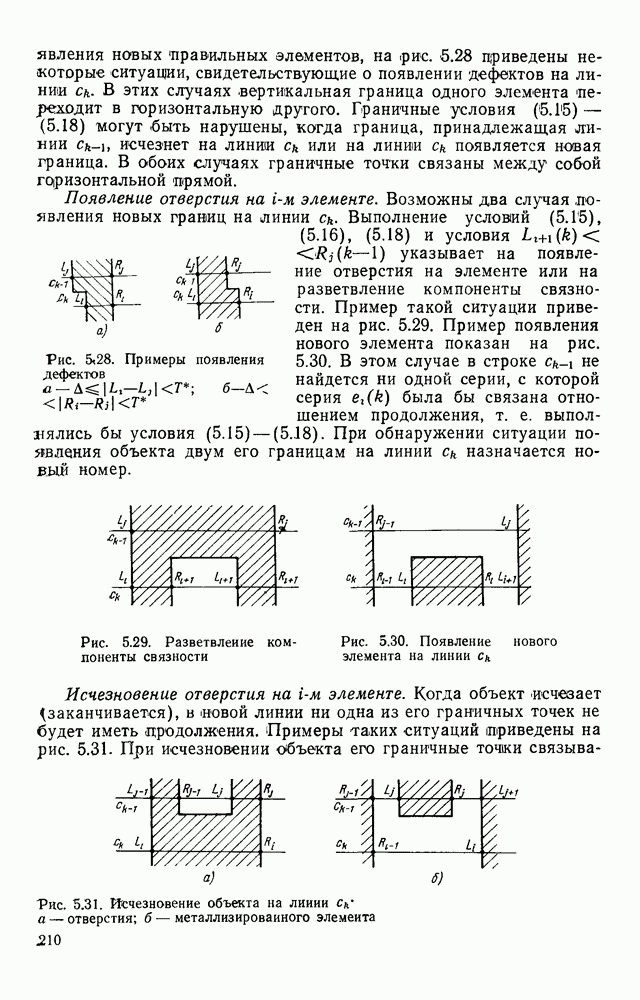
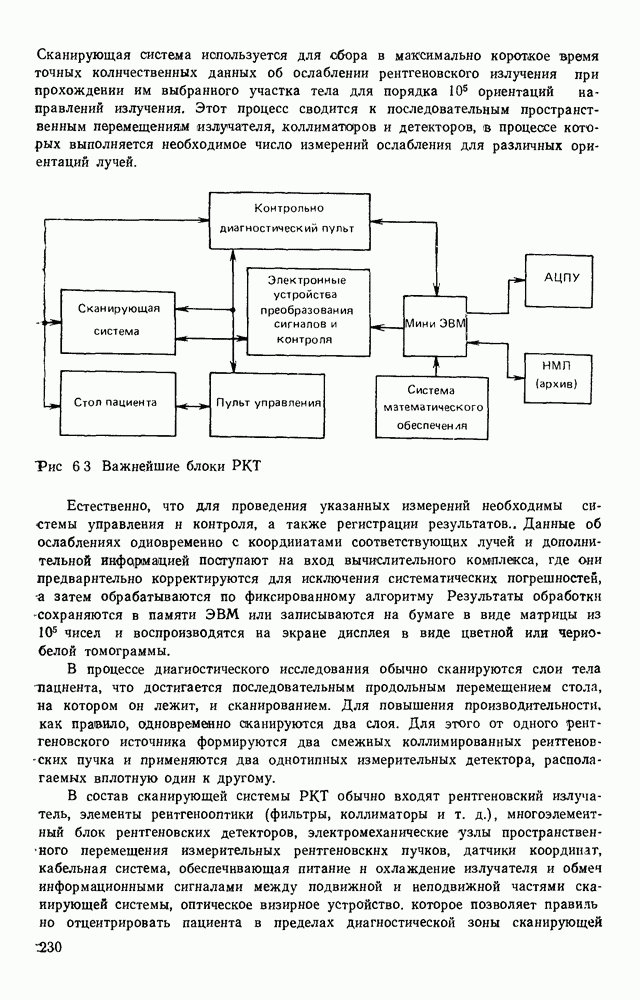
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5. ПРЕДСТАВЛЕНИЕ КОНТУРОВ ФИГУР
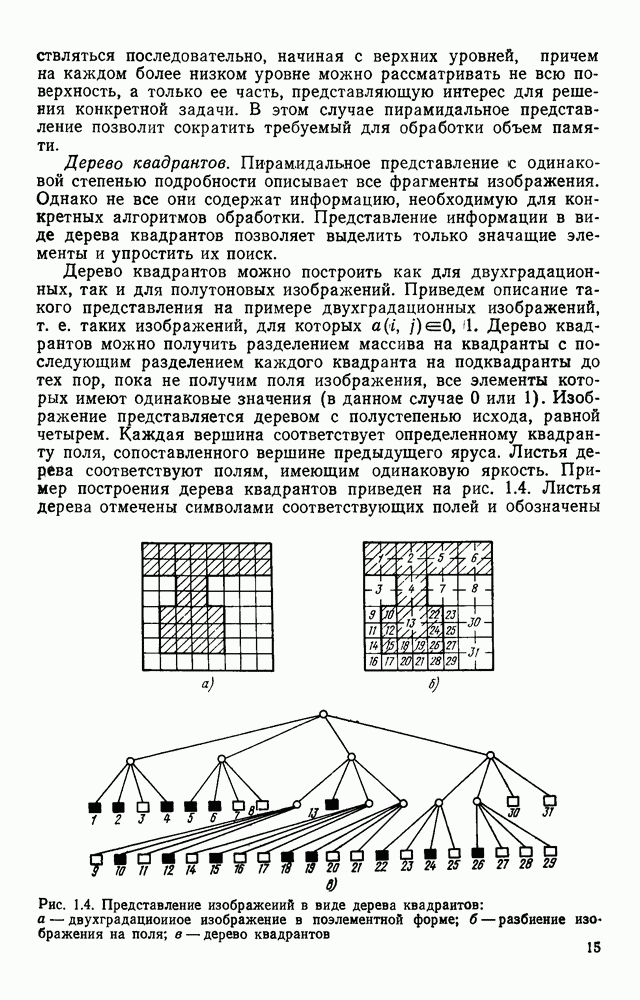
Рассматривается задача кодирования изображений, состоящих из плоских фигур. На рецепторном поле каждая такая фигура представляется множеством принадлежащих ей то чек, образующих некоторую связную область. Точка  находящаяся в этой области, называется граничной или контурной, если хотя бы одна
находящаяся в этой области, называется граничной или контурной, если хотя бы одна  четырех соседних точек рецепторного поля изображению фигуры не принадлежит. Каждая фигура однозначно задается множеством
четырех соседних точек рецепторного поля изображению фигуры не принадлежит. Каждая фигура однозначно задается множеством  граничных точек, в совокупности образующих ее контур. При этом от способа представления контура фигур в существенной степени зависит компактность представления изображения в целом и эффективность его обработки. Обычно контур аппроксимируется ломаной линией или задается параметрически. Некоторые алгоритмы аппроксимации контуров рассматриваются ниже.
граничных точек, в совокупности образующих ее контур. При этом от способа представления контура фигур в существенной степени зависит компактность представления изображения в целом и эффективность его обработки. Обычно контур аппроксимируется ломаной линией или задается параметрически. Некоторые алгоритмы аппроксимации контуров рассматриваются ниже.
Полигональная аппроксимация.
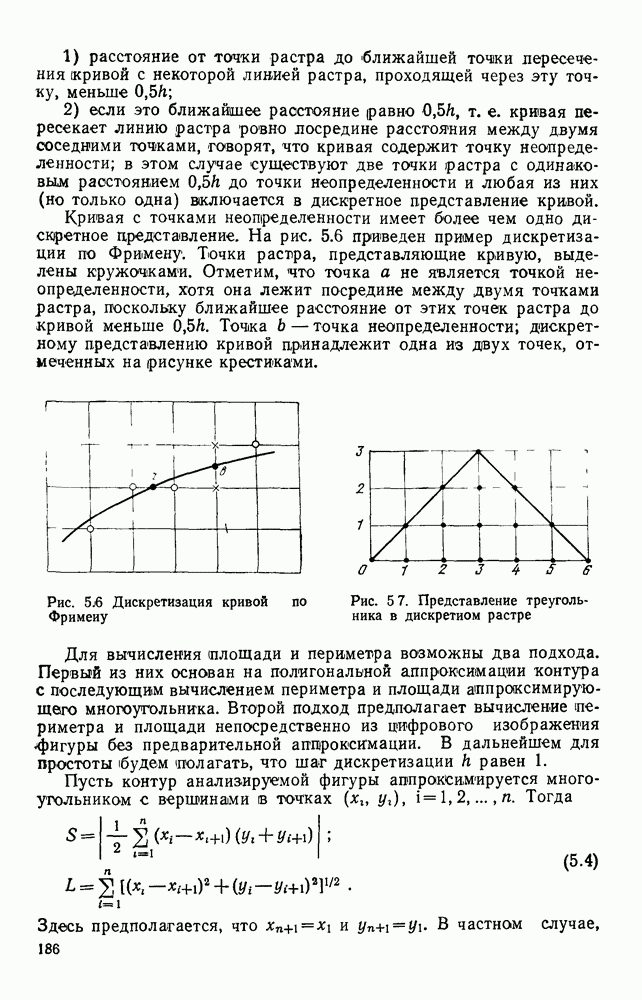
Фигура представляется в виде многоугольника, который задается множеством вершин, называемых узлами аппроксимации. Естественно попытаться построить такой многоугольник, который содержал бы минимальное числа вершин и в то же время представлял фигуру с заданной точностью. Требования к точности аппроксимации сформулируем следующим образом: расстояние от каждой точки  до ближайшей точки пересечения отрезка аппроксимирующей ломаной с некоторой линией растра, проходящей через b», не должно превышать шага рецепторной сетки. Для конкретности положим, что узлы аппроксимации должны выбираться из множества граничных точек.
до ближайшей точки пересечения отрезка аппроксимирующей ломаной с некоторой линией растра, проходящей через b», не должно превышать шага рецепторной сетки. Для конкретности положим, что узлы аппроксимации должны выбираться из множества граничных точек.
При построении каждого отрезка ломаной целесообразно придерживаться следующих положений. Если известна начальная точка то в качестве конца отрезка выбирается максимально удаленная от b точка  такая, что расстояние от каждой точки контура, расположенной между
такая, что расстояние от каждой точки контура, расположенной между  до отрезка
до отрезка  удовлетворяет сформулированным выше требованиям к точности аппроксимации. Для определения такой максимально удаленной точки
удовлетворяет сформулированным выше требованиям к точности аппроксимации. Для определения такой максимально удаленной точки  можно воспользоваться следующим алгоритмом. Поместим начало координат
можно воспользоваться следующим алгоритмом. Поместим начало координат  в известную начальную точку
в известную начальную точку  Свяжем с каждой точкой
Свяжем с каждой точкой  некоторые ограничения на область, в которой может лежать очередной узел аппроксимации. Для этого проведем из начала координат через соседние с
некоторые ограничения на область, в которой может лежать очередной узел аппроксимации. Для этого проведем из начала координат через соседние с  точки растра четыре луча. Выберем два
точки растра четыре луча. Выберем два  так, чтобы образованный ими угол имел максимальное значение. Очевидно, что очередной узел аппроксимации должен принадлежать области
так, чтобы образованный ими угол имел максимальное значение. Очевидно, что очередной узел аппроксимации должен принадлежать области  ограниченной этими лучами. Определение конечной точки
ограниченной этими лучами. Определение конечной точки  осуществляется перебором точек
осуществляется перебором точек  в направлении обхода контура. Пусть на очередном шаге перебора рассматривается точка
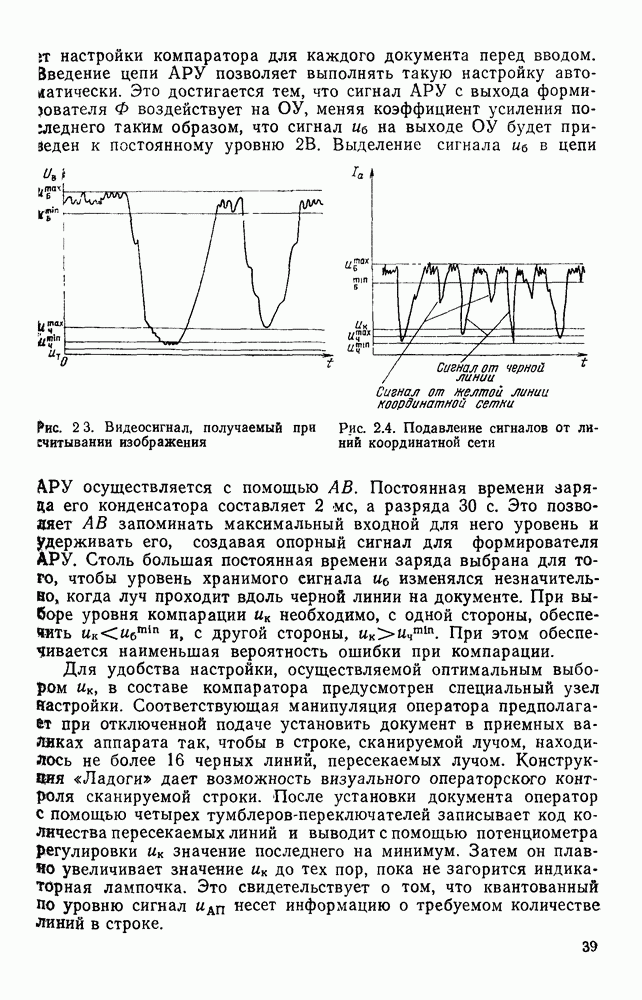
в направлении обхода контура. Пусть на очередном шаге перебора рассматривается точка  результате предшествующих шагов алгоритма определена область
результате предшествующих шагов алгоритма определена область  которой должен принадлежать узел аппроксимации. Тогда при рассмотрении точки
которой должен принадлежать узел аппроксимации. Тогда при рассмотрении точки  эта область
эта область
корректируется по следующему правилу:  Если то полагается, что
Если то полагается, что  В противном случае значение
В противном случае значение  не меняется. В начале реализации алгоритма полагается, что
не меняется. В начале реализации алгоритма полагается, что  равна всей плоскости. Считается, что отрезок построен, если на очередном шаге алгоритма область
равна всей плоскости. Считается, что отрезок построен, если на очередном шаге алгоритма область  пуста.
пуста.
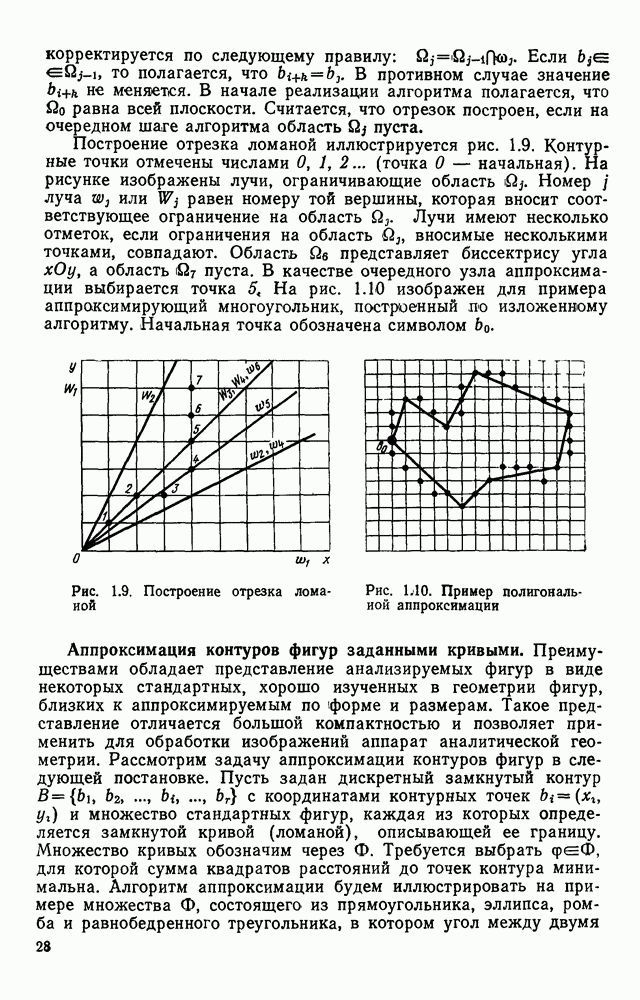
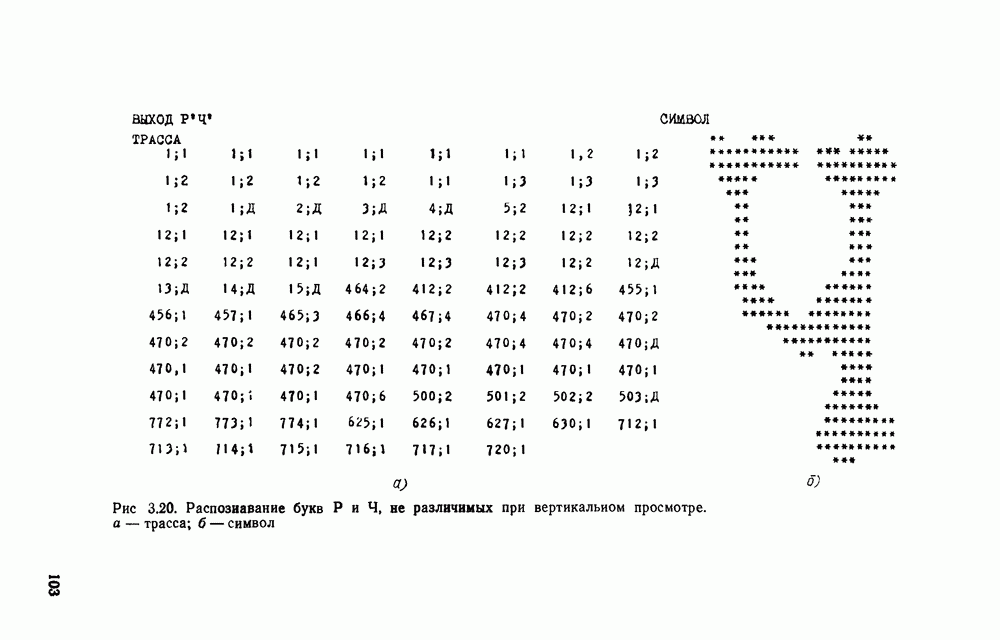
Построение отрезка ломаной иллюстрируется рис. 1.9. Контурные точки отмечены числами  (точка 0 — начальная). На рисунке изображены лучи, ограничивающие область
(точка 0 — начальная). На рисунке изображены лучи, ограничивающие область  Номер
Номер  луча
луча  или
или  равен номеру той вершины, которая вносит соответствующее ограничение на область
равен номеру той вершины, которая вносит соответствующее ограничение на область  . Лучи имеют несколько отметок, если ограничения на область
. Лучи имеют несколько отметок, если ограничения на область  вносимые несколькими точками, совпадают. Область
вносимые несколькими точками, совпадают. Область  представляет биссектрису угла
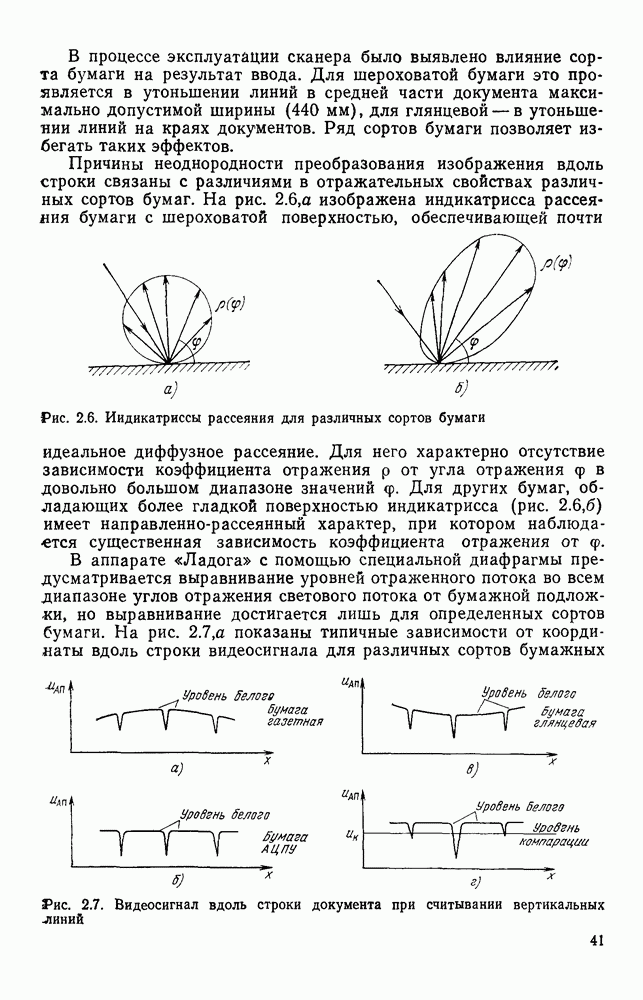
представляет биссектрису угла  а область
а область  пуста. В качестве очередного узла аппроксимации выбирается точка 5, На рис. 1.10 изображен для примера аппроксимирующий многоугольник, построенный по изложенному алгоритму. Начальная точка обозначена символом
пуста. В качестве очередного узла аппроксимации выбирается точка 5, На рис. 1.10 изображен для примера аппроксимирующий многоугольник, построенный по изложенному алгоритму. Начальная точка обозначена символом 

Рис. 1.9. Построение отрезка ломаной

Рис. 1.10. Пример полигональной аппроксимации
Аппроксимация контуров фигур заданными кривыми.
Преимуществами обладает представление анализируемых фигур в виде некоторых стандартных, хорошо изученных в геометрии фигур, близких к аппроксимируемым по форме и размерам. Такое представление отличается большой компактностью и позволяет применить для обработки изображений аппарат аналитической геометрии. Рассмотрим задачу аппроксимации контуров фигур в следующей постановке. Пусть задан дискретный замкнутый контур  с координатами контурных точек
с координатами контурных точек  и множество стандартных фигур, каждая из которых определяется замкнутой кривой (ломаной), описывающей ее границу. Множество кривых обозначим через Ф. Требуется выбрать срез, для которой сумма квадратов расстояний до точек контура минимальна. Алгоритм аппроксимации будем иллюстрировать на примере множества Ф, состоящего из прямоугольника, эллипса, ромба и равнобедренного треугольника, в котором угол между двумя
и множество стандартных фигур, каждая из которых определяется замкнутой кривой (ломаной), описывающей ее границу. Множество кривых обозначим через Ф. Требуется выбрать срез, для которой сумма квадратов расстояний до точек контура минимальна. Алгоритм аппроксимации будем иллюстрировать на примере множества Ф, состоящего из прямоугольника, эллипса, ромба и равнобедренного треугольника, в котором угол между двумя
равными сторонами не превышает 60°. Устраняя некоторую неоднозначность, подчеркнем, что в дальнейшем, говоря о прямоугольнике, эллипсе, ромбе и треугольнике, будем подразумевать не фигуру, а соответствующую кривую (ломаную) линию.
Зафиксируем некоторое каноническое положение кривых относительно осей декартовой системы координат. С этой целью построим для каждой кривой проходящую через ее центр тяжести ось, относительно которой момент инерции кривой [8] принимает минимальное значение. Совместим ось  с этой главной осью тяжести, а центр системы координат — с центром тяжести.
с этой главной осью тяжести, а центр системы координат — с центром тяжести.
Каноническое положение кривых иллюстрируется рис. 1.11. Строго говоря, для треугольника возможны два канонических положения, получающиеся один из другого поворотом треугольника на угол 180°.

Рис. 1.11. Каноническое положение прямоугольника, эллипса, ромба и треугольника относительно осей декартовой системы координат
Удобно различать эти два представления как две различные фигуры. Пусть в множество Ф входит одна из них, а именно та, которая изображена на рисунке. Очевидно, любое расположение кривой в растре может быть сведено к каноническому переносу центра системы координат по оси х и у на расстояния  и повороту осей координат на угол 8. Примем также, что в канонической системе координат аппроксимирующие кривые однозначно определяются двумя параметрами, которые обозначим через u и v, Для кривых множества Ф эти параметры имеют следующий смысл: в прямоугольнике — это длины сторон, в эллипсе — большая и малая полуоси, в ромбе — длины диагоналей, а треугольнике — основание и высота. Задача построения каждой кривой
и повороту осей координат на угол 8. Примем также, что в канонической системе координат аппроксимирующие кривые однозначно определяются двумя параметрами, которые обозначим через u и v, Для кривых множества Ф эти параметры имеют следующий смысл: в прямоугольнике — это длины сторон, в эллипсе — большая и малая полуоси, в ромбе — длины диагоналей, а треугольнике — основание и высота. Задача построения каждой кривой  таким образом, может быть сведена к отысканию компонент вектора
таким образом, может быть сведена к отысканию компонент вектора 
В целом алгоритм аппроксимации разбивается на три этапа. На первом из них решается задача совмещения контура с кривыми множества Ф. При этом определяются  и преобразуется система координат, в которой определены контурные точки. Такое преобразование является общим для совмещения с любой кривой
и преобразуется система координат, в которой определены контурные точки. Такое преобразование является общим для совмещения с любой кривой  . На втором этапе для каждой кривой находят все геометрические параметры
. На втором этапе для каждой кривой находят все геометрические параметры  . Третий этап сводится к выбору из множества построенных на втором этапе кривых такой,
. Третий этап сводится к выбору из множества построенных на втором этапе кривых такой,
сумма квадратов расстояний которой от контурных точек минимальна. Результаты реализации каждого из этапов могут представлять самостоятельный интерес. Например, параметры u и v всех построенных на втором этапе алгоритма кривых могут быть использованы как признаки в задачах классификации. Если требуется найти только положение некоторой фигуры в растре, то достаточно реализовать только первый этап алгоритма. Отметим, что на первых двух этапах алгоритма в качестве меры близости точек контура и аппроксимирующей кривой используется не сумма квадратов соответствующих расстояний, а совпадение некоторых характерных линий и точек. Уравнения этих линий и точек однозначно определяются для кривых уравнениями кривых, а для множества контурных точек — их координатами. Такое изменение критерия позволило существенно упростить вычисление компонент вектора G и придать алгоритму большую степень универсальности.
Будем считать, что аппроксимируемый контур и аппроксимирующая кривая совмещены, если совмещены их центры и главные оси тяжести. При этом главная ось тяжести дискретного контура определяется как прямая, сумма квадратов расстояний от которой до точек контура минимальна. Координаты  центра тяжести вычисляют по формулам:
центра тяжести вычисляют по формулам:  . Уравнение главной оси тяжести представляется в виде
. Уравнение главной оси тяжести представляется в виде  Из условия минимума суммы квадратов расстояний от точек контура определяется угловой коэффициент
Из условия минимума суммы квадратов расстояний от точек контура определяется угловой коэффициент 

Помещаем центр новой системы координат в точку  и совмещаем ось абсцисс с главной осью тяжести. Координаты точек контура
и совмещаем ось абсцисс с главной осью тяжести. Координаты точек контура  в новой системе координат вычисляют по формулам:
в новой системе координат вычисляют по формулам:

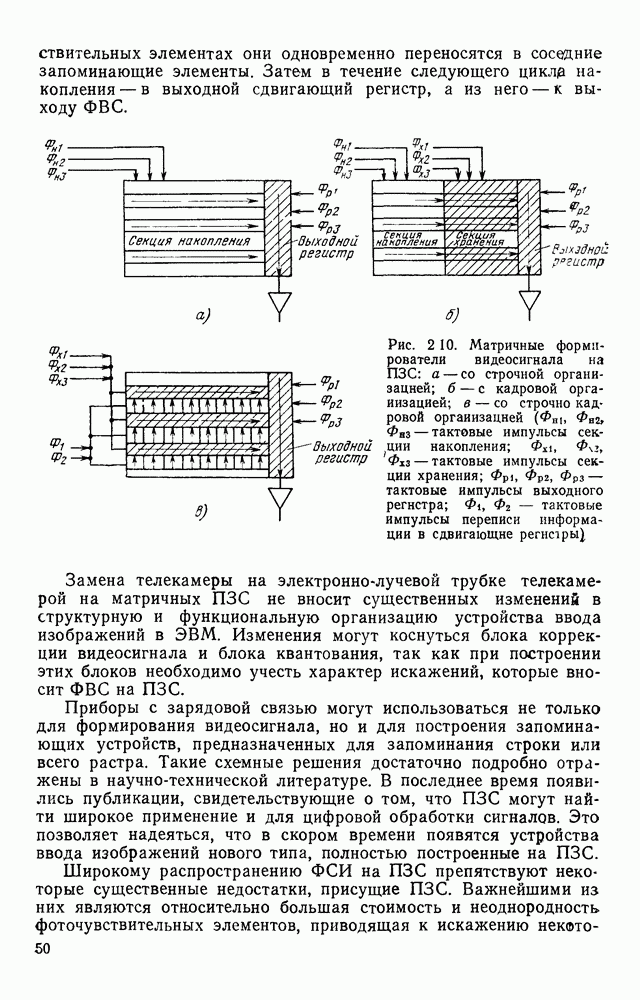
Для определения параметров u и v применим искусственный прием, сводящийся к разбиению множества контурных точек и кривых  на части. Положим, что исходный контур распадается, как показано на рис. 1.12, на две пары замкнутых контуров, образованных соответственно точками контура, лежащими в верхней, нижней, левой и правой полуплоскостях, а также точками пересечения осей координат с линиями координатной сетки. Все преобразования делают в новой системе координат. Обозначим через
на части. Положим, что исходный контур распадается, как показано на рис. 1.12, на две пары замкнутых контуров, образованных соответственно точками контура, лежащими в верхней, нижней, левой и правой полуплоскостях, а также точками пересечения осей координат с линиями координатной сетки. Все преобразования делают в новой системе координат. Обозначим через
 среднее расстояние от оси у центров тяжести двух контуров, расположенных в левой и правой полуплоскостях. Аналогично через
среднее расстояние от оси у центров тяжести двух контуров, расположенных в левой и правой полуплоскостях. Аналогично через  обозначим такие расстояния от оси
обозначим такие расстояния от оси  для контуров, расположенных в верхней и нижней полуплоскостях. Величины
для контуров, расположенных в верхней и нижней полуплоскостях. Величины  могут быть определены из соотношений:
могут быть определены из соотношений:

где  — соответствующие координаты точек пересечения контура с осями координат.
— соответствующие координаты точек пересечения контура с осями координат.

Рис. 1.12. Определение парамет ров аппроксимирующих кривых
Параметры u и v могут быть определены, исходя из значений  для каждой из кривых, принадлежащих множеству
для каждой из кривых, принадлежащих множеству  . Так, например, в аппроксимирующем прямоугольнике величины
. Так, например, в аппроксимирующем прямоугольнике величины  найденные тем же способом, что и для исходного контура, определяются соотношениями:
найденные тем же способом, что и для исходного контура, определяются соотношениями:

где  — длины сторон прямоугольника. Отсюда
— длины сторон прямоугольника. Отсюда  Нетрудно также получить соотношения, определяющие размеры большой «а и малой
Нетрудно также получить соотношения, определяющие размеры большой «а и малой  полуосей эллипса
полуосей эллипса  . Аналогично вычисляются диагонали
. Аналогично вычисляются диагонали  ромба:
ромба:

а также основание  и высота
и высота  треугольника:
треугольника:

На третьем этапе алгоритма каждой кривой  сопоставляется оценка
сопоставляется оценка  вычисляемая по формуле
вычисляемая по формуле  где
где  - расстояние от точки контура
- расстояние от точки контура  до кривой
до кривой  . Из множества кривых в качестве аппроксимирующей выбирают кривую с минимальным значением оценки. Обозначим через
. Из множества кривых в качестве аппроксимирующей выбирают кривую с минимальным значением оценки. Обозначим через  расстояние в преобразованной системе координат от некоторой точки
расстояние в преобразованной системе координат от некоторой точки  до прямоугольника, эллипса, ромба и треугольника соответственно. Значения
до прямоугольника, эллипса, ромба и треугольника соответственно. Значения  вычисляют по формулам:
вычисляют по формулам:


где  Вычисление точных значений параметра
Вычисление точных значений параметра  для эллипса связано со значительными аналитическими трудностями. Поэтому
для эллипса связано со значительными аналитическими трудностями. Поэтому  определяют приближенно, как половину модуля разности между суммой расстояний от i-й точки контура до фокусов эллипса и константой эллипса
определяют приближенно, как половину модуля разности между суммой расстояний от i-й точки контура до фокусов эллипса и константой эллипса 

где  — половина фокусного расстояния эллипса.
— половина фокусного расстояния эллипса.
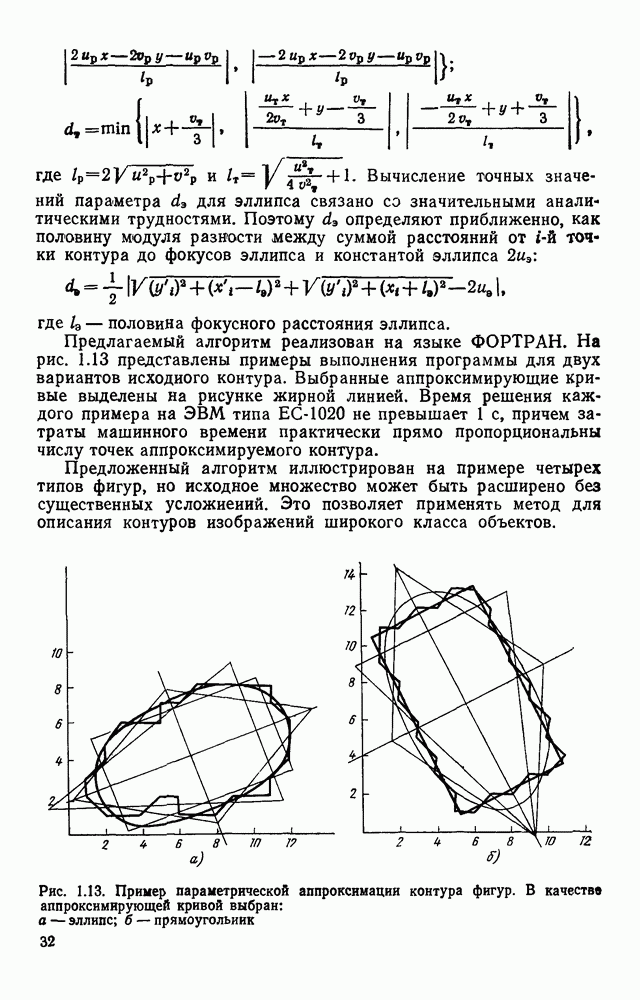
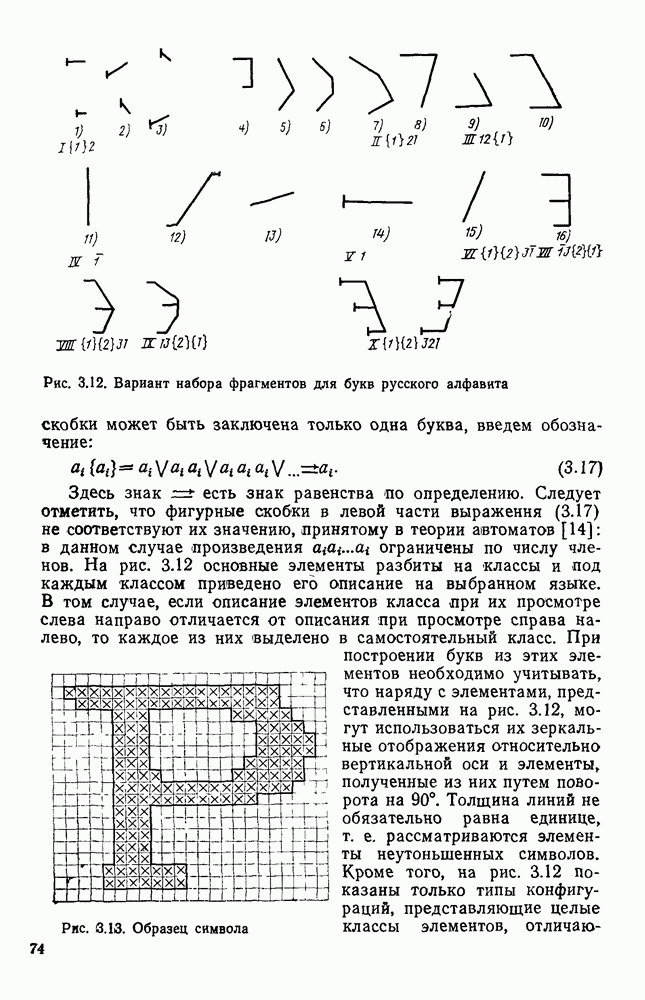
Предлагаемый алгоритм реализован на языке ФОРТРАН. На рис. 1.13 представлены примеры выполнения программы для двух вариантов исходного контура. Выбранные аппроксимирующие кривые выделены на рисунке жирной линией. Время решения каждого примера на ЭВМ типа  не превышает 1 с, причем затраты машинного времени практически прямо пропорциональны числу точек аппроксимируемого контура.
не превышает 1 с, причем затраты машинного времени практически прямо пропорциональны числу точек аппроксимируемого контура.
Предложенный алгоритм иллюстрирован на примере четырех типов  но исходное множество может быть расширено без существенных усложнений. Это позволяет применять метод для описания контуров изображений широкого класса объектов.
но исходное множество может быть расширено без существенных усложнений. Это позволяет применять метод для описания контуров изображений широкого класса объектов.

Рис. 1.13. Пример параметрической аппроксимаций контура фигур. В качестве аппроксимирующей кривой выбран: а — эллипс; б — прямоугольник
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ КОДИРОВАНИЯ И СЖАТИЯ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
- 1.2. ОСНОВНЫЕ МЕТОДЫ КОДИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.3. ВТОРИЧНОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ
- 1.4. КОДИРОВАНИЕ ДВУХГРАДАЦИОННЫХ ИЗОБРАЖЕНИЙ
- 1.5. ПРЕДСТАВЛЕНИЕ КОНТУРОВ ФИГУР
- ГЛАВА 2. АППАРАТНЫЕ СРЕДСТВА ВВОДА ИЗОБРАЖЕНИЙ
- 2.1. УСТРОЙСТВА ВВОДА НА ОСНОВЕ ФАКСИМИЛЬНЫХ АППАРАТОВ
- 2.2. ВВОД ИЗОБРАЖЕНИЙ С ТЕЛЕКАМЕРЫ
- 2.3. ОСОБЕННОСТИ ПОСТРОЕНИЯ УСТРОЙСТВ ВВОДА НА ПРИБОРАХ С ЗАРЯДОВОЙ СВЯЗЬЮ
- 2.4. ПРОМЫШЛЕННОЕ УСТРОЙСТВО СЧИТЫВАНИЯ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
- ГЛАВА 3. АВТОМАТИЧЕСКОЕ РАСПОЗНАВАНИЕ ПЕЧАТНЫХ И СТИЛИЗОВАННЫХ РУКОПИСНЫХ ПИСЬМЕННЫХ ЗНАКОВ
- 3.1. МЕСТО РАЗЛИЧНЫХ ВИДОВ СИМВОЛЬНОЙ ИНФОРМАЦИИ В ОБЩЕЙ ЗАДАЧЕ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 3.2. СТРУКТУРНО-ЛИНГВИСТИЧЕСКИЙ ПОДХОД К ОБРАБОТКЕ ИЗОБРАЖЕНИЙ
- 3.3. ОБЩАЯ СТРУКТУРА И ОРГАНИЗАЦИЯ СИСТЕМЫ РАСПОЗНАВАНИЯ
- 3.4. АЛГОРИТМЫ ПРЕДВАРИТЕЛЬНОЙ ОБРАБОТКИ
- 3.5. ЯЗЫК ОПИСАНИЯ ИЗОБРАЖЕНИЙ
- 3.6. АЛГОРИТМИЗАЦИЯ АБСТРАКТНОГО СИНТЕЗА РАСПОЗНАЮЩЕГО АВТОМАТА
- 3.7. ПОСТРОЕНИЕ ТАБЛИЦ ПЕРЕХОДОВ
- 3.8. МИНИМИЗАЦИЯ ЧИСЛА СОСТОЯНИИ РАСПОЗНАЮЩЕГО АВТОМАТА
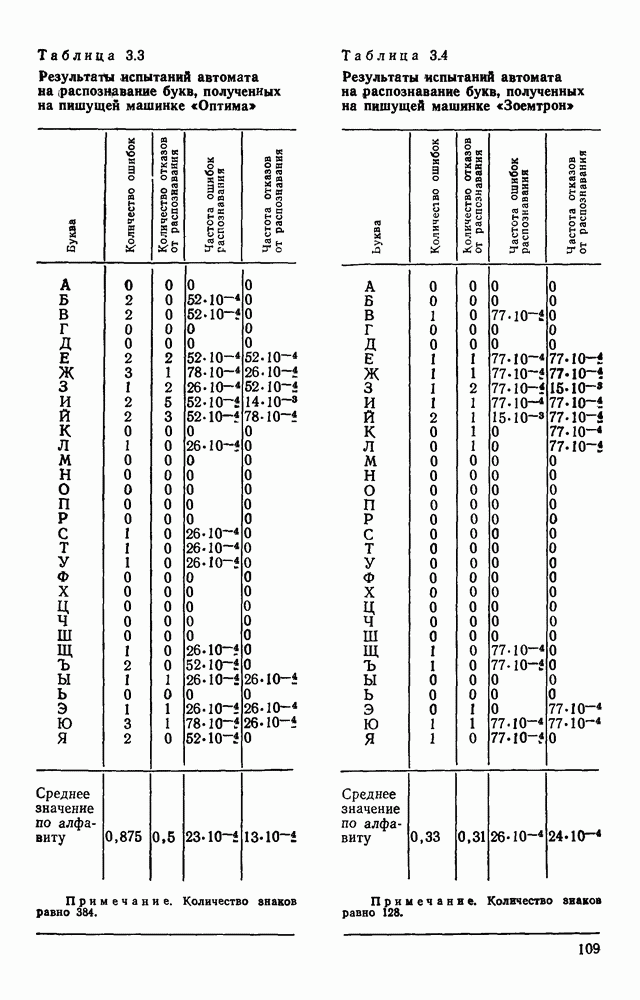
- 3.9. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА РАБОТЫ СИСТЕМЫ
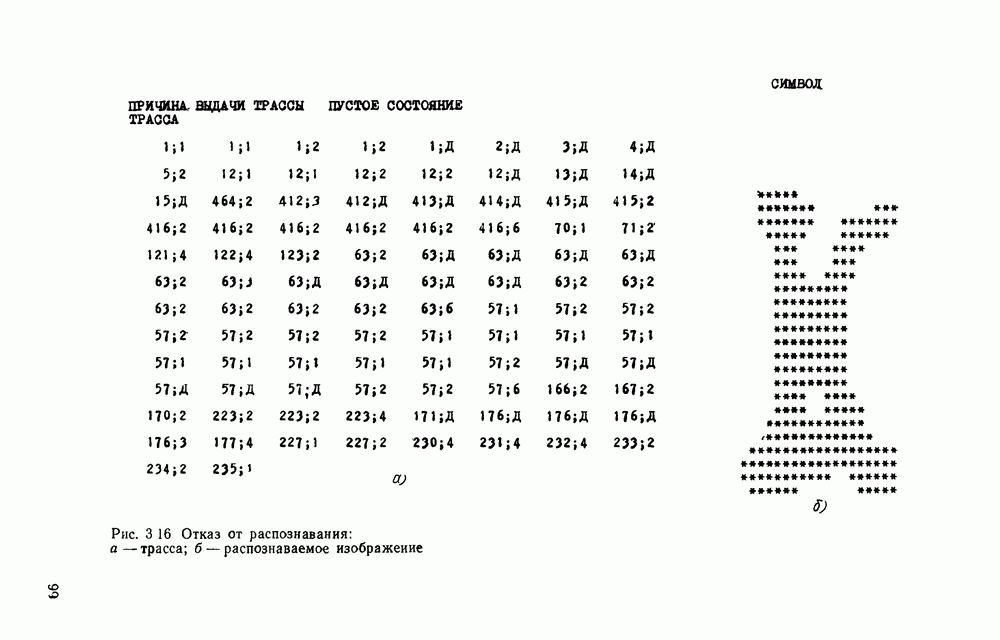
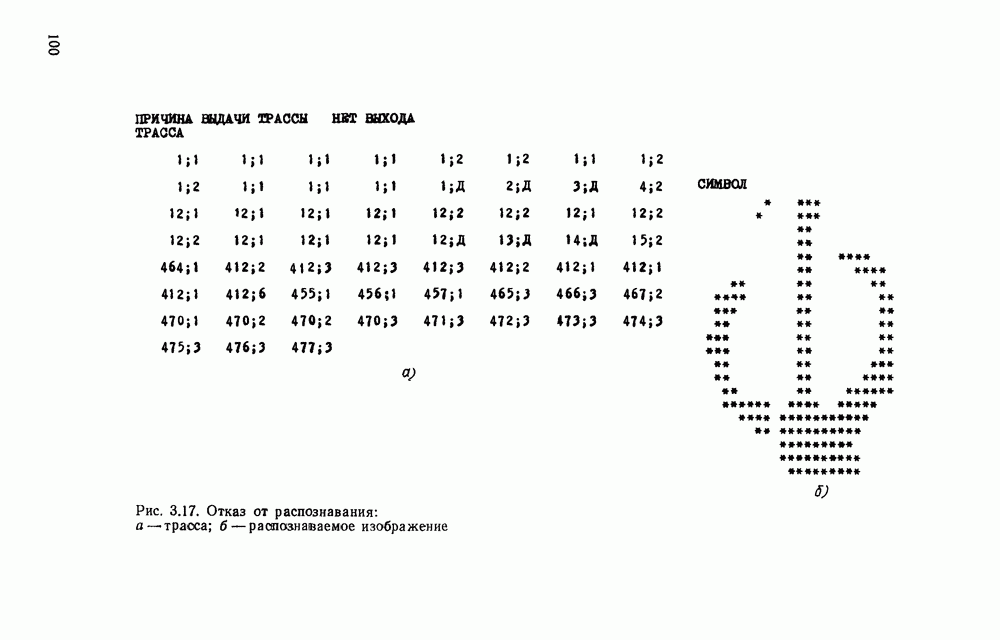
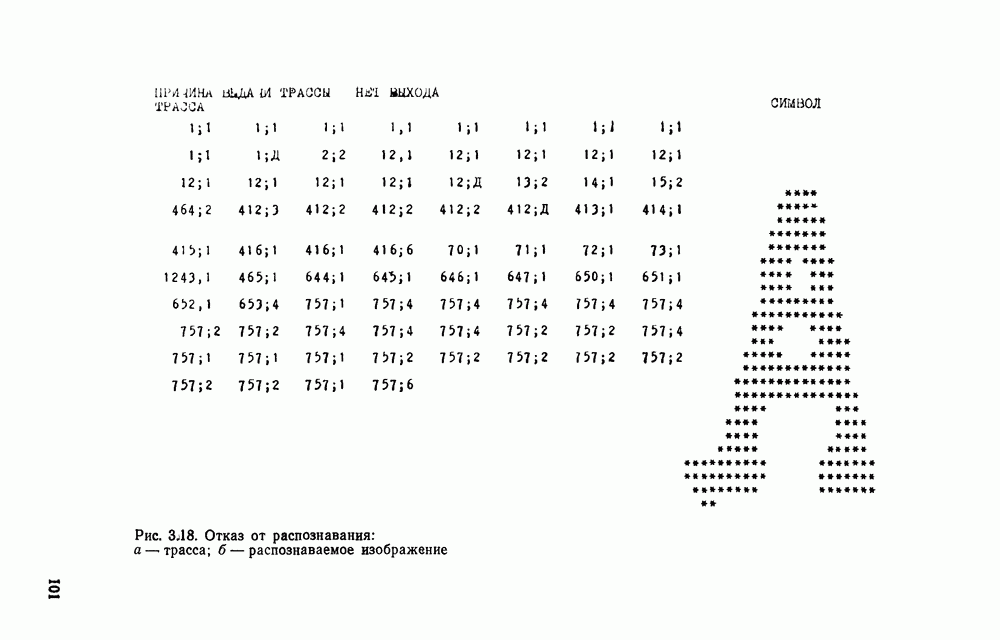
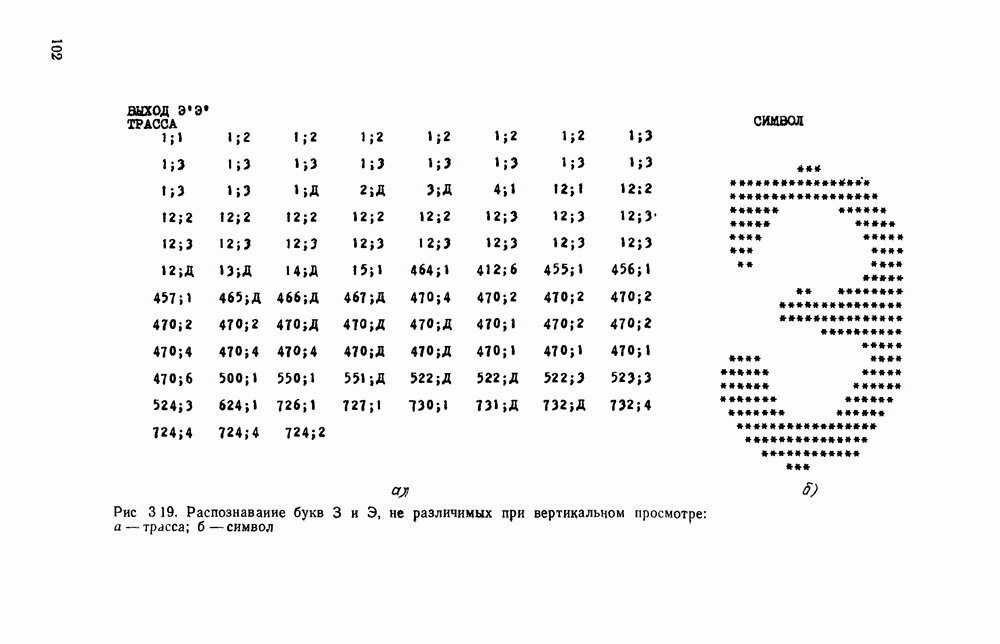
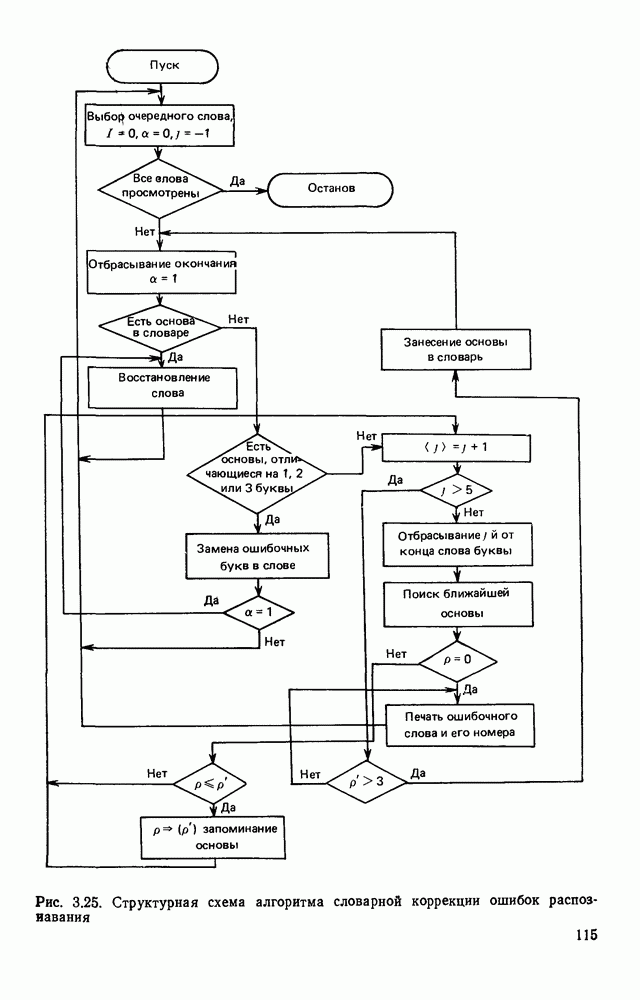
- 3.10. ОБНАРУЖЕНИЕ И ИСПРАВЛЕНИЕ ОШИБОК РАСПОЗНАВАНИЯ
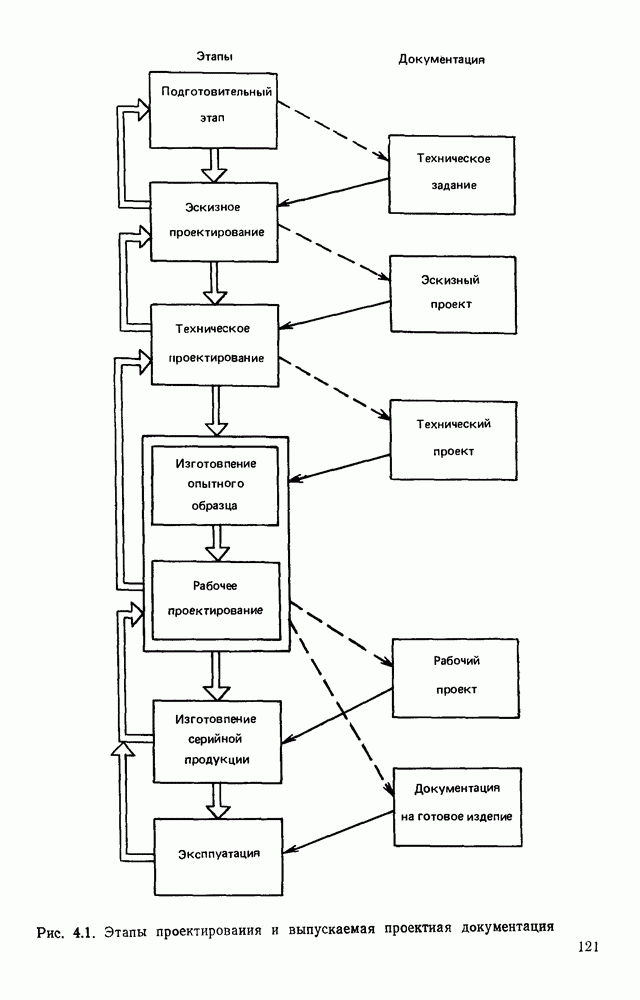
- ГЛАВА 4. АВТОМАТИЗАЦИЯ ПРОЕКТИРОВАНИЯ ПЕЧАТНЫХ ПЛАТ РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ
- 4.1. ВЗАИМОДЕЙСТВИЕ РАЗРАБОТЧИКА РЭА С СИСТЕМОЙ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
- 4.2. ТРЕБОВАНИЯ К ДОКУМЕНТАМ, АВТОМАТИЧЕСКИ СЧИТЫВАЕМЫМ СИСТЕМОЙ
- 4.3. ЭКСПЕРИМЕНТАЛЬНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО ЧТЕНИЯ ЭСКИЗОВ СЛОЕВ ТОПОЛОГИИ ПЛАТ ПЕЧАТНОГО МОНТАЖА
- 4.4. УНИВЕРСАЛЬНЫЙ ЭТАП ОБРАБОТКИ ИЗОБРАЖЕНИИ, АВТОМАТИЧЕСКИ СЧИТАННЫХ С КОНСТРУКТОРСКИХ ДОКУМЕНТОВ
- 4.5. СПЕЦИАЛИЗИРОВАННАЯ ОБРАБОТКА ИЗОБРАЖЕНИИ ДЛЯ ЭСКИЗОВ СЛОЕВ ТОПОЛОГИИ ПЛАТ ПЕЧАТНОГО МОНТАЖА
- 4.6. СПЕЦИАЛИЗИРОВАННАЯ ОБРАБОТКА ИЗОБРАЖЕНИИ ДЛЯ ПРИНЦИПИАЛЬНЫХ ЭЛЕКТРИЧЕСКИХ СХЕМ
- 4.7. ОБЕСПЕЧЕНИЕ ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ ЧТЕНИЯ
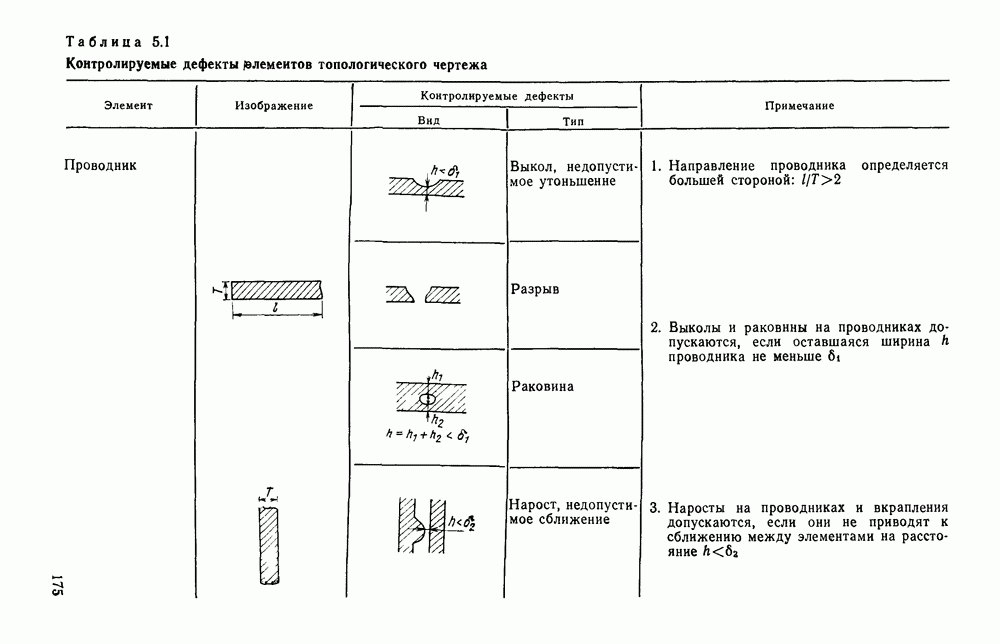
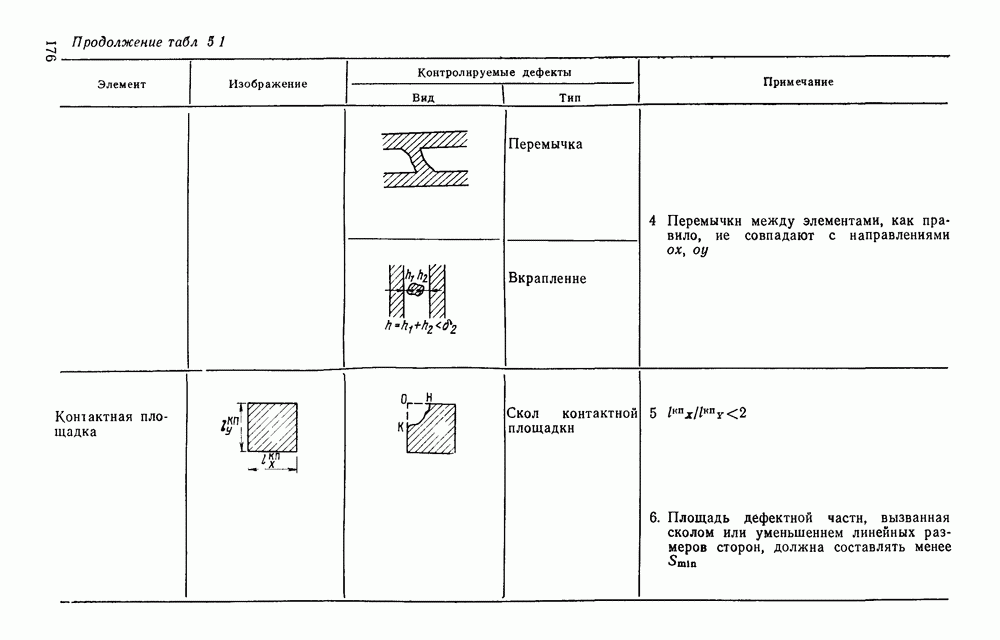
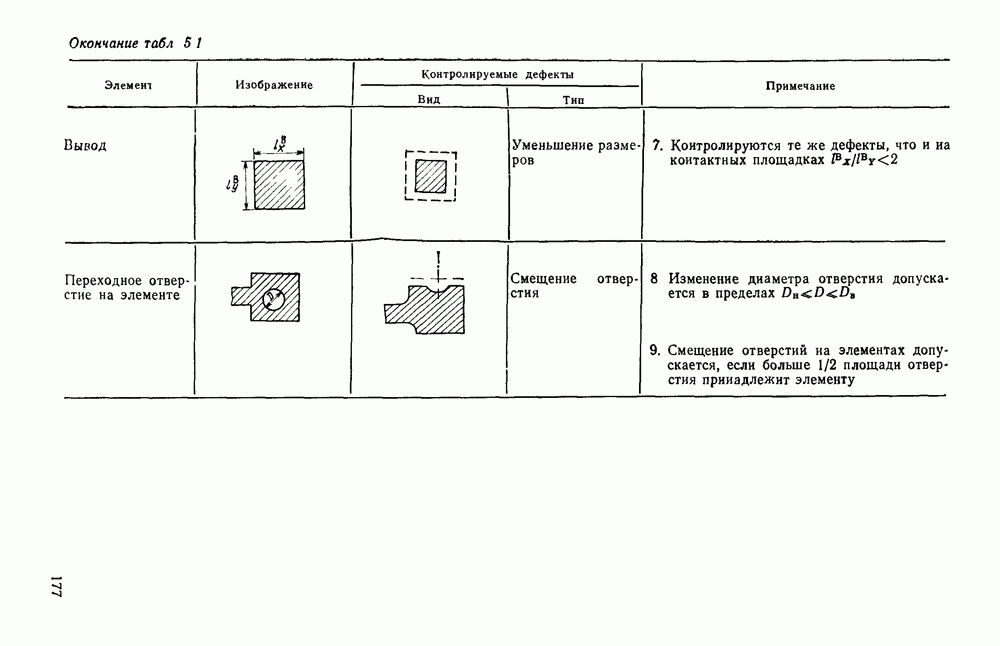
- ГЛАВА 5. КОНТРОЛЬ КАЧЕСТВА ПЕЧАТНЫХ ПЛАТ И МИКРОСХЕМ ПО ИХ ВНЕШНЕМУ ВИДУ
- 5.2. СТРУКТУРА АВТОМАТИЧЕСКОЙ СИСТЕМЫ КОНТРОЛЯ
- 5.3. КОНТРОЛЬ КАЧЕСТВА ИЗГОТОВЛЕНИЯ ТЕХНОЛОГИЧЕСКИХ ОТВЕРСТИИ
- 5.4. ПРОГРАММНАЯ КОРРЕКЦИЯ ИСКАЖЕНИЙ ВВОДА
- 5.5. АЛГОРИТМЫ КОНТРОЛЯ КАЧЕСТВА ИЗГОТОВЛЕНИЯ ЭЛЕМЕНТОВ ПЕЧАТНОГО МОНТАЖА
- 5.6. ОПТИМАЛЬНОЕ РАСПОЛОЖЕНИЕ КОНТРОЛЬНЫХ ЛОСТОВ В ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССАХ
- ГЛАВА 6. ПРИМЕРЫ СИСТЕМ ОБРАБОТКИ ИЗОБРАЖЕНИЙ
- 6.1. АВТОМАТИЗИРОВАННАЯ ОБРАБОТКА СНИМКОВ ЗЕМНОЙ ПОВЕРХНОСТИ, ПОЛУЧАЕМЫХ С ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
- 6.2. РЕКОНСТРУКТИВНАЯ КОМПЬЮТЕРНАЯ ТОМОГРАФИЯ
- СПИСОК ЛИТЕРАТУРЫ