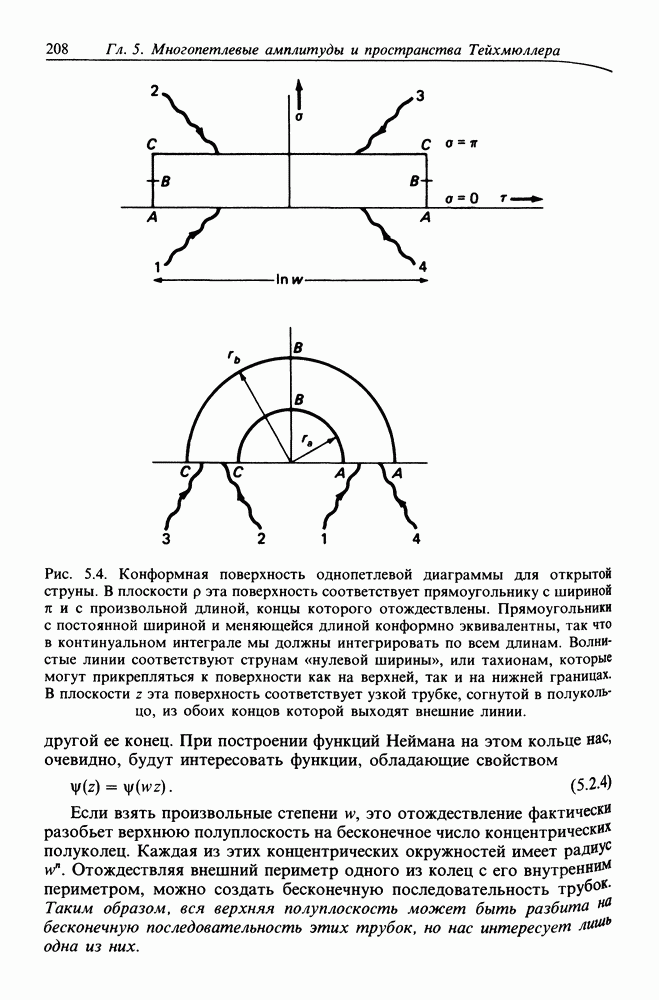
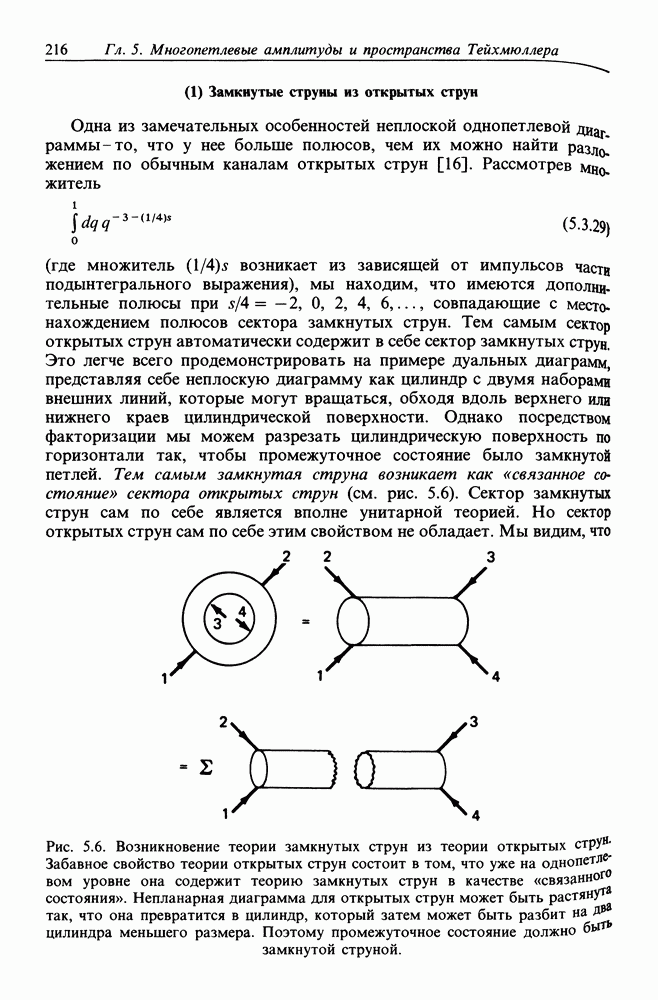
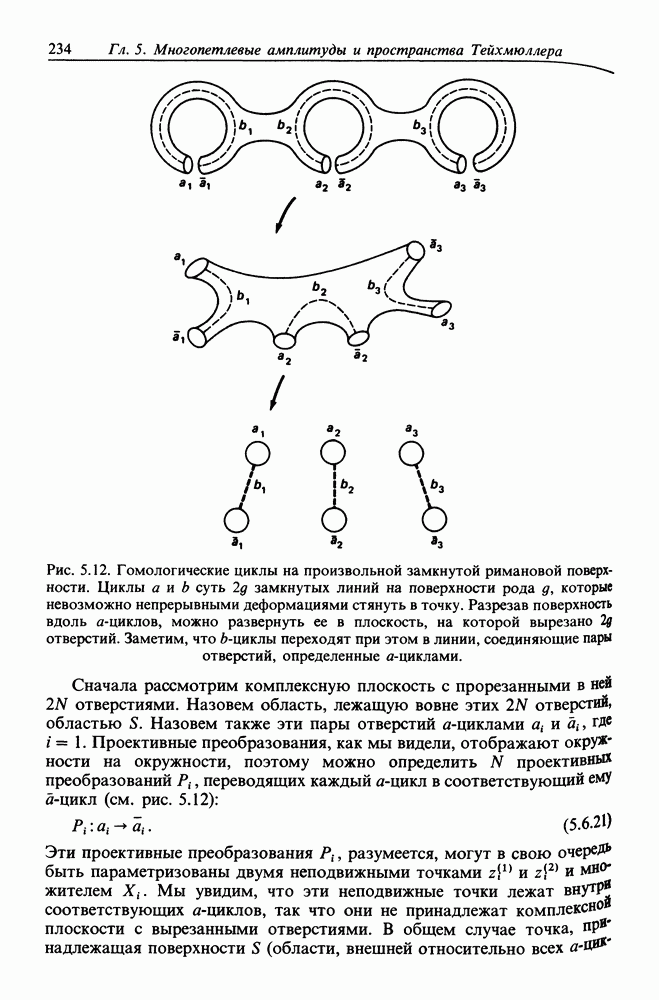
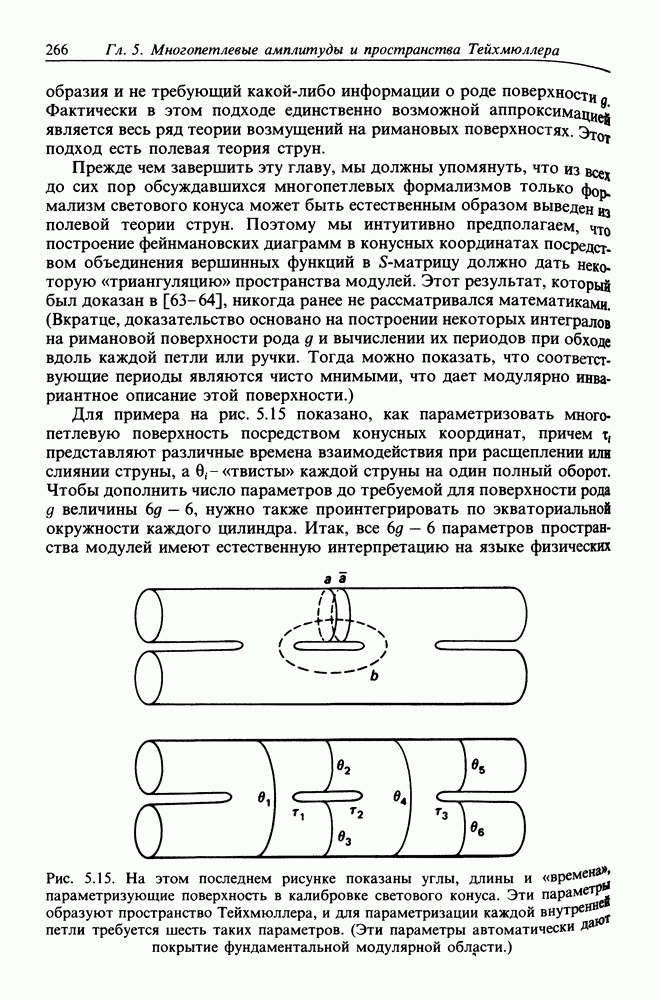
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 11.3. КОГОМОЛОГИИ И ГОМОЛОГИИ
Какова связь между группами гомологий и когомологий для компактного многообразия? Можно показать, что из-за дуальности этих групп их размерности совпадают. Определим числа Бетти как размерности групп Н:

Пусть  набор циклов, определенных на компактном многообразии М. Пусть
набор циклов, определенных на компактном многообразии М. Пусть  набор определенных на М замкнутых форм. Теперь введем матрицу
набор определенных на М замкнутых форм. Теперь введем матрицу 

Матрица  называется матрицей периодов (см. (5.6.31) и (5.11.8)), и при достаточно общих предположениях можно показать, что эта матрица обратима. Поэтому она является
называется матрицей периодов (см. (5.6.31) и (5.11.8)), и при достаточно общих предположениях можно показать, что эта матрица обратима. Поэтому она является  -матрицей с ненулевым детерминантом. Но если матрица периодов является квадратной матрицей, действующей в пространстве
-матрицей с ненулевым детерминантом. Но если матрица периодов является квадратной матрицей, действующей в пространстве  измерений, то размерность пространства замкнутых форм со равна размерности пространства циклов
измерений, то размерность пространства замкнутых форм со равна размерности пространства циклов  что доказывает совпадение чисел Бетти для групп гомологий и когомологий. Это очень важный результат, потому что он означает, что можно использовать либо локальные (когомологии), либо глобальные (гомологии) свойства заданного многообразия для подсчета его чисел Бетти.
что доказывает совпадение чисел Бетти для групп гомологий и когомологий. Это очень важный результат, потому что он означает, что можно использовать либо локальные (когомологии), либо глобальные (гомологии) свойства заданного многообразия для подсчета его чисел Бетти.
Важно также понимать, что числа Бетти являются топологическими числами, зависящими только от топологии многообразия. Таким образом, любая линейная комбинация чисел Бетти также является топологическим числом. В частности, наиболее важным среди них является эйлерова характеристика:

Для того чтобы понять свойства чисел Бетти, введем несколько операторов, в том числе лапласиан. Введем оператор Ходжа  преобразующий
преобразующий  -формы в
-формы в  -формы:
-формы:

где является полностью антисимметричным тензором в пространстве  измерений. Заметим, что
измерений. Заметим, что

В  -мерном пространстве внешнее произведение
-мерном пространстве внешнее произведение  -формы и
-формы и
 -формы дает
-формы дает  -форму, пропорциональную форме объема
-форму, пропорциональную форме объема  Таким образом, можно брать интеграл от внешнего произведения формы и
Таким образом, можно брать интеграл от внешнего произведения формы и  -формы и получать вещественное число. Определим еще одно внутреннее произведение:
-формы и получать вещественное число. Определим еще одно внутреннее произведение:

Введение определения скалярного произведения форм тотчас же позволяет нам определить оператор  , сопряженный к оператору
, сопряженный к оператору  внешнего дифференцирования:
внешнего дифференцирования:

В явном виде сопряженный к  оператор
оператор  дается формулой
дается формулой

Мы также имеем

Отметим, что сопряженный оператор уменьшает степень дифференциальной формы на единицу, в то время как  увеличивает ее на единицу. Определим теперь лапласиан как
увеличивает ее на единицу. Определим теперь лапласиан как

Определим гармонические  -формы условием:
-формы условием:

Определим козамкнутые  -формы условием:
-формы условием:

Говорим, что  -форма является коточной, если она может быть записана в виде
-форма является коточной, если она может быть записана в виде

для некоторой  -формы а.
-формы а.
Теперь мы можем сформулировать следующую важную теорему.
Теорема Ходжа. На компактном многообразии без края любая Рформа может быть единственным образом разложена на сумму точной, коточной и гармонической форм, т. е.

где  - гармоническая форма.
- гармоническая форма.
Это сильный результат, поскольку можно показать, что каждый Когомологический класс содержит только одну гармоническую форму.
Чтобы увидеть это, построим сначала внутреннее произведение формы и лаплассиана от нее:

Таким образом, утверждение о гармоничности формы (которое дает  ) эквивалентно точности и коточности формы (так как
) эквивалентно точности и коточности формы (так как  ). Действительно, можно показать, что
). Действительно, можно показать, что

Но если  то это означает, что
то это означает, что  и поэтому
и поэтому  Следовательно, (11.3.14) редуцируется к
Следовательно, (11.3.14) редуцируется к

Таким образом, в каждом классе когомологий содержится единственный гармонический представитель.
Тот факт, что в каждом классе эквивалентности точных форм содержится один гармонический представитель, позволяет по-другому определить числа Бетти. Мы можем также сказать, что числа Бетти подсчитывают, сколько независимых гармонических форм существует на данном многообразии. Получаем следующее эквивалентное описание чисел Бетти:

Тем самым мы можем использовать любой из этих эквивалентных формализмов для вычисления чисел Бетти.
Последняя формулировка чисел Бетти (через независимые гармонические формы) дает нам еще одно определение. Множество гармонических форм можно рассматривать как ядро лаплассиана (т. е. те формы, которые этот оператор отображает в нуль). Итак, числа Бетти можно определить так:

Как мы увидим, полезно изучить свойства некоторых из этих чисел Бетти. Во-первых, всегда можно определить скалярное произведение для  -мерного многообразия:
-мерного многообразия:

Поэтому эти два пространства содержат одинаковое число независимых
элементов. Следовательно,

Изоморфизм пространств  и
и  называется дуальностью Пуанкаре. Обычно мы будем брать
называется дуальностью Пуанкаре. Обычно мы будем брать  тогда и
тогда и 
Другой способ доказательства дуальности Пуанкаре связан с тем обстоятельством, что если выбрана гармоническая форма, то и дуальная форма также является гармонической:

Поскольку число независимых гармонических форм равно числу Бетти, а оператор Ходжа переводит  -формы в
-формы в  -формы, то мы снова получаем дуальность Пуанкаре.
-формы, то мы снова получаем дуальность Пуанкаре.
Наконец, если мы имеем произведение многообразий, тогда эйлерова характеристика произведения многообразий равна произведению эйлеровых характеристик каждого многообразия:

Если переписать это через числа Бетти согласно (11.3.3), то получим

так называемую форму Кюннета для произведения многообразий.
Возьмем теперь несколько простейших поверхностей и вычислим их числа Бетти.
(1) Двумерный тор
Двумерный тор может быть разбит на циклы при помощи двух разрезов. Число независимых  -циклов, которые можно натянуть на тор, равно двум. Итак,
-циклов, которые можно натянуть на тор, равно двум. Итак,  Далее, согласно дуальности Пуанкаре, имеем
Далее, согласно дуальности Пуанкаре, имеем

Таким образом, эйлерова характеристика (11.3.3) тора равна

(2) Риманова поверхность
Как было показано в гл. 5, существует  разрезов, которыми можно разделить риманову поверхность рода
разрезов, которыми можно разделить риманову поверхность рода  на независимые циклы. Каждой дырке или ручке соответствуют два таких цикла. Следовательно,
на независимые циклы. Каждой дырке или ручке соответствуют два таких цикла. Следовательно,  . Имеем
. Имеем

Таким образом, эйлерова характеристика замкнутой римановой поверхности равна

(3) N-сфера
Циклы на сфере  конечно, всегда могут быть стянуты в точку. Поэтому на
конечно, всегда могут быть стянуты в точку. Поэтому на  не существует независимых циклов. Следовательно,
не существует независимых циклов. Следовательно,

Для эйлеровой характеристики получаем

В частности, поскольку

можно использовать правило произведения эйлеровых характеристик и показать, что эйлерова характеристика тора равна

что согласуется с приведенным выше вычислением.
(4) Произведение сфер
Используя (11.3.24), можно показать, что для произведения  числа Бетти суть
числа Бетти суть

Мы находим, что эйлерова характеристика равна нулю, как и следовало ожидать, поскольку эйлерова характеристика трехмерной сферы также равна нулю:

Аналогично можно взять произведение  числа Бетти которого равны
числа Бетти которого равны

Для эйлеровой характеристики получаем

(5) Четырехмерный тор
Можно представить  -мерный тор как
-мерный тор как

В качестве простого упражнения можно показать, что формула Кюннета (11.3.24) для произведения многообразий дает

Подставляя полученные числа Бетти в формулу для эйлеровой характеристики, находим

как и следовало ожидать.
(6) Шестимерный тор
Для шестимерного тора  имеем
имеем

Поэтому мы можем использовать формулу Кюннета для нахождения чисел Бетти произведения многообразий. Легко показать, что

Отсюда получаем, что эйлерова характеристика равна нулю:

Это следует также и из того факта, что каждый цикл в  имеет нулевую эйлерову характеристику. Используя сформулированные выше простые правила, можно легко получить числа Бетти для
имеет нулевую эйлерову характеристику. Используя сформулированные выше простые правила, можно легко получить числа Бетти для 
(7) Вещественное и комплексное проективные пространства
Пространство  получается, если взять обычное комплексное
получается, если взять обычное комплексное  -мерное пространство и отождествить
-мерное пространство и отождествить

для некоторого ненулевого комплексного числа X. Это отождествление превращает комплексное  -мерное пространство в комплексное проективное
-мерное пространство в комплексное проективное  -мерное пространство.
-мерное пространство.  является обобщением вещественного проективного пространства
является обобщением вещественного проективного пространства  которое получается после отождествления точек в
которое получается после отождествления точек в  -мерном вещественном пространстве по формуле
-мерном вещественном пространстве по формуле

для некоторого ненулевого вещественного к. Пространство  можно также получить отождествлением противоположных точек сферы
можно также получить отождествлением противоположных точек сферы  Примерами вещественных и комплексных проективных пространств служат
Примерами вещественных и комплексных проективных пространств служат

Числа Бетти для них будут следующими:

и

Следовательно,

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Часть I. ПЕРВИЧНОЕ КВАНТОВАНИЕ И КОНТИНУАЛЬНЫЕ ИНТЕГРАЛЫ
- Глава 1 КОНТИНУАЛЬНЫЕ ИНТЕГРАЛЫ И ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 1.2. ИСТОРИЧЕСКИЙ ОБЗОР КАЛИБРОВОЧНОЙ ТЕОРИИ
- § 1.3. КОНТИНУАЛЬНЫЙ ИНТЕГРАЛ И ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 1.4. РЕЛЯТИВИСТСКИЕ ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 1.5. ПЕРВИЧНОЕ И ВТОРИЧНОЕ КВАНТОВАНИЕ
- § 1.6. КВАНТОВАНИЕ ФАДДЕЕВА-ПОПОВА
- § 1.7. ВТОРИЧНОЕ КВАНТОВАНИЕ
- § 1.8. ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
- § 1.9. ТОКИ И ВТОРИЧНОЕ КВАНТОВАНИЕ
- § 1.10. РЕЗЮМЕ
- Глава 2. СТРУНЫ НАМБУ-ГОТО
- § 2.1. БОЗОННЫЕ СТРУНЫ
- § 2.2. КВАНТОВАНИЕ ГУПТЫ-БЛЕЙЛЕРА
- § 2.3. КВАНТОВАНИЕ В КАЛИБРОВКЕ СВЕТОВОГО КОНУСА
- § 2.4. BRST-КВАНТОВАНИЕ
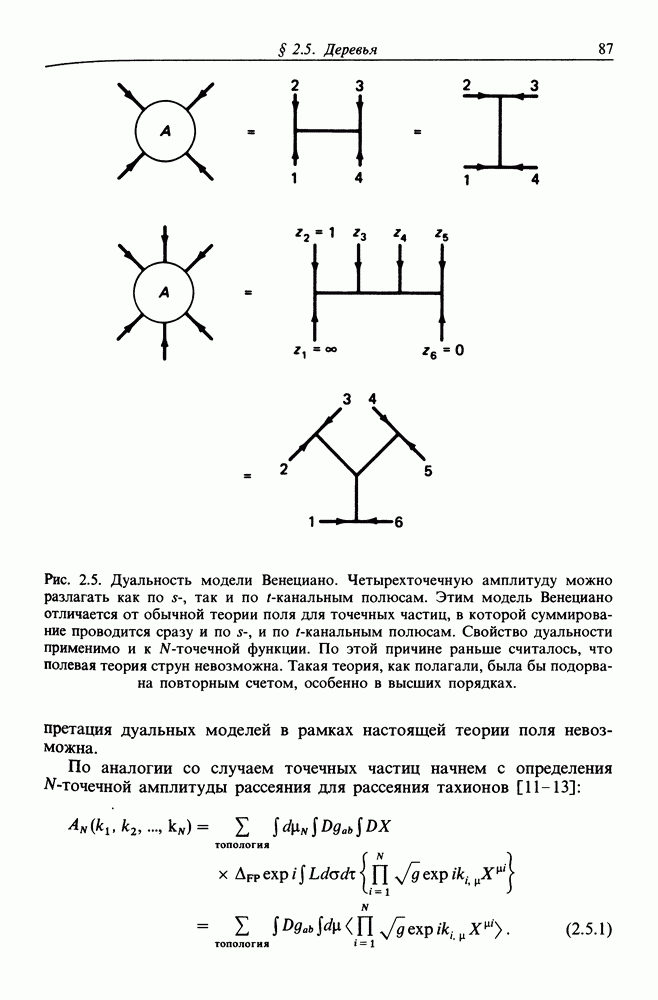
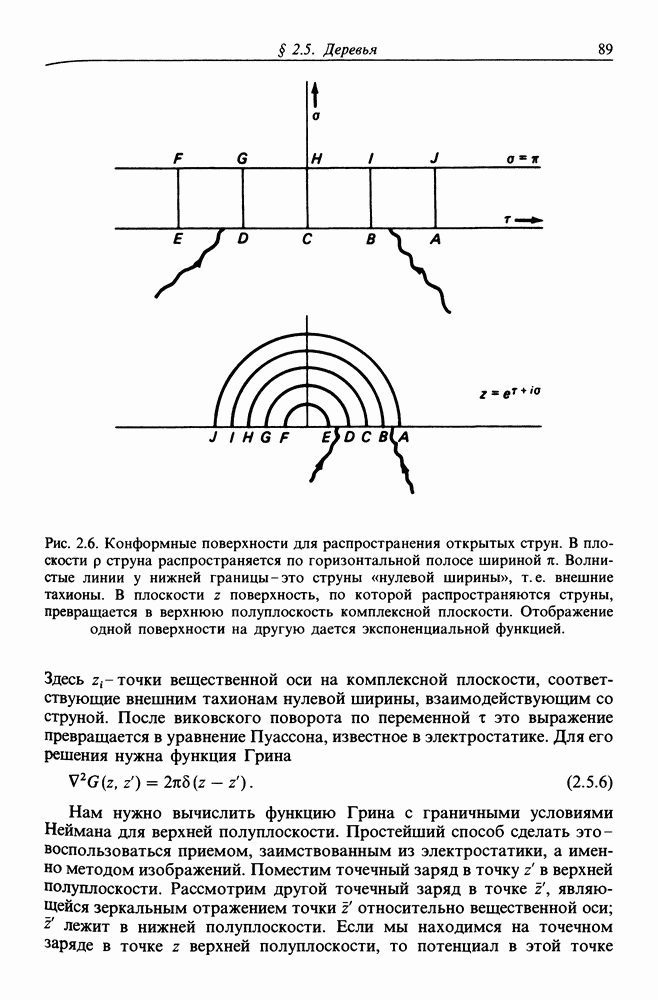
- § 2.5. ДЕРЕВЬЯ
- § 2.6. ОТ КОНТИНУАЛЬНОГО ИНТЕГРАЛА К ОПЕРАТОРАМ
- § 2.7. ПРОЕКТИВНАЯ ИНВАРИАНТНОСТЬ И ТВИСТЫ
- § 2.8. ЗАМКНУТЫЕ СТРУНЫ
- § 2.9. УНИЧТОЖЕНИЕ ДУХОВ
- § 2.10. РЕЗЮМЕ
- Глава 3. СУПЕРСТРУНЫ
- § 3.1. СУПЕРСИММЕТРИЧНЫЕ ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 3.2. ДВУМЕРНАЯ СУПЕРСИММЕТРИЯ
- § 3.3. ДЕРЕВЬЯ
- § 3.4. ЛОКАЛЬНАЯ ДВУМЕРНАЯ СУПЕРСИММЕТРИЯ
- § 3.5. КВАНТОВАНИЕ
- § 3.6. ПРОЕКЦИЯ GSO
- § 3.7. СУПЕРСТРУНЫ
- § 3.8. КВАНТОВАНИЕ ДЕЙСТВИЯ ГРИНА-ШВАРЦА В КОНУСНЫХ ПЕРЕМЕННЫХ
- § 3.9. ВЕРШИНЫ И ДЕРЕВЬЯ
- § 3.10 РЕЗЮМЕ
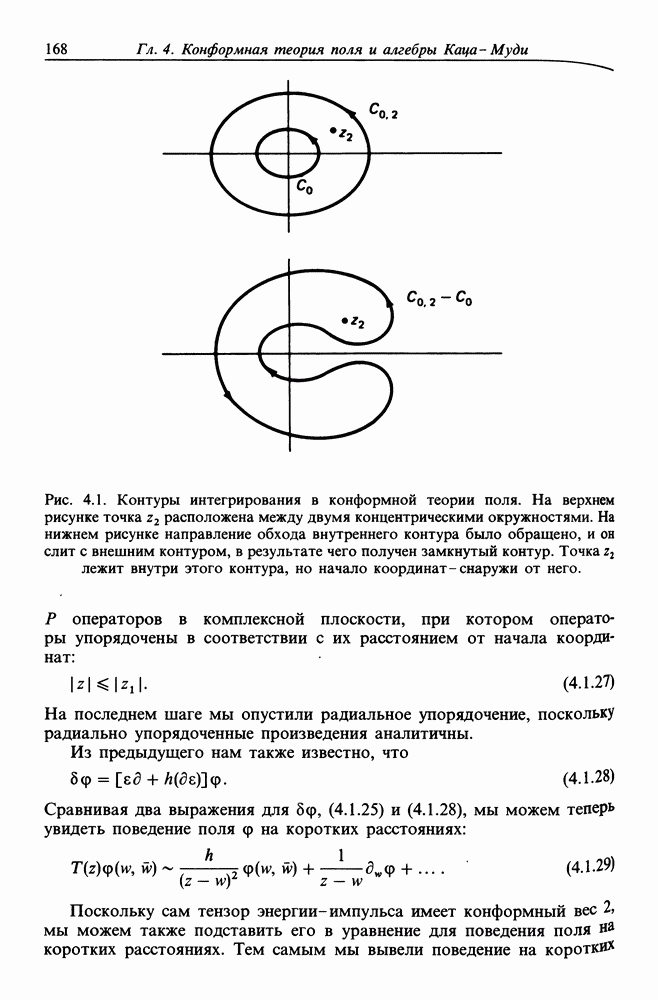
- Глава 4. КОНФОРМНАЯ ТЕОРИЯ ПОЛЯ И АЛГЕБРЫ КАЦА-МУДИ
- § 4.2. СУПЕРКОНФОРМНАЯ ТЕОРИЯ ПОЛЯ
- § 4.3. СПИНОВЫЕ ПОЛЯ
- § 4.4. СУПЕРКОНФОРМНЫЕ ДУХИ
- § 4.5. ФЕРМИОННЫЙ ВЕРШИННЫЙ ОПЕРАТОР
- § 4.6. СПИНОРЫ И ДЕРЕВЬЯ
- § 4.7. АЛГЕБРЫ КАЦА-МУДИ
- § 4.8. СУПЕРСИММЕТРИЯ
- § 4.9. РЕЗЮМЕ
- Глава 5. МНОГОПЕТЛЕВЫЕ АМПЛИТУДЫ И ПРОСТРАНСТВА ТЕЙХМЮЛЛЕРА
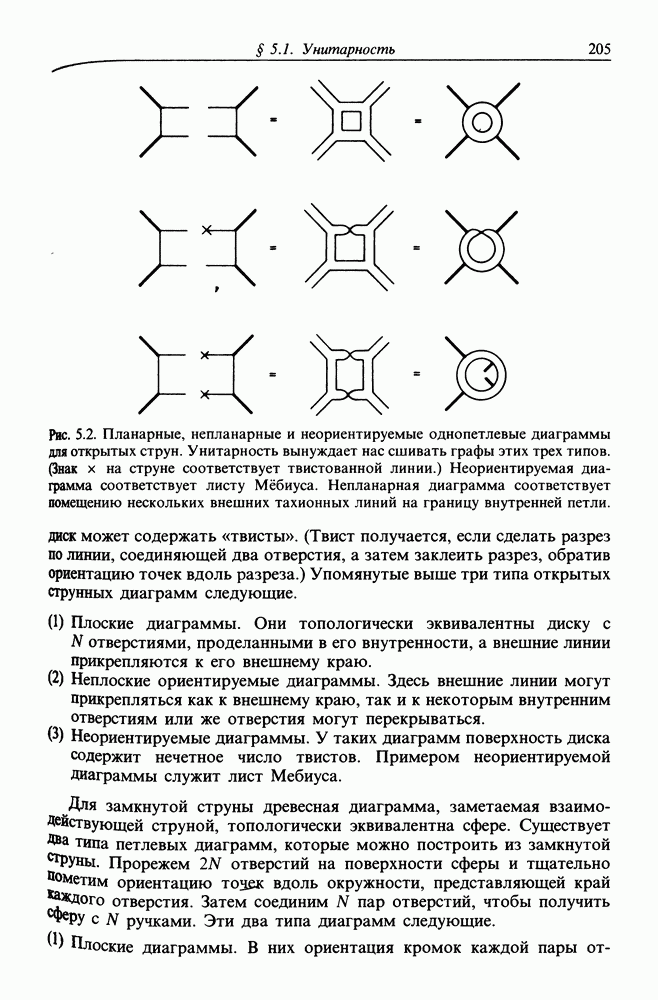
- § 5.2. ОДНОПЕТЛЕВЫЕ АМПЛИТУДЫ
- § 5.3. ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
- § 5.4. ОДНОПЕТЛЕВЫЕ АМПЛИТУДЫ СУПЕРСТРУН
- § 5.5. ОДНОПЕТЛЕВЫЕ ДИАГРАММЫ ЗАМКНУТЫХ СТРУН
- § 5.6. МНОГОПЕТЛЕВЫЕ АМПЛИТУДЫ
- § 5.7. РИМАНОВЫ ПОВЕРХНОСТИ И ПРОСТРАНСТВА ТЕЙХМЮЛЛЕРА
- § 5.8. КОНФОРМНАЯ АНОМАЛИЯ
- § 5.9. СУПЕРСТРУНЫ
- § 5.10. ДЕТЕРМИНАНТЫ И СИНГУЛЯРНОСТИ
- § 5.11. ПРОСТРАНСТВА МОДУЛЕЙ И ГРАССМАНИАНЫ
- § 5.12. РЕЗЮМЕ
- Часть II. ВТОРИЧНОЕ КВАНТОВАНИЕ И ПОИСКИ ГЕОМЕТРИИ
- Глава 6. ПОЛЕВАЯ ТЕОРИЯ В КАЛИБРОВКЕ СВЕТОВОГО КОНУСА
- § 6.2 ВЫВОД ПОЛЕВОЙ ТЕОРИИ ТОЧЕЧНЫХ ЧАСТИЦ
- § 6.3. ПОЛЕВАЯ ТЕОРИЯ В КАЛИБРОВКЕ СВЕТОВОГО КОНУСА
- § 6.4. ВЗАИМОДЕЙСТВИЯ
- § 6.5. МЕТОД ФУНКЦИЙ НЕЙМАНА
- § 6.6. ЭКВИВАЛЕНТНОСТЬ АМПЛИТУД РАССЕЯНИЯ
- § 6.7. ЧЕТЫРЕХСТРУННОЕ ВЗАИМОДЕЙСТВИЕ
- § 6.8. ПОЛЕВАЯ ТЕОРИЯ СУПЕРСТРУН
- § 6.9. РЕЗЮМЕ
- Глава 7. ПОЛЕВАЯ ТЕОРИЯ BRST
- § 7.1. КОВАРИАНТНАЯ ПОЛЕВАЯ ТЕОРИЯ СТРУН
- § 7.2. ПОЛЕВАЯ ТЕОРИЯ BRST
- § 7.3. ФИКСАЦИЯ КАЛИБРОВКИ
- § 7.4. ВЗАИМОДЕЙСТВИЯ
- § 7.5. АКСИОМАТИЧЕСКАЯ ФОРМУЛИРОВКА
- § 7.6. ДОКАЗАТЕЛЬСТВО ЭКВИВАЛЕНТНОСТИ
- § 7.7. ЗАМКНУТЫЕ СТРУНЫ И СУПЕРСТРУНЫ
- § 7.8. РЕЗЮМЕ
- Глава 8. ГЕОМЕТРИЧЕСКАЯ ПОЛЕВАЯ ТЕОРИЯ СТРУН
- § 8.2. СТРУННАЯ ГРУППА
- § 8.3. ОБЪЕДИНЕННАЯ СТРУННАЯ ГРУППА
- § 8.4. ПРЕДСТАВЛЕНИЯ ГРУППЫ USG
- § 8.5. ДУХОВЫЙ СЕКТОР И КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- § 8.6. СВЯЗНОСТИ И КОВАРИАНТНЫЕ ПРОИЗВОДНЫЕ
- § 8.7. ГЕОМЕТРИЧЕСКИЙ ВЫВОД ДЕЙСТВИЯ
- § 8.8. ИНТЕРПОЛЯЦИОННАЯ КАЛИБРОВКА
- § 8.9. ЗАМКНУТЫЕ СТРУНЫ И СУПЕРСТРУНЫ
- § 8.10. РЕЗЮМЕ
- Часть III. ФЕНОМЕНОЛОГИЯ И ПОСТРОЕНИЕ МОДЕЛЕЙ
- Глава 9. АНОМАЛИИ И ТЕОРЕМА АТЬИ-ЗИНГЕРА
- § 9.2. АНОМАЛИИ И ФЕЙНМАНОВСКИЕ ДИАГРАММЫ
- § 9.3. АНОМАЛИИ В ФУНКЦИОНАЛЬНОМ ФОРМАЛИЗМЕ
- § 9.4. АНОМАЛИИ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
- § 9.5. ИНДЕКС ОПЕРАТОРА ДИРАКА
- § 9.6. ГРАВИТАЦИОННЫЕ И КАЛИБРОВОЧНЫЕ АНОМАЛИИ
- § 9.7. СОКРАЩЕНИЕ АНОМАЛИЙ В ТЕОРИИ СТРУН
- § 9.8. ПРОСТОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ АТЬИ-ЗИНГЕРА ОБ ИНДЕКСЕ
- § 9.9. РЕЗЮМЕ
- Глава 10. ГЕТЕРОТИЧЕСКИЕ СТРУНЫ И КОМПАКТИФИКАЦИЯ
- § 10.2. ГЕТЕРОТИЧЕСКАЯ СТРУНА
- § 10.3. СПЕКТР СОСТОЯНИЙ
- § 10.4. КОВАРИАНТНАЯ И ФЕРМИОННАЯ ФОРМУЛИРОВКИ
- § 10.5. ДЕРЕВЬЯ
- § 10.6. ОДНОПЕТЛЕВАЯ АМПЛИТУДА
- § 10.7. ГРУППА Е8 И АЛГЕБРЫ КАЦА-МУДИ
- § 10.8. ДЕСЯТИМЕРНАЯ ТЕОРИЯ БЕЗ СУПЕРСИММЕТРИИ
- § 10.9. ЛОРЕНЦЕВЫ РЕШЕТКИ
- § 10.10. РЕЗЮМЕ
- Глава 11. ПРОСТРАНСТВА КАЛАБИ-ЯУ И ОРБИОБРАЗИЯ
- § 11.2. ОБЗОР ТЕОРИИ КОГОМОЛОГИЙ ДЕ РАМА
- § 11.3. КОГОМОЛОГИИ И ГОМОЛОГИИ
- § 11.4. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- § 11.5. ВЛОЖЕНИЕ СПИНОВОЙ СВЯЗНОСТИ
- § 11.6. ПОКОЛЕНИЯ ФЕРМИОНОВ
- § 11.7. ВИЛЬСОНОВСКИЕ ЛИНИИ
- § 11.8. ОРБИОБРАЗИЯ
- § 11.9. ЧЕТЫРЕХМЕРНЫЕ СУПЕРСТРУНЫ
- § 11.10. РЕЗЮМЕ
- § 11.11. ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЕ
- § П.1. КРАТКОЕ ВВЕДЕНИЕ В ТЕОРИЮ ГРУПП
- СОВПАДЕНИЯ
- § П.2. КРАТКОЕ ВВЕДЕНИЕ В ОБЩУЮ ТЕОРИЮ ОТНОСИТЕЛЬНОСТИ
- § П.3. КРАТКОЕ ВВЕДЕНИЕ В ТЕОРИЮ ФОРМ
- § П.4. КРАТКОЕ ВВЕДЕНИЕ В СУПЕРСИММЕТРИЮ
- § П.5. КРАТКОЕ ВВЕДЕНИЕ В ТЕОРИЮ СУПЕРГРАВИТАЦИИ
- § П.6. СЛОВАРИК ТЕРМИНОВ
- П.7. ОБОЗНАЧЕНИЯ