3.3. Средние значения

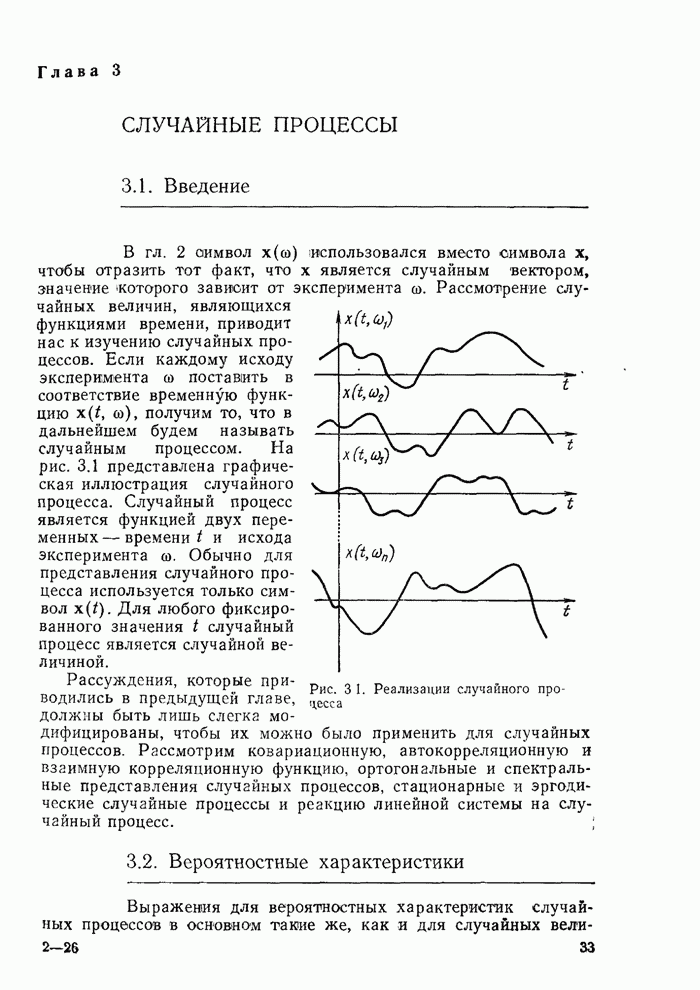
Как было указано в предыдущем разделе, общие методы исследования средних значений, изложенные в § 2.5, могут быть непосредственно применены к случайным процессам. Однако из-за введения временного аргумента некоторые средние случайных процессов не имеют прямого аналога в теории случайных величин. В частности, отметим связь между понятиями усреднения по времени и по ансамблю и понятиями стационарности и эргодичности.                                                                            

Среднее значение. Вектор математического ожидания случайного векторного процесса определяется как

                    (3.7)

Если  не зависит от времени, то говорят, что процесс стационарный по среднему значению. Достаточным условием независимости  от времени является то, что   не зависит от времени. Это условие, однако, не необходимо.

Когда случайный процесс стационарен по среднему значению, среднее по времени этого процесса    

                                         (3.8)

Если среднее по времени  стационарного по среднему значению случайного процесса [см. (3.8)] равно (с вероятностью 1) постоянному среднему по ансамблю [см. (3.7)], то процесс эргодичен по среднему значению, или просто в среднем.

Вместо оценки вектора средних путем усреднения по непрерывному времени можно ввести оценку, полученную усреднением по дискретному времени. Для эргодического в среднем процесса вектор среднего по дискретному времени имеет вид

                         (3.9)

где  — интервал квантования во времени. В реальных измерениях невозможно использовать ф-лы (3.7) и (3.8) с бесконечными пределами. Поэтому усреднение осуществляется по конечному числу выборок.

Среднеквадратическое значение и дисперсия. Матрица среднеквадратических значений векторного случайного процесса имеет вид

                 (3.10)

Это выражение в точности соответствует (2.116). Если среднеквадратическое значение не является функцией времени, должно быть выполнено другое необходимое условие стационарности случайного процесса. Если процесс и стационарен и эргодичен, то среднеквадратическое значение, вычисленное путем усреднения по ансамблю реализаций, равно (с вероятностью 1) среднему по времени от произведения  :

                                             (3.11)

Нетрудно записать дискретный аналог ф-лы (3.11). Матрица среднеквадратических значений эргодического процесса, полученная усреднением по дискретному времени, равна

                                (3.12)

Матрица дисперсий векторного случайного процесса имеет вид

        (3.13)

Отсюда непосредственно следует, что

                                          (3.14)

Будем опускать индекс  в обозначении матрицы дисперсий   в тех случаях, когда это не вызовет путаницы.

Корреляционные и ковариационные функции. Рассмотрим матрицу средних произведения двух значений векторного случайного процесса с временным сдвигам

                                        (3.15)

которую называют матрицей автокорреляционных функций. Используя результаты § 2.5, нетрудно получить следующее выражение для  :

              (3.16)

Введем также матрицу взаимных корреляционных функций двух векторных случайных процессов:

                                        (3.17)

Подобным же образом вводятся матрицы ковариационных и взаимных ковариационных функций. Матрица ковариационных функций (называемая также ядром ковариации) определяется следующим образом:

         (3.18)

т. е. представляет собой среднее произведения центрированных случайных процессов в моменты времени    и  . Ясно, что

                                 (3.19)

Матрица взаимных ковариационных функций равна

       (3.20)

Легко показать, что матрицы средних дисперсий и ковариационных функций связаны соотношением

                                         (3.21)

а матрицы соответствующих смешанных моментов — соотношением

                                      (3.22)

Важность первых двух статистических моментов, которые определяют среднее значение, среднеквадратическое значение, дисперсию, корреляционную и ковариационную функции случайного процесса, обусловлена двумя факторами. Во-первых, обычно намного легче найти среднее значение или ковариационную функцию случайного процесса, чем закон распределения. Во-вторых, многие важные фундаментальные задачи, связанные со случайными процессами, могут быть решены на основе знания вектора среднеквадратического значения и матрицы ковариационных функций. В частности, задачи «линейной оценки» могут быть легко решены, если основываться на знании этих вероятностных характеристик.

Однако важно не переоценить надежды, возлагаемые на использование векторов средних и матрицы ковариационных функций Можно показать, например, что для определения ошибок при оценивании дисперсии случайного сигнала по его конечной длительности потребуется четвертый момент распределения. Таким образом, с помощью только первых двух моментов можно решить хотя и большое число задач, но не все.

Стационарность и эргодичность. Случайные процессы делятся на два широких класса — стационарные и нестационарные (называемые также эволюционными). Стационарным называется процесс, в котором совместное распределение или плотность вероятности инвариантны во времени. Случайный процесс является строго стационарным -го порядка, если совместное распределение или плотность -гo порядка не зависят от временного сдвига, так что

 для любого       (3.23)

Процесс является строго стационарным, если он строго стационарен -го порядка при .

Можно указать поистине фантастическое число работ по определению стационарности в строгом смысле. Поэтому нас обычно будет удовлетворять определение стационарности в широком смысле, для которой требуется независимость от выбора начала отсчета времени только первых двух моментов. Если процесс строго стационарный второго порядка, он стационарен в широком смысле, обратное не справедливо. Для стационарности в широком смысле требуется, чтобы вектор среднего значения не зависел от времени, так что

                              (3.24)

и чтобы матрица корреляционных функций была функцией только временного сдвига:

  (3.25)

Матрица корреляционных функций стационарного в широком смысле процесса может быть записана в виде

                                                         (3.26)

Более слабым, чем стационарность в широком смысле, во все же очень полезным для дальнейшего изложения является понятие ковариационной стационарности. Случайный процесс является ковариационно стационарным, если матрица ковариационных функций зависит только от временного сдвига  ,  так что

                                                 (3.27)

или

                                                 (3.28)

Можно легко связать понятия стационарности в широком смысле и ковариационной стационарности. Так как

                                    (3.29)

то для ковариационно стационарного случайного процесса  из ф-лы (3.27) находим

                        (3.30)

Таким образом, случайный процесс стационарен в широком смысле (или является стационарным второго порядка), если он ковариационно стационарен и если он стационарен в среднем. При этом  в (3.30) можно заменить на .

Как отмечалось выше, в некоторых случаях усреднение по ансамблю можно заменить усреднением по времени. Строго стационарный процесс  является эргодическим, если для любой функции  средние от этой функции по времени на конечном (интервале времени или по выборке конечного размера сходятся (с вероятностью 1) к среднему по ансамблю [56].

Таким образом, для эргодического процесса при произвольной  

.             (3.31)

Случайный процесс называется эргодическим в среднем, если средние по времени на конечном интервале и по выборке конечного размера

                             (3.32)

сходятся к константе при увеличении длины реализации. Другими словами, если

                                            (3.33)

так что средние от реализации конечной длительности стремятся к средним по ансамблю, то процесс эргодичен в среднем. Можно показать [182], что необходимым и достаточным условием эргодичности в среднем является_сходимость к нулю ковариации случайных величин   : 

                (3.34)

при , т. е.

                     (3.35)

Необходимым условием эргодичности является строгая стационарность. Таким образом, все эргодические процессы стационарны, но не все стационарные процессы эргодические.