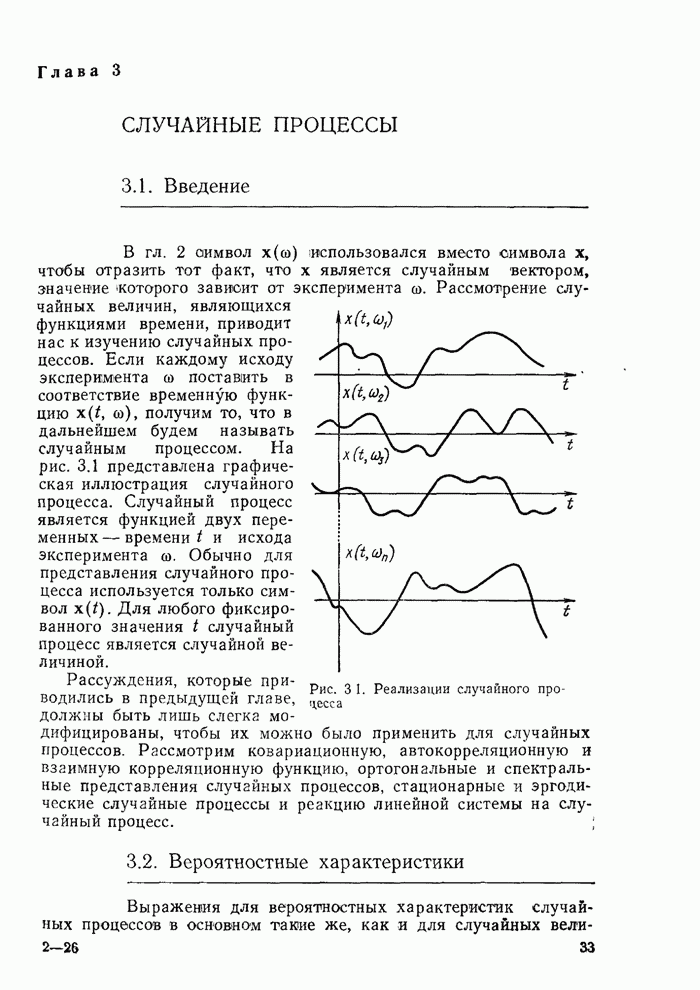
5.6. Последовательный анализ

В предыдущих разделах данной главы предполагалось, что объем выборки, на основе которой выносится решение, фиксирован. В § 5.3 уже отмечалось, что значение риска, связанного с принятием решений, уменьшается при увеличении числа наблюдений. Вообще механизм вынесения решений может быть «выбран таким образом, чтобы» кроме основных решений, он позволял определять и необходимый объем выборки. Можно ожидать, что в этом случае удалось бы сократить время от начала наблюдения до принятия решения при том же самом значении было бы построено правило выбора решения, которое следовало бы признать лучше правила, основанного на выборке фиксированного объема. В данном параграфе будут изучены два таких последовательных правила (выбора решения для простого бинарного случая. Одно из них называется байесовским, а другое — последовательным правилом Вальда [86, 88, 166, 272].

Напомним, что при проверке гипотез по выборке фиксированного объема отношение правдоподобия  сравнивается с порогом . При последовательном анализе используются два порога  и , которые  могут изменяться с изменением числа наблюдений . Если на -м шаге отношение правдоподобия больше порога , то принимается гипотеза . Если оно меньше, чем , то принимается гипотеза . Если же значение отношения правдоподобия лежит между этими порогами, то необходимо произвести очередное наблюдение.

Отношение правдоподобия

,             (5.106)

где  - совместная плотность вероятности выборки  при гипотезе , (полученной за первые  шагов. Для вычисления порога непоследовательного правила выбора решения необходимо знать априорные вероятности гипотез  и . Аналогично для определения порогов последовательного правила на -м шаге необходимо знать априорные вероятности  и    этих гипотез перед -м  шагом. Эти априорные вероятности можно рассматривать как апостериорные, вычисляемые после первых  шагов. Их можно определить из соотношений:

 ;            (5.107)

        (5.108)

Поделив обе части последнего выражения на соответствующие части предыдущего, получим простое выражение для отношения априорных вероятностей на -м шаге

.              (5.109)

В качестве начального значения в этом соотношении следует выбрать отношение ,  которое использовалось бы при построении непоследовательного правила. На каждом шаге отношение априорных вероятностей подстраивается путем умножения на отношение правдоподобия :

.                           (5.110)

зависящее только от результатов наблюдений на предшествующих шагах. Если элементы выборки независимы, то отношение правдоподобия для «всей выборки можно записать как произведение отношений правдоподобия для наблюдений на разных шагах:

.                       (5.111)

Так как

,                           (5.112)

то рекуррентное соотношение (5.109) можно записать в следующей полезной форме:

.                          (5.113)

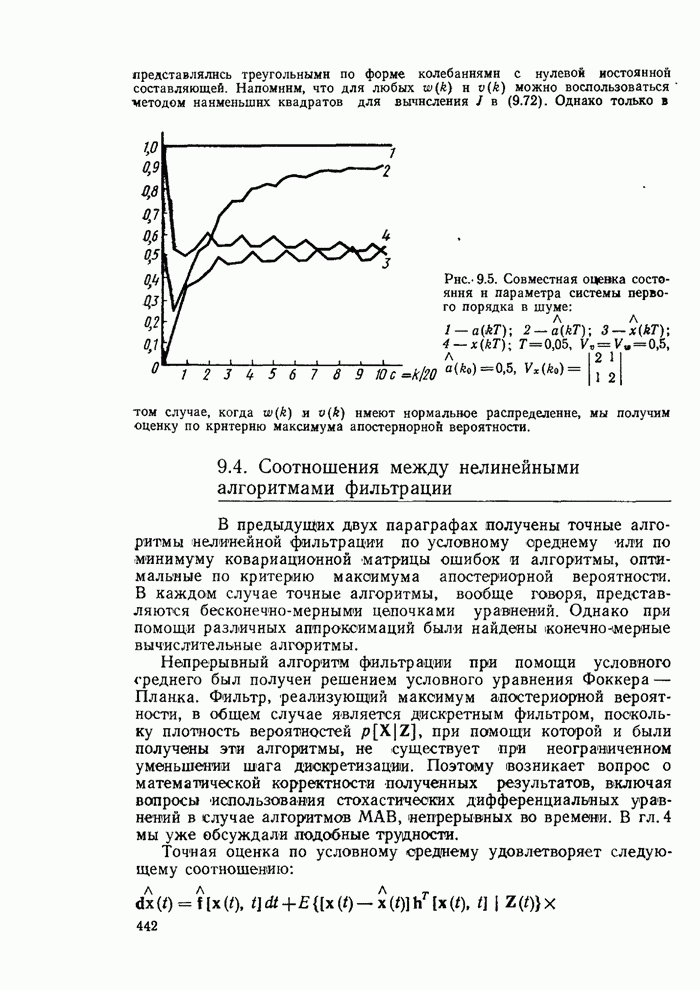
Определить среднее значение потерь при наличии решений о продолжении наблюдений (что необходимо при рассмотрении байесовского последовательного правила) довольно трудно. Поэтому обратимся к более простому подходу, предложенному Вальдом [272]. Это правило, называемое обычно последовательным правилом Вальда, является модификацией непоследовательного правила Неймана-Пирсона.

Покажем, что пороги  и  последовательного правила Вальда связаны простыми соотношениями с вероятностями ложной тревоги и пропуска сигнала. Предположим, что при  отношение правдоподобия оказалось равным порогу .

Следовательно, на этом шаге принимается гипотеза  и

.                   (5.114)

Умножая обе части последнего равенства на величину и интегрируя в области принятия гипотезы  получим

.     (5.115)

Это равенство можно записать следующим образом:

.                     (5.116)

Если отношение правдоподобия равно значению порога , то принимается гипотеза . Поскольку при этом

,                         (5.117)

то нетрудно установить равенство, аналогичное равенству (5.116)

,                    (5.118)

Из равенств (5.116) и (5.118) следует, что для обеспечения заданных значений вероятностей ложной тревоги и пропуска сигнала следует выбрать следующие значения порогов:

                 (5.119)

Из этих выражений, в частности, следует, что значения порогов последовательного правила Вальда не зависят от номера наблюдения , если вероятности  и  не зависят от .

При использовании последовательного правила объем выборки, при котором принимается одна из рассмотренных гипотез, оказывается случайным (можно показать, что одна из гипотез всегда принимается в результате конечного числа шагов). Поэтому желательно определить хотя бы среднее значение необходимого числа наблюдений. Предположим, что пересечение порогов невозможно Тогда существуют всего две возможности при завершении проверки: достигается либо порог , либо порог  . Поскольку при этом может быть справедливой либо гипотеза , либо гипотеза , то возможны следующие четыре комбинации при окончании проверки на -м шаге:

          (5.120)

Среднее значение отношения правдоподобия при окончании наблюдений (при объеме выборки )

                 (5.121)

Вычислим теперь отношение правдоподобия  для , предположив для простоты, что элементы выборки независимы и одинаково распределены. В этом случае справедливо представление (5.111) при .  Поэтому можно записать

.       (5.122)

Правую часть этого равенства можно рассматривать как произведение двух независимых случайных величин. Вычисляя натуральный логарифм от обеих частей этого равенства, получим

.              (5.123)

Найдем теперь математические ожидания обеих частей полученного равенства:

         (5.124)

Здесь предполагается, что математическое ожидание  не зависит от номера наблюдения . Равенство (5.124) записано с учетом того, что

.            (5.125)

Формулу (5.121) можно записать в несколько ином виде:

               (5.126)

Учитывая теперь равенство (5.125), для математического ожидания  объема выборки получаем

                  (5.127)

Интересно сравнить последовательное правило с аналогичным правилом, использующим выборку фиксированного объема. Такое сравнение для задачи с нормальными случайными величинами, дисперсии которых известны и одинаковы при рассматриваемых гипотезах, проведено в примере 5.5. Результаты сравнения для случая непрерывного времени будут приведены позже.

Пример 5.5. Снова рассмотрим простую задачу различения двух гипотез:

где положительный параметр  известен, т.е. гипотеза о среднем значении нормальной случайной величины с известной дисперсией проверяется против простой альтернативы. Как уже отмечалось ранее, при отыскании правила различения гипотез можно использовать различные подходы. Найдем теперь последовательное правило выбора решения. Ради простоты будем предполагать, что элементы выборки независимы (иногда в таком случае говорят, что шум измерения белый)

Согласно ф-ле (5.106) отношение правдоподобия

Значения порогов последовательного правила можно вычислить по ф-ле (5.119), если задать и считать постоянными вероятности ложной тревоги и пропуска сигнала, так что

Таким образом, последовательное правило выбора решения можно записать следующим образом если

,

то принимается гипотеза , если 

,

то следует провести еще одно наблюдение, если

,

то принимается гипотеза .

Как и при выборке фиксированного объема, функцию от выборки  можно рассматривать как достаточную статистику Пороги построенного таким образом последовательного правила изменяются с ростом номера наблюдения, (см рис.5.9). Разница между значениями порогов постоянна и равна

.

Рис.5.9 Пороги как функции числа наблюдений, тангенс угла наклона соответствующих прямых равен

Так как , то

Средний объем выборки, необходимой для принятия одной из рассматриваемых гипотез, можно вычислить по ф-ле (5.127) В результате получаем

Сравним теперь средний объем выборки, требуемый для принятия окончательного решения с помощью последовательного правила, с объемом выборки, который необходим для достижения тех же значений вероятностей ложной тревоги и пропуска сигнала при применении непоследовательного правила В примере 5.2 уже было показано, что для рассмотренного там непоследовательного правила выбора решения можно записать

;

,

где порог  при использовании достаточной статистики определяется соотношением ,  а  - порог этого правила. Зададим теперь некоторые значения вероятностей ложной тревоги и пропуска сигнала для этого непоследовательного правила Неймана-Пирсона и найдем требуемый объем выборки. Из трех предыдущих равенств получаем

Отсюда объем выборки, необходимый для обеспечения заданных вероятностей ошибок при использовании правила Неймана-Пирсона,

.

Это выражение получено из двух предыдущих равенств путем исключения переменной . Таким образом, для обоих рассматриваемых правил необходимое число наблюдений растет с увеличением дисперсии  и уменьшается с ростом .

Интересно отметить, что объем выборки явно не зависит от порога правила , как это следовало бы ожидать, поскольку порог должен выбираться так, чтобы обеспечить заданные значения вероятностей  и . Особенно важным является отношение .  Значение этого отношения при заданных вероятностях  и  зависит от того, какая из гипотез справедлива.  На рис 5.10 приведены графики изменения этого отношения при гипотезе .

Рис.5.10  Отношение объема выборки непоследовательного правила к среднему объему выборки последовательного правила при вероятностях ложной тревоги и пропуска сигнала, одинаковых для обоих правил, справедлива гипотеза

Оказывается что при использован и последовательного правила требуется в среднем меньший объем выборки, чем для непоследовательного. И эта экономия среднего числа наблюдений становится существенной при малых значениях вероятностей  и .

Пример 5.6. Рассмотрим теперь задачу предыдущего примера, предположив, однако, что число отсчетов значений наблюдаемого процесса на конечном интервале времени может быть неограниченно увеличено. Это позволит построить последовательное правило выбора решения при непрерывном времени. Рассматриваемые гипотезы можно описать следующим образом:

где значение параметра  известно, a  - стационарный белый нормальный шум, среднее значение которого равно нулю, а ковариационная функция

.

Начнем с отсчетов непрерывного наблюдаемого процесса в дискретные моменты времени и примем, что

,

т.е. при любом  элементы выборки предполагаются независимыми. Для этого частного случая отношение правдоподобия, рассматривавшееся в предыдущем примере, примет вид

.

Положим теперь, что число отсчетов на конечном интервале наблюдения неограниченно увеличивается, т. е. . Нетрудно выписать предел отношения правдоподобия

,

где  - известный момент начала наблюдения, a  - неизвестный момент прекращения наблюдения, который определяется последовательным правилом. Пороги, с которыми сравнивается значение отношения правдоподобия при непрерывном времени, остаются такими же, как и в предыдущем примере. Последовательное правило можно записать следующим образом: если

,

то принимается гипотеза ; если

,

то интервал наблюдения следует увеличить; если

,

то принимается гипотеза .

Пороги данного правила являются функциями времени наблюдения. Можно вычислить среднее время от момента начала наблюдения до принятия окончательного решения и оценить выигрыш, обеспечиваемый последовательным правилом по сравнению с непоследовательным при фиксированных вероятностях ложной тревоги и пропуска сигнала. Полученные здесь результаты аналогичны результатам, приведенным в предыдущем примере.

Полученные в этом разделе соотношения можно легко модифицировать с тем, чтобы охватить задачи проверки сложных гипотез с помощью последовательных правил. Последовательность рассуждений при этом полностью совпадает с той, которая подробно описана в § 5.4.

Здесь следует использовать отношение правдоподобия

                                                        ,
которое при наличии случайного параметра  можно записать следующим образом:

.          (5.128)

Последовательное правило проверки сложных гипотез после этого строится, как последовательное правило проверки соответствующих простых гипотез.

Вероятности ложной тревоги и пропуска сигнала в этом случае зависят от значения параметра, таr как

;              (5.129)

.           (5.130)

Средние значения вероятностей ложной тревоги и пропуска сигнала могут быть определены с помощью соотношений:

;              (5.131)

.            (5.132)

Значения порогов для рассматриваемых последовательных правил вычисляются по формулам: . Как и ранее, эти вероятности и пороги иногда могут зависеть от номера наблюдения .

Если векторный параметр  не случаен и его значение неизвестно, то можно воспользоваться обобщенным отношением правдоподобия [cм. также ф-лу (5.100)]

,                   (5.133)

в котором оценки максимального правдоподобия неизвестного параметра  отыскиваются путем максимизации соответствующих условных плотностей вероятности но допустимым областям значений  при фиксированной выборке .

Можно рассмотреть также задачу проверки нескольких гипотез с помощью последовательного правила. При этом необходимо ввести вероятности нескольких ошибок, которые служат аналогами вероятностей ложного обнаружения и пропуска сигнала. Соотношения, получающиеся при решении этой задачи, полностью аналогичны тем, которые были получены для бинарного случая.

Поскольку объем  выборки, используемой для вынесения окончательного решения с помощью последовательного правила, является случайной величиной с математическим ожиданием  то может оказаться необходимым ограничить максимально допустимое число наблюдений или время наблюдения. То есть, если после получения  наблюдений окончательное решение с помощью последовательного правила не принято, то для выбора одной из рассматривающихся гипотез используется другое правило:

.

Вальд [272] указал границы для вероятностей ложной тревоги и пропуска сигнала подобных усеченных последовательных правил.

В примерах данного раздела были рассмотрены простые задачи последовательного анализа для нормальных случайных величин. Теперь перейдем к анализу более полезного варианта этой задачи, который будет играть очень важную роль при изложении в гл. 7 результатов, полученных Калманом при решении задач фильтрации.