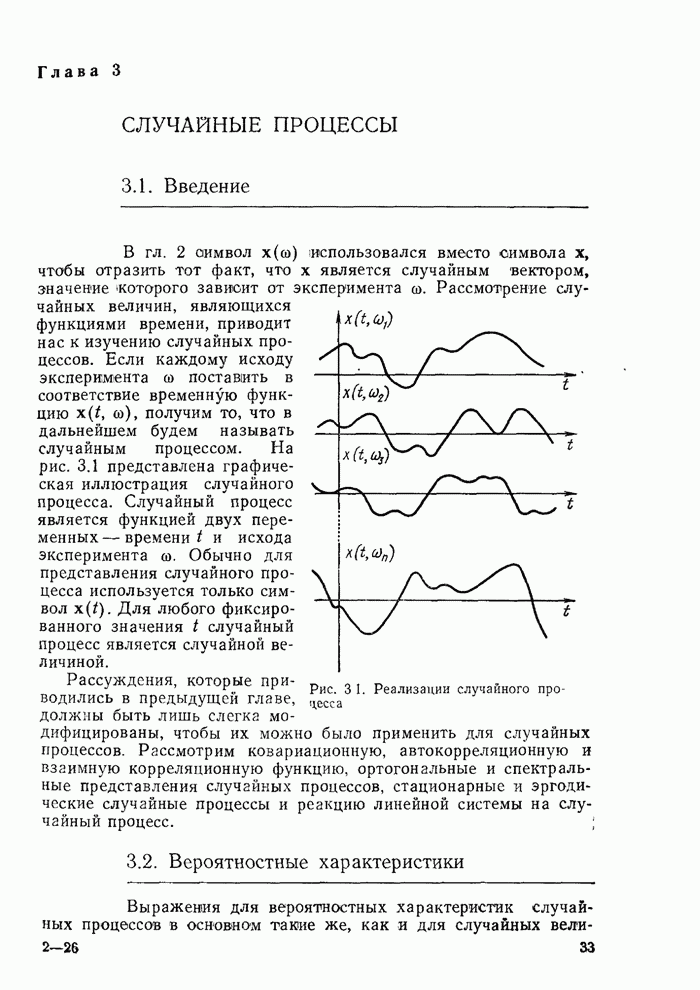
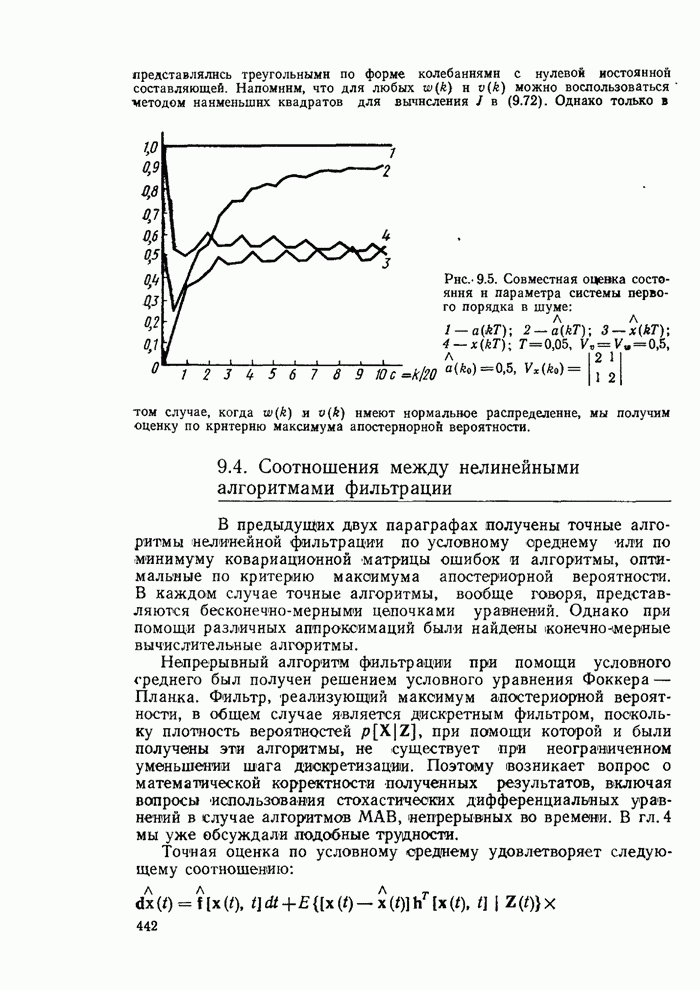
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.5. Асимптотические свойства
В этом параграфе мы обсудим некоторые
асимптотические свойства фильтра Калмана. Так как этот вопрос очень мало
изучен, изложение будет кратким и будет состоять, главным образом, из
формулировок отдельных положений, доказательство которых не будет приводиться
вообще, либо будет приводиться в сокращенном виде. Доказательства этих свойств,
хотя и не очень трудные, опираются на теоремы устойчивости по Ляпунову [223],
[85], [107], [111]. Из-за непреодолимых трудностей, которые возникают при
изучении асимптотического поведения случайного процесса ![]() , основное внимание здесь будет
уделено изучению ур-ний (7.33) и (7.34) для дискретного случая и (7.24) для
непрерывного случая.
, основное внимание здесь будет
уделено изучению ур-ний (7.33) и (7.34) для дискретного случая и (7.24) для
непрерывного случая.
При изучении случайного процесса обычно можно сделать ряд утверждений относительно свойств процесса, таких, как непрерывность, ограниченность, используя понятие сходимости почти наверно или с вероятностью единица. При анализе поведения дисперсии ошибки оценивания можно избежать этих тонкостей, так как уравнение для дисперсии ошибки — детерминированное.
Существуют два связанных друг с другом вопроса, касающиеся асимптотического поведения алгоритма фильтрации Калмана, которые будут рассмотрены в данном параграфе. Во-первых, определим условия существования стационарного решения уравнения дисперсии. Ответ на этот вопрос полезен тем, что он позволяет определить, когда существует решение стационарной задачи оценивания (задачи Винера), и указывает условия, выполнение которых необходимо для того, чтобы процесс оценивания оставался эффективным при увеличении интервала наблюдения.
Второй и несомненно более важный
вопрос касается устойчивости алгоритма фильтрации. Если фильтр устойчив, то
влияние любой небольшой ошибки в априорных данных о начальном состоянии при
увеличении времени будет постепенно ослабевать. Практическое значение
устойчивого в вычислительном отношении алгоритма фильтрации трудно
переоценить, поскольку очень редко имеются точные сведения о начальном
распределении состояния ![]() . Перед тем как приступить к обсуждению
каждого из этих вопросов, необходимо ввести понятия управляемости и
наблюдаемости.
. Перед тем как приступить к обсуждению
каждого из этих вопросов, необходимо ввести понятия управляемости и
наблюдаемости.
Понятия управляемости и наблюдаемости были использованы Калманом [105], [106] для описания совокупности условий, которые были связаны с существованием решений некоторых линейных задач управления.
Подробное изложение этого вопроса можно найти в литературе [42], [105]—[108], [114], [120], [202], [223].
Чтобы облегчить обсуждение
понятий управляемости и наблюдаемости, удобно рассматривать входной шум ![]() в модели сообщения
как входной сигнал управления, который может быть выбран произвольно. Кроме
того, предположим, что шум измерений
в модели сообщения
как входной сигнал управления, который может быть выбран произвольно. Кроме
того, предположим, что шум измерений ![]() отсутствует.
отсутствует.
Управляемость, грубо говоря, означает, как можно было догадаться по названию термина, способность каждой переменной изменяться под действием входного сигнала управления. С другой стороны, под наблюдаемостью подразумевается способность каждой переменной состояния влиять на выходной сигнал системы. Определим каждое из этих понятий более точно.
Модели сообщения, описываемые
ур-ниями (7.1) или (7.82), называются управляемыми в момент времени ![]() , если существуют
такие момент времени
, если существуют
такие момент времени ![]() и управление
и управление ![]() , заданные на интервале
, заданные на интервале ![]() , которые, вообще
говоря, зависят от
, которые, вообще
говоря, зависят от ![]() ,
и
,
и ![]() такое,
что
такое,
что ![]() . Если
может быть найдено управление для каждого состояния
. Если
может быть найдено управление для каждого состояния ![]() , то говорят, что модель
сообщения является вполне управляемой в момент времени
, то говорят, что модель
сообщения является вполне управляемой в момент времени ![]() и если это справедливо при
любом
и если это справедливо при
любом ![]() , то
модель сообщения является вполне управляемой.
, то
модель сообщения является вполне управляемой.
В ходе последующих рассуждений
будут особенно важны свойства абсолютной и равномерно абсолютной
управляемости. Для непрерывного случая легко показать, что модель сообщения, определяемая
ур-нием (7,82), является вполне управляемой тогда и только тогда, когда для
любого ![]() существует
такое
существует
такое ![]() , что
симметричная матрица Грамма [74]
, что
симметричная матрица Грамма [74]
 .
(7.214)
.
(7.214)
положительно определена. Здесь ![]() — переходная матрица
состояний, которая определяется уравнением
— переходная матрица
состояний, которая определяется уравнением
![]() . (7.215)
. (7.215)
Если для некоторого ![]() и всех
и всех ![]() матрицы
матрицы ![]() и
и ![]() — положительно
определенные и ограниченные независимо от
— положительно
определенные и ограниченные независимо от ![]() , то модель сообщения является
равномерно вполне управляемой.
, то модель сообщения является
равномерно вполне управляемой.
При изучении закона изменения дисперсии в линейных системах в § 3.5 отмечалось, что удобно преобразовать интегральное уравнение, которое по форме совпадает с ур-нием (7.214), в дифференциальное. Этот же прием может быть использован и здесь. Вычислим частную производную:

Так как ![]() — переходная матрица, которая
удовлетворяет ур-нию (7.215), то это выражение можно представить в виде
— переходная матрица, которая
удовлетворяет ур-нию (7.215), то это выражение можно представить в виде

Отсюда следует [см. (7.214)], что
 . (7.216)
. (7.216)
Так как ![]() , то
, то ![]() однозначно определяется для
всех
однозначно определяется для
всех ![]() решением
обыкновенного дифференциального ур-ния (7.216) в обратном времени. Одно из
главных достоинств этого метода заключается в том, что здесь нет необходимости
вычислять переходную матрицу
решением
обыкновенного дифференциального ур-ния (7.216) в обратном времени. Одно из
главных достоинств этого метода заключается в том, что здесь нет необходимости
вычислять переходную матрицу ![]() .
.
Для непрерывных систем с постоянными
коэффициентами, в которых ![]() и
и ![]() — матрицы постоянных коэффициентов,
свойство равномерности всегда соблюдается, и модель является (равномерно)
вполне управляемой тогда и только тогда, когда удовлетворяется условие
— матрицы постоянных коэффициентов,
свойство равномерности всегда соблюдается, и модель является (равномерно)
вполне управляемой тогда и только тогда, когда удовлетворяется условие
![]() .
(7.217)
.
(7.217)
Легко показать, используя теорему
Кели—Гамильтона, что это условие является прямым следствием условия,
сформулированного выше в терминах ![]() . Достаточное условие полной управляемости,
аналогичное ур-нию (7.217), существует также и для систем с переменными
параметрами [42].
. Достаточное условие полной управляемости,
аналогичное ур-нию (7.217), существует также и для систем с переменными
параметрами [42].
В дискретном случае модель
сообщения [см. (7.1)] является полностью управляемой тогда и только тогда,
когда для любого ![]() существует
такое
существует
такое ![]() , что
симметричная матрица Грама, определяемая как
, что
симметричная матрица Грама, определяемая как
 . (7.218)
. (7.218)
положительно определена. Условия
для равномерной полной управляемости записываются точно так же, как и в
непрерывном случае, за исключением разве того, что ![]() в этом случае может принимать
только целые значения. Для дискретной системы с постоянными параметрами
необходимое и достаточное условие равномерно полной управляемости модели
сообщения записывается в виде
в этом случае может принимать
только целые значения. Для дискретной системы с постоянными параметрами
необходимое и достаточное условие равномерно полной управляемости модели
сообщения записывается в виде
![]() . (7.219)
. (7.219)
Можно также получить разностное
уравнение для ![]() ,
эквивалентное ур-нию (7.216) для непрерывного случая.
,
эквивалентное ур-нию (7.216) для непрерывного случая.
Как можно будет убедиться в
дальнейшем, понятие наблюдаемости по сравнению с понятием управляемости в
задаче оценивания является до некоторой степени более фундаментальным. Калман
[105] впервые ввел понятие наблюдаемости и исследовал его, рассматривая
систему, дуальную исходной. Дуальная система оказывалась управляемой, когда
исходная система была наблюдаемой. Подход, развитый Калманом, здесь
использоваться не будет, хотя он имеет определенные преимущества. Вместо этого
рассмотрим непосредственно проблему наблюдаемости. При обсуждении этой
проблемы необходимо рассматривать модели наблюдения и сообщения совместно, так
что под системой в широком смысле будем понимать комбинацию этих моделей. Будем
также полагать, что ![]() и
и
![]() тождественно
равны нулю.
тождественно
равны нулю.
Невозмущенная система называется
вполне наблюдаемой на ![]() , если для данного
, если для данного ![]() и
и ![]() любое состояние
любое состояние ![]() может быть однозначно
определено по известному наблюдению
может быть однозначно
определено по известному наблюдению ![]() на интервале
на интервале ![]() . Если для любого
. Если для любого ![]() существует
существует ![]() , которое может
зависеть от
, которое может
зависеть от ![]() ,
так что система является вполне наблюдаемой на
,
так что система является вполне наблюдаемой на ![]() , то систему принято называть вполне
наблюдаемой. Так же, как и в случае управляемости, наблюдаемость системы может
быть установлена при анализе матрицы Грама. Можно непосредственно показать, что
непрерывная система является вполне наблюдаемой на
, то систему принято называть вполне
наблюдаемой. Так же, как и в случае управляемости, наблюдаемость системы может
быть установлена при анализе матрицы Грама. Можно непосредственно показать, что
непрерывная система является вполне наблюдаемой на ![]() , если симметричная матрица
Грама, определяемая как
, если симметричная матрица
Грама, определяемая как
 , (7.220)
, (7.220)
есть положительно определенная
или несингулярная матрица. Если для некоторого ![]() и для всех
и для всех ![]() матрицы
матрицы ![]() и
и ![]() — положительно определенные ограниченные
независимо от
— положительно определенные ограниченные
независимо от ![]() ,
то модель сообщения равномерно вполне наблюдаема. Для дискретной системы
,
то модель сообщения равномерно вполне наблюдаема. Для дискретной системы ![]() определяется
дискретным аналогом ур-ния (7.220), определяемым как
определяется
дискретным аналогом ур-ния (7.220), определяемым как
 . (7.221)
. (7.221)
Эти же условия должны быть
соблюдены для различных форм наблюдаемости. В частном случае, когда ![]() ,
, ![]() — нормальный случайный
процесс с нулевым средним значением и единичной дисперсией, матрица
— нормальный случайный
процесс с нулевым средним значением и единичной дисперсией, матрица ![]() совпадает с известной
в математической статистике информационной матрицей Фишера. В этом случае
дисперсия любой несмещенной оценки
совпадает с известной
в математической статистике информационной матрицей Фишера. В этом случае
дисперсия любой несмещенной оценки ![]() состояния
состояния ![]() удовлетворяет неравенству Крамера — Рао
(6.43):
удовлетворяет неравенству Крамера — Рао
(6.43):
![]() . (7.222)
. (7.222)
где ![]() — любая действительная линейная функция
— любая действительная линейная функция ![]() . Калман назвал
. Калман назвал ![]() смежным состоянием,
поскольку оно связано с введенным им понятием дуальной системы и понятием
дуальности в линейной алгебре. Для любого смежного состояния
смежным состоянием,
поскольку оно связано с введенным им понятием дуальной системы и понятием
дуальности в линейной алгебре. Для любого смежного состояния ![]() существует
несмещенная оценка с минимальной дисперсией, для которой в выражении (7.222)
выполняется знак равенства тогда и только тогда, когда
существует
несмещенная оценка с минимальной дисперсией, для которой в выражении (7.222)
выполняется знак равенства тогда и только тогда, когда ![]() положительно определенная
матрица.
положительно определенная
матрица.
Для систем с постоянными параметрами свойство равномерности всегда соблюдается, и можно показать [105], что непрерывная система с постоянными параметрами является (равномерно) вполне наблюдаемой тогда и только тогда, когда
![]() . (7.223)
. (7.223)
В дискретном случае необходимо выполнение следующего условия:
![]() . (7.224)
. (7.224)
Опираясь на введенные понятия управляемости и наблюдаемости, можно приступить к анализу уравнения дисперсии. Для простоты ограничимся рассмотрением непрерывного случая; обобщение результатов применительно к дискретному случаю выполняется достаточно просто. Рассмотрим сначала вопрос о существовании решения уравнения дисперсии (7.105):
![]() . (7.225)
. (7.225)
Для любого заданного
фиксированного начального момента времени ![]() и неотрицательно определенной
симметричной матрицы
и неотрицательно определенной
симметричной матрицы ![]() ур-ние (7.105) имеет единственное
решение
ур-ние (7.105) имеет единственное
решение
![]() . (7.226)
. (7.226)
для всех ![]() , таких, что
, таких, что ![]() — является достаточно
малой. Для того чтобы подчеркнуть, что решение ур-ния (7.105) зависит от начальной
условий, в ф-лу (7.226) введены аргументы, указывающие условия. Существование
и единственность решения для достаточно малых значений
— является достаточно
малой. Для того чтобы подчеркнуть, что решение ур-ния (7.105) зависит от начальной
условий, в ф-лу (7.226) введены аргументы, указывающие условия. Существование
и единственность решения для достаточно малых значений ![]() прямо следуют из того факта,
что ур-ние. (7.105) удовлетворяет условию Липшица [110].
прямо следуют из того факта,
что ур-ние. (7.105) удовлетворяет условию Липшица [110].
Так как ур-ние (7.105)
нелинейное, то существование решения для достаточно малых значений ![]() — еще не гарантирует
существования решения уравнения для всех
— еще не гарантирует
существования решения уравнения для всех ![]() . Однако Калман показал [107], что
решение этого уравнения существует для всех
. Однако Калман показал [107], что
решение этого уравнения существует для всех ![]() и однозначно определяется выбором
и однозначно определяется выбором ![]() . Следовательно, для
всех задач, в которых интервал наблюдения конечен, существование и
единственность решения уравнения дисперсии, а значит, и уравнения для
коэффициента усиления гарантируются выбором
. Следовательно, для
всех задач, в которых интервал наблюдения конечен, существование и
единственность решения уравнения дисперсии, а значит, и уравнения для
коэффициента усиления гарантируются выбором ![]() . Заметим, что до сих пор никакие
ограничения не накладывались на модели сообщения и наблюдений, которые первоначально
были введены в § 7.3. Чтобы исследовать задачу с бесконечным интервалом
наблюдений, т. е. при
. Заметим, что до сих пор никакие
ограничения не накладывались на модели сообщения и наблюдений, которые первоначально
были введены в § 7.3. Чтобы исследовать задачу с бесконечным интервалом
наблюдений, т. е. при ![]() , необходимо ввести не очень сильное
ограничение либо на модель сообщения, либо на модель наблюдений. Например, если
, необходимо ввести не очень сильное
ограничение либо на модель сообщения, либо на модель наблюдений. Например, если
![]() , то
, то ![]() для всех
для всех ![]() и если модель является
неустойчивой, то
и если модель является
неустойчивой, то ![]() и,
следовательно,
и,
следовательно, ![]() будут
неограниченно возрастать пря
будут
неограниченно возрастать пря ![]() .
.
Решение задачи с бесконечным интервалом наблюдений будет: существовать в том смысле, что
![]() . (7.227)
. (7.227)
существует для всех ![]() и является решением
ур-ния (7.105), когда либо модель сообщения является равномерно асимптотически
устойчивой, либо система является вполне наблюдаемой [85].
и является решением
ур-ния (7.105), когда либо модель сообщения является равномерно асимптотически
устойчивой, либо система является вполне наблюдаемой [85].
Если система является вполне
наблюдаемой, то всегда можно оценить ![]() с конечной ошибкой и, следовательно,
с конечной ошибкой и, следовательно, ![]() будет оставаться
конечной. Как мы убедимся в дальнейшем, решение
будет оставаться
конечной. Как мы убедимся в дальнейшем, решение ![]() , определяемое ур-нием (7.226), можно
рассматривать как «движущуюся» точку равновесия уравнения дисперсии.
, определяемое ур-нием (7.226), можно
рассматривать как «движущуюся» точку равновесия уравнения дисперсии.
В стационарной задаче оценивания ![]() , определяемое ур-нием
(7.226), представляет собой матрицу постоянных коэффициентов. Следовательно,
введенные выше условия устойчивости или наблюдаемости гарантируют
существование решения задачи фильтрации Винера. Таким образом, необязательно,
чтобы модель сообщения была устойчивой, важно, чтобы система была наблюдаемой.
, определяемое ур-нием
(7.226), представляет собой матрицу постоянных коэффициентов. Следовательно,
введенные выше условия устойчивости или наблюдаемости гарантируют
существование решения задачи фильтрации Винера. Таким образом, необязательно,
чтобы модель сообщения была устойчивой, важно, чтобы система была наблюдаемой.
Существование стационарного
решения на бесконечном интервале наблюдений, определяемого выражением (7.226),
выражает одну из форм устойчивости алгоритма фильтрации. Мы уверены в том, что
если при ![]() наблюдение
начинается с
наблюдение
начинается с ![]() ,
то уравнение дисперсии имеет решение для всех
,
то уравнение дисперсии имеет решение для всех ![]() . Гораздо более важным является ответ на
следующий вопрос: если решение уравнения дисперсии на конечном интервале
выполняется при неправильном значении начальной дисперсии, то будет ли это
решение стремиться к решению, которое получалось бы при правильном выборе начальной
дисперсии? Правильное решение в действительности определяется выражением
(7.226) для
. Гораздо более важным является ответ на
следующий вопрос: если решение уравнения дисперсии на конечном интервале
выполняется при неправильном значении начальной дисперсии, то будет ли это
решение стремиться к решению, которое получалось бы при правильном выборе начальной
дисперсии? Правильное решение в действительности определяется выражением
(7.226) для ![]() ,
но, разумеется, начинать вычисления при
,
но, разумеется, начинать вычисления при ![]() совершенно нереально.
совершенно нереально.
Чтобы установить, что
стационарное решение ![]() , определяемое выражением (7.226), представляет
устойчивую траекторию в том смысле, что некоторое возмущение траектории
полностью затухает при
, определяемое выражением (7.226), представляет
устойчивую траекторию в том смысле, что некоторое возмущение траектории
полностью затухает при ![]() , необходимо ввести достаточно жесткое
ограничение на модели сообщения и наблюдений. Если модели сообщения и
наблюдений являются равномерно вполне управляемыми и равномерно вполне
наблюдаемыми, если матрицы
, необходимо ввести достаточно жесткое
ограничение на модели сообщения и наблюдений. Если модели сообщения и
наблюдений являются равномерно вполне управляемыми и равномерно вполне
наблюдаемыми, если матрицы ![]() и
и ![]() ,
, ![]() соответственно положительно определенные
и положительно полуопределенные, а также ограниченные для всех
соответственно положительно определенные
и положительно полуопределенные, а также ограниченные для всех ![]() , и, кроме того,
ограниченной для всех
, и, кроме того,
ограниченной для всех ![]() является матрица
является матрица ![]() , то оптимальный фильтр
равномерно асимптотически устойчив. Кроме того, решение
, то оптимальный фильтр
равномерно асимптотически устойчив. Кроме того, решение ![]() сходится к стационарному
решению
сходится к стационарному
решению ![]() ,
определяемому согласно (7.227) при
,
определяемому согласно (7.227) при ![]() , для любой симметричной неотрицательной
определенной матрицы
, для любой симметричной неотрицательной
определенной матрицы ![]() .
.
Значение устойчивости алгоритма фильтрации
Калмана трудно переоценить. Если алгоритм устойчив, то любая ошибка в выборе
начального значения дисперсии ошибки [а ошибка весьма вероятна, поскольку часто
мы выбираем ![]() до
некоторой степени произвольно] будет стремиться к нулю при
до
некоторой степени произвольно] будет стремиться к нулю при ![]() и в конечном счете будут
обеспечиваться оптимальные качественные показатели. Оценка скорости сходимости,
которая часто оказывается достаточно высокой, может быть выполнена с помощью
второго метода Ляпунова [107]. Чувствительность алгоритма фильтрации к ошибкам
в выборе значений статистических моментов, а также моделей сообщения и
наблюдений будет проанализирована в следующей главе. Кроме того, там будет
показано, что при практической реализации алгоритма фильтрации часто можно
наблюдать расходимость или неустойчивость даже в тех случаях, когда алгоритм в
вычислительном отношении является устойчивым.
и в конечном счете будут
обеспечиваться оптимальные качественные показатели. Оценка скорости сходимости,
которая часто оказывается достаточно высокой, может быть выполнена с помощью
второго метода Ляпунова [107]. Чувствительность алгоритма фильтрации к ошибкам
в выборе значений статистических моментов, а также моделей сообщения и
наблюдений будет проанализирована в следующей главе. Кроме того, там будет
показано, что при практической реализации алгоритма фильтрации часто можно
наблюдать расходимость или неустойчивость даже в тех случаях, когда алгоритм в
вычислительном отношении является устойчивым.
В заключение главы интересно, хотя бы вкратце, рассмотреть один из способов аналитического решения нелинейного уравнения дисперсии путем решения системы линейных матричных дифференциальных уравнений. В вычислительном отношении этот метод не представляет большой ценности, поскольку, за исключением случая стационарных моделей сообщения и наблюдений, получающиеся при этом уравнения не могут быть достаточно легко решены. С другой стороны, этот метод часто оказывается весьма полезным при формулировке общих выводов о характере решения уравнения дисперсии.
Пусть ![]() — переходная матрица размера
— переходная матрица размера ![]() для
для ![]() -мерного векторного
дифференциального уравнения
-мерного векторного
дифференциального уравнения
![]() , (7.228)
, (7.228)
где ![]() и
и ![]() матрица размера
матрица размера ![]() определяемая в структурной
форме как
определяемая в структурной
форме как
 . (7.229)
. (7.229)
Если ![]() записать в виде
записать в виде
 , (7.230)
, (7.230)
где каждый элемент ![]() — матрица размера
— матрица размера ![]() , то получим решение
уравнения дисперсии (7.105) для произвольной неотрицательно определенной
матрицы
, то получим решение
уравнения дисперсии (7.105) для произвольной неотрицательно определенной
матрицы ![]() :
:
![]() . (7.231)
. (7.231)
Доказательство этого результата, которое сводится к подстановке (7.230) в ур-ние (7.105), предоставляется читателю. Непреодолимые трудности, которые возникают при попытке получить аналитически решение уравнения дисперсии даже для системы первого порядка [202], не позволяют рассматривать этот метод в качестве реального метода решения уравнения дисперсии.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие к русскому изданию
- Глава 1. Обзор содержания книги
- Глава 2. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 2.1. Введение
- 2.2. Теория вероятностей
- 2.3. Случайные величины
- 2.4. Алгебраические действия над случайными величинами
- 2.5. Средние значения
- Глава 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 3.1. Введение
- 3.2. Вероятностные характеристики
- 3.3. Средние значения
- 3.4. Спектральные и ортогональные представления
- 3.5. Реакция линейных систем
- Глава 4. НОРМАЛЬНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ И СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 4.1. Введение
- 4.2. Нормальные случайные процессы
- 4.3. Марковские случайные процессы
- 4.4. Стохастические дифференциальные уравнения
- 4.5. Среднее значение и дисперсия процесса на выходе нелинейной системы
- Глава 5. ТЕОРИЯ РЕШЕНИЙ
- 5.1. Введение
- 5.2. Выбор решения при однократном наблюдении
- 5.3. Выбор решения при многократных наблюдениях
- 5.4. Проверка сложных гипотез
- 5.5. Проверка многих гипотез
- 5.6. Последовательный анализ
- 5.7. Последовательное обнаружение марковских сигналов в нормальном шуме
- Глава 6. ОСНОВЫ ТЕОРИИ ОЦЕНИВАНИЯ
- 6.1. Введение
- 6.2. Байесовские оценки
- 6.3. Оценки максимального правдоподобия
- 6.4. Свойства оценок
- 6.5. Точность оценок и априорная информация
- 6.6. Линейные оценки с минимальной среднеквадратической ошибкой
- 6.7. Оценки наименьших квадратов
- Глава 7. ОПТИМАЛЬНЫЙ ЛИНЕЙНЫЙ ФИЛЬТР
- 7.1. Введение
- 7.2. Оптимальный линейный дискретный фильтр
- 7.3. Оптимальный линейный непрерывный фильтр
- 7.4. Стационарные процессы и фильтр Винера
- 7.5. Асимптотические свойства
- Глава 8. ОБОБЩЕНИЕ АЛГОРИТМА ОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ФИЛЬТРАЦИИ
- 8.1. Введение
- 8.2. Небелый шум
- 8.3. Сглаживание и предсказание
- 8.4. Анализ ошибок и априорные данные
- 8.5. Расходимость
- Глава 9. НЕЛИНЕЙНОЕ ОЦЕНИВАНИЕ
- 9.1. Введение
- 9.2 Оценивание при помощи условного среднего
- 9.3. Оценивание по максимуму апостериорной вероятности
- 9.4. Соотношения между нелинейными алгоритмами фильтрации
- 9.5. Нелинейное сглаживание
- Список литературы