| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.5. Проверка многих гипотез
Результаты, полученные при решении задачи проверни
двух гипотез, в этом разделе будут обобщены на случай проверки ![]() гипотез. Как и ранее,
в качестве критерия оптимальности здесь будет использован минимум среднего
риска. Выражение для среднего риска (5.23) при
гипотез. Как и ранее,
в качестве критерия оптимальности здесь будет использован минимум среднего
риска. Выражение для среднего риска (5.23) при ![]() гипотезах принимает вид
гипотезах принимает вид
 , (5.101)
, (5.101)
где ![]() - потери при
принятии гипотезы
- потери при
принятии гипотезы ![]() ,
когда на самом деле справедлива гипотеза
,
когда на самом деле справедлива гипотеза ![]() ;
; ![]() - априорная вероятность гипотезы
- априорная вероятность гипотезы ![]() ;
; ![]() - плотность вероятности
выборки при
- плотность вероятности
выборки при![]() -ой
гипотезе;
-ой
гипотезе; ![]() -
выборочное пространство при гипотезе
-
выборочное пространство при гипотезе ![]() ;
; - выборочное
пространство.
- выборочное
пространство.
Повторив рассуждения, проведенные для бинарного
случая, можно переписать выражение (5.101) и получить правило выбора одной из ![]() гипотез, основанное
на использовании отношения правдоподобия [163]. Согласно этому правилу
принимается та гипотеза
гипотез, основанное
на использовании отношения правдоподобия [163]. Согласно этому правилу
принимается та гипотеза ![]() , для которой справедливо неравенство
, для которой справедливо неравенство
 (5.102)
(5.102)
для всех ![]() . Рассмотрим здесь более подробно
следующий частный случай. Пусть потери при правильных решениях равны нулю, а
при ошибочных — одинаковы; предположим также, что все рассматриваемые гипотезы
равновероятны. На основании ф-лы (5.102) гипотеза
. Рассмотрим здесь более подробно
следующий частный случай. Пусть потери при правильных решениях равны нулю, а
при ошибочных — одинаковы; предположим также, что все рассматриваемые гипотезы
равновероятны. На основании ф-лы (5.102) гипотеза ![]() принимается, если
принимается, если
![]() (5.103)
(5.103)
для всех ![]() . Воспользовавшись формулой Байеса,
неравенство (5.103) можно записать следующим образом:
. Воспользовавшись формулой Байеса,
неравенство (5.103) можно записать следующим образом:
![]() . (5.104)
. (5.104)
Таким образом, следует вычислить апостериорные вероятности
![]() рассматриваемых
гипотез и принять ту гипотезу, апостериорная вероятность которой максимальна.
рассматриваемых
гипотез и принять ту гипотезу, апостериорная вероятность которой максимальна.
Можно рассмотреть также задачу проверки ![]() сложных гипотез. В
частности, оказывается, что при назначении потерь таким образом, как это было
сделано выше, для принятия решения необходимо вычислять интегралы
сложных гипотез. В
частности, оказывается, что при назначении потерь таким образом, как это было
сделано выше, для принятия решения необходимо вычислять интегралы
 . (5.105)
. (5.105)
Принимается гипотеза ![]() с таким индексом
с таким индексом ![]() , для которого
интеграл (5.105) оказывается наибольшим.
, для которого
интеграл (5.105) оказывается наибольшим.
Пример 5.4. Рассмотрим задачу проверки ![]() следующих гипотез (
следующих гипотез (![]() ):
):
![]()
где ![]() - нормальный шум с нулевым средним значением и
дисперсией
- нормальный шум с нулевым средним значением и
дисперсией ![]() .
Значение параметра
.
Значение параметра ![]() будем считать известным и положительным,
а все рассматриваемые гипотезы равновероятными. Примем также что потери при
правильных решениях равны нулю, а при любых неправильных — единице.
будем считать известным и положительным,
а все рассматриваемые гипотезы равновероятными. Примем также что потери при
правильных решениях равны нулю, а при любых неправильных — единице.
После проведения
наблюдений будем принимать ту гипотезу ![]() , апостериорная вероятность которой при
полученной выборке наибольшая. Согласно формуле Байеса
, апостериорная вероятность которой при
полученной выборке наибольшая. Согласно формуле Байеса
![]() .
.
Так как ![]() для любой
рассматриваемой гипотезы, то отыскание гипотезы, апостериорная вероятность
которой максимальна, сводится к отысканию гипотезы
для любой
рассматриваемой гипотезы, то отыскание гипотезы, апостериорная вероятность
которой максимальна, сводится к отысканию гипотезы ![]() при которой значение плотности
при которой значение плотности
![]()
при полученном
единственном наблюдении оказывается наибольшим. Здесь ![]() обозначает
возможные значения сигнала
обозначает
возможные значения сигнала ![]() . Этот способ принятия решения приводит
к выбору гипотезы
. Этот способ принятия решения приводит
к выбору гипотезы ![]() с
наименьшим значением модуля
с
наименьшим значением модуля ![]() . Границы областей принятия отдельных
гипотез определяются просто как проекции точек пересечения функций плотности
вероятности наблюдаемой величины при этих гипотезах (см. рис. 5.8).
. Границы областей принятия отдельных
гипотез определяются просто как проекции точек пересечения функций плотности
вероятности наблюдаемой величины при этих гипотезах (см. рис. 5.8).

Рис. 5.8 Области принятия отдельных гипотез (пример 5.4)

Значение байесовского риска для этого примера совпадает с вероятностью ошибки и может быть выполнено по формуле
 ,
,
Из рис 5.7 следует, что вероятность ошибки определяется выражением

Путем введения новой
переменной интегрирования все интегралы этого выражения можно выразить через
интеграл от стандартной нормальной плотности вероятности. В результате получим
 . Как и следовало
ожидать, вероятность ошибки уменьшается с ростом
. Как и следовало
ожидать, вероятность ошибки уменьшается с ростом ![]() и уменьшением
и уменьшением ![]() . Полученные в этом примере
соотношения можно без труда обобщить на случай выборки объема
. Полученные в этом примере
соотношения можно без труда обобщить на случай выборки объема ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие к русскому изданию
- Глава 1. Обзор содержания книги
- Глава 2. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 2.1. Введение
- 2.2. Теория вероятностей
- 2.3. Случайные величины
- 2.4. Алгебраические действия над случайными величинами
- 2.5. Средние значения
- Глава 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
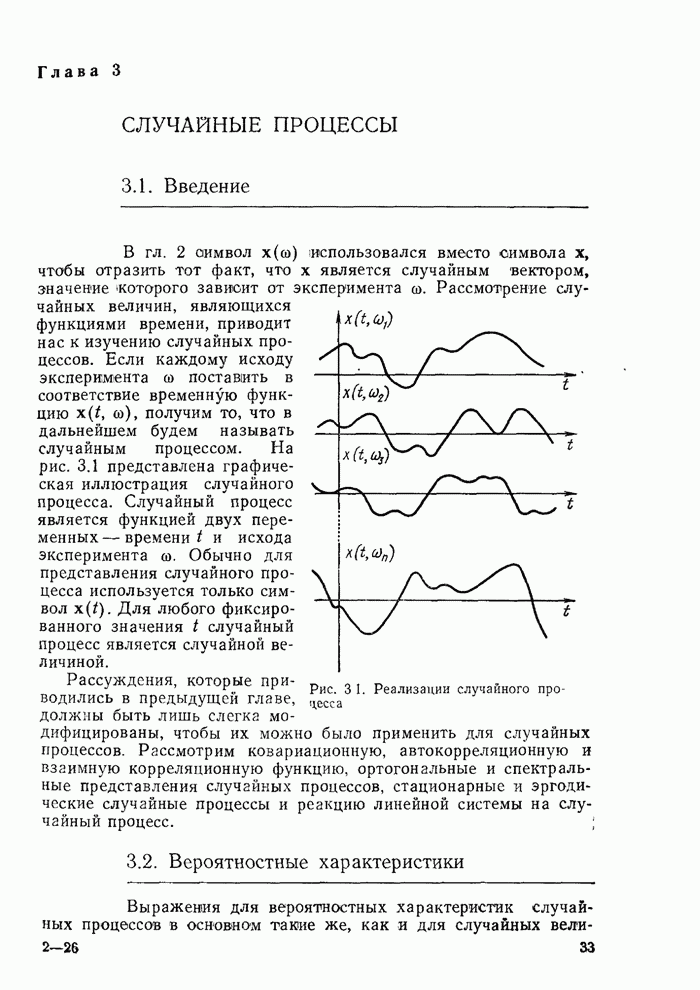
- 3.1. Введение
- 3.2. Вероятностные характеристики
- 3.3. Средние значения
- 3.4. Спектральные и ортогональные представления
- 3.5. Реакция линейных систем
- Глава 4. НОРМАЛЬНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ И СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 4.1. Введение
- 4.2. Нормальные случайные процессы
- 4.3. Марковские случайные процессы
- 4.4. Стохастические дифференциальные уравнения
- 4.5. Среднее значение и дисперсия процесса на выходе нелинейной системы
- Глава 5. ТЕОРИЯ РЕШЕНИЙ
- 5.1. Введение
- 5.2. Выбор решения при однократном наблюдении
- 5.3. Выбор решения при многократных наблюдениях
- 5.4. Проверка сложных гипотез
- 5.5. Проверка многих гипотез
- 5.6. Последовательный анализ
- 5.7. Последовательное обнаружение марковских сигналов в нормальном шуме
- Глава 6. ОСНОВЫ ТЕОРИИ ОЦЕНИВАНИЯ
- 6.1. Введение
- 6.2. Байесовские оценки
- 6.3. Оценки максимального правдоподобия
- 6.4. Свойства оценок
- 6.5. Точность оценок и априорная информация
- 6.6. Линейные оценки с минимальной среднеквадратической ошибкой
- 6.7. Оценки наименьших квадратов
- Глава 7. ОПТИМАЛЬНЫЙ ЛИНЕЙНЫЙ ФИЛЬТР
- 7.1. Введение
- 7.2. Оптимальный линейный дискретный фильтр
- 7.3. Оптимальный линейный непрерывный фильтр
- 7.4. Стационарные процессы и фильтр Винера
- 7.5. Асимптотические свойства
- Глава 8. ОБОБЩЕНИЕ АЛГОРИТМА ОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ФИЛЬТРАЦИИ
- 8.1. Введение
- 8.2. Небелый шум
- 8.3. Сглаживание и предсказание
- 8.4. Анализ ошибок и априорные данные
- 8.5. Расходимость
- Глава 9. НЕЛИНЕЙНОЕ ОЦЕНИВАНИЕ
- 9.1. Введение
- 9.2 Оценивание при помощи условного среднего
- 9.3. Оценивание по максимуму апостериорной вероятности
- 9.4. Соотношения между нелинейными алгоритмами фильтрации
- 9.5. Нелинейное сглаживание
- Список литературы