| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. Средние значения
В предыдущих разделах рассматривались понятия вероятности, плотности вероятностей и функции распределения вероятностей для одной и более чем одной случайной величины. Мы видели, что вероятности соответствуют относительным частотам появления событий и не удивительно поэтому, что средние значения (математические ожидания) случайных величин или векторов могут быть определены из функции распределения вероятностей случайных величин.
Рассмотрим
дискретную случайную величину ![]() , которая принимает
, которая принимает ![]() возможных значений:
возможных значений: ![]() . Если, как и раньше, обозначим через
. Если, как и раньше, обозначим через ![]() число
случаев появления события
число
случаев появления события ![]() и
положим, что общее число событий равно
и
положим, что общее число событий равно ![]() , то найдем среднее значение
дискретной случайной величины
, то найдем среднее значение
дискретной случайной величины ![]() в виде
в виде
 (2.101)
(2.101)
Вероятность
наступления события ![]() определялась
нами из предельного соотношения
определялась
нами из предельного соотношения
![]() (2.102)
(2.102)
Объединяя (2.101) и (2.102), получим выражение среднего значения через вероятность наступления событий
 (2.103)
(2.103)
При возрастании ![]() число дискретных
событий увеличивается и, наконец, для очень больших
число дискретных
событий увеличивается и, наконец, для очень больших ![]() можно рассматривать
можно рассматривать ![]() как непрерывную
величину, которая аппроксимирует дискретную величину, принимающую значения
как непрерывную
величину, которая аппроксимирует дискретную величину, принимающую значения ![]() с вероятностью
с вероятностью ![]() . Таким образом,
(2.103) преобразуется к виду
. Таким образом,
(2.103) преобразуется к виду
 (2.104)
(2.104)
При ![]() сумма в ф-ле
(2.104) может быть заменена интегралом, который определяет среднее значение
непрерывной случайной величины
сумма в ф-ле
(2.104) может быть заменена интегралом, который определяет среднее значение
непрерывной случайной величины
 (2.105)
(2.105)
Когда распределение дискретное
 (2.106)
(2.106)
подстановка (2.106) в (2.105) непосредственно приводит к ф-ле (2.103) для среднего значения дискретной случайной величины.
С помощью рассуждений, аналогичных тем, которые использовались при выводе ф-лы (2.105), получим выражение для среднего значения случайного вектора
 (2.107)
(2.107)
Понятие
среднего может быть распространено и на случайный вектор ![]() , полученный преобразованием
случайного вектора
, полученный преобразованием
случайного вектора ![]() :
:
![]() (2.108)
(2.108)
при помощи основной теоремы о среднем значении
 (2.109)
(2.109)
С помощью этой теоремы можно получить математические ожидания значений степеней случайного вектора. Таким образом, определяют различные статистические моменты. Величина
 (2.110)
(2.110)
называется ![]() -м моментом случайной величины
-м моментом случайной величины ![]() . Первый момент
. Первый момент ![]() называется средним
значением или математическим ожиданием и обозначается
называется средним
значением или математическим ожиданием и обозначается ![]() . Центральные моменты случайной
величины определяются как
. Центральные моменты случайной
величины определяются как
 (2.111)
(2.111)
Особенно
важными являются среднее значение ![]() , среднеквадратическое значение
, среднеквадратическое значение ![]() и дисперсия
и дисперсия ![]() случайной величины:
случайной величины:
 (2.112)
(2.112)
 (2.113)
(2.113)
 (2.114)
(2.114)
Эти
понятия можно без каких-либо изменений применять и для векторного случая, когда
вводятся понятия среднего значения вектора, матрицы среднеквадратических
значений и ковариационной матрицы вектора ![]() . Эти величины определяются следующим
образом:
. Эти величины определяются следующим
образом:
 (2.115)
(2.115)
 (2.116)
(2.116)
 (2.117)
(2.117)
где
![]() —
симметричная матрица размера
—
симметричная матрица размера ![]() :
:
 (2.118)
(2.118)
Отсюда следует,
что члены главной диагонали ковариационной матрицы представляют собой дисперсию
случайных величин, образующих случайный вектор. Можно определить моменты непосредственно
из характеристических функций, которые получаются,
если положить в (2.108) ![]() так что
так что
 (2.119)
(2.119)
Тогда
 (2.120)
(2.120)
 (2.121)
(2.121)
Для
скалярной случайной величины ![]() -й момент
-й момент
 (2.122)
(2.122)
Используя приведенные результаты, легко показать, что среднее значение суммы случайных величин равно сумме средних значений слагаемых. Важно отметить, что при этом нет необходимости в специальной оговорке относительно статистической независимости.
В большинстве задач, которые рассматриваются в дальнейшем, появляются случайные величины, зависящие от других случайных величин. Поэтому закончим главу определением моментов случайных величин, зависящих от других случайных величин.
Условное среднее
значение случайной величины ![]() , когда зависимая от нее случайная
величина приняла определенное значение, равна
, когда зависимая от нее случайная
величина приняла определенное значение, равна
 (2.122)
(2.122)
Безусловное
среднее значение случайной величины ![]()
 .
(2.123)
.
(2.123)
Так как индивидуальная
плотность вероятности ![]() , может быть получена из совместной
плотности
, может быть получена из совместной
плотности  , то совместная, условная и индивидуальная плотности
связаны соотношением
, то совместная, условная и индивидуальная плотности
связаны соотношением ![]() . Тогда можно записать эквивалентное
(2.123) выражение в виде
. Тогда можно записать эквивалентное
(2.123) выражение в виде

В этом выражении легко выделить условное математическое ожидание (2.122). Таким образом, получим соотношение между условным и безусловным средними значениями
 (2.124)
(2.124)
или
![]() (2.125)
(2.125)
где индексация используется для выделения случайной величины, для которой находится среднее. Как правило, мы не будем использовать индексацию моментов распределения, если только это не будет необходимо для ясности.
Условная
дисперсия ![]() ,
если задан
,
если задан ![]() ,
будет обозначаться как
,
будет обозначаться как ![]() или
или ![]() . Имеем
. Имеем
 (2.126)
(2.126)
Для условных дисперсий можно получить выражения, аналогичные ф-лам (2.124) и (2.125). Легко показать, что
 (2.127)
(2.127)
где все символы
усреднения относятся к ![]() или к
или к ![]() , зависящему от
, зависящему от ![]() . Если теперь рассмотреть
усреднение по
. Если теперь рассмотреть
усреднение по ![]() в
ур-ниях (2.127), то получим:
в
ур-ниях (2.127), то получим:
![]() ;
;
![]() (2.128)
(2.128)
![]()
где
введены индексы для дисперсий, чтобы исключить возможную путаницу. Объединив
полученные результаты (с 2.127), увидим, что дисперсия
случайной величины ![]() эквивалентна
среднему по
эквивалентна
среднему по ![]() условной
дисперсии
условной
дисперсии ![]() плюс
дисперсия по
плюс
дисперсия по ![]() условного
математического ожидания
условного
математического ожидания ![]() . Это утверждение можно записать следующим
образом:
. Это утверждение можно записать следующим
образом:
![]() (2.129)
(2.129)
Определяя условную характеристическую функцию
 (2.130)
(2.130)
можно использовать ее для получения различных моментов. В частности, имеем
 (2.131)
(2.131)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие к русскому изданию
- Глава 1. Обзор содержания книги
- Глава 2. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 2.1. Введение
- 2.2. Теория вероятностей
- 2.3. Случайные величины
- 2.4. Алгебраические действия над случайными величинами
- 2.5. Средние значения
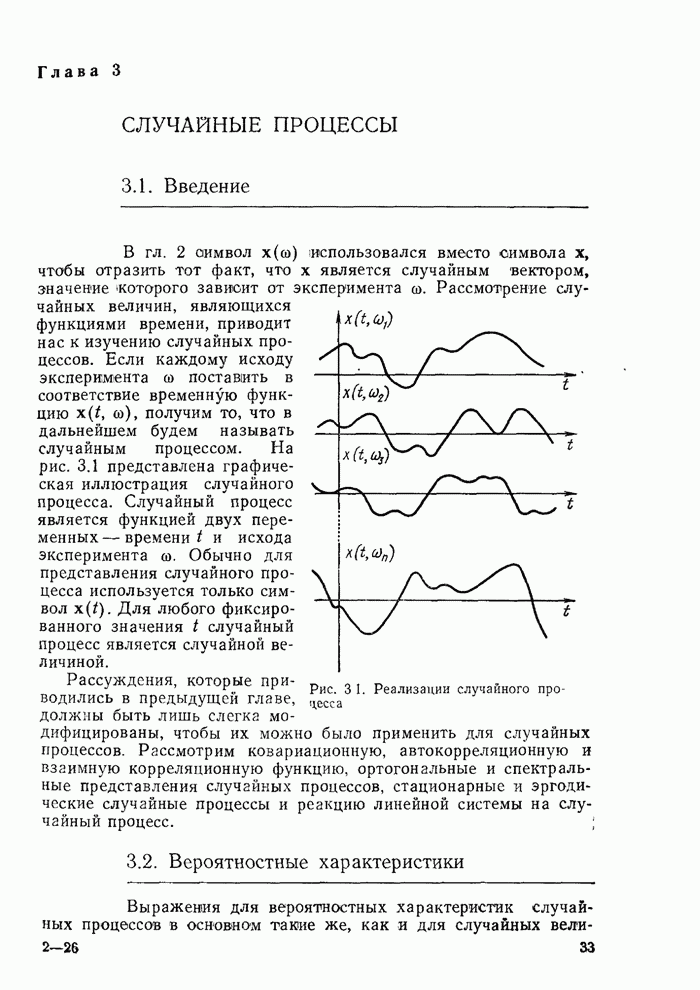
- Глава 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 3.1. Введение
- 3.2. Вероятностные характеристики
- 3.3. Средние значения
- 3.4. Спектральные и ортогональные представления
- 3.5. Реакция линейных систем
- Глава 4. НОРМАЛЬНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ И СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 4.1. Введение
- 4.2. Нормальные случайные процессы
- 4.3. Марковские случайные процессы
- 4.4. Стохастические дифференциальные уравнения
- 4.5. Среднее значение и дисперсия процесса на выходе нелинейной системы
- Глава 5. ТЕОРИЯ РЕШЕНИЙ
- 5.1. Введение
- 5.2. Выбор решения при однократном наблюдении
- 5.3. Выбор решения при многократных наблюдениях
- 5.4. Проверка сложных гипотез
- 5.5. Проверка многих гипотез
- 5.6. Последовательный анализ
- 5.7. Последовательное обнаружение марковских сигналов в нормальном шуме
- Глава 6. ОСНОВЫ ТЕОРИИ ОЦЕНИВАНИЯ
- 6.1. Введение
- 6.2. Байесовские оценки
- 6.3. Оценки максимального правдоподобия
- 6.4. Свойства оценок
- 6.5. Точность оценок и априорная информация
- 6.6. Линейные оценки с минимальной среднеквадратической ошибкой
- 6.7. Оценки наименьших квадратов
- Глава 7. ОПТИМАЛЬНЫЙ ЛИНЕЙНЫЙ ФИЛЬТР
- 7.1. Введение
- 7.2. Оптимальный линейный дискретный фильтр
- 7.3. Оптимальный линейный непрерывный фильтр
- 7.4. Стационарные процессы и фильтр Винера
- 7.5. Асимптотические свойства
- Глава 8. ОБОБЩЕНИЕ АЛГОРИТМА ОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ФИЛЬТРАЦИИ
- 8.1. Введение
- 8.2. Небелый шум
- 8.3. Сглаживание и предсказание
- 8.4. Анализ ошибок и априорные данные
- 8.5. Расходимость
- Глава 9. НЕЛИНЕЙНОЕ ОЦЕНИВАНИЕ
- 9.1. Введение
- 9.2 Оценивание при помощи условного среднего
- 9.3. Оценивание по максимуму апостериорной вероятности
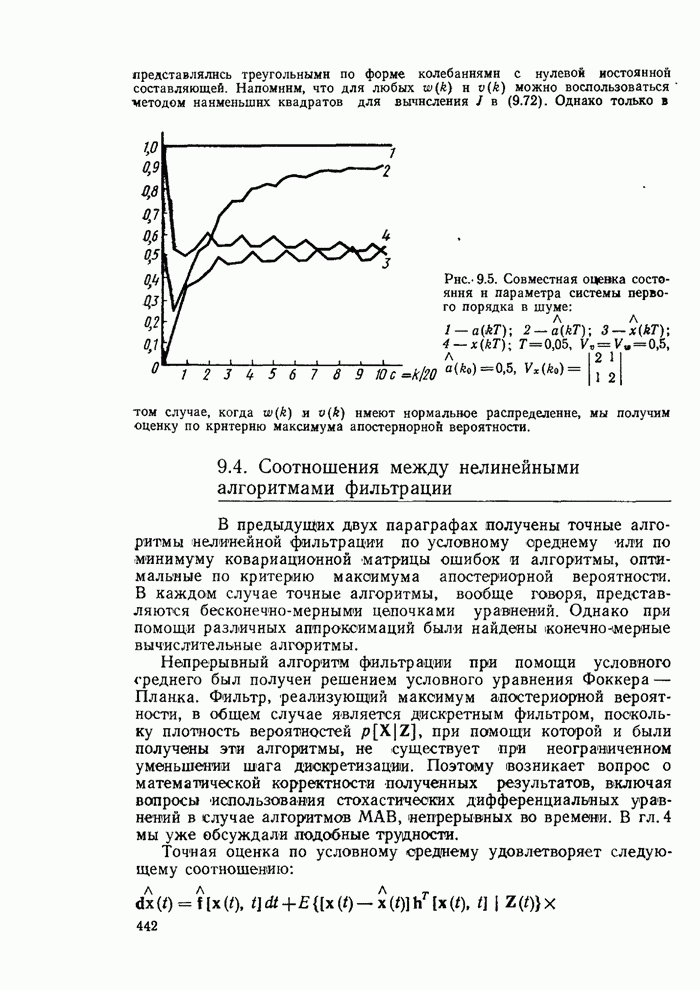
- 9.4. Соотношения между нелинейными алгоритмами фильтрации
- 9.5. Нелинейное сглаживание
- Список литературы