| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.5. Расходимость
В некоторых приложениях можно
обнаружить, что истинные ошибки оценивания во много раз превышают теоретически
предсказанные ошибки, характеризуемые дисперсией ![]() Действительно, реальная ошибка может
увеличиваться безгранично, даже если теоретическая ошибка калмановской
фильтрации пренебрежимо мала. Это явление, называемое расходимостью
(неустойчивостью) или насыщением информации, может вызвать серьезные возражения
по поводу целесообразности применения фильтра Калмана. Впервые возможность
нестабильного поведения фильтра была проанализирована самим Калманом [105] и
позднее в работах Кнолла и Эдельштейна [117] и других, посвященных применению
алгоритмов калмановской фильтрации в задачах пространственной навигации и
определения орбит.
Действительно, реальная ошибка может
увеличиваться безгранично, даже если теоретическая ошибка калмановской
фильтрации пренебрежимо мала. Это явление, называемое расходимостью
(неустойчивостью) или насыщением информации, может вызвать серьезные возражения
по поводу целесообразности применения фильтра Калмана. Впервые возможность
нестабильного поведения фильтра была проанализирована самим Калманом [105] и
позднее в работах Кнолла и Эдельштейна [117] и других, посвященных применению
алгоритмов калмановской фильтрации в задачах пространственной навигации и
определения орбит.
Может показаться, что утверждение о расходимости резко противоречит результатам по устойчивости, полученным в § 7.5. Однако на самом деле это не так, поскольку расходимость вызывается такими ошибками, которые учтены в этом параграфе не были. Одними из главных причин расходимости являются: неточность задания процесса, моделирующего сообщение и наблюдение, линеаризация уравнений, отсутствие полной информации о реальной физической задаче, а также всякого рода упрощающие предположения, позволяющие дать математическое описание задачи. Кроме того, неустойчивость могут вызывать ошибки, связанные с моделированием вероятностных характеристик шума и неизвестных входных сигналов. Неустойчивость могут вызвать также ошибки округления, неизбежно возникающие при цифровом моделировании алгоритмов фильтрации и которые могут привести к потере положительной определенности и симметрии ковариационной матрицы ошибок.
Для того чтобы выяснить, каким образом возникает расходимость и как ее можно проконтролировать с помощью простой модификации алгоритма фильтрации, рассмотрим простой пример, в котором расходимость возникает в результате неточного задания модели сообщения.
Допустим, что необходимо оценить состояние дискретного процесса
![]() (8.266)
(8.266)
где ![]() - постоянная. Однако модель сообщения,
которую мы используем, задана в виде
- постоянная. Однако модель сообщения,
которую мы используем, задана в виде
![]() . (8.267)
. (8.267)
Модель наблюдения
![]() (8.268)
(8.268)
где ![]() - последовательность случайных
независимых нормальных величин с нулевыми средними и одинаковой единичной дисперсией.
Положим, что
- последовательность случайных
независимых нормальных величин с нулевыми средними и одинаковой единичной дисперсией.
Положим, что ![]() и
и
![]() , иными
словами, у нас нет информации о начальном состоянии.
, иными
словами, у нас нет информации о начальном состоянии.
Используя
алгоритмы табл. 7.2, легко показать, что оценка после ![]() наблюдений
определится соотношением
наблюдений
определится соотношением
 , (8.269)
, (8.269)
а дисперсия ошибки, согласно фильтрации по Калману, равна
![]() .
(8.270)
.
(8.270)
Следовательно, при увеличении ![]() дисперсия будет стремиться к
нулю, и оценка будет очень точной. Однако легко убедиться, что это неверно,
если вычислить действительную дисперсию ошибки.
дисперсия будет стремиться к
нулю, и оценка будет очень точной. Однако легко убедиться, что это неверно,
если вычислить действительную дисперсию ошибки.
Действительное состояние после ![]() наблюдений равно
наблюдений равно
![]() . (8.271)
. (8.271)
Поэтому действительная ошибка оценивания равна разности между (8.271) и (8.269):
 (8.272)
(8.272)
Следовательно, действительная среднеквадратическая ошибка равна
![]() , (8.273)
, (8.273)
откуда
(видно, что при увеличении ![]() ошибка
неограниченно возрастает и оценка расходится.
ошибка
неограниченно возрастает и оценка расходится.
Может показаться, что подобная задача тривиальна, поскольку мы просто игнорируем константу, которую должны были бы учесть. Однако даже если и включить константу в модель сообщения, то оценка все равно могла бы разойтись, до тех пор пока два входных сигнала не станут абсолютно равными, что, к сожалению, практически трудно сделать. Если, например, модель сообщения задать в виде
![]() , (8.274)
, (8.274)
то очень просто показать, что действительная среднеквадратическая ошибка равна
![]() (8.275)
(8.275)
и оценка снова будет расходиться до тех пор, пока ![]() будет не равна
будет не равна ![]() .
.
Основная причина, вызывающая
расходимость в фильтре Калмана, состоит в том, что коэффициент передачи
(усиления) ![]() фильтра
очень быстро стремиться к нулю. Поэтому оценка перестает быть зависимой от
последовательности наблюдений и растущая ошибка наблюдений на нее не влияет.
фильтра
очень быстро стремиться к нулю. Поэтому оценка перестает быть зависимой от
последовательности наблюдений и растущая ошибка наблюдений на нее не влияет.
Эта трудность может быть
преодолена одной из простых модификаций алгоритма фильтрации. Можно, например,
просто ограничить снизу коэффициент передачи ![]() так, чтобы он не становился меньше
некоторого значения, скажем,
так, чтобы он не становился меньше
некоторого значения, скажем, ![]() . Другими словами, после
. Другими словами, после ![]() наблюдений считаем
наблюдений считаем ![]() постоянной величиной
для всех будущих наблюдений. Для того чтобы продемонстрировать этот прием,
найдем среднее значение действительной ошибки оценивания. В случае
немодифицированных уравнений — это линейная оценка по минимуму дисперсии и
поэтому из ур-ния (8.272) получим следующий результат (поскольку
постоянной величиной
для всех будущих наблюдений. Для того чтобы продемонстрировать этот прием,
найдем среднее значение действительной ошибки оценивания. В случае
немодифицированных уравнений — это линейная оценка по минимуму дисперсии и
поэтому из ур-ния (8.272) получим следующий результат (поскольку ![]() для всех
для всех ![]() ):
):
![]() . (8.276)
. (8.276)
Так как, с другой стороны, мы
ограничили ![]() снизу
величиной
снизу
величиной ![]() ,
то легко показать (см. задачу 8.24), что
,
то легко показать (см. задачу 8.24), что
 . (8.277)
. (8.277)
Тогда при ![]() ошибка стремится к нулю и фильтр не возбуждается.
Можно возразить, что при этом фильтр перестает быть оптимальным, и это на самом
деле правильно. Однако немодифицированный фильтр также не является оптимальным,
поскольку моделью входной сигнал не учитывается. Если
ошибка стремится к нулю и фильтр не возбуждается.
Можно возразить, что при этом фильтр перестает быть оптимальным, и это на самом
деле правильно. Однако немодифицированный фильтр также не является оптимальным,
поскольку моделью входной сигнал не учитывается. Если ![]() равно нулю, то можно показать,
что дисперсия модифицированного фильтра будет больше немодифицированного. Однако,
если нет оснований считать
равно нулю, то можно показать,
что дисперсия модифицированного фильтра будет больше немодифицированного. Однако,
если нет оснований считать ![]() равной нулю, то можно пойти на такое
ухудшение качества, являющееся платой за сохранение устойчивости.
равной нулю, то можно пойти на такое
ухудшение качества, являющееся платой за сохранение устойчивости.
Другой подход к устранению расходимости в
указанной выше задаче возникает в случае, когда в рассматриваемой модели a есть неизвестное состояние
некоторой динамической системы, управляемой белым шумом. Хотя эта процедура
часто дает хорошие результаты, она имеет неприятную особенность, связанную с
повышением порядка рассматриваемой задачи. Так как порядок фильтра и алгоритма вычисления дисперсии для ![]() -мерной модели
сообщения равен
-мерной модели
сообщения равен ![]() ,
то даже небольшое увеличение
,
то даже небольшое увеличение ![]() может
привести « значительному усложнению вычислительных процедур. К примеру, если
сначала
может
привести « значительному усложнению вычислительных процедур. К примеру, если
сначала ![]() и
просто добавить одно новое состояние в модели в качестве неизвестного входного
сигнала, то порядок уравнений (число их) увеличится с 20 до 27. Если увеличить
и
просто добавить одно новое состояние в модели в качестве неизвестного входного
сигнала, то порядок уравнений (число их) увеличится с 20 до 27. Если увеличить ![]() с 5 до 7, то придется
добавить еще 15 новых уравнений. Даже если не обращать внимания .на вычислительный
аспект задачи, все равно нужно помнить, что эффективное решение можно получить
в случае, если требования к вычислениям не являются основной проблемой и если
«природа» неизвестного сигнала такова, что его можно представить эффективной
моделью.
с 5 до 7, то придется
добавить еще 15 новых уравнений. Даже если не обращать внимания .на вычислительный
аспект задачи, все равно нужно помнить, что эффективное решение можно получить
в случае, если требования к вычислениям не являются основной проблемой и если
«природа» неизвестного сигнала такова, что его можно представить эффективной
моделью.
Выводы, полученные при рассмотрении этой простой задачи, имеют фундаментальное значение и в общем случае. Расходимость может возникнуть из-за слишком малого веса новой информации или, наоборот, из-за слишком большого веса прошлых наблюдений. Поэтому расходимость (насыщение информацией) — явление противоречивое. Как уже известно из гл. 7, в том случае, когда входной шум мал по сравнению с наблюдениями, дисперсия ошибки калмановской фильтрации и, следовательно, коэффициент усиления имеют тенденцию быстро уменьшаться при увеличении времени. В том случае, когда модель сообщения вообще не содержит управляющего шума, коэффициент усиления асимптотически стремится к нулю. Эта особенность, которая в общем не является неожиданной, поскольку (каждый отсчет (в среднем) содержит гораздо больше нежелаемого шума наблюдения, чем информации об управляющем шуме, имеет тенденцию «отключать» фильтр от последовательности наблюдений и таким образом вызывать неустойчивость. Итак, мы приходим к тому, что ситуации, в которых управляющий шум слабо сравним с шумом наблюдения, приводят к проблемам неустойчивости. Насколько сильно проявляется расходимость и в каких случаях она возникнет вообще, все это зависит от длины интервала наблюдения и от точности моделирования реального процесса.
Основываясь на предыдущих рассуждениях, можно предложить определенные модификации фильтра Калмана, устраняющие расходимость. В работе [221] рассматриваются несколько простых методов устранения неустойчивости в специфических задачах определения орбит. Основная идея этих подходов связана с ограничением коэффициента усиления для того, чтобы избежать «нечувствительности» к наблюдениям. Эти методы можно разбить на три широких класса:
- уменьшение матричных коэффициентов усиления;
- ограничение дисперсии ошибок;
- искусственное увеличение мощности управляющего шума сигнала.
Рассмотрим каждый из этих методов.
Существует несколько способов непосредственного уменьшения матричных коэффициентов усиления. Так, можно использовать процедуру, развитую в рассмотренном выше примере, и ограничить элементы матрицы снизу некоторой заранее выбранной величиной. Можно просто добавить к элементам матрицы некоторую величину или использовать менее очевидные способы для увеличения усиления. Например, в работе [222] матрица коэффициентов усиления представлена в виде
![]() . (8.287)
. (8.287)
Подобно тому, как можно ограничивать снизу элементы матрицы коэффициентов усиления, аналогичная методика может быть применена для ограничения элементов матрицы дисперсий ошибок. Легко видеть, что из-за неизбежной неопределенности в формулировке начальных условий физически невозможно иметь ошибку, равную нулю. Однако точную нижнюю границу дисперсии ошибки также трудно найти, если не использовать эксперимент. Можно показать, что, имея минимальное значение дисперсии ошибок, можно избавиться от расходимости.
Поскольку основная причина, из-за которой матричные коэффициенты становятся малыми и возникает неустойчивость, состоит в том, что управляющий шум модели значительно слабее, чем шум наблюдения, то очевидное решение задачи состоит в искусственном увеличении дисперсии управляющего шума. Несмотря на то, что можно вычислить величину необходимой добавки к дисперсии управляющего шума, точная ее величина должна находиться экспериментально.
Нетрудно видеть, что при использовании перечисленных выше методов дисперсия ошибки будет большей, если модель сообщения на самом деле точная. Другими словами, контроль расходимости может быть осуществлен только за счет увеличения дисперсии ошибки свыше «теоретического» минимума. Конечно, если оптимальный фильтр неустойчив, то модифицированный неоптимальный фильтр будет иметь дисперсию ошибки, меньшую, чем действительная дисперсия ошибки «оптимальной» фильтрации.
Другой подход, позволяющий контролировать расходимость, состоит в вычислении квадратного корня из матрицы ковариаций ошибок оценивания. Подобный способ был развит в работах [21], [23], [5]. Эта процедура полезна в случаях, когда неустойчивость вызывают ошибки округления. Тогда лучше вычислять квадратный корень из дисперсии, чем саму дисперсию, потому что число необходимых операций при счете сокращается в два раза. Рассматривая этот способ, предположим, что шум модели равен нулю; мы уже видели, что неустойчивость возникает чаще всего при малом шуме модели, поэтому наше предположение не является ограничительным. В случае ненулевого шума можно воспользоваться алгоритмом, разработанным в [58].
В дискретном времени
уравнения для ковариационной матрицы ошибок оценивания при ![]() записываются в виде
записываются в виде
![]() (8.279)
(8.279)
![]() (8.280)
(8.280)
Легко показать прямой подстановкой, что корень из матрицы ковариаций равен
![]() (8.281)
(8.281)
 (8.282)
(8.282)
где используется нижняя треугольная матрица корней из дисперсий. Аналогичные выражения для случая непрерывного времени были получены в [5].
Другой подход [96] состоит в том,
что оценку получают только по прошлым ![]() –наблюдениями, где
–наблюдениями, где ![]() — некоторое фиксированное
число отсчетов, достаточно большое, чтобы его еще можно было бы наблюдать в
системе. К сожалению, этот метод требует одновременного использования
алгоритмов фильтрации и предсказания и, следовательно, становится практически
непригодным, если алгоритм фильтрации расходится, что и является его основным
ограничением. Однако в [96] была предложена подоптимальная процедура,
позволяющая снять это ограничение и исключить тем самым проблему
неустойчивости.
— некоторое фиксированное
число отсчетов, достаточно большое, чтобы его еще можно было бы наблюдать в
системе. К сожалению, этот метод требует одновременного использования
алгоритмов фильтрации и предсказания и, следовательно, становится практически
непригодным, если алгоритм фильтрации расходится, что и является его основным
ограничением. Однако в [96] была предложена подоптимальная процедура,
позволяющая снять это ограничение и исключить тем самым проблему
неустойчивости.
Для устранения неустойчивости можно воспользоваться адаптивными алгоритмами фильтрации [97], [208], [243]. Применение этих алгоритмов может оказаться более целесообразным, поскольку при этом ошибка из-за расходимости становится большой, а значит, и большее количество информации можно использовать для адаптации.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие к русскому изданию
- Глава 1. Обзор содержания книги
- Глава 2. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 2.1. Введение
- 2.2. Теория вероятностей
- 2.3. Случайные величины
- 2.4. Алгебраические действия над случайными величинами
- 2.5. Средние значения
- Глава 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
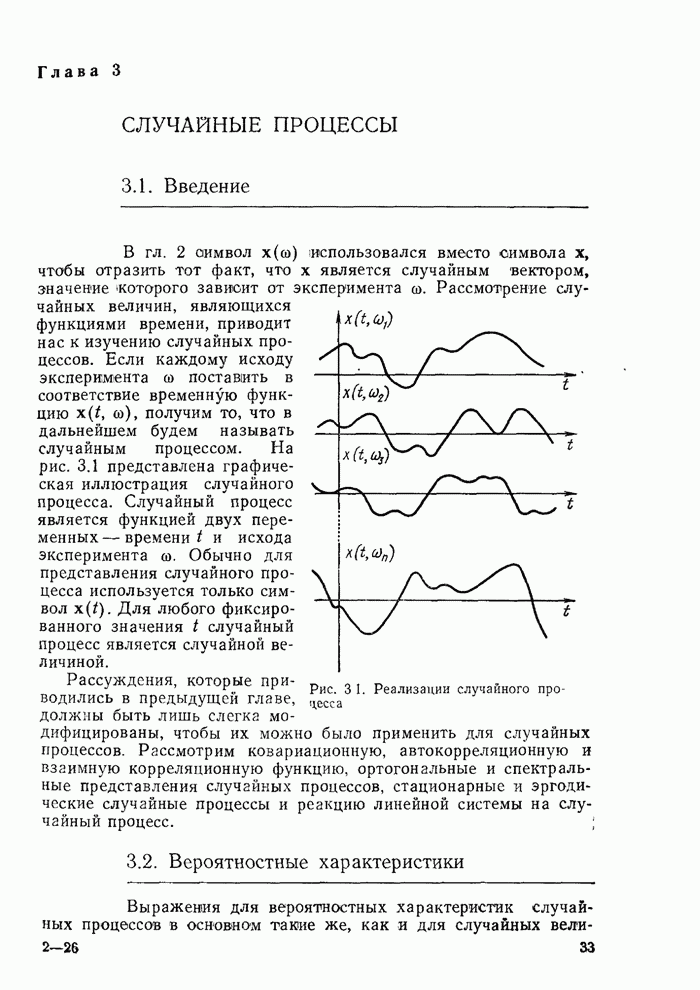
- 3.1. Введение
- 3.2. Вероятностные характеристики
- 3.3. Средние значения
- 3.4. Спектральные и ортогональные представления
- 3.5. Реакция линейных систем
- Глава 4. НОРМАЛЬНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ И СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 4.1. Введение
- 4.2. Нормальные случайные процессы
- 4.3. Марковские случайные процессы
- 4.4. Стохастические дифференциальные уравнения
- 4.5. Среднее значение и дисперсия процесса на выходе нелинейной системы
- Глава 5. ТЕОРИЯ РЕШЕНИЙ
- 5.1. Введение
- 5.2. Выбор решения при однократном наблюдении
- 5.3. Выбор решения при многократных наблюдениях
- 5.4. Проверка сложных гипотез
- 5.5. Проверка многих гипотез
- 5.6. Последовательный анализ
- 5.7. Последовательное обнаружение марковских сигналов в нормальном шуме
- Глава 6. ОСНОВЫ ТЕОРИИ ОЦЕНИВАНИЯ
- 6.1. Введение
- 6.2. Байесовские оценки
- 6.3. Оценки максимального правдоподобия
- 6.4. Свойства оценок
- 6.5. Точность оценок и априорная информация
- 6.6. Линейные оценки с минимальной среднеквадратической ошибкой
- 6.7. Оценки наименьших квадратов
- Глава 7. ОПТИМАЛЬНЫЙ ЛИНЕЙНЫЙ ФИЛЬТР
- 7.1. Введение
- 7.2. Оптимальный линейный дискретный фильтр
- 7.3. Оптимальный линейный непрерывный фильтр
- 7.4. Стационарные процессы и фильтр Винера
- 7.5. Асимптотические свойства
- Глава 8. ОБОБЩЕНИЕ АЛГОРИТМА ОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ФИЛЬТРАЦИИ
- 8.1. Введение
- 8.2. Небелый шум
- 8.3. Сглаживание и предсказание
- 8.4. Анализ ошибок и априорные данные
- 8.5. Расходимость
- Глава 9. НЕЛИНЕЙНОЕ ОЦЕНИВАНИЕ
- 9.1. Введение
- 9.2 Оценивание при помощи условного среднего
- 9.3. Оценивание по максимуму апостериорной вероятности
- 9.4. Соотношения между нелинейными алгоритмами фильтрации
- 9.5. Нелинейное сглаживание
- Список литературы