| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. Алгебраические действия над случайными величинами
Задачи теории оценивания довольно часто приводят к необходимости вычисления результатов комбинации двух или более случайных величин, а также линейных или нелинейных операций над одной или более случайными величинами. В этом параграфе последуют комбинации двух или более случайных величин и результаты алгебраических действий над ними.
Начнем с простого случая линейного преобразования скалярной случайной величины:
![]() ,
, ![]() (2.66)
(2.66)
где ![]() и
и
![]() известные постоянные
величины. Известна также плотность вероятности
известные постоянные
величины. Известна также плотность вероятности ![]() и требуется получить плотность вероятности
и требуется получить плотность вероятности ![]() . Определим событие
. Определим событие ![]() и
событие
и
событие ![]() . Поскольку оба события относятся к одному
и тому же исходу, ясно, что
. Поскольку оба события относятся к одному
и тому же исходу, ясно, что
![]() и
и ![]() (2.67)
(2.67)
Если обозначить ![]() , то
, то
![]() (2.68)
(2.68)
Искомая функция плотности вероятности новой величины ![]() получается при дифференцировании этого выражения
по
получается при дифференцировании этого выражения
по ![]() :
:
![]() для
для ![]() (2.69)
(2.69)
Если ![]() отрицательна, то необходимо переопределить
события
отрицательна, то необходимо переопределить
события ![]() и
и ![]() так, чтобы
так, чтобы ![]() и
и ![]() . Так же, как было получено выражение (2.68),
находим
. Так же, как было получено выражение (2.68),
находим
![]() для
для ![]() (2.70)
(2.70)
Объединяя (2.69) и (2.70), получим ![]()
Несколько более сложное преобразование получается при прохождении
случайной величины ![]() с известной
функцией плотности вероятности через устройство с квадратичной характеристикой.
Пусть
с известной
функцией плотности вероятности через устройство с квадратичной характеристикой.
Пусть
![]() . (2.71)
. (2.71)
Преобразование от данного ![]() к значению
к значению ![]() однозначное. Однако обратное преобразование
неоднозначно. Данному значению
однозначное. Однако обратное преобразование
неоднозначно. Данному значению ![]() соответствуют
два значения
соответствуют
два значения ![]() .
.
Таким образом, для случайной величины ![]() событие
событие ![]() при
при ![]() соответствует событию
соответствует событию  , так что имеем
, так что имеем ![]() . Это означает, что
. Это означает, что
 (2.72)
(2.72)
Дифференцируя предыдущее распределение по ![]() , получим плотность вероятности для преобразования
, получим плотность вероятности для преобразования ![]()
 (2.73)
(2.73)
Если функция плотностей вероятности ![]() симметрична
относительно
симметрична
относительно ![]() , то из ф-лы (2 .73) следует
, то из ф-лы (2 .73) следует
 (2.74)
(2.74)
Теперь исследуем общий случай нелинейного безынерционного преобразования скалярной случайной величины (рис. 2.2):
![]() (2.75)
(2.75)
Событие ![]() определим
как
определим
как ![]() . Как показано на рис. 2.2, может существовать некоторое
число интервалов на оси
. Как показано на рис. 2.2, может существовать некоторое
число интервалов на оси ![]() соответствующих
одному и тому же интервалу на оси
соответствующих
одному и тому же интервалу на оси ![]() . Таким образом, определим событие для
. Таким образом, определим событие для ![]() как
как ![]() , так что
, так что ![]() . При малых
. При малых ![]() имеем
имеем
 (2.76)
(2.76)
где взяты абсолютные значения ![]() и
и ![]() , так как плотности вероятности должны быть неотрицательны.
Поделив это выражение на
, так как плотности вероятности должны быть неотрицательны.
Поделив это выражение на ![]() и перейдя к пределу
при
и перейдя к пределу
при ![]() и
и ![]() , стремящихся к нулю,
получим плотность вероятности для случайной величины
, стремящихся к нулю,
получим плотность вероятности для случайной величины ![]()
 (2.77)
(2.77)
где ![]() распространяется на все значения
распространяется на все значения
![]() , которые
соответствуют
, которые
соответствуют ![]() . Значения
. Значения ![]() и
и
![]() связаны между
собой ур-нием (2.75). Если множество решений ур-ния (2.75) имеет вид
связаны между
собой ур-нием (2.75). Если множество решений ур-ния (2.75) имеет вид
![]() (2.78)
(2.78)
то окончательно имеем
 . (2.79)
. (2.79)

Рис 2.2. Общий вид нелинейного безынерционного преобразования
Этот
результат является наиболее общим выражением для плотности вероятности
скалярной случайной величины ![]() , полученной с помощью алгебраического преобразования
скалярной случайной величины
, полученной с помощью алгебраического преобразования
скалярной случайной величины ![]() .
.
Во многих
задачах теории оценивания две или более случайные величины комбинируются для
формирования скалярной или векторной случайной величины. Например, одной из
важных задач, которая будет изложена ниже, является оценка сигнального вектора
![]() по наблюдаемому процессу
по наблюдаемому процессу ![]() , который является аддитивной смесью шума
, который является аддитивной смесью шума ![]() и нелинейного преобразования сигнала
и нелинейного преобразования сигнала
![]() (2.80)
(2.80)
Вначале рассмотрим несколько простых вариантов комбинаций случайных величин, а затем перейдем к более сложным. Одной из самых простых комбинаций является сумма двух скалярных случайных входных сигналов
![]() . (2.81)
. (2.81)
Предположим,
что известна совместная плотность вероятности ![]() и
и ![]() и необходимо определить плотность
и необходимо определить плотность ![]() . Если обозначить события
. Если обозначить события ![]() и
и ![]() , то
, то ![]() и
и
![]() (2.82)
(2.82)
Дифференцируя это выражение по ![]() , получим
, получим
![]() (2.83)
(2.83)
Но согласно (2.51) совместные плотности вероятности являются произведениями условных и индивидуальных плотностей, т. е.
![]() (2.84)
(2.84)
![]() (2.85)
(2.85)
Умножая обе частя (2.83) на ![]() , получим
, получим
![]() (2.86)
(2.86)
Так как индивидуальные плотности можно получить интегрированием совместной плотности, то искомая плотность вероятностей
 . (2.87)
. (2.87)
Формула (2.87) выражает функцию
плотности вероятностей ![]() через совместную плотность
вероятностей
через совместную плотность
вероятностей ![]() и
и ![]() .
.
Возможен и чиной метод получения
этого результата при другом подходе к решению таких задач Вероятность того,
что ![]() меньше некоторой величины
меньше некоторой величины ![]() , эквивалентна тому, что все значения
, эквивалентна тому, что все значения ![]() и
и ![]() лежат слева от линии
лежат слева от линии ![]() , как это показано на рис 2.3. Для
определения этой вероятности рассмотрим вероятность попадания в полосу шириной
, как это показано на рис 2.3. Для
определения этой вероятности рассмотрим вероятность попадания в полосу шириной ![]() всех
значений
всех
значений ![]() от
от ![]() до
до ![]() .
.


Рис. 2.3. Допустимые значения ![]() и
и ![]() для
для ![]()
Для получения искомой функции распределения ![]() следует проинтегрировать
последнее выражение по
следует проинтегрировать
последнее выражение по ![]() от
от ![]() до
до ![]() :
:
 (2.88)
(2.88)
Дифференцируя (2.89), получим функцию плотности вероятности
 (2.89)
(2.89)
Это же выражение может быть записано иначе:
 (2.90)
(2.90)
Если случайные величины
![]() и
и ![]() статистически
независимы, из ф-лы (2.90) получаем
статистически
независимы, из ф-лы (2.90) получаем
 (2.91)
(2.91)
т. е. ![]() представляет собой
свертку двух функций плотности вероятности.
представляет собой
свертку двух функций плотности вероятности.
Если ![]() , где
, где ![]() и
и ![]() независимы,
то с помощью ур-ния (2.91) можно вычислить
независимы,
то с помощью ур-ния (2.91) можно вычислить
![]() . Аналогично, если
. Аналогично, если ![]() , где
, где ![]() и
и ![]() независимы, можно получить, используя (2.91)
следующее выражение для плотности вероятности случайной величины
независимы, можно получить, используя (2.91)
следующее выражение для плотности вероятности случайной величины ![]() :
:
 (2.92)
(2.92)
Рассмотрим теперь общий метод
определения плотностей вероятности для комбинаций случайных величин.
Рассмотрим векторную ![]() -мерную случайную величину
-мерную случайную величину ![]() , полученную из векторной
, полученную из векторной ![]() -мерной случайной величины
-мерной случайной величины ![]() с помощью векторного преобразования
с помощью векторного преобразования
![]() (2.93)
(2.93)
которое является обратимым в том смысле, что обратное преобразование существует и оно единственное, т. е.
![]() (2.94)
(2.94)
Определим событие ![]() и
соответствующее событие
и
соответствующее событие![]() . Вероятностные связи величин
. Вероятностные связи величин ![]() и
и ![]() определяются
из равенства
определяются
из равенства ![]() , которое можно записать через функции
распределения
, которое можно записать через функции
распределения
![]() (2.95)
(2.95)
или через интегралы от плотностей:
 (2.96)
(2.96)
Если продифференцировать кратные
интегралы по каждой из компонент ![]() , то, как легко убедиться, получим
, то, как легко убедиться, получим
 (2.97)
(2.97)
Здесь ![]() представляет матрицу размера
представляет матрицу размера ![]() x
x![]() , элемент которой равен
, элемент которой равен ![]() . Таким
образом,
. Таким
образом,
 (2.98)
(2.98)
и ![]() — определитель матрицы (его часто
называют якобианом преобразования
— определитель матрицы (его часто
называют якобианом преобразования ![]() ). Символ
). Символ ![]() обозначает абсолютную величину якобиана
преобразования.
обозначает абсолютную величину якобиана
преобразования.
Другой метод доказательства ф-лы (2.97) получим путем замены переменной в (2.96):
![]() ;
;  (2.99)
(2.99)
Тогда ф-ла (2.96) принимает вид

Дифференцирование этого кратного интеграла по каждой составляющей
![]() непосредственно
приводит к ф-ле (2.97). Эту формулу будем часто использовать в дальнейшем.
непосредственно
приводит к ф-ле (2.97). Эту формулу будем часто использовать в дальнейшем.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие к русскому изданию
- Глава 1. Обзор содержания книги
- Глава 2. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 2.1. Введение
- 2.2. Теория вероятностей
- 2.3. Случайные величины
- 2.4. Алгебраические действия над случайными величинами
- 2.5. Средние значения
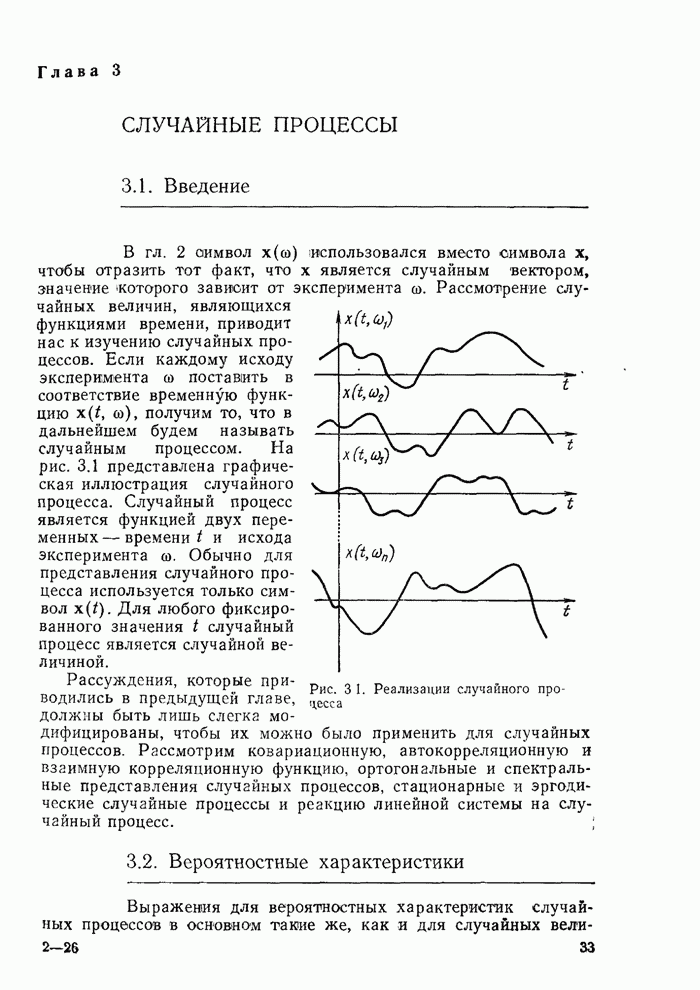
- Глава 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 3.1. Введение
- 3.2. Вероятностные характеристики
- 3.3. Средние значения
- 3.4. Спектральные и ортогональные представления
- 3.5. Реакция линейных систем
- Глава 4. НОРМАЛЬНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ И СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 4.1. Введение
- 4.2. Нормальные случайные процессы
- 4.3. Марковские случайные процессы
- 4.4. Стохастические дифференциальные уравнения
- 4.5. Среднее значение и дисперсия процесса на выходе нелинейной системы
- Глава 5. ТЕОРИЯ РЕШЕНИЙ
- 5.1. Введение
- 5.2. Выбор решения при однократном наблюдении
- 5.3. Выбор решения при многократных наблюдениях
- 5.4. Проверка сложных гипотез
- 5.5. Проверка многих гипотез
- 5.6. Последовательный анализ
- 5.7. Последовательное обнаружение марковских сигналов в нормальном шуме
- Глава 6. ОСНОВЫ ТЕОРИИ ОЦЕНИВАНИЯ
- 6.1. Введение
- 6.2. Байесовские оценки
- 6.3. Оценки максимального правдоподобия
- 6.4. Свойства оценок
- 6.5. Точность оценок и априорная информация
- 6.6. Линейные оценки с минимальной среднеквадратической ошибкой
- 6.7. Оценки наименьших квадратов
- Глава 7. ОПТИМАЛЬНЫЙ ЛИНЕЙНЫЙ ФИЛЬТР
- 7.1. Введение
- 7.2. Оптимальный линейный дискретный фильтр
- 7.3. Оптимальный линейный непрерывный фильтр
- 7.4. Стационарные процессы и фильтр Винера
- 7.5. Асимптотические свойства
- Глава 8. ОБОБЩЕНИЕ АЛГОРИТМА ОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ФИЛЬТРАЦИИ
- 8.1. Введение
- 8.2. Небелый шум
- 8.3. Сглаживание и предсказание
- 8.4. Анализ ошибок и априорные данные
- 8.5. Расходимость
- Глава 9. НЕЛИНЕЙНОЕ ОЦЕНИВАНИЕ
- 9.1. Введение
- 9.2 Оценивание при помощи условного среднего
- 9.3. Оценивание по максимуму апостериорной вероятности
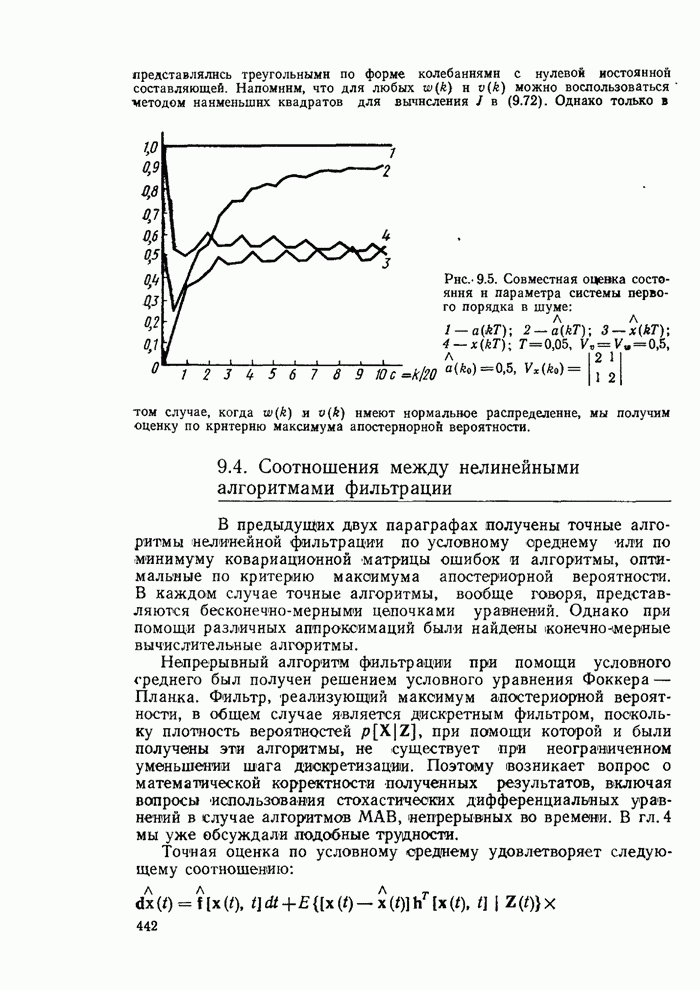
- 9.4. Соотношения между нелинейными алгоритмами фильтрации
- 9.5. Нелинейное сглаживание
- Список литературы