| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. Случайные величины
Случайная
величина ![]() представляет
собой действительную функцию, значение которой определяется результатом
представляет
собой действительную функцию, значение которой определяется результатом ![]() произвольного
эксперимента. Иначе говоря, случайная величина присваивает вещественное
значение каждой точке выборочного пространства. В предыдущем разделе мы
определяли вероятности конечных совокупностей событий, вычисляя относительную
частоту появления каждого события. Для определения плотности вероятности и
функции распределения непрерывных случайных величин, определенных на
бесконечных множествах событий, используется предельный переход. Важными для
дальнейшего изложения будут понятия вероятности по времени и вероятности по
ансамблю, которые непосредственно приводят к определению случайного процесса
как выборочного пространства, состоящего из событий, являющихся функциями
времени. Таким образом, случайный процесс можно представить как совокупность
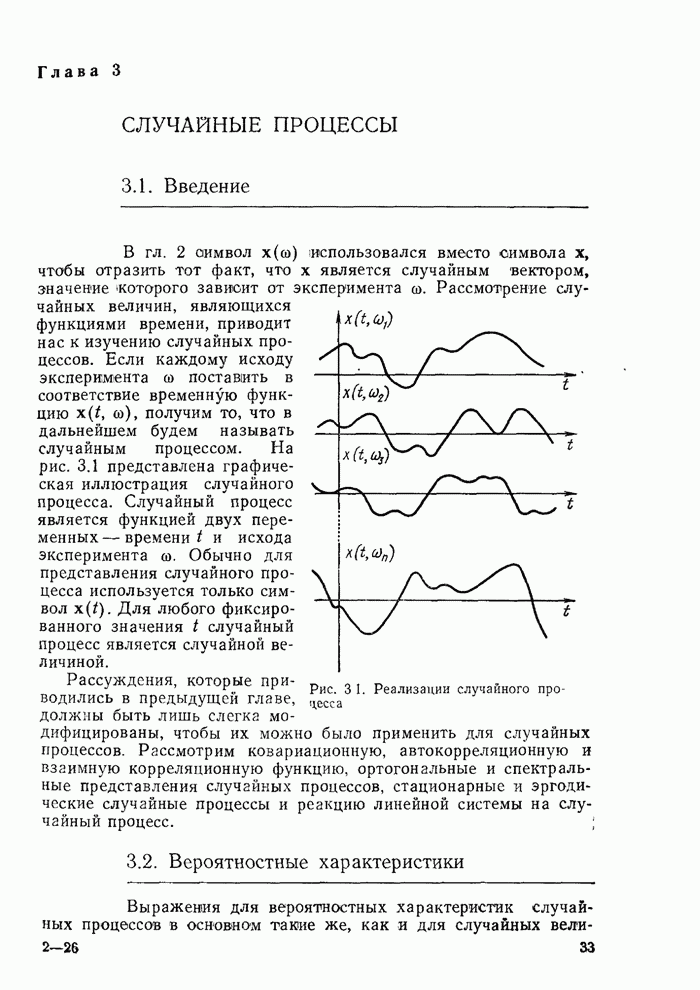
функций времени. В гл. 3 будет дан обзор теории случайных процессов. В этой
главе ограничимся только случайными величинами.
произвольного
эксперимента. Иначе говоря, случайная величина присваивает вещественное
значение каждой точке выборочного пространства. В предыдущем разделе мы
определяли вероятности конечных совокупностей событий, вычисляя относительную
частоту появления каждого события. Для определения плотности вероятности и
функции распределения непрерывных случайных величин, определенных на
бесконечных множествах событий, используется предельный переход. Важными для
дальнейшего изложения будут понятия вероятности по времени и вероятности по
ансамблю, которые непосредственно приводят к определению случайного процесса
как выборочного пространства, состоящего из событий, являющихся функциями
времени. Таким образом, случайный процесс можно представить как совокупность
функций времени. В гл. 3 будет дан обзор теории случайных процессов. В этой
главе ограничимся только случайными величинами.
Когда выборочное
пространство для случайного эксперимента состоит из непрерывного, а значит, из
бесконечного множества значений, вероятность получения одного определенного
значения или элемента множества равна нулю. Однако сумма (вероятностей по
бесконечному числу элементов во всем выборочном пространстве должна равняться
единице. В этих случаях удобно определить функцию распределения вероятностей ![]() следующим образом:
следующим образом:
![]() (2.15)
(2.15)
где ![]() представляет собой
вероятность того, что
представляет собой
вероятность того, что ![]() меньше
или равен
меньше
или равен ![]() .
Чтобы связать это с полученной ранее дискретной вероятностью, следует лишь
отметить, что мы просто определяем событие
.
Чтобы связать это с полученной ранее дискретной вероятностью, следует лишь
отметить, что мы просто определяем событие
![]() как
то, что
как
то, что ![]() ,
или, выражаясь более строго, что событие
,
или, выражаясь более строго, что событие ![]() является
совокупностью исходов
является
совокупностью исходов ![]() , принадлежащих выборочному пространству
, принадлежащих выборочному пространству ![]() , таких, что
, таких, что ![]() , т. е.
, т. е.
![]()
![]() .
(2.16)
.
(2.16)
Если ![]() представляет
собой событие
представляет
собой событие
![]() ,
(2.17)
,
(2.17)
то,
используя ф-лу (2.16), получим, что вероятность события ![]()
![]() (2.18)
(2.18)
Если
![]() , то из
предыдущего выражения находим
, то из
предыдущего выражения находим
![]() (2.19)
(2.19)
Предел в ф-ле
(2.19) при ![]() ,
если он существует, называют функцией плотности вероятности
,
если он существует, называют функцией плотности вероятности ![]() :
:
![]() (2.20)
(2.20)
Из определения ![]() согласно (2.18) и события
согласно (2.18) и события ![]() согласно (2.17)
следует, что
согласно (2.17)
следует, что
![]() . (2.21)
. (2.21)
Таким образом,
вероятность того, что событие ![]() больше
больше ![]() , но меньше или равно
, но меньше или равно ![]() , равно значению
функции плотности вероятности
, равно значению
функции плотности вероятности ![]() , умноженной на
, умноженной на ![]() . Из ур-ния (2.20) следует, что
функцию распределения вероятностей можно получить интегрированием функции
плотности вероятности
. Из ур-ния (2.20) следует, что
функцию распределения вероятностей можно получить интегрированием функции
плотности вероятности
 .
(2.22)
.
(2.22)
Некоторые свойства плотностей вероятностей и функций распределения, на которые следует обратить внимание, приведены ниже:
![]() (2.23а)
(2.23а)
![]() (2.23б)
(2.23б)
![]() для всех
для всех ![]() (2.23в)
(2.23в)
![]() для всех
для всех ![]() (2.23г)
(2.23г)
 (2.23д)
(2.23д)
Приведем некоторые
примеры часто используемых непрерывных распределений (ниже во всех случаях ![]() ,
, ![]() ):
):
Равномерное:


Экспоненциальное:


Импульсное:


Релеевское:


Гауссовское(нормальное):

![]()
Здесь ![]() - дельта-функция;
- дельта-функция; ![]() - единичная ступенчатая
функция, начинающаяся при
- единичная ступенчатая
функция, начинающаяся при ![]() ;
; ![]() - табулированный интеграл
- табулированный интеграл
 .
.
Графики приведенных выше функций даны на рис 2.1. Импульсное распределение показывает, что дискретные распределения могут быть представлены как непрерывные с плотностями в виде дельта-функций. Нормальное распределение является весьма важным, в чем мы сможем убедиться в дальнейшем.

Рис 2.1 Примеры непрерывных распределений вероятности: а)равномерное; б)экспонециальное; в) импульсное; г)релеевское; д)гауссовское
Если
имеются две случайные величины ![]() и
и ![]() , можно определить
двумерную функцию распределения вероятностей:
, можно определить
двумерную функцию распределения вероятностей:
![]() , (2.24)
, (2.24)
которая
представляет собой вероятность того, что ![]() меньше или равно
меньше или равно ![]() и
и ![]() меньше или равно
меньше или равно
![]() .
Чтобы связать эту функцию с двумерной дискретной функцией распределения
вероятностей, следует лишь заметить, как и в одномерном случае, что мы определяем
событие
.
Чтобы связать эту функцию с двумерной дискретной функцией распределения
вероятностей, следует лишь заметить, как и в одномерном случае, что мы определяем
событие ![]() , как
событие, при котором
, как
событие, при котором ![]() ,
,
![]() ; другими
словами
; другими
словами
![]()
![]() (2.25)
(2.25)
Определим теперь
событие ![]() следующим
образом:
следующим
образом:
![]() (2.26)
(2.26)
тогда вероятность
наступления события ![]()
![]() ,
(2.27)
,
(2.27)
где события ![]() ,
,![]() ,
,![]() и
и ![]() определены как
определены как
![]() ;
;
![]() ;
;
![]() ; (2.28)
; (2.28)
![]() ;
;
Обе
части ф-лы (2.25) можно разделить на ![]() и записать через функции распределения:
и записать через функции распределения:
![]() (2.29)
(2.29)
Переходя
к пределу ![]() ,
получим
,
получим
 .
(2.30)
.
(2.30)
Если теперь
определить предел при ![]() , получим следующий важный результат:
, получим следующий важный результат:
 .
(2.31)
.
(2.31)
Выражение ![]() представляет собой
совместную функцию плотности вероятности двух случайных величин. Из определения
события
представляет собой
совместную функцию плотности вероятности двух случайных величин. Из определения
события ![]() видно,
что
видно,
что
![]() (2.32)
(2.32)
Это выражение
является другим определением плотности вероятности двух случайных величин.
Вероятность того, что ![]() и
и ![]() лежат в прямоугольной области,
образованной приращениями
лежат в прямоугольной области,
образованной приращениями ![]()
![]() , равна значению функции плотности
вероятности, умноженному на площадь прямоугольника, образованного приращениями.
, равна значению функции плотности
вероятности, умноженному на площадь прямоугольника, образованного приращениями.
Функцию распределения вероятности можно записать, проинтегрировав выражение (2.31):
 . (2.33)
. (2.33)
Некоторые свойства двумерных плотностей и функций распределения, на которые следует обратить внимание, приведены ниже:
![]() (2.34а)
(2.34а)
![]() (2.34б)
(2.34б)
![]() для всех
для всех ![]() ; (2.34в)
; (2.34в)
![]() для всех
для всех ![]() ; (2.34г)
; (2.34г)
![]() (2.34д)
(2.34д)
![]() (2.34е)
(2.34е)
![]() для всех
для всех ![]() и
и ![]() (2.34ж)
(2.34ж)
 (2.34з)
(2.34з)
Если имеются
больше чем две случайные величины, система обозначений, которой мы до сих пор
пользовались, становится громоздкой. Гораздо выгоднее использовать векторную
запись. Поэтому удобно определить ![]() -мерный вектор-столбец как
-мерный вектор-столбец как
![]() (2.35)
(2.35)
где символ ![]() означает
транспонирование. Нам понадобится
также приращение
означает
транспонирование. Нам понадобится
также приращение ![]() -мерного
вектора
-мерного
вектора ![]() ,
которое будем определять как
,
которое будем определять как
![]() (2.36)
(2.36)
Здесь ![]() является скалярным
элементом. Следует быть внимательными и отличать его от дифференциального
вектора
является скалярным
элементом. Следует быть внимательными и отличать его от дифференциального
вектора ![]() , который
будем определять как
, который
будем определять как
![]() (2.37)
(2.37)
Для удобства будем говорить, что один вектор меньше другого, когда каждая составляющая первого меньше соответствующей составляющей второго. Таким образом, следующие записи эквивалентны:
![]() (2.38)
(2.38)
В векторной форме:
![]() (2.39)
(2.39)
 (2.40)
(2.40)
 (2.41)
(2.41)
![]() (2.42)
(2.42)
где интеграл с
векторными пределами является ![]() -мерным интегралом. Мы сможем
неоднократно убедиться в том, что векторное представление случайных величин
значительно проще для их понимания и операций над ними, чем эквивалентное скалярное
представление.
-мерным интегралом. Мы сможем
неоднократно убедиться в том, что векторное представление случайных величин
значительно проще для их понимания и операций над ними, чем эквивалентное скалярное
представление.
Часто представляет интерес возможность получения распределения или плотности только одной величины по совместному распределению или плотности. Для двух случайных величин из ф-л (2.33) и (2.34д) следует
 (2.43)
(2.43)
Таким образом, индивидуальная плотность вероятности
 (2.44)
(2.44)
Для ![]() -мерного
случая индивидуальная плотность вероятности одной величины
-мерного
случая индивидуальная плотность вероятности одной величины ![]() (
(![]() -й компоненты вектора
-й компоненты вектора ![]() ) может быть легко выражена, если
определить
) может быть легко выражена, если
определить ![]() -мерный вектор
-мерный вектор ![]() как исходный
вектор
как исходный
вектор ![]() , в
котором исключена
, в
котором исключена ![]() -я
компонента, т. е.
-я
компонента, т. е.
![]() (2.45)
(2.45)
Так как функция плотности вероятности случайного вектора является функцией совместной плотности, то индивидуальная плотность вероятности может быть представлена в виде
 (2.46)
(2.46)
Этот результат
легко распространяется на случай, когда нужно получить совместную плотность
для более чем одной случайной величины из совместной плотности для ![]() случайных величин.
случайных величин.
Во многих
(случаях для определения непрерывных случайных величин нужно знать условные функции
распределения и плотности. Начнем с двух случайных скалярных величин ![]() и
и ![]() , а затем
распространим результат на векторные случайные величины
, а затем
распространим результат на векторные случайные величины ![]() и
и ![]()
Определим
два события ![]() и
и
![]() :
:
![]() ,
, ![]() (2.47)
(2.47)
Тогда согласно
(2.10) вероятность того, что ![]() больше, чем
больше, чем ![]() , но меньше или равен
, но меньше или равен ![]() при условии, что значение
при условии, что значение ![]() лежит в интервале от
лежит в интервале от
![]() до
до ![]() , равна
, равна
![]() (2.48)
(2.48)
Используя функции плотностей вероятности, можно это выражение представить в виде
 (2.49)
(2.49)
Так как
вероятность того, что ![]() при условии, что
при условии, что ![]() уже
получена, то теперь нужно получить функцию распределения
уже
получена, то теперь нужно получить функцию распределения ![]() при условии, что
при условии, что
![]() задано.
Действительно, при
задано.
Действительно, при ![]() мы
должны получить функцию распределения. Однако возникают некоторые трудности,
так как знаменатель в правой части (2.49) будет равен нулю почти во всех
случаях, когда
мы
должны получить функцию распределения. Однако возникают некоторые трудности,
так как знаменатель в правой части (2.49) будет равен нулю почти во всех
случаях, когда ![]() .
Если положить
.
Если положить ![]() ,
то
,
то


Таким
образом, при ![]() условная
функция распределения вероятности для
условная
функция распределения вероятности для ![]() при условии
при условии ![]() имеет вид
имеет вид
 (2.50)
(2.50)
Условная плотность вероятности определяется как производная от условной функции распределения:
 (2.51)
(2.51)
Интересно отметить, что это выражение имеет тот же вид, что и (2.48). Точно также можно показать, что
 (2.52)
(2.52)
где условная плотность вероятности
![]() (2.53)
(2.53)
Выражения,
подобные (2.51) и (2.53), весьма часто используются при оценке и обнаружении
сигналов. Например, если ![]() представляет собой переданное,
а
представляет собой переданное,
а ![]() — принятое
сообщение, то условная средняя оценка включает определение
— принятое
сообщение, то условная средняя оценка включает определение ![]() . Поэтому при
изложении вопросов обнаружения и оценки сигналов будут широко использоваться
условные плотности вероятности. Когда условные плотности или распределения не
зависят от случайных величин, две случайные величины независимы, т. е. для
независимых случайных величин
. Поэтому при
изложении вопросов обнаружения и оценки сигналов будут широко использоваться
условные плотности вероятности. Когда условные плотности или распределения не
зависят от случайных величин, две случайные величины независимы, т. е. для
независимых случайных величин
![]() ( 2.54)
( 2.54)
или
![]() (2.55)
(2.55)
Из (2.51) следует, что если две случайные величины независимы, то
![]() (2.56)
(2.56)
Объединяя ф-лы
(2.51) и (2.53) так, чтобы исключить ![]() , получим формулу Байеса для
плотностей вероятностей
, получим формулу Байеса для
плотностей вероятностей
![]() (2.57)
(2.57)
Это выражение аналогично формуле Байеса для дискретных событий (2.15):

Понятия условной плотности остаются справедливыми и для векторного случая, для которого имеем следующие выражения для условных плотностей вероятностей через совместные:
![]() (2.58)
(2.58)
![]() (2.59)
(2.59)
и для индивидуальных плотностей:
 (2.60)
(2.60)
 (2.61)
(2.61)
Для
двух независимых случайных векторов ![]() и
и ![]() имеем:
имеем:
![]() (2.62)
(2.62)
![]() (2.63)
(2.63)
![]() (2.64)
(2.64)
Формулу Байеса можно также непосредственно применить к векторному случаю, и она имеет такой же вид, как и (2.57):
![]() .
(2.65)
.
(2.65)
Во многих случаях в теории оценивания и ее применении в связи и управлении необходимо вычислить плотность вероятности функции случайных величин. Обратим теперь внимание на эту важную задачу.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие к русскому изданию
- Глава 1. Обзор содержания книги
- Глава 2. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 2.1. Введение
- 2.2. Теория вероятностей
- 2.3. Случайные величины
- 2.4. Алгебраические действия над случайными величинами
- 2.5. Средние значения
- Глава 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 3.1. Введение
- 3.2. Вероятностные характеристики
- 3.3. Средние значения
- 3.4. Спектральные и ортогональные представления
- 3.5. Реакция линейных систем
- Глава 4. НОРМАЛЬНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ И СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 4.1. Введение
- 4.2. Нормальные случайные процессы
- 4.3. Марковские случайные процессы
- 4.4. Стохастические дифференциальные уравнения
- 4.5. Среднее значение и дисперсия процесса на выходе нелинейной системы
- Глава 5. ТЕОРИЯ РЕШЕНИЙ
- 5.1. Введение
- 5.2. Выбор решения при однократном наблюдении
- 5.3. Выбор решения при многократных наблюдениях
- 5.4. Проверка сложных гипотез
- 5.5. Проверка многих гипотез
- 5.6. Последовательный анализ
- 5.7. Последовательное обнаружение марковских сигналов в нормальном шуме
- Глава 6. ОСНОВЫ ТЕОРИИ ОЦЕНИВАНИЯ
- 6.1. Введение
- 6.2. Байесовские оценки
- 6.3. Оценки максимального правдоподобия
- 6.4. Свойства оценок
- 6.5. Точность оценок и априорная информация
- 6.6. Линейные оценки с минимальной среднеквадратической ошибкой
- 6.7. Оценки наименьших квадратов
- Глава 7. ОПТИМАЛЬНЫЙ ЛИНЕЙНЫЙ ФИЛЬТР
- 7.1. Введение
- 7.2. Оптимальный линейный дискретный фильтр
- 7.3. Оптимальный линейный непрерывный фильтр
- 7.4. Стационарные процессы и фильтр Винера
- 7.5. Асимптотические свойства
- Глава 8. ОБОБЩЕНИЕ АЛГОРИТМА ОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ФИЛЬТРАЦИИ
- 8.1. Введение
- 8.2. Небелый шум
- 8.3. Сглаживание и предсказание
- 8.4. Анализ ошибок и априорные данные
- 8.5. Расходимость
- Глава 9. НЕЛИНЕЙНОЕ ОЦЕНИВАНИЕ
- 9.1. Введение
- 9.2 Оценивание при помощи условного среднего
- 9.3. Оценивание по максимуму апостериорной вероятности
- 9.4. Соотношения между нелинейными алгоритмами фильтрации
- 9.5. Нелинейное сглаживание
- Список литературы